多种群合作学习的多模态多目标路径规划算法

赵萌; 路辉; 王诗琪; 杨思旖; 王赞

doi:10.13700/j.bh.1001-5965.2021.0274

多种群合作学习的多模态多目标路径规划算法

doi: 10.13700/j.bh.1001-5965.2021.0274

北京航空航天大学电子信息工程学院，北京 100191

基金项目: 国家自然科学基金(61671041)；陕西省组合与智能导航重点实验室开放基金(SKLIIN-20190201)

详细信息

通讯作者:
E-mail：mluhui@buaa.edu.cn

中图分类号: TP181
计量
- 文章访问数: 448
- HTML全文浏览量: 101
- PDF下载量: 77
- 被引次数: 0
出版历程
- 收稿日期: 2021-05-27
- 录用日期: 2021-08-22
- 网络出版日期: 2021-09-29
- 整期出版日期: 2023-03-30

A multimodal multi-objective path planning algorithm based on multi-swarm cooperative learning

School of Electronic and Information Engineering，Beihang University，Beijing 100191，China

Funds: National Natural Science Foundation of China (61671041); The Foundation of Shaanxi Key Laboratory of Integrated and Intelligent Navigation (SKLIIN-20190201)

More Information

Corresponding author: E-mail：mluhui@buaa.edu.cn

摘要

摘要:
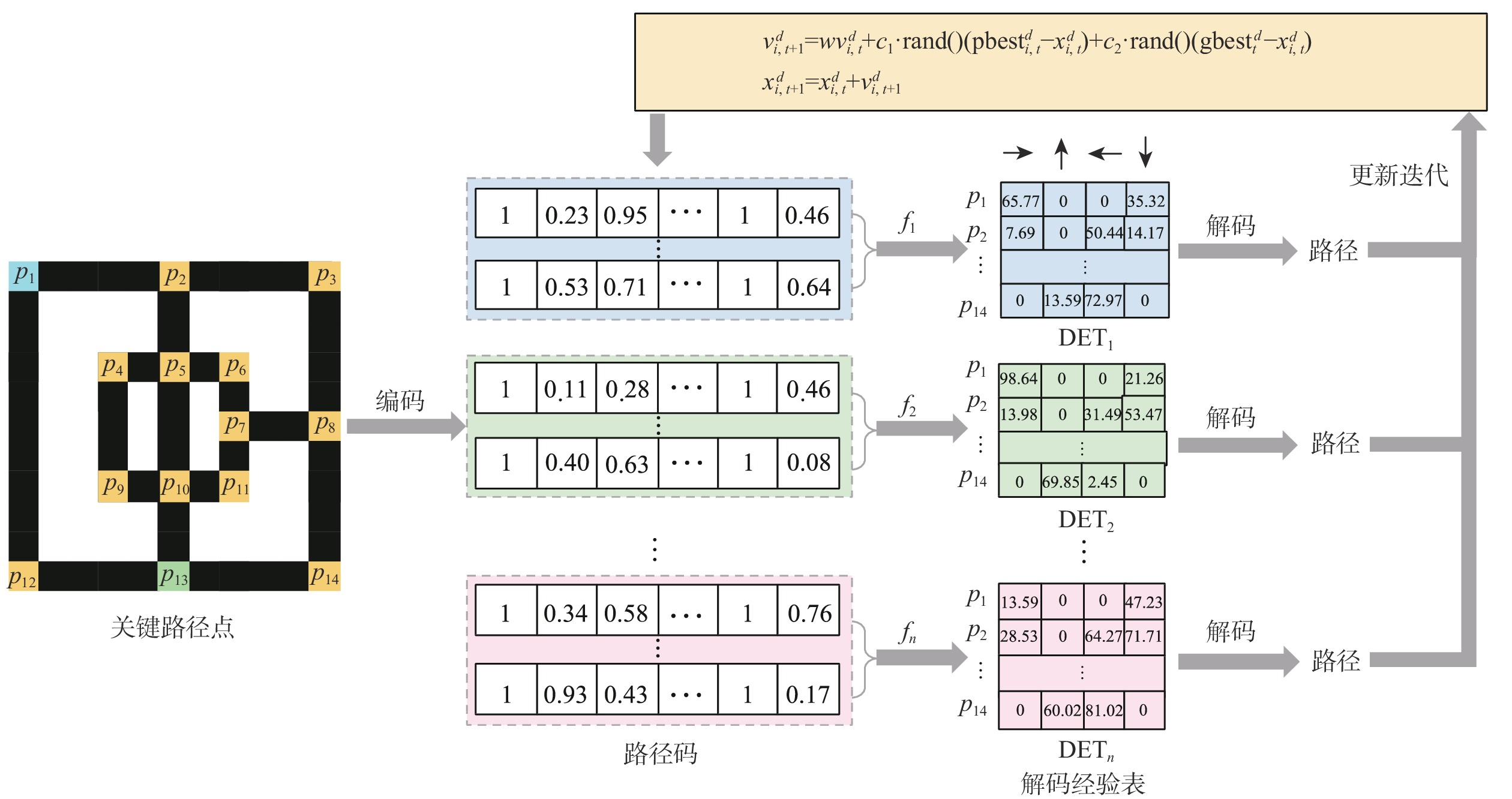
为同时规划出满足多种目标需求的多条可行路径，提高规划路径的鲁棒性与实用性，提出一种基于多种群合作学习的路径规划算法。基于粒子群算法的基本思想，先针对单一种群在多维目标空间内搜索时容易陷入局优的问题，提出基于多目标分解的子种群划分策略，平衡算法在目标空间内各个维度上的搜索能力。再依据地图中栅格点的出入度信息提取关键路径点。在编码阶段，根据关键路径点提供的维度信息，利用实数编码的方式初始化种群，降低解空间大小；在解码阶段，提出利用精英解的解码经验指导可行解的快速搜索，使解码经验能够被有效传递，降低解码的不确定性，提高了算法的寻优能力。最后，将多个种群的搜索结果进行非支配排序，得到满足优化目标的所有路径。实验结果表明：与标准粒子群算法相比，基于解码经验表指导的多种群合作学习算法具有更强的搜索能力和寻优能力，能够解决多模态多目标路径规划问题。
- 多模态多目标优化 /
- 路径规划 /
- 粒子群算法 /
- 子种群划分 /
- 解码经验表
Abstract:
An algorithm based on multi-swarm cooperative learning was proposed to plan multiple optimal paths to meet multiple objectives, which can improve the robustness and practicability of the planned paths. The concept of the particle swarm optimization algorithm served as the algorithm's guidance. First, to address the issue that a single population is easy to trap in local optimum in the multi-dimensional target space, a strategy of sub-swarm division was proposed. The population was divided into many sub-swarms according to the number of objectives, balancing the searching ability of the algorithm in each dimension of the target space. Second, key path points were extracted according to the in-degree and out-degree of the path points in the map. In the coding process, real coding was used to initialize the population. The dimension of the path code was equal to the number of key path points, reducing the size of the solution space. In the decoding process, the decoding experience of the elite solutions guided the fast search for feasible solutions. This method can transfer the decoding experience efficiently and reduce the uncertainty of decoding, which improved the optimization ability of the algorithm. Finally, the search results of all sub-swarms were sorted by the non-dominated sorting method to obtain the paths satisfying the planning objectives. The path planning algorithm based on the multi-swarm cooperative learning outperforms the standard particle swarm optimization algorithm in terms of search and optimization ability and is capable of solving the multimodal multi-objective path planning problem.
- multimodal multi-objective optimization /
- path planning /
- particle swarm optimization algorithm /
- sub-swarm division /
- decoding experience table

HTML全文

图 1 多种群合作学习算法框架

Figure 1. Framework of the proposed algorithm

下载: 全尺寸图片幻灯片

图 2 关键路径点的提取

Figure 2. Extraction of key path points

下载: 全尺寸图片幻灯片

图 3 有3个优化目标时单一种群的粒子群寻优过程

Figure 3. Optimization process of particles when there are three objectives to be optimized

下载: 全尺寸图片幻灯片

图 4 有3个优化目标时基于子种群划分策略的粒子群寻优过程

Figure 4. Optimization process of particles when there are three objectives to be optimized

下载: 全尺寸图片幻灯片

图 5 粒子的寻优过程

Figure 5. The optimization process of the particles.

下载: 全尺寸图片幻灯片

图 6 解码经验表

Figure 6. Decoding experience table

下载: 全尺寸图片幻灯片

图 7 一个多模态多目标路径规划问题的应用实例

Figure 7. An application example of MMOPP problem

下载: 全尺寸图片幻灯片

图 8 多种群合作学习算法流程

Figure 8. Flowchart of multi-swarm cooperative learning algorithm

下载: 全尺寸图片幻灯片

图 9 种群（路径码）初始化结果

Figure 9. Result of initialing particle swarm (path codes)

下载: 全尺寸图片幻灯片

图 10 以种群1为例的路径解码过程

Figure 10. Path decoding process of the first sub-swarm that is responsible for optimizing path length

下载: 全尺寸图片幻灯片

图 11 第1类MMOPP测试问题实例

Figure 11. An example of the first kind of MMOPP test problem

下载: 全尺寸图片幻灯片

图 12 第2类MMOPP测试问题实例

Figure 12. An example of the second kind of MMOPP test problem

下载: 全尺寸图片幻灯片

图 13 第3类MMOPP测试问题实例

Figure 13. An example of the third kind of MMOPP test problem

下载: 全尺寸图片幻灯片

图 14 不同算法搜索到的最优路径数量

Figure 14. Number of the optimal paths searched by different algorithms

下载: 全尺寸图片幻灯片

图 15 不同算法规划路径所需时间

Figure 15. Time used in path planning for different algorithms

下载: 全尺寸图片幻灯片

表 1 实验参数

Table 1. Experimental parameters

参数	数值	测试问题	迭代次数
${c_1}$	2	TP1	5
${c_2}$	2	TP2	10
${v_{\min }}$	0.4	TP3	15
${v_{\max }}$	0.9	TP4	10
${x_{\min }}$	0	TP5	150
${x_{\max }}$	1	TP6	10
$\alpha $	0.9	TP7	50
$\gamma $	0.1	TP8	300
$\varepsilon $	0.5	TP9	300
$\delta $	100	TP10	300
$\beta $	10	TP11	10
$n$	50	TP12	300

下载: 导出CSV

表 2 不同算法的求解时间

Table 2. Solving time of different algorithms

测试问题	求解时间/s
测试问题	PSO	PSOK	PSOD	MSCL
TP1	0.07	0.07	0.11	0.13
TP2	0.16	0.18	0.27	0.36
TP3	0.26	0.29	0.43	0.63
TP4	0.18	0.20	0.30	0.41
TP5	2.89	3.26	6.34	8.09
TP6	0.14	0.15	0.21	0.25
TP7	0.79	0.90	1.52	1.47
TP8	8.21	9.05	21.99	16.60
TP9	11.30	11.81	35.35	21.66
TP10	24.32	25.63	60.52	40.94
TP11	0.18	0.20	0.31	0.33
TP12	5.41	6.21	10.88	12.05

下载: 导出CSV

表 3 不同算法搜索到的路径数量

Table 3. Number of paths searched by different algorithms

测试问题	路径数量
测试问题	PSO	PSOK	PSOD	MSCL
TP1	7.08	7.24	8.56	8.66
TP2	8.14	7.86	10.44	12.02
TP3	3.52	3.48	5.86	3.56
TP4	5.38	5.56	7.28	7.78
TP5	5.38	5.1	11.26	16.86
TP6	4.5	4.54	4.62	4.62
TP7	15.32	15.32	12.98	15.58
TP8	44.34	45.02	33.66	44.1
TP9	73.32	74.54	51.64	81.68
TP10	111	108.8	150.02	215.42
TP11	3.98	4	4	4
TP12	7.88	7.62	10.5	12

下载: 导出CSV

表 4 不同算法的搜索到的最优路径数量对比

Table 4. Number of optimal paths searched by different algorithms

测试问题	最优路径数量
测试问题	PSO	PSOK	PSOD	MSCL
TP1	5.72	5.82	7.48	7.78
TP2	6.74	6.82	9.82	11.62
TP3	0.54	0.58	2.14	2.58
TP4	3.2	3.46	7.08	7.34
TP5	3.4	2.76	10.48	15.28
TP6	4.4	4.34	4.56	4.5
TP7	15.1	15.16	12.08	15.38
TP8	30.52	31.48	22.32	37.74
TP9	68.48	69.26	48.54	79.98
TP10	73.82	72.78	109.16	179.56
TP11	3.96	4	4	4
TP12	5.64	5.08	9.8	11.94

下载: 导出CSV

表 5 不同算法搜索到的最优路径占比

Table 5. Proportion of optimal paths in paths searched by different algorithms

测试问题	最优路径占比/%
测试问题	PSO	PSOK	PSOD	MSCL
TP1	63.56	64.67	83.11	86.44
TP2	51.85	52.46	75.54	89.38
TP3	13.50	14.50	53.50	64.50
TP4	40.00	43.25	88.50	91.75
TP5	17.89	14.53	55.16	80.42
TP6	88.00	86.80	91.20	90.00
TP7	94.38	94.75	75.50	96.13
TP8	63.58	65.58	46.50	78.63
TP9	65.22	65.96	46.23	76.17
TP10	4.96	4.89	7.34	12.08
TP11	99.00	100.00	100.00	100.00
TP12	40.29	36.29	70.00	85.29

下载: 导出CSV

表 6 测试问题难度等级分析

Table 6. Analysis of difficulty level of test problems

测试问题	目标数量	地图边长/格	编码维度	最优路径数量	求解难度等级
TP3	3	50	71	4	1
TP6	2	40	45	5	1
TP1	2	40	45	9	2
TP4	3	50	63	8	2
TP2	3	40	46	13	3
TP7	3	40	46	16	4
TP5	3	84	139	19	5
TP8	4	50	71	48	5
TP9	5	50	63	105	5
TP10	7	84	139	1487	6

下载: 导出CSV

参考文献(25)

[1]	DEB K. Multi-objective genetic algorithms: Problem difficulties and construction of test problems[J]. Evolutionary Computation, 1999, 7(3): 205-230. doi: 10.1162/evco.1999.7.3.205
[2]	FENG G, KORKMAZ T. Finding multi-constrained multiple shortest paths[J]. IEEE Transactions on Computers, 2015, 64(9): 2559-2572. doi: 10.1109/TC.2014.2366762
[3]	王树西, 李安渝. Dijkstra算法中的多邻接点与多条最短路径问题[J]. 计算机科学, 2014, 41(6): 217-224. doi: 10.11896/j.issn.1002-137X.2014.06.043 WANG S X, LI A Y. Multi-adjacent-vertexes and multi-shortest-paths problem of Dijkstra algorithm[J]. Computer Science, 2014, 41(6): 217-224(in Chinese). doi: 10.11896/j.issn.1002-137X.2014.06.043
[4]	HAYAT S, YANMAZ E, BROWN T X, et al. Multi-objective UAV path planning for search and rescue[C]//IEEE International Conference on Robotics and Automation. Piscataway: IEEE Press, 2017, 5569-5574.
[5]	马小铭, 靳伍银. 基于改进蚁群算法的多目标路径规划研究[J]. 计算技术与自动化, 2020, 39(4): 100-105. doi: 10.16339/j.cnki.jsjsyzdh.202004018 MA X M, JIN W Y. Multi-objective path planning based on improved and colony algorithm[J]. Computing Technology and Automation, 2020, 39(4): 100-105(in Chinese). doi: 10.16339/j.cnki.jsjsyzdh.202004018
[6]	DENG Y T, RONG D C, SHANGGUAN W, et al. Multi-objective path optimization method in terminal building based on improved genetic algorithm[C]//Chinese Automation Congress. 2020, 3181-3186.
[7]	NAZARAHARI M, KHANMIRZA E, DOOSTIE S. Multi-objective multi-robot path planning in continuous environment using an enhanced genetic algorithm[J]. Expert Systems with Applications, 2018, 115: 106-120.
[8]	LI Z J, LIU Y, YANG Z. An effective kernel search and dynamic programming hybrid heuristic for a multimodal transportation planning problem with order consolidation[J]. Transportation Research Part E:Logistics and Transportation Review, 2021, 152: 102408. doi: 10.1016/j.tre.2021.102408
[9]	WANG Z Z, ZHANG M H, CHU R J, et al. Modeling and planning multimodal transport paths for risk and energy efficiency using AND/OR graphs and discrete ant colony optimization[J]. IEEE Access, 2020, 8: 132642-132654.
[10]	张启钱, 许卫卫, 张洪海, 等. 复杂低空物流无人机路径规划[J]. 北京航空航天大学学报, 2020, 46(7): 1275-1286. doi: 10.13700/j.bh.1001-5965.2019.0455 ZHANG Q Q, XU W W, ZHANG H H, et al. Plan planning for logistics UAV in complex low-altitude airspace[J]. Journal of Beijing University of Aeronautics and Astronautics, 2020, 46(7): 1275-1286(in Chinese). doi: 10.13700/j.bh.1001-5965.2019.0455
[11]	MIAO C, GHEN G, YAN C, et al. Path planning optimization of indoor mobile robot based on adaptive ant colony algorithm[J]. Computers & Industrial Engineering, 2021, 156: 107230.
[12]	ZHOU X, WANG X, GU X. Welding robot path planning problem based on discrete MOEA/D with hybrid environment selection[J]. Neural Computing and Applications, 2021, 4: 12881-12903.
[13]	肖博. 基于多目标优化的震后应急物流路径规划研究[D]. 西安: 长安大学, 2019: 10-14. XIAO B. Study on post-earthquake emergency logistics path planning based on multi-objective optimization[D]. Xi’an: Chang’an University, 2019: 10-14(in Chinese).
[14]	CHOU Y T, HSIA S Y, LAN C H. A hybrid approach on multi-objective route planning and assignment optimization for urban lorry transportation[C]//International Conference on Applied System Innovation. Piscataway: IEEE Press, 2017: 1006-1009.
[15]	蒋强, 易春林, 张伟, 等. 基于蚁群算法的移动机器人多目标路径规划[J]. 计算机仿真, 2021, 38(2): 318-325. doi: 10.3969/j.issn.1006-9348.2021.02.068 JIANG Q, YI C L, ZHANG W, et al. The multi-objective path planning for mobile robot based on ant colony algorithm[J]. Computer Simulation, 2021, 38(2): 318-325(in Chinese). doi: 10.3969/j.issn.1006-9348.2021.02.068
[16]	王晨宇. 基于智能优化算法的多目标路径规划方法研究[D]. 桂林: 桂林电子科技大学, 2020: 18-27. WANG C Y. Research on multi-objective path planning method based on intelligent optimization algorithm[D]. Guilin: Guilin University of Electronic Technology, 2020: 18-27(in Chinese).
[17]	熊昕霞, 何利力. 基于混合粒子群算法的移动机器人路径规划[J]. 计算机系统应用, 2021, 30(4): 153-159. doi: 10.15888/j.cnki.csa.007865 XIONG X X, HE L L. Path planning for mobile robot based on improved particle swarm optimization algorithm[J]. Computer Systems & Applications, 2021, 30(4): 153-159(in Chinese). doi: 10.15888/j.cnki.csa.007865
[18]	GUL F, RAHIMAN W, ALHADY S S N, et al. Meta-heuristic approach for solving multi-objective path planning for autonomous guided robot using PSO-GWO optimization algorithm with evolutionary programming[J]. Journal of Ambient Intelligence and Humanized Computing, 2021, 12: 7873-7890. doi: 10.1007/s12652-020-02514-w
[19]	HIDALGO-PANIAGUA A, VEGA-RODRÍGUEZ M A, FERRUZ J, et al. Solving the multi-objective path planning problem in mobile robotics with a firefly-based approach[J]. Soft Computing, 2017, 21(4): 1-16.
[20]	段益琴. 基于多目标优化的多机器人路径规划研究[D]. 重庆: 重庆邮电大学, 2020: 23-34. DUAN Y Q. Research on multi-robot path planning based on multi-objective optimization[D]. Chongqing: Chongqing University of Posts and Telecommunications, 2020: 23-34(in Chinese).
[21]	樊娇, 雷涛, 董南江, 等. 基于改进NSGA-Ⅱ算法的多目标无人机路径规划[J]. 火力与指挥控制, 2022, 47(2): 43-48. doi: 10.3969/j.issn.1002-0640.2022.02.008 FAN J, LEI T, DONG N J, et al. Multi-objective UAV path planning based on an improved NSGA-Ⅱ[J]. Fire Control & Command Control, 2022, 47(2): 43-48(in Chinese). doi: 10.3969/j.issn.1002-0640.2022.02.008
[22]	DHIKARI D, KIM E, REZA H. A fuzzy adaptive differential evolution for multi-objective 3D UAV path optimization[C]//IEEE Congress on Evolutionary Computation. Piscataway: IEEE Press, 2017: 2258-2265.
[23]	SHI Y, EBERHART R. A modified particle swarm optimizer[C]//IEEE World Congress on Computational Intelligence. Piscataway: IEEE Press, 1998: 69-73.
[24]	EBERHART R, KENNEDY J. A new optimizer using particle swarm theory[C]//Proceedings of the Sixth International Symposium on Micro Machine and Human Science. Piscataway: IEEE Press, 1995: 39-43.
[25]	LIANG J, YUE C, LI G, et al. Problem definitions and evaluation criteria for the CEC 2021 on multimodal multiobjective path planning optimization[EB/OL]. (2020-12)[2021-05-24]. https://cec2021.mini.pw.edu.pl/en/program/competitions-C-8.