-
摘要:
针对麻雀搜索算法前期易陷入局部极值点、后期寻优精度不高等问题,提出一种自适应变异麻雀搜索算法(AMSSA)。先通过猫映射混沌序列初始化种群,增强初始种群的随机性、遍历性,提高算法的全局搜索能力;再引入柯西变异和Tent混沌扰动,拓展局部搜索能力,使陷入局部极值点的个体跳出限制继续搜索;最后,提出探索者-跟随者数量自适应调整策略,利用各阶段探索者和跟随者数量的改变增强算法前期的全局搜索能力和后期的局部深度挖掘能力,提高算法的寻优精度。选取16个基准函数和Wilcoxon检验进行验证,实验结果表明:所提算法与其他算法相比,寻优精度、收敛速度和稳定性都取得较大提升。
Abstract:To address the problems that the sparrow search algorithm is prone to fall into local extremum points in the early stage and not high accuracy in the later stage of the search, an adaptive variational sparrow search algorithm (AMSSA) is proposed. Firstly, the initial population is initialized by cat mapping chaotic sequences to enhance the randomness and ergodicity of the initial population and improve the global search ability of the algorithm; Secondly, the Cauchy mutation and Tent chaos disturbance are introduced to expand the local search ability, so that the individuals caught in the local extremum can jump out of the limit and continue the search. Finally, the explorer-follower number adaptive adjustment strategy the adaptive adjustment strategy of explorer-follower number is proposed to enhance the global search ability in the early stage and the local depth mining ability in the later stage of the algorithm by using the change of the explorer and follower numbers in each stage to improve the optimization-seeking accuracy of the algorithm. Sixteen benchmark functions and the Wilcoxon test are selected for validation, and the experimental results show that the AMSSA achieves greater improvement in search accuracy, convergence speed and stability compared with other algorithms.
-
Key words:
- sparrow search algorithm /
- cat map chaos /
- Cauchy mutation /
- Tent chaos /
- adaptive adjustment strategy
-
表 1 参数
${\boldsymbol{m}}$ 对SSA2的影响Table 1. Influence of parameter
${\boldsymbol{m}}$ on SSA2m 最佳值 平均值 标准差 平均收敛次数 1.0 0 5.509×10−72 3.120×10−71 891 1.5 0 0 0 723 2.0 0 0 0 151 2.5 0 7.505×10−35 4.747×10−34 289 3.0 0 0 0 224 3.5 0 0 0 557 4.0 0 0 0 292 表 2 基准函数
Table 2. Benchmark function
编号 函数名称 函数式 维度 定义域 最佳值 f1 Sphere ${f_1}(x) = \displaystyle\sum\limits_{i = 1}^N{x_i^2}$ 30 [−100,100] 0 f2 Schwefel’s ${f_2}(x) = \displaystyle\sum\limits_{i = 1}^N {\left| { {x_i} } \right|} + \displaystyle\prod\limits_{i = 1}^N {\left| { {x_i} } \right|}$ 30 [−10,10] 0 f3 Quadric ${f_3}(x) = {\displaystyle\sum\limits_{i = 1}^N {\left( {\displaystyle\sum\limits_{j = 1}^N { {x_j} } } \right)} ^2}$ 30 [−100,100] 0 f4 Rosenbrock ${f_4}(x){\text{ = } }\displaystyle\sum\limits_{i = 1}^{N - 1} {\left[ {100{ {({x_{i + 1} } - x_i^2)}^2} + { {({x_i} - 1)}^2} } \right]}$ 30 [−30,30] 0 f5 Step ${f_5}(x){\text{ = } }\displaystyle\sum\limits_{i = 1}^N { { {(\left| { {x_i} + 0.5} \right|)}^2} }$ 30 [−100,100] 0 f6 Quartic ${f_6}(x){\text{ = } }\displaystyle\sum\limits_{i = 1}^N {ix_i^4} + {\rm{random} }[0,1]$ 30 [−1.28,1.28] 0 f7 Schwefel ${f_7}(x){\text{ = } }\displaystyle\sum\limits_{i = 1}^N { - {x_i} } \sin \left( {\sqrt {\left| { {x_i} } \right|} } \right)$ 30 [−500,500] −418.9829N f8 Rastrigrin ${f_8}(x){\text{ = } }\displaystyle\sum\limits_{i = 1}^N {\left[ {x_i^2 - 10\cos\; (2{\text{π}} {x_i}) + 10} \right]}$ 30 [−5.12,5.12] 0 f9 Ackley ${f_9}(x) = - 20{\rm{exp} }\left( - 0 { {.2} }\sqrt {\dfrac{1}{N}\displaystyle\sum\limits_{i = 1}^N {x_i^2} } \right) - {\rm{exp}} \left( \dfrac{1}{N}\displaystyle\sum\limits_{i = 1}^N {\cos \;(2\text{π} {x_i})} \right) + 20 + {\rm{e} }$ 30 [−32,32] 0 f10 Griewing ${f_{10} }(x){\text{ = } }\dfrac{1}{ {4\;000} }\displaystyle\sum\limits_{i = 1}^N {x_i^2} - \displaystyle\prod\limits_{i = 1}^N {\cos \left( {\dfrac{ { {x_i} } }{ {\sqrt i } } } \right)} + 1$ 30 [−600,600] 0 f11 Generalized penalized ${f_{11} }(x){\text{ = } }\dfrac{\text{π} }{N}\left\{ {10{ {\sin }^2}(\text{π} {y_1}) + \displaystyle\sum\limits_{i = 1}^{N - 1} { { {({y_i} - 1)}^2}\left[ {1 + 10{ {\sin }^2}(\text{π} {y_{i + 1} })} \right]} } \right\} + {({y_N} - 1)^2}$ 30 [−50,50] 0 f12 Foxholes ${f_{12} }(x){\text{ = } }{\left( {\dfrac{1}{ {500} }{\text{ + } }\displaystyle\sum\limits_{j = 1}^{25} {\dfrac{1}{ {j + \displaystyle\sum\limits_{i = 1}^2 { { {({x_i} - {a_{ij} })}^6} } } } } } \right)^{ - 1} }$ 2 [−65,65] 1 f13 Hartmann 6-D ${f_{13} }(x){{ = - } }\displaystyle\sum\limits_{i = 1}^4 { {c_i} } \exp \left( { - \displaystyle\sum\limits_{j = 1}^6 { {a_{ij} }{ {\left( { {x_j} - {p_{ij} } } \right)}^2} } } \right)$ 6 [0,1] −3.32237 f14 Schkel ${f_{14} }(x){ { = - } }{\displaystyle\sum\limits_{i = 1}^{10} {\left[ {\left( { {\boldsymbol{X} } - {{\boldsymbol{a}}_i} } \right){ {\left( { {\boldsymbol{X} } - {{\boldsymbol{a}}_i} } \right)}^{\rm{T} } } + {c_i} } \right]} ^{ - 1} }$ 4 [0,10] −10.5363 f15 Six-Hump Camel ${f_{15} }(x){\text{ = 4} }x_1^2 - 2.1x_1^4 + \dfrac{1}{3}x_1^6 + {x_1}{x_2} - 4x_2^2 - 4x_2^4$ 2 [−5,5] −1.0316 f16 Kowalik ${f_{16} }(x){\text{ = } }{\displaystyle\sum\limits_{i = 1}^{11} {\left[ { {a_i} - \dfrac{ { {x_1}\left( {b_i^2 + {b_i}{x_2} } \right)} }{ {b_i^2 + {b_i}{x_3} + {x_4} } } } \right]} ^2}$ 4 [−5,5] 0.000307 表 3 基准函数测试结果对比
Table 3. Comparison of benchmark function test results
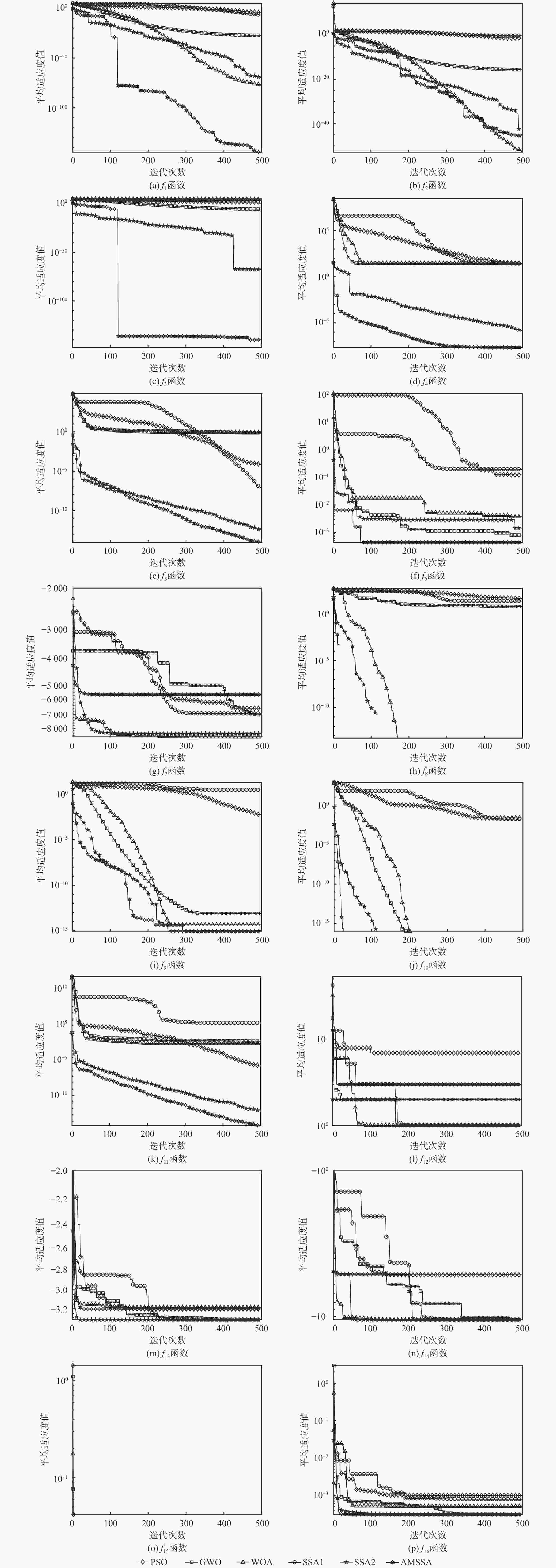
编号 算法 最佳值 平均值 标准值 编号 算法 最佳值 平均值 标准值 f1 PSO 1.057×10−5 1.422×10−4 2.013×10−4 f9 PSO 2.200×10−3 1.381×10−1 3.759×10−1 GWO 2.026×10−29 1.522×10−27 1.998×10−27 GWO 7.550×10−14 1.021×10−13 1.668×10−14 WOA 2.579×10−87 6.403×10−73 2.573×10−72 WOA 8.882×10−16 4.530×10−15 2.955×10−15 SSA1 2.628×10−8 1.302×10−7 1.163×10−7 SSA1 9.313×10−1 2.648 1.245 SSA2 0 1.227×10−51 7.761×10−51 SSA2 8.882×10−16 8.882×10−16 0 AMSSA 0 1.010×10−182 0 AMSSA 8.882×10−16 8.882×10−16 0 f2 PSO 5.100×10−3 4.260×10−2 6.160×10−2 f10 PSO 1.354×10−6 1.030×10−1 9.200×10−3 GWO 2.312×10−17 8.104×10−17 3.908×10−17 GWO 0 3.200×10−3 8.000×10−3 WOA 4.803×10−58 1.678×10−51 7.650×10−51 WOA 0 0 0 SSA1 4.260×10−2 2.371 1.860 SSA1 6.545×10−4 1.330×10−2 1.050×10−2 SSA2 1.129×10−118 5.065×10−31 3.185×10−30 SSA2 0 0 0 AMSSA 0 4.831×10−35 2.656×10−34 AMSSA 0 0 0 f3 PSO 2.569×10 7.363×10 3.642×10 f11 PSO 9.907×10−8 1.040×10−2 3.930×10−2 GWO 2.630×10−5 7.351×10−5 1.307×10−5 GWO 1.280×10−2 4.300×10−2 1.470×10−2 WOA 3.610×103 4.822×104 1.793×104 WOA 4.500×10−3 2.920×10−2 4.220×10−2 SSA1 2.330×102 1.467×103 7.677×102 SSA1 2.115 6.832 3.754 SSA2 2.774×10−5 4.129×10−5 1.628×10−5 SSA2 2.785×10−16 9.587×10−13 3.536×10−12 AMSSA 0 1.168×10−167 0 AMSSA 1.335×10−22 3.992×10−15 8.391×10−15 f4 PSO 1.563×10 9.915×10 5.719×10 f12 PSO 9.980×10−1 3.635 2.619 GWO 2.610×10 2.693×10 6.457×10−1 GWO 9.980×10−1 3.792 3.810 WOA 2.707×10 2.798×10 4.642×10−1 WOA 9.980×10−1 2.838 3.215 SSA1 2.430×10 1.659×102 2.593×102 SSA1 9.980×10−1 1.097 3.762×10−1 SSA2 6.711×10−9 3.419×10−5 1.144×10−4 SSA2 9.980×10−1 4.847 5.242 AMSSA 1.658×10−13 8.871×10−7 3.077×10−6 AMSSA 9.980×10−1 9.611 4.962 f5 PSO 1.008×10−5 1.894×10−4 3.878×10−4 f13 PSO −3.322 −3.274 5.900×10−2 GWO 7.462×10−5 7.011×10−1 3.678×10−1 GWO −3.322 −3.254 8.450×10−2 WOA 7.440×10−2 4.005×10−1 2.182×10−1 WOA −3.322 −3.209 1.158×10−1 SSA1 2.344×10−8 2.011×10−7 2.792×10−7 SSA1 −3.322 −3.220 6.150×10−2 SSA2 1.179×10−14 1.538×10−11 3.735×10−11 SSA2 −3.322 −3.280 5.740×10−2 AMSSA 2.101×10−23 7.744×10−15 1.533×10−14 AMSSA −3.322 −3.216 3.114×10−2 f6 PSO 4.340×10−2 1.793×10−1 5.150×10−2 f14 PSO −1.054×10 −9.165 2.805 GWO 3.836×10−4 1.900×10−3 8.773×10−4 GWO −1.054×10 −1.033×10 1.283 WOA 3.416×10−5 2.700×10−3 3.400×10−3 WOA −1.054×10 −7.119 3.386 SSA1 6.170×10−2 1.766×10−1 6.360×10−2 SSA1 −1.054×10 −8.422 3.343 SSA2 8.384×10−5 1.700×10−3 1.400×10−3 SSA2 −1.054×10 −8.508 2.652 AMSSA 2.468×10−6 8.001×10−4 7.674×10−4 AMSSA −1.054×10 −1.006×10 6.803×10−15 f7 PSO −7.082×103 −4.601×103 1.108×103 f15 PSO −1.032 −1.032 2.043×10−16 GWO −7.586×103 −5.865×103 9.074×102 GWO −1.032 −1.032 2.281×10−8 WOA −1.257×104 −1.057×104 1.769×103 WOA −1.032 −1.032 5.898×10−10 SSA1 −9.017×103 −7.584×103 6.607×102 SSA1 −1.032 −1.032 3.233×10−14 SSA2 −9.618×103 −8.525×103 5.415×102 SSA2 −1.032 −1.032 1.067×10−16 AMSSA −8.839×103 −6.541×103 6.724×102 AMSSA −1.032 −1.032 2.073×10−18 f8 PSO 3.609×10 6.026×10 1.460×10 f16 PSO 3.275×10−4 8.612×10−4 1.552×10−4 GWO 0 3.174 4.412 GWO 3.075×10−4 3.900×10−3 7.700×10−3 WOA 0 0 0 WOA 3.229×10−4 7.261×10−4 4.383×10−4 SSA1 2.388×10 5.313×10 2.077×10 SSA1 4.024×10−4 1.400×10−3 3.100×10−3 SSA2 0 0 0 SSA2 3.075×10−4 3.219×10−4 5.463×10−5 AMSSA 0 0 0 AMSSA 3.075×10−4 3.075×10−4 8.314×10−10 表 4 Wilcoxon秩和检验p值
Table 4. p-value for Wilcoxon’s rank-sum test
函数 PSO GWO WOA SSA1 SSA2 p R p R p R p R p R f1 8.25×10−15 + 8.25×10−15 + 8.64×10−11 + 9.55×10−15 + 5.57×10−10 + f2 1.17×10−14 + 1.26×10−14 + 1.85×10−5 + 1.17×10−14 + 1.98×10−7 + f3 1.29×10−14 + 9.55×10−15 + 9.55×10−15 + 9.55×10−15 + 2.69×10−7 + f4 1.43×10−14 + 1.43×10−14 + 1.43×10−14 + 1.43×10−14 + 1.94×10−10 + f5 1.43×10−14 + 1.43×10−14 + 1.43×10−14 + 1.43×10−14 + 8.40×10−13 + f6 1.43×10−14 + 6.54×10−2 − 6.94×10−4 + 1.43×10−14 + 9.57×10−1 − f7 3.46×10−11 + 2.40×10−3 + 2.83×10−10 + 9.92×10−7 + 2.89×10−13 + f8 1.96×10−16 + 1.90×10−16 + NaN = 1.96×10−16 + NaN = f9 1.96×10−16 + 1.77×10−16 + 1.90×10−11 + 1.96×10−16 + NaN = f10 1.96×10−16 + 4.18×10−4 + NaN = 1.96×10−16 + NaN = f11 1.43×10−14 + 1.43×10−14 + 1.43×10−14 + 1.43×10−14 + 5.12×10−11 + f12 1.17×10−5 + 1.12×10−1 − 5.10×10−3 + 2.90×10−8 + 7.00×10−3 + f13 3.77×10−2 + 2.27×10−8 + 9.88×10−12 + 6.32×10−13 + 3.40×10−1 − f14 1.62×10−2 + 7.18×10−5 + 2.61×10−6 + 9.02×10−7 + 5.68×10−1 − f15 9.60×10−8 + 2.93×10−15 + 2.93×10−15 + 6.88×10−15 + 6.32×10−1 − f16 1.43×10−14 + 8.66×10−12 + 1.05×10−13 + 1.79×10−14 + 6.68×10−1 − 表 5 模型消融实验结果
Table 5. Experimental results of model ablation
算法 f1 f2 f3 Mean Std Mean Std Mean Std SSA 2.526×10−60 1.050×10−59 1.212×10−26 7.105×10−26 7.076×10−26 3.363×10−25 ASSA 1.690×10−75 1.069×10−74 9.746×10−29 6.164×10−28 5.576×10−29 1.763×10−28 MSSA 1.679×10−67 1.032×10−66 4.333×10−37 1.978×10−36 5.084×10−29 1.605×10−28 AMSSA 1.034×10−181 0 1.966×10−37 1.243×10−36 1.026×10−155 3.243×10−155 算法 f4 f5 f6 Mean Std Mean Std Mean Std SSA 9.633×10−5 2.729×10−4 5.003×10−11 1.924×10−10 1.600×10−3 1.300×10−3 ASSA 3.436×10−6 8.914×10−6 2.327×10−14 3.221×10−14 1.600×10−3 1.800×10−3 MSSA 3.527×10−6 7.135×10−6 2.300×10−14 3.999×10−14 2.000×10−3 1.800×10−3 AMSSA 4.318×10−7 8.616×10−7 2.029×10−14 3.859×10−14 1.400×10−3 8.627×10−4 算法 f7 f8 f9 f10 Mean Std Mean Std Mean Std Mean Std SSA −8.463×103 5.314×102 0 0 8.882×10−16 0 0 0 ASSA −8.492×103 5.921×102 0 0 8.882×10−16 0 0 0 MSSA −8.726×103 9.075×102 0 0 8.882×10−16 0 0 0 AMSSA −8.759×103 4.052×102 0 0 8.882×10−16 0 0 0 算法 f11 f12 f13 Mean Std Mean Std Mean Std SSA 3.474×10−12 1.105×10−11 6.260 5.454 −3.263 6.270×10−2 ASSA 6.636×10−15 1.377×10−14 7.620 5.746 −3.274 6.140×10−2 MSSA 1.356×10−15 2.427×10−15 9.980×10−1 1.480×10−16 −3.298 5.010×10−2 AMSSA 1.045×10−15 8.414×10−16 9.980×10−1 1.655×10−16 −3.274 6.140×10−2 算法 f14 f15 f16 Mean Std Mean Std Mean Std SSA −8.373 2.793 −1.032 1.958×10−16 3.456×10−4 8.718×10−5 ASSA −8.914 2.612 −1.032 1.958×10−16 3.404×10−4 1.040×10−4 MSSA −8.914 2.612 −1.032 2.094×10−16 3.215×10−4 6.452×10−5 AMSSA −9.455 2.280 −1.032 1.958×10−16 3.075×10−4 8.442×10−10 -
[1] YANG L N, SUN X, LI Z L. An efficient framework for remote sensing parallel processing: Integrating the artificial bee colony algorithm and multiagent technology[J]. Remote Sensing, 2019, 11(2): 152. doi: 10.3390/rs11020152 [2] SHAFFIEE HAGHSHENAS S, PIROUZ B, SHAFFIEE HAGHSHENAS S, et al. Prioritizing and analyzing the role of climate and urban parameters in the confirmed cases of COVID-19 based on artificial intelligence applications[J]. International Journal of Environmental Research and Public Health, 2020, 17(10): 3730. doi: 10.3390/ijerph17103730 [3] DASH J, DAM B, SWAIN R. Implementation of narrow-width automatic digital tuner using popular swarm intelligence technique[J]. Engineering Applications of Artificial Intelligence, 2019, 79: 87-99. doi: 10.1016/j.engappai.2018.12.009 [4] HU P, PAN J S, CHU S C. Improved binary grey wolf optimizer and its application for feature selection[J]. Knowledge-Based Systems, 2020, 195: 105746. doi: 10.1016/j.knosys.2020.105746 [5] KENNEDY J, EBERHART R. Particle swarm optimization[C]//Proceedings of International Conference on Neural Networks. Piscataway: IEEE Press, 1995 : 1942-1948. [6] MIRJALILI S, MIRJALILI S M, LEWIS A. Grey wolf optimizer[J]. Advances in Engineering Software, 2014, 69: 46-61. doi: 10.1016/j.advengsoft.2013.12.007 [7] MIRJALILI S, LEWIS A. The whale optimization algorithm[J]. Advances in Engineering Software, 2016, 95: 51-67. doi: 10.1016/j.advengsoft.2016.01.008 [8] MIRJALILI S, GANDOMI A H, MIRJALILI S Z. Salp swarm algorithm: A bio-inspired optimizer for engineering design problems[J]. Advances in Engineering Software, 2017, 114: 163-191. doi: 10.1016/j.advengsoft.2017.07.002 [9] MIRJALILI S. SCA: A sine cosine algorithm for solving optimization problems[J]. Knowledge-Based Systems, 2016, 96: 120-133. doi: 10.1016/j.knosys.2015.12.022 [10] XUE J K, SHEN B. A novel swarm intelligence optimization approach: Sparrow search algorithm[J]. Systems Science & Control Engineering, 2020, 8(1): 22-34. [11] 陈忠云, 张达敏, 辛梓芸. 多子群的共生非均匀高斯变异樽海鞘群算法[J]. 自动化学报, 2022, 48(5): 1307-1317. doi: 10.16383/j.aas.c190684CHEN Z Y, ZHANG D M, XIN Z Y. Multi-subpopulation based symbiosis and non-uniform Gaussian mutation salp swarm algorithm[J]. Acta Automatica Sinica, 2022, 48(5): 1307-1317(in Chinese). doi: 10.16383/j.aas.c190684 [12] 刘景森, 袁蒙蒙, 左方. 面向全局搜索的自适应领导者樽海鞘群算法[J]. 控制与决策, 2021, 36(9): 2152-2160. doi: 10.13195/j.kzyjc.2020.0090LIU J S, YUAN M M, ZUO F. Global search-oriented adaptive leader salp swarm algorithm[J]. Control and Decision, 2021, 36(9): 2152-2160(in Chinese). doi: 10.13195/j.kzyjc.2020.0090 [13] 周娇, 王力, 陈小青. 基于改进鲸鱼优化算法的最大2维熵图像分割[J]. 激光技术, 2021, 45(3): 378-385. doi: 10.7510/jgjs.issn.1001-3806.2021.03.020ZHOU J, WANG L, CHEN X Q. Image segmentation of 2-D maximum entropy based on the improved whale optimization algorithm[J]. Laser Technology, 2021, 45(3): 378-385(in Chinese). doi: 10.7510/jgjs.issn.1001-3806.2021.03.020 [14] 周璟. 混沌狼群围捕算法的车间机器人导航路径规划[J]. 机械设计与制造, 2020(1): 251-255. doi: 10.19356/j.cnki.1001-3997.2020.01.062ZHOU J. Workshop used robot navigation path planning method based on chaotic wolf pack besieging algorithm[J]. Machinery Design & Manufacture, 2020(1): 251-255(in Chinese). doi: 10.19356/j.cnki.1001-3997.2020.01.062 [15] YAN C, LI M X, LIU W. Prediction of bank telephone marketing results based on improved whale algorithms optimizing S_Kohonen network[J]. Applied Soft Computing, 2020, 92: 106259. doi: 10.1016/j.asoc.2020.106259 [16] LI X G, HAN S F, GONG C Q. Analysis and improvement of fireworks algorithm[J]. Algorithms, 2017, 10(1): 26. doi: 10.3390/a10010026 [17] 何庆, 林杰, 徐航. 混合柯西变异和均匀分布的蝗虫优化算法[J]. 控制与决策, 2021, 36(7): 1558-1568. doi: 10.13195/j.kzyjc.2019.1609HE Q, LIN J, XU H. Hybrid Cauchy mutation and uniform distribution of grasshopper optimization algorithm[J]. Control and Decision, 2021, 36(7): 1558-1568(in Chinese). doi: 10.13195/j.kzyjc.2019.1609 [18] 吕鑫, 慕晓冬, 张钧, 等. 混沌麻雀搜索优化算法[J]. 北京航空航天大学学报, 2021, 47(8): 1712-1720. doi: 10.13700/j.bh.1001-5965.2020.0298LYU X, MU X D, ZHANG J, et al. Chaos sparrow search optimization algorithm[J]. Journal of Beijing University of Aeronautics and Astronautics, 2021, 47(8): 1712-1720(in Chinese). doi: 10.13700/j.bh.1001-5965.2020.0298 [19] LIU G Y, SHU C, LIANG Z W, et al. A modified sparrow search algorithm with application in 3d route planning for UAV[J]. Sensors, 2021, 21(4): 1224. doi: 10.3390/s21041224 [20] YUAN J H, ZHAO Z W, LIU Y P, et al. DMPPT control of photovoltaic microgrid based on improved sparrow search algorithm[J]. IEEE Access, 2021, 9: 16623-16629. doi: 10.1109/ACCESS.2021.3052960 [21] CHEN S R, WANG S Y. An optimization method for an integrated energy system scheduling process based on NSGA-II improved by tent mapping chaotic algorithms[J]. Processes, 2020, 8(4): 426. doi: 10.3390/pr8040426 [22] 张娜, 赵泽丹, 包晓安, 等. 基于改进的Tent混沌万有引力搜索算法[J]. 控制与决策, 2020, 35(4): 893-900. doi: 10.13195/j.kzyjc.2018.0795ZHANG N, ZHAO Z D, BAO X A, et al. Gravitational search algorithm based on improved Tent chaos[J]. Control and Decision, 2020, 35(4): 893-900(in Chinese). doi: 10.13195/j.kzyjc.2018.0795 [23] 郭振洲, 王平, 马云峰, 等. 基于自适应权重和柯西变异的鲸鱼优化算法[J]. 微电子学与计算机, 2017, 34(9): 20-25. doi: 10.19304/j.cnki.issn1000-7180.2017.09.005GUO Z Z, WANG P, MA Y F, et al. Whaleoptimization algorithm based on adaptive weight and cauchy mutation[J]. Microelectronics & Computer, 2017, 34(9): 20-25(in Chinese). doi: 10.19304/j.cnki.issn1000-7180.2017.09.005 [24] DERRAC J, GARCIA S, MOLINA D, et al. A practical tutorial on the use of nonparametric statistical tests as a methodology for comparing evolutionary and swarm intelligence algorithms[J]. Swarm and Evolutionary Computation, 2011, 1(1): 3-18. doi: 10.1016/j.swevo.2011.02.002 -







 下载:
下载: