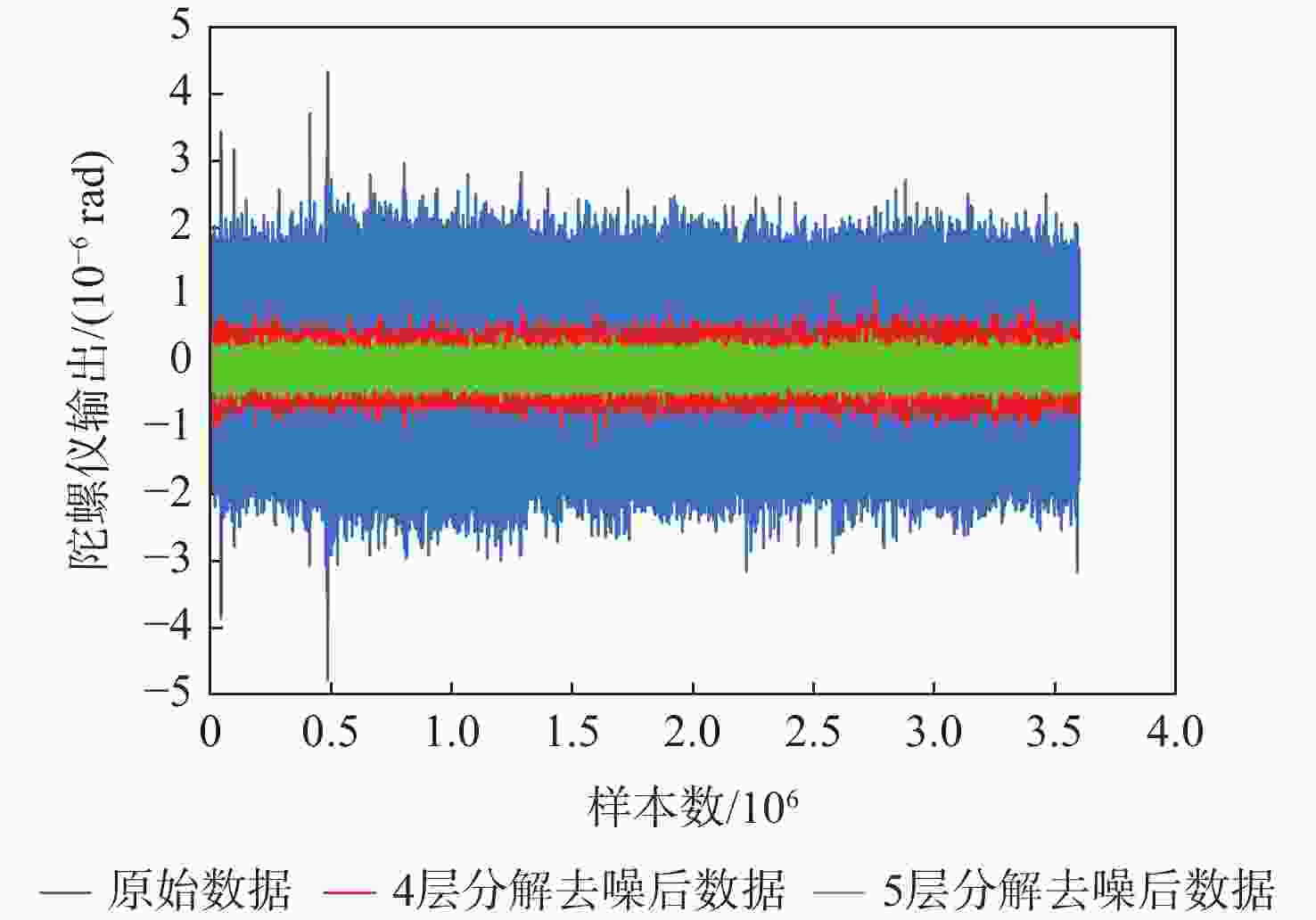
A quality evaluation method for wavelet denoising based on combinatorial weighting method
-
摘要:
针对传统质量评价指标在小波阈值去噪中理论依据不足的问题，提出了一种基于组合赋权法的小波去噪质量评价方法，能够为小波去噪参数的选择提供有效评价。通过分析在真值未知情况下均方根误差（RMSE）、信噪比（SNR）、平滑度等单项指标的特点，选取RMSE与平滑度作为小波去噪指标，对其进行归一化处理，采用信息熵权与变异系数的方法进行组合赋权，将归一化指标与对应权值线性组合，得到一种新的指标即为复合评价指标，其值越小，说明去噪效果越好，所选参数越优。仿真实验表明，在真值已知情况下，该评价指标具有更高的准确性，能够适用于不同的分解层数与小波基函数，具有比传统方法更好的适用性;实测数据表明，所提方法得出的小波去噪峰值域更加光滑，波形更加平稳，去噪效果更佳。
Abstract:Addressing such a problem with the traditional indicator system for quality evaluation as an insufficient theoretical basis for wavelet threshold denoising, a combination weighting approach-based method for evaluation of wavelet denoising quality is proposed with the expectation of effectively evaluating the selection of wavelet denoising parameters. Through analysis of characteristics of individual indicators such as root-mean-square error (RMSE), signal-noise ratio (SNR) and smoothness with the truth-value unknown, RMSE and smoothness are selected as wavelet denoising indicators. They are first normalized, then processed with information entropy and coefficient of variation for combination weighting, and, in the end, linearly combined with the corresponding weights to produce a new indicator, i.e., the composite index. A smaller composite index indicates better denoising effect and better parameters selected. According to a simulated experiment, the index outperforms the conventional approach in terms of accuracy given the truth-value and is applicable to various decomposition levels and wavelet base functions. According to experimental data, this method achieves smoother wavelet denoising peak regions, steadier waveforms, and a better denoising effect.
-
图 1 真值已知的多普勒信号的单一评价指标趋势
Figure 1. Trends of single evaluation index of Doppler signal with known truth value
图 2 真值未知的陀螺输出数据的单一评价指标趋势
Figure 2. Trends of single evaluation index of gyro output data with unknown truth value
图 3 原始信号与降噪信号时域曲线
Figure 3. Time-domain curves of original signal and denoising signal
图 5 原始信号与降噪信号功率谱密度图
Figure 5. Power spectral density diagram of original signal and denoising signal
表 1 真值未知时评价指标特点
Table 1. Characteristics of evaluation indexes when truth value is unknown
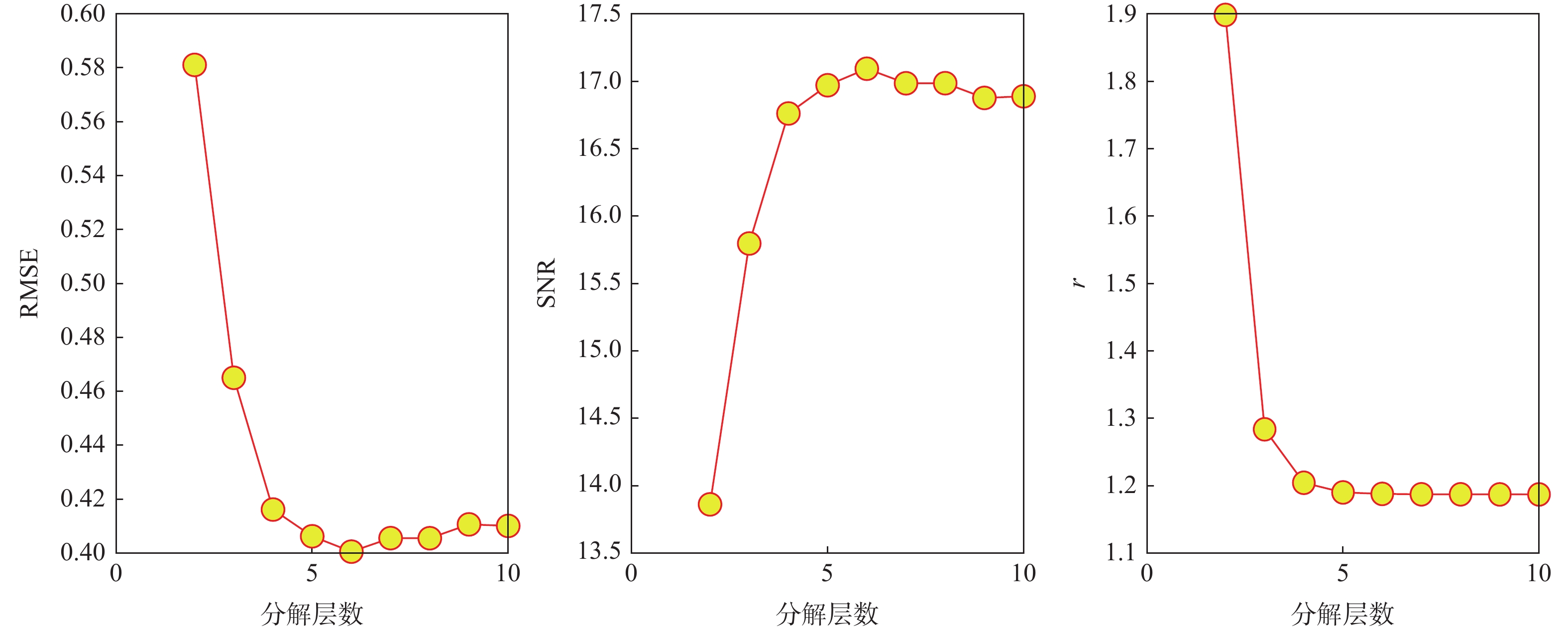
评价指标 关注信息 与分解层数相关性 RMSE 细节信息 正相关 SNR 细节信息 负相关 平滑度 近似信息 负相关 
下载: 导出CSV
表 2 不同分解层数利用sym4小波基处理的评价指标
Table 2. Evaluation indexes of sym4 wavelet basis processing for different decomposition layers
分解层数 真值已知 真值未知 T S H RMSE SNR RMSE r 2 0.581 1 13.861 7 0.778 1 0.103 0 0.866 5 0.890 3 0.899 5 3 0.465 0 15.796 9 0.844 7 0.069 7 0.212 3 0.256 6 0.193 3 4 0.416 2 16.761 3 0.856 8 0.065 4 0.132 8 0.233 3 0.105 9 5 0.406 2 16.970 8 0.866 2 0.064 6 0.128 8 0.122 3 0.097 9 6 0.400 6 17.093 4 0.867 2 0.064 5 0.127 5 0.146 2 0.096 2 7 0.405 6 16.985 4 0.869 9 0.064 4 0.130 6 0.109 7 0.098 3 8 0.405 5 16.986 0 0.869 9 0.064 4 0.130 6 0.116 4 0.098 3 9 0.418 7 16.876 8 0.870 4 0.064 4 0.131 2 0.132 0 0.098 7 10 0.410 1 16.888 8 0.872 1 0.064 3 0.133 5 0.100 5
下载: 导出CSV
表 3 不同分解层数利用db5小波基处理的评价指标
Table 3. Evaluation indexes of db5 wavelet basis processing for different decomposition layers
分解层数 真值已知 真值未知 T S H RMSE SNR RMSE r 2 0.5411 14.4805 0.8219 0.0808 0.8593 0.8925 0.8933 3 0.456 1 15.965 5 0.883 3 0.050 0 0.236 9 0.267 8 0.219 0 4 0.414 9 16.788 0 0.895 5 0.045 7 0.156 1 0.248 9 0.129 6 5 0.382 5 17.492 8 0.905 7 0.044 4 0.140 3 0.157 4 0.108 7 6 0.375 8 17.648 3 0.909 4 0.044 1 0.139 7 0.119 5 0.106 5 7 0.375 2 17.662 2 0.910 3 0.044 0 0.140 0 0.109 5 0.10627 8 0.379 5 17.562 9 0.910 7 0.044 0 0.140 1 0.108 7 0.106 3 9 0.379 7 17.558 6 0.910 9 0.044 0 0.140 7 0.107 5 0.106 5 10 0.380 2 17.546 3 0.911 0 0.044 0 0.144 5 0.106 7
下载: 导出CSV
表 4 不同小波基对应的最优分解层数
Table 4. Number of optimal decomposition layers corresponding to different wavelet bases
下载: 导出CSV
表 5 SPAN-ISA-100C陀螺仪Allan方差分析结果
Table 5. Allan variance analysis results of SPAN-ISA-100C gyroscope
坐标轴 角度随机游走/
$({(^\circ )}\cdot{ {\text{h} }^{-\frac{ {1} }{ {2} } } })$零偏不稳定性/
$((^\circ) \cdot{\text{h} }^{-1})$角速率随机游走/
$((^\circ )\cdot{ {\text{h} }^{-\frac{ {3} }{ {2} } } })$x轴 0.030 4 0.045 5 0.054 2 y轴 0.026 9 0.120 8 0.185 7 z轴 0.025 4 0.043 0 0.057 9
下载: 导出CSV
表 6 MP-M39陀螺仪Allan方差分析结果
Table 6. Allan variance analysis results of MP-M39 gyroscope
坐标轴 角度随机游走/
$({(^\circ )}\cdot{ {\text{h} }^{-\frac{ {1} }{ {2} } } })$零偏不稳定性/
$((^\circ) \cdot{\text{h} }^{-1})$角速率随机游走/
$((^\circ )\cdot{ {\text{h} }^{-\frac{ {3} }{ {2} } } })$x轴 0.199 3 9.504 1 28.599 4 y轴 0.136 3 4.198 7 14.920 2 z轴 0.186 8 7.591 2 29.389 7
下载: 导出CSV
表 7 陀螺数据对应的最优分解层数
Table 7. Number of optimal decomposition layers corresponding to gyro data
方法 陀螺数据 x1 y1 z1 x2 y2 z2 本文 4 5 5 5 5 5 文献[9] 4 4 4 4 4 4
下载: 导出CSV
表 8 陀螺数据对应的最佳小波基函数
Table 8. Optimal wavelet basis functions corresponding to gyro data
陀螺数据 x1 y1 z1 x2 y2 z2 小波基 sym6 sym4 db8 db7 db7 db7
下载: 导出CSV
-
[1] SHI Y B, ZHANG J J, JIAO J J, et al. Calibration analysis of high-G MEMS accelerometer sensor based on wavelet and wavelet packet denoising[J]. Sensors, 2021, 21(4): 1231. doi: 10.3390/s21041231 [2] 吴保锋, 夏林元, 吴东金, 等. 基于改进小波阈值的MEMS陀螺去噪算法[J]. 电子器件, 2020, 43(5): 1104-1107. doi: 10.3969/j.issn.1005-9490.2020.05.028WU B F, XIA L Y, WU D J, et al. Denoising algorithm of MEMS gyroscope based on improved threshold function[J]. Chinese Journal of Electron Devices, 2020, 43(5): 1104-1107(in Chinese). doi: 10.3969/j.issn.1005-9490.2020.05.028 [3] JANG Y I, SIM J Y, YANG J R, et al. The optimal selection of mother wavelet function and decomposition level for denoising of DCG signal[J]. Sensors, 2021, 21(5): 1851. doi: 10.3390/s21051851 [4] 李文华, 汪立新, 沈强, 等. 基于EMD的MEMS陀螺仪随机漂移分析方法[J]. 北京航空航天大学学报, 2021, 47(9): 1927-1932.LI W H, WANG L X, SHEN Q, et al. Random drift analysis method of MEMS gyroscope based on EMD[J]. Journal of Beijing University of Aeronautics and Astronautics, 2021, 47(9): 1927-1932(in Chinese). [5] 景冰洁, 韩跃平, 张鹏, 等. 改进提升小波阈值法在MEMS陀螺仪误差分析中的应用[J]. 仪表技术与传感器, 2020(12): 95-100. doi: 10.3969/j.issn.1002-1841.2020.12.019JING B J, HAN Y P, ZHANG P, et al. Application of improved lifting wavelet threshold method in error analysis of MEMS gyroscope[J]. Instrument Technique and Sensor, 2020(12): 95-100(in Chinese). doi: 10.3969/j.issn.1002-1841.2020.12.019 [6] 刘晓光, 胡静涛, 高雷, 等. 基于改进小波阈值的微机械陀螺去噪方法[J]. 中国惯性技术学报, 2014, 22(2): 233-236. doi: 10.13695/j.cnki.12-1222/o3.2014.02.017LIU X G, HU J T, GAO L, et al. Micro mechanical gyro denoising method based on improved wavelet threshold[J]. Journal of Chinese Inertial Technology, 2014, 22(2): 233-236(in Chinese). doi: 10.13695/j.cnki.12-1222/o3.2014.02.017 [7] 邵旋, 康兴无, 王旭平, 等. 基于多元信息融合的小波降噪质量综合评估指标[J]. 兵器装备工程学报, 2020, 41(12): 155-160. doi: 10.11809/bqzbgcxb2020.12.029SHAO X, KANG X W, WANG X P, et al. Comprehensive evaluation index of wavelet denoising quality based on multi-information fusion[J]. Journal of Ordnance Equipment Engineering, 2020, 41(12): 155-160(in Chinese). doi: 10.11809/bqzbgcxb2020.12.029 [8] 陶珂, 朱建军. 多指标融合的小波去噪最佳分解尺度选择方法[J]. 测绘学报, 2012, 41(5): 749-755.TAO K, ZHU J J. A hybrid indicator for determining the best decomposition scale of wavelet denoising[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(5): 749-755(in Chinese). [9] 朱建军, 章浙涛, 匡翠林, 等. 一种可靠的小波去噪质量评价指标[J]. 武汉大学学报(信息科学版), 2015, 40(5): 688-694.ZHU J J, ZHANG Z T, KUANG C L, et al. A reliable evaluation indicator of wavelet de-noising[J]. Geomatics and Information Science of Wuhan University, 2015, 40(5): 688-694(in Chinese). [10] 王旭, 王昶. 一种基于熵权法的小波去噪复合评价指标[J]. 大地测量与地球动力学, 2018, 38(7): 698-702. doi: 10.14075/j.jgg.2018.07.008WANG X, WANG C. A kind of wavelet de-noising composite evaluation index based on entropy method[J]. Journal of Geodesy and Geodynamics, 2018, 38(7): 698-702(in Chinese). doi: 10.14075/j.jgg.2018.07.008 [11] 冯明, 周程瑜, 张坤, 等. 回转误差测试中系统噪声分离技术[J]. 北京航空航天大学学报, 2020, 46(4): 666-673. doi: 10.13700/j.bh.1001-5965.2019.0316FENG M, ZHOU C Y, ZHANG K, et al. Separation technology of system noise in error motion test[J]. Journal of Beijing University of Aeronautics and Astronautics, 2020, 46(4): 666-673(in Chinese). doi: 10.13700/j.bh.1001-5965.2019.0316 [12] 孔玲军. MATLAB小波分析超级学习手册[M]. 北京: 人民邮电出版社, 2014.KONG L J. MATLAB super Learning handbook of wavelet analysis[M]. Beijing: Post&Telecom Press, 2014(in Chinese). [13] 赵宣懿, 孔雪博, 熊智, 等. 基于低成本MEMS陀螺的小波阈值去噪应用研究[J]. 传感器与微系统, 2017, 36(12): 54-56.ZHAO X Y, KONG X B, XIONG Z, et al. Research of application of wavelet threshold de-noising based on low-cost MEMS gyro[J]. Transducer and Microsystem Technologies, 2017, 36(12): 54-56(in Chinese). [14] SOLTANI A A, SHAHRTASH S M. Decision tree-based method for optimum decomposition level determination in wavelet transform for noise reduction of partial discharge signals[J]. IET Science, Measurement & Technology, 2020, 14(1): 9-16. [15] LI Y N, LI Z H. Application of a novel wavelet shrinkage scheme to partial discharge signal denoising of large generators[J]. Applied Sciences, 2020, 10(6): 2162. doi: 10.3390/app10062162 [16] BALDAZZI G, SOLINAS G, DEL VALLE J, et al. Systematic analysis of wavelet denoising methods for neural signal processing[J]. Journal of Neural Engineering, 2020, 17(6): 11-27. [17] ROUIS M, OUAFI A, SBAA S. Optimal level and order detection in wavelet decomposition for PCG signal denoising[J]. Biomedizinische Technik Biomedical Engineering, 2019, 64(2): 163-176. doi: 10.1515/bmt-2018-0001 [18] 谈渊, 甘学辉, 张东剑, 等. 基于小波去噪的激光多普勒振动信号处理[J]. 激光技术, 2022, 46(1): 129-133. doi: 10.7510/jgjs.issn.1001-3806.2022.01.014TAN Y, GAN X H, ZHANG D J, et al. Laser Doppler vibration signal processing based on wavelet denoising[J]. Laser Technology, 2022, 46(1): 129-133(in Chinese). doi: 10.7510/jgjs.issn.1001-3806.2022.01.014 [19] 王永弟, 许承权, 范千. 熵权、变异系数及模糊多准则决策在测量平差中的综合应用[J]. 工程勘察, 2012, 40(9): 58-61.WANG Y D, XU C Q, FAN Q. Integrated application of entropy theory, variation coefficient and fuzzy multi-criteria decision making in surveying adjustment[J]. Geotechnical Investigation & Surveying, 2012, 40(9): 58-61(in Chinese). [20] 严恭敏, 李四海, 秦永元. 惯性仪器测试与数据分析[M]. 北京: 国防工业出版社, 2012: 143-146.YAN G M, LI S H, QIN Y Y. Inertial instrument testing and data analysis[M]. Beijing: National Defense Industry Press, 2012: 143-146 (in Chinese). -
下载:
点击查看大图
计量
- 文章访问数: 368
- HTML全文浏览量: 90
- PDF下载量: 45
- 被引次数: 0
