无人直升机LPV控制律设计

段镖; 杨庶; 李爱军

doi:10.13700/j.bh.1001-5965.2021.0340

无人直升机LPV控制律设计

doi: 10.13700/j.bh.1001-5965.2021.0340

西北工业大学自动化学院，西安 710072

详细信息

通讯作者:
E-mail：syang@nwpu.edu.cn

中图分类号: V212.4；V249.1
计量
- 文章访问数: 310
- HTML全文浏览量: 83
- PDF下载量: 45
- 被引次数: 0
出版历程
- 收稿日期: 2021-06-22
- 录用日期: 2021-10-29
- 网络出版日期: 2021-11-16
- 整期出版日期: 2023-04-30

Design of LPV control law for unmanned helicopter

School of Automation，Northwestern Polytechnical University，Xi’an 710072，China

More Information

Corresponding author: E-mail：syang@nwpu.edu.cn

摘要

摘要:
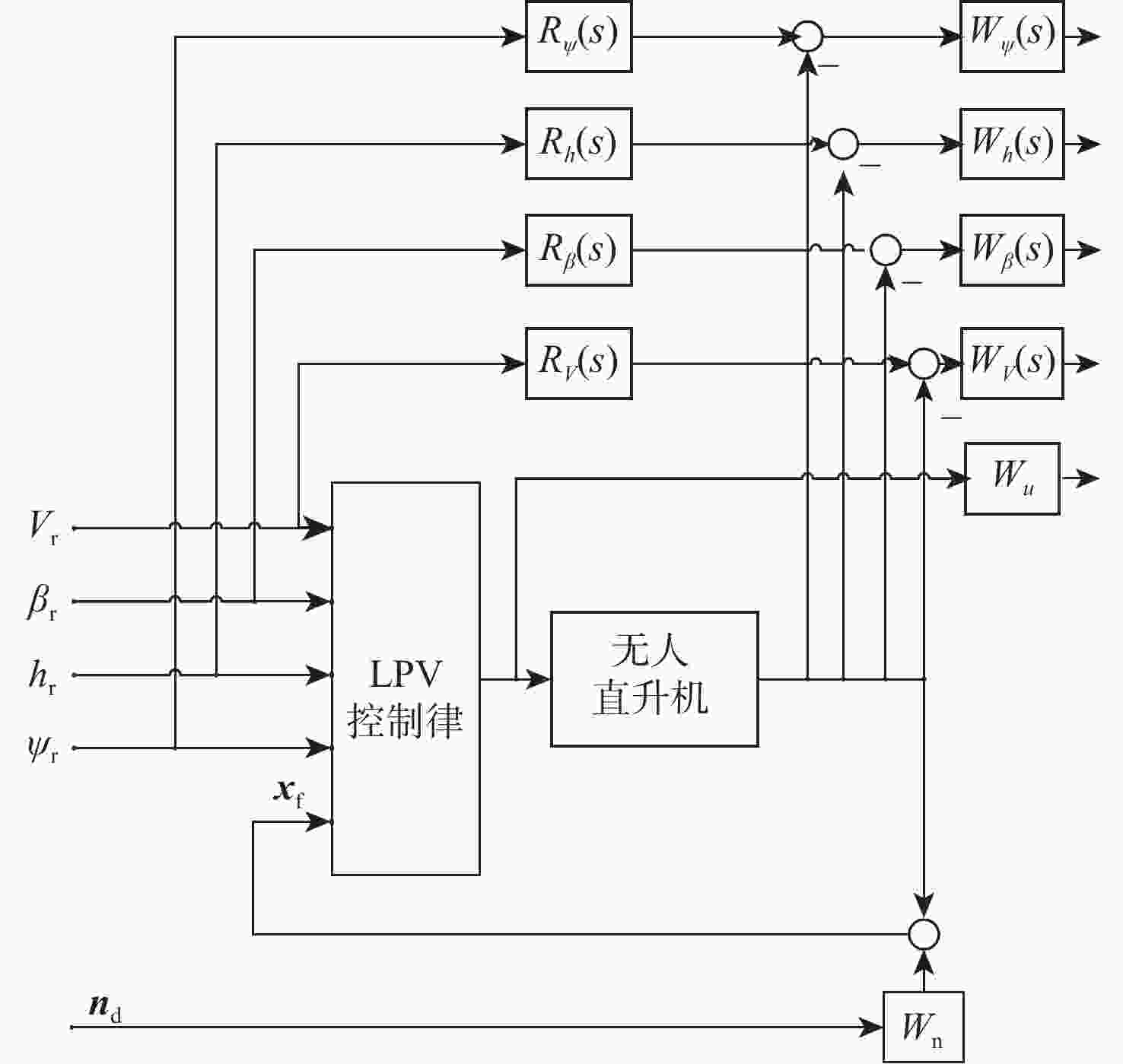
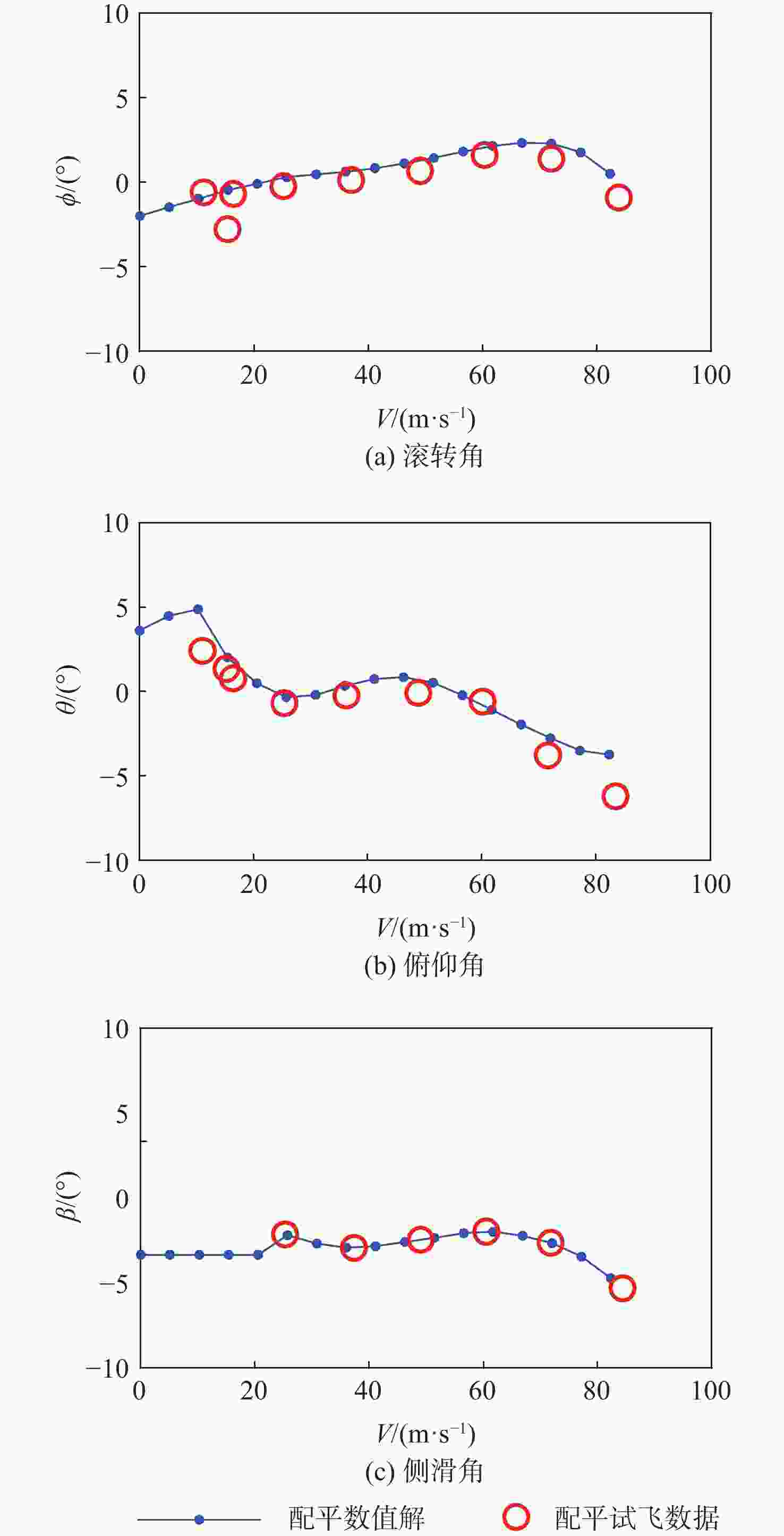
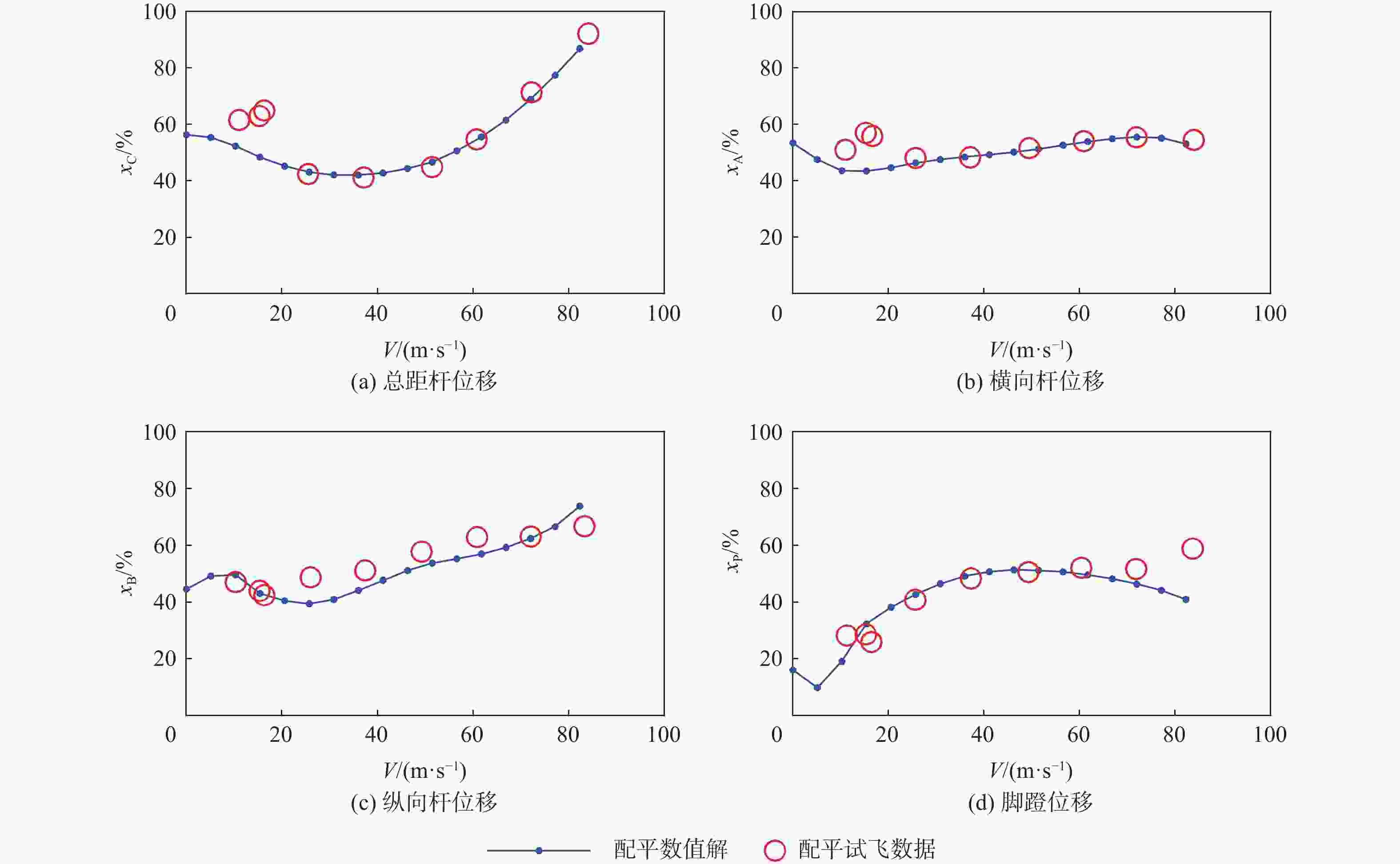
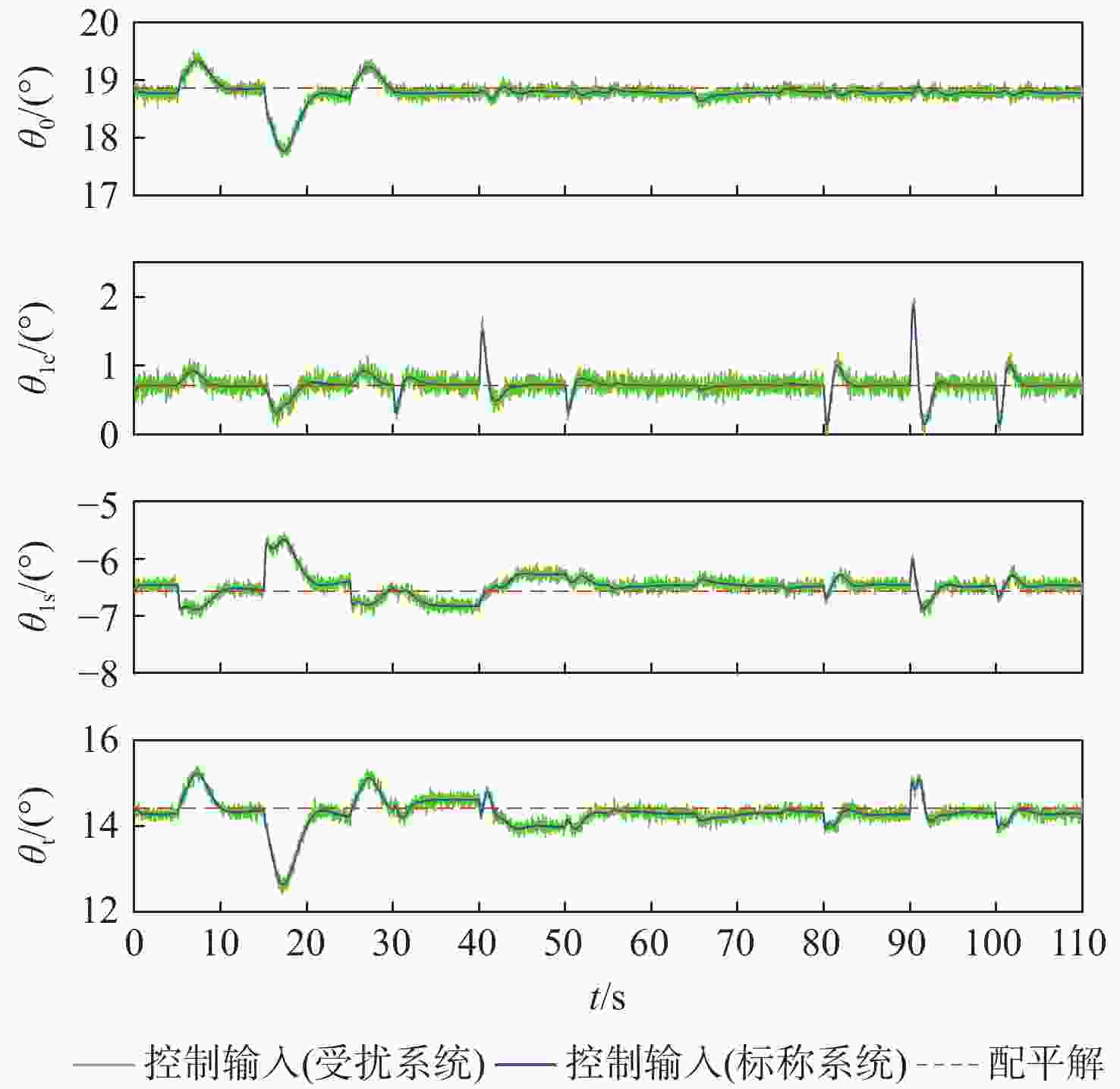
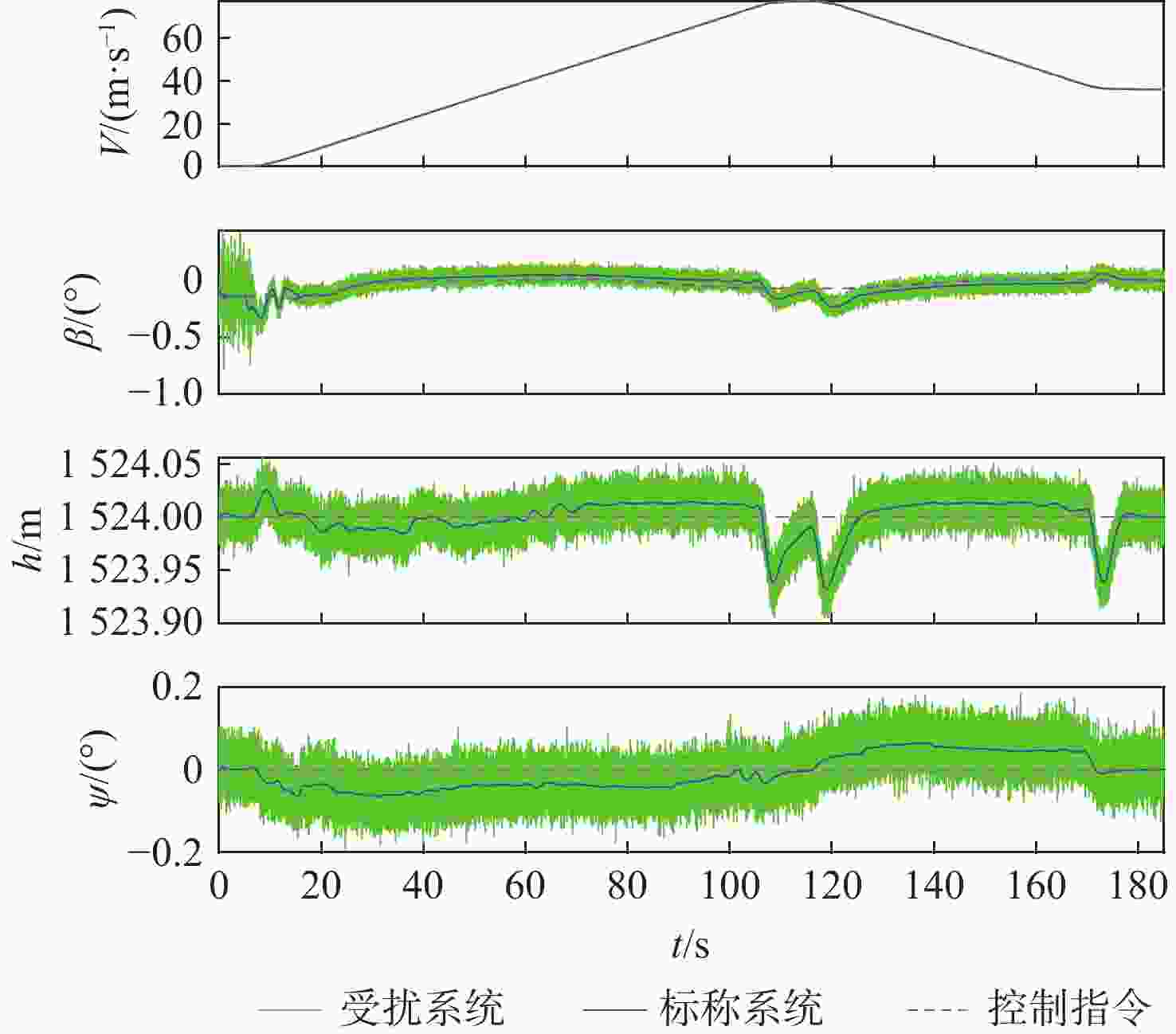
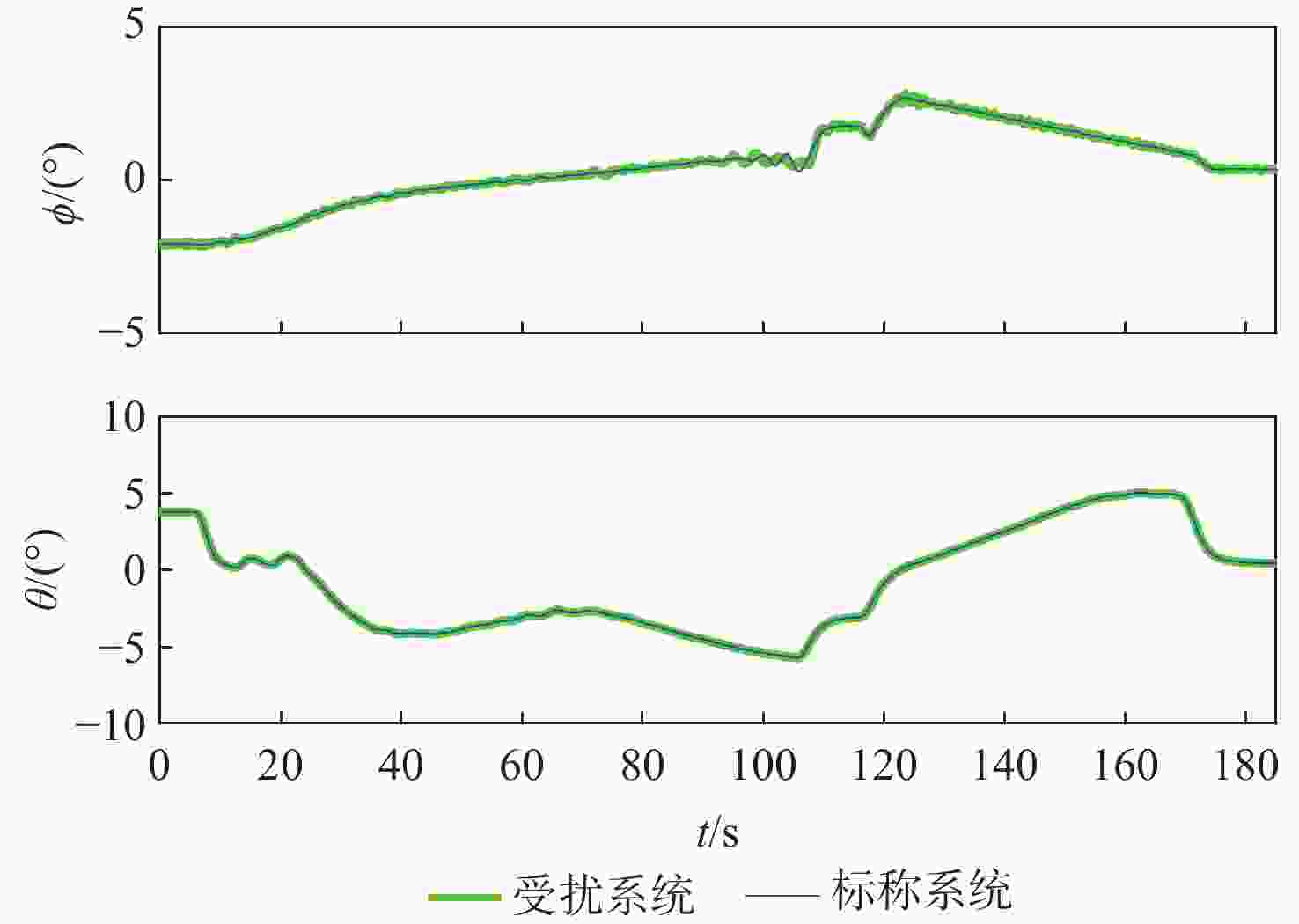
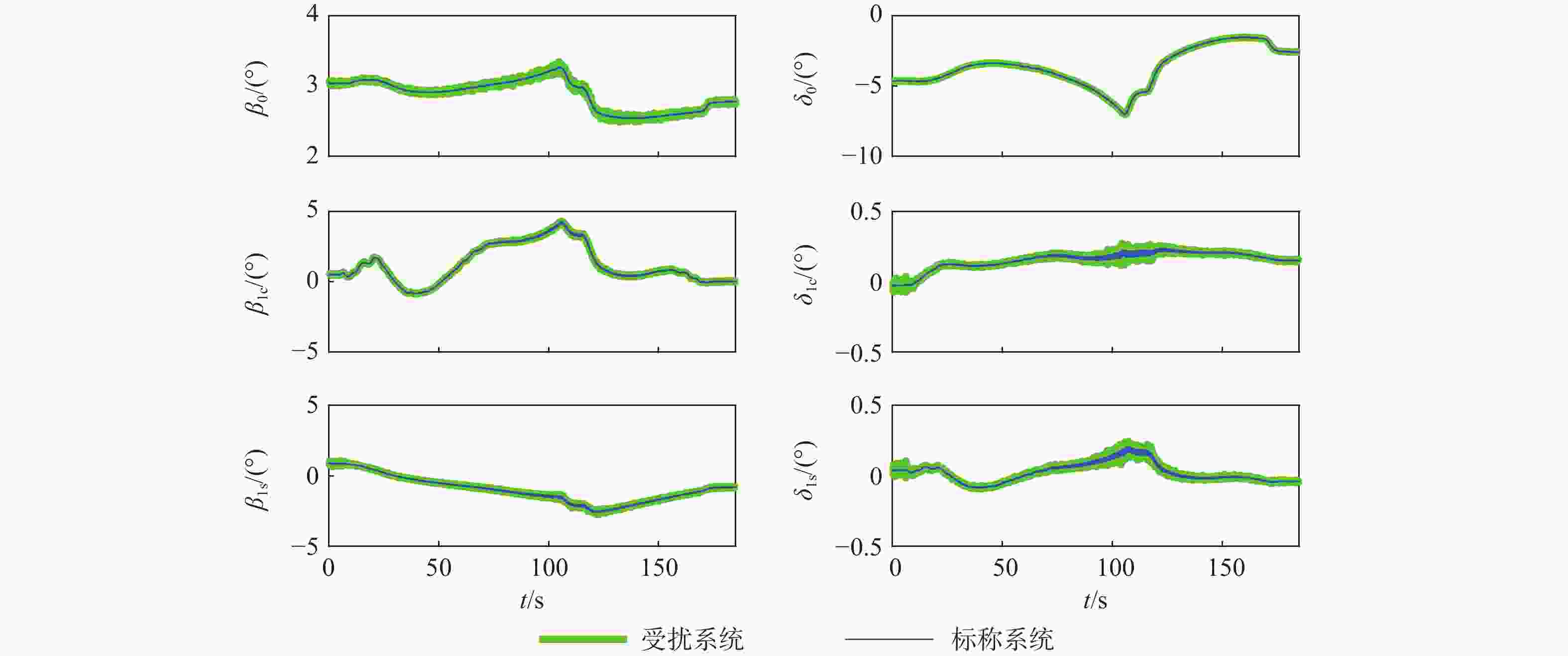
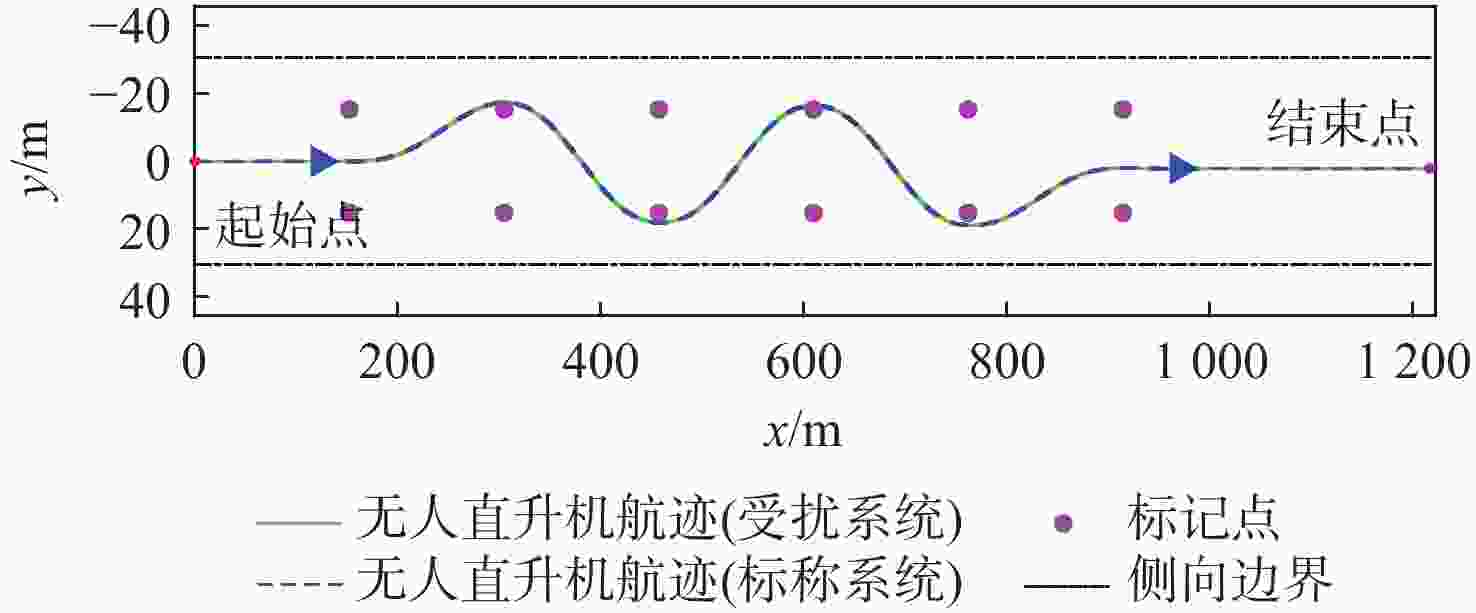
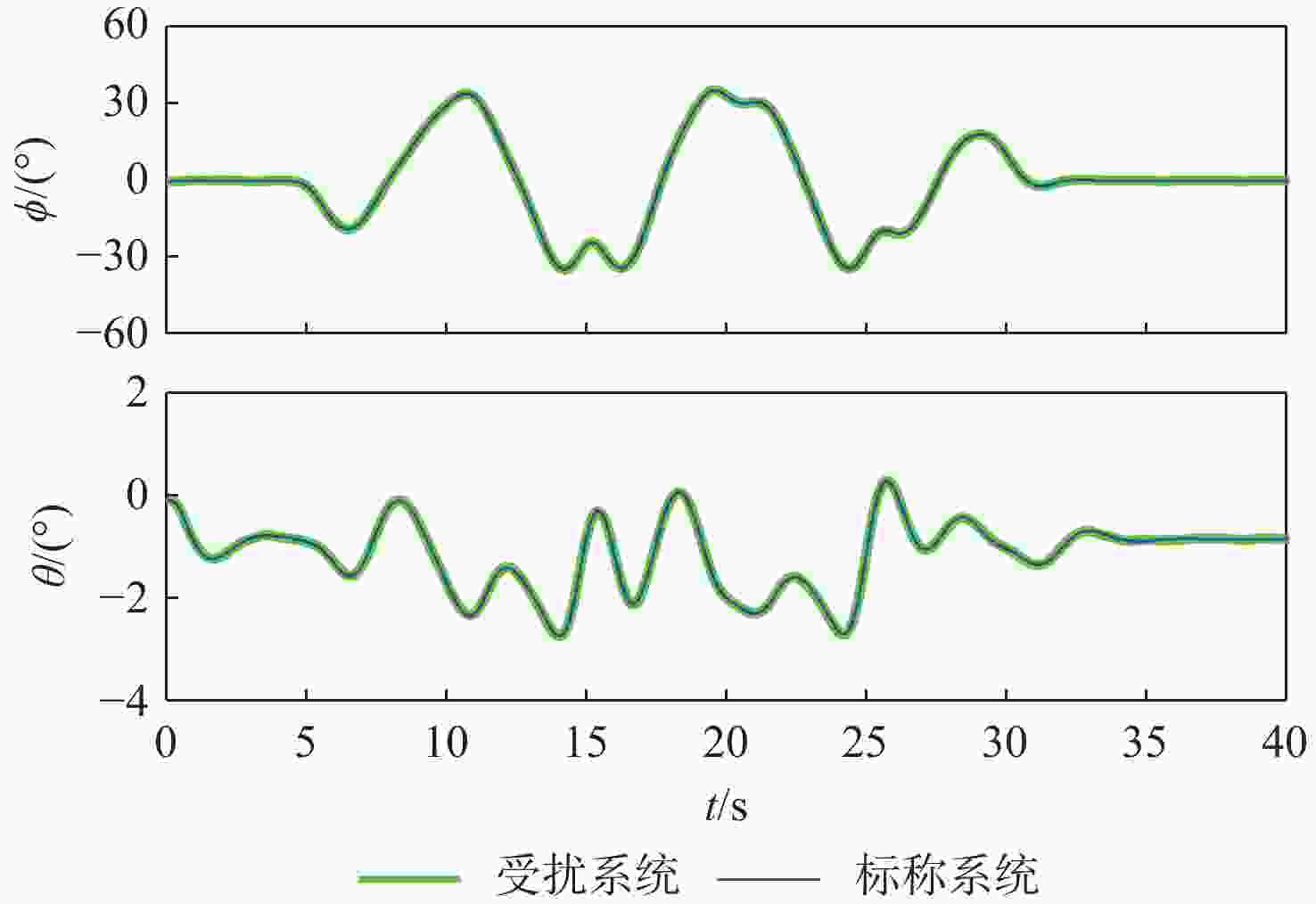
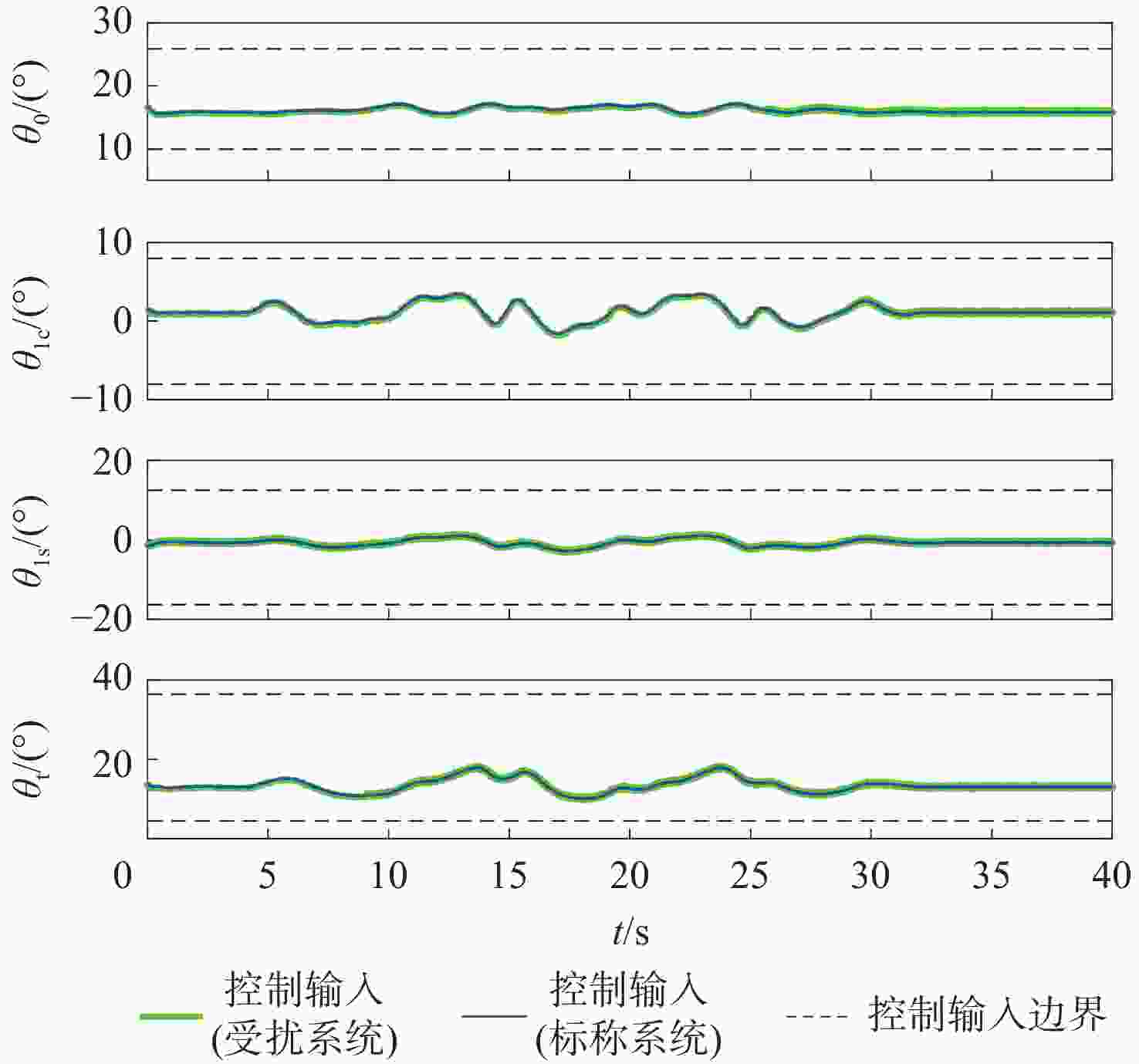
针对无人直升机航迹控制要求，提出一种基于线性变参数(LPV)控制理论的无人直升机一体化式飞行控制律设计方法，通过速度、侧滑角、高度和偏航角控制通道的显模型跟踪控制，实现无人直升机航迹控制。建立了无人直升机高阶非线性动力学模型，模型中考虑了旋翼桨叶挥舞和摆振运动、旋翼动态入流、机体运动之间的运动耦合，用于检验直升机高阶运动特性对控制律性能和闭环系统稳定性的影响。由于无人直升机的非线性动力学模型是典型的周期性系统，基于简谐平衡方法进行无人直升机的配平和模型线性化计算，在速度包线内得到用于控制律设计的无人直升机LPV模型，通过凸函数优化方法求解LPV控制律的参数。基于典型直升机机动，采用数值仿真方法对LPV控制律在传感器噪声影响下的控制性能进行检验，仿真结果表明：LPV控制律在速度包线内具有良好的控制性能和鲁棒性，无人直升机闭环系统在机动飞行中满足给定的性能要求。
- 无人直升机 /
- 高阶动力学模型 /
- 一体化式飞行控制 /
- 鲁棒控制 /
- 线性变参数控制 /
- 显模型跟踪
Abstract:
An LPV control scheme is proposed to design integrated flight control laws for unmanned helicopters. The LPV control law achieves explicit model following performance for an unmanned helicopter in velocity, sideslip angle, altitude, and yaw angle control channels, leading to desired flight path control performance. A nonlinear mathematical model is developed for an unmanned helicopter to take into consideration the coupling among rotor blade flapping and lead-lag dynamics, rotor inflow dynamics, and fuselage dynamics. Since helicopter dynamics is periodic, harmonic balance method is employed to conduct trim and model linearization, leading to an LPV model used to perform LPV control design in a velocity envelope. Parameters of the LPV control law are determined by solving a convex optimization problem. Numerical simulations are conducted to examine the performance of the LPV control law based on typical helicopter maneuvers under sensor noise. Results show that the proposed law has good performance and robustness in helicopter velocity envelope, satisfying performance standards of each maneuver of an unmanned helicopter.
- unmanned helicopter /
- high-order dynamics model /
- integrated flight control /
- robust control /
- linear parameter varying control /
- explicit model following

HTML全文

图 1 主旋翼桨叶的广义坐标

Figure 1. Generalized coordinates of main rotor blades

下载: 全尺寸图片幻灯片

图 2 LPV控制律设计的系统连接结构

Figure 2. System interconnections for LPV control

下载: 全尺寸图片幻灯片

图 3 滚转角、俯仰角和侧滑角配平结果

Figure 3. Trim results of roll, pitch, and sideslip angles

下载: 全尺寸图片幻灯片

图 4 杆输入配平结果

Figure 4. Trim results of stick inputs

下载: 全尺寸图片幻灯片

图 5 对偶输入指令和无人直升机响应（V = 2.5 m/s ）

Figure 5. Doublet input commands and unmanned helicopter responses (V = 2.5 m/s )

下载: 全尺寸图片幻灯片

图 6 对偶输入指令和无人直升机响应（V = 61.7 m/s ）

Figure 6. Doublet input commands and unmanned helicopter responses (V = 61.7 m/s )

下载: 全尺寸图片幻灯片

图 7 控制输入（V = 2.5 m/s ）

Figure 7. Control inputs (V = 2.5 m/s )

下载: 全尺寸图片幻灯片

图 8 控制输入（V = 61.7 m/s ）

Figure 8. Control inputs (V = 61.7 m/s )

下载: 全尺寸图片幻灯片

图 9 控制指令和无人直升机响应（水平加减速机动）

Figure 9. Control commands and unmanned helicopter responses (level acceleration and deceleration)

下载: 全尺寸图片幻灯片

图 10 滚转角和俯仰角响应（水平加减速机动）

Figure 10. Responses of roll and pitch angles (level acceleration and deceleration)

下载: 全尺寸图片幻灯片

图 11 旋翼多桨叶坐标响应（水平加减速机动）

Figure 11. Responses of rotor multi-blade coordinates (level acceleration and deceleration)

下载: 全尺寸图片幻灯片

图 12 控制输入（水平加减速机动）

Figure 12. Control inputs (level acceleration and deceleration)

下载: 全尺寸图片幻灯片

图 13 无人直升机航迹（穿桩回旋机动）

Figure 13. Unmanned helicopter trajectory (slalom)

下载: 全尺寸图片幻灯片

图 14 控制指令和无人直升机响应（穿桩回旋机动）

Figure 14. Control commands and unmanned helicopter responses (slalom)

下载: 全尺寸图片幻灯片

图 15 滚转角和俯仰角响应（穿桩回旋机动）

Figure 15. Responses of roll and pitch angles (slalom)

下载: 全尺寸图片幻灯片

图 16 旋翼多桨叶坐标响应（穿桩回旋机动）

Figure 16. Responses of rotor multi-blade coordinates (slalom)

下载: 全尺寸图片幻灯片

图 17 控制输入（穿桩回旋机动）

Figure 17. Control inputs (slalom)

下载: 全尺寸图片幻灯片

参考文献(31)

[1]	TAKAHASHI M D, FUJIZAWA B T, LUSARDI J A, et al. Autonomous guidance and flight control on a partial-authority Black Hawk helicopter[C]//Proceedings of AIAA Aviation Forum. Reston: AIAA, 2020: 1-39.
[2]	TAKAHASHI M D, WHALLEY M S, FLETCHER J W, et al. Development and flight testing of a flight control law for autonomous operations research on the RASCAL JUH-60A[J]. Journal of the American Helicopter Society, 2014, 59: 032007.
[3]	HALBE O, HAJEK M. Robust helicopter sliding mode control for enhanced handling and trajectory following[J]. Journal of Guidance, Control, and Dynamics, 2020, 43(10): 1805-1821. doi: 10.2514/1.G005183
[4]	GREER W B, SULTAN C. Infinite horizon model predictive control tracking application to helicopters[J]. Aerospace Science and Technology, 2020, 98: 105675. doi: 10.1016/j.ast.2019.105675
[5]	GREER W B, SULTAN C. Shrinking horizon model predictive control method for helicopter-ship touchdown[J]. Journal of Guidance, Control, and Dynamics, 2020, 43(5): 884-900. doi: 10.2514/1.G004374
[6]	陈南宇, 蒙志君, 黄俊. 无人直升机飞行品质要求探讨[J]. 北京航空航天大学学报, 2016, 42(2): 337-344. doi: 10.13700/j.bh.1001-5965.2015.0125 CHEN N Y, MENG Z J, HUANG J. Research on flying quality of unmanned helicopter[J]. Journal of Beijing University of Aeronautics and Astronautics, 2016, 42(2): 337-344(in Chinese). doi: 10.13700/j.bh.1001-5965.2015.0125
[7]	吴超, 王浩文, 姜辰, 等. 基于LADRC的直升机姿态解耦控制及参数整定[J]. 北京航空航天大学学报, 2015, 41(11): 2085-2094. doi: 10.13700/j.bh.1001-5965.2014.0710 WU C, WANG H W, JIANG C, et al. LADRC-based attitude decoupling control for helicopter and parameters tuning[J]. Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(11): 2085-2094(in Chinese). doi: 10.13700/j.bh.1001-5965.2014.0710
[8]	汪庆, 王永, 彭程, 等. 直升机两步法抗饱和控制[J]. 北京航空航天大学学报, 2011, 37(7): 888-894. doi: 10.13700/j.bh.1001-5965.2011.07.025 WANG Q, WANG Y, PENG C, et al. Two-step anti-windup control of helicopter[J]. Journal of Beijing University of Aeronautics and Astronautics, 2011, 37(7): 888-894(in Chinese). doi: 10.13700/j.bh.1001-5965.2011.07.025
[9]	赵佳, 申功璋, 陈胜功. 基于多点逆模型组的直升机慢切换姿态控制[J]. 北京航空航天大学学报, 2010, 36(7): 798-802. doi: 10.13700/j.bh.1001-5965.2010.07.028 ZHAO J, SHENG G Z, CHEN S G. Helicopter slow switching attitude control based on multiple points inversion models group[J]. Journal of Beijing University of Aeronautics and Astronautics, 2010, 36(7): 798-802(in Chinese). doi: 10.13700/j.bh.1001-5965.2010.07.028
[10]	RUGH W J, SHAMMA J S. Research on gain scheduling[J]. Automatica, 2000, 36: 1401-1425. doi: 10.1016/S0005-1098(00)00058-3
[11]	WU F, YANG X H, PACKARD A, et al. Induced L₂-norm control for LPV systems with bounded parameter variation rates[J]. International Journal of Robust and Nonlinear Control, 1996, 6: 983-998. doi: 10.1002/(SICI)1099-1239(199611)6:9/10<983::AID-RNC263>3.0.CO;2-C
[12]	HUGHES H, WU F. H_∞ LPV state feedback control for flexible hypersonic vehicle longitudinal dynamics[C]//Proceedings of AIAA Guidance, Navigation, and Control Conference. Reston: AIAA, 2010: 1-13.
[13]	SIGTHORSSON D O, SERRANI A, BOLENDER M A, et al. LPV control design for over-actuated hypersonic vehicles models[C]//Proceedings of AIAA Guidance, Navigation, and Control Conference. Reston: AIAA, 2009: 1-24.
[14]	BALAS G J, FIALHO I, PACK A, et al. On the design of LPV controllers for the F-14 aircraft lateral-directional axis during powered approach[C]//Proceedings of the 1997 American Control Conference. Reston: AIAA, 1997: 123-127.
[15]	BITTANTI S, CUZZOLA F A, LOVERA M, et al. An LPV-LMI approach to generalised active control of vibrations in helicopters[C]//Proceedings of the 1999 European Control Conference. Piscataway: IEEE Press, 1999: 2783-2788.
[16]	SUN X D, POSTLETHWAITE I. Affine LPV modelling and its use in gain-scheduled helicopter control[C]//Proceedings of UKACC International Conference on Control. Piscataway: IEEE Press, 1998: 1504-1509.
[17]	POSTLETHWAITE I, KONSTANTOPOULOS I K, SUN X D, et al. Design, flight simulation, and handling qualities evaluation of an LPV gain-scheduled helicopter flight control system[J]. European Journal of Control, 2000, 6: 553-566. doi: 10.1016/S0947-3580(00)71119-8
[18]	CHEN R T N, HINDSON W S. Influence of high-order dynamics on helicopter flight-control system bandwidth[J]. Journal of Guidance, Control, and Dynamics, 1986, 9(2): 190-197. doi: 10.2514/3.20089
[19]	DRYFOOS J B, KOTHMANN B D, MAYO J. An approach to reducing rotor-body coupled roll oscillations on the RAH-66 Comanche using modified roll rate feedback[C]//Proceedings of the American Helicopter Society 55th Annual Forum. Fairfax: AHS, 1999: 1-14.
[20]	HOWLETT J J. UH-60A Black Hawk engineering simulation program: Volume 1 - mathematical model: NASA CR 166309[R]. Washington, D. C.: NASA, 1981: 5-361.
[21]	PADFIELD G D. Helicopter flight dynamics[M]. 2nd ed. Oxford: Blackwell Publishing Ltd, 2007: 175-179.
[22]	STEVENS B L, LEWIS F L, JOHNSON E N. Aircraft control and simulation[M]. 3rd ed. Hoboken: John Wiley & Sons Inc, 2015: 34-45.
[23]	DUVAL R W. Inertial dynamics of a general purpose rotor model: NASA TM-78557[R]. Washington, D. C.: NASA, 1979: 6-34.
[24]	PITT D M, PETERS D A. Theoretical prediction of dynamics inflow derivatives[J]. Vertica, 1981, 5(1): 21-34.
[25]	BALLIN M G. Validation of a real-time engineering simulation of the UH-60A helicopter: NASA TM-88360[R]. Washington, D. C.: NASA, 1987: 23-26.
[26]	KIM F D, CELI R, TISCHLER M B. Forward flight trim and frequency response validation of a helicopter simulation model[J]. Journal of Aircraft, 1993, 30(6): 854-863. doi: 10.2514/3.46427
[27]	NOCEDAL J, WRIGHT S J. Numerical optimization[M]. Berlin: Springer, 2006: 136-142.
[28]	JOHNSON W. Rotorcraft aeromechanics[M]. New York: Cambridge University Press, 2013: 549-562.
[29]	MARCOS A, BALAS G J. Development of linear-parameter-varying models for aircraft[J]. Journal of Guidance, Control, and Dynamics, 2004, 27(2): 218-228. doi: 10.2514/1.9165
[30]	AKARIAN P, ADAMS R J. Advanced gain-scheduling techniques for uncertain systems[J]. IEEE Transactions on Control System Technology, 1998, 6(1): 21-32. doi: 10.1109/87.654874
[31]	BASKETT B J. Aeronautical design standard performance specification handling qualities requirements for military rotorcraft: ADS-33E-PRF[S]. Alabama: United States Army Aviation and Missile Command, 2000: 35-36.