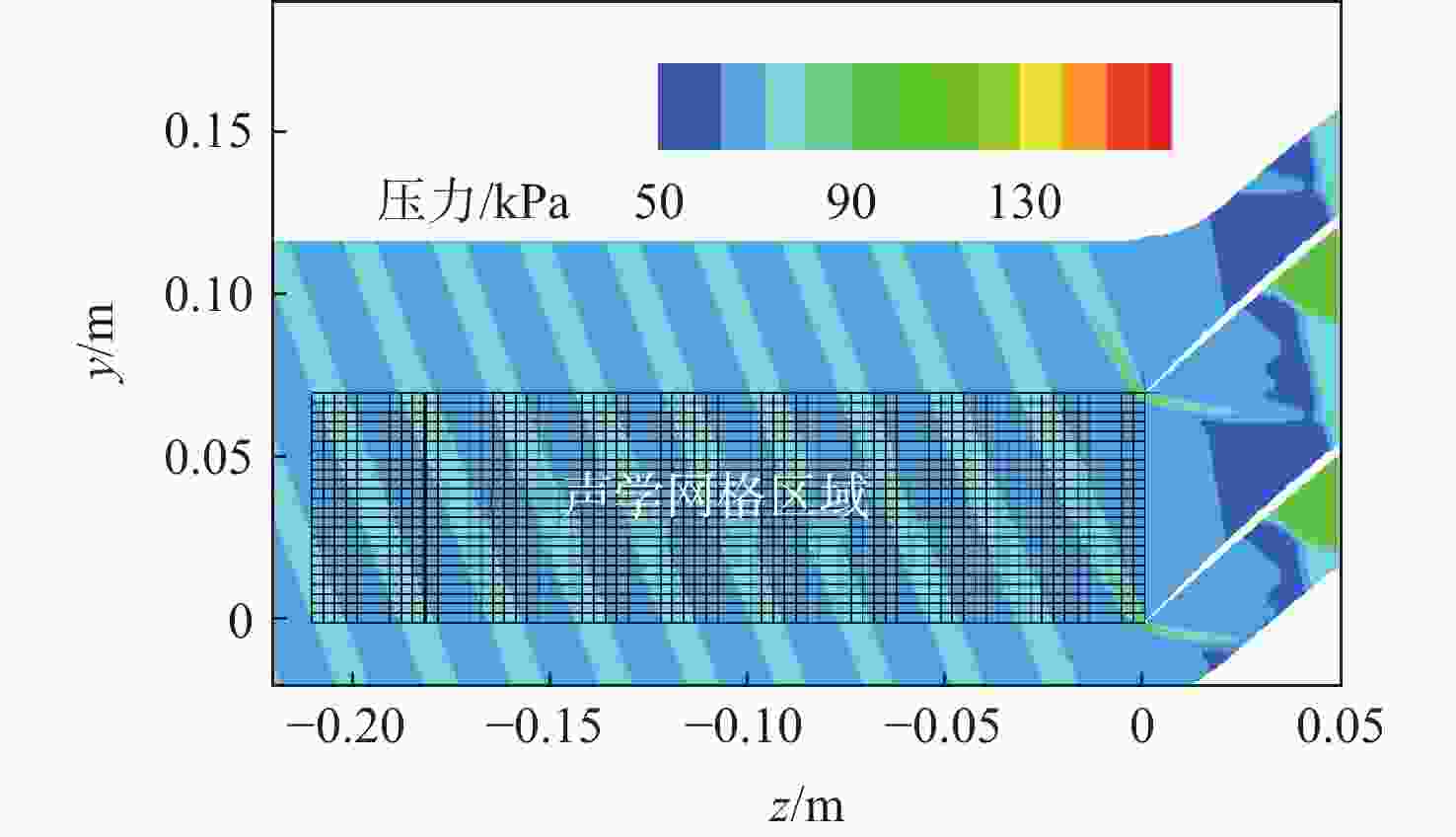
-
摘要:
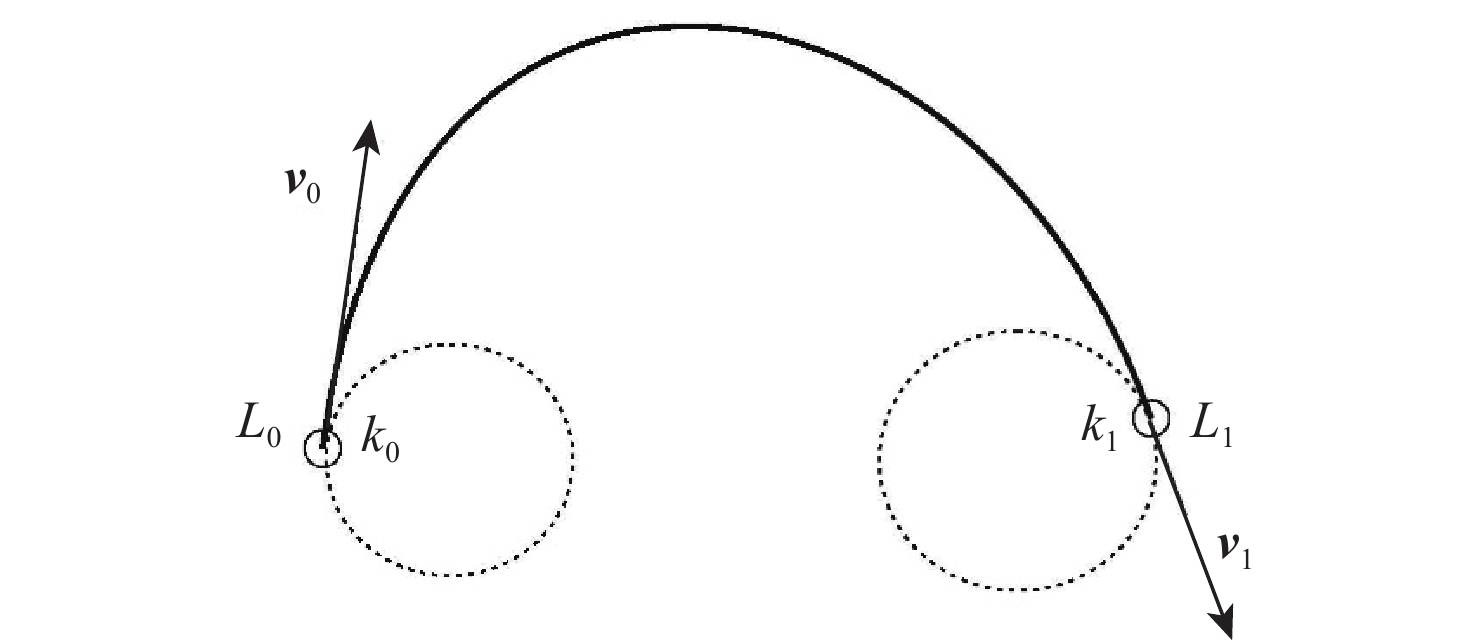
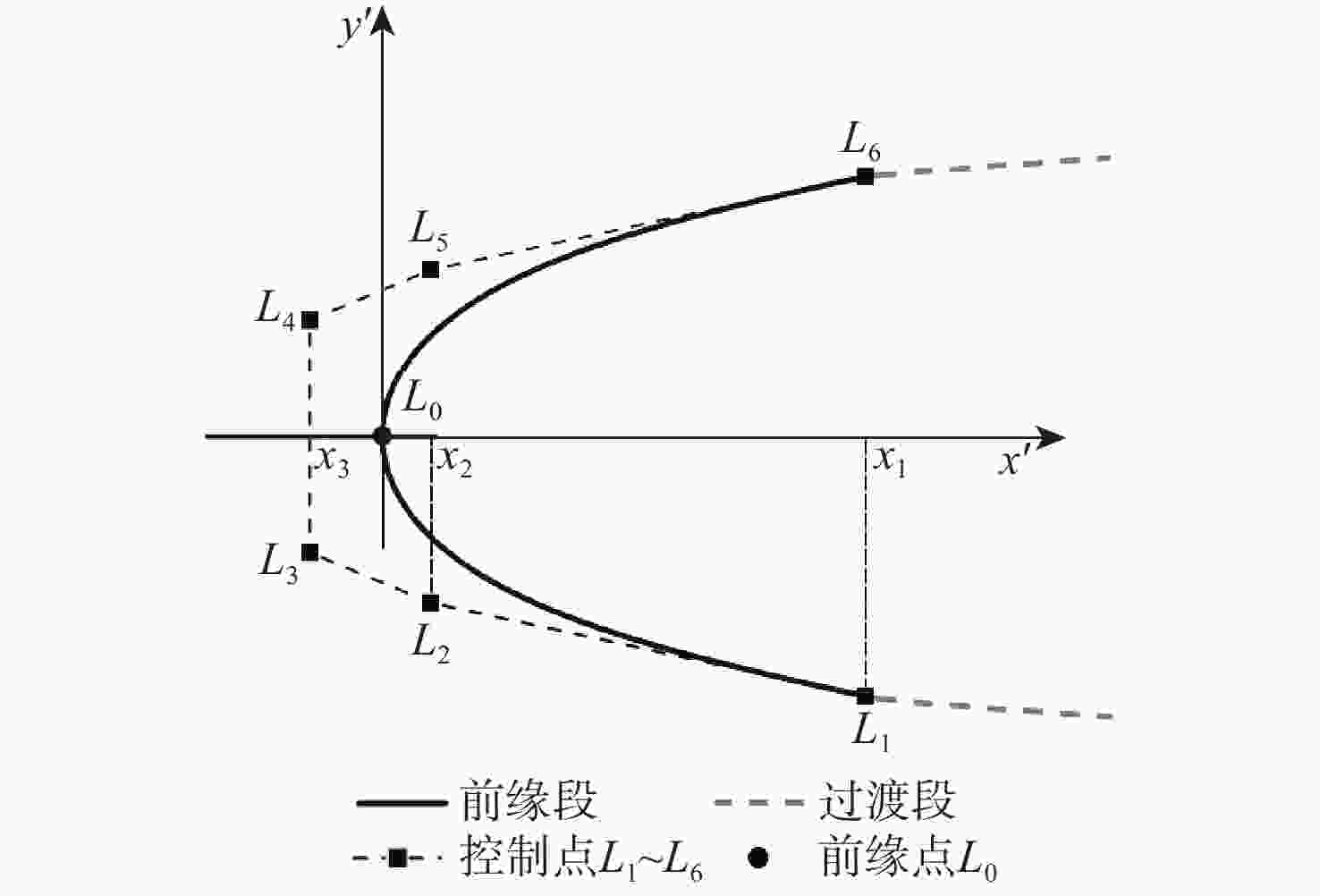
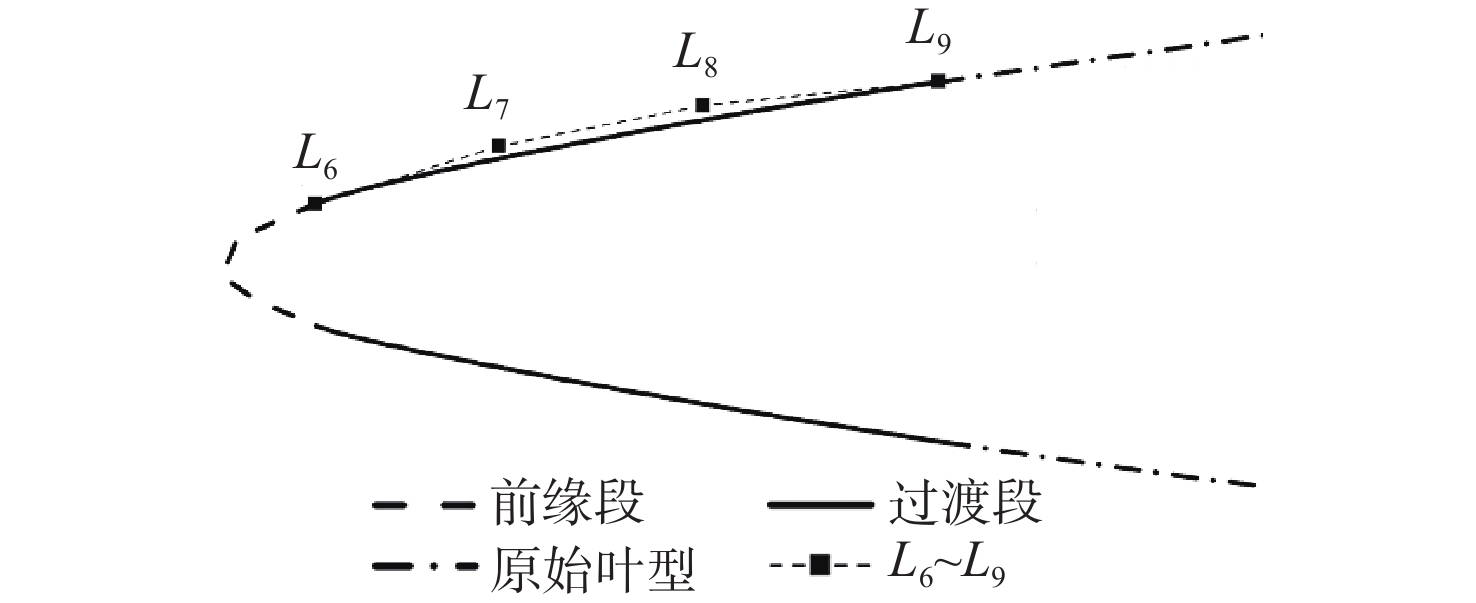
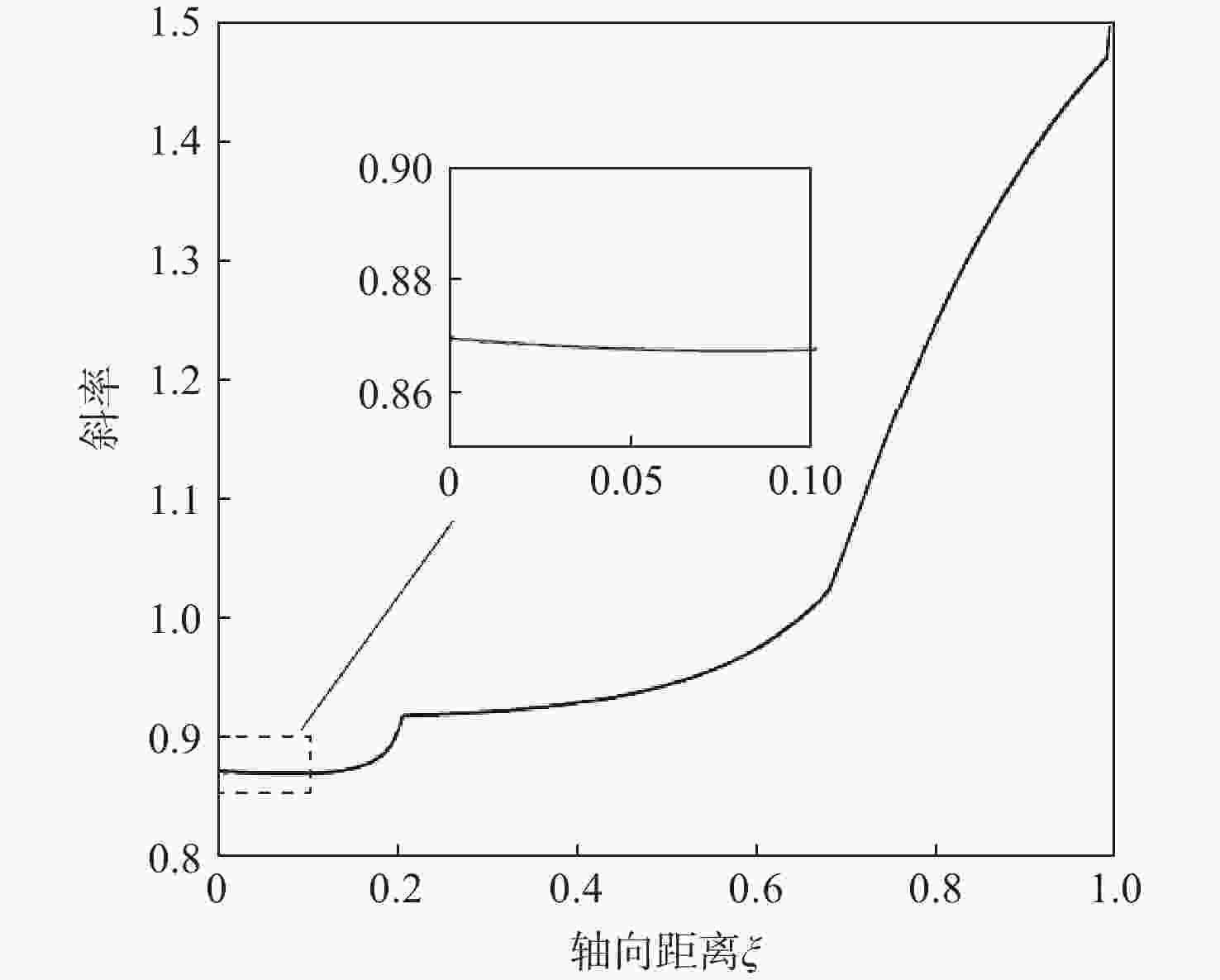
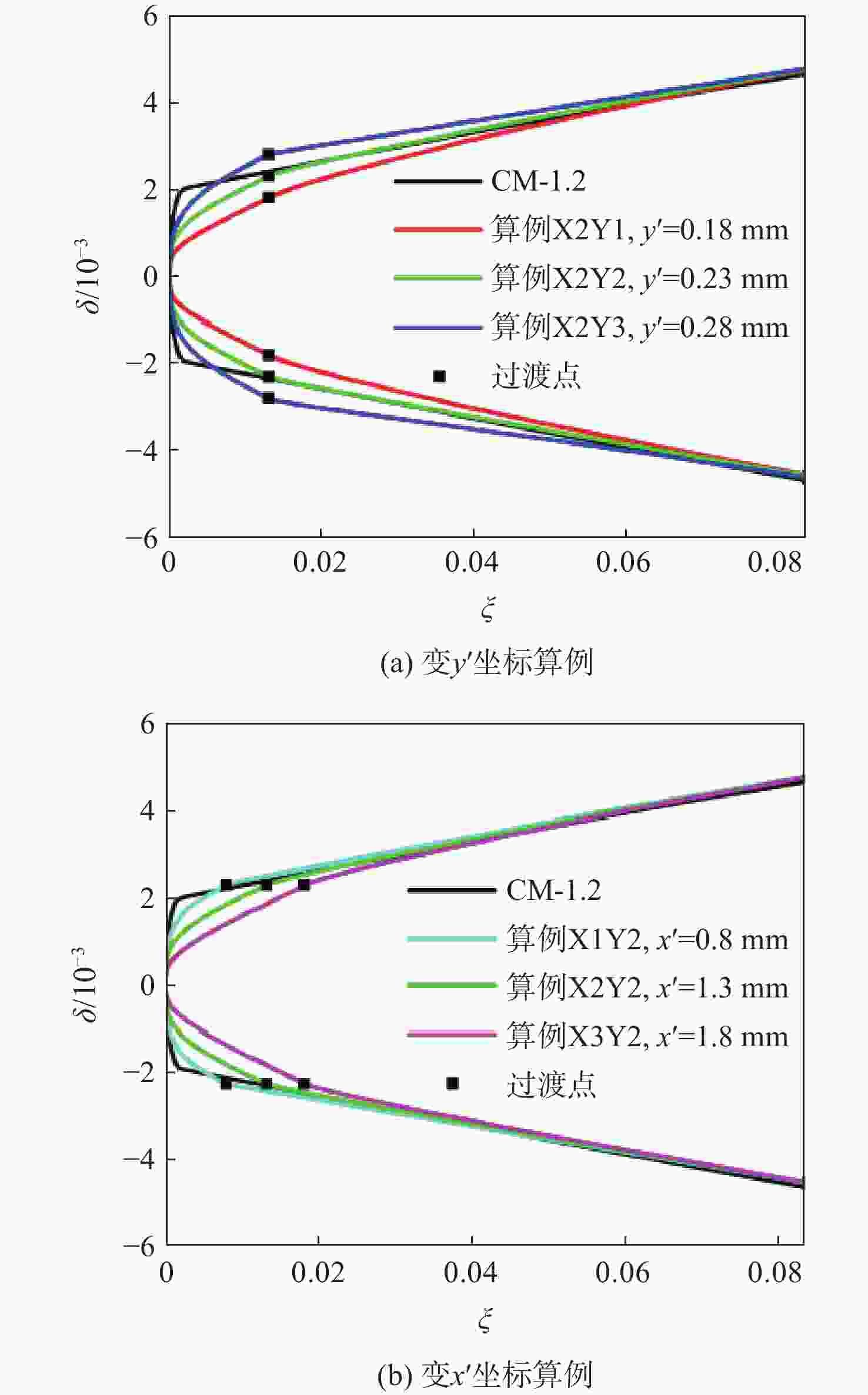
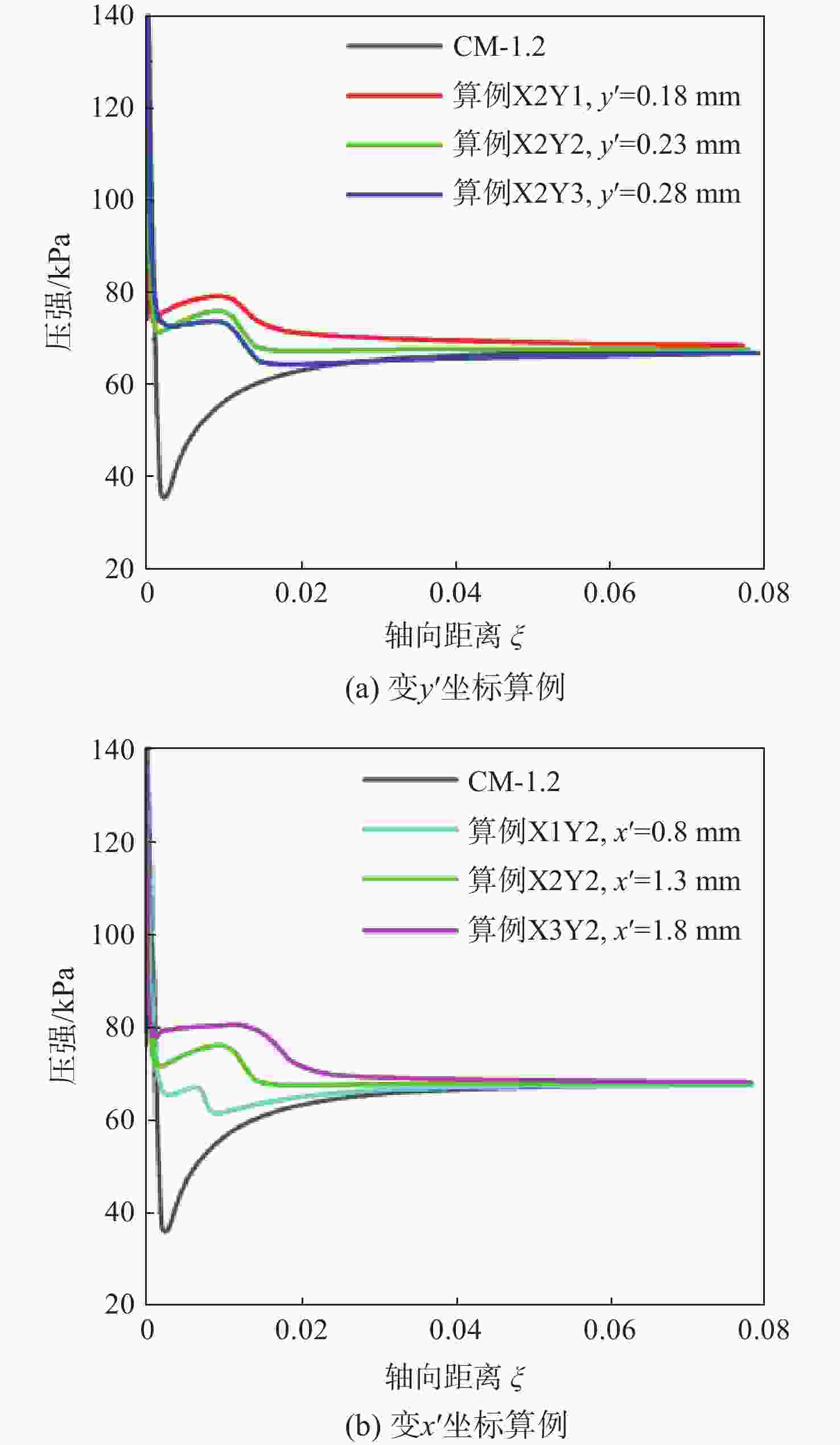
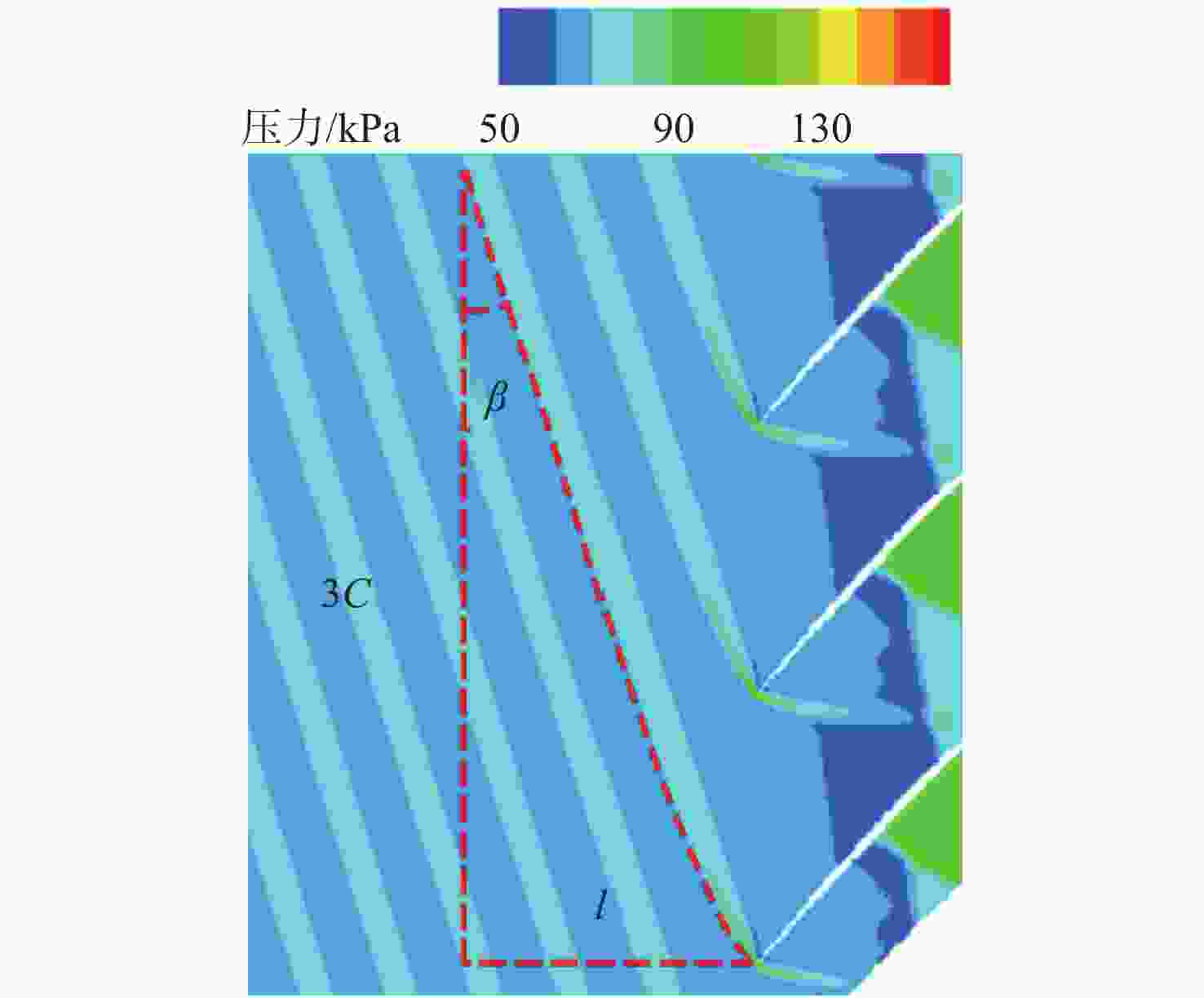
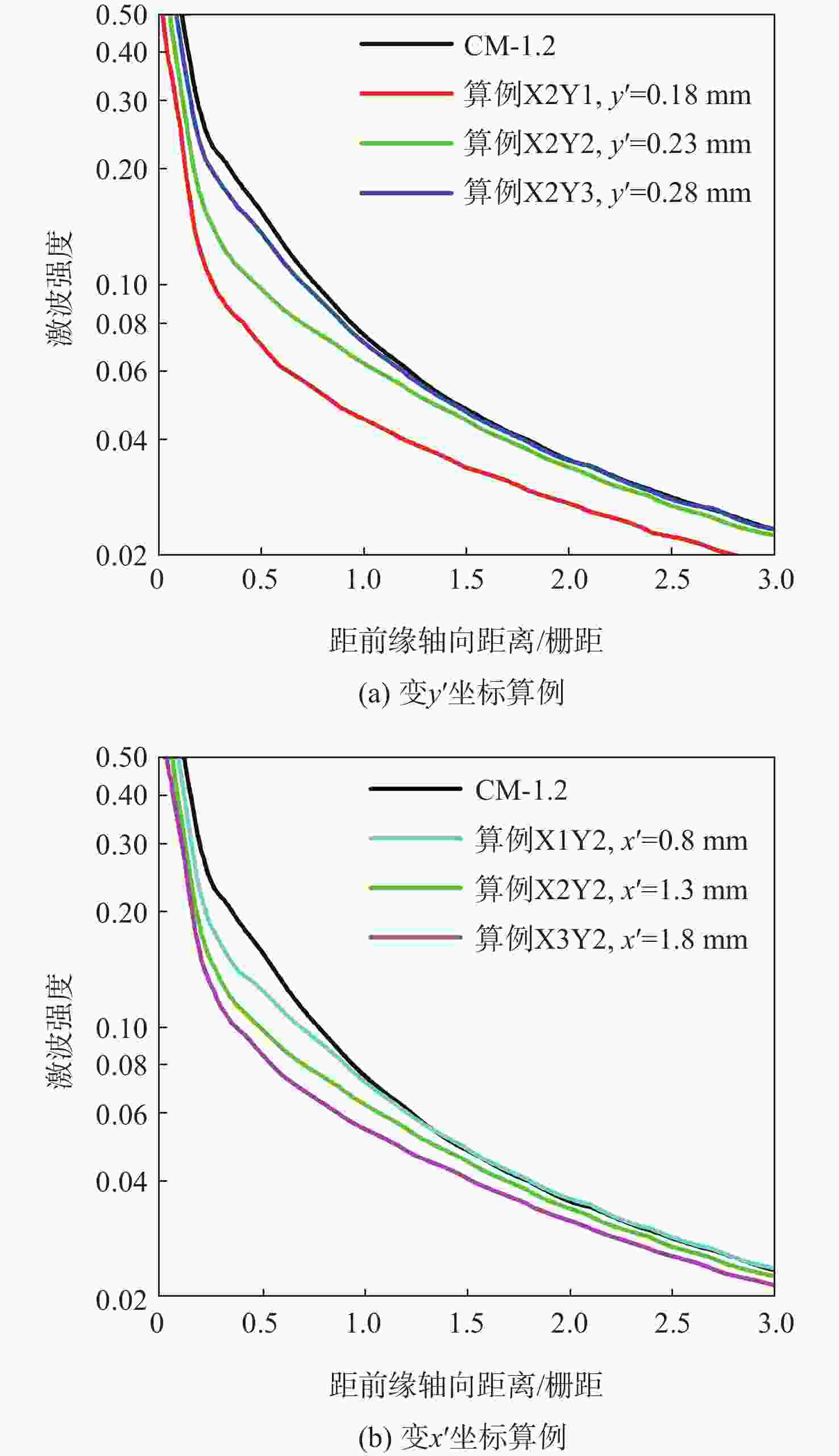
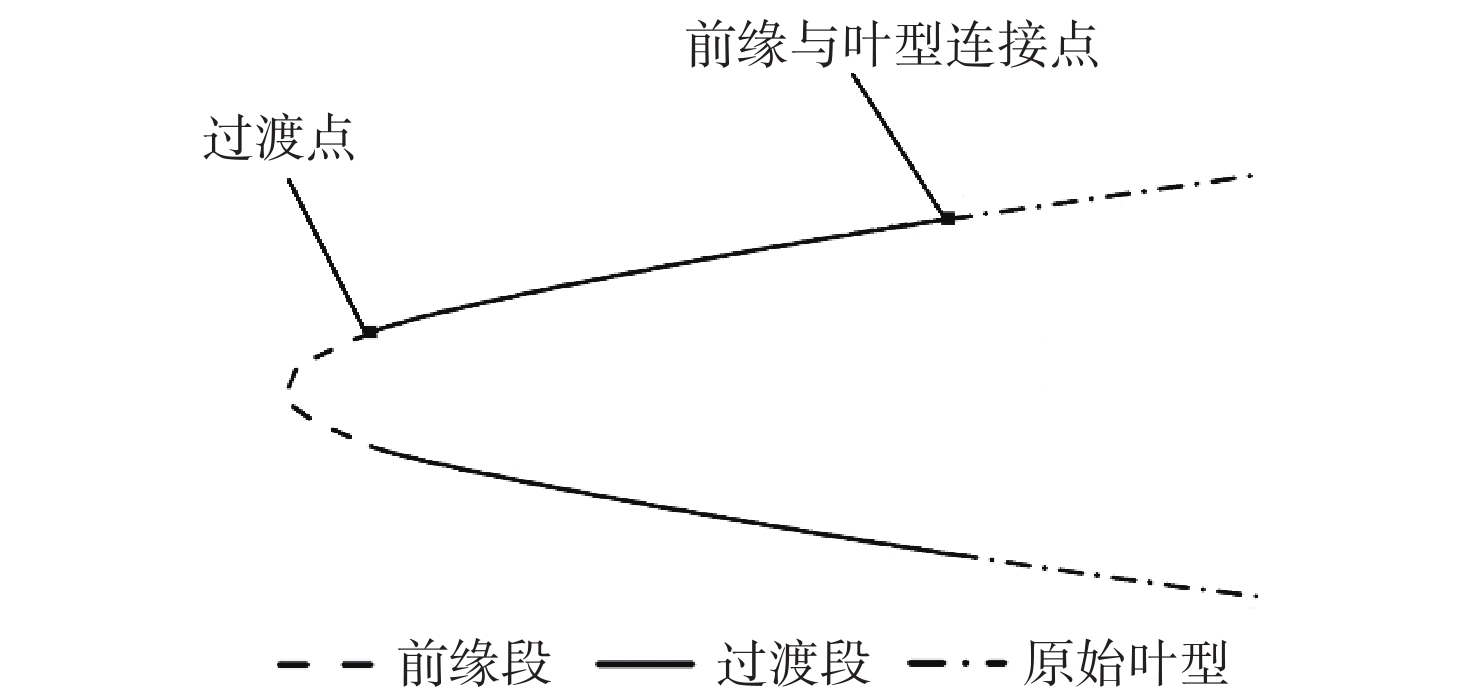
激波噪声是大涵道比涡扇发动机噪声的主要来源。为降低风扇/压气机叶片叶尖产生的激波噪声,对轴向亚音、相对超音的基元级叶型前缘脱体激波系进行研究。基于几何Hermit差值法(GHI)思想,提出一种3段式贝塞尔(Bezier)曲线构造曲率连续前缘叶型的方法,在完成改型设计时拥有更高的自由度。通过改变前缘上3段Bezier曲线间过渡点位置,探究局部曲率优化、整体曲率优化及带厚度补偿的改型方式对前缘处外伸激波强度和激波噪声的影响。通过对比研究不同数值模拟,结果表明:曲率连续前缘设计能减小叶型前缘处过膨胀区大小,减小由此产生的逆压梯度;局部曲率优化和整体曲率优化的方式能够分别在距前缘1倍弦长处降低噪声1.6 dB和4.6 dB。
Abstract:Buzz-saw noise generated by fan/compressor blade tips is one of the main noise sources in high bypass ratio Turbofan engine. To reduce the noise, the detached shock-wave system at the blade leading edge of a relative supersonic and subsonic axial two-dimensional cascade is studied. First, based on the geometric hermit interpolation (GHI) method, a three-segment Bezier curve was proposed to construct a continuous-curvature leading edge, which has higher degree of freedom in modification design. Next, by changing the position of the transition points between the three Bezier curves on the leading edge, the effects of local curvature optimization, overall curvature optimization, and optimization with extra thickness upon the strength of the shock-wave and noise level at the leading edge were explored. A comparison of numerical results showed that the continuous curvature design could decrease the size of the over expanded zone at the leading edge of the blade, thus reducing the reverse pressure gradient. Through local curvature optimization and overall curvature optimization, noise level at one chord length upstream from the leading edge could be lowered by 1.6 dB and 4.6 dB.
-
表 1 算例过渡点坐标数据
Table 1. Example of transition points coordinate data
算例名 x′/mm y′/mm 算例X2Y1 1.3 0.18 算例X2Y2 1.3 0.23 算例X2Y3 1.3 0.28 算例X1Y2 0.8 0.23 算例X2Y2 1.3 0.23 算例X3Y2 1.8 0.23 表 2 激波角及真实马赫数数据
Table 2. Shock-wave angle and real mach number
算例名 x′/mm y′/mm 激波角/(°) 真实马赫数 CM-1.2 19.5 1.2035 算例X2Y1 1.3 0.18 17.5 1.2082 算例X2Y2 1.3 0.23 18.5 1.2068 算例X2Y3 1.3 0.28 18.8 1.2056 算例X1Y2 0.8 0.23 19.0 1.2059 算例X2Y2 1.3 0.23 18.5 1.2068 算例X3Y2 1.8 0.23 18.0 1.2074 表 3 降噪效果
Table 3. Noise reduction
算例名 x′/mm y′/mm 降噪效果/dB 算例X2Y1 1.3 0.18 1.63 算例X2Y2 1.3 0.23 0.25 算例X2Y3 1.3 0.28 0 算例X1Y2 0.8 0.23 −0.1 算例X3Y2 1.8 0.23 0.70 -
[1] 梁春华, 孙广华. 商用飞机发动机先进降噪技术[J]. 航空科学技术, 2011, 22(4): 48-52. doi: 10.3969/j.issn.1007-5453.2011.04.015LIANG C H, SUN G H. Advanced noise reduction technology for large commercial aircraft engines[J]. Aeronautical Science & Technology, 2011, 22(4): 48-52(in Chinese). doi: 10.3969/j.issn.1007-5453.2011.04.015 [2] International Civil Aviation Organization. AN16-1 Environmental protection: Volume I: Aircraft noise ANN-00016-001-01[S]. Quebec: International Civil Aviation Organization, 2017: 1-250 [3] ELDREDGE J D. On the interaction of higher duct modes with a perforated liner system with bias flow[J]. Journal of Fluid Mechanics, 2004, 510: 303-331. doi: 10.1017/S0022112004009504 [4] FITE E B. Aerodynamic performance measurements for a forward swept low noise fan: NASA/TM-2006-214413[R]. Washington D. C.: National Aeronautics and Space Administration, 2006. [5] 周振华. 前缘形状对风扇/压气机激波噪声的影响[D]. 北京: 北京航空航天大学, 2015: 1-72ZHOU Z H. Influence of leading edge shape on shock noise of fan/compressor[D]. Beijing: Beihang University, 2015: 1-72(in Chinese). [6] 葛健. 风扇激波噪声的降噪研究[D]. 北京: 北京航空航天大学, 2017: 1-83.GE J. Research on noise reduction of fan shock wave noise[D]. Beijing: Beihang University, 2017: 1-83(in Chinese). [7] 葛健, 柳阳威, 周振华, 等. 吸力面波系分布对风扇激波噪声的影响[J]. 工程热物理学报, 2018, 39(11): 2389-2397.GE J, LIU Y W, ZHOU Z H, et al. The influence of wave system on the suction surface on the buzz-saw noise of turbofan[J]. Journal of Engineering Thermophysics, 2018, 39(11): 2389-2397(in Chinese). [8] 陆宏志, 徐力平. 压气机叶片的带平台圆弧形前缘[J]. 推进技术, 2003, 24(6): 532-536. doi: 10.3321/j.issn:1001-4055.2003.06.014LU H Z, XU L P. Circular leading edge with a flat for compressor blades[J]. Journal of Propulsion Technology, 2003, 24(6): 532-536(in Chinese). doi: 10.3321/j.issn:1001-4055.2003.06.014 [9] 靳军, 刘波, 南向谊, 等. 超声速叶型前缘几何形状对叶栅气动性能的影响[J]. 航空动力学报, 2007, 22(4): 660-665. doi: 10.3969/j.issn.1000-8055.2007.04.022JIN J, LIU B, NAN X Y, et al. Influence effect of supersonic airfoil’s leading edge geometric shape on aero-dynamical performance of cascade[J]. Journal of Aerospace Power, 2007, 22(4): 660-665(in Chinese). doi: 10.3969/j.issn.1000-8055.2007.04.022 [10] 宋寅, 顾春伟. 曲率连续的压气机叶片前缘设计方法[J]. 推进技术, 2013, 34(11): 1474-1481.SONG Y, GU C W. Continuous curvature leading edge of compressor blading[J]. Journal of Propulsion Technology, 2013, 34(11): 1474-1481(in Chinese). [11] 宋寅, 顾春伟. 叶片前缘形状对压气机气动性能的影响[J]. 工程热物理学报, 2013, 34(6): 1051-1054.SONG Y, GU C W. Effect of leading edge shape on the aerodynamic performance of compressor[J]. Journal of Engineering Thermophysics, 2013, 34(6): 1051-1054(in Chinese). [12] 刘宝杰, 袁春香, 于贤君. 前缘形状对可控扩散叶型性能影响[J]. 推进技术, 2013, 34(7): 890-897.LIU B J, YUAN C X, YU X J. Effects of leading-edge geometry on aerodynamic performance in controlled diffusion airfoil[J]. Journal of Propulsion Technology, 2013, 34(7): 890-897(in Chinese). [13] 杨炯, 宁涛, 席平. 前缘点曲率可控的曲率连续前缘几何设计[J]. 计算机辅助设计与图形学学报, 2016, 28(7): 1195-1200. doi: 10.3969/j.issn.1003-9775.2016.07.021YANG J, NING T, XI P. Geometric design of leading edge with specified curvature at leading edge point[J]. Journal of Computer-Aided Design & Computer Graphics, 2016, 28(7): 1195-1200(in Chinese). doi: 10.3969/j.issn.1003-9775.2016.07.021 [14] 施恒涛, 刘宝杰, 于贤君. 基于多项式的曲率连续前缘造型方法及应用[J]. 航空动力学报, 2020, 35(2): 397-409.SHI H T, LIU B J, YU X J. Polynomial-based continuous-curvature leading edge design method and its application[J]. Journal of Aerospace Power, 2020, 35(2): 397-409(in Chinese). [15] PRASAD D, FENG J Z. Propagation and decay of shock waves in turbofan engine inlets[J]. Journal of Turbomachinery, 2005, 127(1): 118-127. doi: 10.1115/1.1811102 [16] HAN F, SHARMA A, PALIATH U, et al. Multiple pure tone noise prediction[J]. Journal of Sound and Vibration, 2014, 333(25): 6942-6959. doi: 10.1016/j.jsv.2014.08.006 [17] LEWY S, POLACSEK C, BARRIER R. Analytical and numerical prediction of harmonic sound power in the inlet of aero-engines with emphasis on transonic rotation speeds[J]. Journal of Sound and Vibration, 2014, 333(26): 7165-7182. doi: 10.1016/j.jsv.2014.06.013 [18] MOECKEL W E. Approximate method for predicting from and location of detached shock waves ahead of plane or axially symmetric bodies: NACA-TN-1921 [R]. Washington D. C.: National Aeronautics and Space Administration, 1949. [19] DE BOOR C, HÖLLIG K, SABIN M. High accuracy geometric Hermite interpolation[J]. Computer Aided Geometric Design, 1987, 4(4): 269-278. doi: 10.1016/0167-8396(87)90002-1 [20] 徐良宏, 孟勇, 陈铁. 给定两端点及端点处切方向和曲率的空间Bezier曲线的插值问题[J]. 数值计算与计算机应用, 2001, 22(2): 81-86. doi: 10.3969/j.issn.1000-3266.2001.02.001XU L H, MENG Y, CHEN T. Space curve interpolation of given end points tangent directions and curvatures[J]. Journal of Unmerical Methods and Computer Applications, 2001, 22(2): 81-86(in Chinese). doi: 10.3969/j.issn.1000-3266.2001.02.001 [21] 邱名. 高级压比轴流压气机转子通道内激波组织研究[D]. 南京: 南京航空航天大学, 2014: 186-188.QIU M. Investigation of shock organization in axial compressor passages of high pressure ratio[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2014: 186-188(in Chinese). [22] PRASAD A. Evolution of upstream propagating shock waves from a transonic compressor rotor[J]. Journal of Turbomachinery, 2003, 125(1): 133-140. doi: 10.1115/1.1516813 [23] VAN LEER B. Towards the ultimate conservative difference scheme. V. A second-order sequel to Godunov’s method[J]. Journal of Computational Physics, 1979, 32(1): 101-136. doi: 10.1016/0021-9991(79)90145-1 [24] MORFEY C L. The acoustics of axial flow machines[J]. Journal of Sound and Vibration, 1972, 22(4): 445-466. doi: 10.1016/0022-460X(72)90455-5 -






 下载:
下载: