-
摘要:
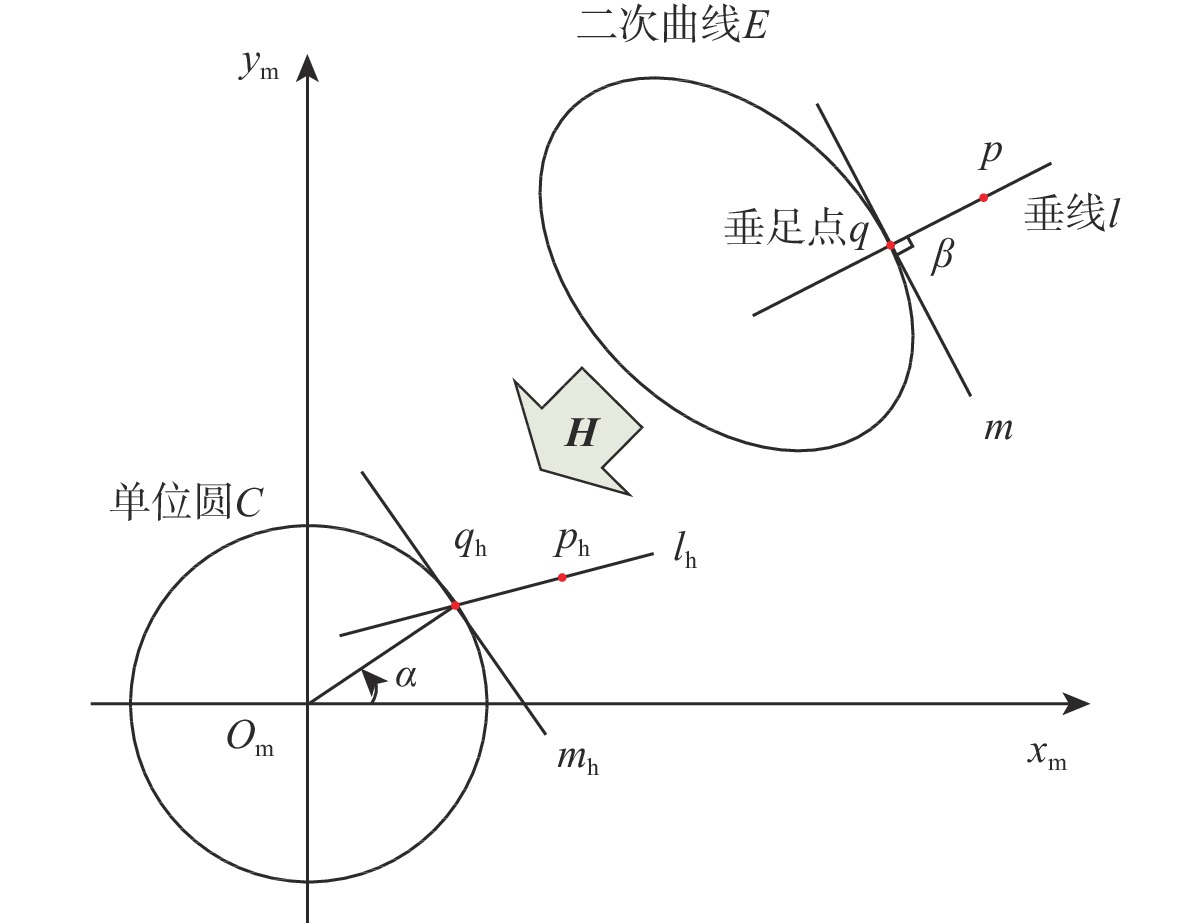
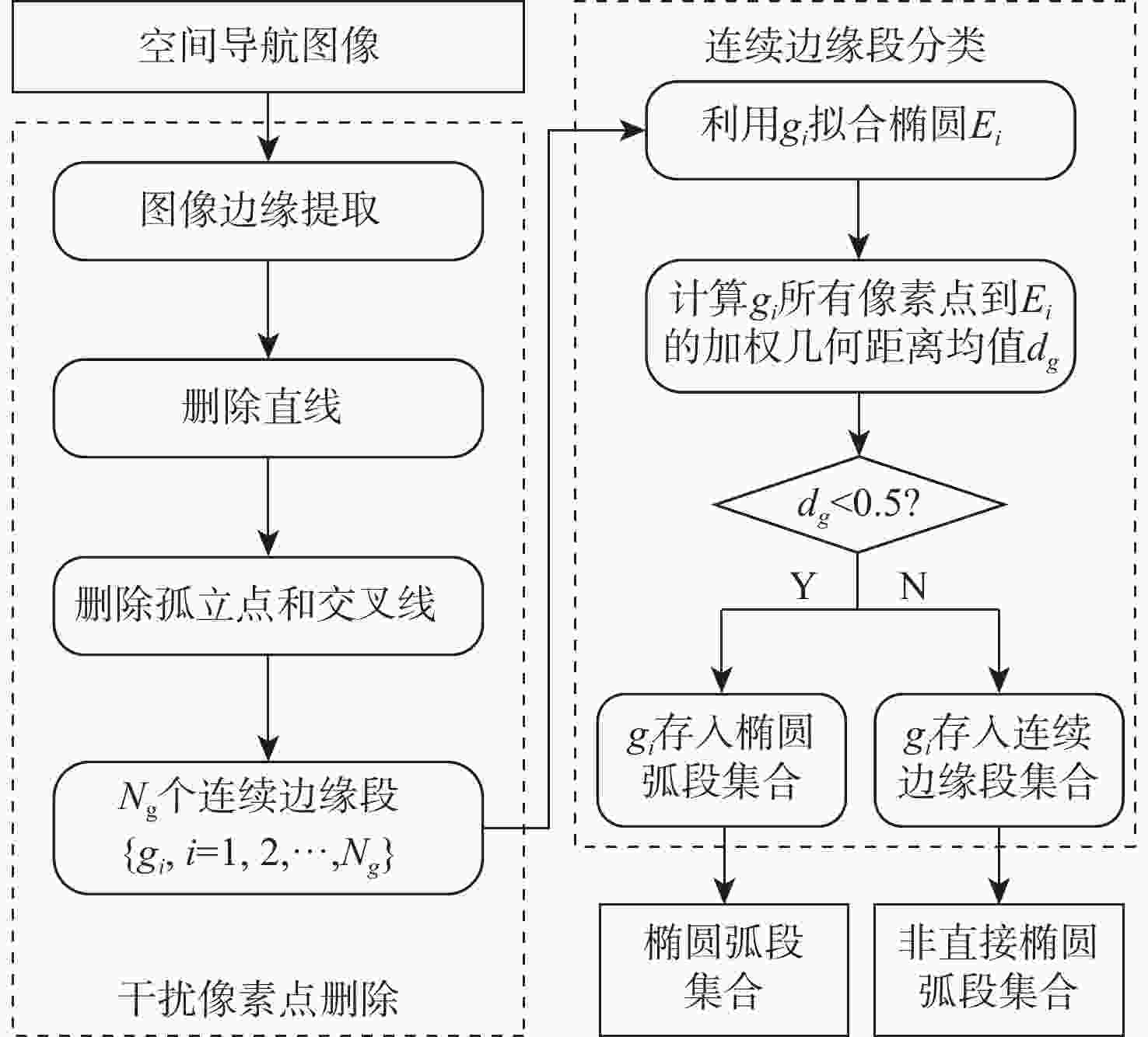
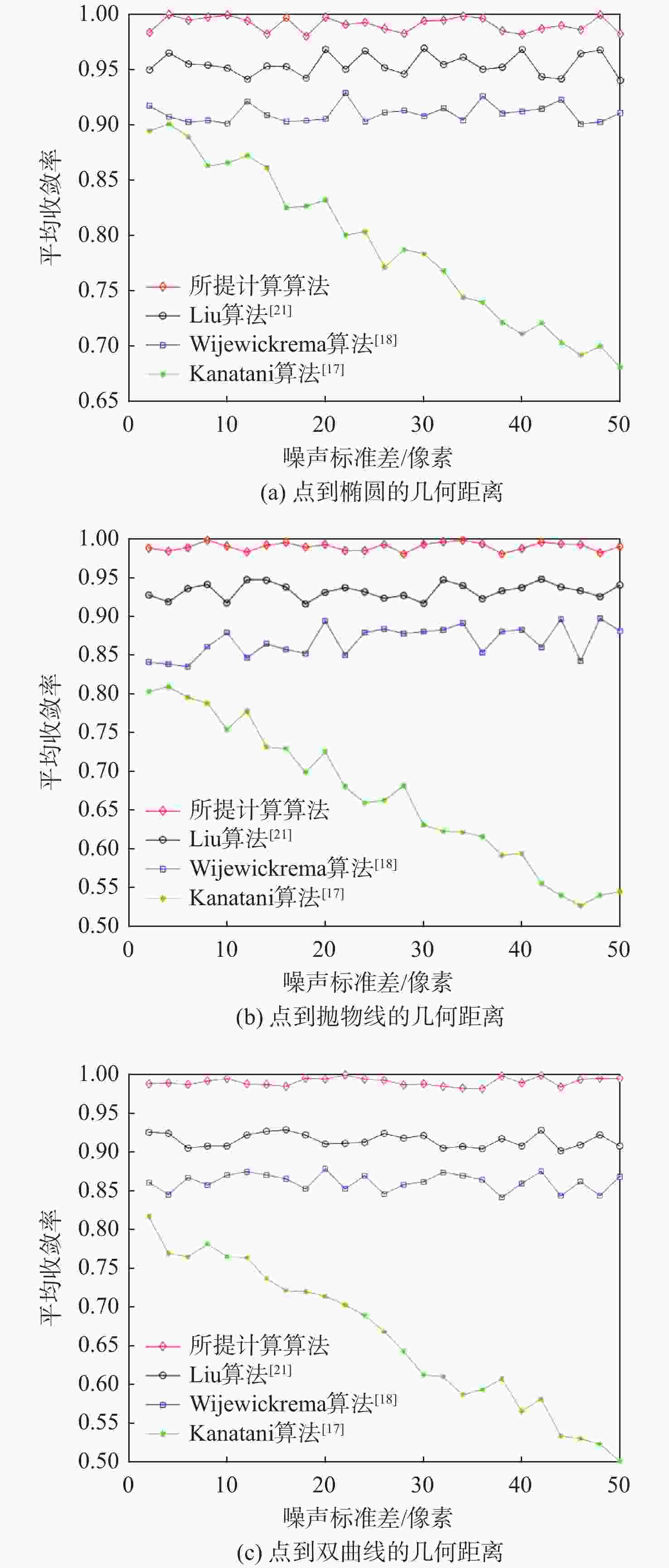
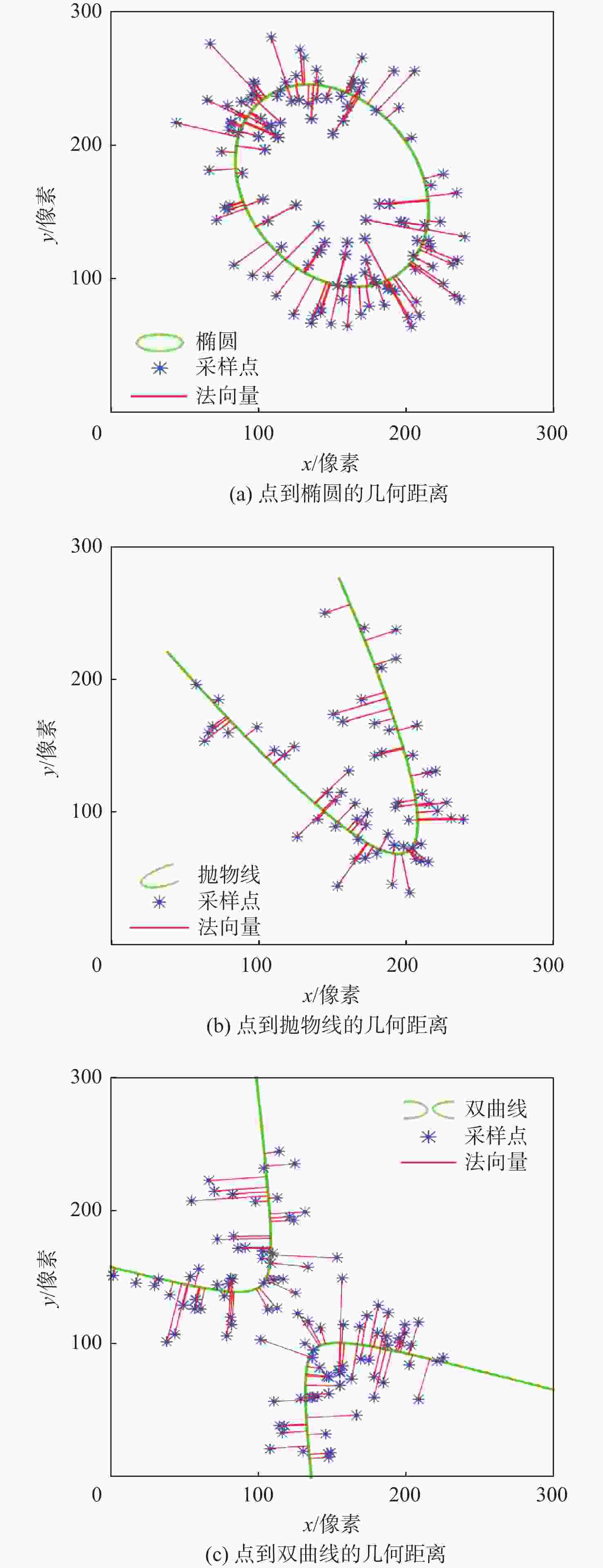
基于椭圆特征的空间飞行器视觉导航技术是一种新颖的高精度空间探测自主导航方法，如何对空间目标的环形边缘进行精准提取和高效拟合是实现空间飞行器视觉导航的必要条件。针对该问题，提出一种面向空间飞行器视觉导航的椭圆检测算法。利用多项式逼近导航图像连续边缘段的方式提取椭圆弧段；通过基于极大似然假设检验理论构建的模型选择判据，对来自同一个椭圆的椭圆弧段进行准确合并；对合并后的椭圆弧段进行拟合，得到空间飞行器视觉导航的椭圆检测结果。大量的仿真实验表明：与传统的椭圆检测算法相比，所提算法具有较高的精度和更高的鲁棒性，可以广泛应用于空间飞行器视觉导航图像椭圆检测，为空间飞行器视觉导航算法提供精准的二次曲线输入。
Abstract:The ellipse-based optical navigation technology has become a novel and precise autonomous navigation method. Therefore, how to fit the elliptic edge of the space object is the essential condition of the optical navigation method. We propose an ellipse detection algorithm for the spacecraft optical navigation in this paper. First, the elliptic curves are extracted by utilizing the polygonal curve to approximate the edge in edge map of the navigation image. Second, the elliptic curves are merged accurately by a model selection criterion derived from the maximal likelihood ratio hypothesis test. Finally, the ellipses in the navigation image are detected by fitting the merged elliptic curves. The experimental results demonstrate that the proposed algorithm can detect ellipses with higher accuracy and robustness than the traditional ellipse detection methods, and can be applied in the ellipse detection for the spacecraft optical navigation method to provide the precise curves as the inputs.
-
Key words:
- space objects /
- elliptic edge /
- ellipse fitting /
- ellipse detection /
- optical navigation
-
图 2 点到二次曲线几何距离计算示意图
Figure 2. Schematic diagram of calculating geometrical distance from point to conic
图 3 空间导航图像预处理算法基本流程
Figure 3. Basic flowchart of spacecraft navigation image pre-processing algorithm
图 5 椭圆弧段合并必要条件示意图
Figure 5. Examples of necessary condition of elliptic curves mergence
图 6 基于极大似然假设检验的椭圆弧段合并的模型
Figure 6. Mergence models of elliptic curves based on maximum likelihood ratio test
图 7 四种点到二次曲线几何距离计算算法平均计算时间
Figure 7. Mean calculation time of four geometric distance calculation algorithms from point to curve
图 8 四种点到二次曲线几何距离计算算法平均收敛率
Figure 8. Mean rate of convergence of four geometric distance calculation algorithms
图 9 本文几何距离计算算法的典型计算结果
Figure 9. Typical calculation results of the proposed geometric distance algorithms
图 13 交叉椭圆数据集上椭圆检测结果图例
Figure 13. Examples of ellipse detection results on crossing ellipse dataset
图 15 交叠椭圆数据集上椭圆检测结果图例
Figure 15. Examples of ellipse detection results on occluded ellipse dataset
图 16 椒盐噪声椭圆数据集中椭圆示例
Figure 16. Instances of ellipses in ellipse dataset with impulsive noise
图 17 椒盐噪声数据集上椭圆检测结果图例
Figure 17. Examples of ellipse detection results on ellipse dataset with impulsive noise
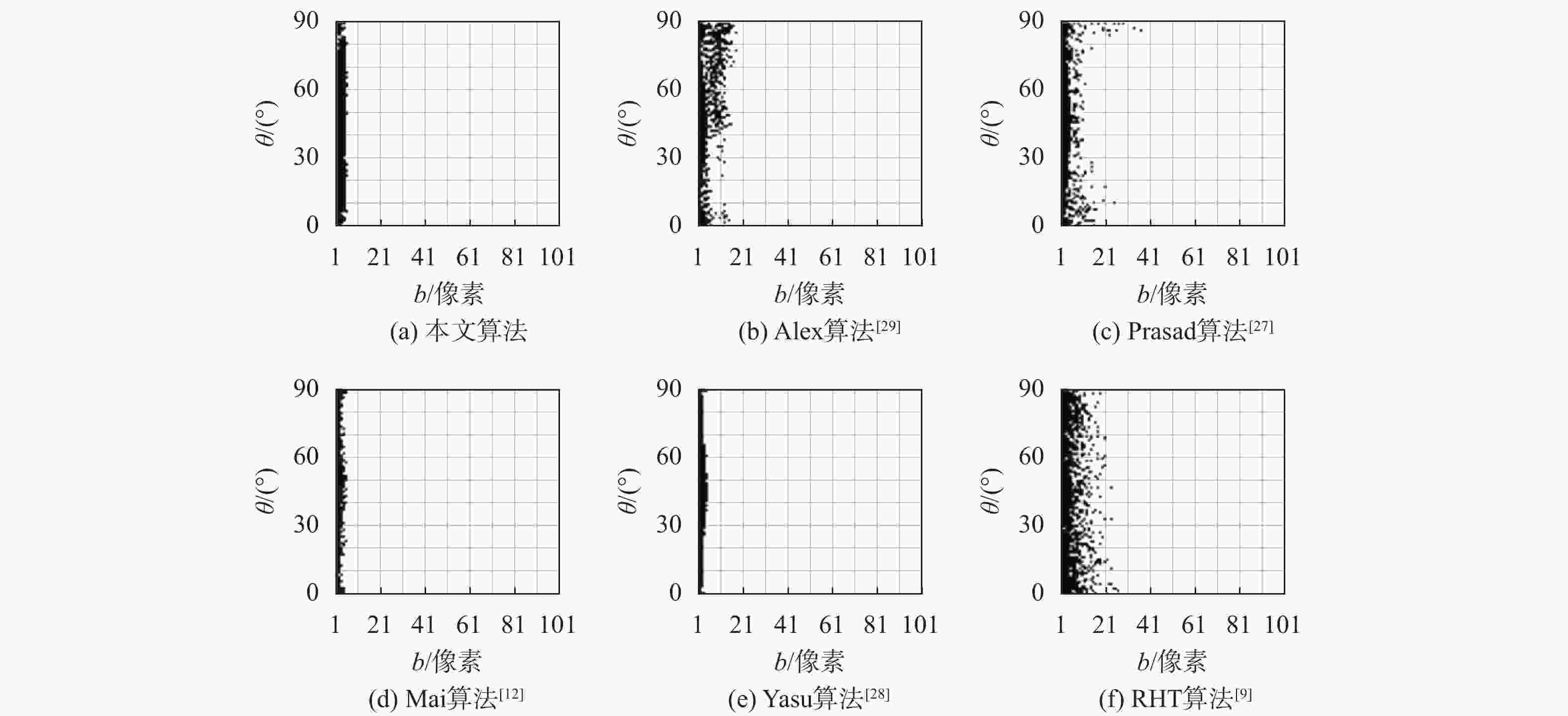
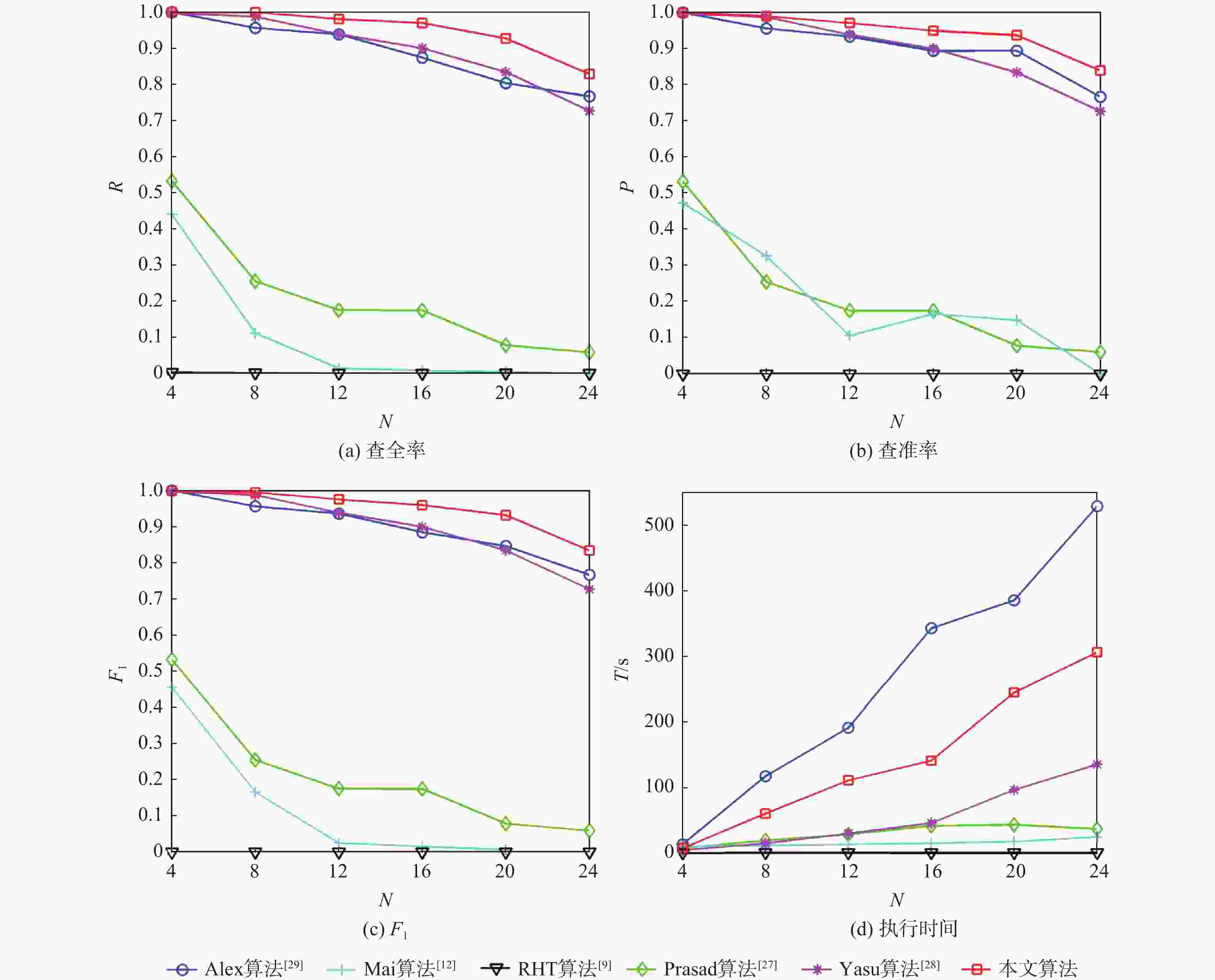
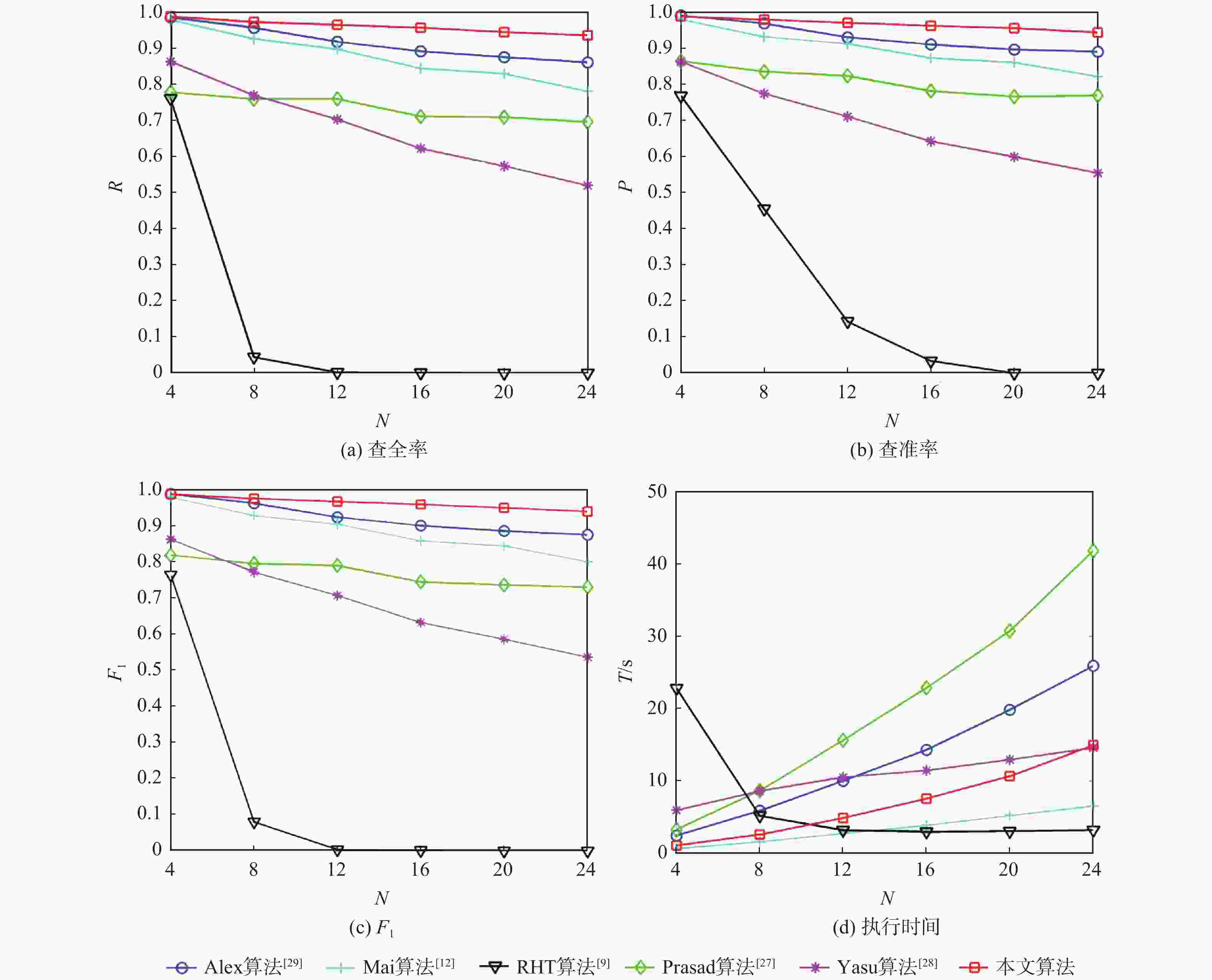
表 1 椭圆检测算法对几何参数鲁棒性测试数据集
Table 1. Dataset testing robustness of ellipse detection algorithm to geometric parameters
数据集 图像数量 图像尺寸/像素 半长轴a/像素 半短轴b/像素 长短轴之比a/b 旋转角θ/(°) 数据集1 9100 400×400 100 区间[1,100]，步长为1 不需设定，由a和b确定 区间[0,90]，步长为1 数据集2 10000 400×400 区间[1,100]，步长为1 不需设定，由a和a/b确定 [0.01,1]，步长为0.01 60 
下载: 导出CSV
-
[1] LIU C, HU W. Relative pose estimation for cylinder-shaped spacecrafts using single image[J]. IEEE Transactions on Aerospace and Electronic Systems, 2014, 50(4): 3036-3056. doi: 10.1109/TAES.2014.120757 [2] LU T, HU W, LIU C, et al. Relative pose estimation of a lander using crater detection and matching[J]. Optical Engineering, 2016, 55(2): 023102. doi: 10.1117/1.OE.55.2.023102 [3] SU S, LUO Y, YANG K, et al. A novel camera calibration method based on multilevel-edge-fitting ellipse-shaped analytical model[J]. IEEE Sensors Journal, 2020, 20(11): 5818-5826. doi: 10.1109/JSEN.2020.2972615 [4] 梁琼, 赵慧民, 葛任贤, 等. 基于椭圆拟合的改进Hough变换算法在眼控系统中的应用研究[J]. 广东技术师范大学学报, 2020, 41(3): 9-15. doi: 10.3969/j.issn.1672-402X.2020.06.003LIANG Q, ZHAO H M, GE R X, et al. Application of improved Hough transform algorithm based on ellipse fitting in eye-control system[J]. Journal of Guangdong Polytechnic Normal University, 2020, 41(3): 9-15(in Chinese). doi: 10.3969/j.issn.1672-402X.2020.06.003 [5] 李迎松, 郑顺义, 夏远鑫, 等. 自然环境下圆形禁令交通标志检测[J]. 武汉大学学报(信息科学版), 2016, 41(12): 1619-1625.LI Y S, ZHENG S Y, XIA Y X, et al. Detection of round ban traffic signs in natural environment[J]. Geomatics and Information Science of Wuhan University, 2016, 41(12): 1619-1625(in Chinese). [6] 段志达, 魏利胜, 刘小珲, 等. 基于Hough变换圆检测和边缘模板匹配的轴承缺陷检测与定位[J]. 安徽工程大学学报, 2020, 35(4): 60-68. doi: 10.3969/j.issn.2095-0977.2020.04.007DUAN Z D, WEI L S, LIU X H, et al. Bearing defect detection and location based on Hough transform circle detection and edge template matching[J]. Journal of Anhui Polytechnic University, 2020, 35(4): 60-68(in Chinese). doi: 10.3969/j.issn.2095-0977.2020.04.007 [7] DUAD R O. Use of the Hough transformation to detect lines and curves in pictures[J]. Communications of the ACM, 1972, 15(1): 11-15. [8] MUKHOPADHYAY P, CHAUDHURI B B. A survey of Hough transform[J]. Pattern Recognition, 2015, 48(3): 993-1010. [9] MCLAUGHLIN R A. Randomized Hough transform: Improved ellipse detection with comparison[J]. Pattern Recognition Letters, 1998, 19(3-4): 299-305. doi: 10.1016/S0167-8655(98)00010-5 [10] KIRYATI N, ELDAR Y, BRUCKSTEIN A M. A probabilistic Hough transform[J]. Pattern Recognition, 1991, 24(4): 303-316. doi: 10.1016/0031-3203(91)90073-E [11] LU W, TAN J. Detection of incomplete ellipse in images with strong noise by iterative randomized Hough transform (IRHT)[J]. Pattern Recognition, 2008, 41(4): 1268-1279. doi: 10.1016/j.patcog.2007.09.006 [12] KIM E, HASEYAMA M, KITAJIMA H. Fast and robust ellipse extraction from complicated images[C]//Proceedings of the First International Conference on Information Technology and Applications. Piscataway: IEEE Press, 2002: 357-362. [13] HAHN K, JUNG S, HAN Y, et al. A new algorithm for ellipse detection by curve segments[J]. Pattern Recognition Letters, 2008, 29(13): 1836-1841. doi: 10.1016/j.patrec.2008.05.025 [14] MAI F, HUNG Y S, ZHONG H, et al. A hierarchical approach for fast and robust ellipse extraction[J]. Pattern Recognition, 2008, 41(8): 2512-2524. doi: 10.1016/j.patcog.2008.01.027 [15] LIU Z Y, QIAO H. Multiple ellipses detection in noisy environments: A hierarchical approach[J]. Pattern Recognitio, 2009, 42(11): 2421-2433. [16] NGUYEN T M, AHUJA S, WU Q, et al. A real-time ellipse detection based on edge grouping[C]//Proceedings of IEEE International Conference on Systems, Man and Cybernetics. Piscataway: IEEE Press, 2009: 3280-3286. [17] KANATANI K, SUGAYA Y. Compact algorithm for strictly ML ellipse fitting[C]//Proceedings of International Conference on Pattern Recognition. Piscataway: IEEE Press, 2009: 1-4. [18] WIJEWICKREMA S, ESSON C, PAPLINSKI A. Orthogonal distance least squares fitting: A novel approach[C]//Proceedings of International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications. Piscataway: IEEE Press, 2010: 255-268. [19] 吴福朝. 计算机视觉中的数学方法[M]. 北京: 科学出版社, 2008: 40-60.WU C F. Mathematical methods in computer vision[M]. Beijing: Science Press, 2008: 40-60(in Chinese). [20] CANN J. A computational approach to edge detection[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1986, 8(6): 679-698. [21] LIU C, HU W. Effective method for ellipse extraction and integration for spacecraft images[J]. Optical Engineering, 2013, 52(5): 057002. [22] ZHANG S C, LIU Z Q. A robust, real-time ellipse detector[J]. Pattern Recognition, 2005, 38(2): 273-287. doi: 10.1016/j.patcog.2004.03.014 [23] FITZGIBBON A, PILU M, FISHER R B. Direct least square fitting of ellipses[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1999, 21(5): 476-480. [24] IMAI H, IRI M. Polygonal approximations of a curve—Formulations and algorithms[J]. Machine Intelligence and Pattern Recognition, 1988, 6: 71-86. [25] PRASAD D K, LEUNG M K H, CHAI Q, et al. A novel framework for making dominant point detection methods non-parametric[J]. Image and Vision Computing, 2012, 30(11): 843-859. [26] KANATANI K. Statistical optimization for geometric computation: Theory and practice[M]. New York: Elsevier Science, 1996: 115-125. [27] PRASAD D K, LEUNG M K H, CHO S Y. Edge curvature and convexity based ellipse detection method[J]. Pattern Recognition, 2012, 45(9): 3204-3221. doi: 10.1016/j.patcog.2012.02.014 [28] SUGAYA Y. Ellipse detection by combining division and model selection based integration of edge points[C]//Proceedings of 4th Pacific-Rim Symposium on Image and Video Technology Image and Video Technology. Piscataway: IEEE Press, 2010: 64-69. [29] CHIA A Y, RAHARDJA S, RAJAN D, et al. A split and merge based ellipse detector with self-correcting capability[J]. IEEE Transactions on Image Processing, 2011, 20(7): 1991-2006. doi: 10.1109/TIP.2010.2099127 [30] 陆婷婷, 张尧, 阎岩, 等. 一种基于自动特征学习的陨石坑区域检测算法[J]. 北京航空航天大学学报, 2021, 47(5): 939-952.LU T T, ZHANG Y, YAN Y, et al. A crater region detection algorithm based on automatic feature learning[J]. Journal of Beijing University of Aeronautics and Astronautics, 2021, 47(5): 939-952(in Chinese). -
下载:
点击查看大图
计量
- 文章访问数: 356
- HTML全文浏览量: 68
- PDF下载量: 41
- 被引次数: 0
