-
摘要:
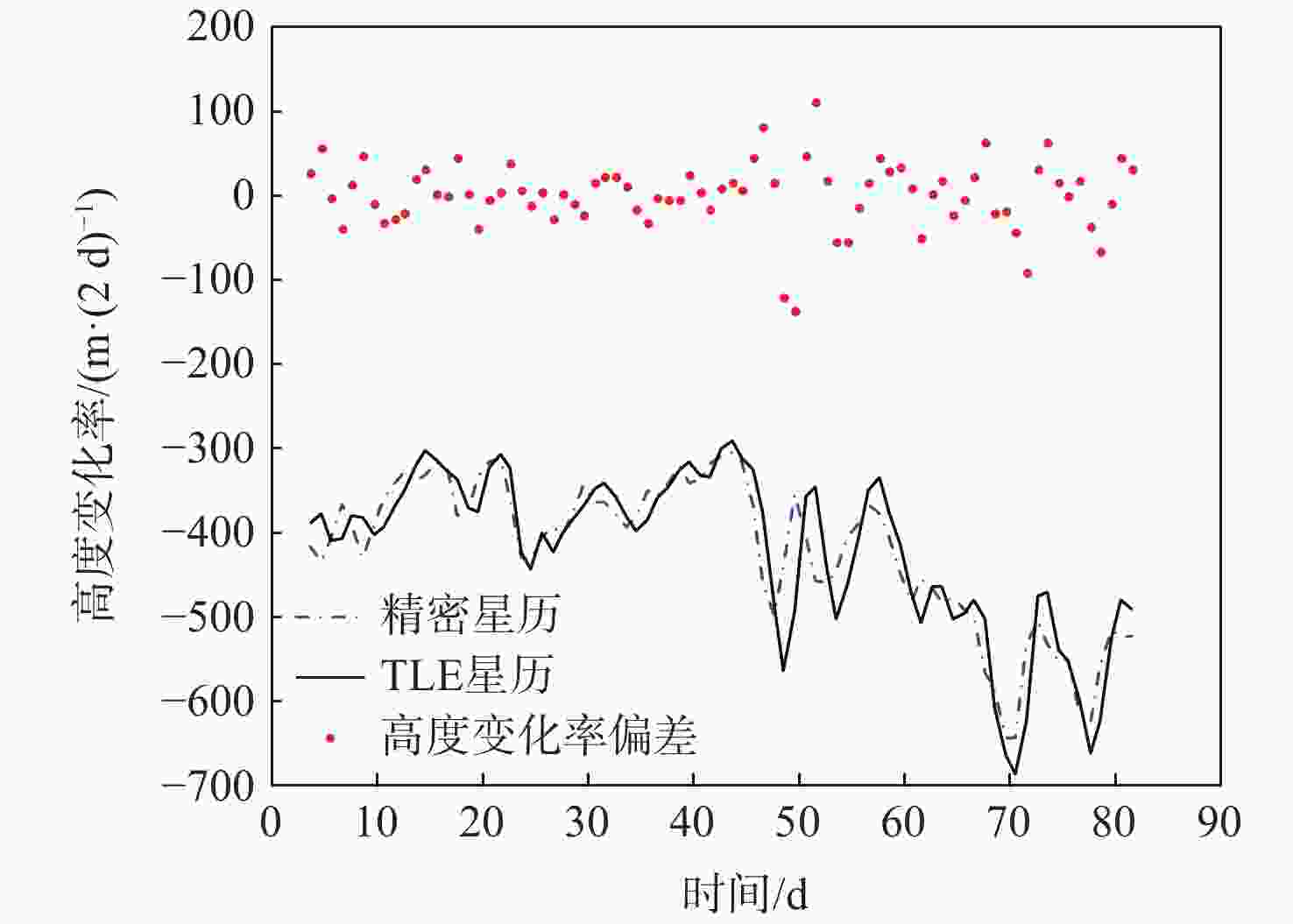
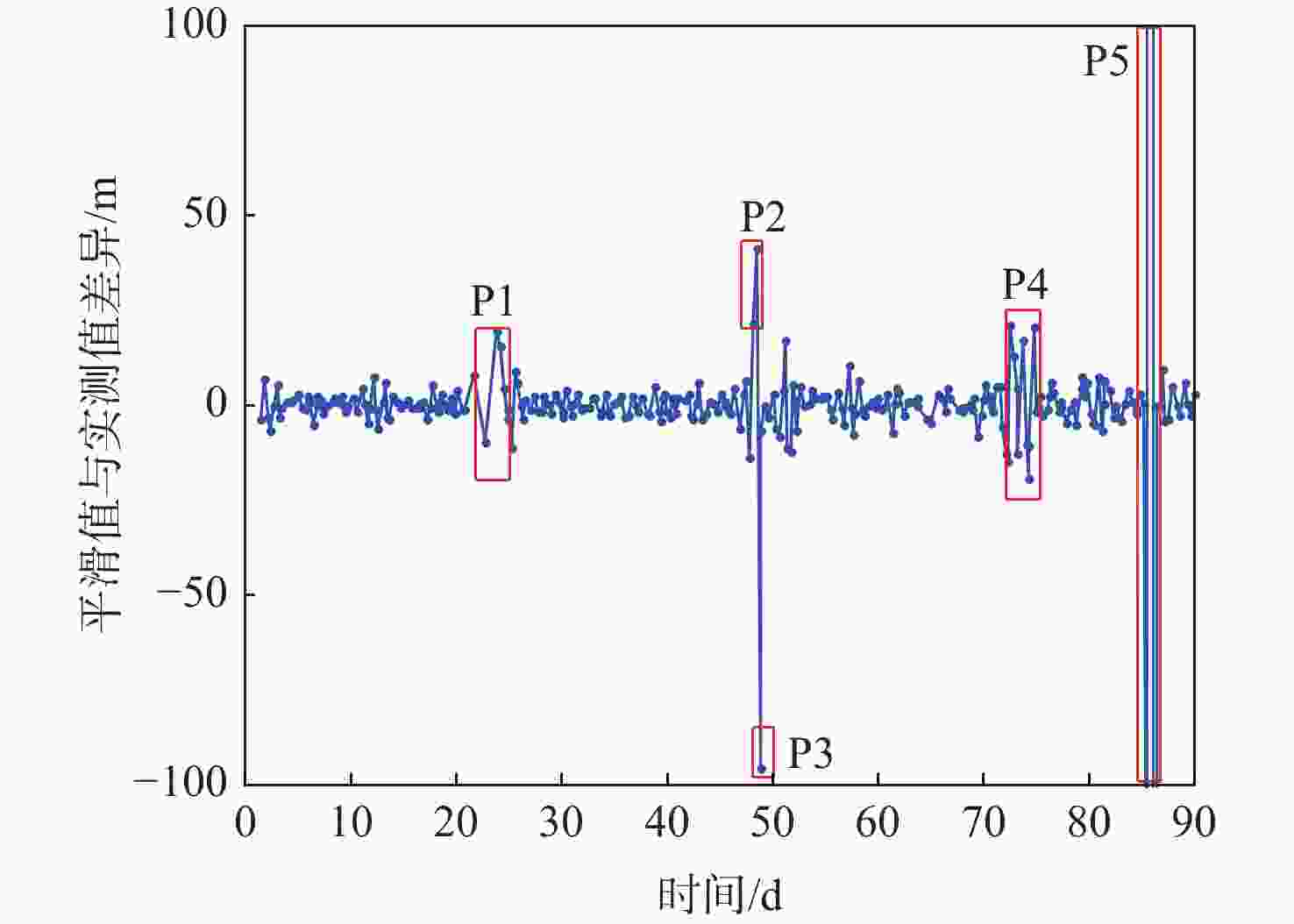
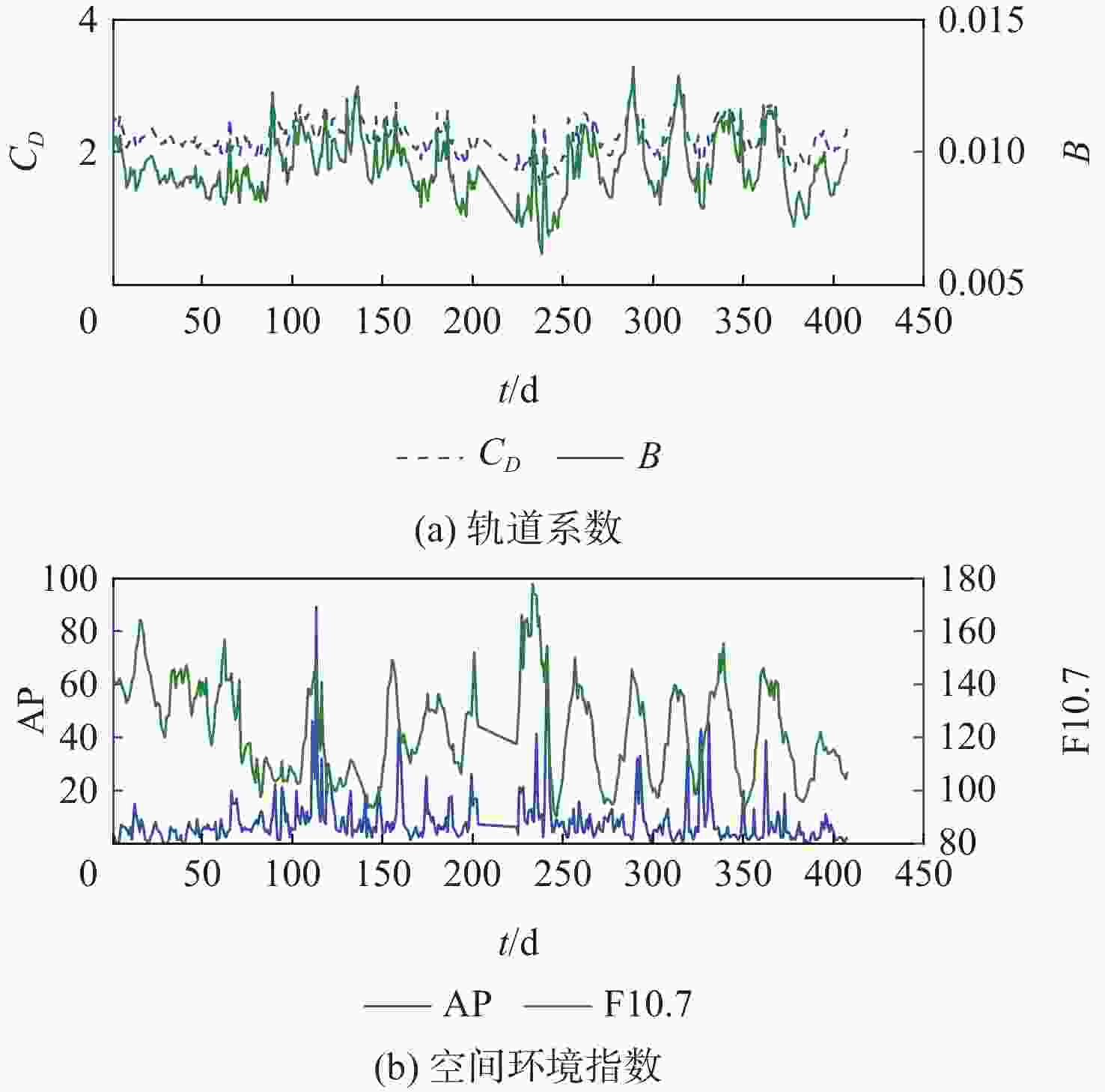
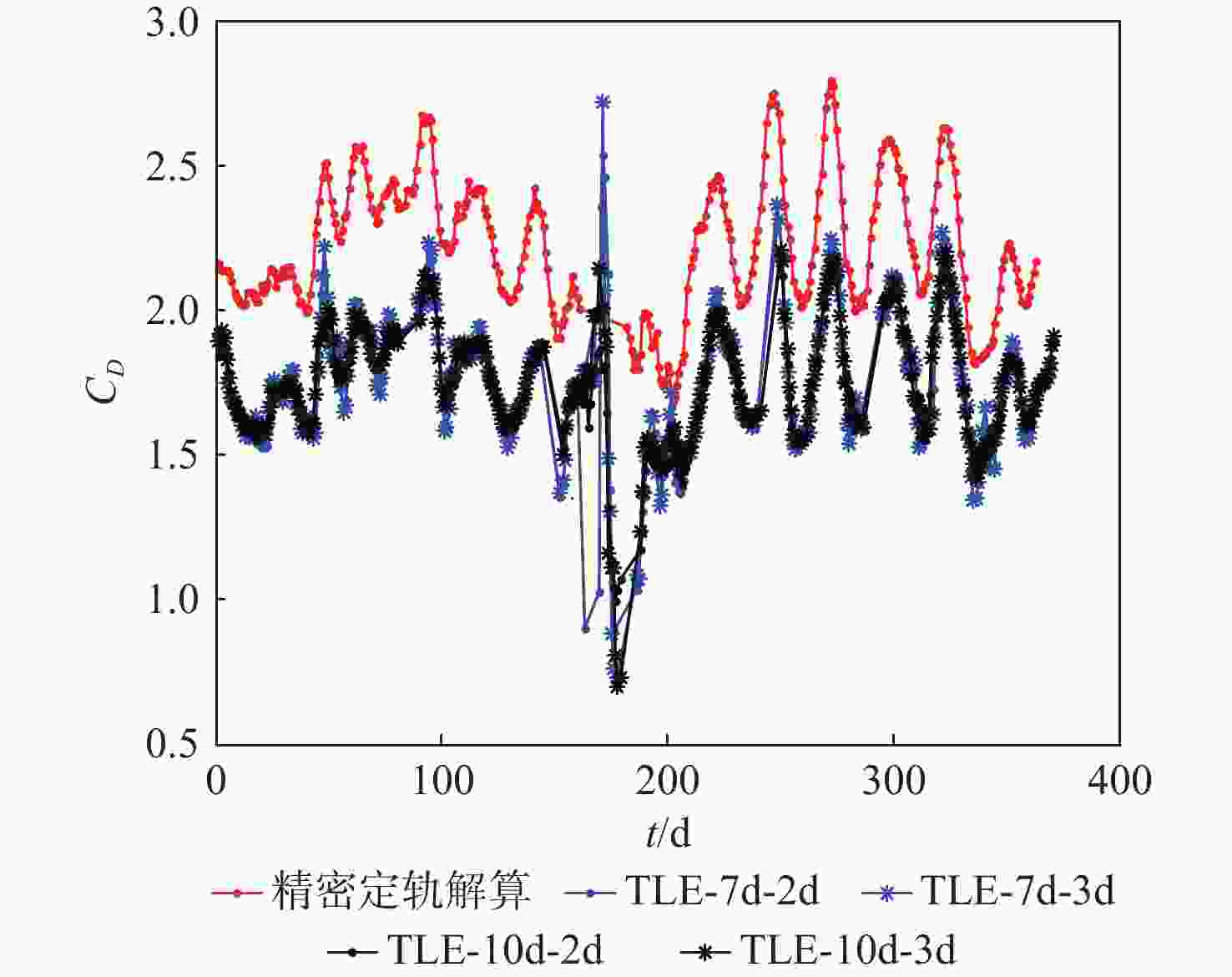
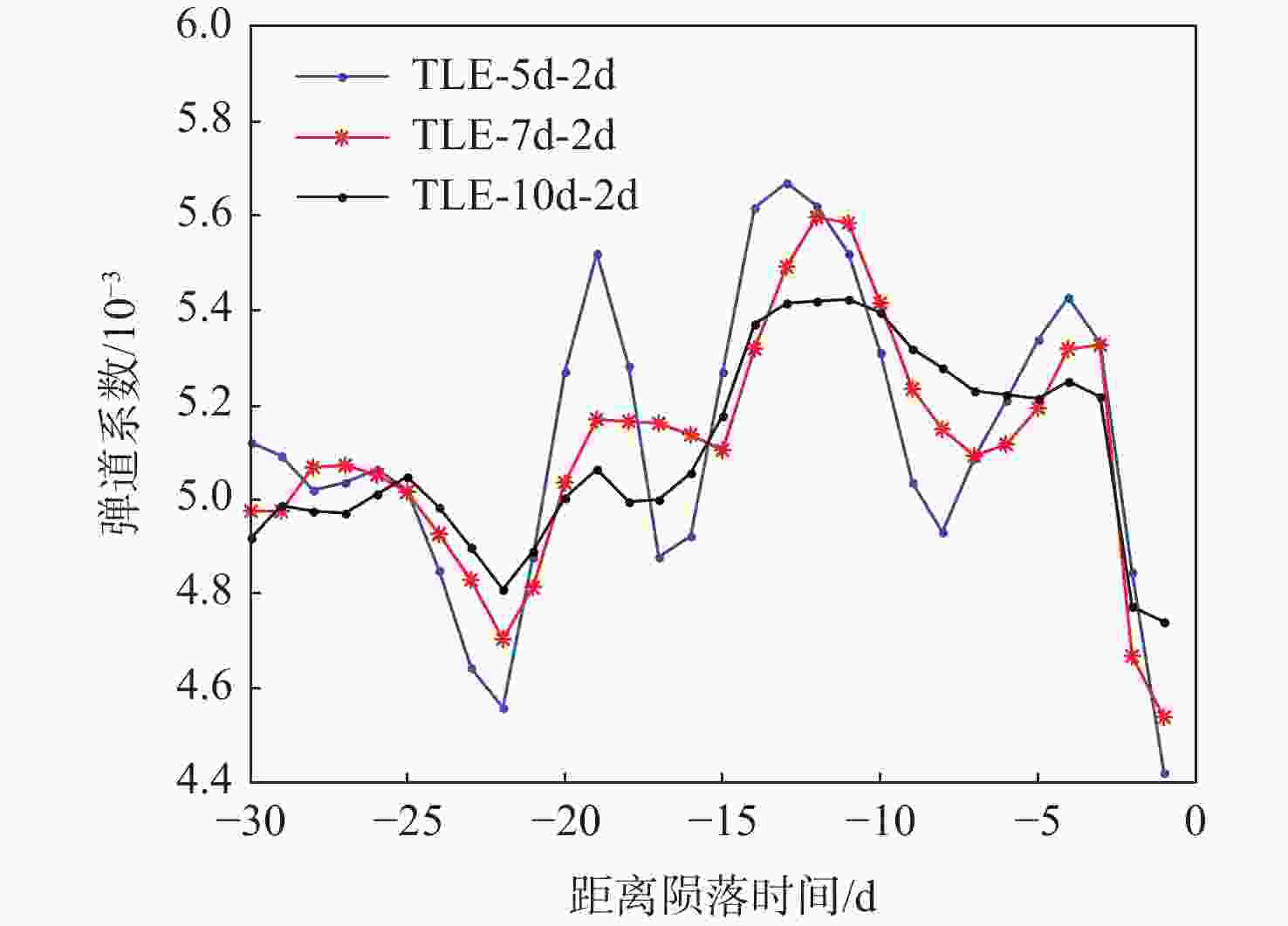
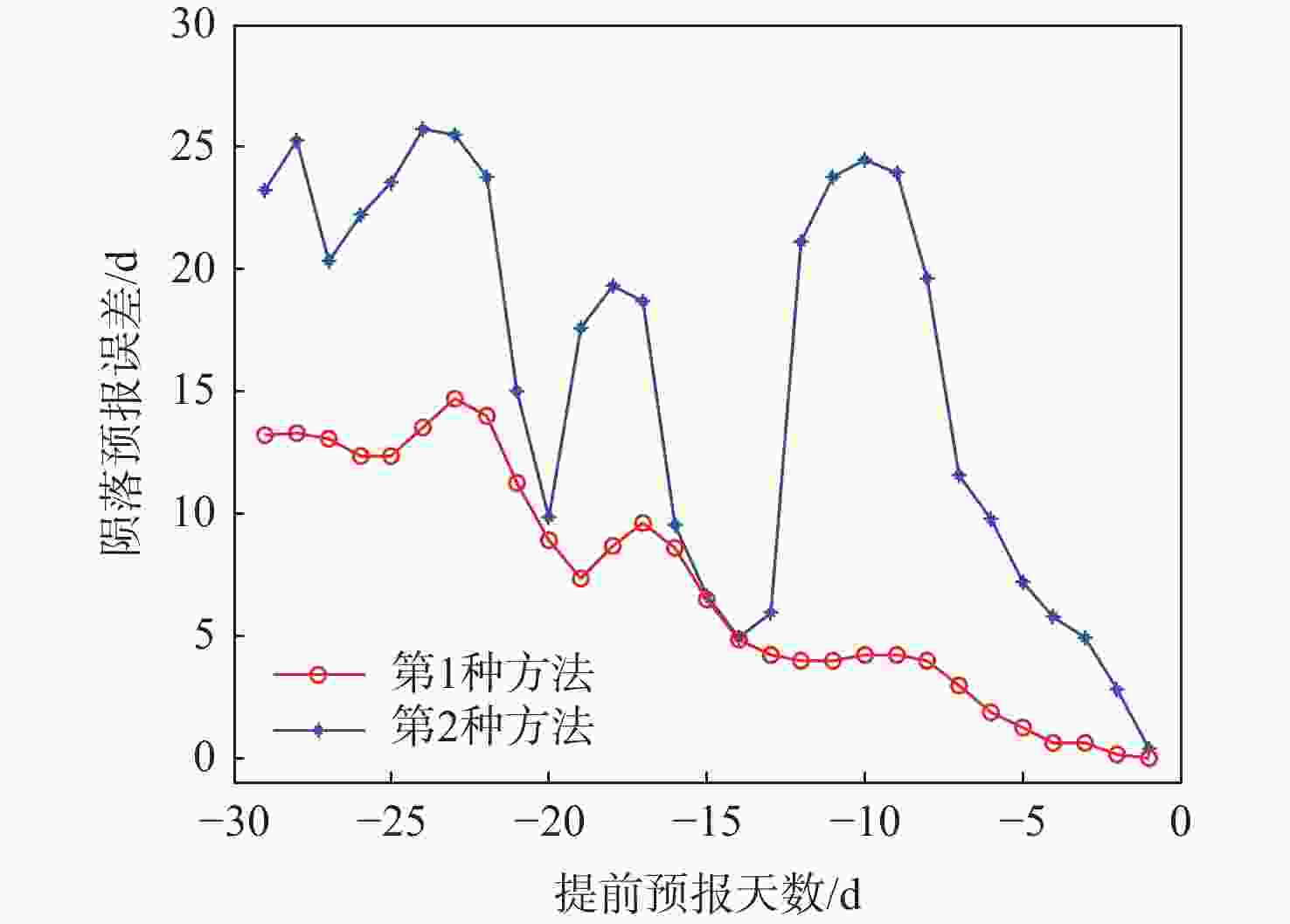
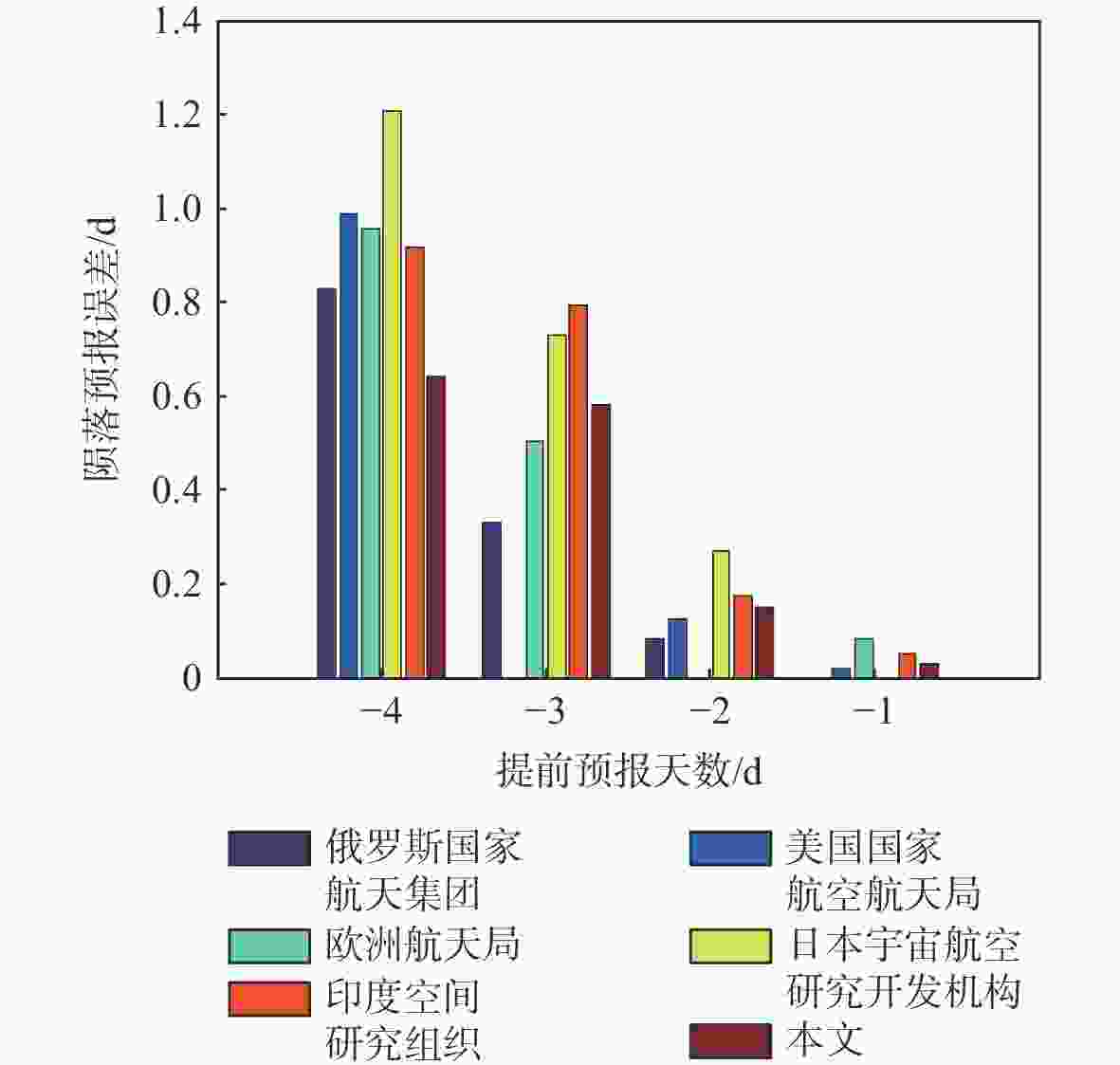
弹道系数是非合作目标轨道预报的重要参数,对于数目庞大的非合作目标,利用有限的测控资源进行弹道系数的快速解算是空间目标监测的迫切需求。基于双行根数(TLE)的半长轴衰减信息,提出了一种改进的弹道系数解算算法。通过多项式平滑检测和二次判别,识别出野值、轨道机动和地磁暴3种情况;分析了构造半长轴衰减观测量的依据,比较了不同观测弧长对弹道系数解算的影响;利用天宫一号数据对所提算法解算的弹道系数进行精度评估,并将解算结果在天宫一号陨落预报中进行验证。结果表明:基于TLE解算的弹道系数稳定、准确,适用于非合作目标轨道预报。
Abstract:The ballistic coefficient is an important source of error in the orbit prediction of non-cooperative targets. For a large number of non-cooperative targets, calculating quickly the ballistic coefficient with the limited measurement and control resources is an urgent need. In this paper, based on the semi-major axis attenuation information of the two line element (TLE), an improved ballistic coefficient calculation algorithm is studied. Through polynomial smooth detection and quadratic discrimination, three situations, ie. outliers, orbital maneuvers and geomagnetic storms are identified. The basis for constructing semi-major axis attenuation observations is analyzed, and the influence of different observation arc lengths on the calculation of ballistic coefficients is compared. The accuracy of the ballistic coefficients is evaluated using the data of Tiangong-1, and the ballistic coefficients are used in the prediction of Tiangong-1’s reentry. The results show that the ballistic coefficients calculated based on the TLE elements are stable and accurate, and are suitable for non-cooperative target orbit prediction.
-
Key words:
- non-cooperative targets /
- orbit forecast /
- two line element /
- ballistic coefficient /
- reentry prediction
-
-
[1] AILOR W. Spacecraft end-of-life disposal[M]//BLOCKLEY R, SHYY W. Encyclopedia of aerospace engineering. New York: John Wiley & Sons Ltd, 2010: 105-120. [2] 李翠兰, 欧阳琦, 陈明, 等. 大型低轨航天器与星座卫星的碰撞风险研究[J]. 宇航学报, 2020, 41(9): 1158-1165.LI C L, OUYANG Q, CHEN M, et al. Analysis of collision risk between constellation satellites and large low-orbit spacecraft[J]. Journal of Astronautics, 2020, 41(9): 1158-1165(in Chinese). [3] CORLEY B. International space station debris avoidance process [EB/OL]. (2016-08-01) [2021-07-20]. https://orbitaldebris.jsc.nasa.gov/quarterly-news/pdfs/odqnv2014.pdf. [4] 王晓楠, 高山, 程柏林. 基于不敏卡尔曼滤波平滑的再入弹头弹道系数提取[J]. 火力与指挥控制, 2011, 36(6): 89-92.WANG X N, GAO S, CHENG B L. Extraction of ballistic coefficient of reentry warhead based on unscented Kalman filtering smoothing[J]. Fire Control & Command Control, 2011, 36(6): 89-92(in Chinese). [5] 张金凤, 何重阳, 梁彦. 面向再入目标跟踪的估计与辨识联合优化算法[J]. 航空学报, 2016, 37(5): 1634-1643.ZHANG J F, HE C Y, LIANG Y. Joint optimization algorithm of estimation and identification for reentry target tracking[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(5): 1634-1643(in Chinese). [6] 刘舒莳, 龚建村, 刘四清, 等. 中长期轨道预报中大气阻力系数补偿算法的研究[J]. 宇航学报, 2013, 34(2): 157-162.LIU S S, GONG J C, LIU S Q, et al. Atmospheric drag coefficient calibration in medium-term orbit prediction[J]. Journal of Astronautics, 2013, 34(2): 157-162(in Chinese). [7] LIDTKE A A, GONDELACH D J, ARMELLIN R, et al. Processing two line element sets to facilitate re-entry prediction of spent rocket bodies from the geostationary transfer orbit[C]//Proceedings of the 6th International Conference on Astrodynamics Tools and Techniques, 2016: 1-5. [8] 许晓丽, 熊永清. 基于历史TLE的空间目标轨道预报误差演化规律研究[J]. 天文学报, 2019, 60(4): 28-40.XU X L, XIONG Y Q. Study on orbit prediction error of space objects based on historical TLE[J]. Acta Astronomica Sinica, 2019, 60(4): 28-40(in Chinese). [9] GUPTA S, ANILKUMAR A K. Integrated model for prediction of reentry time of risk objects[J]. Journal of Spacecraft and Rockets, 2015, 52(1): 295-299. doi: 10.2514/1.A32704 [10] SHOEMAKER M A, VAN DER HA J C, FUJITA K. Trajectory reconstruction of Hayabusa’s atmospheric reentry[J]. Acta Astronautica, 2012, 71: 151-162. doi: 10.1016/j.actaastro.2011.08.006 [11] SHARMA R K, BANDYOPADHYAY P, ADIMURTHY V. Lifetime estimation of upper stages re-entering from GTO by genetic algorithm with response surface approximation[C]//Proceedings of the International Astronautical Congress, 2006: 1-4. [12] SANG J Z, BENNETT J C, SMITH C H. Estimation of ballistic coefficients of low altitude debris objects from historical two line elements[J]. Advances in Space Research, 2013, 52(1): 117-124. doi: 10.1016/j.asr.2013.03.010 [13] SAUNDERS A, LEWIS H G, SWINERD G G. A new tool for satellite reentry predictions[C]//5th European Conference of Space Debris, 2009: 1-3. [14] SAUNDERS A, SWINERD G G, LEWIS H G. Deriving accurate satellite ballistic coefficients from two-line element data[J]. Journal of Spacecraft and Rockets, 2012, 49(1): 175-184. doi: 10.2514/1.A32023 [15] 唐歌实, 李勰. 载人航天轨道确定技术及在交会对接中的应用[M]. 北京: 国防工业出版社, 2013: 121-143.TANG G S, LI X. Orbit determination technology of manned spacecraft and application in rendezvous and docking[M]. Beijing: National Defense Industry Press, 2013: 121-143(in Chinese). [16] 汤锡生, 陈贻迎, 朱民才. 载人飞船轨道确定和返回控制[M]. 北京: 国防工业出版社, 2002: 47-52.TANG X S, CHEN Y Y, ZHU M C. Orbit determination and reentry control for manned spacecraft[M]. Beijing: National Defense Industry Press, 2002: 47-52(in Chinese). [17] HOOTS F R, ROEHRHICH R L. Models for propagation of NORAD element sets[R]. [S.l.]: Office of Astrodynamics, Aerospace Defense Center, U. S. , 1980: 10-31. [18] COOK G E. Satellite drag coefficients[J]. Planetary and Space Science, 1965, 13(10): 929-946. doi: 10.1016/0032-0633(65)90150-9 [19] MEHTA P M, WALKER A, LAWRENCE E, et al. Modeling satellite drag coefficients with response surfaces[J]. Advances in Space Research, 2014, 54(8): 1590-1607. doi: 10.1016/j.asr.2014.06.033 [20] RUSSEL R, ARORA N, VITTALDEV V, et al. Ballistic coefficient prediction for resident space objects[C]//Proceedings of the Advanced Maui Optical and Space Surveillance Technologies Conference, 2012: 1-6. [21] NWANKWO V U J, DENIG W, CHAKRABARTI S K, et al. Atmospheric drag effects on modelled low Earth orbit (LEO) satellites during the July 2000 Bastille Day event in contrast to an interval of geomagnetically quiet conditions[J]. Annales Geophysicae, 2021, 39: 397-412. doi: 10.5194/angeo-39-397-2021 [22] MOE K, MOE M M. Gas-surface interactions and satellite drag coefficients[J]. Planetary and Space Science, 2005, 53(8): 793-801. doi: 10.1016/j.pss.2005.03.005 -







 下载:
下载: