基于深度强化学习的跳跃式导弹轨迹优化算法

龚开奇; 魏宏夔; 李嘉玮; 宋晓; 李勇; 李怡昕; 张岳

doi:10.13700/j.bh.1001-5965.2021.0436

基于深度强化学习的跳跃式导弹轨迹优化算法

doi: 10.13700/j.bh.1001-5965.2021.0436

1.
北京航空航天大学网络空间安全学院，北京 100191
2.
北京电子工程总体研究所，北京 100191

基金项目: 国家重点研发计划(2018YFB1702703)

详细信息

通讯作者:
E-mail：songxiao@buaa.edu.cn

中图分类号: V448.23；TP183
计量
- 文章访问数: 381
- HTML全文浏览量: 80
- PDF下载量: 75
- 被引次数: 0
出版历程
- 收稿日期: 2021-08-02
- 录用日期: 2021-11-11
- 网络出版日期: 2021-12-14
- 整期出版日期: 2023-06-30

Trajectory optimization algorithm of skipping missile based on deep reinforcement learning

1.
School of Cyber Science and Technology，Beihang University，Beijing 100191，China
2.
Beijing Institute of Electronic System Engineering，Beijing 100191，China

Funds: National Key R& D Program of China (2018YFB1702703)

More Information

Corresponding author: E-mail：songxiao@buaa.edu.cn

摘要

摘要:
导弹的跳跃飞行过程可建模为时变非线性微分方程组，该方程组难以得到解析解，给导弹的轨迹优化带来很大的困难。针对该问题，提出一种基于双深度Q网络的带网络优选（NEO）策略的深度强化学习（NEO-DDQN）算法，所提算法以跳跃导弹航程最大化为优化目标，在热流密度、动压、过载及末速度等约束下，求解跳跃导弹的轨迹优化问题。设计问题的动作空间、状态空间和奖励函数；确定算法关键参数学习率的取值及合适的贪心策略，并提出NEO策略，得到所提NEO-DDQN算法；开展与最优恒定攻角（OCAOA）方案、遗传算法(GA)的对比实验。结果表明：NEO策略有效提升了算法的求解稳定性且将航程提升了2.52%；与OCAOA方案、GA相比，所提算法使跳跃导弹航程分别提高了2.61%和1.33%；所提算法还避免了直接求解复杂非线性微分方程，为轨迹优化问题提供了一种新型的基于学习的算法。
- 导弹 /
- 跳跃飞行 /
- 轨迹优化 /
- 深度强化学习 /
- 网络优选
Abstract:
The skipping flight process of the skipping missile can be modeled as a set of time-varying nonlinear differential equations which cannot be solved analytically. Therefore, it brings great difficulties to optimize the trajectory optimization of the skipping missile. To solve this problem, a deep reinforcement learning trajectory optimization method based on double deep Q-network (DDQN) is proposed to maximize the range of the missile under certain constraints of heat flux, dynamic pressure, and overload. The procedure of this method is as follows. Firstly, the action space, state space, and reward function of the algorithm are designed. The appropriate greedy strategy is then determind, along with the learning rate, an important algorithmic parameter. Further, the network optimization (NEO) strategy is introduced and then the NEO-DDQN algorithm is proposed. Finally, comparison experiments with the optional constant angle of attack (OCAOA) scheme and genetic algorithm (GA) are designed. Results show that the network optimization strategy effectively improves the stability of the algorithm and increases the flight range by 2.52%. Compared with OCAOA scheme and GA, the NEO-DDQN method improves the range of skipping missiles by 2.61% and 1.33% respectively. In addition, the proposed method successfully avoids directly dealing with complex nonlinear differential equations and innovatively provides a learning-based method for the trajectory optimization of the missile.
- missile /
- skipping flight /
- trajectory optimization /
- deep reinforcement learning /
- network optimization

HTML全文

图 1 跳跃导弹的三维模型

Figure 1. Three dimensional model of skipping missile

下载: 全尺寸图片幻灯片

图 2 导弹受力分析

Figure 2. Force analysis of missile

下载: 全尺寸图片幻灯片

图 3 导弹跳跃飞行示意图

Figure 3. Diagram of skipping flight of missile

下载: 全尺寸图片幻灯片

图 4 DQN（DDQN）算法的训练模型

Figure 4. Training model of DQN (DDQN) algorithm

下载: 全尺寸图片幻灯片

图 5 NEO-DDQN算法的训练模型

Figure 5. Training model of NEO-DDQN algorithm

下载: 全尺寸图片幻灯片

图 6 5种学习率的训练迭代

Figure 6. Training iteration for 5 learning rates

下载: 全尺寸图片幻灯片

图 7 5种贪心策略的训练迭代

Figure 7. Training iteration under 5 greedy strategies

下载: 全尺寸图片幻灯片

图 8 3种算法的热流密度、动压、过载与约束界限的关系

Figure 8. Relationship between heat flux, dynamic pressure, overload and restraint for three algorithms

下载: 全尺寸图片幻灯片

图 9 3种算法的航程-海拔图

Figure 9. Range-altitude diagram of three algorithms

下载: 全尺寸图片幻灯片

图 10 3种算法的攻角序列图

Figure 10. Sequence diagram of three algorithms of angle of attack

下载: 全尺寸图片幻灯片

图 11 导弹跳跃飞行的性能分析

Figure 11. Performance analysis of missile skipping flight

下载: 全尺寸图片幻灯片

表 1 导弹跳跃飞行仿真参数

Table 1. Simulation parameters of missile skipping flight

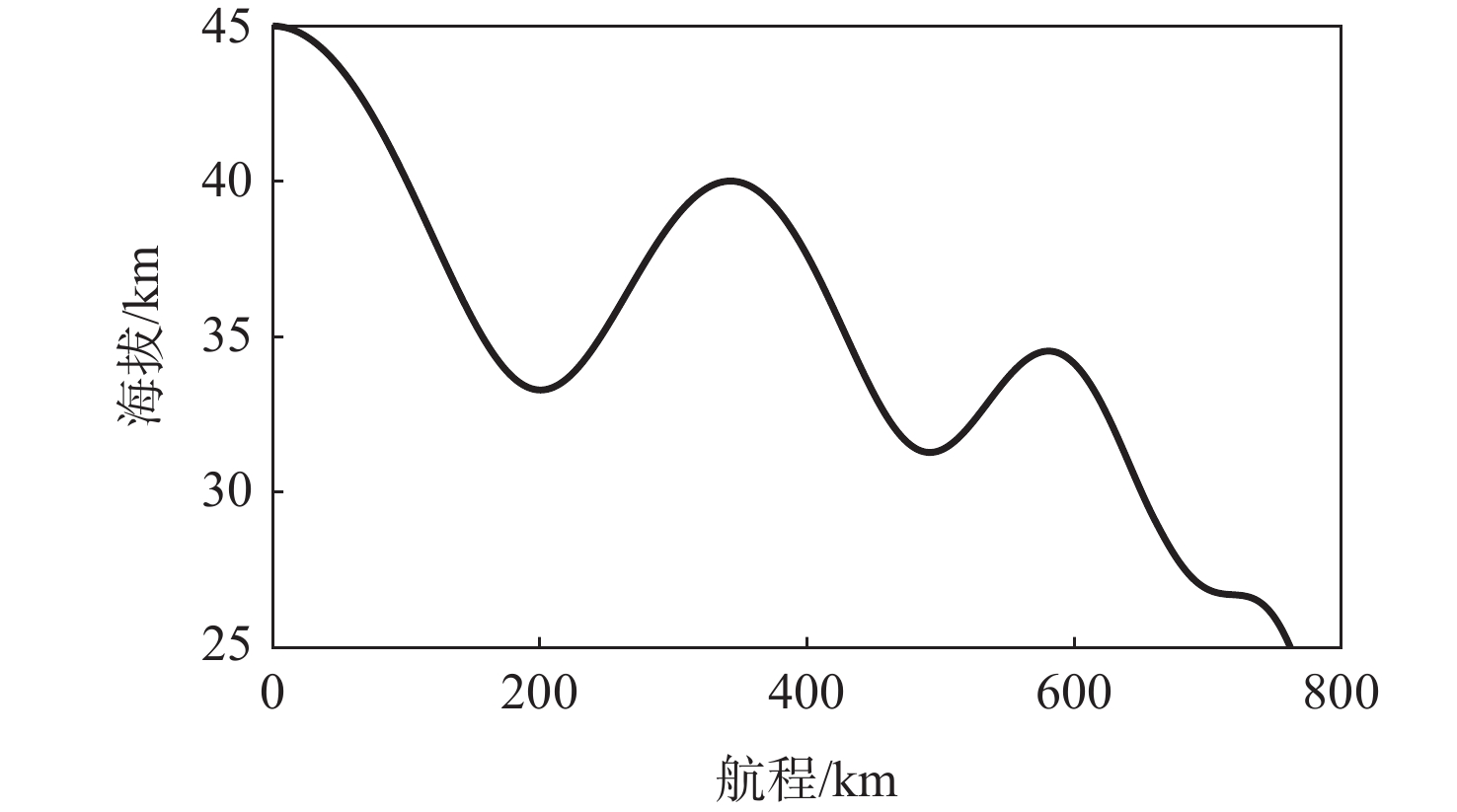
参数	数值
初始位置/m	(0, 45000)
初速度大小/（m·s⁻¹）	2224
初始速度倾角/（°）	0
质量/kg	574
特征面积/m²	0.203
高度约束/km	25~ 45

下载: 导出CSV

表 2 不同时间间隔对训练的影响

Table 2. Influence of different time intervals on training

分段时间间隔/s	航程/m
10	747878
20	776593
40	775804
50	768351

下载: 导出CSV

表 3 网络结构参数

Table 3. Parameters of network structure

层数	神经元个数
输入层	5
隐含层1	40
隐含层2	40
输出层	1

下载: 导出CSV

表 4 NEO-DDQN算法参数

Table 4. Parameters of NEO-DDQN algorithm

参数	数值
观察期回合数N₁	500
训练期回合数N₂	59500
训练频率N₃	20
更新频率N₄	200
折扣因子$ \gamma $	0.95
批大小B	32
记忆池大小M	4000

下载: 导出CSV

表 5 5种学习率最终航程的收敛值

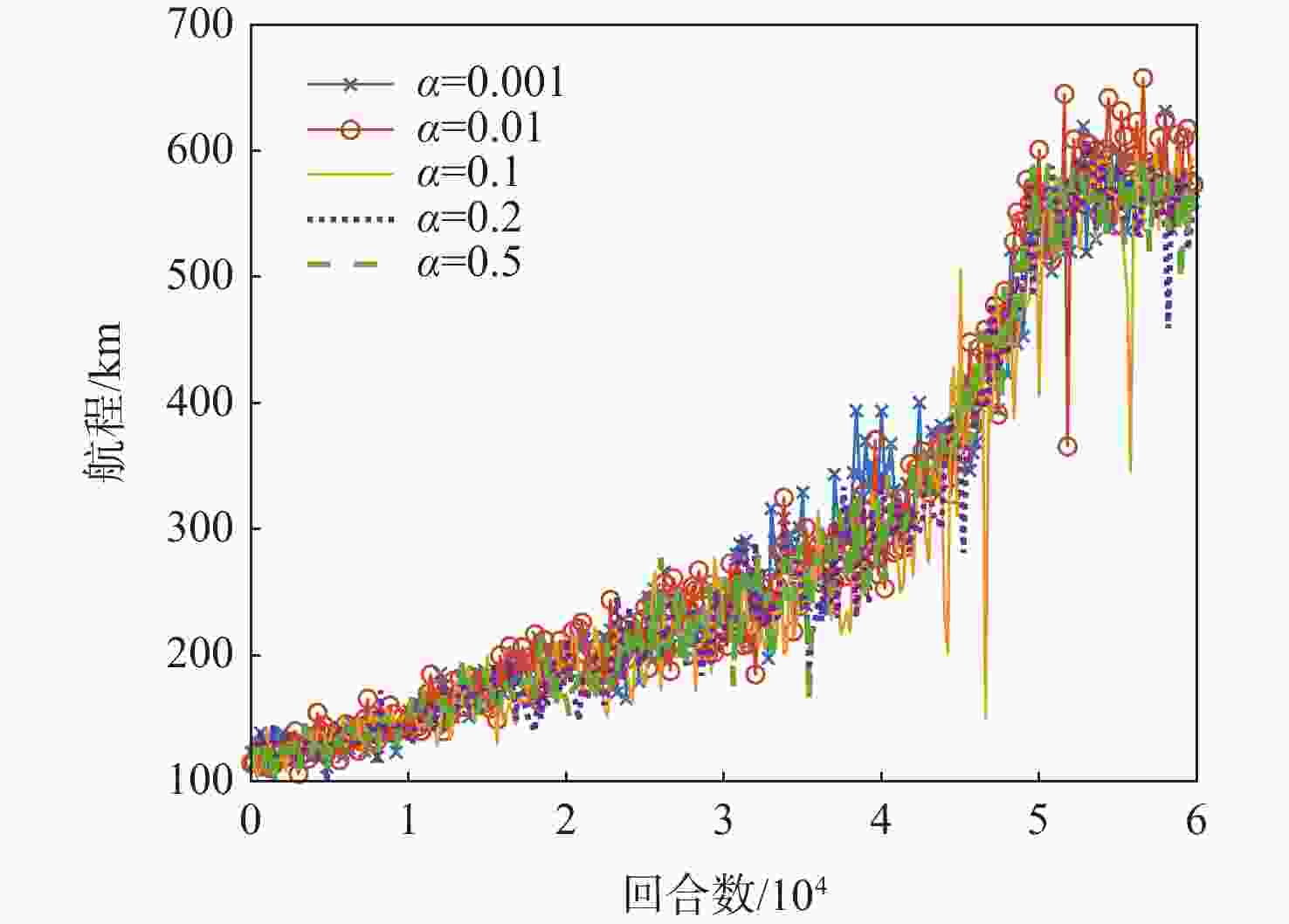
Table 5. Final range convergence values of 5 learning rates

学习率	收敛值/m
0.001	745654
0.01	781434
0.1	774864
0.2	743651
0.5	746867

下载: 导出CSV

表 6 5种贪心策略最终航程的收敛值

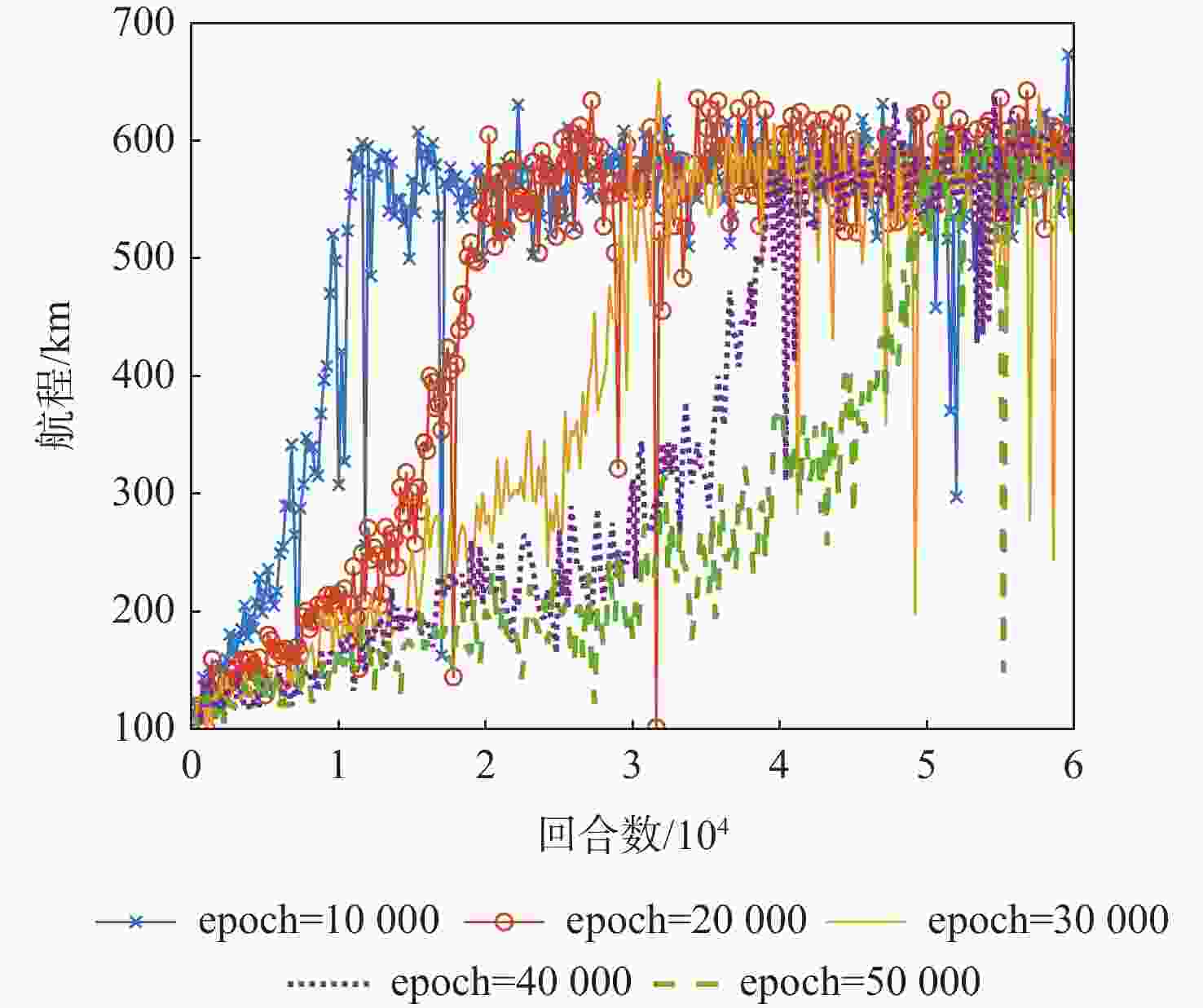
Table 6. Final range convergence values of 5 greedy strategies

epoch	收敛值/m
10000	771926
20000	778832
30000	771433
40000	764878
50000	776593

下载: 导出CSV

表 7 NEO策略对算法结果的影响

Table 7. Influence of NEO strategy on algorithm results

编号	$ \theta_{1} $/m	$ \theta_{2} $/m	$ \theta_{2} $−$ \theta_{1} $/m
1	767040	771830	4790
2	760609	774440	13831
3	767642	769734	2092
4	770645	771134	489
5	771587	784626	13039
6	702365	781316	78951
7	762389	785295	22906
8	764834	783575	18741
9	754677	777747	23070
10	755698	768921	13223
平均值	757748	776861	19113

下载: 导出CSV

表 8 GA的参数设置

Table 8. Parameters setting of genetic algorithm

参数	数值
时间间隔T/s	20
攻角/（°）	0~30（整数）
种群大小N₅	10
交叉概率P_c	0.8
变异概率P_v	0.9
迭代次数I	100

下载: 导出CSV

表 9 GA的优化结果

Table 9. Optimization results of genetic algorithm

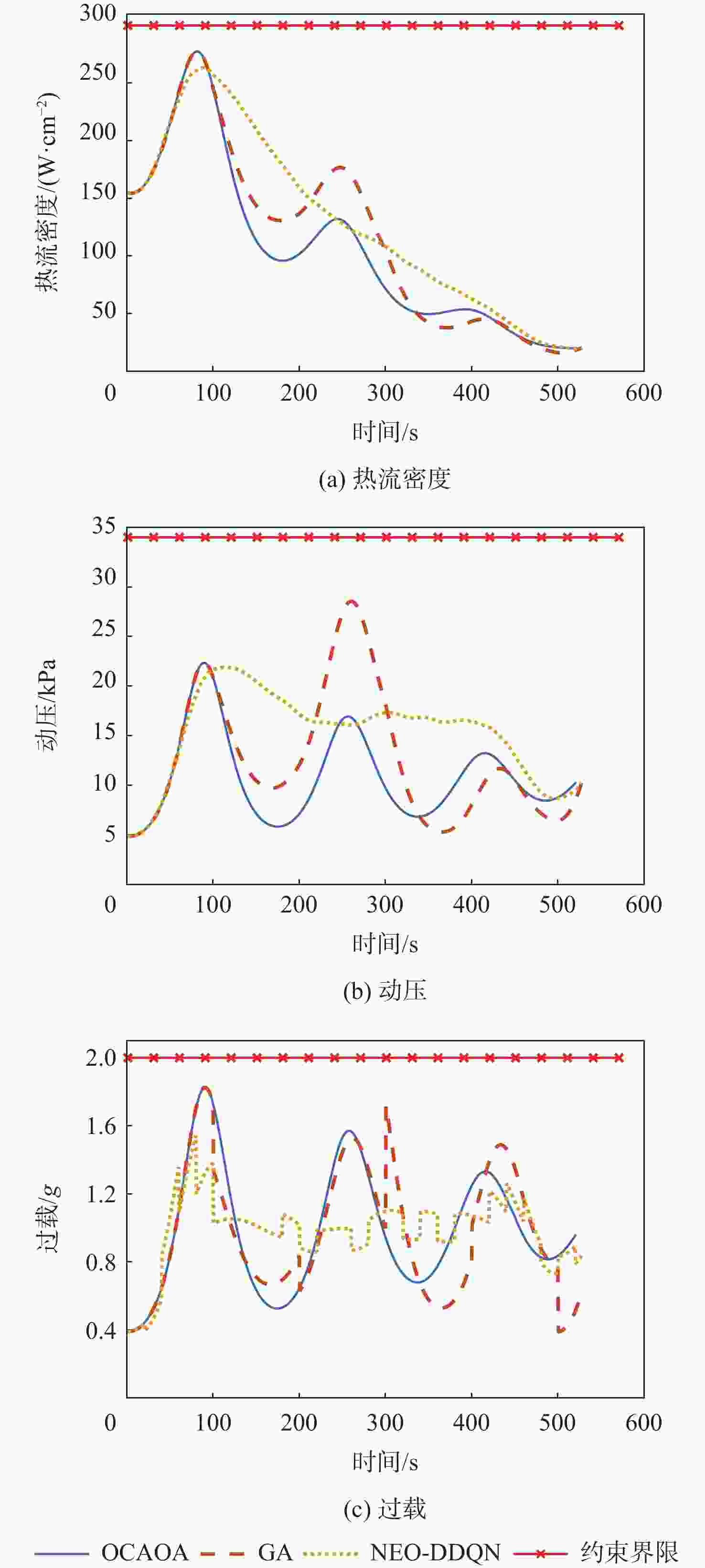
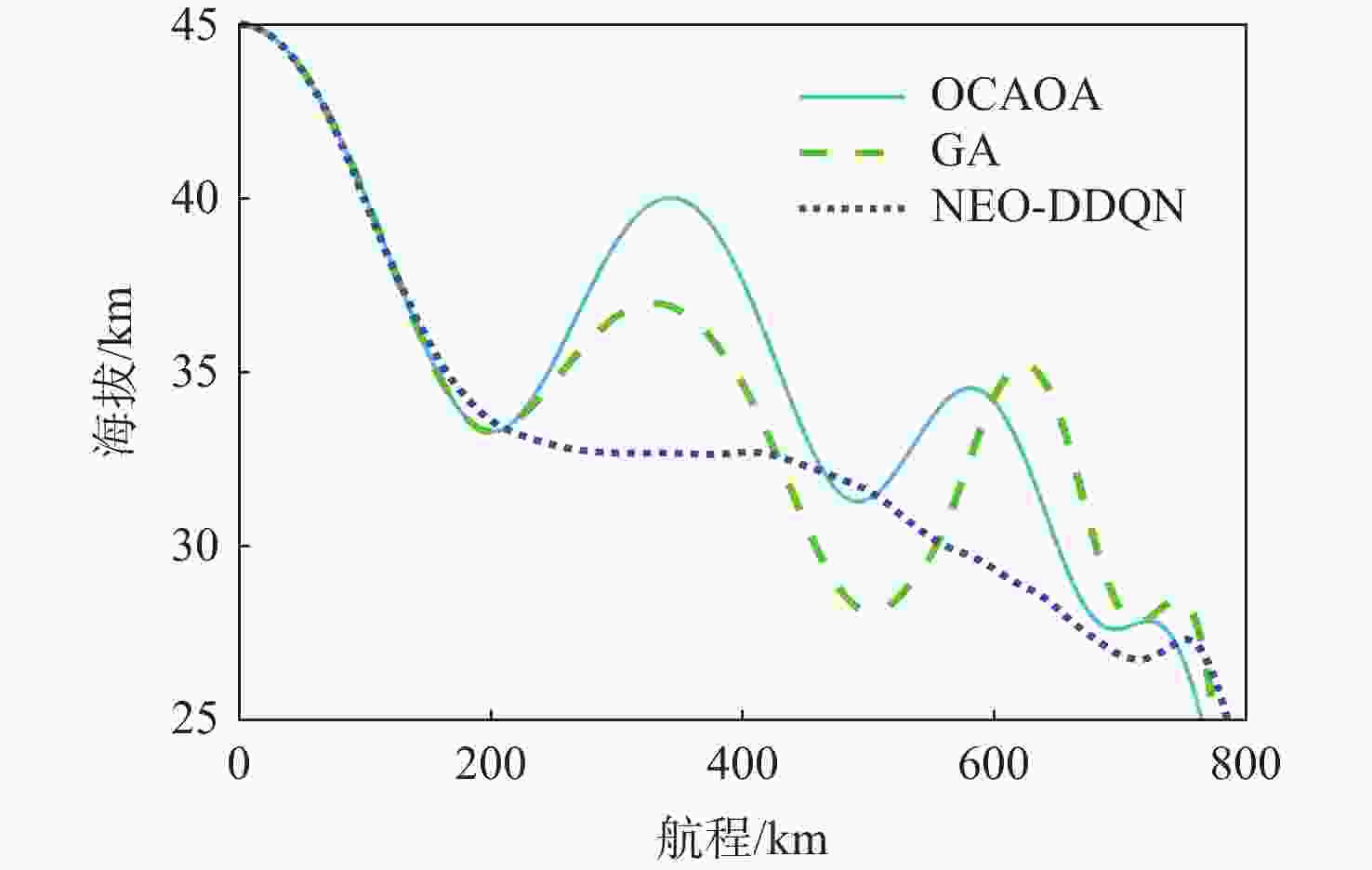
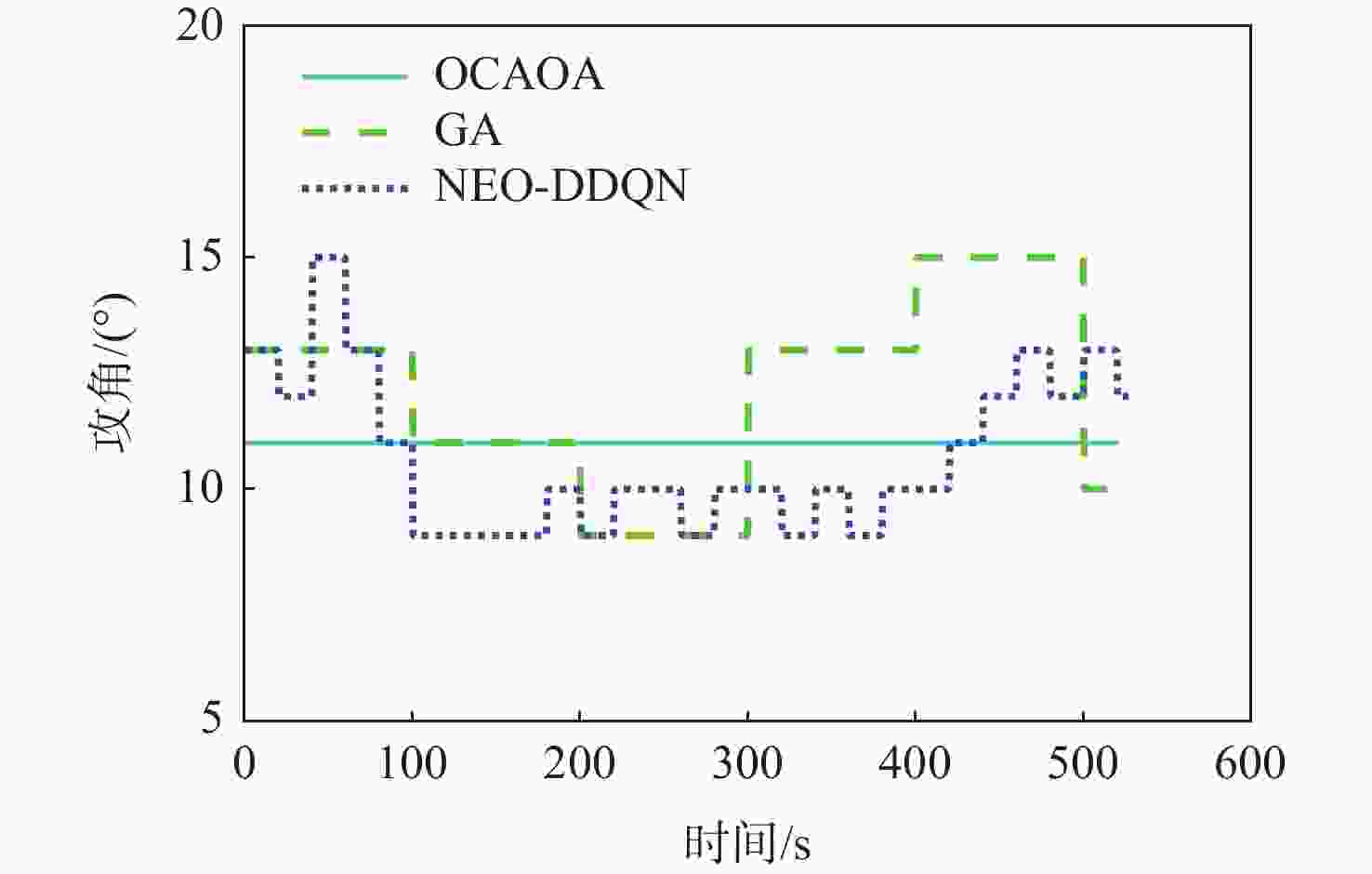
编号	航程 /m
1	741955
2	767656
3	752029
4	730913
5	721760
6	775017
7	764682
8	751243
9	744770
10	761691

下载: 导出CSV

表 10 3种算法的优化结果

Table 10. Optimization results of three algorithms

算法	航程 /m	末速度/（m·s⁻¹）	航程提升 /%
OCAOA	765343	715	0.00
GA	775017	722	1.26
NEO-DDQN	785295	713	2.61

下载: 导出CSV

参考文献(26)

[1]	王在铎, 王惠, 丁楠, 等. 高超声速飞行器技术研究进展[J]. 科技导报, 2021, 39(11): 59-67. doi: 10.3981/j.issn.1000-7857.2021.11.007 WANG Z D, WANG H, DING N, et al. Research on the development of hypersonic vehicle technology[J]. Science & Technology Review, 2021, 39(11): 59-67(in Chinese). doi: 10.3981/j.issn.1000-7857.2021.11.007
[2]	邵雷, 雷虎民, 赵锦. 临近空间高超声速飞行器轨迹预测方法研究进展[J]. 航空兵器, 2021, 28(2): 34-39. doi: 10.12132/ISSN.1673-5048.2020.0138 SHAO L, LEI H M, ZHAO J. Research progress in trajectory prediction for near space hypersonic vehicle[J]. Aero Weaponry, 2021, 28(2): 34-39(in Chinese). doi: 10.12132/ISSN.1673-5048.2020.0138
[3]	陈小庆, 侯中喜, 刘建霞. 高超声速滑翔式飞行器再入轨迹多目标多约束优化[J]. 国防科技大学学报, 2009, 31(6): 77-83. doi: 10.3969/j.issn.1001-2486.2009.06.015 CHEN X Q, HOU Z X, LIU J X. Multi-objective optimization of reentry trajectory for hypersonic glide vehicle with multi-constraints[J]. Journal of National University of Defense Technology, 2009, 31(6): 77-83(in Chinese). doi: 10.3969/j.issn.1001-2486.2009.06.015
[4]	AN K, GUO Z Y, XU X P, et al. A framework of trajectory design and optimization for the hypersonic gliding vehicle[J]. Aerospace Science and Technology, 2020, 106: 106110. doi: 10.1016/j.ast.2020.106110
[5]	何烈堂, 柳军, 侯中喜, 等. 无动力跳跃式跨大气层飞行的可行性研究[J]. 弹箭与制导学报, 2008, 28(2): 155-157. doi: 10.3969/j.issn.1673-9728.2008.02.048 HE L T, LIU J, HOU Z X, et al. Feasibility study of unpropulsive skipping trans-atmospheric flight[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2008, 28(2): 155-157(in Chinese). doi: 10.3969/j.issn.1673-9728.2008.02.048
[6]	国海峰, 黄长强, 丁达理, 等. 考虑随机干扰的高超声速滑翔飞行器轨迹优化[J]. 北京航空航天大学学报, 2014, 40(9): 1281-1290. doi: 10.13700/j.bh.1001-5965.2013.0755 GUO H F, HUANG C Q, DING D L, et al. Trajectory optimization for hypersonic gliding vehicle considering stochastic disturbance[J]. Journal of Beijing University of Aeronautics and Astronautics, 2014, 40(9): 1281-1290(in Chinese). doi: 10.13700/j.bh.1001-5965.2013.0755
[7]	GATH P F, WELL K H, MEHLEM K. Initial guess generation for rocket ascent trajectory optimization using indirect methods[J]. Journal of Spacecraft and Rockets, 2002, 39(4): 515-521. doi: 10.2514/2.3864
[8]	BARRON R L, CHICK C M. Improved indirect method for air-vehicle trajectory optimization[J]. Journal of Guidance, Control, and Dynamics, 2006, 29(3): 643-652. doi: 10.2514/1.16228
[9]	ROSA SENTINELLA M, CASALINO L. Genetic algorithm and indirect method coupling for low-thrust trajectory optimization[C]//42nd AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit. Reston: AIAA, 2006: 4468.
[10]	李瑜, 杨志红, 崔乃刚. 洲际助推-滑翔导弹全程突防弹道优化[J]. 固体火箭技术, 2010, 33(2): 125-130. doi: 10.3969/j.issn.1006-2793.2010.02.002 LI Y, YANG Z H, CUI N G. Optimization of overall penetration trajectory for intercontinental boost-glide missile[J]. Journal of Solid Rocket Technology, 2010, 33(2): 125-130(in Chinese). doi: 10.3969/j.issn.1006-2793.2010.02.002
[11]	涂良辉, 袁建平, 岳晓奎, 等. 基于直接配点法的再入轨迹优化设计[J]. 西北工业大学学报, 2006, 24(5): 653-657. doi: 10.3969/j.issn.1000-2758.2006.05.026 TU L H, YUAN J P, YUE X K, et al. Improving design of reentry vehicle trajectory optimization using direct collocation method[J]. Journal of Northwestern Polytechnical University, 2006, 24(5): 653-657(in Chinese). doi: 10.3969/j.issn.1000-2758.2006.05.026
[12]	RAO A, CLARKE K. Performance optimization of a maneuvering re-entry vehicle using a Legendre pseudospectral method[C]//AIAA Atmospheric Flight Mechanics Conference and Exhibit. Reston: AIAA, 2002: 4885.
[13]	COTTRILL G C, HARMON F G. Hybrid Gauss pseudospectral and generalized polynomial chaos algorithm to solve stochastic optimal control problems[C]//AIAA Guidance, Navigation, and Control Conference. Reston: AIAA, 2011: 6572.
[14]	KUMAR G N, AHMED M S, SARKAR A K, et al. Reentry trajectory optimization using gradient free algorithms[J]. IFAC-Papers OnLine, 2018, 51(1): 650-655. doi: 10.1016/j.ifacol.2018.05.109
[15]	CHAI R Q, SAVVARIS A, TSOURDOS A, et al. Solving multi-objective aeroassisted spacecraft trajectory optimization problems using extended NSGA-II[C]// AIAA SPACE and Astronautics Forum and Exposition. Reston: AIAA, 2017: 5193.
[16]	ZHAO J, ZHOU R. Particle swarm optimization applied to hypersonic reentry trajectories[J]. Chinese Journal of Aeronautics, 2015, 28(3): 822-831. doi: 10.1016/j.cja.2015.04.007
[17]	SHAHZAD SANA K, HU W D. Hypersonic reentry trajectory planning by using hybrid fractional-order particle swarm optimization and gravitational search algorithm[J]. Chinese Journal of Aeronautics, 2021, 34(1): 50-67. doi: 10.1016/j.cja.2020.09.039
[18]	SONG X, HAN D L, SUN J H, et al. A data-driven neural network approach to simulate pedestrian movement[J]. Physica A: Statistical Mechanics and its Applications, 2018, 509(11): 827-844.
[19]	桑晨, 郭杰, 唐胜景, 等. 基于DDPG算法的变体飞行器自主变形决策[J]. 北京航空航天大学学报, 2022, 48(5): 910-919. SANG C, GUO J, TANG S J, et al. Autonomous deformation decision making of morphing aircraft based on DDPG algorithm[J]. Journal of Beijing University of Aeronautics and Astronautics, 2022, 48(5): 910-919(in Chinese).
[20]	许轲, 吴凤鸽, 赵军锁. 基于深度强化学习的软件定义卫星姿态控制算法[J]. 北京航空航天大学学报, 2018, 44(12): 2651-2659. doi: 10.13700/j.bh.1001-5965.2018.0357 XU K, WU F G, ZHAO J S. Software defined satellite attitude control algorithm based on deep reinforcement learning[J]. Journal of Beijing University of Aeronautics and Astronautics, 2018, 44(12): 2651-2659(in Chinese). doi: 10.13700/j.bh.1001-5965.2018.0357
[21]	NI W J, WU D, MA X P. Energy-optimal flight strategy for solar-powered aircraft using reinforcement learning with discrete actions[J]. IEEE Access, 2021, 9: 95317-95334. doi: 10.1109/ACCESS.2021.3095224
[22]	JIANG L, NAN Y, LI Z H. Realizing midcourse penetration with deep reinforcement learning[J]. IEEE Access, 2021, 9: 89812-89822.
[23]	GAO J S, SHI X M, CHENG Z T, et al. Reentry trajectory optimization based on deep reinforcement learning[C]//2019 Chinese Control and Decision Conference (CCDC). Piscataway: IEEE Press, 2019: 2588-2592.
[24]	MNIH V, KAVUKCUOGLU K, SILVER D, et al. Human-level control through deep reinforcement learning[J]. Nature, 2015, 518(7540): 529-533. doi: 10.1038/nature14236
[25]	MNIH V, KAVUKCUOGLU K, SILVER D, et al. Playing atari with deep reinforcement learning[EB/OL]. (2013-03-02) [2021-05-15]. http://arxiv.org/abs/1312.5602.
[26]	VAN HASSELT H, GUEZ A, SILVER D. Deep reinforcement learning with double Q-learning[C]//Proceedings of the AAAI Conference on Artificial Intelligence. New York: ACM, 2016: 2094–2100.