Reduced order method for large flexible wing structure based on dynamic response data
-
摘要:
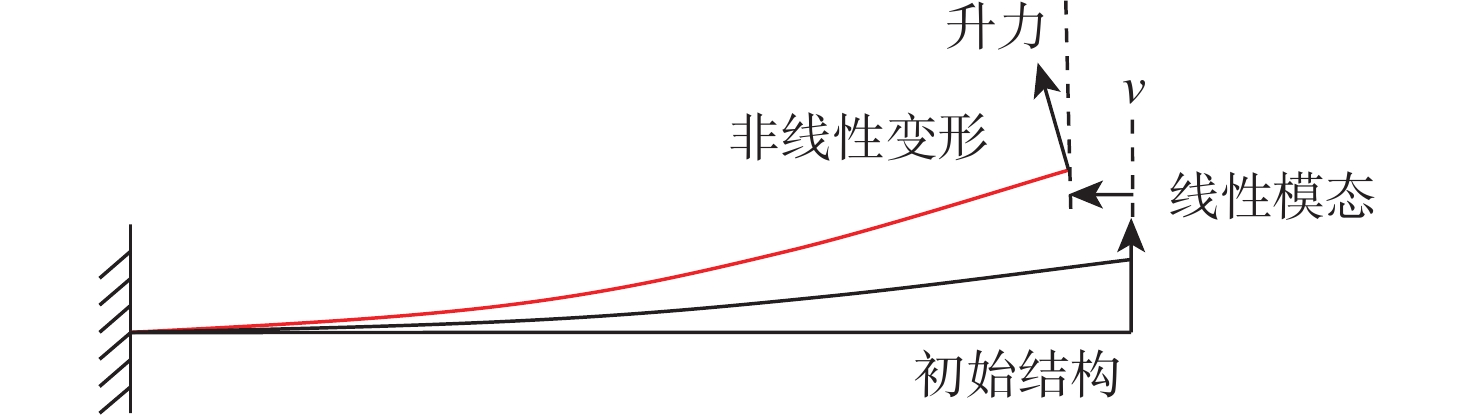
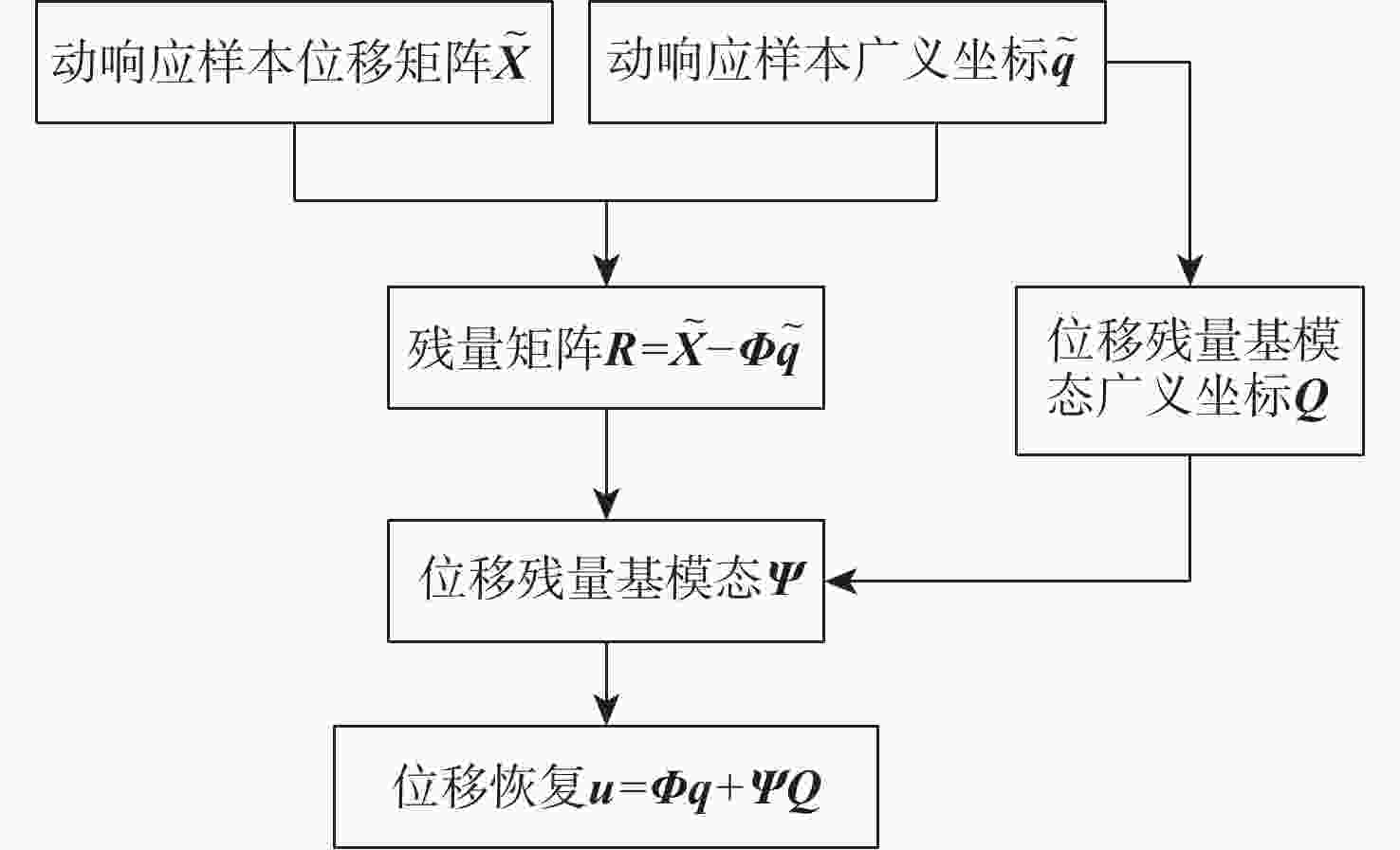
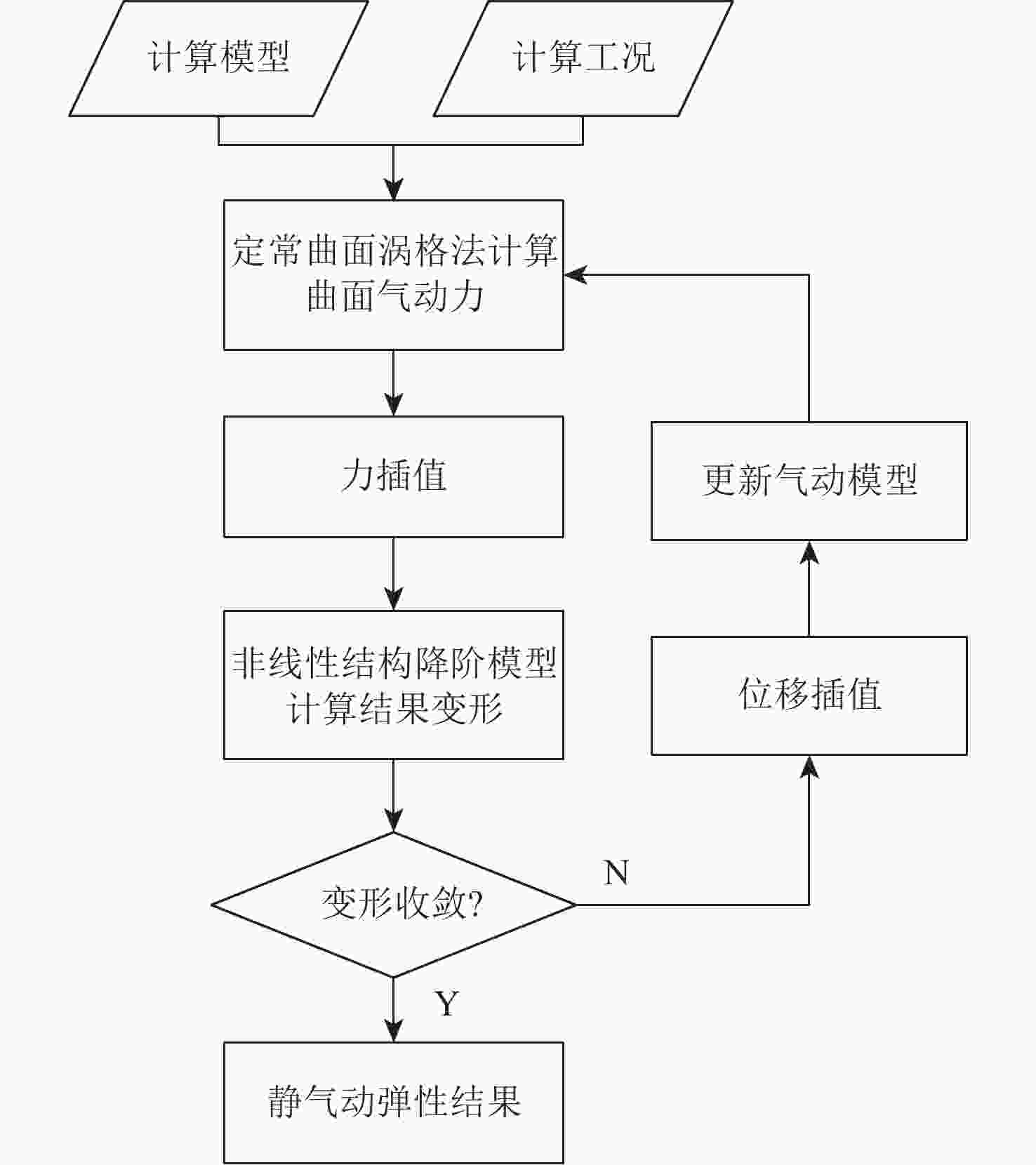
现代飞行器机翼柔性大，几何非线性问题不可忽略。基于动响应数据样本，基于谐波平衡和快速Fourier变换对结构动力学方程中的非线性刚度系数进行识别，建立非线性结构降阶模型。引入位移残量基模态，进行柔性机翼大变形的位移恢复。结合曲面涡格法和三维曲面插值方法搭建大柔性机翼几何非线性气动弹性分析框架。相比传统基于静力学数据回归分析的几何非线性结构降阶方法，该方法需要的载荷集数目小，提高了分析效率。计算结果表明：与非线性有限元方法相比，非线性结构降阶模型准确度高，能够有效应用于大柔性机翼几何非线性静气动弹性分析，而传统的线性计算方法与非线性方法相比结果差异较大。
Abstract:Due to the flexibility of modern aircraft wing, geometric nonlinearity cannot be neglected. Based on dynamic response data samples, non-linear stiffness coefficients in structural dynamics equation are identified based on harmonic balance and fast Fourier transform, and a non-linear structural order reduction model is established. The basic mode of displacement residue is introduced to recover the displacement of large flexible wings. A geometrically nonlinear aeroelastic analysis framework for large flexible wings is established by combining non-planar vortex lattice method and non-planar spline interpolation method. Compared with reduced order model for the traditional geometric nonlinear structure based on static data regression analysis, the proposed method requires a small number of load sets and improves analysis efficiency. Results show that compared with the nonlinear finite element method, the proposed model has high accuracy and can be effectively applied to the geometric nonlinear static aeroelastic analysis of large flexible wings. The result of traditional linear calculation method is significantly different from that of the nonlinear method.
-
图 6 大柔性机翼静气动弹性分析流程
Figure 6. Static aeroelastic analysis flowchart of large flexible wing
图 9 垂直一弯模态的广义力功率谱密度及方波输入
Figure 9. Power spectral density and square wave input of generalized force of 1st bending mode
图 11 不同来流风速下的主梁垂直位移
Figure 11. Vertical displacement of main beam with different flow velocities
图 12 不同来流风速下的主梁展向位移
Figure 12. Spanwise displacement of main beam with different flow velocities
图 13 不同来流风速下的翼尖垂直位移
Figure 13. Vertical displacement of wing tip with different flow velocities
图 14 不同来流风速下的翼尖展向位移
Figure 14. Spanwise displacement of wing tip with different flow velocities
图 15 不同来流风速下静气动弹性垂直位移
Figure 15. Static aeroelastic vertical displacement with different flow velocities
图 16 不同来流风速下的静气动弹性展向位移
Figure 16. Static aeroelastic spanwise displacement with different flow velocities
图 17 不同来流风速下的静气动弹性扭转角
Figure 17. Static aeroelastic twist with different flow velocities
图 18 不同来流风速下的翼尖静气动弹性位移
Figure 18. Static aeroelastic tip displacement with different flow velocities
表 1 机翼模型设计参数
Table 1. Design parameters of wing model
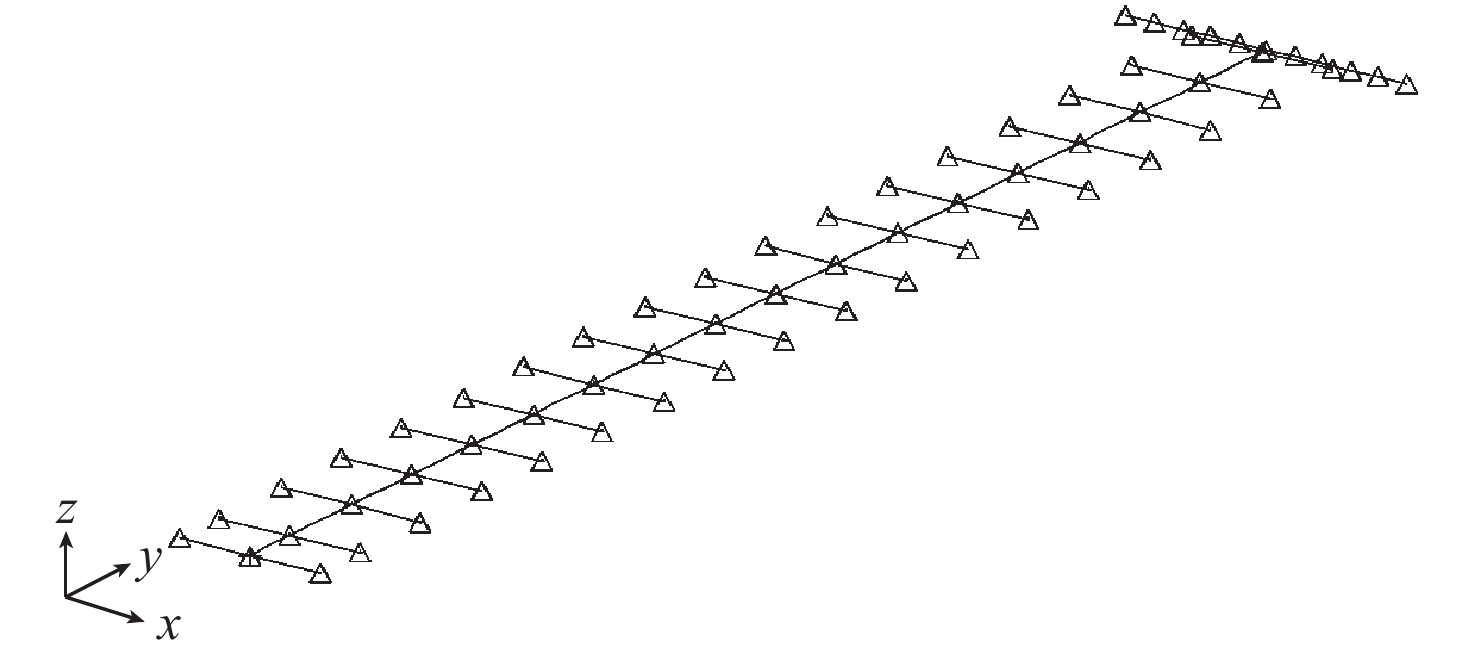
模型参数 取值 半翼展/mm 1000 弦长/mm 100 弹性轴位置 50%机翼弦长 主梁密度/ (kg·m−3) 7.75×103 主梁截面形状 35 mm×1.5 mm(矩形) 配重杆长度/mm 200 配重杆质量/g 62 
下载: 导出CSV
表 2 前六阶模态
Table 2. First six modes
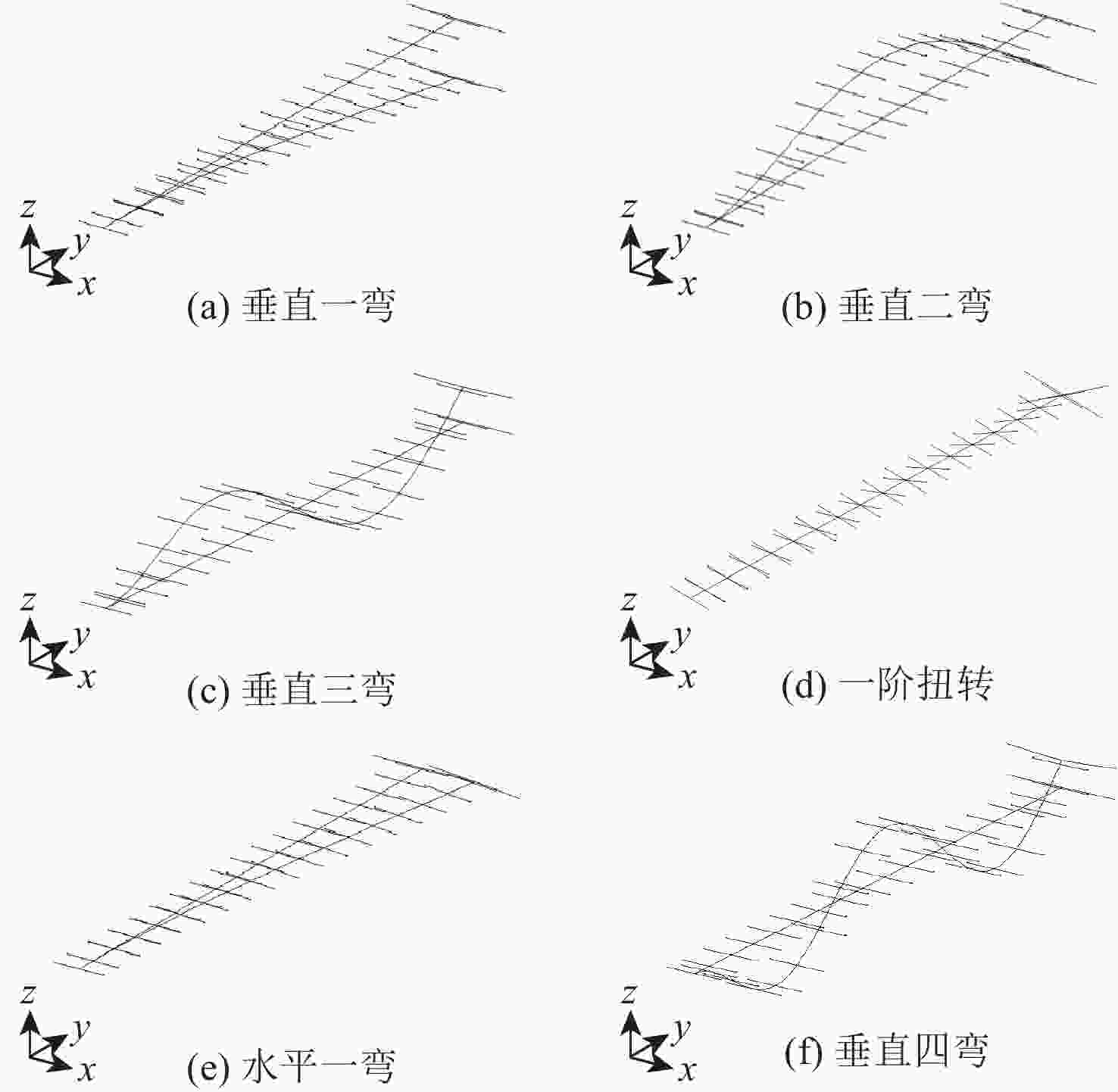
模态编号 模态振型 模态频率/Hz 1 垂直一弯 1.179 2 垂直二弯 7.724 3 垂直三弯 22.19 4 一阶扭转 22.95 5 水平一弯 27.47 6 垂直四弯 44.27
下载: 导出CSV
表 3 翼尖垂直位移对比
Table 3. Comparison of tip vertical displacement
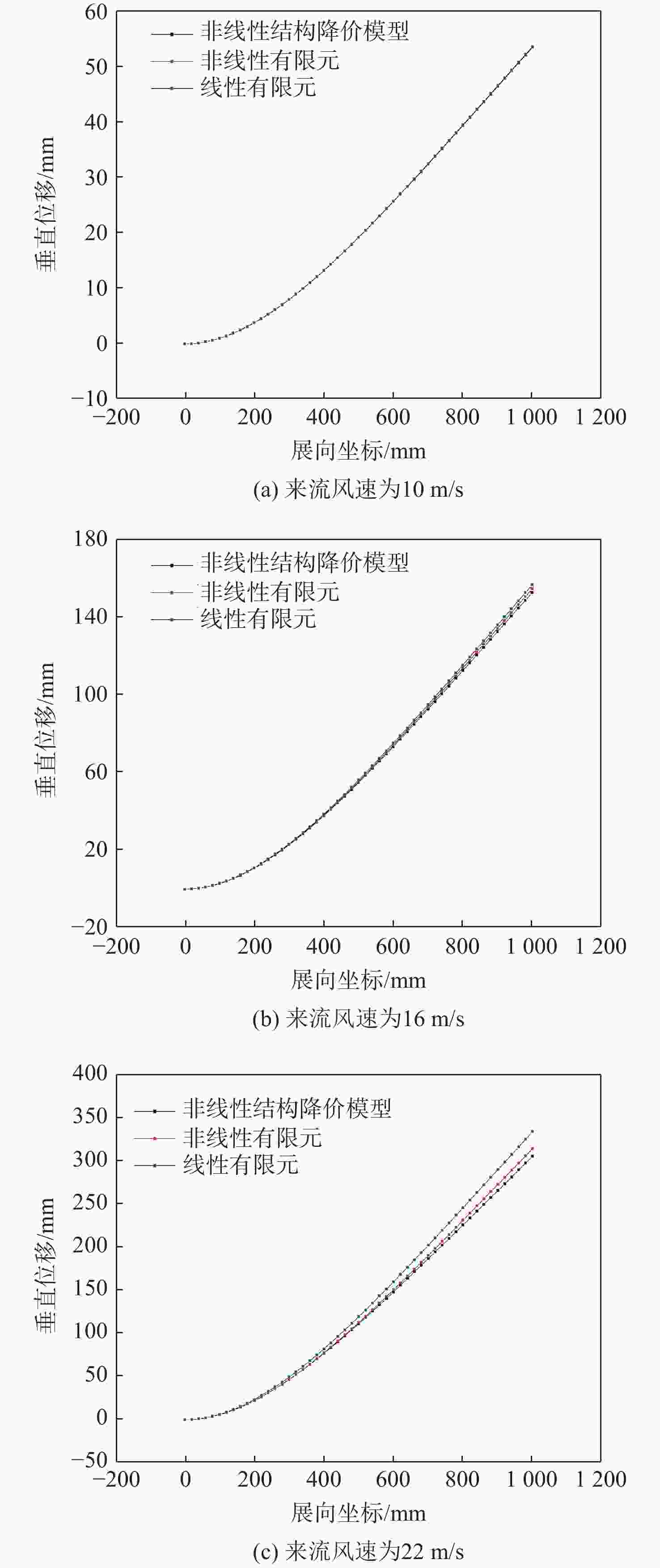
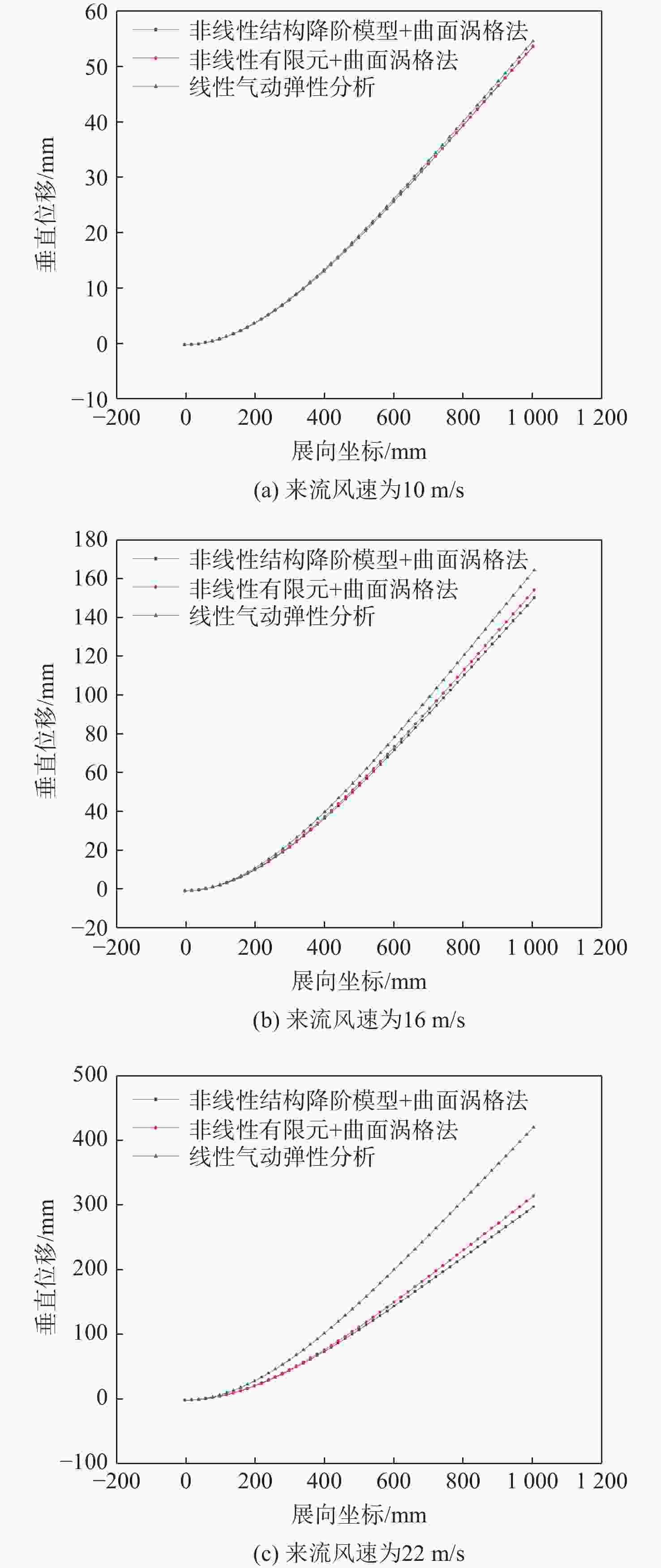
来流风速/(m·s−1) 垂直位移/mm 相对误差/% 非线性有限元 非线性结构降阶模型 10 53.4 53.3 0.2 16 153.7 151.8 1.2 22 313.0 304.3 2.8
下载: 导出CSV
表 4 静气动弹性垂直位移对比
Table 4. Comparison of static aeroelastic vertical displacement
来流风速/
(m·s−1)垂直位移/mm 非线性
有限元非线性结构
降阶模型线性气动
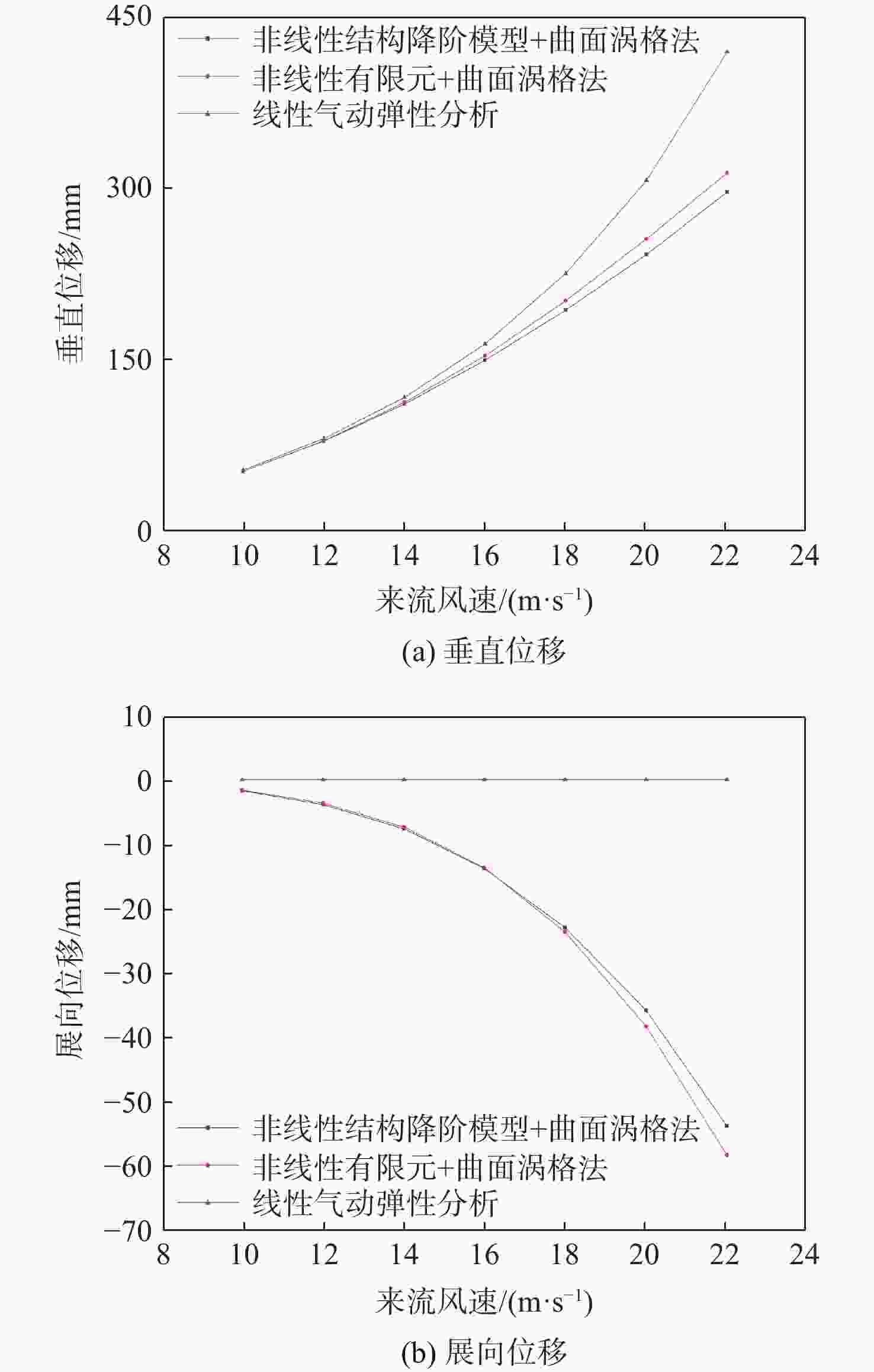
弹性分析10 53.4 53.3 54.3 16 153.7 149.9 164.0 22 313.0 296.6 418.2
下载: 导出CSV
表 5 静气动弹性展向位移对比
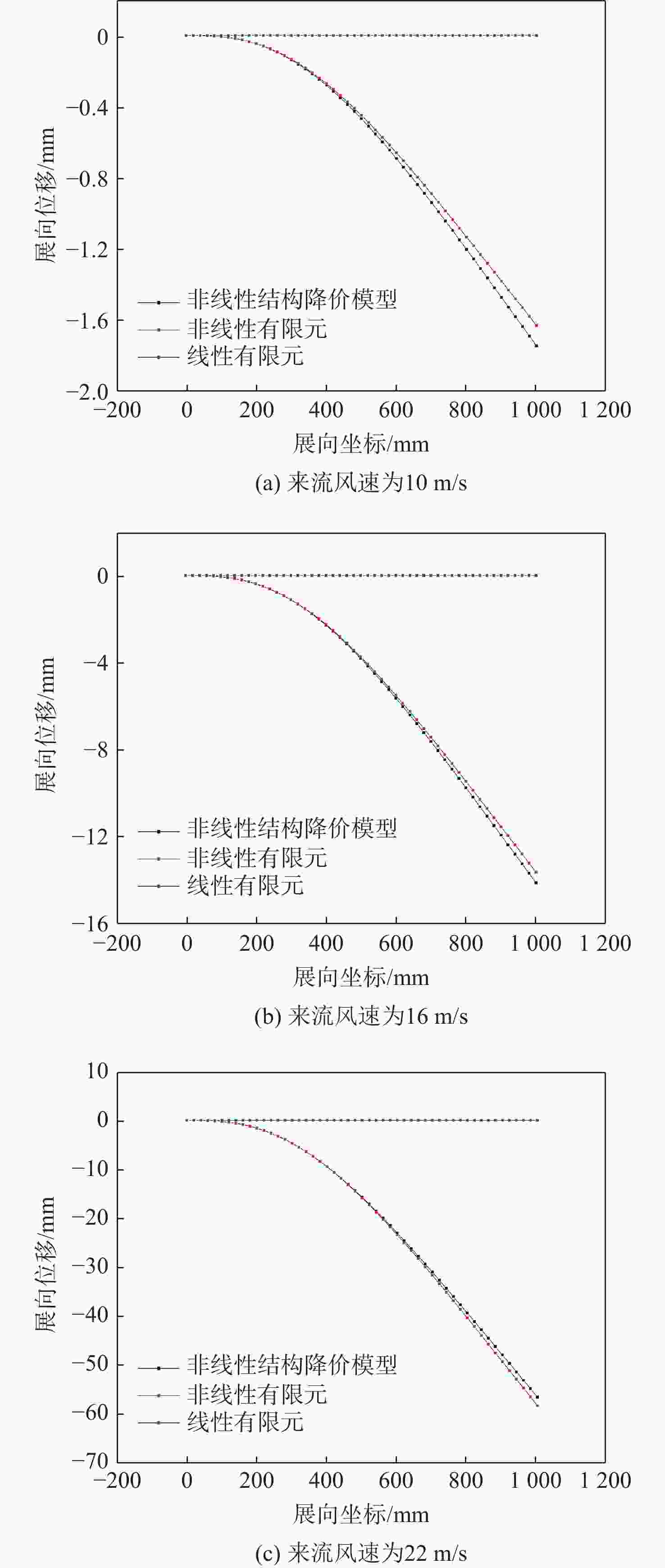
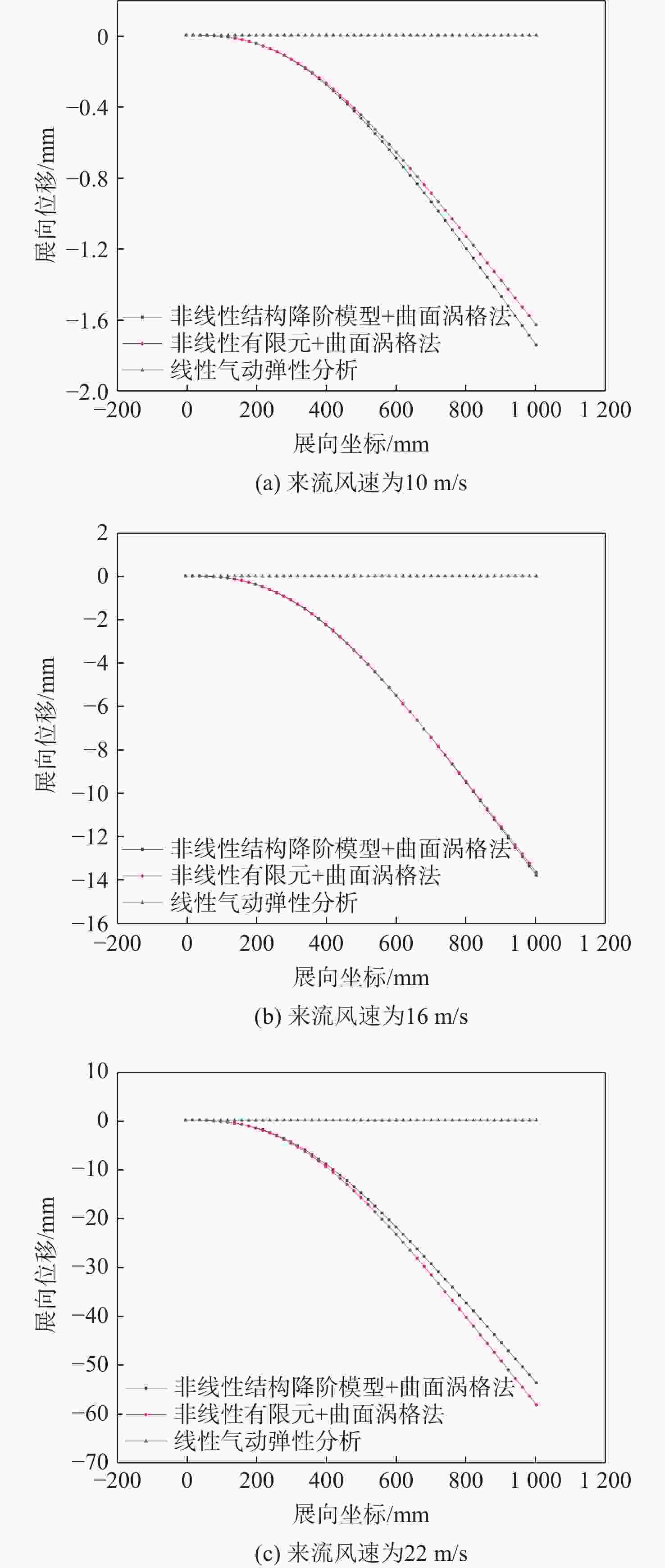
Table 5. Comparison of static aeroelastic spanwise displacement
来流风速/
(m·s−1)展向位移/mm 非线性有限元 非线性结构降阶模型 线性气动弹性分析 10 −1.6 −1.7 0 16 −13.6 −13.7 0 22 −57.9 −53.5 0
下载: 导出CSV
表 6 静气动弹性扭转角对比
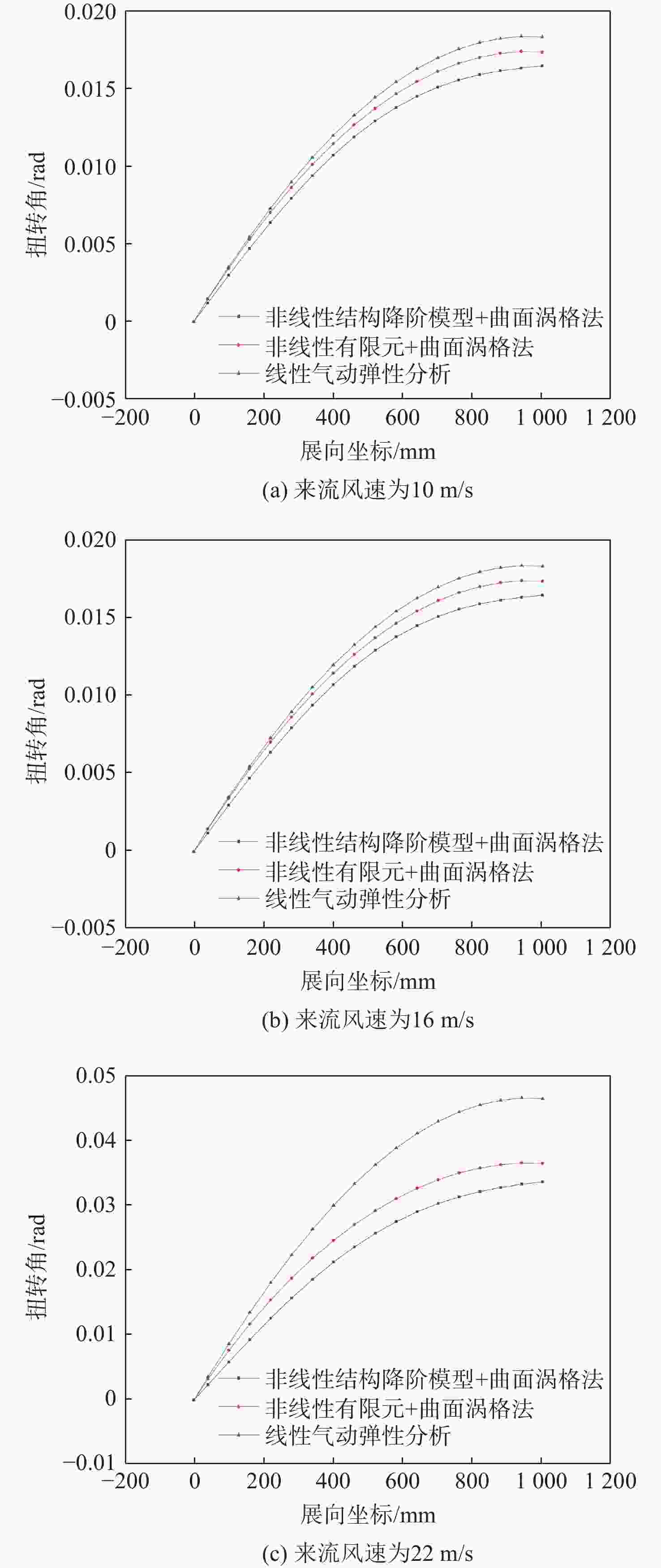
Table 6. Comparison of static aeroelastic twist
来流风速/
(m·s−1)扭转角/(°) 非线性有限元 非线性结构降阶模型 线性气动弹性分析 10 0.343 0.341 0.348 16 0.990 0.939 1.045 22 2.078 1.917 2.645
下载: 导出CSV
-
[1] 谢长川, 吴志刚, 杨超. 大展弦比柔性机翼的气动弹性分析[J]. 北京航空航天大学学报, 2003, 29(12): 1087-1090. doi: 10.13700/j.bh.1001-5965.2003.12.007XIE C C, WU Z G, YANG C. Aeroelastic analysis of flexible large aspect ratio wing[J]. Journal of Beijing University of Aeronautics and Astronautics, 2003, 29(12): 1087-1090(in Chinese). doi: 10.13700/j.bh.1001-5965.2003.12.007 [2] HODGES D H, DOWELL E H. Nonlinear equations of motion for the elastic bending and torsion of twisted nonuniform rotor blades: NASA-TN-D-7818[R]. Washington, D. C. : NASA, 1974. [3] HODGES D H. Review of composite rotor blade modeling[J]. AIAA Journal, 1990, 28(3): 561-565. doi: 10.2514/3.10430 [4] SIMO J C. A finite strain beam formulation. The three-dimensional dynamic problem. Part I[J]. Computer Methods in Applied Mechanics and Engineering, 1985, 49(1): 55-70. doi: 10.1016/0045-7825(85)90050-7 [5] CASTELLANI M, COOPER J E, LEMMENS Y. Nonlinear static aeroelasticity of high aspect ratio wing aircraft by FEM and multibody methods[C]//15th Dynamics Specialists Conference. Reston: AIAA, 2016. [6] MIGNOLET M P, PRZEKOP A, RIZZI S A, et al. A review of indirect/non-intrusive reduced order modeling of nonlinear geometric structures[J]. Journal of Sound and Vibration, 2013, 332(10): 2437-2460. doi: 10.1016/j.jsv.2012.10.017 [7] MCEWAN M I, WRIGHT J R, COOPER J E, et al. A combined modal/finite element analysis technique for the dynamic response of a non-linear beam to harmonic excitation[J]. Journal of Sound and Vibration, 2001, 243(4): 601-624. doi: 10.1006/jsvi.2000.3434 [8] MIGNOLET M P, SOIZE C. Stochastic reduced order models for uncertain geometrically nonlinear dynamical systems[J]. Computer Methods in Applied Mechanics and Engineering, 2008, 197(45-48): 3951-3963. doi: 10.1016/j.cma.2008.03.032 [9] HOLLKAMP J J, GORDON R W, SPOTTSWOOD S M. Nonlinear modal models for sonic fatigue response prediction: A comparison of methods[J]. Journal of Sound and Vibration, 2005, 284(3-5): 1145-1163. doi: 10.1016/j.jsv.2004.08.036 [10] HOLLKAMP J J, GORDON R W. Reduced-order models for nonlinear response prediction: Implicit condensation and expansion[J]. Journal of Sound and Vibration, 2008, 318(4-5): 1139-1153. doi: 10.1016/j.jsv.2008.04.035 [11] GUO X, PRZEKOP A. Energy-based modal basis selection procedures for reduced-order nonlinear simulation[C]//Proceeding of the 51st Structures, Structural Dynamics and Materials Conference. Reston: AIAA, 2010. [12] HARMIN M Y, COOPER J E. Aeroelastic behavior of a wing including geometric nonlinearities[J]. The Aeronautical Journal, 2011, 115(1174): 767-777. doi: 10.1017/S0001924000006515 [13] XIE C C, AN C, LIU Y, et al. Static aeroelastic analysis including geometric nonlinearities based on reduced order model[J]. Chinese Journal of Aeronautics, 2017, 30(2): 638-650. doi: 10.1016/j.cja.2016.12.031 [14] AN C, YANG C, XIE C C, et al. Gust load alleviation including geometric nonlinearities based on dynamic linearization of structural ROM[J]. International Journal of Aerospace Engineering, 2019, 2019: 1-20. [15] MEDEIROS R R, CESNIK C E S, COETZEE E B. Computational aeroelasticity using modal-based structural nonlinear analysis[J]. AIAA Journal, 2020, 58(1): 362-371. doi: 10.2514/1.J058593 [16] 张骥. 一种基于FFT计算离散小波变换的方法[J]. 计算机与数字工程, 2009, 37(10): 29-31. doi: 10.3969/j.issn.1672-9722.2009.10.009ZHANG J. Discrete wavelet transform algorithm-based on fast Fourier transform algorithm[J]. Computer & Digital Engineering, 2009, 37(10): 29-31(in Chinese). doi: 10.3969/j.issn.1672-9722.2009.10.009 [17] 窦苏广, 叶敏. 基于谐波平衡的参激系统非线性参数识别频域法[J]. 振动与冲击, 2009, 28(12): 123-127. doi: 10.3969/j.issn.1000-3835.2009.12.030DOU S G, YE M. Nonlinear identification in frequency domain for parametric excitation system based on harmonic balance principle[J]. Journal of Vibration and Shock, 2009, 28(12): 123-127(in Chinese). doi: 10.3969/j.issn.1000-3835.2009.12.030 [18] IBRAHIM S R. An approach for reducing computational requirements in modal identification[J]. AIAA Journal, 1986, 24(10): 1725-1727. doi: 10.2514/3.9516 [19] 殷有泉. 非线性有限元基础[M]. 北京: 北京大学出版社, 2007: 272-273.YIN Y Q. Nonlinear finite element foundation[M]. Beijing: Peking University Press, 2007: 272-273(in Chinese). [20] 安朝. 大柔性飞行器大柔性飞行器结构建模方法及气动弹性分析研究[D]. 北京: 北京航空航天大学, 2020.AN C. Structure modeling methodology and aeroelastic analysis of large flexible aircraft[D]. Beijing: Beihang University, 2020(in Chinese). [21] 刘燚. 大柔性飞机气动弹性稳定性及动响应分析[D]. 北京: 北京航空航天大学, 2016.LIU Y. Aeroelastic stability and dynamic response analysis of large flexible aircraft [D]. Beijing: Beihang University, 2016 (in Chinese). [22] 刘燚, 杨澜, 谢长川. 基于曲面涡格法的柔性飞机静气动弹性分析[J]. 工程力学, 2018, 35(2): 249-256.LIU Y, YANG L, XIE C C. Study on the static aeroelasticity for flexible aircrat based on non-planar vortex lattice method[J]. Engineering Mechanics, 2018, 35(2): 249-256(in Chinese). [23] XIE C C, YANG C. Surface splines generalization and large deflection interpolation[J]. Journal of Aircraft, 2007, 44(3): 1024-1026. doi: 10.2514/1.24571 -
下载:
点击查看大图
计量
- 文章访问数: 221
- HTML全文浏览量: 57
- PDF下载量: 41
- 被引次数: 0
