Data processing technology of balanced dynamic characteristics based on wavelet reconstruction
-
摘要:
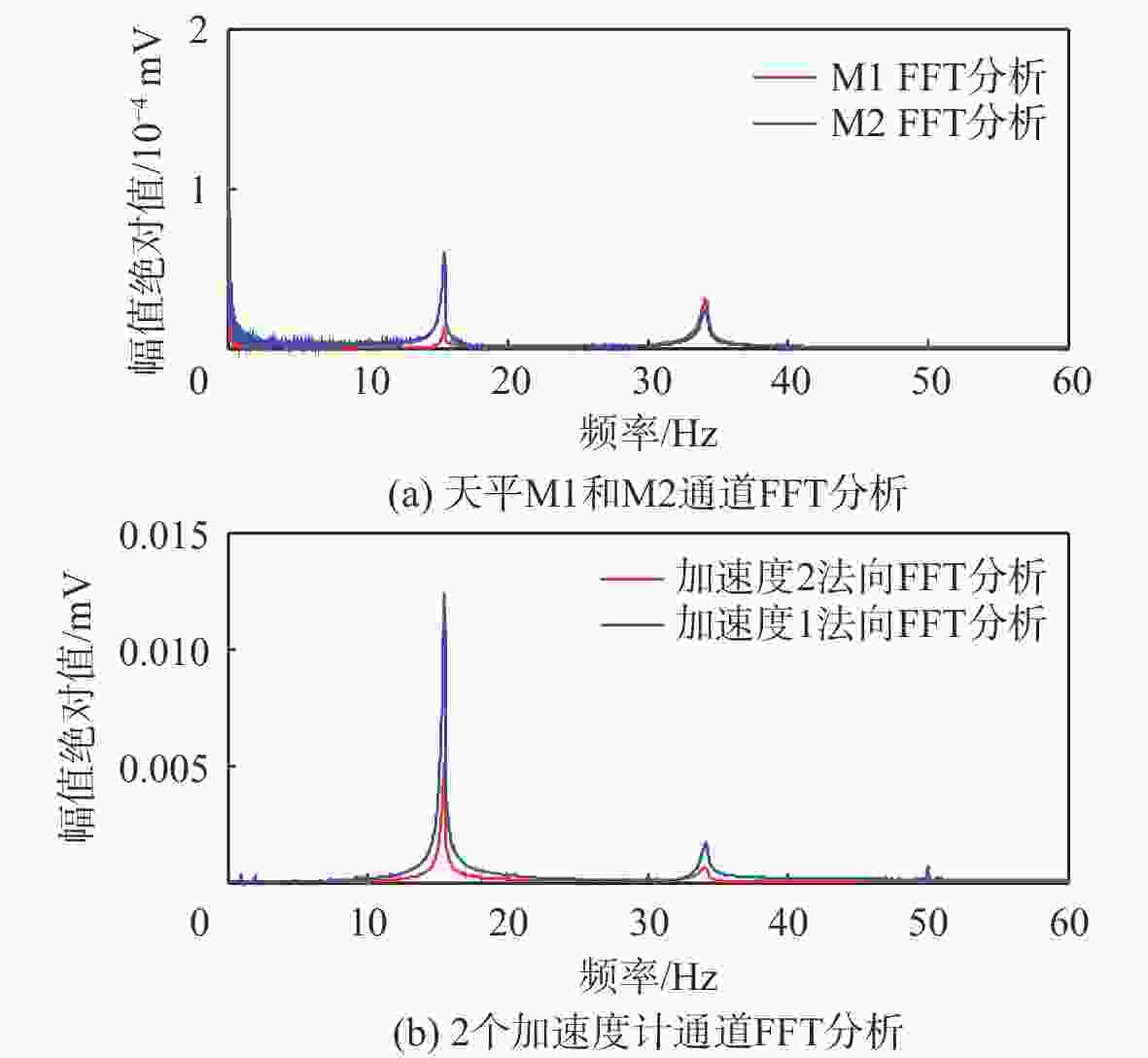
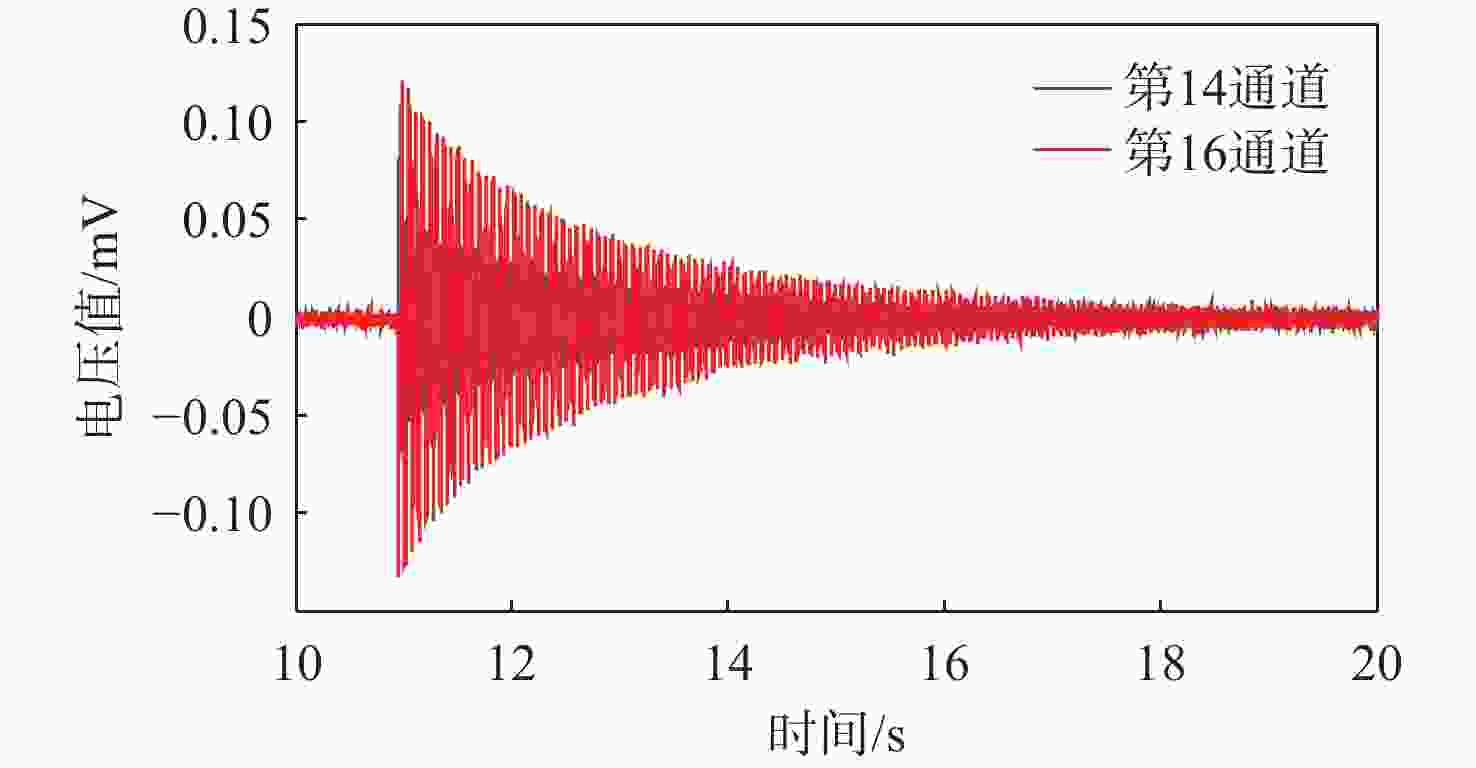
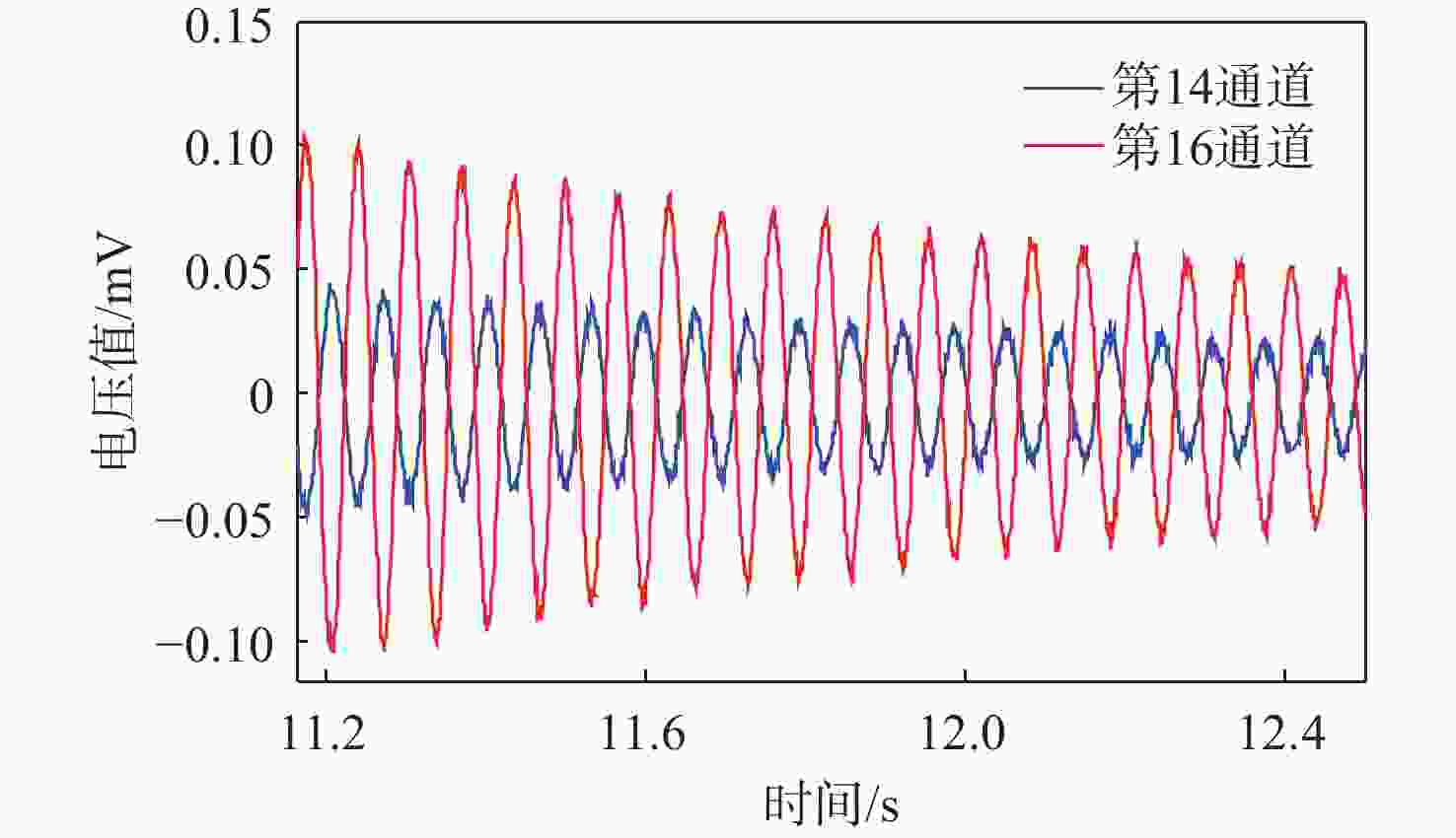
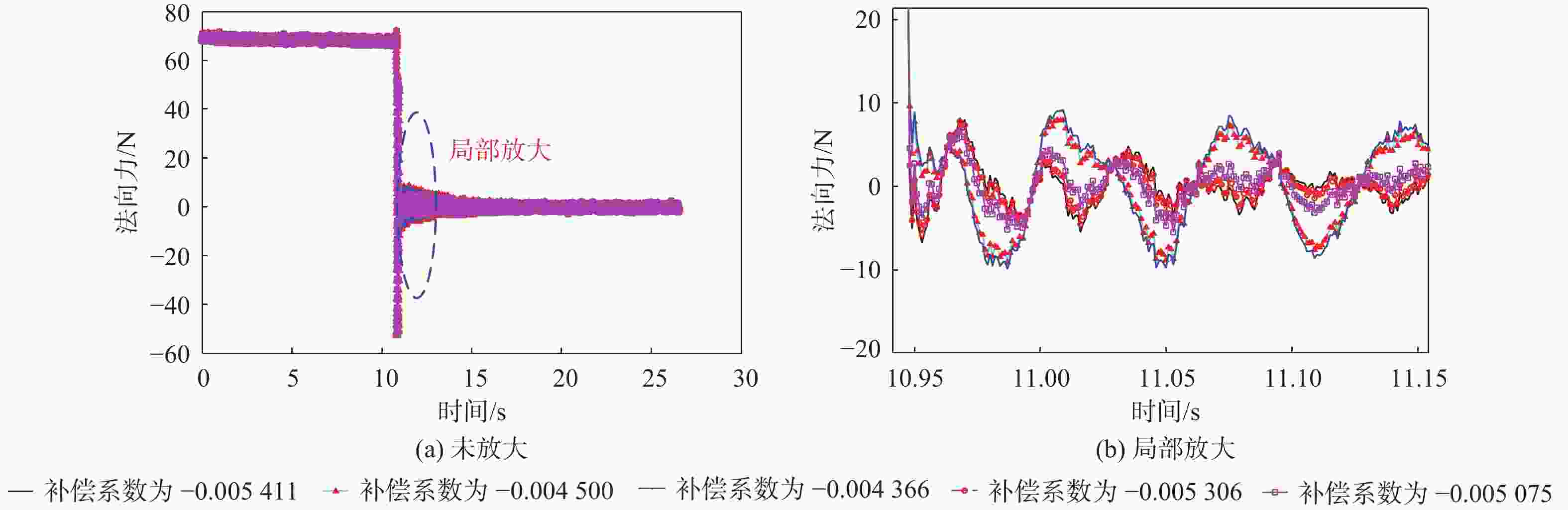
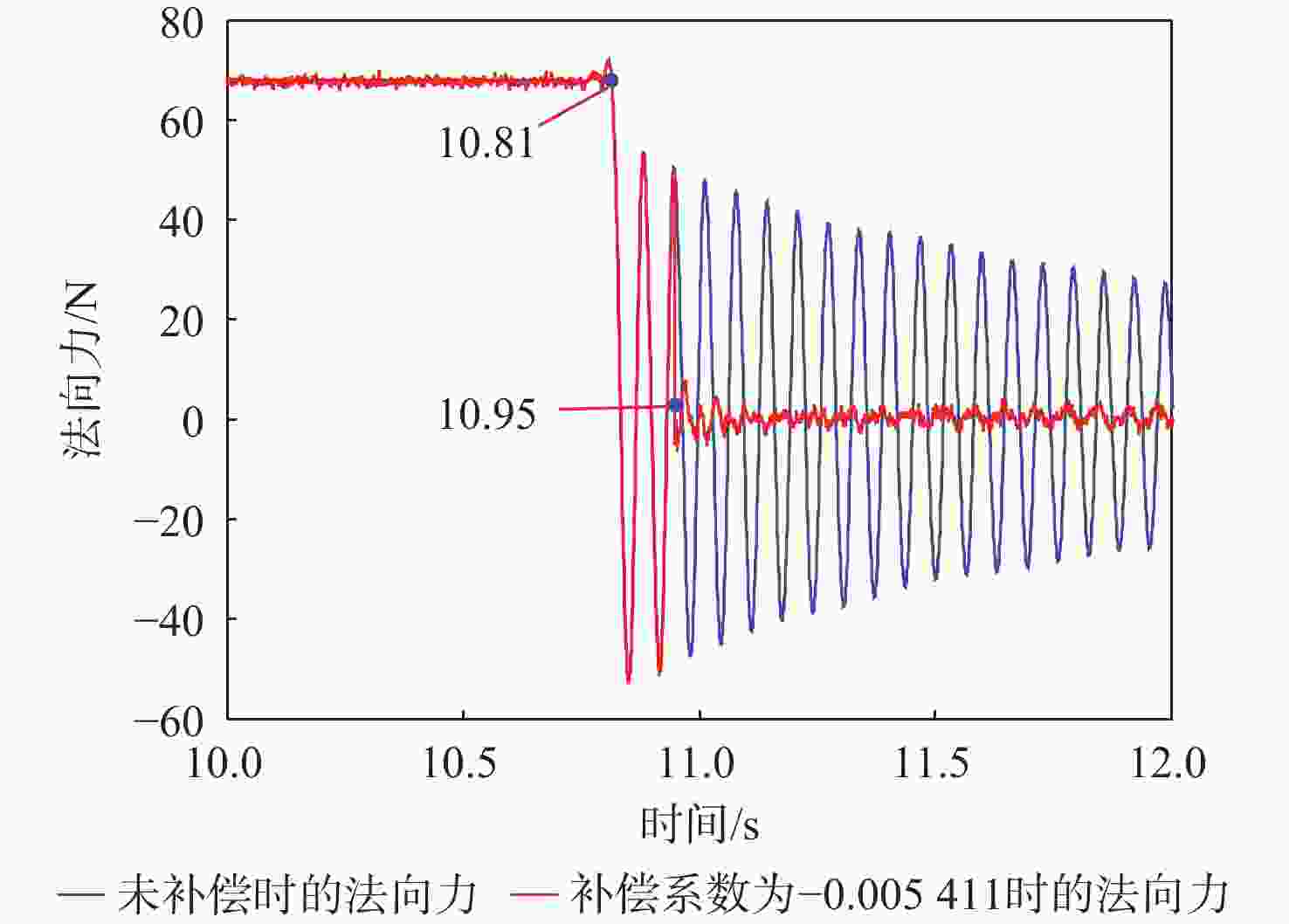
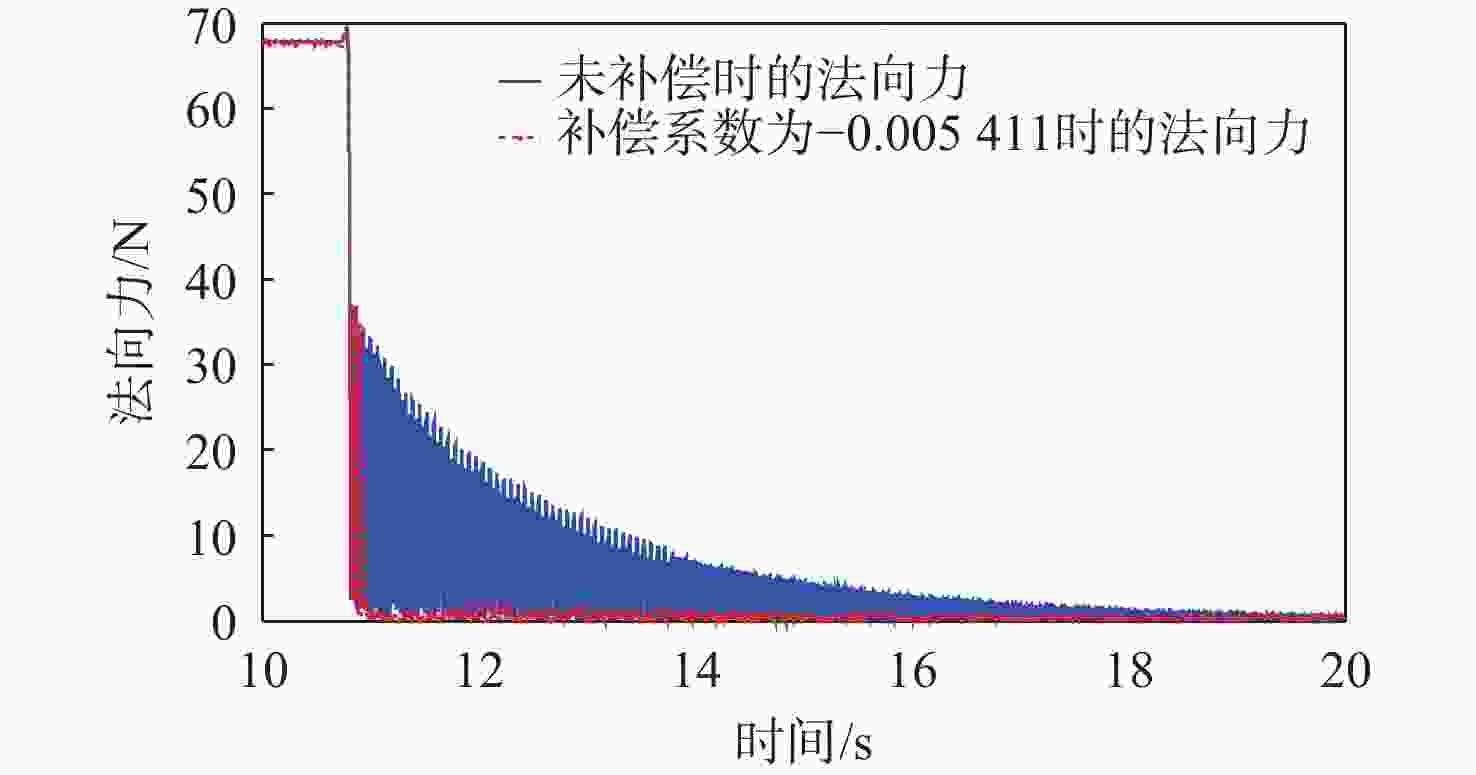
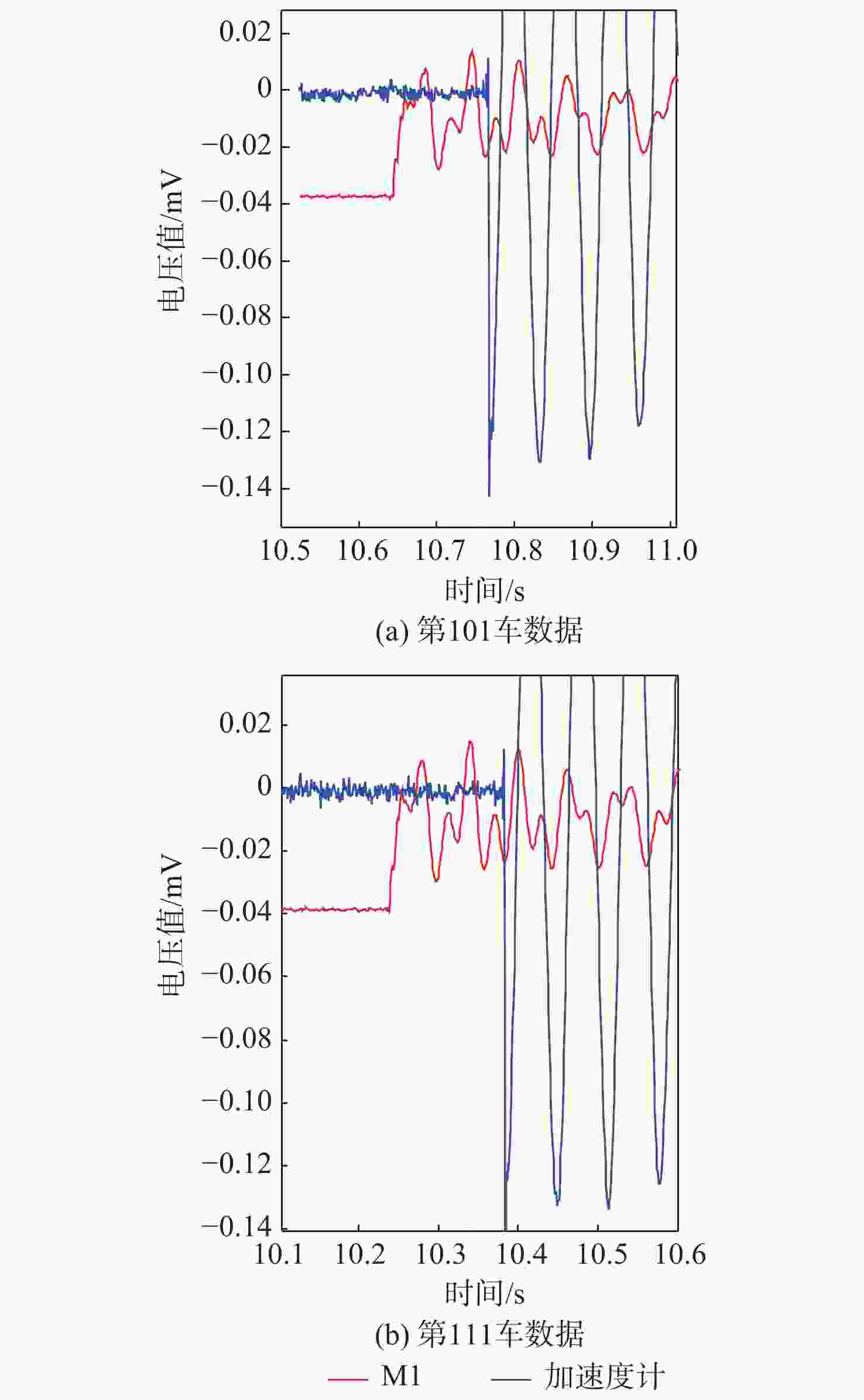
针对风洞试验模型会产生受迫振动，测力天平测量的数据是模型受迫振动和受到气动力的混叠影响测力数据精度的问题，提出基于小波重构的天平动态特性数据处理技术。通过在模型上安装加速度计敲击模型获取受迫振动数据，再对受迫振动数据通过快速傅里叶变换(FFT)分析确定滤波频率阈值，采用小波重构技术实现滤波。通过投影公式计算动态补偿系数，通过补偿系数对天平测量的气动力实现补偿。试验数据分析发现，基于小波重构的天平动态特性数据处理技术，可得到固定的补偿系数，在试验环境中，干扰信号最大能衰减到15.69%，具有重要的工程应用价值。
Abstract:Forced vibration occurs in wind tunnel experiments, thus, the data measured by balance is the aliasing of forced vibration and the aerodynamic force of a model. This affects the accuracy of force data. To address this problem, data processing technology of balanced dynamic characteristics is proposed based on wavelet reconstruction. Acceleration sensors are installed on the model, with vibration data obtained by knocking model, and natural frequency analyzed by fast Fourier transform (FFT). The filtering threshold is determined, and then the wavelet reconstruction is used for filtering. Finally, the dynamic compensation coefficient is calculated by projection equation. The aerodynamic data measured by the balances compensated by the compensation coefficient. Through the analysis of the experimental data, model forced vibration interference data can be processed by balance dynamic characteristics based on wavelet reconstruction. This study shows important application potential of the proposed technology in engineering.
-
Key words:
- wavelet reconstruction /
- balance /
- dynamic compensation /
- data processing /
- compensation coefficient
-
图 2 第34车手动法向激励振动数据FFT分析
Figure 2. FFT analysis of vibration data of manual normal force applied in the 34th test
图 3 第14和第16通道法向加速度计测量值
Figure 3. Normal accelerometer measuremer in channel 14th and 16th
图 4 第14和第16通道法向加速度计阻尼部分放大
Figure 4. Enlarged view of damping data of normal acceleration in channel 14th and 16th
图 5 迎角α=0°时激振不同补偿系数的补偿效果
Figure 5. Compensation effect of different compensation coefficients with angle of attack α=0°
图 6 第1次激振补偿系数为−0.005411的补偿结果局部放大
Figure 6. Enlarged view of compensation effect with compensation coefficient being −0.005411 in firet test
图 8 第2次试验施加法向力60 N时补偿系数
Figure 8. Compensation coefficients in second test with normal external force being 60 N
图 9 第101车不同补偿系数对比
Figure 9. Comparison of different compensation coefficients of the 101th text
图 10 第101车和第111车原始数据相位差对比
Figure 10. Phase difference comparison of original data between the 101th and 111th text
表 1 原始数据采集信息
Table 1. Information of original data collection
类别 通道编号 天平通道 自由度 天平 2 M4 侧向 天平 3 M3 侧向 天平 4 M1 法向 天平 5 MA 轴向 天平 6 M2 法向 天平 7 MX1 扭转 天平 8 MX2 扭转 加速度计 14 加速度计2 法向 加速度计 15 加速度计1X 侧向 加速度计 16 加速度计1Y 法向 加速度计 17 加速度计1Z 轴向 加速度计 18 加速度计3X 侧向 加速度计 19 加速度计3Y 轴向 加速度计 20 加速度计3Z 法向 
下载: 导出CSV
表 2 第1次试验车状态
Table 2. Train status of the first test
迎角α/（°） 法向力/N 车编号/车 0 60 1～4 0 50 5 0 30 6 5 60 7～10 5 50 11 5 30 12 10 60 13～16 10 50 17 10 30 18 −5 60 19～22 −5 50 23 −5 30 24 −10 60 25～28 −10 50 29 −10 30 30 −13～+13 60 33 0 * 34 −13～+13 0 31、37、39 +13～−13 0 38、40 注：*表示手动法向激励。
下载: 导出CSV
表 3 第2次试验车状态
Table 3. Train status of the second test
迎角α/（°） 法向力/N 车编号/车 0 60 101～115 5 60 116～130
下载: 导出CSV
表 4 第1次试验施加法向力补偿系数
Table 4. Normal force compensation coefficient was applied in the first test
迎角α/（°） 法向力/N 第14通道
补偿系数第16通道
补偿系数补偿后
比值0 60 0.012824 −0.005411 −0.421925 0 60 0.010763 −0.004500 −0.418090 0 60 0.010327 −0.004366 −0.422540 0 60 0.005670 −0.002443 −0.431073 0 50 0.012531 −0.005306 −0.423713 0 30 0.011855 −0.005075 −0.427627 5 60 0.004661 −0.002044 −0.437842 5 60 0.006692 −0.002880 −0.430394 5 60 0.007321 −0.003130 −0.427911 5 60 0.012919 −0.005445 −0.421602 5 50 0.001888 −0.000865 −0.458178 5 30 0.008786 −0.003789 −0.431455 10 60 0.008082 −0.003429 −0.424709 10 60 0.007105 −0.003047 −0.428880 10 60 0.008364 −0.003548 −0.424486 10 60 0.007097 −0.002997 −0.423050 10 50 0.012182 −0.005118 −0.419921 10 30 0.010568 −0.004592 −0.434781 −5 60 0.004229 −0.001772 −0.418425 −5 60 0.004980 −0.002097 −0.421170 −5 60 0.004763 −0.002036 −0.427668 −5 60 0.007867 −0.003330 −0.423102 −5 50 0.003732 −0.001593 −0.426389 −5 30 0.004905 −0.002142 −0.436893 −10 60 0.010633 −0.004510 −0.424398 −10 60 0.005843 −0.002507 −0.429957 −10 60 0.009871 −0.004162 −0.422217 −10 60 0.005725 −0.002392 −0.417780 −10 50 0.003583 −0.001508 −0.420557 −10 30 0.008918 −0.003736 −0.418899
下载: 导出CSV
表 5 第1次试验施加法向力补偿系数平均值
Table 5. Normal force mean value of compensation coefficient was applied in the first test
迎角α/（°） 第14通道补偿系数均值 第16通道补偿系数均值 0 0.01130 −0.00476 5 0.00622 −0.00268 10 0.00766 −0.00326 −5 0.00466 −0.00197 −10 0.00802 −0.00339
下载: 导出CSV
表 6 第2次试验施加法向力2种情形下的补偿系数
Table 6. Compensation coefficients under two conditions of appluing normal force in the second text
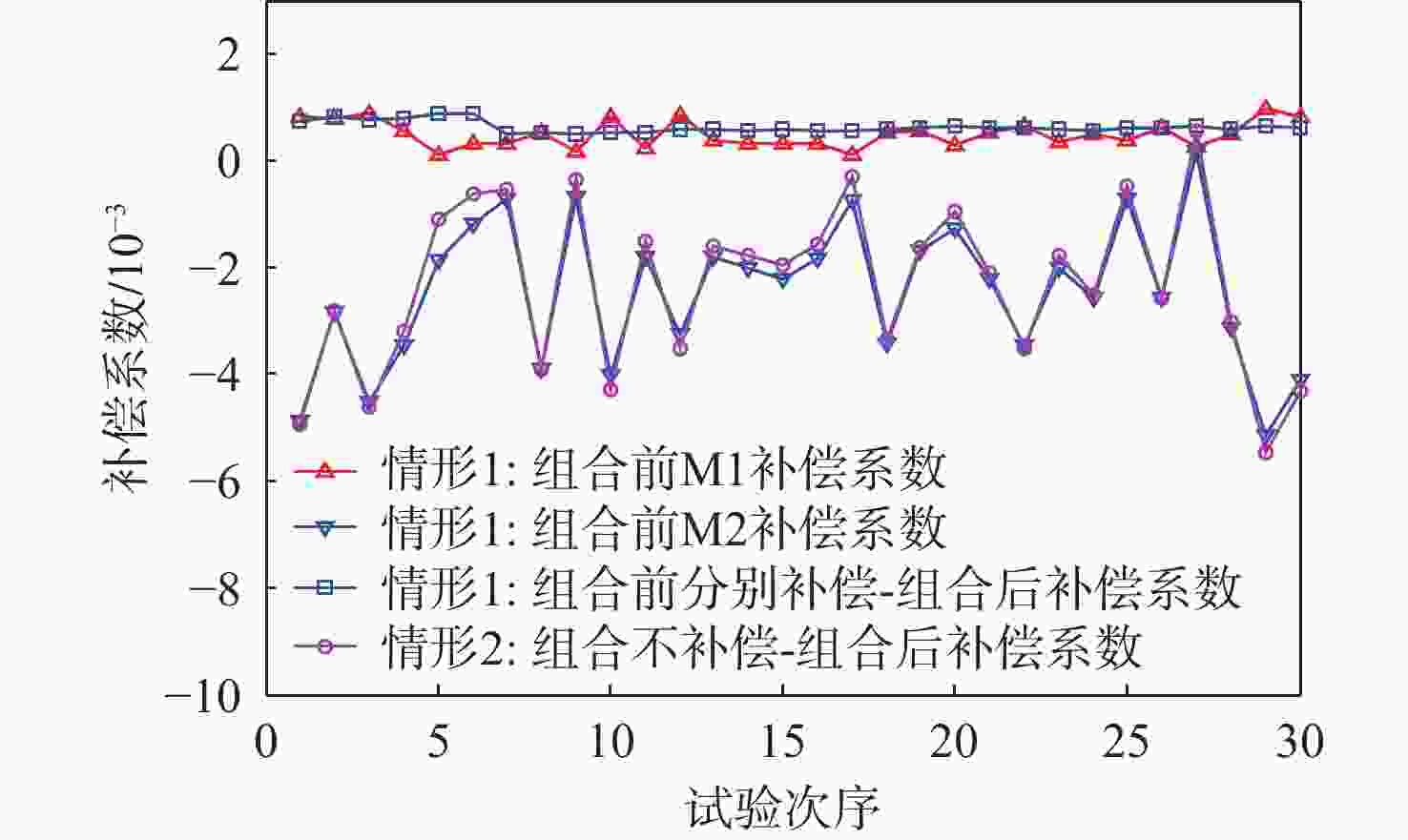
迎角α/（°） 试验车编号/车 组合前后同时补偿系数（情形1） 组合后补偿系数（情形2） 组合前M1补偿系数 组合前M2补偿系数 组合后补偿系数 0 101 0.000819 −0.004866 0.000737 −0.00484 102 0.000801 −0.002836 0.000815 −0.00292 103 0.000890 −0.004508 0.000780 −0.00449 104 0.000564 −0.003444 0.000812 −0.00329 105 0.000126 −0.001848 0.000883 −0.00124 106 0.000312 −0.001182 0.000880 −0.00077 107 0.000334 −0.000715 0.000504 −0.00072 108 0.000531 −0.003894 0.000529 −0.00396 109 0.000178 −0.000692 0.000510 −0.00053 110 0.000820 −0.004008 0.000532 −0.00435 111 0.000238 −0.001797 0.000519 −0.00166 112 0.000848 −0.003259 0.000592 −0.00360 113 0.000395 −0.001796 0.000583 −0.00175 114 0.000317 −0.002019 0.000563 −0.00192 115 0.000324 −0.002229 0.000592 −0.00209 5 116 0.000313 −0.001817 0.000574 −0.00171 117 0.000129 −0.000734 0.000575 −0.00045 118 0.000544 −0.003413 0.000606 −0.00344 119 0.000571 −0.001697 0.000631 −0.00179 120 0.000301 −0.001281 0.000644 −0.00109 121 0.000520 −0.002220 0.000634 −0.00223 122 0.000653 −0.003465 0.000608 −0.00360 123 0.000353 −0.002022 0.000587 −0.00193 124 0.000502 −0.002565 0.000561 −0.00262 125 0.000382 −0.000710 0.000613 −0.00064 126 0.000613 −0.002582 0.000628 −0.00270 127 0.000253 0.000168 0.000656 0.00039 128 0.000497 −0.003134 0.000602 −0.00313 129 0.000968 −0.005145 0.000643 −0.00541 130 0.000831 −0.004115 0.000636 −0.00437
下载: 导出CSV
表 7 第2次试验施加法向力2种情形下的补偿系数平均值
Table 7. Mean value of compensation coefficients under two conditions of applying normal force in the second test
迎角α/（°） 组合前后同时偿系数均值（情形1） 组合后补偿系数均值（情形2） 组合前M1补偿系数 组合前M2补偿系数 组合后补偿系数 0 0.000500 −0.002606 0.000655 −0.002444 5 0.000513 −0.002493 0.000610 −0.002390
下载: 导出CSV
表 8 第2次试验施加法向力加速度相位移动后的补偿系数（第1组）
Table 8. Compensation coefficient after normal application of acceleration phase shift of external force in the second text (the first group)
试验车
编号/车与101车比较 相位差点数移动数量 相位对齐时
补偿系数校正值 校差值 −20 −19 −18 −17 −16 −15 −14 −13 −12 −11 0 1 2 3 101 0 0 0.00291 −0.00598 0.00100 0.00556 −0.00253 −0.00530 0.00189 0.00573 0.00097 −0.00479 −0.00484 −0.00526 −0.00549 −0.00544 −0.00484 102 0 −16 −0.00497 −0.00132 0.00591 −0.00147 −0.00549 0.00191 0.00560 −0.00013 −0.00548 −0.00355 −0.00292 −0.00223 −0.00121 0.00040 −0.00549 103 3 1 0.00361 −0.00587 0.00021 0.00583 −0.00180 −0.00562 0.00114 0.00581 0.00174 −0.00435 −0.00449 −0.00502 −0.00539 −0.00556 −0.00556 104 0 −14 −0.00475 −0.00177 0.00597 −0.00104 −0.00567 0.00149 0.00573 0.00031 −0.00539 −0.00391 −0.00329 −0.00264 −0.00165 −0.00005 0.00573 105 0 −18 −0.00585 0.00077 0.00542 −0.00334 −0.00450 0.00367 0.00482 −0.00209 −0.00568 −0.00184 −0.00124 −0.00040 0.00068 0.00223 0.00542 106 0 −19 −0.00600 0.00132 0.00521 −0.00380 −0.00416 0.00409 0.00454 −0.00258 −0.00564 −0.00135 −0.00077 0.00010 0.00117 0.00268 0.00132 107 0 −20 −0.00600 0.00144 0.00514 −0.00388 −0.00407 0.00416 0.00447 −0.00267 −0.00561 −0.00125 −0.00072 0.00019 0.00125 0.00275 −0.00600 108 0 −12 −0.00403 −0.00270 0.00585 −0.00004 −0.00583 0.00050 0.00577 0.00129 −0.00494 −0.00455 −0.00396 −0.00344 −0.00253 −0.00101 −0.00494 109 0 −20 −0.00603 0.00165 0.00503 −0.00403 −0.00392 0.00430 0.00433 −0.00285 −0.00557 −0.00105 −0.00053 0.00037 0.00144 0.00291 −0.00603 110 0 −12 −0.00360 −0.00323 0.00576 0.00053 −0.00590 −0.00006 0.00577 0.00184 −0.00467 −0.00489 −0.00435 −0.00387 −0.00302 −0.00155 −0.00467 注：①红色是经过移动相位差对应的补偿系数，蓝色是经过移动相位补偿系数异常标注，以上扣除了异常127车；②校正值代表经过自动计算的相位差点数，校差值代表人工对校正值的修正，表中的加粗的数据代表经过校正值后的补偿系数。
下载: 导出CSV
表 9 第2次试验施加法向力加速度相位移动后的补偿系数（第2组）
Table 9. Compensation coefficient after normal application of acceleration phase shift of external force in the second test (the second group)
试验车
编号/车与101车比较 相位差点数移动数量 相位对齐时
补偿系数校正值 校差值 −20 −19 −18 −17 −16 −15 −14 −13 −12 −11 0 1 2 3 111 0 −17 −0.00578 0.00039 0.00559 −0.00303 −0.00476 0.00337 0.00505 −0.00171 −0.00571 −0.00222 −0.00166 −0.00082 0.00025 0.00183 −0.00303 112 0 −14 −0.00446 −0.00213 0.00591 −0.00064 −0.00572 0.00108 0.00573 0.00072 −0.00518 −0.00416 −0.00360 −0.00298 −0.00203 −0.00047 0.00573 113 0 −18 −0.00576 0.00027 0.00564 −0.00294 −0.00483 0.00328 0.00511 −0.00161 −0.00572 −0.00232 −0.00175 −0.00092 0.00015 0.00174 0.00564 114 0 −18 −0.00569 0.00010 0.00570 −0.00279 −0.00493 0.00314 0.00519 −0.00145 −0.00571 −0.00248 −0.00192 −0.00109 −0.00001 0.00159 0.00570 115 −15 −17 −0.00561 −0.00014 0.00576 −0.00257 −0.00505 0.00294 0.00528 −0.00122 −0.00570 −0.00267 −0.00209 −0.00130 −0.00023 0.00137 0.00294 116 0 −17 −0.00579 0.00036 0.00563 −0.00301 −0.00480 0.00336 0.00509 −0.00169 −0.00573 −0.00227 −0.00171 −0.00086 0.00022 0.00181 −0.00301 117 0 −19 −0.00605 0.00174 0.00498 −0.00411 −0.00386 0.00437 0.00428 −0.00292 −0.00556 −0.00098 −0.00045 0.00045 0.00150 0.00298 0.00174 118 0 −13 −0.00467 −0.00190 0.00597 −0.00090 −0.00571 0.00134 0.00575 0.00047 −0.00533 −0.00403 −0.00344 −0.00280 −0.00182 −0.00023 0.00047 119 0 −18 −0.00570 0.00021 0.00563 −0.00287 −0.00484 0.00323 0.00511 −0.00156 −0.00570 −0.00236 −0.00179 −0.00096 0.00011 0.00170 0.00563 120 −18 −19 −0.00595 0.00101 0.00535 −0.00355 −0.00438 0.00386 0.00473 −0.00229 −0.00569 −0.00166 −0.00109 −0.00023 0.00085 0.00239 0.00535 注：①红色是经过移动相位差对应的补偿系数，蓝色是经过移动相位补偿系数异常标注，以上扣除了异常127车；②校正值代表经过自动计算的相位差点数，校差值代表人工对校正值的修正，表中的加粗的数据代表经过校正值后的补偿系数。
下载: 导出CSV
表 10 第2次试验施加法向力加速度相位移动后的补偿系数（第3组）
Table 10. Compensation coefficient after normal application of acceleration phase shift of external force in the second test (the third group)
试验车
编号/车与101车比较 相位差点数移动数量 相位对齐时
补偿系数校正值 校差值 −20 −19 −18 −17 −16 −15 −14 −13 −12 −11 0 1 2 3 121 −15 −17 −0.00553 −0.00033 0.00580 −0.00240 −0.00513 0.00278 0.00535 −0.00105 −0.00569 −0.00283 −0.00223 −0.00145 −0.00039 0.00121 0.00278 122 0 −14 −0.00454 −0.00210 0.00597 −0.00069 −0.00577 0.00114 0.00578 0.00068 −0.00525 −0.00418 −0.00360 −0.00298 −0.00202 −0.00044 0.00578 123 −16 −17 −0.00569 0.00008 0.00571 −0.00277 −0.00495 0.00313 0.00521 −0.00143 −0.00573 −0.00251 −0.00193 −0.00111 −0.00004 0.00157 −0.00495 124 0 −16 −0.00531 −0.00080 0.00590 −0.00197 −0.00535 0.00237 0.00552 −0.00060 −0.00562 −0.00322 −0.00262 −0.00188 −0.00084 0.00078 −0.00535 125 0 −20 −0.00600 0.00153 0.00506 −0.00393 −0.00398 0.00420 0.00438 −0.00272 −0.00557 −0.00117 −0.00064 0.00024 0.00130 0.00278 −0.00600 126 0 −16 −0.00528 −0.00088 0.00592 −0.00191 −0.00539 0.00231 0.00555 −0.00053 −0.00561 −0.00328 −0.00270 −0.00194 −0.00090 0.00072 −0.00539 128 −13 −15 −0.00494 −0.00148 0.00596 −0.00132 −0.00559 0.00175 0.00568 0.00006 −0.00546 −0.00372 −0.00313 −0.00245 −0.00144 0.00017 0.00006 129 2 −5 0.00063 −0.00584 0.00318 0.00439 −0.00436 −0.00400 0.00382 0.00506 −0.00121 −0.00561 −0.00541 −0.00554 −0.00537 −0.00473 −0.00537 130 0 −12 −0.00360 −0.00324 0.00576 0.00055 −0.00590 −0.00008 0.00577 0.00186 −0.00466 −0.00490 −0.00437 −0.00388 −0.00304 −0.00157 −0.00466 注：①红色是经过移动相位差对应的补偿系数，蓝色是经过移动相位补偿系数异常标注，以上扣除了异常127车；②校正值代表经过自动计算的相位差点数，校差值代表人工对校正值的修正，表中的加粗的数据代表经过校正值后的补偿系数。
下载: 导出CSV
-
[1] 史玉杰, 黄勇, 田正波. 小展弦比飞翼布局高速标模测力天平研制[J]. 实验流体力学, 2015, 29(5): 50-54.SHI Y J, HUANG Y, TIAN Z B. Strain gauge balance development for force test on small aspect ratio flying wing high speed standard model[J]. Journal of Experiments in Fluid Mechanics, 2015, 29(5): 50-54(in Chinese). [2] 罗华云, 赖传兴, 王月贵, 等. 喷管模型试验器六分量天平校准技术[J]. 航空动力学报, 2013, 28(1): 67-73.LUO H Y, LAI C X, WANG Y G, et al. Six-component balance calibration technology for nozzle model testing facility[J]. Journal of Aerospace Power, 2013, 28(1): 67-73(in Chinese). [3] 吕金洲, 张小庆, 陈光雄, 等. 基于惯性补偿的脉冲风洞测力天平瞬态研究[J]. 振动与冲击, 2018, 37(2): 216-222.LV J Z, ZHANG X Q, CHEN G X, et al. Transient simulation for dynamic output of force measuring balance in animpulse combustion wind tunnel based on inertia compensation[J]. Journal of Vibration and Shock, 2018, 37(2): 216-222(in Chinese). [4] 王锋, 武龙, 吴东升, 等. 脉冲风洞天平短时振荡测力数据稳态值提取的优化识别方法[J]. 振动与冲击, 2018, 37(8): 153-158.WANG F, WU L, WU D S, et al. An optimization method of recovering steady-state value from short-time oscillatory signal of force balance for impulse tunnel[J]. Journal of Vibration and Shock, 2018, 37(8): 153-158(in Chinese). [5] 徐科军, 杨双龙, 张进, 等. 杆式风洞应变天平动态实验、建模与补偿[J]. 仪器仪表学报, 2009, 30(10): 2123-2130.XU K J, YANG S L, ZHANG J, et al. Dynamic experiment, modeling and compensation of bar-shaped strain gauge balance for wind tunnel[J]. Chinese Journal of Scientific Instrument, 2009, 30(10): 2123-2130(in Chinese). [6] 郭晨曦, 郝新红, 栗苹,等. 毫米波调频引信的优化二维FFT信号处理算法[J]. 北京航空航天大学学报, 2020, 46(1): 220-228.GUO C X, HAO X H, LI P, et al. Optimized two-dimensional FFT signal processing algorithm for millimeter-wave FM fuze[J]. Journal of Beijing University of Aeronautics and Astronautics, 2020, 46(1): 220-228(in Chinese). [7] RENE DE JESUS R T. Multirate signal processing to improve FFT-based analysis for detecting faults in induction motors[J]. IEEE Transactions on Industrial Informatics, 2017, 13(3): 1291-1300. doi: 10.1109/TII.2016.2603968 [8] SOBIA B, USMAN A, HAFIZ M A, et al. Closed-form BER expression for Fourier and wavelet transform-based pulse-shaped data in downlink NOMA[J]. IEEE Communications Letters, 2019, 23(4): 592-595. doi: 10.1109/LCOMM.2019.2903083 [9] ZHOU Q G, CHEN D. Improving wavelet reconstruction algorithm to achieve comprehensive application of thermal infrared remote sensing data from TM and MODIS[J]. High Technology Letters, 2015, 21(2): 224-230. [10] KEYLOCK C J, SINGH K, GEORGIOU E F. The complexity of gravel bed river topography examined with gradual wavelet reconstruction[J]. Journal of Geophysical Research: Earth Surface, 2014, 119(3): 682-700. doi: 10.1002/2013JF002999 [11] 吴央, 袁运能. 基于小波包分解和FCM聚类的纹理图像分割方法[J]. 北京航空航天大学学报, 2008, 34(5): 572-575.WU Y, YUAN Y N. Texture image segmentation method based on wavelet packet transform and FCM clustring[J], Journal of Beijing University of Aeronautics and Astronautics, 2008, 34(5): 572-575 (in Chinese). [12] LIU W X, WANG Y J, LIU X, et al. Weak thruster fault detection for AUV based on stochastic resonance and wavelet reconstruction[J]. Journal of Central South University, 2016, 23(11): 2883-2895. doi: 10.1007/s11771-016-3352-1 [13] LEMING Q, PARTHA S R, PHIL D A. Wavelet reconstruction of nonuniformly sampled signals[J]. IEEE Signal Processing Letters, 2009, 16(2): 73-76. [14] 陈浩, 郭军海, 齐巍. 基于经验小波变换的目标加速度估计算法[J]. 北京航空航天大学学报, 2015, 41(1): 154-159.CHEN H, GUO J H, QI W. Estimation of target’s acceleration based on empirical wavelet transform[J]. Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(1): 154-159(in Chinese). [15] JEON Y J, CHOI D C, LEE S J, et al. Defect detection for corner cracks in steel billets using a wavelet reconstruction method[J]. Journal of the Optical Society of America A, Optics, Image Science, and Vision, 2014, 31(2): 227-237. doi: 10.1364/JOSAA.31.000227 [16] 姚裕, 吴洪涛. 大膨胀比喷管试验台的六分量天平研究[J]. 南京理工大学学报, 2011, 35(4): 547-551.YAO Y, WU H T. Six-component force balance for big expansion ratio nozzle test-bed[J]. Journal of Nanjing University of Science and Technology, 2011, 35(4): 547-551(in Chinese). -
下载:
点击查看大图
计量
- 文章访问数: 199
- HTML全文浏览量: 69
- PDF下载量: 13
- 被引次数: 0
