-
摘要:
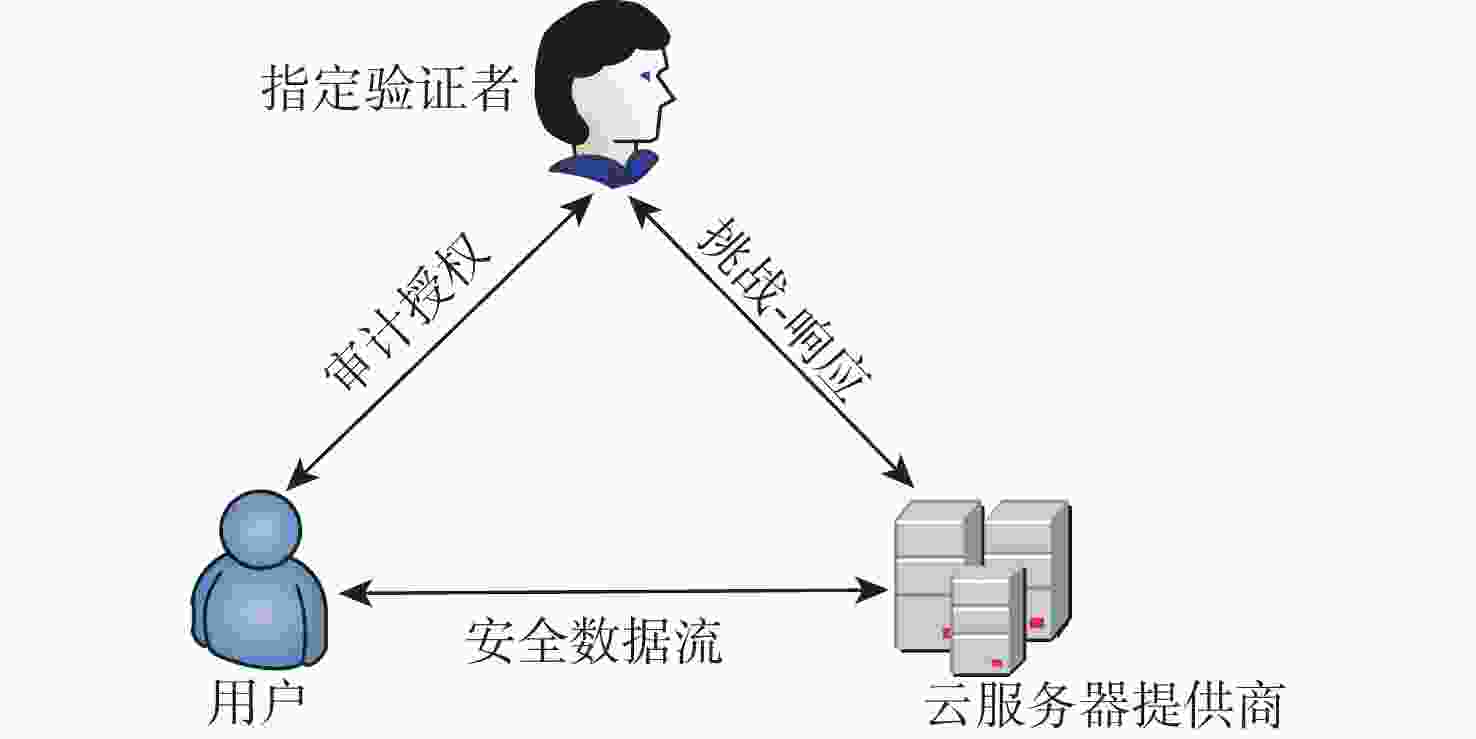
强指定验证者签名(SDVS)方案允许签名者指定一个验证者,只有指定的验证者才能确保签名是由签名者生成。利用陷门生成算法构造了一种基于格的强指定验证者签名方案,并给出了签名方案的正确性证明。基于改进的小整数解(SIS)问题,在标准模型中证明了所提方案在适应性选择消息攻击下是存在性不可伪造的,基于误差学习(LWE)问题证明了所提方案的不可转移性及签名人身份的隐私性。将所提方案应用到云计算的数据完整性审计机制中,使得只有授权的第三方才拥有数据验证权利,有效保护了用户的隐私。
-
关键词:
- 格 /
- 强指定验证者签名方案 /
- 小整数解问题 /
- 误差学习问题 /
- 强不可伪造性
Abstract:The signer can identify a verifier using the strong designated verifier signature (SDVS) scheme. Only the selected verifier can confirm that the signature was created by the signer. Using the trapdoor generation process, we first built a lattice-based strongly designated verifier signature scheme and demonstrated its accuracy. At the same time, based on the improved small integer solution (SIS) problem, the existential unforgeability of the scheme under adaptive chosen message attack is proved in the standard model. The non-transferability of the technique and the secrecy of the signer’s identity are demonstrated utilizing learning with errors (LWE) problem. In order to successfully protect the user’s privacy, the signature technique is then used to the data integrity audit mechanism in cloud computing. As a result, only the approved third party has the right to verify the data.
-
[1] JAKOBSSON M, SAKO K, IMPAGLIAZZO R. Designated verifier proofs and their applications[C]//International Conference on the Theory and Applications of Cryptographic Techniques. Berlin: Springer, 1996: 143-154. [2] STEINFELD R, BULL L, WANG H, et al. Universal designated verifier signatures[C]//International Conference on the Theory and Application of Cryptology and Information Security. Berlin: Springer, 2003: 523-542. [3] SAEEDNIA S, KREMER S, MARKOWITCH O. An efficient strong designated verifier signature Scheme[C]//Proceedings of the 6th International Conference on Information Security and Cryptology. Berlin: Springer, 2003: 40-54. [4] LAGUILLAUMIE F, VERGNAUD D. Designated verifier signatures: Anonymity and efficient construction fromany bilinear map[C]//International Conference on Security in Communication Networks. Berlin: Springer, 2004, 3352: 105-119. [5] HUANG Q, YANG G, WONG D S, et al. Efficient strong designated verifier signature schemes without random oracle or with non-delegatability[J]. International Journal of Information Security, 2011, 10: 373-385. doi: 10.1007/s10207-011-0146-1 [6] KI J H, HWANG J Y, NYANG D H, et al. Constructing strong identity-based designated verifier signatures with self-unverifiability[J]. ETRI Journal, 2012, 34(2): 235-244. doi: 10.4218/etrij.12.0111.0597 [7] 李继国, 钱娜, 黄欣沂, 等. 基于证书强指定验证者签名方案[J]. 计算机学报, 2012, 35(8): 1579-1587. doi: 10.3724/SP.J.1016.2012.01579LI J G, QIAN N, HUANG X Y, et al. Certificate-based strong designated verifier signature scheme[J]. Chinese Journal of Computers, 2012, 35(8): 1579-1587(in Chinese). doi: 10.3724/SP.J.1016.2012.01579 [8] YANG X, CHEN G, LI T, et al. Strong designated verifier signature scheme with undeniability and strong unforgeability in the standard model[J]. Applied Sciences, 2019, 9(10): 2062. doi: 10.3390/app9102062 [9] WANG F, HU Y, WANG B. Lattice-based strong designate verifier signature and its applications[J]. Malaysian Journal of Computer Science, 2012, 25(1): 11-22. [10] 李明祥, 郑艳娟. 格基强指定验证者签名方案[J]. 小型微型计算机系统, 2013, 34(10): 2363-2366. doi: 10.3969/j.issn.1000-1220.2013.10.027LI M X, ZHENG Y J. Lattice-based strong designated verifier signature scheme[J]. Journal of Chinese Mini-Micro Computer Systems, 2013, 34(10): 2363-2366(in Chinese). doi: 10.3969/j.issn.1000-1220.2013.10.027 [11] GEONTAE N, IK R J. Strong designated verifier signature scheme from lattices in the standard model[J]. Security and Communication Networks, 2017, 9(18): 6202-6214. [12] CAI J, HAN J, ZHANG P, et al. An efficient strong designated verifier signature based on R-SIS assumption[J]. IEEE Access, 2019, 7: 3938-3947. doi: 10.1109/ACCESS.2018.2889242 [13] GENTRY C, PEIKERT C, VAIKUNTANATHAN V. Trapdoors for hard lattices and new cryptographic constructions[C]//The 40th Annual ACM Symposium on the Theory of Computing. New York: ACM, 2008: 197-206. [14] AJTAI M. Generating hard instances of lattice problems[C]//The 28th ACM Symposium on the Theory of Computing. New York: ACM, 1996: 99-108. [15] MICCIANCIO D, REGEV O. Worst-case to average-case reductions based on Gaussian measures[J]. SIAM Journal on Computing, 2007, 37(1): 267-302. doi: 10.1137/S0097539705447360 [16] REGEV O. On lattices, learning with errors, random linear codes, and cryptography[J]. Journal of the ACM, 2009, 56(6): 84-93. [17] LYUBASHEVSKY V, MICCIANCIO D. On bounded distance decoding, unique shortest vectors, and the minimum distance problem[C]//Annual International Cryptology Conference. Berlin: Springer, 2009, 5677: 577-594. [18] MICCIANCIO D, PEIKERT C. Trapdoors for lattices: Simpler, tighter, faster, smaller[C]//The 31st Annual International Conference on Theory and Applications of Cryptographic. Berlin: Springer, 2012: 700-718. [19] WORKU S G, XU C, ZHAO J. Cloud data auditing with designated verifier[J]. Frontiers of Computer Science Springer, 2014, 8(3): 503-512. doi: 10.1007/s11704-013-3138-7 [20] 岳峰. 高效的指定验证者签名体制及其应用研究[D]. 成都: 电子科技大学, 2016.YUE F. Researching of efficient designated verifier signature scheme and application[D]. Chengdu: University of Electronic Science and Technology, 2016(in Chinese). -






 下载:
下载:



