GNSS instantaneous attitude determination method based on multi-variable constraints
-
摘要:
传统的直接定姿法或最小二乘法依赖于整周模糊度的成功固定。当卫星数目较少或存在干扰的情形下，模糊度固定成功率会大大降低，进而导致定姿结果不准确。因此，提出基于多变量约束的姿态确定方法，所提方法将整周模糊度和姿态确定视作联合问题进行解算且对基线长度没有限制。利用天线的几何信息和姿态矩阵的正交特性对观测模型进行多变量约束，能够有效提升模糊度固定成功率并实现瞬时定姿。仿真结果表明：即使在信号观测精度非常低的场景下，所提方法也能达到75.7%的模糊度固定成功率；即使只有4颗卫星，所提方法也能达到90%以上的成功率。且在使用超短基线的前提下，所提方法能够达到0.93°的定姿精度。
Abstract:The traditional direct attitude determination or least square method depends on the correct fixation of the ambiguity. When the number of satellites is small or there is interference, the success rate of ambiguity will be greatly reduced, which will lead to inaccurate attitude determination results. This study employs the multivariate constraint-based attitude determination method, which treats attitude determination and ambiguity as a single problem to be solved and does not place any strict restrictions on the baseline's length. This paper uses the geometric information of the antennas and the orthogonal characteristics of the attitude matrix to perform multivariate constraints on the observation model. It can effectively improve the success rate of ambiguity and achieve instantaneous attitude determination. The simulation results show that the multivariable constraint method can achieve 75.7% ambiguity fixed success rate even in the scene with very low signal observation accuracy. Even if there are only four satellites, the success rate of this method can reach more than 90%. Under the premise of using the ultra-short baseline, this method can achieve an attitude accuracy of 0.93°.
-
图 4 4组数据对应的模糊度固定成功率
Figure 4. Ambiguity fixed success rate corresponding to the four sets of data
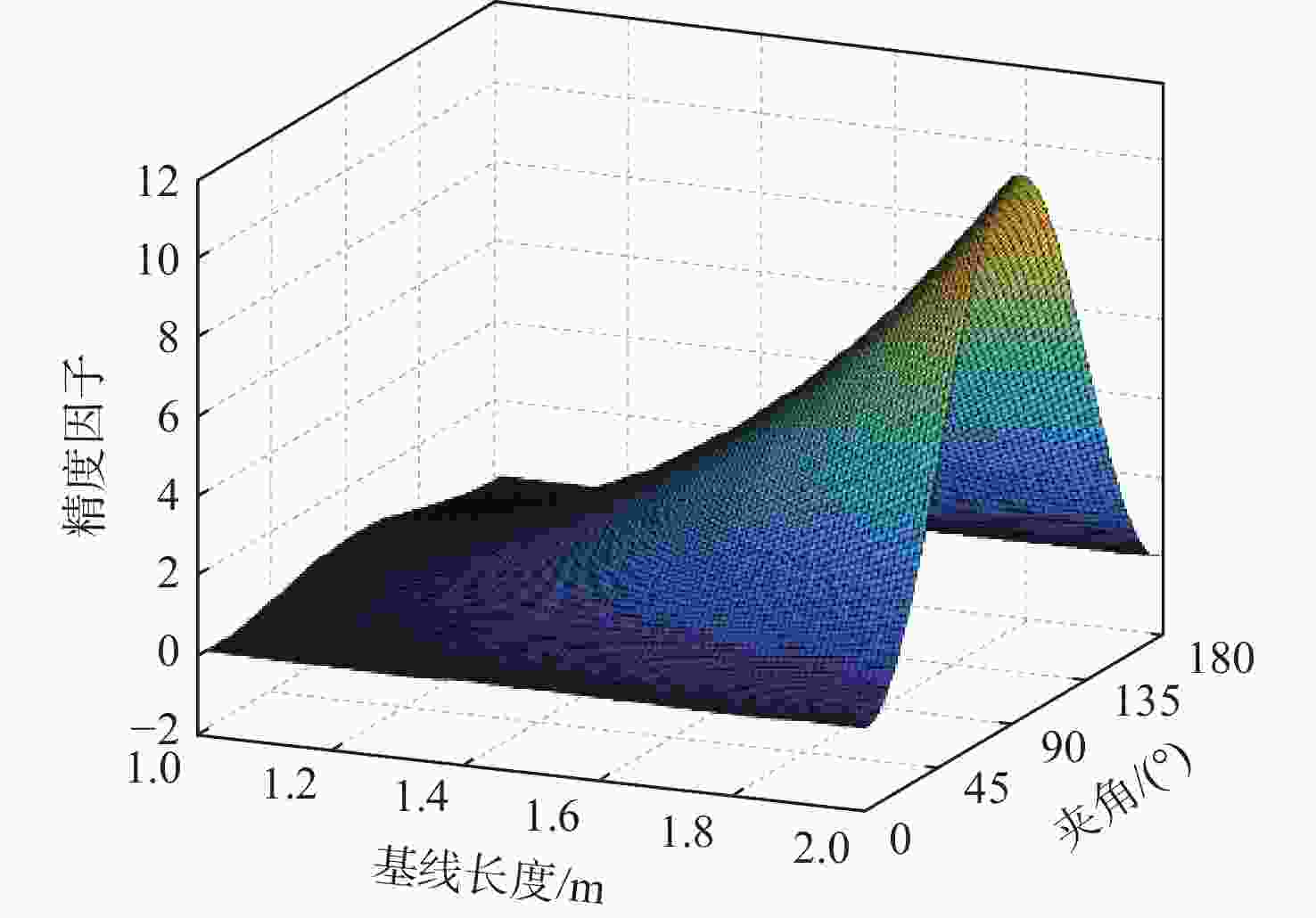
表 1 4组天线布局的参数
Table 1. Parameters of four antenna configurations
组别 基线1长度/m 基线2长度/m 夹角/（°） 精度因子v 第1组 1.0 2.0 100 5.2 第2组 1.5 2.0 90 12 第3组 2.0 2.0 60 16 第4组 2.0 2.0 90 21.3 
下载: 导出CSV
表 2 不同卫星数目下的模糊度固定成功率
Table 2. Success rate of ambiguity under different number of satellites
% 卫星数 第1组模糊度固定成功率 第2组模糊度固定成功率 无约束 多变量约束 无约束 多变量约束 4 0.6 90.3 0.5 90.5 5 6.7 95.4 5.8 96.6 6 33.3 100 34.5 100 7 65.9 100 65.2 100 8 95.4 100 96.2 100 9 99.9 100 99.7 100
下载: 导出CSV
表 3 姿态角的均值和标准差
Table 3. Mean and standard deviation of attitude angle
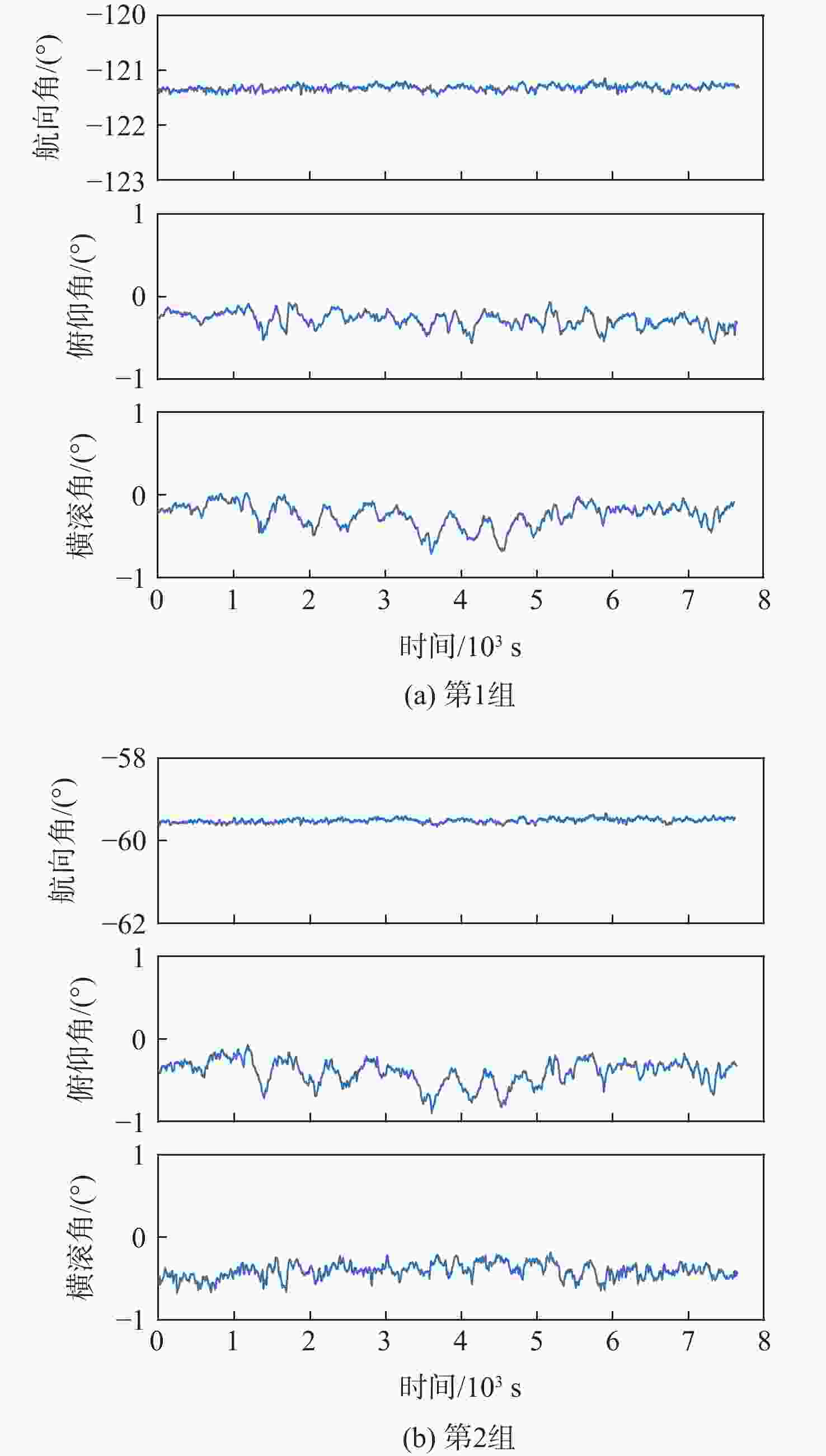
(°) 组别 航向角 俯仰角 横滚角 均值 标准差 均值 标准差 均值 标准差 第1组 −123.32 0.216 −0.28 0.472 −0.25 0.670 第2组 −59.51 0.212 −0.41 0.740 −0.41 0.395
下载: 导出CSV
表 4 3组天线布局的参数
Table 4. Parameters of three antenna configurations
组别 基线1长度/m 基线2长度/m 夹角/（°） 精度因子v 第1组 0.73 0.35 90 0.09 第2组 0.73 0.35 60 0.07 第3组 0.73 0.22 60 0.03
下载: 导出CSV
表 5 姿态角估计值的标准差
Table 5. Standard deviation of estimated attitude angle
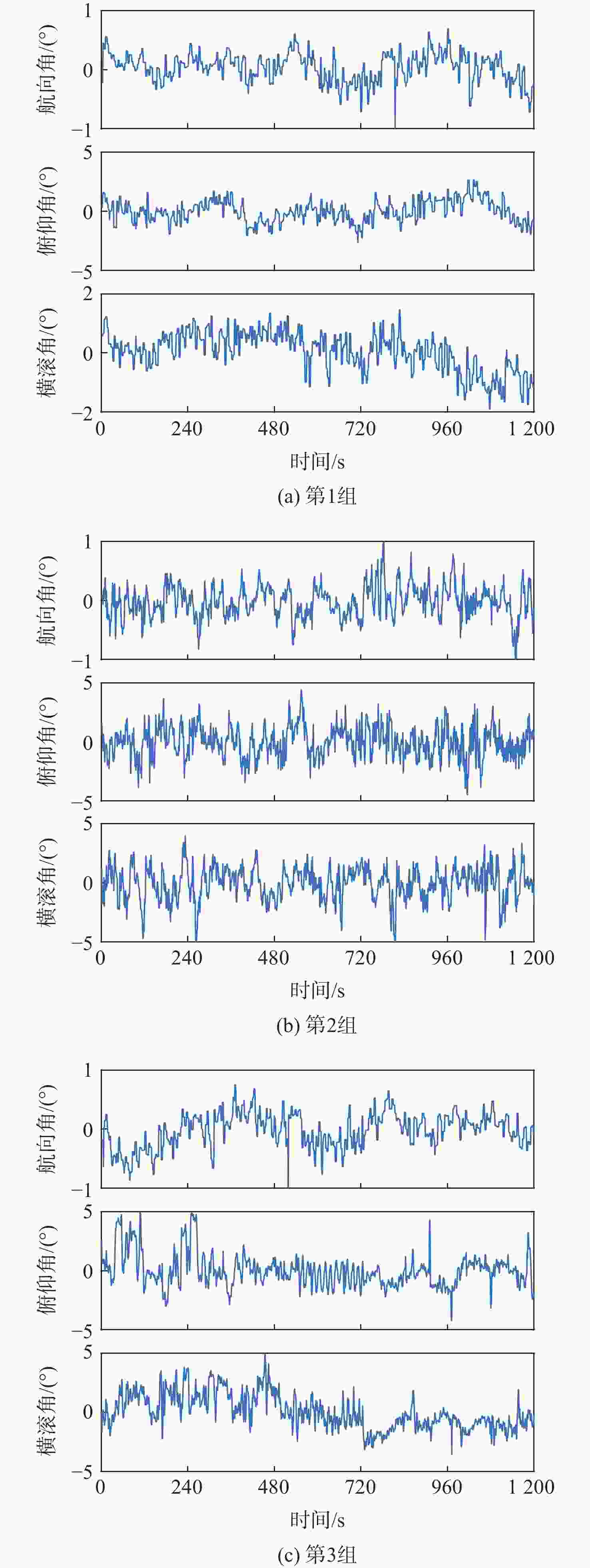
(°) 组别 航向角 俯仰角 横滚角 第1组 0.27 0.93 0.68 第2组 0.28 1.33 1.42 第3组 0.29 1.42 1.56
下载: 导出CSV
-
[1] DMITRIYEV S P, STEPANOV O A, SHEPEL S V. Nonlinear filtering methods application in INS alignment[J]. IEEE Transactions on Aerospace and Electronic Systems, 1997, 33(1): 260-272. [2] WU M, WU Y, HU X, et al. Optimization-based alignment for inertial navigation systems: Theory and algorithm[J]. Aerospace Science and Technology, 2011, 15(1): 1-17. doi: 10.1016/j.ast.2010.05.004 [3] HAUSCHILD A, GRILLMAYER G, MONTENBRUCK O, et al. GPS based attitude determination for the flying laptop satellite[C]//Small Satellites for Earth Observation. Berlin: Springer, 2008: 211-220. [4] 郑坤, 董绪荣, 刘亚涛, 等. GNSS载波相位多天线实时测姿系统的设计与实现[J]. 测绘科学技术学报, 2014, 31(2): 136-139.ZHENG K, DONG X R, LIU Y T, et al. Attitude determination with a GNSS multiple-antenna system[J]. Journal of Geomatics Science and Technology, 2014, 31(2): 136-139(in Chinese). [5] KIM D, LEE S, LEE S, et al. Application of a new efficient attitude determination algorithm on a ground simulator[J]. International Journal of Control, Automation and Systems, 2011, 9(5): 998-1004. [6] 张方照, 柴艳菊, 柴华, 等. 两种多天线GNSS定姿方法的精度分析[J]. 中国惯性技术学报, 2016, 24(1): 30-35.ZHANG F Z, CHAI Y J, CHAI H, et al. Analysis on precision of two attitude determination methods using GNSS multi-antenna data[J]. Journal of Chinese Inertial Technology, 2016, 24(1): 30-35(in Chinese). [7] WANG Y, ZHAN X, ZHANG Y. Improved ambiguity function method based on analytical resolution for GPS attitude determination[J]. Measurement Science and Technology, 2007, 18(9): 2985-2990. [8] BO W, MIAO L, WANG S, et al. A constrained LAMBDA method for GPS attitude determination[J]. GPS Solutions, 2009, 13(2): 97-107. doi: 10.1007/s10291-008-0103-2 [9] BALLAL T, BLEAKLEY C J. GNSS instantaneous ambiguity resolution and attitude determination exploiting the receiver antenna configuration[J]. IEEE Transactions on Aerospace and Electronic Systems, 2014, 50(3): 2061-2069. [10] 龚昂, 赵修斌, 庞春雷, 等. 基线矢量约束GNSS单频单历元可靠姿态解算方法[J]. 华中科技大学学报(自然科学版), 2017, 45(1): 103-107.GONG A, ZHAO X B, PANG C L, et al. Reliable GNSS single frequency single epoch attitude determination algorithm with baseline vector constraints[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2017, 45(1): 103-107(in Chinese). [11] GIORGI G, TEUNISSEN P, VERHAGEN S, et al. Improving the GNSS attitude ambiguity success rate with the multivariate constrained LAMBDA method[J]. Iag-geodesy for Planet Earth Symposium on Mathematical Geodesy, 2009, 136(3): 941-948. [12] CHEN J, XU Y, YUAN H, et al. A new GNSS spoofing detection method using two antennas[J]. IEEE Access, 2020, 8: 110738-110747. [13] GIORGI G. GNSS carrier phase-based attitude determination estimation and applications[D]. Deft: Deft University of Technology, 2011: 71-80. [14] TEUNISSEN P. The lambda method for the GNSS compass[J]. Artificial Satellites, 2006, 41(3): 89-103. [15] ZHANG P, ZHAO Y Z, LIN H, et al. A novel GNSS attitude determination method based on primary baseline switching for a multi-antenna platform[J]. Remote Sensing, 2020, 12(5): 747. doi: 10.3390/rs12050747 -
下载:
点击查看大图
计量
- 文章访问数: 292
- HTML全文浏览量: 60
- PDF下载量: 35
- 被引次数: 0
