四旋翼的改进PSO-RBF神经网络自适应滑模控制

唐志勇; 马福源; 裴忠才

doi:10.13700/j.bh.1001-5965.2021.0477

四旋翼的改进PSO-RBF神经网络自适应滑模控制

doi: 10.13700/j.bh.1001-5965.2021.0477

北京航空航天大学自动化科学与电气工程学院，北京 100191

详细信息

通讯作者:
E-mail：peizc@buaa.edu.cn

中图分类号: V249.122
计量
- 文章访问数: 539
- HTML全文浏览量: 95
- PDF下载量: 125
- 被引次数: 0
出版历程
- 收稿日期: 2021-08-19
- 录用日期: 2021-11-19
- 网络出版日期: 2021-12-16
- 整期出版日期: 2023-07-31

Improved PSO-RBF neural network adaptive sliding mode control for quadrotor systems

School of Automation Science and Electrical Engineering，Beihang University，Beijing 100191，China

More Information

Corresponding author: E-mail：peizc@buaa.edu.cn

摘要

摘要:
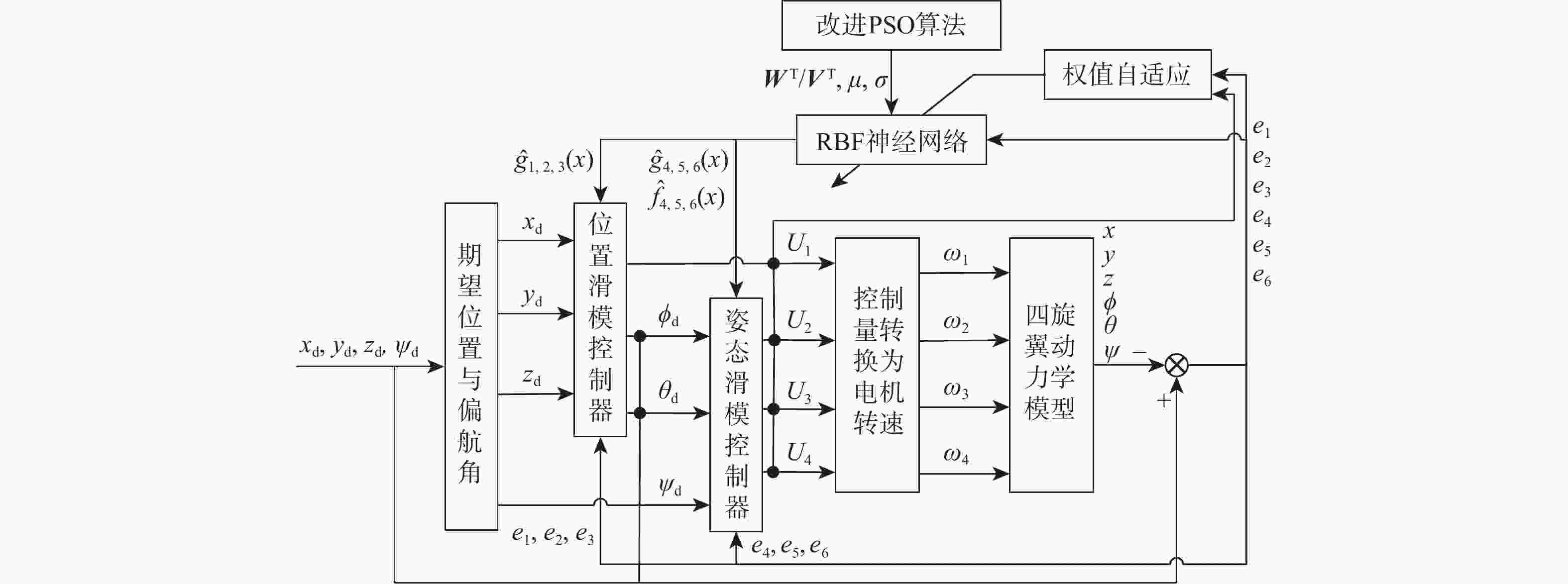
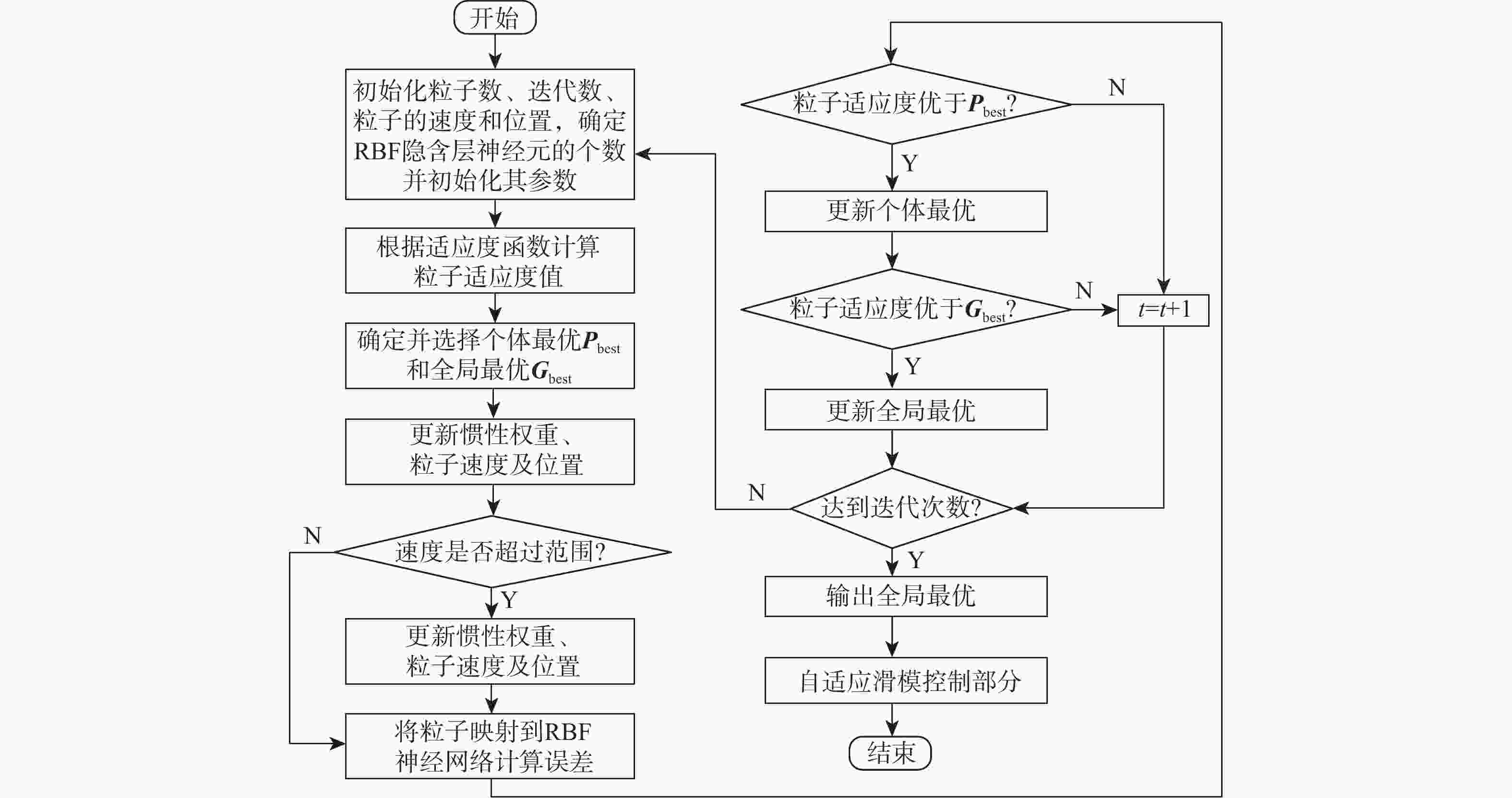
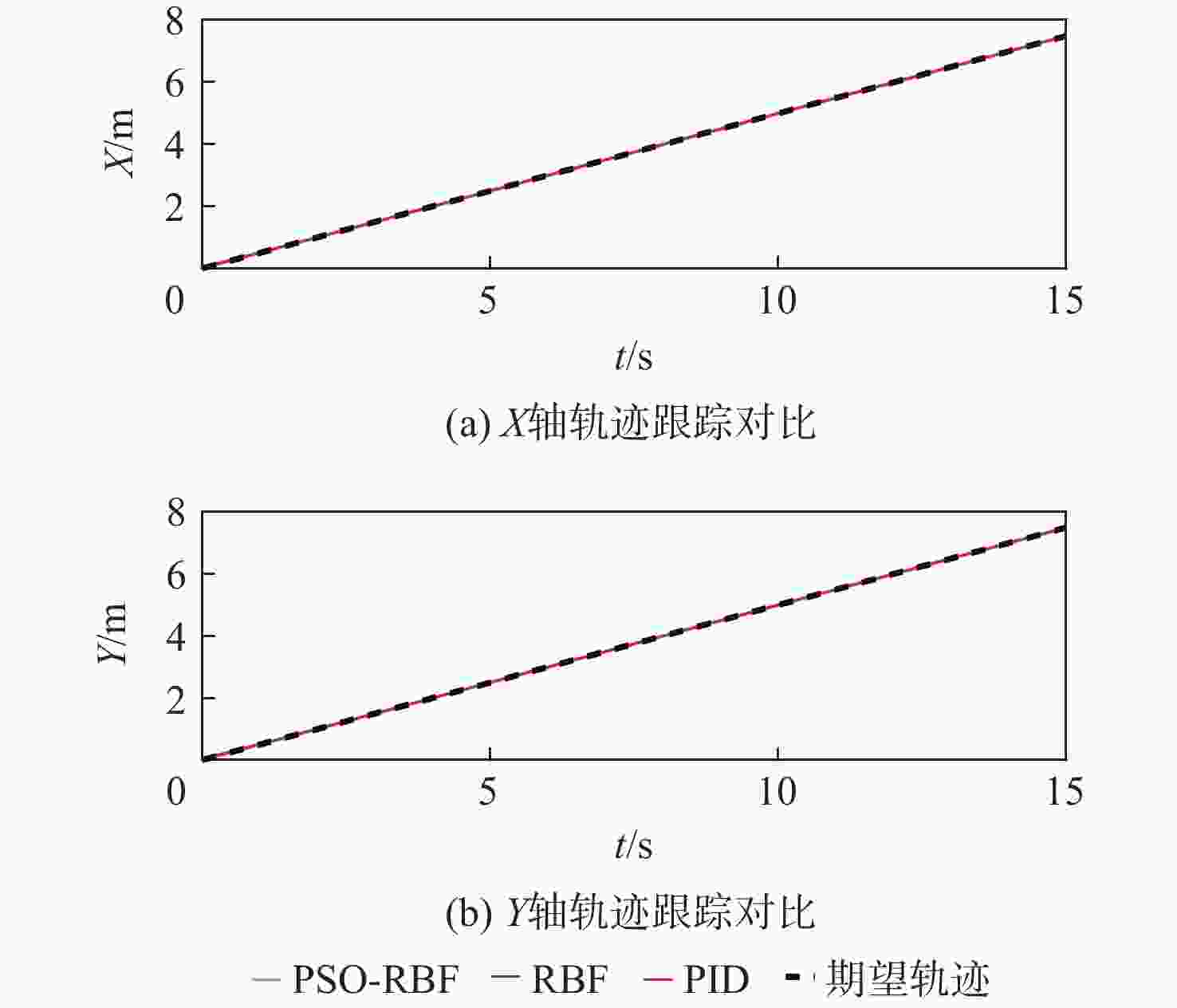
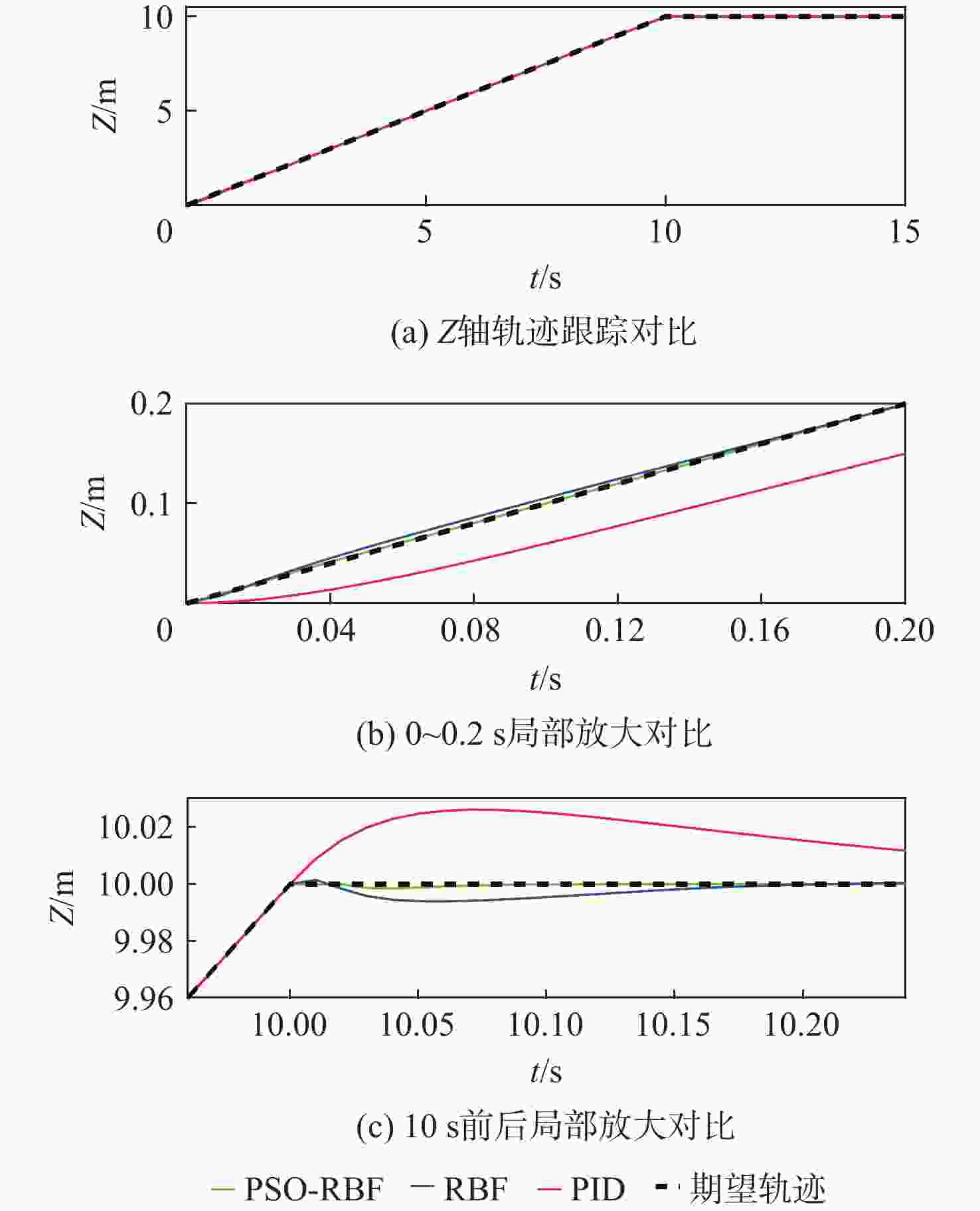
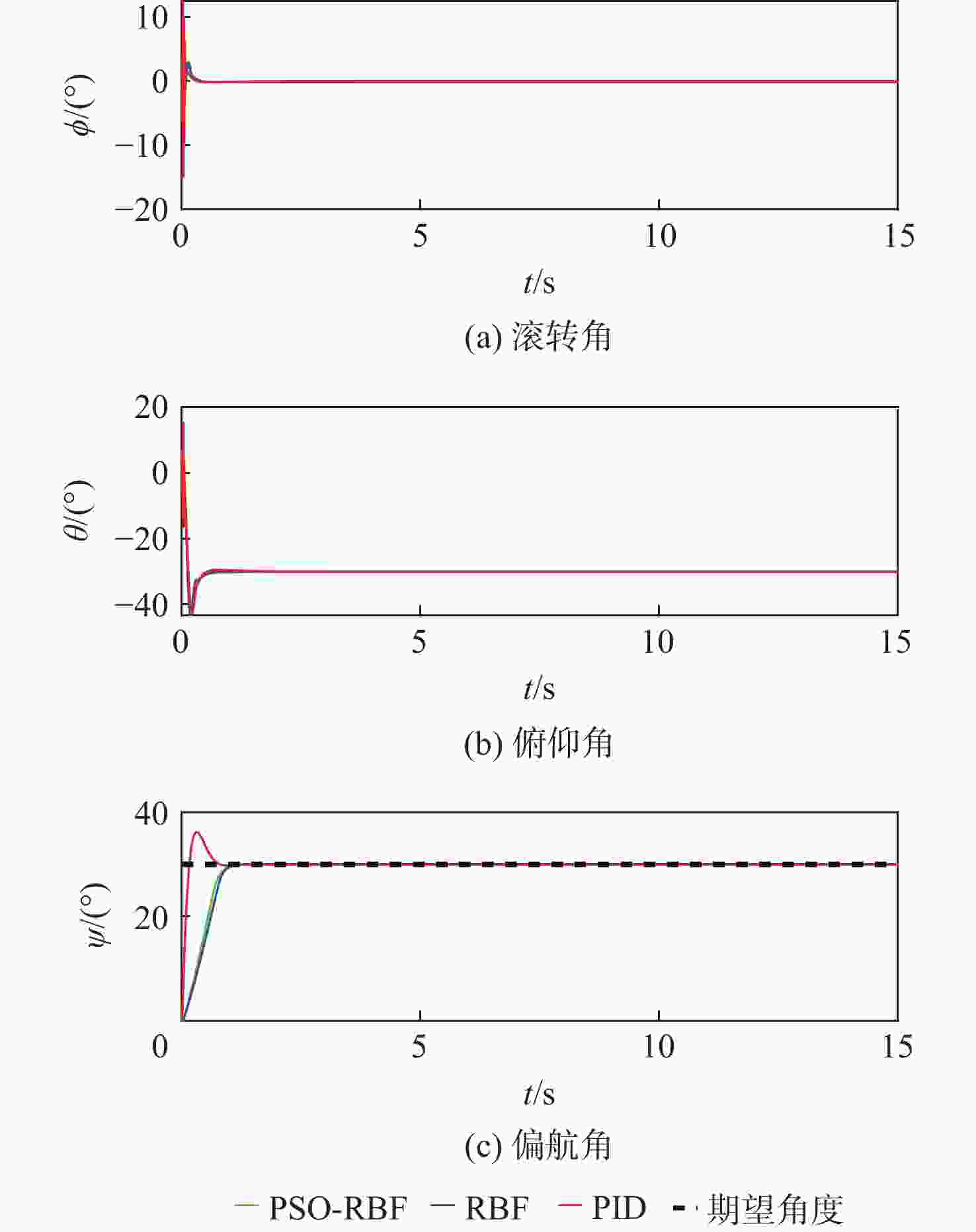
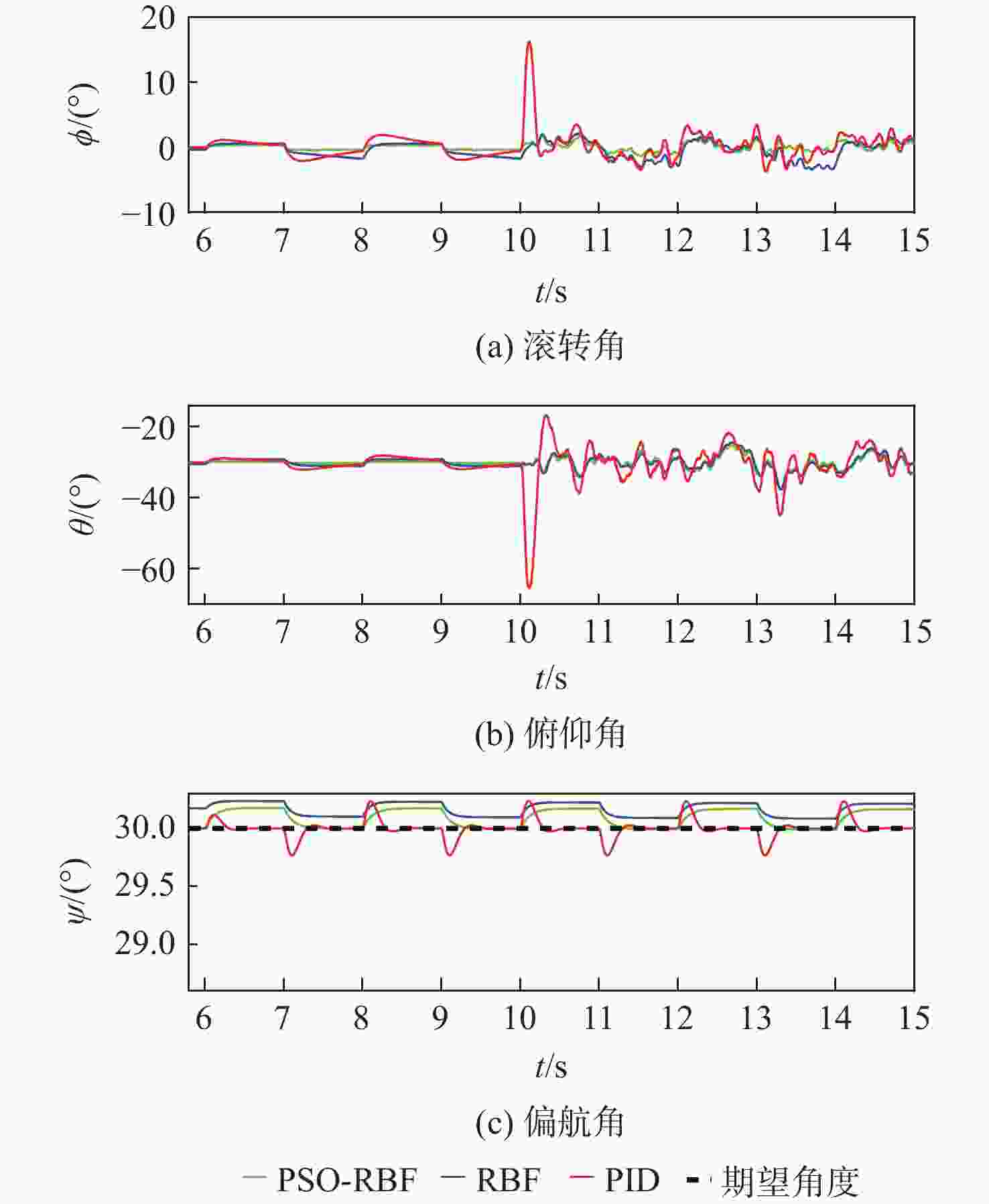
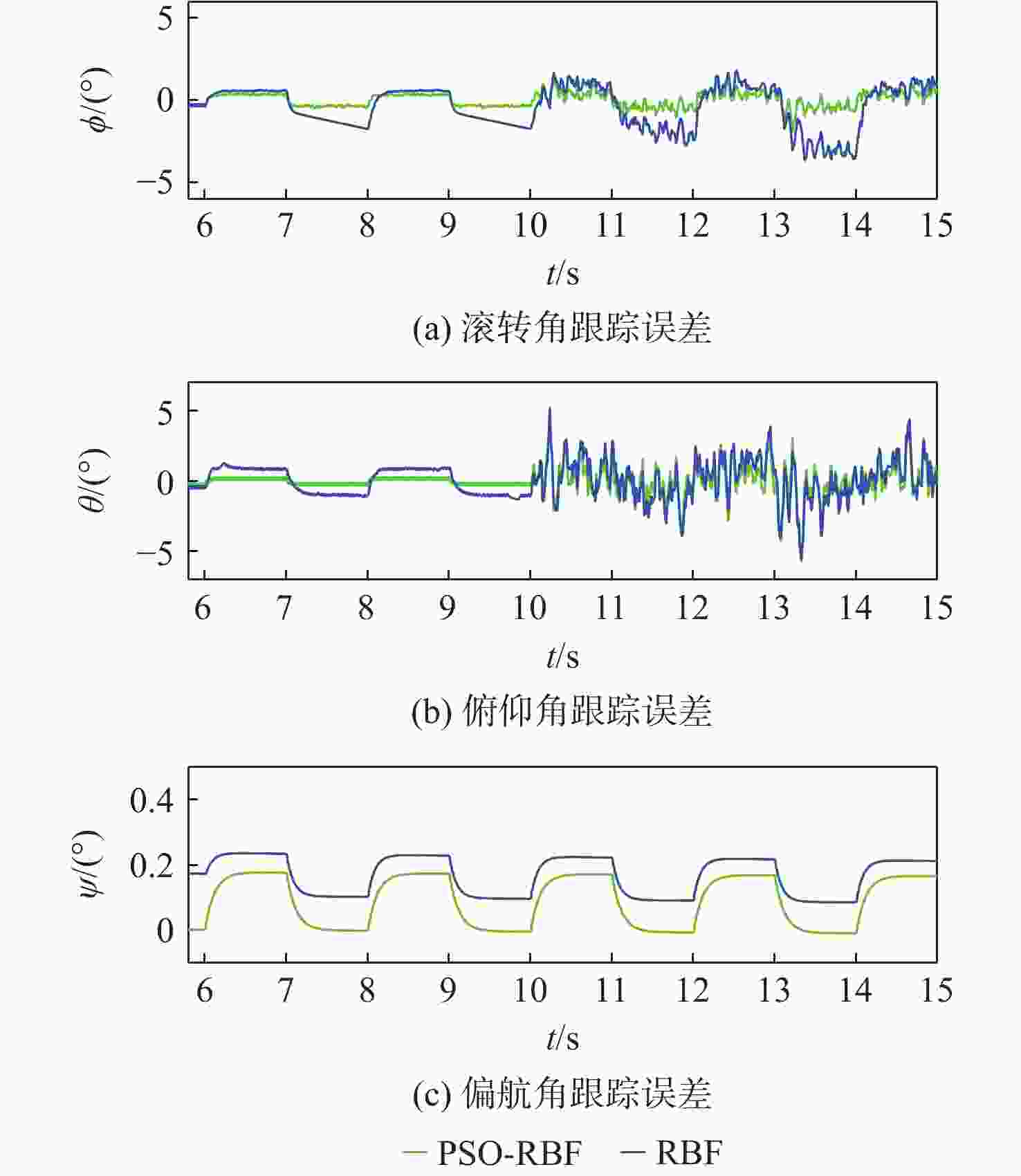
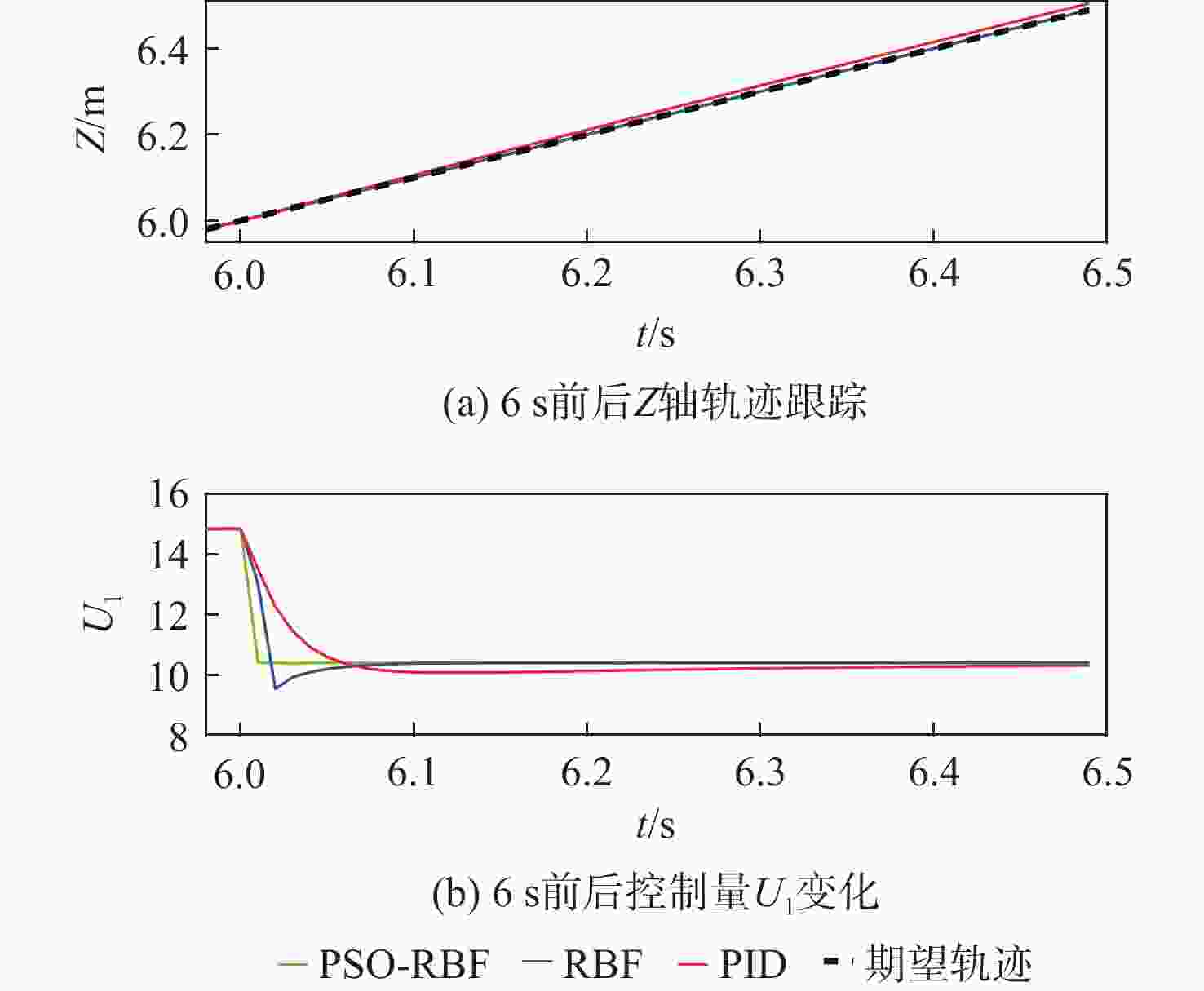
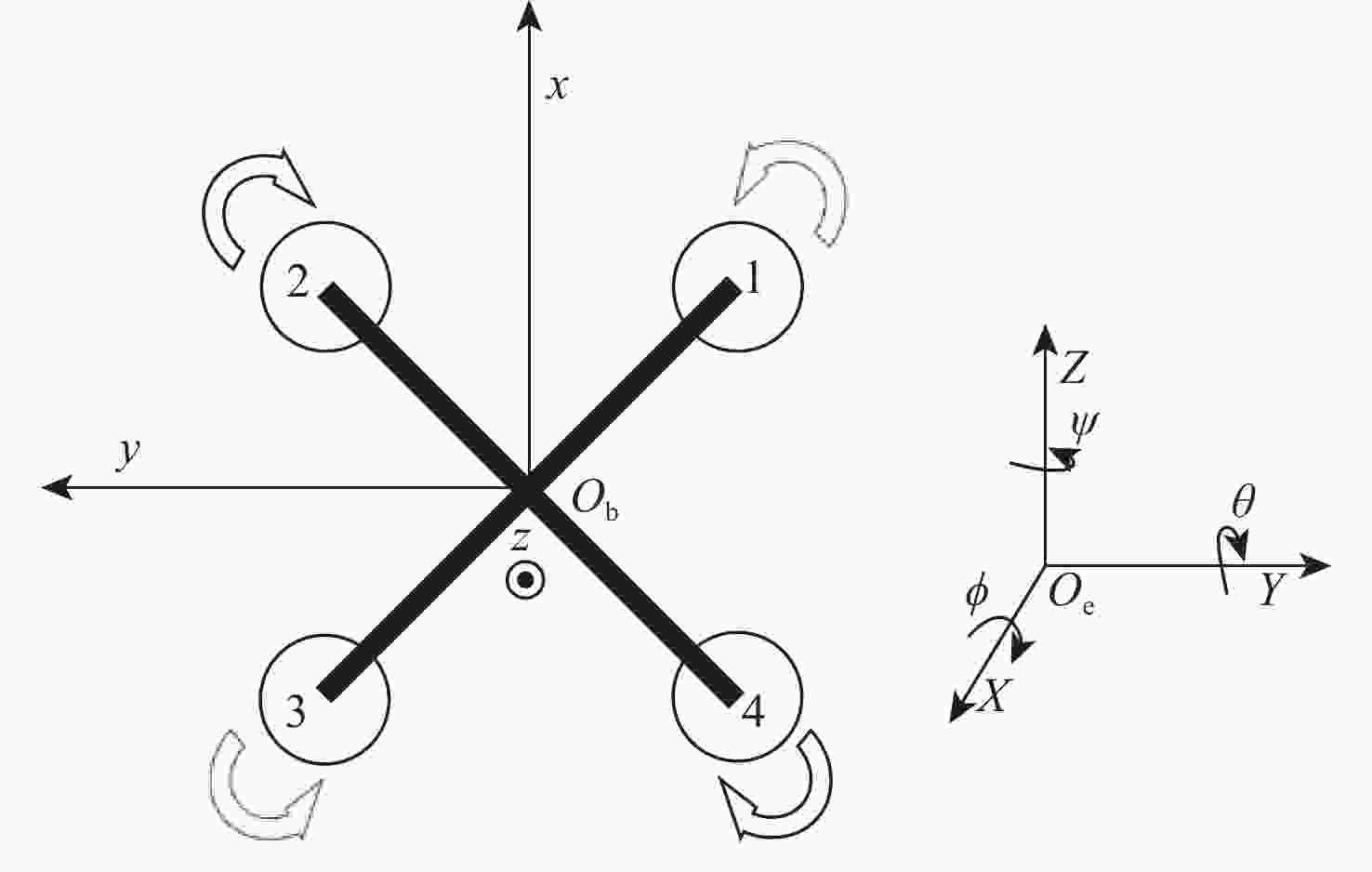
针对非线性、强耦合并带有不确定性干扰的四旋翼无人机模型，提出了一种改进粒子群算法-径向基(PSO-RBF)神经网络自适应滑模控制器。在对RBF神经网络自适应滑模控制器进行控制量平滑改进的基础上，利用改进的具有全局寻优能力的PSO算法来调整RBF神经网络的拟合参数，从而进一步提升网络的拟合能力。根据实际四旋翼的模型参数，搭建四旋翼的动力学模型，通过Lyapunov理论验证了系统的稳定性。仿真结果表明：与RBF神经网络自适应滑模控制器和双闭环PID控制器相比，改进PSO-RBF神经网络自适应滑模控制器可以在一个控制周期内寻找到合适的控制量，其调节时间分别提升约50%和75%；改进PSO-RBF神经网络自适应滑模控制器具有轨迹跟踪速度快且准、抗干扰能力强和鲁棒性好的特点。
- 四旋翼无人机 /
- 粒子群算法 /
- 径向基神经网络 /
- 自适应滑模控制 /
- 轨迹跟踪 /
- 抗干扰
Abstract:
An improved particle swarm optimization-radial basis function (PSO-RBF) neural network adaptive sliding mode controller is proposed for quadrotor systems with nonlinearity, strong coupling, and inaccurate interference. First, based on smooth improvement of the control amount of the RBF neural network sliding mode controller, an improved particle swarm optimization with global optimization capability was used to adjust the fitting parameters of the RBF neural network, thus improving the fitting ability of the network. Next, a dynamic model of quadrotor was built according to themodel parameters of actual quadrotors, the stability of which was then proved by Lyapunov theory.In contrast to the RBF neural network adaptive sliding mode controller and the double closed-loop PID controller, the improved PSO-RBF neural network adaptive sliding mode controller can find the appropriate control quantity in one control cycle, and its adjustment time is about 50% and 75% faster than that of RBF neural network adaptive sliding mode controller and double closed-loop PID controller, respectively. The simulation results show that the improved PSO-RBF neural network adaptive sliding mode controller featuresfasttrack speed with high accuracy, strong disturbance rejection and better robustness.
- quadrotor /
- particle swarm optimization /
- radial basis function neural network /
- adaptive sliding mode control /
- trajectory tracking /
- anti-interference

HTML全文

图 1 坐标系和四旋翼模型

Figure 1. Coordinate system and quadrotor model

下载: 全尺寸图片幻灯片

图 2 控制系统结构

Figure 2. Control system structure

下载: 全尺寸图片幻灯片

图 3 改进PSO-RBF神经网络自适应滑模控制流程

Figure 3. Flow chart of improved PSO-RBF neural network adaptive sliding mode controller

下载: 全尺寸图片幻灯片

图 4 水平位置轨迹跟踪对比

Figure 4. Comparison of horizontal position trajectory tracking

下载: 全尺寸图片幻灯片

图 5 高度位置轨迹跟踪对比

Figure 5. Comparison of height position trajectory tracking

下载: 全尺寸图片幻灯片

图 6 3种控制器的姿态控制对比

Figure 6. Comparison of attitude control of three kinds of controllers

下载: 全尺寸图片幻灯片

图 7 引入干扰情况下3种控制器姿态控制对比

Figure 7. Comparison of attitude control of three kinds of controllers when interference is introduced

下载: 全尺寸图片幻灯片

图 8 改进PSO算法对姿态角跟踪误差影响的对比

Figure 8. Comparison of influence of improved PSO algorithm on attitude angle tracking error

下载: 全尺寸图片幻灯片

图 9 3种控制器对Z轴的控制和产生的控制量U₁对比

Figure 9. Control of Z-axis by three kinds of controllers and generated control quantity U₁

下载: 全尺寸图片幻灯片

表 1 四旋翼无人机的动力学参数

Table 1. Dynamic parameters of quadrotor

参数	数值
升力系数K₁/(${\rm{N}} \cdot {{\rm{s}}^2}\cdot { {\rm{rad} }^{-2} }$)	9.138 × 10⁻⁶
反扭矩系数K₂/(${{\rm{N}}} \cdot {{\rm{m}}} \cdot { {{\rm{s}}}^{2} }\cdot{ {{\rm{rad}}}^{-2} }$)	1.368 × 10⁻⁷
沿x轴转动惯量I_xx/(${\rm{kg}} \cdot {{\rm{m}}^2}$)	1.762 × 10⁻²
沿y轴转动惯量I_yy/(${\rm{kg}} \cdot {{\rm{m}}^2}$)	1.769 × 10⁻²
沿z轴转动惯量I_zz/(${\rm{kg}}\cdot {{\rm{m}}^2}$)	2.805 × 10⁻²
四旋翼质量m/kg	1.311
臂长d/m	0.24

下载: 导出CSV

表 2 3种控制器的调节时间

Table 2. Settling time of three kinds of controllers s

控制器	初始轨迹调节时间	10 s定高调节时间
改进PSO-RBF神经网络自适应滑模控制器	0.08	0.1
RBF神经网络自适应滑模控制器	0.18	0.2
双闭环PID控制器	0.38	0.4

下载: 导出CSV

参考文献(20)

[1]	FU J, CHAI T, SU C, et al. Motion/force tracking control of nonholonomic mechanical systems via combining cascaded design and backstepping[J]. Automatica, 2013, 49(12): 3682-3686. doi: 10.1016/j.automatica.2013.09.004
[2]	李众, 沈炜皓. 四旋翼无人机的反步RBF网络自适应控制[J]. 指挥控制与仿真, 2020, 42(2): 89-94. doi: 10.3969/j.issn.1673-3819.2020.02.017 LI Z, SHEN W H. Backstepping sliding mode RBF network adaptive attitude control for quadrotor unmanned aerial vehicle[J]. Fire Control & Command Control, 2020, 42(2): 89-94(in Chinese). doi: 10.3969/j.issn.1673-3819.2020.02.017
[3]	韩业壮, 华容. 四旋翼飞行器的RBF网络自适应滑模控制[J]. 电光与控制, 2017, 24(11): 22-27. doi: 10.3969/j.issn.1671-637X.2017.11.005 HAN Y Z, HUA R. RBF neural network adaptive sliding mode control for quadrotor aerial vehicle[J]. Electronics Optics & Control, 2017, 24(11): 22-27(in Chinese). doi: 10.3969/j.issn.1671-637X.2017.11.005
[4]	陈骥. 基于双环PID的四旋翼飞行器自主飞行研究[J]. 机电一体化, 2018, 24(7): 22-27. doi: 10.16413/j.cnki.issn.1007-080x.2018.07.004 CHEN J. Research on autonomous flight of quadrotor based on double-loop PID[J]. Mechatronics, 2018, 24(7): 22-27(in Chinese). doi: 10.16413/j.cnki.issn.1007-080x.2018.07.004
[5]	马敏, 许中冲, 常辰飞, 等. 基于PID和LQR的四旋翼无人机控制系统研究[J]. 测控技术, 2016, 35(10): 42-45. doi: 10.3969/j.issn.1000-8829.2016.10.011 MA M, XU Z C, CHANG C F, et al. Research on four-rotor UAV control system based on PID and LQR[J]. Measurement & Control Technology, 2016, 35(10): 42-45(in Chinese). doi: 10.3969/j.issn.1000-8829.2016.10.011
[6]	刘慧博, 彭亮, 赵旭. 四旋翼飞行器姿态控制方法研究[J]. 自动化应用, 2020(12): 4-7. doi: 10.19769/j.zdhy.2020.12.002 LIU H B, PENG L, ZHAO X. Research on attitude control method of quadrotor[J]. Automation Application, 2020(12): 4-7(in Chinese). doi: 10.19769/j.zdhy.2020.12.002
[7]	TAN L, LU L, JIN G. Attitude stabilization control of a quadrotor helicopter using integral backstepping[C]//International Conference on Automatic Control and Artificial Intelligence. London: IET, 2012.
[8]	姜洋. 四旋翼垂直起降机的鲁棒控制问题研究[D]. 哈尔滨: 哈尔滨工业大学, 2009. JIANG Y. Research of four rotor vertical take-offs and landings aircraft robust control[D]. Harbin: Harbin Instituteof Technology, 2009(in Chinese).
[9]	高福海, 胡盛斌, 王晨悦. 基于内外环的四旋翼飞行器的双模糊滑模控制[J]. 智能计算机与应用, 2020, 10(7): 158-165. GAO F H, HU S B, WANG C Y. Double fuzzy sliding mode control of four rotor vehicle based on inner and outer rings[J]. Intelligent Computer and Applications, 2020, 10(7): 158-165(in Chinese).
[10]	王翼虎, 王思明. 基于改进粒子群算法的无人机路径规划[J]. 计算机工程与科学, 2020, 42(9): 1690-1696. doi: 10.3969/j.issn.1007-130X.2020.09.020 WANG Y H, WANG S M. UAV path planning based on improved particle swarm optimization[J]. Computer Engineering & Science, 2020, 42(9): 1690-1696(in Chinese). doi: 10.3969/j.issn.1007-130X.2020.09.020
[11]	SESHAGIRI S, KHALIL H K. Output feedback control of nonlinear systems using RBF neural networks[J]. IEEE Transactions on Neural Networks, 2000, 11(1): 69-79. doi: 10.1109/72.822511
[12]	孙瑞华, 郑重, 幸家正, 等. 基于RBF神经网络优化的四旋翼PID控制系统设计[J]. 自动化应用, 2018(5): 3-4. doi: 10.3969/j.issn.1674-778X.2018.05.002 SUN R H, ZHENG Z, XING J Z, et al. Design of quadrotor PID control system based on RBF neural networks[J]. Automation Application, 2018(5): 3-4(in Chinese). doi: 10.3969/j.issn.1674-778X.2018.05.002
[13]	LIN X, WANG Y, LIU Y. Neural network-based robust terminal sliding-mode control of quadrotor[J]. Asian Journal of Control, 2022, 24(1): 427-438. doi: 10.1002/asjc.2478
[14]	郝海燕, 王新军. 基于改进PSO-RBF滑模控制的光伏系统控制方法[J]. 电源技术, 2020, 44(8): 1148-1151. doi: 10.3969/j.issn.1002-087X.2020.08.019 HAO H Y, WANG X J. Method of tracking maximum power point of photovoltaic system based on improved PSO-RBF sliding mode control[J]. Chinese Journal of Power Sources, 2020, 44(8): 1148-1151(in Chinese). doi: 10.3969/j.issn.1002-087X.2020.08.019
[15]	付兴武, 胡洋. 基于改进粒子群算法的三维路径规划[J]. 电光与控制, 2021, 28(3): 86-89. doi: 10.3969/j.issn.1671-637X.2021.03.017 FU X W, HU Y. Three-dimensional path planning based on improved PSO algorithm[J]. Electronics Optics & Control, 2021, 28(3): 86-89(in Chinese). doi: 10.3969/j.issn.1671-637X.2021.03.017
[16]	MAHONY R, KUMAR V, CORKE P. Multi-rotor aerial vehicles: Modeling, estimation, and control of quadrotor[J]. IEEE Robotics and Automation Magazine, 2012, 19(3): 20-32. doi: 10.1109/MRA.2012.2206474
[17]	朱毅飞, 林德福, 莫雳, 等. 四旋翼无人机旋翼对机身非定常气动干扰特性[J]. 兵工学报, 2022, 43(2): 410-422. doi: 10.3969/j.issn.1000-1093.2022.02.019 ZHU Y F, LIN D F, MO L, et al. Transient aerodynamic interference between rotor and fuselage for a quadcopter[J]. Acta Armamentarii, 2022, 43(2): 410-422(in Chinese). doi: 10.3969/j.issn.1000-1093.2022.02.019
[18]	刘金琨. 滑模变结构控制MATLAB仿真[M]. 3版. 北京: 清华大学出版社, 2015: 15-28. LIU J K. Sliding mode control design and MATLAB simulation[M]. 3rd ed. Beijing: Tsinghua University Press, 2015: 15-28(in Chinese).
[19]	申珊颖. 斜十字四旋翼飞行器实验建模与控制技术研究[D]. 南京: 南京航空航天大学, 2013: 20-42. SHEN S Y. Modelling based on experiment and control technology of an oblique cross quadrotor[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2013: 20-42(in Chinese).
[20]	WANG X, CHEN Z, YANG G. Finite-time-convergent differentiator based on singular perturbation technique[J]. IEEE Transactions on Automatic Control, 2007, 52(9): 1731-1737. doi: 10.1109/TAC.2007.904290