基于角度转化的空间碎片测角数据精密定轨方法

张耀; 刘静

doi:10.13700/j.bh.1001-5965.2021.0507

基于角度转化的空间碎片测角数据精密定轨方法

doi: 10.13700/j.bh.1001-5965.2021.0507

张耀^{1, 2, 3},
刘静^{1, 2, 3, ,}

1.
中国科学院国家天文台，北京 100101
2.
中国科学院大学天文与空间科学学院，北京 100049
3.
平湖实验室，嘉兴 314200

基金项目: 国家自然科学基金(12073045,11803052)

详细信息

通讯作者:
E-mail：liujing@bao.ac.cn

中图分类号: P135
计量
- 文章访问数: 208
- HTML全文浏览量: 50
- PDF下载量: 25
- 被引次数: 0
出版历程
- 收稿日期: 2021-09-01
- 录用日期: 2022-01-25
- 网络出版日期: 2022-02-23
- 整期出版日期: 2023-07-31

Precise orbit determination method for angle-only observation data of space debris based on angle conversion theory

ZHANG Yao^{1, 2, 3},
LIU Jing^{1, 2, 3
, ,}

1.
National Astronomical Observatory，Chinese Academy of Science，Beijing 100101，China
2.
School of Astronomy and Space Science，University of Chinese Academy of Science，Beijing 100049，China
3.
Laboratory of Pinghu，Jiaxing 314200，China

Funds: National Natural Science Foundation of China (12073045,11803052)

More Information

Corresponding author: E-mail：liujing@bao.ac.cn

摘要

摘要:
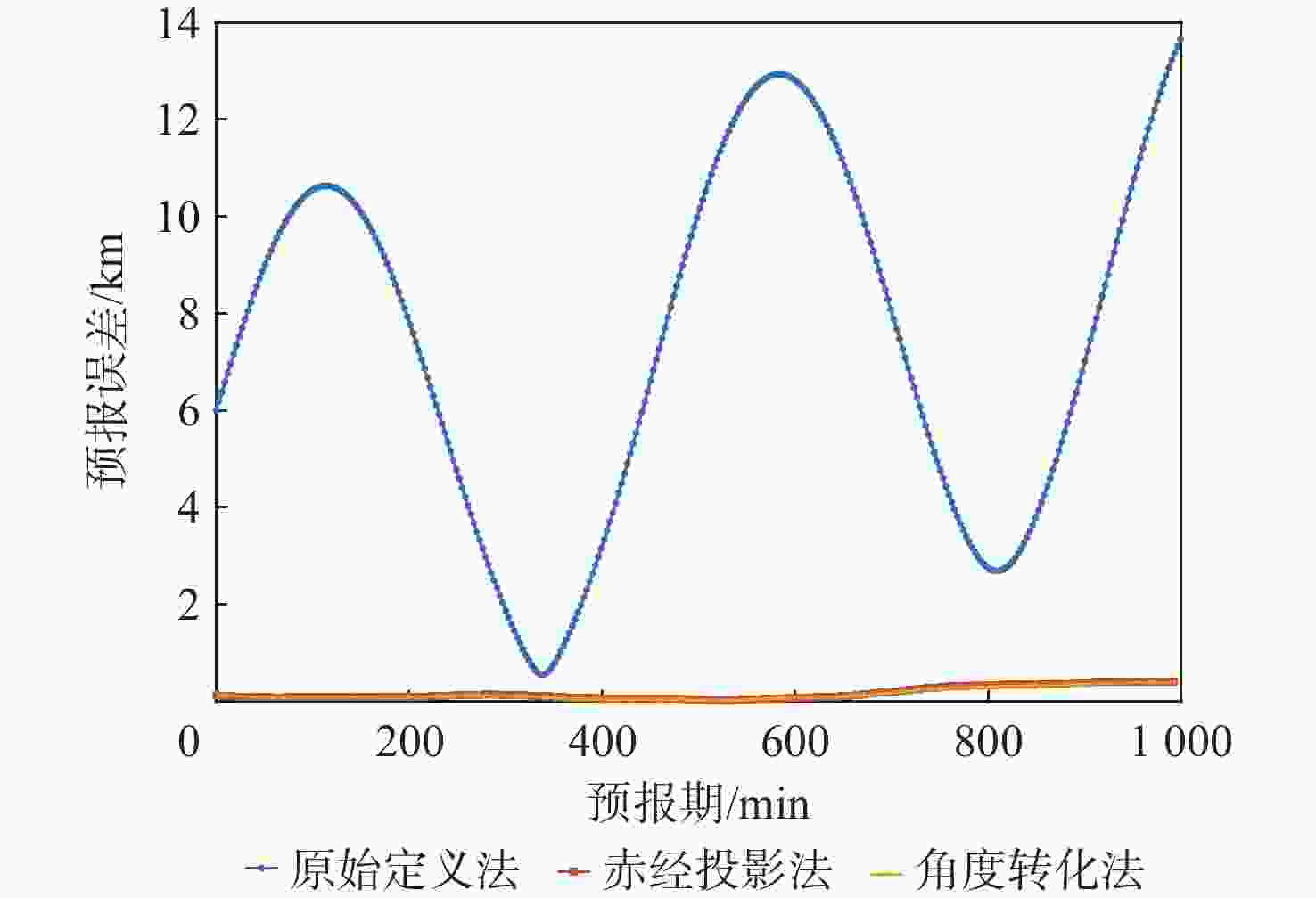
空间碎片对在轨卫星的影响日益增大，持续确定和更新空间碎片轨道日益受到重视。基于角度转化思想，提出了一种空间碎片测角数据精密定轨方法。基于常用的两行根数（TLE）数据应用需求，根据差分思想建立基于SGP4/SDP4预报模型的TLE精密定轨方法；以赤经-赤纬数据为典型场景，分析原始定义法、赤经投影法的优缺点；提出将常规双元素角度资料转化为三元素角度资料的角度转化法。仿真结果表明：当观测数据较多集中于测站天顶方向时，角度转化法能够将精密定轨收敛速度提高25%，轨道精度提高2~10倍。
- 精密定轨 /
- 空间碎片 /
- 测角数据 /
- SGP4/SDP4 /
- 两行根数
Abstract:
On the basis of the angle conversion method, a brand-new accurate orbit determination technique for space debris was developed. First, based on the commonly used two-line-element (TLE) data application requirements, a TLE precise orbit determination model based on the SGP4/SDP4 forecast model was established according to the differential idea. Secondly, the advantages and disadvantages of the original definition method and the right ascension projection method were discussed by taking right ascension-declination observation as an example. Then the angle conversion method was proposed, which converts the two-element angle data into three-element angle data. Finally verifies based on the simulation that when the observation data is concentrated in the direction of the zenith of the station, the angle conversion method could increase the speed of precise orbit determination by about 25%, and increase the accuracy of orbit determination by 2−10 times.
- precise orbit determination /
- space debris /
- angle-only observation data /
- SGP4/SDP4 /
- two-line-element

HTML全文

图 1 赤经和赤纬的定义

Figure 1. Definition of right ascension and declination

下载: 全尺寸图片幻灯片

图 2 新观测量的定义

Figure 2. Definition of new angle

下载: 全尺寸图片幻灯片

图 3 LEO定轨结果预报误差

Figure 3. Propagation errors of LEO orbiting results

下载: 全尺寸图片幻灯片

图 4 MEO定轨结果预报误差

Figure 4. Propagation errors of MEO orbiting results

下载: 全尺寸图片幻灯片

图 5 HEO定轨结果预报误差

Figure 5. Propagation errors of HEO orbiting results

下载: 全尺寸图片幻灯片

表 1 3颗空间碎片的标称轨道根数

Table 1. Nominal orbital elements of 3 debris

轨道	半长轴/km	偏心率	倾角/(°)	升交点赤经/(°)	近地点幅角/(°)	平近点角/(°)	面质比/(m²·kg⁻¹)
LEO	8380.977	0.010582	97.999	0.523	1.006	113.565	0.02
MEO	20002.628	0.009890	97.998	0.023	0.915	48.449	0.02
HEO	41999.169	0.499836	64.988	359.987	180.011	52.964	0.02

下载: 导出CSV

表 2 3颗空间碎片产生的模拟观测数据

Table 2. Simulated observations from 3 debris

轨道	弧段序号	弧长/s	最低赤纬/(°)	最高赤纬/(°)
LEO	1	294.622	66.202	72.912
	2	250.162	63.409	70.409
	3	77.072	66.358	68.833
	4	46.490	64.477	64.818
MEO	1	1623.089	43.099	71.181
	2	1680	35.622	64.044
	3	2825.676	65.381	89.626
	4	6905	−3.112	89.626
	5	3060	23.008	77.662
HEO	1	13080	41.015	71.596
	2	8400	31.787	53.963
	3	6180	−17.460	−28.934
	4	2340	−8.009	−11.759

下载: 导出CSV

表 3 精密定轨结果

Table 3. Results of precise orbit determination

轨道	观测数据处理形式	迭代次数	定轨残差
LEO	原始定义法	18	7.5×10⁻⁵
	赤经投影法	18	5.0×10⁻⁵
	角度转化法	14	4.0×10⁻⁵
MEO	原始定义法	14	1.9×10⁻⁴
	赤经投影法	15	1.4×10⁻⁵
	角度转化法	10	1.0×10⁻⁵
HEO	原始定义法	9	2.0×10⁻⁵
	赤经投影法	9	2.0×10⁻⁵
	角度转化法	9	2.0×10⁻⁵

下载: 导出CSV

参考文献(16)

[1]	BRAUN V, LEMMENS S, REIHS B, et al. Analysis of breakup events[C]//Proceedings of the 7th European Conference on Space Debris, 2017: 1-12.
[2]	PIROVANO L, PRINCIPE G, ARMELLIN R. Data association and uncertainty pruning for tracks determined on short arcs[J]. Celestial Mechanics and Dynamical Astronomy, 2020, 132: 6-30. doi: 10.1007/s10569-019-9947-8
[3]	CICALO S, BECK J, MINISCI E, et al. GOCE radar-based orbit determination for re-entry predictions and comparison with GPS-based POD[C]//Proceedings of the 7th European Conference on Space Debris, 2017: 1-14.
[4]	刘林, 张强, 廖新浩. 人卫精密定轨中的算法问题[J]. 中国科学(A辑), 1998, 28(5): 848-856. LIU L, ZHANG Q, LIAO X H. Algorithm problems in precise orbit determination of artificial earth satellite[J]. Science in China(Series A), 1998, 28(5): 848-856(in Chinese).
[5]	程昊文. 航天器轨道理论在空间目标编目管理中的应用[D]. 南京: 南京大学, 2012: 9-11. CHENG H W. The application of satellite orbit theory in maintaining the space object catalog[D]. Nanjing: Nanjing University, 2012: 9-11(in Chinese).
[6]	MARSHALL J A, LUTHCKE S B. Modeling radiation forces acting on TOPEX/Poseidon for precision orbit determination[J]. Journal of Spacecraft and Rockets, 1994, 31(1): 99-105. doi: 10.2514/3.26408
[7]	BOCK H, HUGENTOBLER U, SPRINGER T A, et al. Efficient precise orbit determination of LEO satellites using GPS[J]. Advances in Space Research, 2002, 30(2): 295-300. doi: 10.1016/S0273-1177(02)00298-3
[8]	张宇, 孔静, 陈明, 等. CE5T拓展试验轨道精度分析[J]. 宇航学报, 2019, 40(9): 1014-1023. doi: 10.3873/j.issn.1000-1328.2019.09.005 ZHANG Y, KONG J, CHEN M, et al. Orbit accuracy analysis for CE5T extended mission[J]. Journal of Astronautics, 2019, 40(9): 1014-1023(in Chinese). doi: 10.3873/j.issn.1000-1328.2019.09.005
[9]	张宇, 周立, 孔静, 等. 长期姿控扰动情况下空间实验室轨道影响分析及建模[J]. 宇航学报, 2017, 38(12): 1273-1280. doi: 10.3873/j.issn.1000-1328.2017.12.003 ZHANG Y, ZHOU L, KONG J, et al. Analysis and modeling of space laboratory orbit under continuous attitude control perturbation[J]. Journal of Astronautics, 2017, 38(12): 1273-1280(in Chinese). doi: 10.3873/j.issn.1000-1328.2017.12.003
[10]	Committee for the Assessment of the U. S. Air Force’s Astrodynamics Standards. Continuing Kepler’s quest: Assessing air force space command’s astrodynamics standards[S]. Washington, D. C. : The National Academies Press, 2012: 21-26.
[11]	GRZEGORZ B, KRZYSZTOF S, RADOSŁAW Z, et al. Determination of precise Galileo orbits using combined GNSS and SLR observations[J]. GPS Solution, 2021, 25: 11. doi: 10.1007/s10291-020-01045-3
[12]	VALLADO D A, FINKLEMAN D. A critical assessment of satellite drag and atmospheric density modeling: AIAA 2008-6442[R]. Reston: AIAA, 2008.
[13]	韦栋, 赵长印. SGP4/SDP4模型精度分析[J]. 天文学报, 2009, 50(3): 332-339. doi: 10.3321/j.issn:0001-5245.2009.03.010 WEI D, ZHAO C Y. Analysis on the accuracy of the SGP4/SDP4 model[J]. Acta Astronomica Sinica, 2009, 50(3): 332-339(in Chinese). doi: 10.3321/j.issn:0001-5245.2009.03.010
[14]	VALLADO D A. Fundamental of astrodynamics and application [M]. Hawthorne: Microcosm Press, 2007: 113-115.
[15]	刘林, 汤靖师. 卫星轨道理论与应用[M]. 北京: 电子工业出版社, 2015: 427-428. LIU L, TANG J S. Satellite orbit theory and application[M]. Beijing: Publishing House of Electronics Industry, 2015: 427-428(in Chinese).
[16]	陈磊, 韩蕾, 百显宗, 等. 空间目标轨道力学与误差分析[M]. 北京: 国防工业出版社, 2010: 93-95. CHEN L, HAN L, BAI X Z, et al. Orbit dynamics and error analysis of space object[M]. Beijing: National Defense Industry Press, 2010: 93-95(in Chinese).