适用于弹性飞机飞行动力学仿真的气动力降阶方法

师妍; 万志强; 吴志刚; 巩轶男

doi:10.13700/j.bh.1001-5965.2021.0510

适用于弹性飞机飞行动力学仿真的气动力降阶方法

doi: 10.13700/j.bh.1001-5965.2021.0510

1.
北京航空航天大学航空科学与工程学院，北京 100191
2.
海鹰航空通用装备有限责任公司，北京 100070

详细信息

通讯作者:
E-mail：wuzhigang@buaa.edu.cn

中图分类号: V212.1；V211；V215.3
计量
- 文章访问数: 215
- HTML全文浏览量: 18
- PDF下载量: 38
- 被引次数: 0
出版历程
- 收稿日期: 2021-09-02
- 录用日期: 2021-11-22
- 网络出版日期: 2021-12-30
- 整期出版日期: 2023-07-31

Aerodynamic order reduction method for elastic aircraft flight dynamics simulation

1.
School of Aeronautic Science and Engineering，Beihang University，Beijing 100191，China
2.
Seahawk Aviation General Equipment Co.，Ltd.，Beijing 100070，China

More Information

Corresponding author: E-mail：wuzhigang@buaa.edu.cn

摘要

摘要:
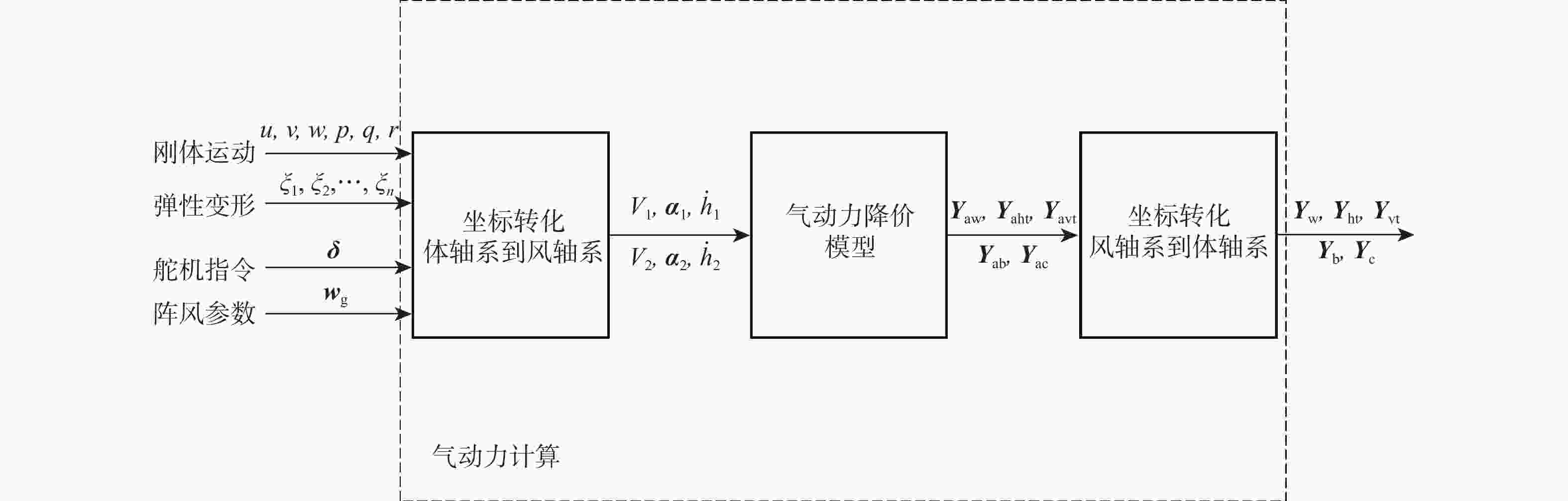
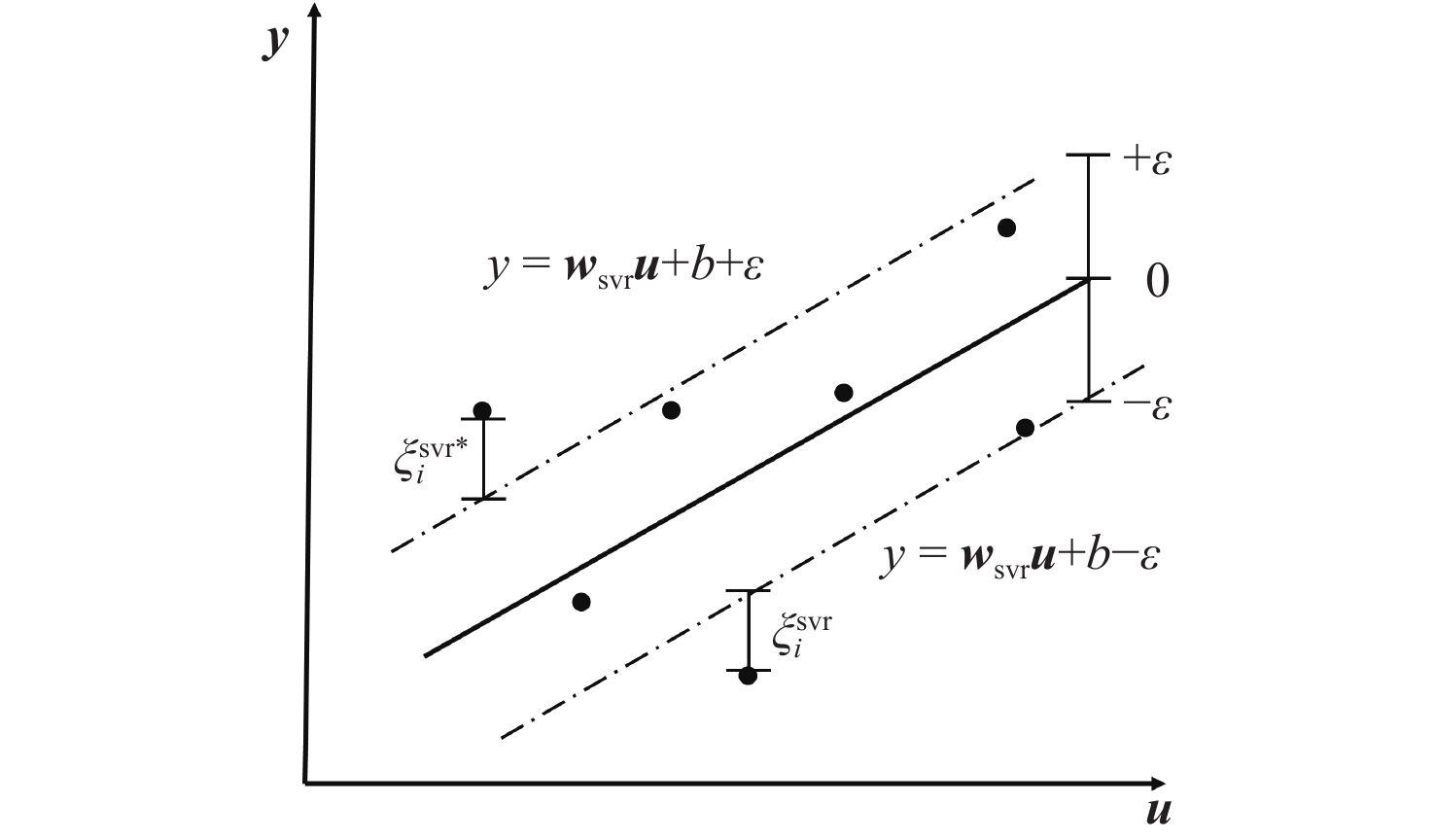
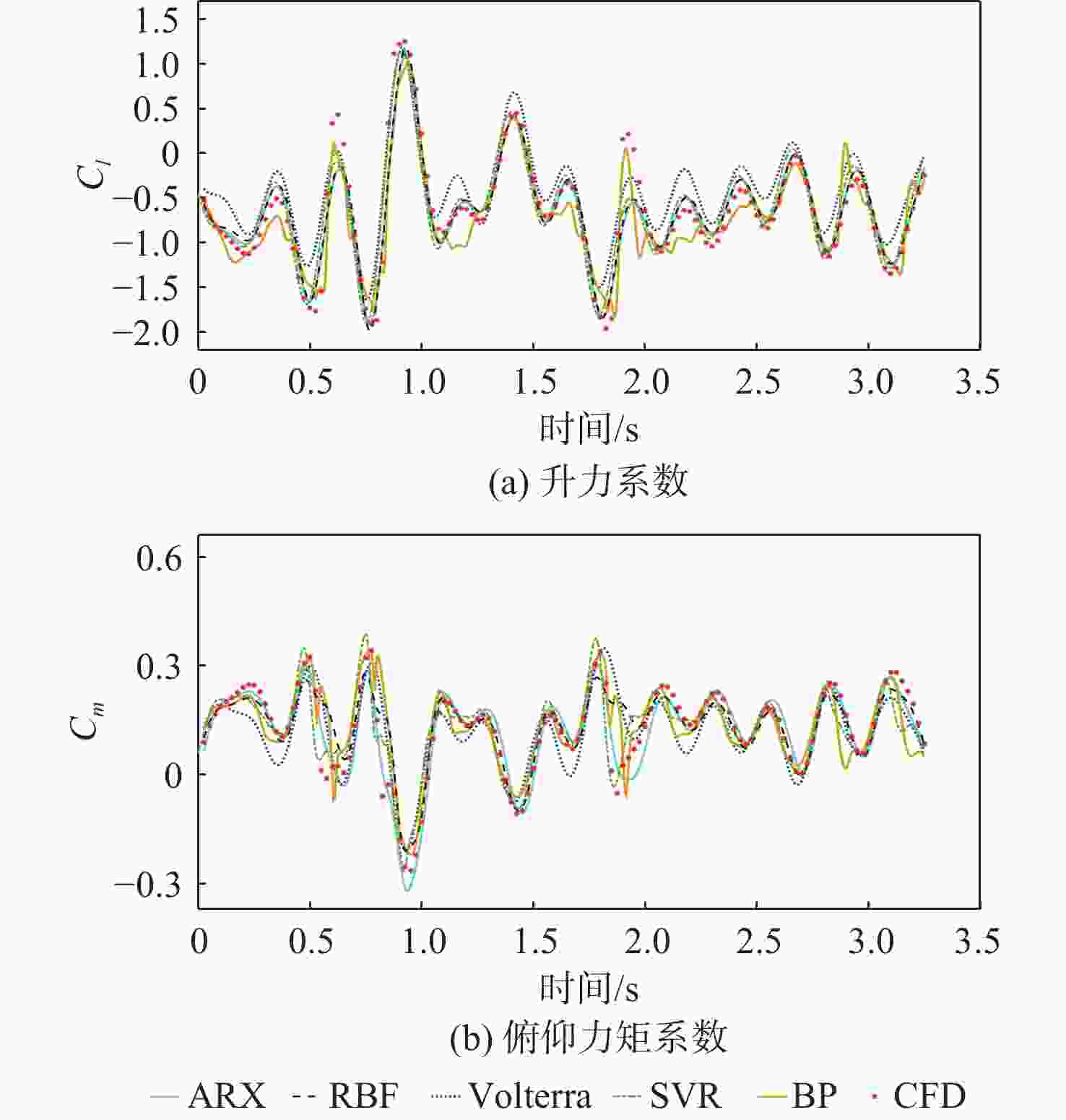
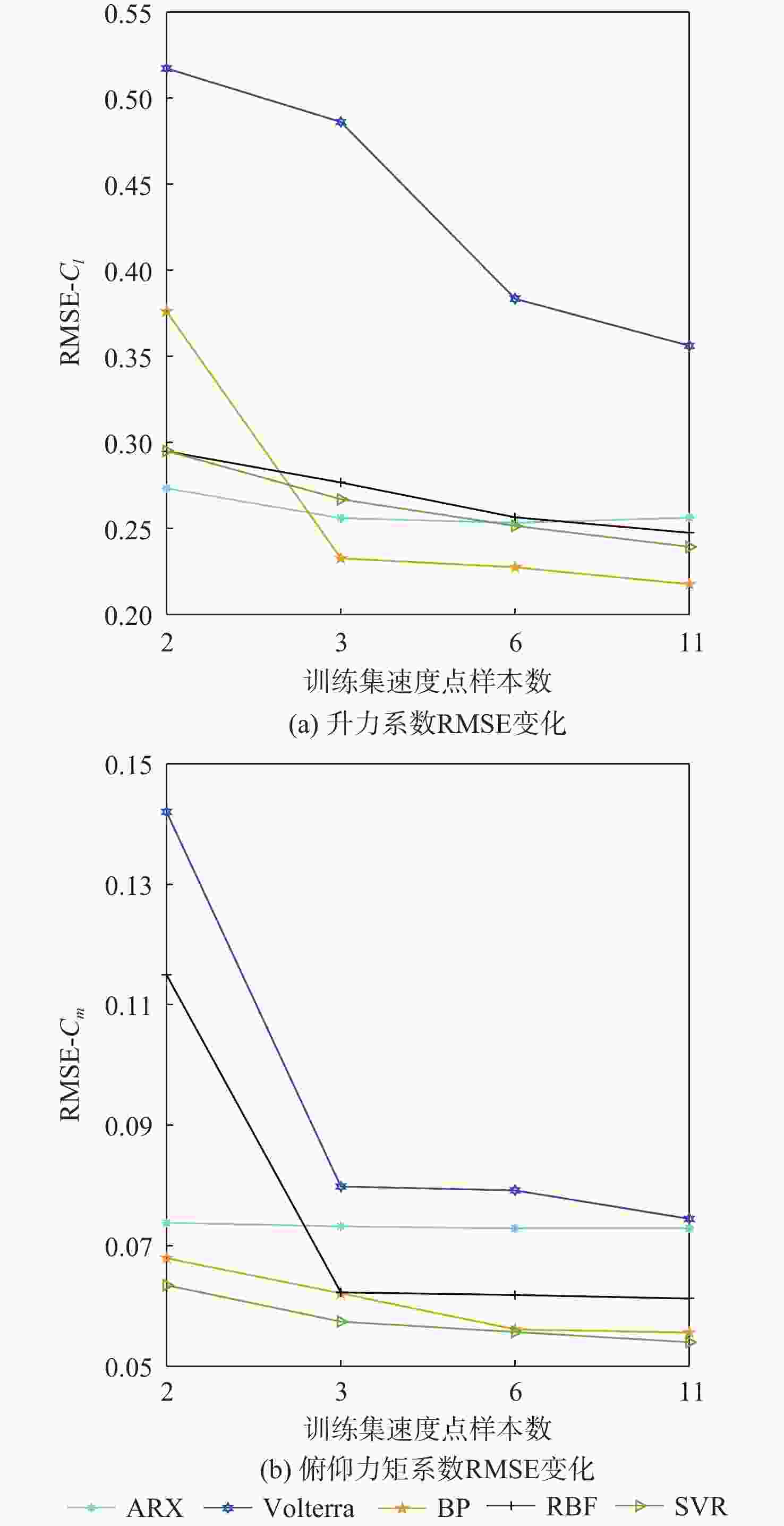
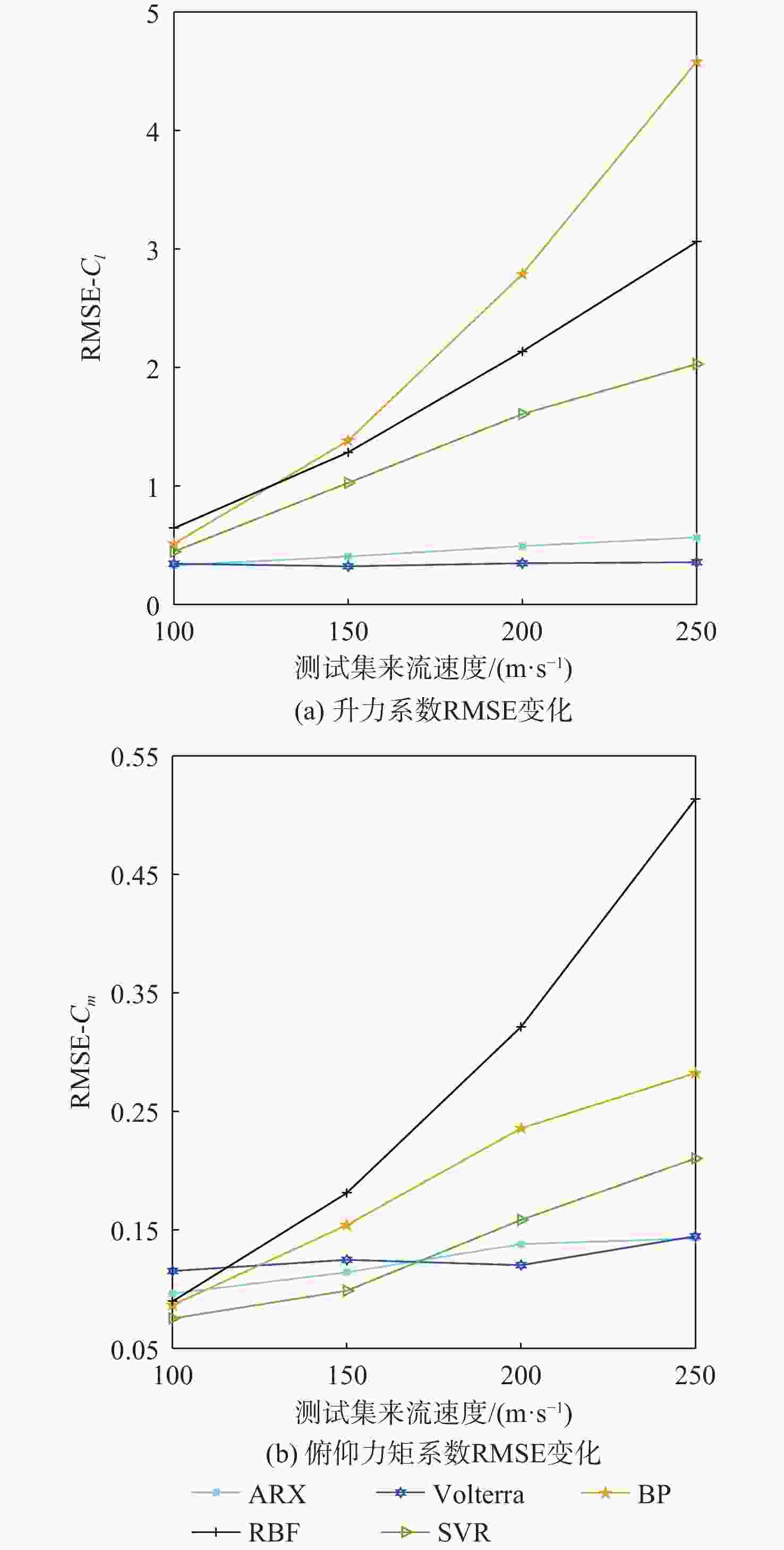
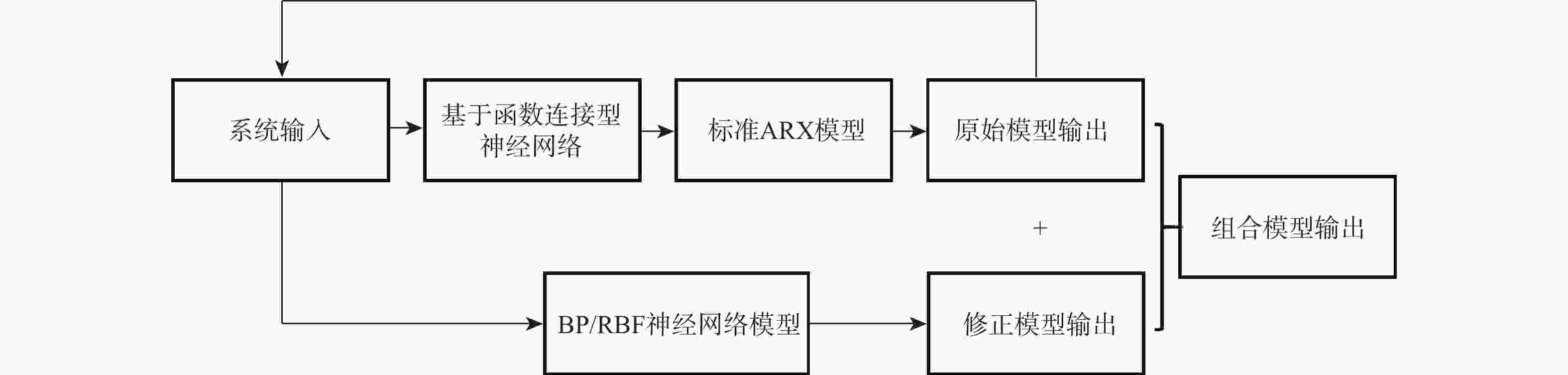
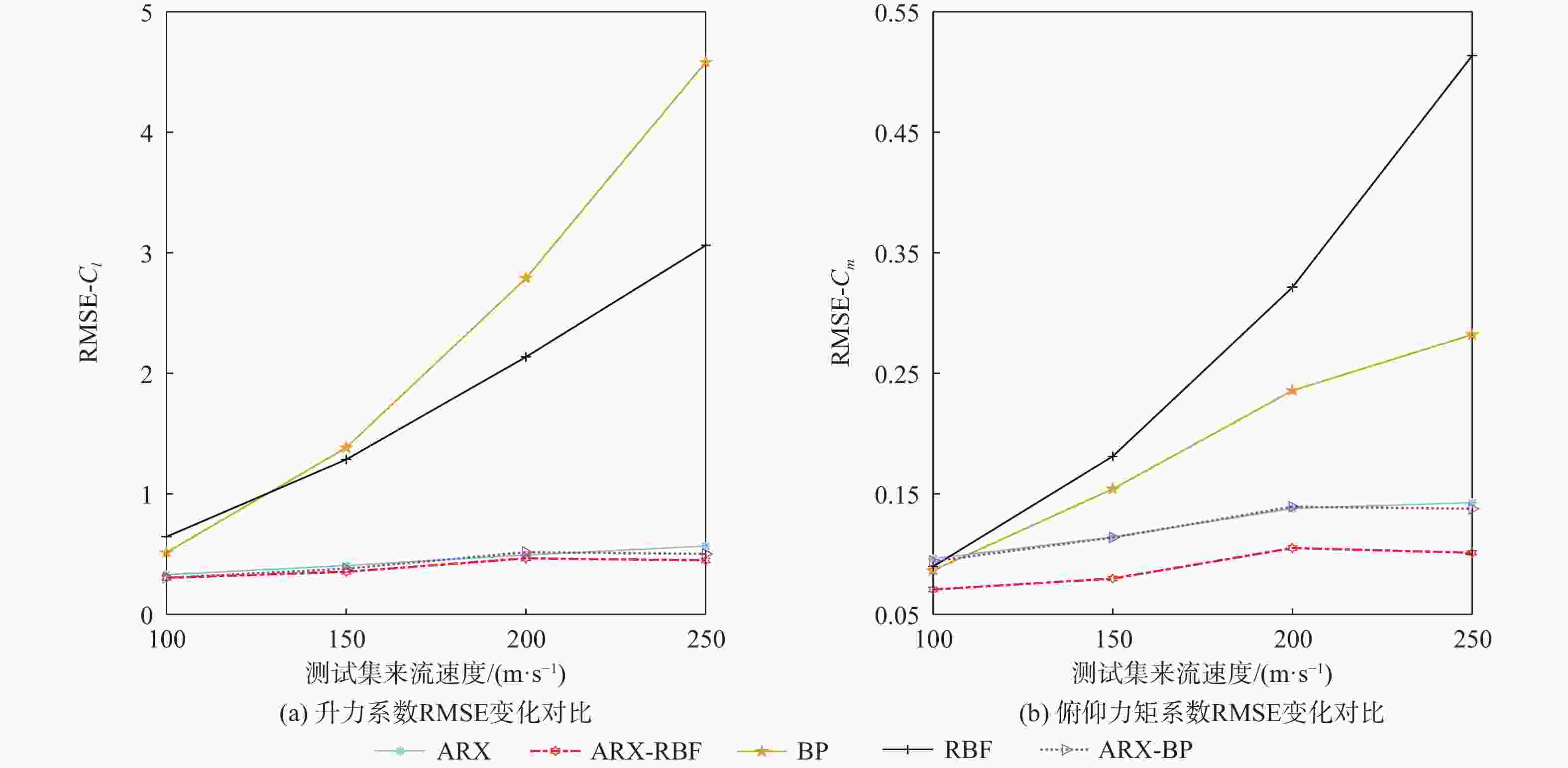
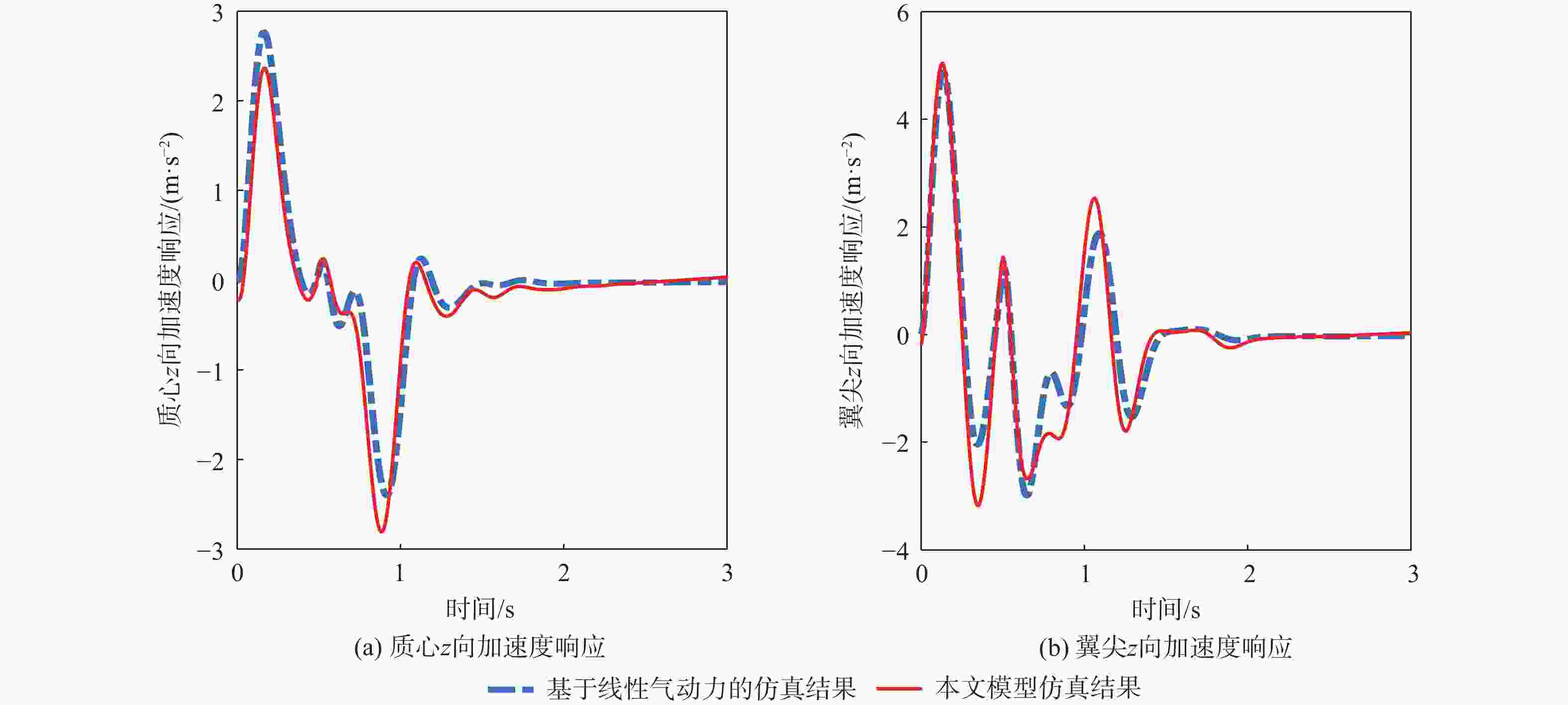
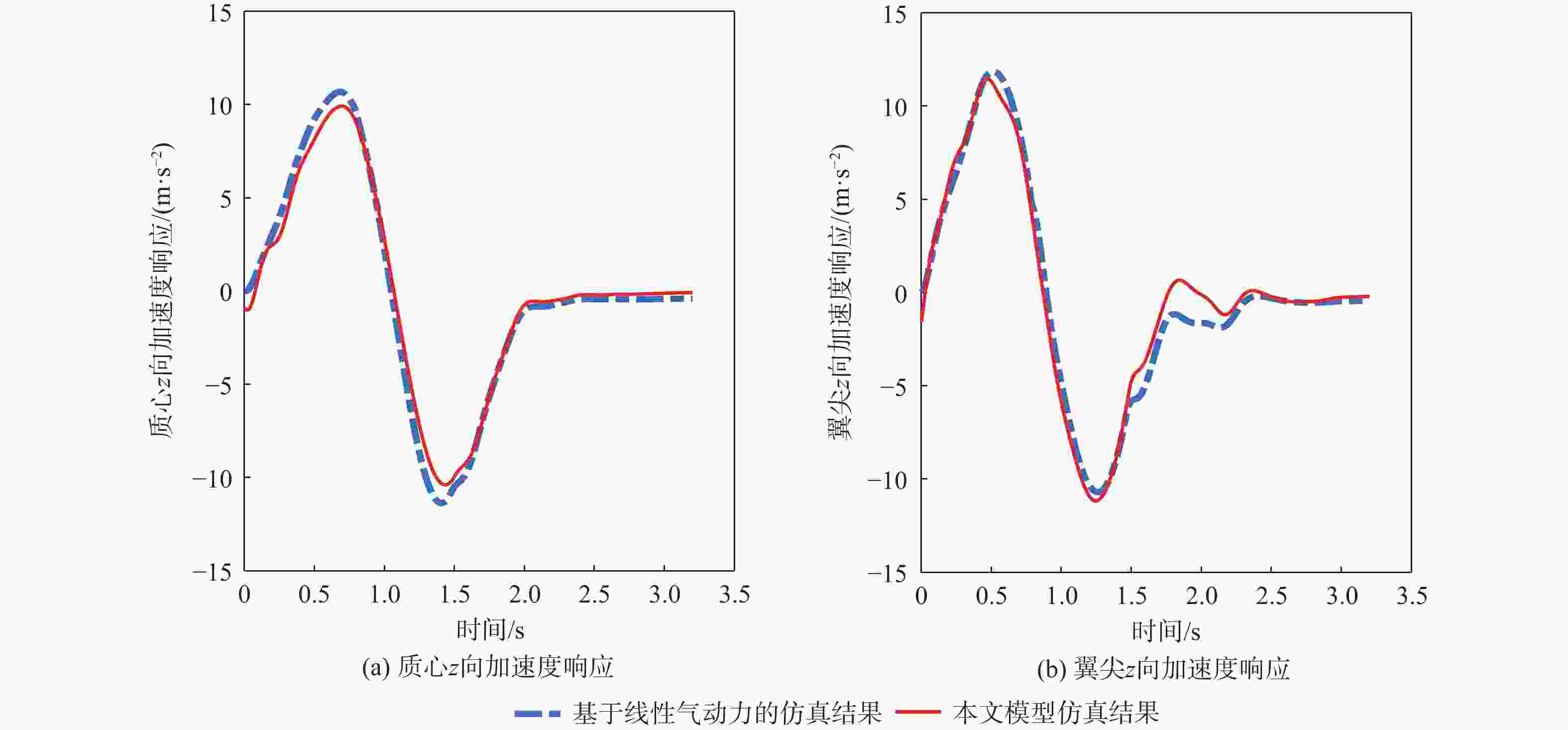
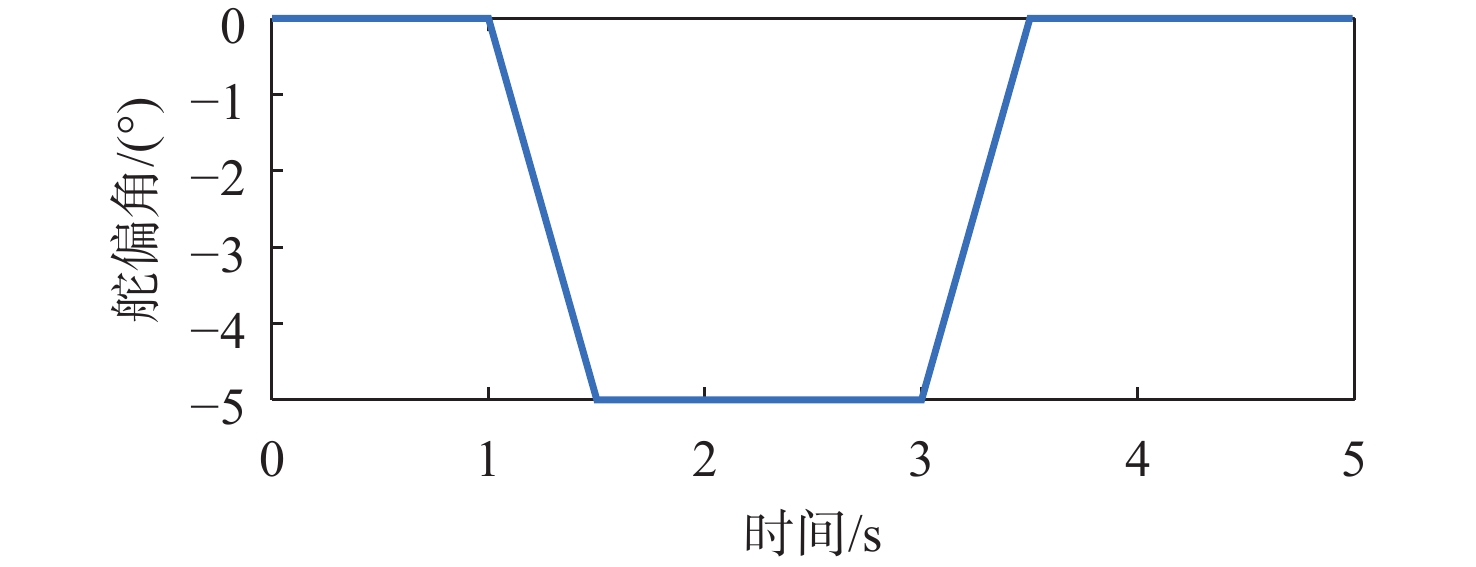
针对低速太阳能无人机在由阵风引起的大迎角非线性气动力情况下的高精度、高效率气动弹性及飞行动力学工程仿真问题，对气动力降阶方法及其在飞行动力学仿真中的应用进行深入探索。以二维翼型为例，分别基于自回归外部输入模型(ARX)方法、多小波Volterra级数方法、反向传播(BP)、径向基函数(RBF)神经网络方法和支持向量回归(SVR)方法建立了非定常气动力降阶模型，并比较了5种方法的收敛性及泛化能力。在此基础之上综合ARX和神经网络方法的优点提出一种计算精度高，收敛性、泛化能力较强的ARX-BP/RBF组合建模方法。将基于ARX-RBF的组合气动力降阶方法和弹性飞机刚弹耦合动力学方程相结合建立基于气动力降阶的弹性飞机飞行动力学仿真模型。以一架太阳能无人机模型为例，开展数值验证，对算例对象在阵风及舵面激励下的响应进行仿真研究，并和计算流体力学(CFD)-计算结构动力学(CSD)结果及基于线性气动力的仿真结果进行对比。结果表明：所建立的弹性飞机仿真模型能有效反映气动力非线性特性，且仿真效率高于CFD-CSD分析方法，适用于工程实践。
- 气动力降阶 /
- 飞行仿真 /
- 刚弹耦合动力学方程 /
- 太阳能无人机 /
- 阵风响应
Abstract:
We develop an aeroelasticity and flight dynamics simulation model with nonlinear aerodynamic reduced order model for low-speed solar unmanned aerial vehicles under high angle of attack caused by gust. Five aerodynamic reduced-order models are created in light of the aforementioned issues, and their use in simulating flight dynamics is further explored. The reduced order models include the model based on the autoregressive model with eXogenous inputs (ARX) method, multi-wavelet Volterra series method, back propagation (BP) neural network, radial basis function (RBF) neural network and support vector regression. Then the convergence and the generalization ability of the five models are compared, and a new model with high precision and strong generalization ability is proposed, which is a combination of ARX and neural network model. Taking a solar UAV model as an example, combining an aerodynamic reduced order model with a rigid-elastic coupling dynamic equation, the flight dynamics simulation model of elastic aircraft is established. Lastly, the computational fluid dynamics-computational structural dynamics (CFD-CSD) outputs and the outcomes of the simulation model based on linear aerodynamics are compared with the simulation results to determine how the UAV model responds to gusts. The results show that the performance of the elastic aircraft simulation model in aerodynamic prediction and gust response analysis is better than that of the model based on linear aerodynamics and is in good agreement with the CFD-CSD model, and the simulation efficiency is much higher than that of the CFD-CSD analysis.
- aerodynamic reduced order model /
- flight simulation /
- rigid elastic coupling dynamic equation /
- solar unmanned aerial vehicle /
- gust response

HTML全文

图 1 弹性飞机飞行动力学仿真框架

Figure 1. Flight dynamics simulation framework

下载: 全尺寸图片幻灯片

图 2 气动力计算模块

Figure 2. Aerodynamic calculation framework

下载: 全尺寸图片幻灯片

图 3 SVR原理示意图

Figure 3. Schematic diagram of SVR

下载: 全尺寸图片幻灯片

图 4 CFD计算结果和实验结果^[20]对比

Figure 4. Comparison of CFD and experimental results^[20]

下载: 全尺寸图片幻灯片

图 5 训练集和测试集部分信号形式

Figure 5. Partial signal form of training and test set

下载: 全尺寸图片幻灯片

图 6 各模型在测试集上的输出结果和CFD计算结果对比

Figure 6. Comparison between output results of different reduced order models and CFD methods ontest data set

下载: 全尺寸图片幻灯片

图 7 各模型随训练速度点样本数增加收敛性对比

Figure 7. Comparison of convergence of each model with increasing sample size of training speed points

下载: 全尺寸图片幻灯片

图 8 各模型对来流速度泛化能力对比

Figure 8. Comparison of generalization ability of each model for incoming flow velocity

下载: 全尺寸图片幻灯片

图 9 ARX-BP/RBF组合模型结构

Figure 9. Structure of ARX-BP/RBF combined model

下载: 全尺寸图片幻灯片

图 10 组合模型和原始模型收敛性对比

Figure 10. Comparison of convergence between combined model and original model

下载: 全尺寸图片幻灯片

图 11 组合模型和原始模型泛化能力对比

Figure 11. Comparison of generalization ability of combined model and original model

下载: 全尺寸图片幻灯片

图 12 太阳能无人机结构模型

Figure 12. Structural model of solar UAV

下载: 全尺寸图片幻灯片

图 13 弹性模态振型

Figure 13. Elastic mode shape

下载: 全尺寸图片幻灯片

图 14 整机外表面网格及局部放大

Figure 14. Grid of external surface and local enlarged view of UAV

下载: 全尺寸图片幻灯片

图 15 气动片条划分俯视图

Figure 15. Top view of slice model

下载: 全尺寸图片幻灯片

图 16 三维气动力降阶模型运行流程

Figure 16. Operation process of three dimensional aerodynamic reduced order model

下载: 全尺寸图片幻灯片

图 17 CFD计算结果的给定运动及变形信号

Figure 17. Motion and deformation signal for CFD calculation

下载: 全尺寸图片幻灯片

图 18 初始、修正模型输出结果与CFD计算结果对比

Figure 18. Comparison of initial and modified model output results with CFD calculation results

下载: 全尺寸图片幻灯片

图 19 飞行仿真模型输出结果与CFD-CSD结果对比

Figure 19. Comparison of flight simulation model output results with CFD-CSD results

下载: 全尺寸图片幻灯片

图 20 阵风算例1加速度响应对比

Figure 20. Comparison of acceleration response under gust case 1

下载: 全尺寸图片幻灯片

图 21 阵风算例2加速度响应对比

Figure 21. Comparison of acceleration response under gust case 2

下载: 全尺寸图片幻灯片

图 22 阵风算例3加速度响应对比

Figure 22. Comparison of acceleration response under gust case 3

下载: 全尺寸图片幻灯片

图 23 舵偏角变化曲线

Figure 23. Variation curve of rudder deflection angle

下载: 全尺寸图片幻灯片

图 24 给定舵偏角变化后加速度响应对比

Figure 24. Comparison of acceleration response for a given rudder deflection angle change

下载: 全尺寸图片幻灯片

表 1 CFD计算验证算例翼型运动参数

Table 1. Airfoil motion parameters of CFD case

翼型弦长/m	来流速度/ (m·s⁻¹)	初始迎角/(°)	俯仰运动幅值/(°)	减缩频率
0.55	40.8	15	10	0.124

下载: 导出CSV

表 2 训练集速度点设置

Table 2. Speed settings for training sets

训练集编号	训练集包含的速度点/(m·s⁻¹)
1	10,60
2	10,35,60
3	10,20,30,40,50,60
4	10,15,20,25,30,35,40,45,50,55,60

下载: 导出CSV

表 3 测试集速度点设置

Table 3. Speed settings for test sets

测试集编号	测试集速度/( m·s⁻¹)
1	55
2	33
3	22
4	12
5	10

下载: 导出CSV

表 4 各模型相同测试集计算时间对比

Table 4. Comparison of calculation efficiency for same test set for each model

模型	计算时间/s
ARX	0.005
Volterra	0.080
BP	0.009
RBF	0.045
SVR	0.052

下载: 导出CSV

表 5 组合模型相同测试集计算时间对比

Table 5. Comparison of calculation efficiency for same test set for each model

模型	计算时间/s
ARX-RBF	0.0505
ARX-BP	0.0120

下载: 导出CSV

表 6 太阳能无人机结构主要参数

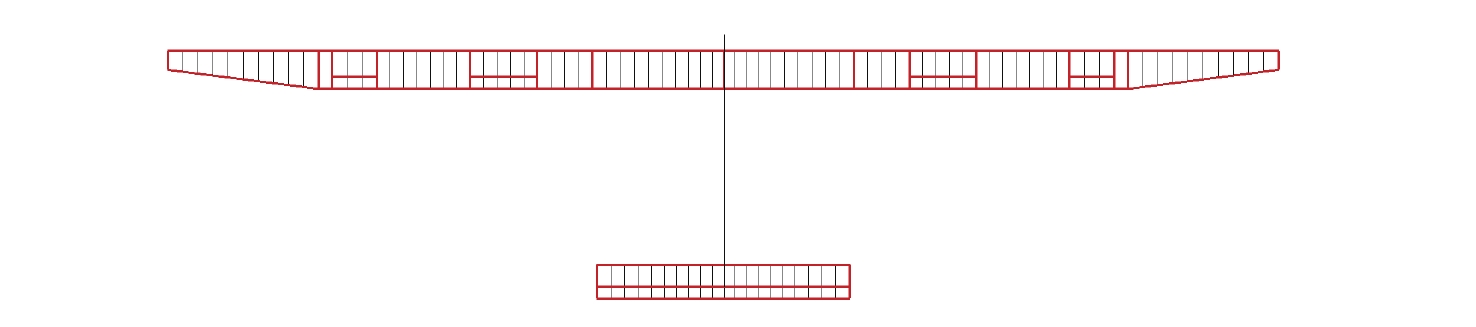
Table 6. Main structural parameters of solar UAV

结构参数	数值
机翼展长/m	50.00
机翼弦长/m	1.72
平尾展长/m	10.20
平尾弦长/m	1.52
垂尾展长/m	4.77
垂尾弦长/m	1.52
质量/kg	424.70
质心到机头距离/m	10.87
转动惯量I_xx/(kg·m²)	5.9387×10⁴
转动惯量/I_yy/(kg·m²)	4.8061×10³
转动惯量/I_zz/(kg·m²)	6.4156×10⁴
转动惯量/I_xz/(kg·m²)	0.2516

下载: 导出CSV

表 7 弹性模态频率

Table 7. Elastic modal frequency

阶数	频率/Hz
1	0.48
2	1.33
3	2.01
4	3.36
5	3.55
6	4.74

下载: 导出CSV

表 8 来流及SIN型阵风参数

Table 8. Incoming flow and SIN type gust parameters

来流风速/（m·s⁻¹）	阵风形式	阵风幅值/（m·s⁻¹）	阵风频率/ Hz
20	SIN型	7	1.2

下载: 导出CSV

表 9 计算效率对比

Table 9. Comparison of calculation efficiency

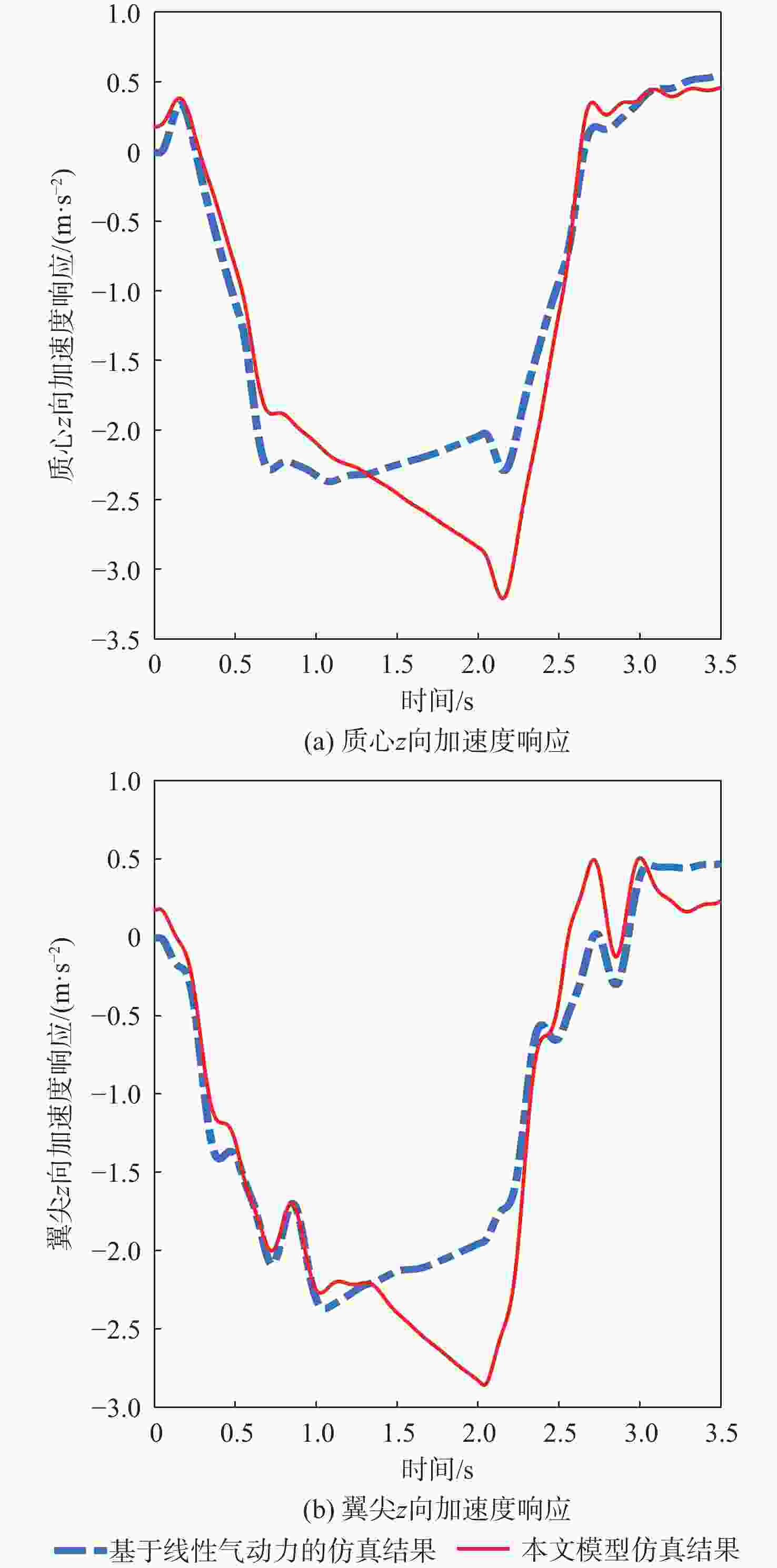
模型	时间步长/s	时间步数	计算时间/min
CFD-CSD	0.001	5000	2398
本文模型	0.001	5000	77

下载: 导出CSV

表 10 来流及1-COS型型阵风参数

Table 10. Incoming flow and 1-COS type gust parameters

编号	来流风速/ （m·s⁻¹）	阵风形式	阵风幅值/ （m·s⁻¹）	尺度L₁/m	尺度L₂/m
1	20	1-COS型	1	30	40
2	20	1-COS型	5	10	40
3	20	1-COS型	7	30	50

下载: 导出CSV

参考文献(20)

[1]	王少奇, 马东立, 杨穆清, 等. 高空太阳能无人机三维航迹优化[J]. 北京航空航天大学学报, 2019, 45(5): 936-943. doi: 10.13700/j.bh.1001-5965.2018.0511 WANG S Q, MA D L, YANG M Q, et al. Three-dimensional optimal path planning for high-altitude solar-powered UAV[J]. Journal of Beijing University of Aeronautics and Astronautics, 2019, 45(5): 936-943(in Chinese). doi: 10.13700/j.bh.1001-5965.2018.0511
[2]	刘藤, 李栋, 黄冉冉, 等. 基于降阶模型的翼型结冰冰形预测方法[J]. 北京航空航天大学学报, 2019, 45(5): 1033-1041. doi: 10.13700/j.bh.1001-5965.2018.0474 LIU T, LI D, HUANG R R, et al. Ice shape prediction method of aero-icing based on reduced order model[J]. Journal of Beijing University of Aeronautics and Astronautics, 2019, 45(5): 1033-1041(in Chinese). doi: 10.13700/j.bh.1001-5965.2018.0474
[3]	杨国伟, 王济康. CFD结合降阶模型预测阵风响应[J]. 力学学报, 2008, 40(2): 145-153. doi: 10.3321/j.issn:0459-1879.2008.02.001 YANG G W, WANG J K. Prediction of gust response by CFD combined with reduced order model[J]. Acta Mechanica Sinica, 2008, 40(2): 145-153(in Chinese). doi: 10.3321/j.issn:0459-1879.2008.02.001
[4]	张伟伟, 叶正寅. 基于气动力降阶模型的跨音速气动弹性稳定性分析[J]. 振动工程学报, 2007, 24(6): 768-772. ZHANG W W, YE Z Y. Transonic aeroelastic stability analysis based on aerodynamic reduced order model[J]. Journal of Vibration Engineering, 2007, 24(6): 768-772(in Chinese).
[5]	师妍, 万志强, 吴志刚, 等. 基于气动力降阶的弹性飞机阵风响应仿真分析及验证[J]. 航空学报, 2022, 43(1): 125474. SHI Y, WAN Z Q, WU Z Q, et al. Gust response analysis and verification of elastic aircraft based on nonlinear aerodynamic reduced order model[J]. Acta Aeronautica et Astronautica Sinica, 2022, 43(1): 125474(in Chinese).
[6]	LIND R, PRAZENICA R J, BRENNER M J, et al. Identifying parameter dependent Volterra kernels to predict aeroelastic instabilities[J]. AIAA Journal, 2005, 43(12): 2496-2502. doi: 10.2514/1.12042
[7]	吴志刚, 杨超. 基于Volterra级数的跨音速非定常气动力建模[J]. 北京航空航天大学学报, 2006, 32(4): 373-376. doi: 10.3969/j.issn.1001-5965.2006.04.001 WU Z G, YANG C. Volterra series based transonic unsteady aerodynamics modeling[J]. Journal of Beijing University of Aeronautics and Astronautics, 2006, 32(4): 373-376(in Chinese). doi: 10.3969/j.issn.1001-5965.2006.04.001
[8]	PRAZENICA R J, REISENTHEL P H, KURDILA A J, et al. Volterra kernel extrapolation for modeling nonlinear aeroelastic systems at novel flight conditions[J]. Journal of Aircraft, 2007, 44(1): 149-162. doi: 10.2514/1.22764
[9]	OMRAN A, NEWMAN B. Full envelope nonlinear parameter- varying model approach for atmospheric flight dynamics[J]. Journal of Guidance, Control, and Dynamics, 2012, 35(1): 270-283. doi: 10.2514/1.51577
[10]	王云海, 韩景龙, 张兵, 等. 空气动力二阶核函数辨识方法[J]. 航空学报, 2014, 35(11): 2949-2957. WANG Y H, HAN J L, ZHANG B, et al. Aerodynamic second order kernel function identification method[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(11): 2949-2957(in Chinese).
[11]	陈森林, 高正红, 饶丹. 基于多小波的Volterra级数非定常气动力建模方法[J]. 航空学报, 2018, 39(1): 121379. CHEN S L, GAO Z H, RAO D. Modeling method of unsteady aerodynamics based on multiwavelet Volterra series[J]. Acta Aeronautica et Astronautica Sinica, 2018, 39(1): 121379(in Chinese).
[12]	王超, 王贵东, 白鹏. 飞行仿真气动力数据机器学习建模方法[J]. 空气动力学学报, 2019, 37(3): 488-497. WANG C, WANG G D, BAI P. Machine learning modeling method for aerodynamic data of flight simulation[J]. Acta Aerodynamics Sinica, 2019, 37(3): 488-497(in Chinese).
[13]	ZHANG W W, WANG B B, YE Z Y, et al. Efficient method for limit cycle flutter analysis based on nonlinear aerodynamic reduced-order models[J]. AIAA Journal, 2012, 50(5): 1019-1028. doi: 10.2514/1.J050581
[14]	KOU J Q, ZHANG W W. Reduced-order modeling for nonlinear aeroelasticity with varying Mach numbers[J]. Journal of Aerospace Engineering, 2018, 31(6): 04018105. doi: 10.1061/(ASCE)AS.1943-5525.0000932
[15]	KOU J Q, ZHANG W W. Multi-kernel neural networks for nonlinear unsteady aerodynamic reduced-order modeling[J]. Aerospace Science and Technology, 2017, 67: 309-326. doi: 10.1016/j.ast.2017.04.017
[16]	JIANG Y, ZHAO Q, ZHU J. Unsteady aerodynamics modeling using SVM and artificial neural network[C]//Proceedings of the 2015 Chinese Intelligent Automation Conference: Intelligent Information Processing. Berlin : Springer, 2015: 577-585.
[17]	WANG Q, QIAN W Q, HE K F. Unsteady aerodynamic modeling at high angles of attack using support vector machines[J]. Chinese Journal of Aeronautics, 2015, 28(3): 659-668. doi: 10.1016/j.cja.2015.03.010
[18]	CHEN S L, GAO Z H, ZHU X Q, et al. Unstable unsteady aerodynamic modeling based on least squares support vector machines with general excitation[J]. Chinese Journal of Aeronautics, 2020, 33(10): 2499-2509. doi: 10.1016/j.cja.2020.03.009
[19]	NARENDRA K, GALLMAN P. An iterative method for the identification of nonlinear systems using a Hammerstein model[J]. IEEE Transactions on Automatic Control, 1966, 11(3): 634-638.
[20]	SHENG W, GALBRAITH R A, COTON F N. A modified dynamic stall model for low mach numbers[J]. Journal of Solar Energy Engineering, 2007, 130(3): 653-653.