Double-loop surrogate model for time-dependent reliability analysis based on NARX and Kriging models
-
摘要:
针对具有动态输出性能的结构系统，传统的求解时变可靠性的代理模型方法在建模时只关注当前瞬间作用于系统的随机变量的作用，而忽视了时间累积效果，使得模型对于时变可靠性的预测效果并不理想。基于此，提出了一种基于带外生输入的非线性自回归(NARX)模型和Kriging模型的时变可靠性分析的双层代理模型方法。所提方法在内层利用NARX模型构建给定随机输入变量下输出响应随时间的变化模型，准确模拟系统的动态行为；在外层基于NARX所得极值构建系统极值与随机变量之间的Kriging模型，得到时变结构系统的可靠性。通过3个算例验证了所提方法在处理具有较强波动性输出系统的可靠性问题时的有效性和准确性。
Abstract:Structural systems with dynamic output performance has gained more and more attention in engineering practice. However, most existing surrogate models for estimating time-dependent reliability of such systems only consider the effect of the random variables which are acting on the system at the current moment, but ignores their effect with time-dependent accumulation. Therefore, these models cannot give an accurate prediction for time-dependent reliability of the dynamic systems. To solve this problem. this paper proposes a double-loop surrogate model method for time-dependent reliability analysis based on the nonlinear autoregressive with exogenous input (NARX) model and Kriging model. In the inner loop of the proposed method, NARX model is used to describe the variation of the output response with time under given random input variables, which can accurately simulate the dynamic behavior of the system. In the outer loop, the Kriging model of the extreme value of the dynamic systems is built based on the random input samples and the corresponding extreme values predicted by the inner NARX model. The reliability of the time-varying structure system then can be easily obtained based on the outer Kriging model. Finally, the effectiveness and accuracy of the proposed method for reliability analysis of dynamic structural systems with fluctuating outputs is verified by three examples.
-
Key words:
- time-dependent reliability /
- failure probability /
- surrogate model /
- NARX model /
- Kriging model
-
图 2 NARX模型与Kriging模型预测的时变均值和标准差与参考解的对比
Figure 2. Comparison of reference resolution with time-dependent mean and standard deviation predicted by NARX model andKriging model
图 3 NARX模型与Kriging模型预测的时变均值和标准差与参考解的对比
Figure 3. Comparison of reference solution with time-dependent mean and standard deviation predicted by NARX model a nd Kriging model
图 6 NARX模型与Kriging模型预测的时变均值和标准差与参考解的对比
Figure 6. Comparison of reference solution with time-dependent mean and standard deviation predicted by NARX model and Kriging model
表 1 随机变量分布参数
Table 1. Variables and parameters
分布
类型运算
输出$\sigma_{{\rm{s}}}/({\rm{N} } \cdot {\rm{m} }^{-2})$ $A /{\rm{m}}^2$ ${J/{\rm{m} }^{4} }$ $n_0/{\rm{s}}^{-1}$ $\rho/({\rm{kg} }\cdot {\rm{m} }^{-3})$ $C$ 正态
分布均值 $1.1 \times {10^9}$ $0.012\;4$ $ 1.22 \times {10^{ - 4}} $ $163$ $8\;240$ $5.67$ 标准差 $1.1 \times {10^8}$ $1.24 \times {10^{ - 3}}$ $1.22 \times {10^{ - 5}}$ $16.3$ $824$ $0.567$ 
下载: 导出CSV
表 2 不同方法的时变可靠性分析结果
Table 2. Time-dependent reliability analysis results of different methods
方法 $ P_{f} $ $\operatorname{Cov}(P_{f})$ 样本量 构建内层模型平均时刻点 构建外层模型样本量 误差/% NARX-Kriging $8.00 \times {10^{ - 5}}$ $0.035\;4$ $172$ $6$ $27$ $2.56$ Double-Kriging $8.76 \times {10^{ - 5}}$ $0.033\;8$ $196$ $5$ $39$ $6.70$ MC $8.21 \times {10^{ - 5}}$ $0.034\;9$ $7 \times {10^9}$
下载: 导出CSV
表 3 分布参数
Table 3. Variables and parameters
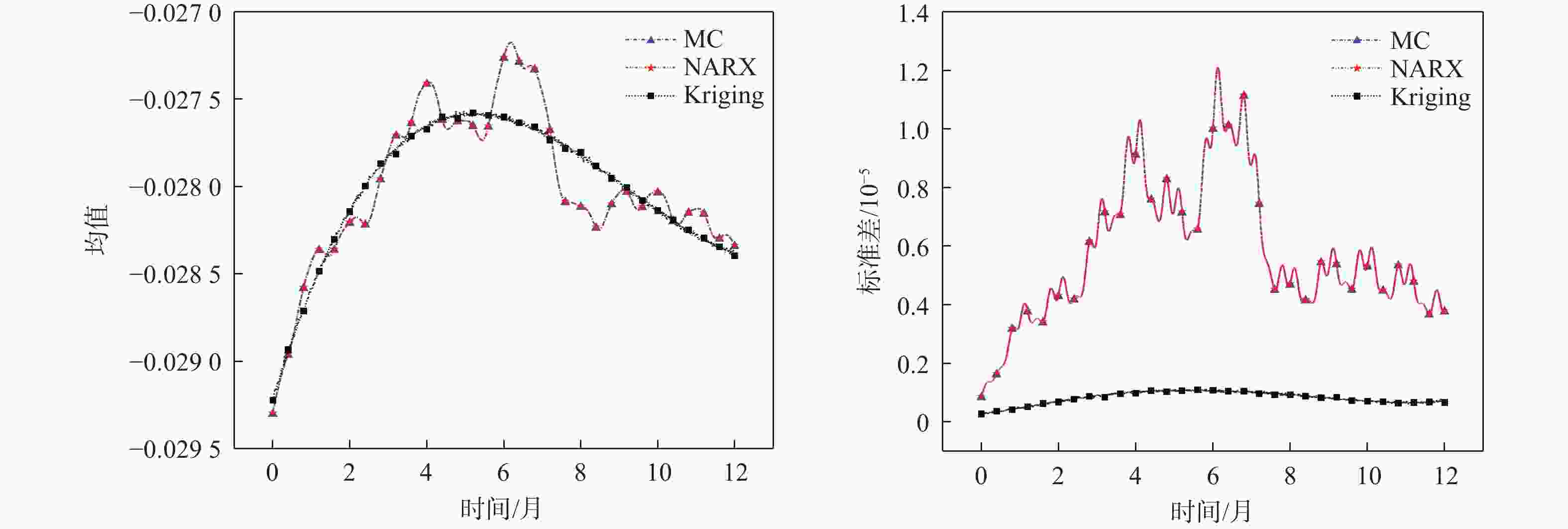
分布类型 运算输出 $\varsigma$ $\omega_{\rm{n}}/({\rm{rad} }\cdot {\rm{s} }^{-1})$ $\alpha$ $A/{\rm{N}}$ $\varphi/({\rm{rad}}\cdot {\rm{s}}^{-1})$ 正态分布 均值 $0.02$ $2\text{π}$ $50$ $1$ $\text{π}$ 标准差 $0.001$ $0.1\text{π}$ $2.5$ $0.05$ $0.05\text{π}$
下载: 导出CSV
表 4 各种方法的时变可靠性分析结果
Table 4. Results of each method
方法 $P_{f}$ $\operatorname{cov}(P_{f})$ 样本量 构建内层模型平均时刻点 构建外层模型样本量 误差/% NARX-Kriging $7.15 \times {10^{ - 4}}$ $0.083\;5$ $9\;900$ $150$ $67$ $1.93$ Double-Kriging MC $7.35 \times {10^{ - 4}}$ $0.082\;4$ $6 \times {10^8}$
下载: 导出CSV
表 5 分布参数
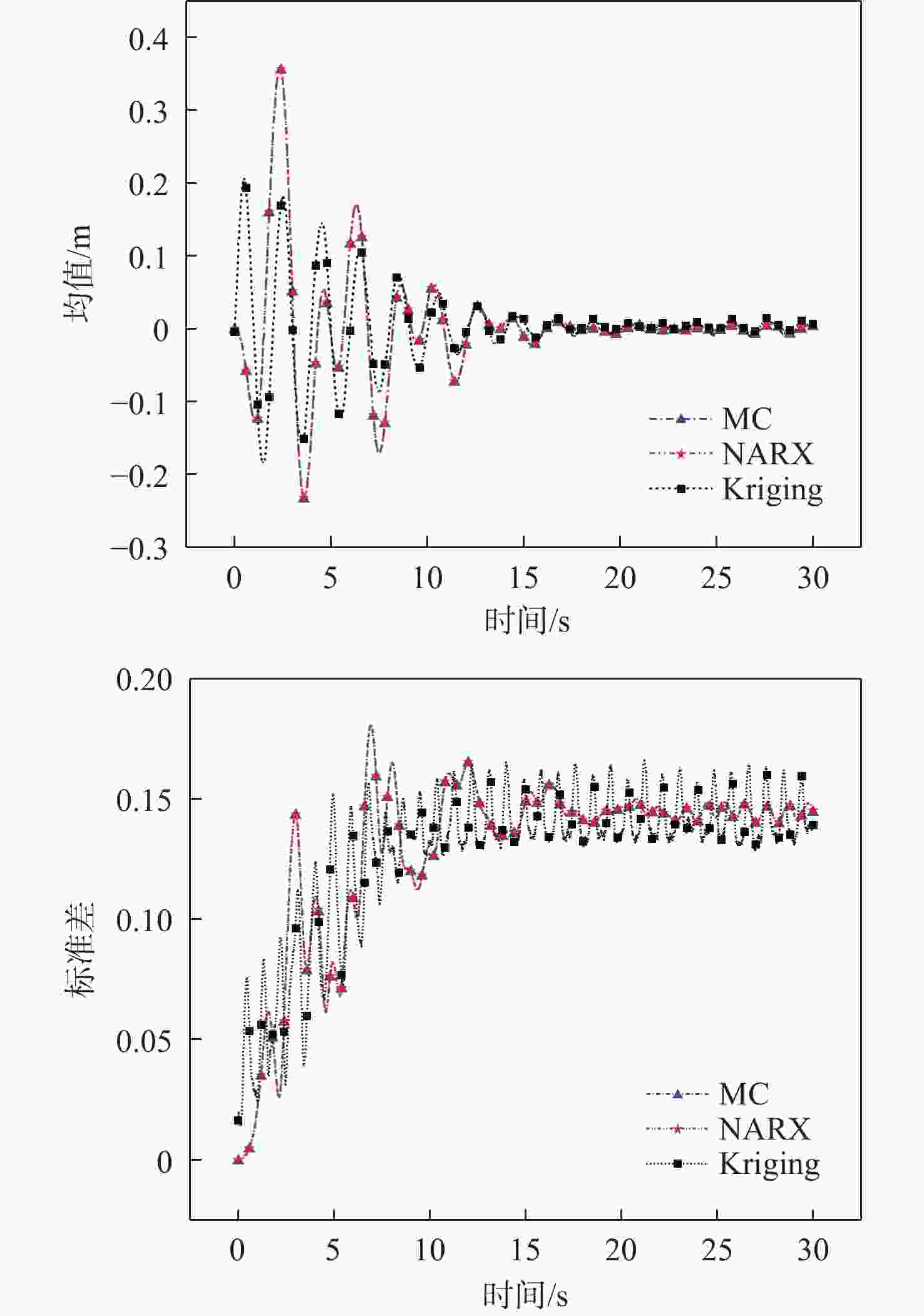
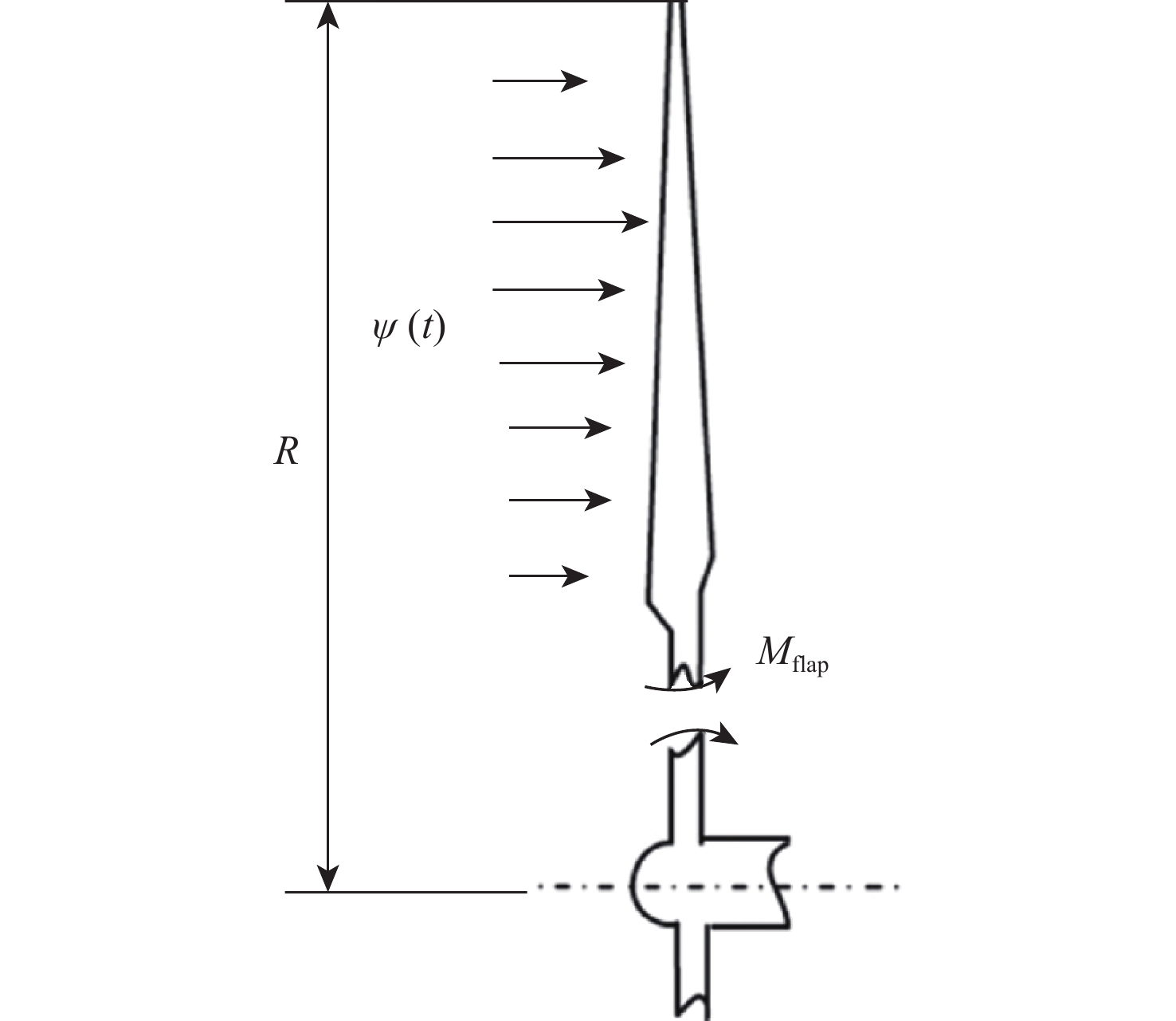
Table 5. Variables and parameters
运算输出 $l_{1}/{\rm{m}}$ $h_{1}/{\rm{m}}$ $h_2 /{\rm{m}}$ $ A_{l} $ $\psi (t)/({\rm{m} }\cdot {\rm{s} }^{-1})$ 均值 $0.22$ $0.025$ $0.019$ $0.030$ $ {\mu _\psi }\left( t \right) $ 标准差 $0.002\;2$ $0.000\;25$ $0.000\;19$ $0.000\;30$ $ {\sigma _\psi }\left( t \right) $ 自相关函数 $ {\rho _\psi }\left( {{t_1},{t_2}} \right) $ 注：l1，h1，h2，Al为正态分布；${\psi}\left( t \right)$为随机过程。
下载: 导出CSV
表 6 各种方法的时变可靠性分析结果
Table 6. Results of each method
方法 Pf Cov(pf) 样本量 构建内层模型平均时刻点 构建外层模型样本量 误差/% 计算结果 NARX-Kriging 6.32×10-4 0.056 3 7 640 40 191 2.27 Double-Kriging MC 6.18×10-4 0.056 8 6×108
下载: 导出CSV
-
[1] 黄贤振, 张义民, 吴茂昌, 等. 基于降维积分的结构系统可靠性分析研究[J]. 力学学报, 2013, 45(3): 456-460. doi: 10.6052/0459-1879-12-326HUANG X Z, ZHANG Y M, WU M C, et al. Research on the method for reliability analysis of structural systems based on the dimensional-reduction integration[J]. Chinese Journal of Theoretical and Applied Mechanics, 2013, 45(3): 456-460(in Chinese). doi: 10.6052/0459-1879-12-326 [2] 杨绿峰, 吴文龙, 余波. 一种不依赖失效路径的结构体系可靠度分析方法[J]. 中国科学:物理学 力学 天文学, 2014, 44(11): 1220-1231.YANG L F, WU W L, YU B. A failure-path independent method for analysis of structural system reliability[J]. Scientia Sinica: Physica, Mechanica & Astronomica, 2014, 44(11): 1220-1231(in Chinese). [3] 亢战, 罗阳军. 基于凸模型的结构非概率可靠性优化[J]. 力学学报, 2006, 38(6): 807-815. doi: 10.3321/j.issn:0459-1879.2006.06.011KANG Z, LUO Y J. On structural optimization for non-probabilistic reliability based on convex models[J]. Chinese Journal of Theoretical and Applied Mechanics, 2006, 38(6): 807-815(in Chinese). doi: 10.3321/j.issn:0459-1879.2006.06.011 [4] 祁武超,邱志平. 基于区间分析的结构非概率可靠性优化设计[J]. 中国科学: 物理学 力学 天文学, 2013, 43(1): 85-93.QI W C, QIU Z P. Non-probabilistic reliability-based structural design optimization based on the interval analysis method[J]. Scientia Sinica: Physica, Mechanica & Astronomica, 2013, 43(1): 85-93(in Chinese). [5] LIANG J H, MOURELATOS Z P, NIKOLAIDIS E. A single-loop approach for system reliability-based design optimization[J]. Journal of Mechanical Design, 2007, 129(12): 1215-1224. doi: 10.1115/1.2779884 [6] DU X P, CHEN W. Sequential optimization and reliability assessment method for efficient probabilistic design[J]. Journal of Mechanical Design, 2004, 126(2): 225-233. doi: 10.1115/1.1649968 [7] RICE S O. Mathematical analysis of random noise[J]. The Bell System Technical Journal, 1944, 23(3): 282-332. doi: 10.1002/j.1538-7305.1944.tb00874.x [8] CRANDALL S H, CHANDIRAMANI K L, COOK R G. Some first-passage problems in random vibration[J]. Journal of Applied Mechanics, 1966, 33(3): 532-538. doi: 10.1115/1.3625118 [9] SUNDAR V S, MANOHAR C S. Time variant reliability model updating in instrumented dynamical systems based on Girsanov’s transformation[J]. International Journal of Non-Linear Mechanics, 2013, 52: 32-40. doi: 10.1016/j.ijnonlinmec.2013.02.002 [10] BREITUNG K, RACKWITZ R. Nonlinear combination of load processes[J]. Journal of Structural Mechanics, 1982, 10(2): 145-166. [11] ZAYED A, GARBATOV Y, GUEDES SOARES C. Time variant reliability assessment of ship structures with fast integration techniques[J]. Probabilistic Engineering Mechanics, 2013, 32: 93-102. doi: 10.1016/j.probengmech.2013.01.002 [12] ANDRIEU-RENAUD C, SUDRET B, LEMAIRE M. The PHI2 method: A way to compute time-variant reliability[J]. Reliability Engineering & System Safety, 2004, 84(1): 75-86. [13] 张德权, 韩旭, 姜潮, 等. 时变可靠性的区间PHI2分析方法[J]. 中国科学:物理学 力学 天文学, 2015, 45(5): 41-53.ZHANG D Q, HAN X, JIANG C, et al. The interval PHI2 analysis method for time-dependent reliability[J]. Scientia Sinica: Physica, Mechanica & Astronomica, 2015, 45(5): 41-53(in Chinese). [14] HU Z, DU X P. A sampling approach to extreme value distribution for time-dependent reliability analysis[J]. Journal of Mechanical Design, 2013, 135(7): 071003. doi: 10.1115/1.4023925 [15] LI J, CHEN J B, FAN W L. The equivalent extreme-value event and evaluation of the structural system reliability[J]. Structural Safety, 2007, 29(2): 112-131. doi: 10.1016/j.strusafe.2006.03.002 [16] CHEN J B, LI J. The extreme value distribution and dynamic reliability analysis of nonlinear structures with uncertain parameters[J]. Structural Safety, 2007, 29(2): 77-93. doi: 10.1016/j.strusafe.2006.02.002 [17] DU X P. Time-dependent mechanism reliability analysis with envelope functions and first-order approximation[J]. Journal of Mechanical Design, 2014, 136(8): 081010. doi: 10.1115/1.4027636 [18] 石岩, 吕震宙, 周易成. 随时间和空间变化可靠性及可靠性全局灵敏度分析的包络函数法[J]. 西北工业大学学报, 2017, 35(4): 591-598. doi: 10.3969/j.issn.1000-2758.2017.04.006SHI Y, LU Z Z, ZHOU Y C. Temporal and spatial reliability and global sensitivity analysis with envelope functions[J]. Journal of Northwestern Polytechnical University, 2017, 35(4): 591-598(in Chinese). doi: 10.3969/j.issn.1000-2758.2017.04.006 [19] CHENG K, LU Z Z. Time-variant reliability analysis based on high dimensional model representation[J]. Reliability Engineering & System Safety, 2019, 188: 310-319. [20] HAWCHAR L, EL SOUEIDY C P, SCHOEFS F. Principal component analysis and polynomial chaos expansion for time-variant reliability problems[J]. Reliability Engineering & System Safety, 2017, 167: 406-416. [21] HU Z, MAHADEVAN S, DU X P. Uncertainty quantification of time-dependent reliability analysis in the presence of parametric uncertainty[J]. ASCE-ASME Journal of Risk and Uncertainty in Engineering Systems Part B: Mechanical Engineering, 2016, 2(3): 031005. doi: 10.1115/1.4032307 [22] WANG Z Q, WANG P F. A nested extreme response surface approach for time-dependent reliability-based design optimization[J]. Journal of Mechanical Design, 2012, 134(12): 121007. doi: 10.1115/1.4007931 [23] HU Z, DU X P. Mixed efficient global optimization for time-dependent reliability analysis[J]. Journal of Mechanical Design, 2015, 137(5): 051401. doi: 10.1115/1.4029520 [24] SPIRIDONAKOS M D, CHATZI E N. Metamodeling of dynamic nonlinear structural systems through polynomial chaos NARX models[J]. Computers & Structures, 2015, 157: 99-113. [25] CHEN S, BILLINGS S A, LUO W. Orthogonal least squares methods and their application to non-linear system identification[J]. International Journal of Control, 1989, 50(5): 1873-1896. doi: 10.1080/00207178908953472 [26] BILLINGS S A. Nonlinear system identification: NARMAX methods in the time, frequence and spatio-temporal domains[M]. New York: John Wiley & Sons, Inc., 2013. [27] CHEN Z H, NI Y Q. On-board identification and control performance verification of an MR damper incorporated with structure[J]. Journal of Intelligent Material Systems and Structures, 2011, 22(14): 1551-1565. doi: 10.1177/1045389X11411212 [28] WEI H L, BILLINGS S A. Model structure selection using an integrated forward orthogonal search algorithm assisted by squared correlation and mutual information[J]. International Journal of Model Identification and Control, 2008, 3(4): 341-356. doi: 10.1504/IJMIC.2008.020543 [29] EFRON B, HASTIE T, JOHNSTONE I, et al. Least angle regression[J]. The Annals of Statistics, 2004, 32(2): 407-499. [30] LV Z Y, LU Z Z, WANG P. A new learning function for Kriging and its applications to solve reliability problems in engineering[J]. Computers & Mathematics with Applications, 2015, 70(5): 1182-1197. [31] KLEINEN J P C. Kringing metamodeling in simulation: A review[J]. Eurpean Journal of Operational Research, 2009, 192(3): 707-716. [32] LOPHAVEN S N, NIELSEN H B, SONDERGAARD J. Aspects of the MATLAB toolbox DACE: IMM-REP-2002-13[R]. Kongens Lyngby: Technical University of Denmark, 2002. [33] ECHARD B, GAYTON N, LEMAIRE M. AK-MCS: An active learning reliability method combining Kriging and Monte Carlo Simulation[J]. Structural Safety, 2011, 33(2): 145-154. doi: 10.1016/j.strusafe.2011.01.002 [34] GHANEM R G, SPANOS P D. Stochastic finite elements: A spectral approach[M]. Berlin: Springer-Verlag, 1991. -
下载:
点击查看大图
计量
- 文章访问数: 498
- HTML全文浏览量: 66
- PDF下载量: 34
- 被引次数: 0
