特征点分段提取的时间序列模式匹配方法

李正欣; 刘畅; 吴诗辉; 郭建胜

doi:10.13700/j.bh.1001-5965.2021.0546

特征点分段提取的时间序列模式匹配方法

doi: 10.13700/j.bh.1001-5965.2021.0546

空军工程大学装备管理与无人机工程学院，西安 710051

详细信息

通讯作者:
E-mail：lizhengxin_2005@163.com

中图分类号: TP391
计量
- 文章访问数: 249
- HTML全文浏览量: 60
- PDF下载量: 46
- 被引次数: 0
出版历程
- 收稿日期: 2021-09-13
- 录用日期: 2021-12-10
- 网络出版日期: 2022-02-15
- 整期出版日期: 2023-07-31

Segmentation extraction of feature points for time series pattern matching

Equipment Management and Unmanned Aerial Vehicle Engineering College，Air Force Engineering University，Xi’an 710051，China

More Information

Corresponding author: E-mail：lizhengxin_2005@163.com

摘要

摘要:
常用的时间序列模式匹配方法难以平衡计算复杂度与匹配精度，针对该问题，提出了一种特征点分段提取的时间序列模式匹配方法。提取时间序列每个变量维度上的特征点，降低序列长度；将特征点序列转化为分位点矩阵，利用欧氏距离对分位点矩阵进行相似性度量；在几组时间序列数据集上对所提方法进行分类实验。结果表明：所提方法在降低计算复杂度的同时，获得了较高的匹配精度。
- 时间序列 /
- 模式匹配 /
- 特征提取 /
- 分位点矩阵 /
- 计算复杂度
Abstract:
It is difficult for the common time series pattern matching methods to balance the computational complexity and matching accuracy. To solve this problem, a time series matching method based on segmented extraction of feature points is proposed. Firstly, the feature points on each variable dimension of the time series are extracted and the sequence length is compressed. Then, the quantile matrix is calculated according to the feature sequence, and the similarity of the quantile matrix is measured by Euclidean distance. Finally, the effectiveness of the proposed method is verified on the application data set. Experimental results show that the proposed method can effectively reduce the computational complexity and ensure high matching accuracy.
- time series /
- pattern matching /
- feature extraction /
- quantile matrix /
- computational complexity

HTML全文

图 1 特征点提取示意图

Figure 1. Schematic diagram of feature point extraction

下载: 全尺寸图片幻灯片

图 2 输入序列(ASL_87, boy)

Figure 2. Input sequence (ASL_87, boy)

下载: 全尺寸图片幻灯片

图 3 不同方法在ASL数据集上寻找的最相似序列

Figure 3. The most similar sequence found by different methods on ASL dataset

下载: 全尺寸图片幻灯片

图 4 滑动窗口因子对匹配精度及计算效率的影响

Figure 4. Influence of sliding window factor on matching accuracy and calculation efficiency

下载: 全尺寸图片幻灯片

图 5 滑动窗口因子对特征点提取的影响

Figure 5. Influence of sliding window factor on feature point extraction

下载: 全尺寸图片幻灯片

图 6 TD、SFP-ED与DTW计算时间比较

Figure 6. Calculation time of TD、SFP-ED and DTW

下载: 全尺寸图片幻灯片

表 1 实验数据集

Table 1. Detail of experimental datasets

数据集	长度	均长	变量个数	样本量	类别
ASL	47~95	59	22	216	8
LP1	15	15	6	88	4
JV	7~29	16	12	640	9
EEG	256	256	64	22	2
WR	128~1918	368	62	44	2
Trace	275	275	1	200	4

下载: 导出CSV

表 2 ASL数据集上的匹配精度

Table 2. Matching accuracy on ASL dataset

k	SVD	DTW	ACM-DTW	TD	PD	SFP-ED
1	0.718	0.977	0.926	0.972	0.579	0.986
5	0.639	0.929	0.870	0.958	0.570	0.947
10	0.570	0.929	0.856	0.906	0.557	0.944

下载: 导出CSV

表 3 6种模式匹配方法在不同准确率下的匹配次数

Table 3. Matching times of 6 pattern matching methods under different accuracy rates

e/%	SVD			DTW			ACM-DTW			TD			PD			SFP-ED
e/%	N=1	N=5	N=10	N=1	N=5	N=10	N=1	N=5	N=10	N=1	N=5	N=10	N=1	N=5	N=10	N=1	N=5	N=10
0	61	20	12	5	0	0	16	9	0	6	0	0	91	33	14	3	0	0
10			19			0			3			0			13			0
20		27	15		0	0		4	0		0	0		25	17		2	0
30			19			1			2			2			28			3
40		34	19		13	0		10	5		4	3		36	18		9	4
50			25			6			5			9			26			1
60		29	26		12	5		10	13		9	8		34	17		6	3
70			7			15			15			7			13			10
80		22	7		14	11		29	17		15	22		23	6		10	7
90			7			30			25			30			12			15
100	155	84	60	211	177	148	200	154	125	210	188	135	125	65	52	213	189	173

下载: 导出CSV

表 4 6组数据集上的匹配精度

Table 4. Accuracy on 6 datasets

数据集	SVD	DTW	ACM-DTW	TD	PD	SFP-ED
ASL	0.718	0.977	0.926	0.972	0.578	0.986
LP1	0.477	0.886	0.909	0.636	0.830	0.921
JV	0.489	0.963	0.759	0.548	0.581	0.958
EEG	0.909	0.727	0.727	1	0.591	0.864
WR	0.977	0.977	0.955	1	1	0.977
Trace		0.995	1	0.930		0.995

下载: 导出CSV

表 5 9个分位点提取结果

Table 5. Nine quantile results

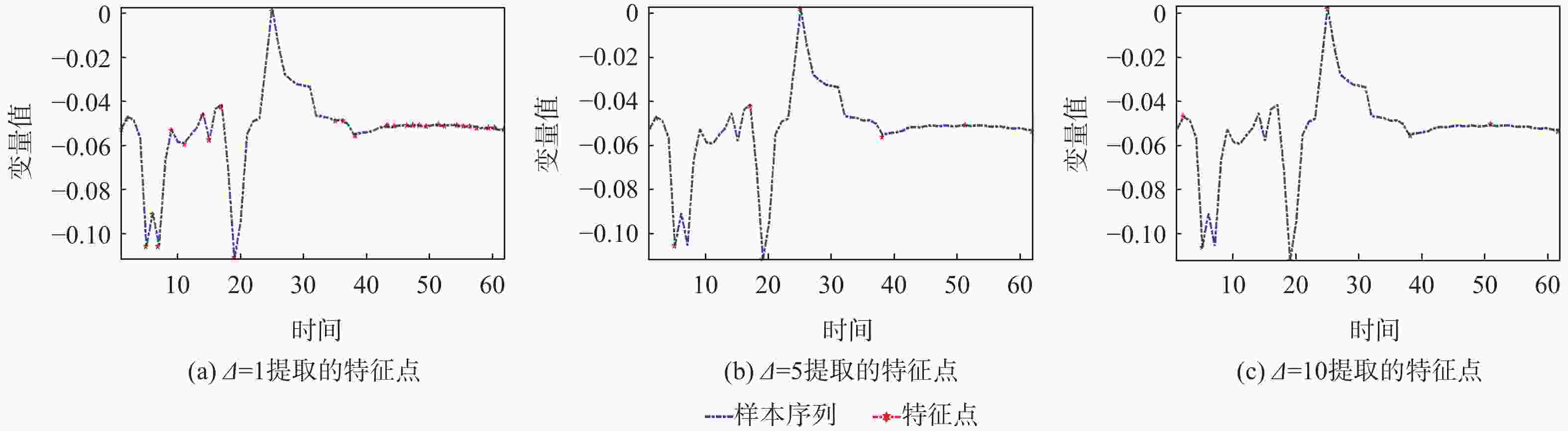
Δ	最小值点	5%	10%	25%	50%	75%	90%	95%	最大值点
1	−0.1111	−0.1052	−0.0975	−0.0528	−0.0512	−0.0506	−0.0460	−0.0414	0.0024
5	−0.1111	−0.1111	−0.1093	−0.0800	−0.0516	−0.0441	−0.0108	0.0024	0.0024
10	−0.1111	−0.1111	−0.1099	−0.0926	−0.0528	−0.0477	−0.0075	0.0024	0.0024

下载: 导出CSV

参考文献(30)

[1]	BOHANNON A W, LAWHERN V J, WAYTOWICH N R, et al. The autoregressive linear mixture model: A time-series model for an instantaneous mixture of network processes[J]. IEEE Transactions on Signal Processing, 2020, 68: 4481-4496. doi: 10.1109/TSP.2020.3012946
[2]	WANG F, LI C, ZENG Z, et al. Cornerstone network with feature extractor: A metric-based few-shot model for Chinese natural sign language[J]. Applied Intelligence, 2021, 51(5): 1-12.
[3]	PAN H, ZHOU H. Study on convolutional neural network and its application in data mining and sales forecasting for E-commerce[J]. Electronic Commerce Research, 2020, 20(2): 297-320. doi: 10.1007/s10660-020-09409-0
[4]	JIANG X Q, ZHANG L C. Stock price fluctuation prediction method based on time series analysis[J]. Discrete and Continuous Dynamical Systems, 2018, 12(4): 915-927.
[5]	WEN S C, YANG C H. Time series analysis and prediction of nonlinear systems with ensemble learning framework applied to deep learning neural networks[J]. Information Sciences, 2021, 572: 167-181. doi: 10.1016/j.ins.2021.04.094
[6]	CABRERA D, SANCHO F, CERRADA M, et al. Knowledge extraction from deep convolutional neural networks applied to cyclo-stationary time-series classification[J]. Information Sciences, 2020, 524: 1-14. doi: 10.1016/j.ins.2020.03.039
[7]	MA Q, CHEN Z, TIAN S, et al. Difference-guided representation learning network for multivariate time series classification[J]. IEEE Transactions on Cybernetics, 2020, 3: 1-11.
[8]	李正欣, 张凤鸣, 李克武, 等. 一种支持DTW距离的多元时间序列索引结构[J]. 软件学报, 2014, 25(3): 560-575. LI Z X, ZHANG F M, LI K W, et al. Index structure for multivariate time series under DTW distance metric[J]. Journal of Software, 2014, 25(3): 560-575(in Chinese).
[9]	SOLEIMANI G, ABESSI M. DLCSS: A new similarity measure for time series data mining[J]. Engineering Applications of Artificial Intelligence, 2020, 92: 103664. doi: 10.1016/j.engappai.2020.103664
[10]	ZHU H, WANG X, CHEN X, et al. Similarity search and performance prediction of shield tunnels in operation through time series data mining[J]. Automation in Construction, 2020, 114: 103178. doi: 10.1016/j.autcon.2020.103178
[11]	LI H. Time works well: Dynamic time warping based on time weighting for time series data mining[J]. Information Sciences, 2021, 547: 592-608. doi: 10.1016/j.ins.2020.08.089
[12]	OKAWA M. Time-series averaging and local stability-weighted dynamic time warping for online signature verification[J]. Pattern Recognition, 2021, 112: 107699. doi: 10.1016/j.patcog.2020.107699
[13]	NIE C X. Nonlinear correlation analysis of time series based on complex network similarity[J]. International Journal of Bifurcation and Chaos, 2020, 14(4): 736-749.
[14]	WANG B Q, JIANG T H, ZHOU X, et al. Time-series classification based on fusion features of sequence and visualization[J]. Applied Sciences, 2020, 10(12): 4124. doi: 10.3390/app10124124
[15]	LI H H, LIU J X, YANG Z L, et al. Adaptively constrained dynamic time warping for time series classification and clustering[J]. Information Sciences, 2020, 534: 97-116. doi: 10.1016/j.ins.2020.04.009
[16]	NISHINO T, HOKUGO A. A stochastic model for time series prediction of the number of post-earthquake fire ignitions in buildings based on the ignition record for the 2011 Tohoku Earthquake[J]. Earthquake Spectra, 2020, 36(1): 232-249. doi: 10.1177/8755293019878184
[17]	WAN Y Q, SI Y W. A hidden semi-Markov model for chart pattern matching in ﬁnancial time series[J]. Soft Computing, 2018, 22: 6525-6544. doi: 10.1007/s00500-017-2703-7
[18]	SUN J, YANG Y, LIU Y, et al. Univariate time series classification using information geometry[J]. Pattern Recognition, 2019, 95: 832-843.
[19]	HUANG W, YUE B, CHI Q, et al. Integrating data-driven segmentation, local feature extraction and fisher kernel encoding to improve time series classification[J]. Neural Processing Letters, 2019, 49(1): 43-66. doi: 10.1007/s11063-018-9798-4
[20]	YOU D G, LIN W W, SHI F, et al. A novel approach for CPU load prediction of cloud server combining denoising and error correction[J]. Computing, 2023, 105(3): 577-594. doi: 10.1007/s00607-020-00865-y
[21]	IOKIBE T, KOYAMA M, TANIGUCHI M. A study for complexity of chaotic time series and prediction accuracy[C]//IEEE International Fuzzy Systems Conference. Piscataway: IEEE Press, 1999: 6430833.
[22]	MONTAGNON C E. Forecasting by splitting a time series using singular value decomposition then using both ARMA and a Fokker Planck equation[J]. Physica A:Statistical Mechanics and its Applications, 2020, 567(3): 536-545.
[23]	THUY H, ANH D T, CHAU V. Efficient segmentation-based methods for anomaly detection in static and streaming time series under dynamic time warping[J]. Journal of Intelligent Information Systems, 2021, 56(3): 373-386.
[24]	孟晓静, 万源. 自适应代价动态时间弯曲的多元时间序列相似性度量[J]. 统计与决策, 2020, 14(2): 25-29. MENG X J, WAN Y. Multivariate time series similarity measure for dynamic time warping of adaptive cost[J]. Statistics and Decision, 2020, 14(2): 25-29(in Chinese).
[25]	李正欣, 张凤鸣, 李克武. 多元时间序列模式匹配方法研究[J]. 控制与决策, 2011, 24(4): 565-570. LI Z X, ZHANG F M, LI K W. Research on pattern matching method of multivariate time series[J]. Control and Decision, 2011, 24(4): 565-570(in Chinese).
[26]	GUIGOU F, COLLET P, PARREND P. SCHEDA: Lightweight euclidean-like heuristics for anomaly detection in periodic time series[J]. Applied Soft Computing, 2019, 82(3): 1432-1443.
[27]	管河山, 姜青山, 王声瑞. 基于点分布特征的多元时间序列模式匹配方法[J]. 软件学报, 2009, 20(1): 67-69. doi: 10.3724/SP.J.1001.2009.00067 GUAN H S, JIANG Q S, WANG S R. Pattern matching method based on point distribution for multivariate time series[J]. Journal of Software, 2009, 20(1): 67-69(in Chinese). doi: 10.3724/SP.J.1001.2009.00067
[28]	GUO X G, HONG P Y, LALEG-KIRATI T M. Calibration and validation for a real-time membrane bioreactor: A sliding window approach[J]. Journal of Process Control, 2021, 98(6): 92-105.
[29]	JILANI T A, BURNEY A S, ARDIL C. A new quantile based fuzzy time series forecasting model[J]. Proceedings of World Academy of Science Engineering & Technology, 2008, 23(1): 32-41.
[30]	刘畅, 李正欣, 张晓丰, 等. 基于特征点界标过滤的时间序列模式匹配方法[J]. 计算机应用研究, 2022, 39(4): 1008-1012. doi: 10.19734/j.issn.1001-3695.2021.09.0396 LIU C, LI Z X, ZHANG X F, et al. Time series pattern matching method based on feature point landmark filtering[J]. Application Research of Computers, 2022, 39(4): 1008-1012(in Chinese). doi: 10.19734/j.issn.1001-3695.2021.09.0396