A sparse estimation method for radar target direction with sliding-window subarray configuration in mainlobe jamming
-
摘要:
雷达抗主瓣干扰(MLJ)一直是雷达领域的难点问题,针对主瓣干扰环境下的雷达目标角度测量问题,提出一种主瓣干扰下基于滑窗子阵的稀疏测角方法,对各子阵进行自适应主瓣干扰抑制处理,并利用自适应后的子阵间相位关系构建角度原子库,采用正交匹配追踪(OMP)算法估计目标角度。当目标与干扰夹角为1/2个3 dB波束宽度时(目标输入信噪比为20 dB),目标角度估计误差小于1/10倍3 dB波束宽度,所提方法无需先验信息,可同时抑制主、副瓣干扰或多个主瓣干扰,并保证较高的目标测角精度。
Abstract:The suppression of mainlobe jamming (MLJ) is a hard task and an open problem in the radar field. This paper considers the problem of radar target direction estimation in MLJ. Hence, we propose a sparse estimation method for radar target direction with sliding-window subarray configuration in MLJ. MLJ is suppressed in each subarray with the proposed method, and the angle atom is constructed according to the phase relationship between the sliding-window subarrays. Finally, the target direction can be estimated with the orthogonal matching pursuit (OMP) algorithm. When the target input signal-to-noise ratio is 20 dB and the angle between the target and MLJ is 1/2 3 dB beam width, the target angle estimation error is smaller than 1/10 3 dB beam width. The accuracy of the angle estimation is well kept and the MLJ can be cancelled without any prior information.
-
Key words:
- mainlobe jamming /
- sliding-window subarray /
- sparse recovery /
- anti-jamming /
- radar
-
表 1 仿真条件设置
Table 1. Simulation parameters setting
条件 设置 阵列天线 20元等距均匀线阵 阵元间距 半波长 滑窗子阵数 15 波束指向/(°) 0 B0.5(3 dB波束宽度)/(°) 5.05 雷达发射信号 线性调频信号,带宽5 MHz,脉宽20 μs,
采样频率10 MHz,阵元级SNRe=0 dB干扰 主瓣压制干扰 目标 位于第100个距离门,空间位置在0° 表 2 干扰环境设置
Table 2. Jamming parameters setting
干扰环境 数量 干噪比/dB 类型 干扰与目标的
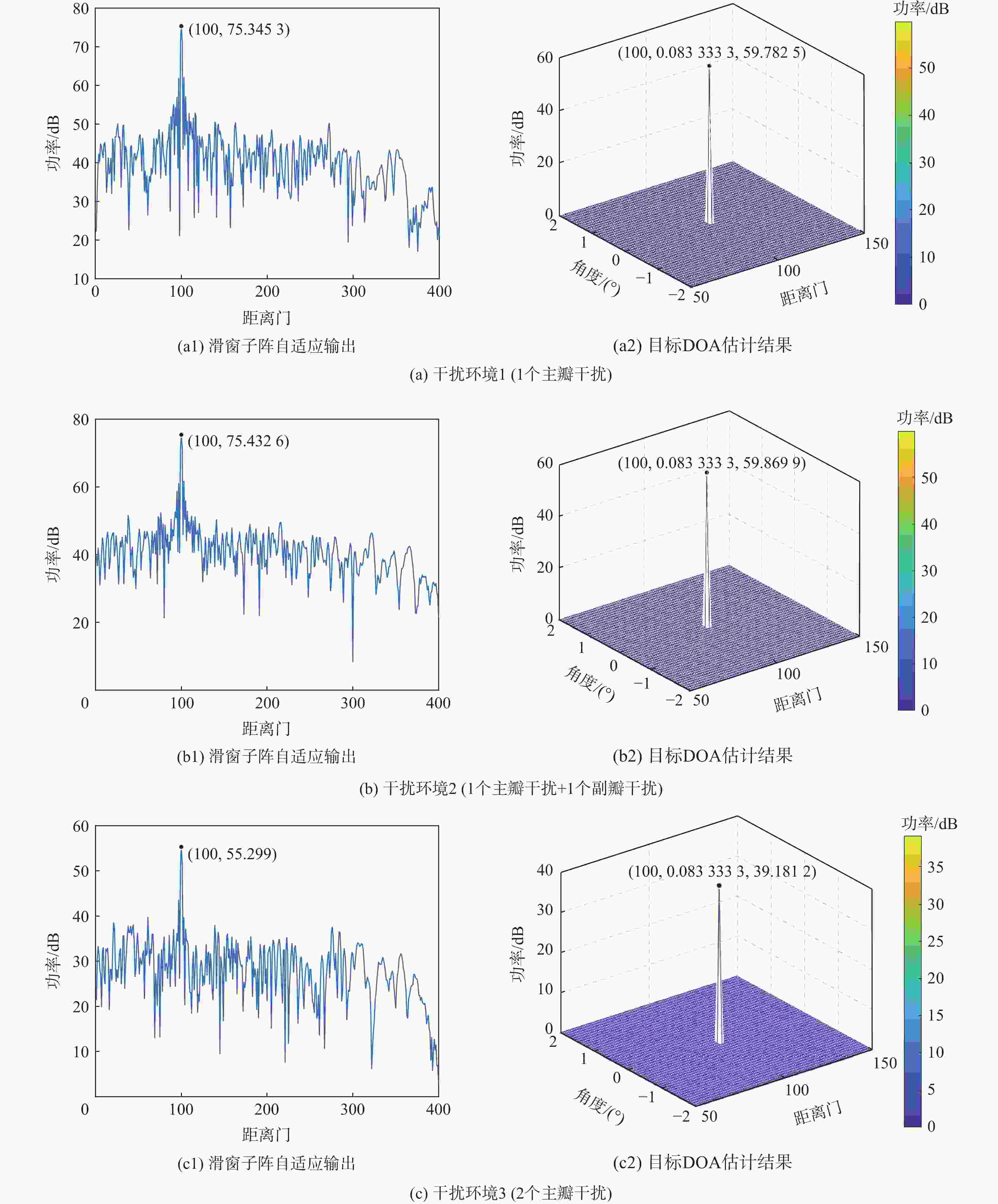
归一化夹角/(°)1 1 50 主瓣噪声
压制干扰0.5 B0.5 2 2 50, 50 主/副瓣噪声
压制干扰0.5 B0.5,10 B0.5 3 2 50, 50 主/主瓣噪声
压制干扰0.5 B0.5, 0.5 B0.5 -
[1] 王永良, 丁前军, 李荣锋. 自适应阵列处理[M]. 北京: 清华大学出版社, 2009.WANG Y L, DING Q J, LI R F. Adaptive array processing[M]. Beijing: Tsinghua University Press, 2009 (in Chinese). [2] 李荣锋, 王永良, 万山虎. 主瓣干扰下自适应方向图保形方法的研究[J]. 现代雷达, 2002, 24(3): 50-53. doi: 10.3969/j.issn.1004-7859.2002.03.015LI R F, WANG Y L, WAN S H. Research of reshaping adapted pattern under mainlobe interference conditions[J]. Modern Radar, 2002, 24(3): 50-53(in Chinese). doi: 10.3969/j.issn.1004-7859.2002.03.015 [3] 李荣锋, 王永良, 万山虎. 一种在主瓣干扰条件下稳健的自适应波束形成方法[J]. 系统工程与电子技术, 2002, 24(7): 61-64. doi: 10.3321/j.issn:1001-506X.2002.07.019LI R F, WANG Y L, WAN S H. Robust adaptive beam forming under main lobe interference conditions[J]. Systems Engineering and Electronics, 2002, 24(7): 61-64(in Chinese). doi: 10.3321/j.issn:1001-506X.2002.07.019 [4] 潘帅, 张永顺, 葛启超, 等. 基于特征投影矩阵的自适应方向图改善方法[J]. 空军工程大学学报(自然科学版), 2019, 20(2): 47-52.PAN S, ZHANG Y S, GE Q C, et al. Research on improvement of adaptive pattern based on eigen-projection matrix[J]. Journal of Air Force Engineering University (Natural Science Edition), 2019, 20(2): 47-52(in Chinese). [5] APPLEBAUM S P, WASIEWICZ R. Main beam jammer cancellation for monopulse sensors: DTIC RADC-TR-86-267[R]. Washington, D. C.: DTIC, 1984. [6] YU K B, MURROW D J. Combining sidelobe canceller and mainlobe canceller for adaptive monopulse radar processing: US6867726[P]. 2005-03-15. [7] YU K B, MURROW D J. Adaptive digital beamforming for angle estimation in jamming[J]. IEEE Transactions on Aerospace and Electronic Systems, 2001, 37(2): 508-523. doi: 10.1109/7.937465 [8] LI R F, RAO C, DAI L Y, et al. Combining sum-difference and auxiliary beams for adaptive monopulse in jamming[J]. Journal of Systems Engineering and Electronics, 2013, 24(3): 372-381. doi: 10.1109/JSEE.2013.00046 [9] 周必雷, 李荣锋, 戴凌燕, 等. 和差四通道及辅助阵元联合自适应单脉冲方法[J]. 系统工程与电子技术, 2017, 39(9): 1905-1914. doi: 10.3969/j.issn.1001-506X.2017.09.01ZHOU B L, LI R F, DAI L Y, et al. Adaptive monopulse algorithm combining four-channel sum-difference beam and auxiliary elements[J]. Systems Engineering and Electronics, 2017, 39(9): 1905-1914(in Chinese). doi: 10.3969/j.issn.1001-506X.2017.09.01 [10] CHEN X Z, SHU T, YU K B, et al. Enhanced ADBF architecture for monopulse angle estimation in multiple jammings[J]. IEEE Antennas and Wireless Propagation Letters, 2017, 16: 2684-2687. doi: 10.1109/LAWP.2017.2740958 [11] YU K B. Mainlobe cancellation, orthogonal nulling and product patterns[C]// 2016 IEEE International Symposium on Phased Array Systems and Technology (PAST). Piscataway: IEEE Press, 2017: 1-7. [12] RAO C, LI R F, DAI L Y. Monopulse estimation with multipoint constrained adaptation in mainlobe jamming[C]// Proceedings of 2011 IEEE CIE International Conference on Radar. Piscataway: IEEE Press, 2012: 1054-1057. [13] 李荣锋, 饶灿, 戴凌燕, 等. 子阵间约束自适应和差单脉冲测角算法[J]. 华中科技大学学报(自然科学版), 2013, 41(9): 6-10. doi: 10.13245/j.hust.2013.09.013LI R F, RAO C, DAI L Y, et al. Algorithm for constrained adaptive sum-difference monopulse among sub-arrays[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2013, 41(9): 6-10(in Chinese). doi: 10.13245/j.hust.2013.09.013 [14] 王文涛, 周青松, 刘兴华, 等. Fast ICA盲分离算法在雷达抗主瓣干扰中的应用研究[J]. 现代雷达, 2015, 37(12): 40-44.WANG W T, ZHOU Q S, LIU X H, et al. A study on radar mainlobe jamming suppression based on blind source separation of fast ICA[J]. Modern Radar, 2015, 37(12): 40-44(in Chinese). [15] 王建明, 伍光新, 周伟光. 盲源分离在雷达抗主瓣干扰中的应用研究[J]. 现代雷达, 2010, 32(10): 46-49. doi: 10.3969/j.issn.1004-7859.2010.10.011WANG J M, WU G X, ZHOU W G. A study on radar mainlobe jamming suppression based on blind source separation algorithm[J]. Modern Radar, 2010, 32(10): 46-49(in Chinese). doi: 10.3969/j.issn.1004-7859.2010.10.011 [16] CAI T T, ZHANG A R. Compressed sensing and affine rank minimization under restricted isometry[J]. IEEE Transactions on Signal Processing, 2013, 61(13): 3279-3290. doi: 10.1109/TSP.2013.2259164 -






 下载:
下载: