基于SMABC算法的FPRM逻辑电路面积优化

秦东阁; 何振学; 陈晨; 李隆昊; 王涛; 王翔

doi:10.13700/j.bh.1001-5965.2021.0579

基于SMABC算法的FPRM逻辑电路面积优化

doi: 10.13700/j.bh.1001-5965.2021.0579

秦东阁¹,
何振学^1, ,,
陈晨¹,
李隆昊²,
王涛³,
王翔⁴

1.
河北农业大学河北省农业大数据重点实验室，保定 071001
2.
河北农业大学现代科技学院，保定 071001
3.
北京信息科技大学信息与通信工程学院，北京 100191
4.
北京航空航天大学电子与信息工程学院，北京 100191

基金项目: 国家自然科学基金(62102130,62001034)；河北省自然科学基金(F2020204003)；河北省高等学校科学技术研究项目(BJ2019008)；河北农业大学引进人才科研专项(YJ201829)

详细信息

通讯作者:
E-mail：hezhenxue@buaa.edu.cn

中图分类号: V443；TP391.72
计量
- 文章访问数: 138
- HTML全文浏览量: 34
- PDF下载量: 13
- 被引次数: 0
出版历程
- 收稿日期: 2021-09-28
- 录用日期: 2022-01-05
- 网络出版日期: 2022-01-19
- 整期出版日期: 2023-08-31

Area optimization of FPRM logic circuits based on SMABC algorithm

1.
Key Laboratory of Agricultural Big Data of Hebei Province, Hebei University of Agricultural, Baoding 071001, China
2.
Institute of Modern Science and Technology, Hebei University of Agricultural, Baoding 071001, China
3.
School of Information and Communication Engineering, Beijing Information Science and Technology University, Beijing 100191, China
4.
School of Electronic and Information Engineering, Beihang University, Beijing 100191, China

Funds: National Natural Science Foundation of China (62102130,62001034); Natural Science Foundation of Hebei Province (F2020204003); Hebei Youth Talents Support Project (BJ2019008); Introducing Talent Research Project of Hebei Agricultural University (YJ201829)

More Information

Corresponding author: E-mail：hezhenxue@buaa.edu.cn

摘要

摘要:
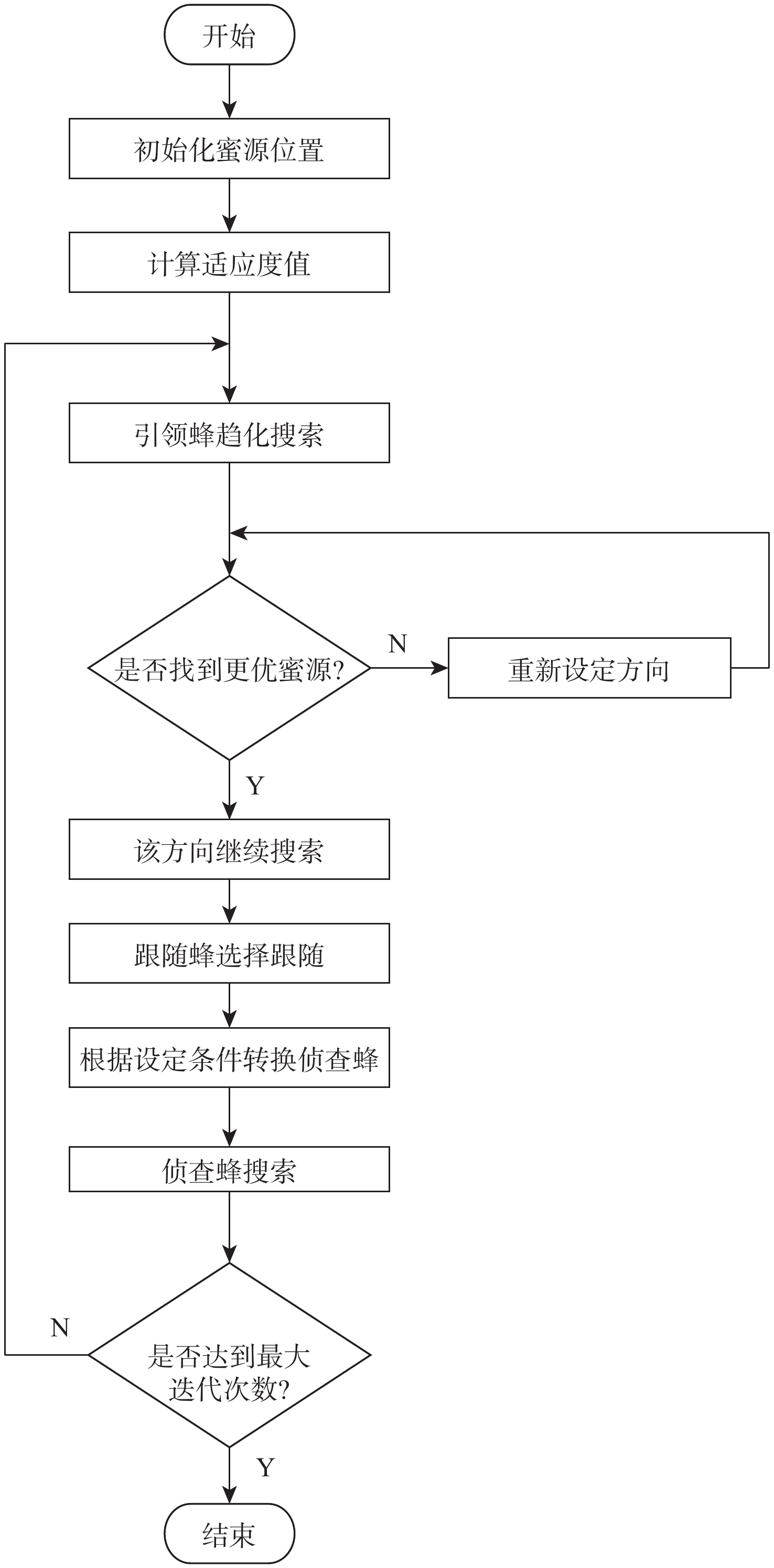
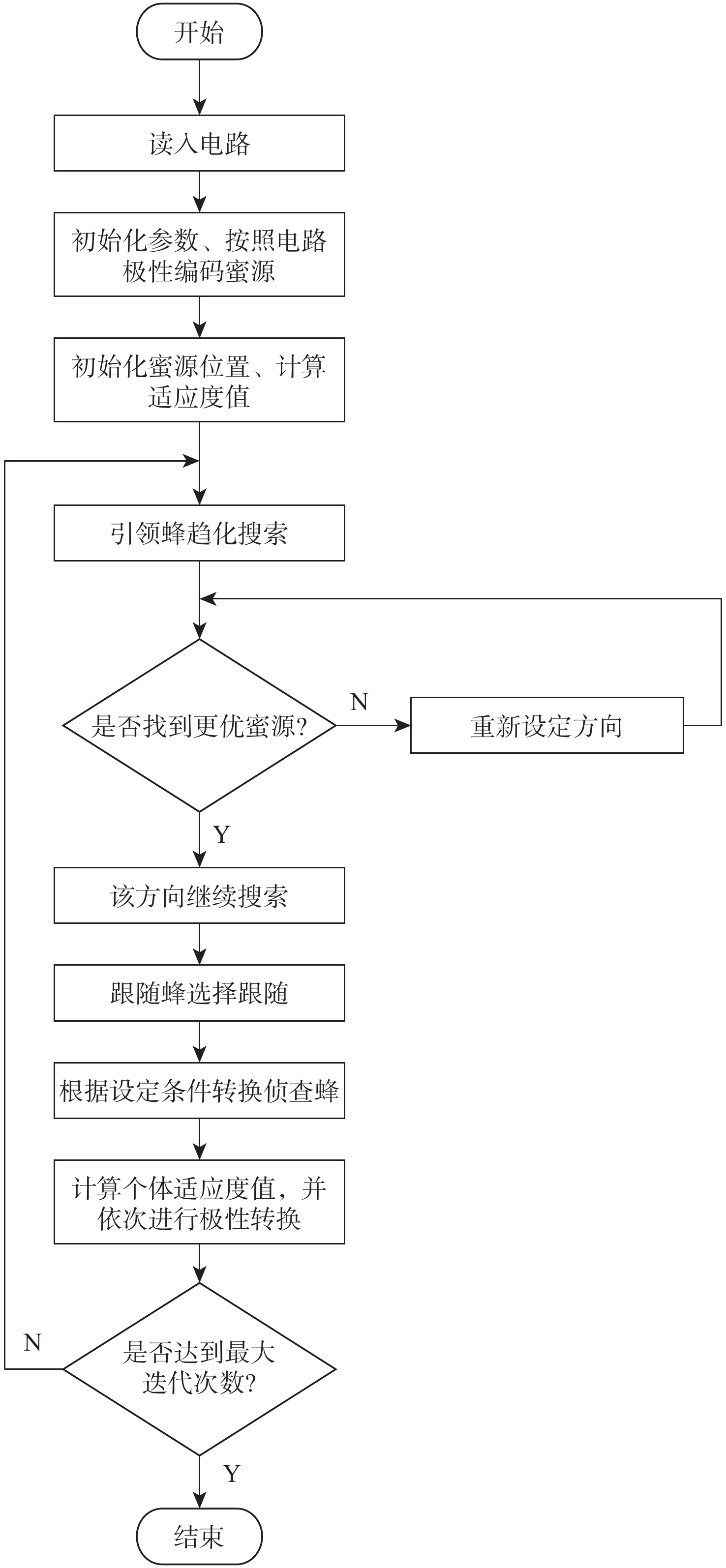
固定极性Reed-Muller (FPRM)逻辑电路面积优化是当前集成电路设计领域的研究热点。但现有FPRM逻辑电路面积优化方法存在优化效率低和优化效果差等问题。FPRM逻辑电路面积优化属于组合优化问题，提出一种自适应混合人工蜂群(SMABC)算法。所提算法在引领蜂搜索阶段引入细菌觅食算法中的细菌趋化行为，使引领蜂向靠近优秀蜜源的方向搜索，提高了所提算法的收敛速度；对跟随蜂的选择概率进行改进使其依据种群的变化自适应改变，提高了所提算法的全局搜索能力；对侦查蜂的转换条件进行改进，增加了侦查蜂在进化过程中的扰动幅度；且在进化过程中引入精英保留策略以提高种群质量。此外，提出一种基于SMABC算法的FPRM逻辑电路面积优化方法，所提方法收敛速度最快且面积优化率最高为54.62%，平均面积优化率为15.33%。
- 面积优化 /
- 组合优化 /
- 人工蜂群算法 /
- 细菌觅食算法 /
- 固定极性Reed-Muller 逻辑电路
Abstract:
The area optimization of fixed polarity Reed-Muller (FPRM) circuits is one of the most important research hotspots in the field of integrated circuit design. However, the existing area optimization methods have problems such as low optimization efficiency and poor optimization effect. Since the area optimization of FPRM logic circuits is a combinatorial optimization problem, a self-adaptive mixed artificial bee colony (SMABC) algorithm is proposed. The algorithm introduces chemotaxis behavior of bacterial foraging algorithm in the stage of the leader bee searching, which enables the leader bee to search in the direction toward good nectar sources, and improves the convergence speed of the algorithm. The algorithm also improves both the selection probability of the following bees for adaptive change, and the global search ability. The transformation conditions of scout bees are improved, and the disturbance amplitude in the evolution process of scout bees is increased. The elite retention strategy is then introduced to improve the population quality. In addition, a method of area optimization of FPRM logic circuits based on SMABC algorithm is proposed, which has the fastest convergence, and that the the maximum optimization rate of the area reaches 54.62% while the average area optimization rate is 15.33%.
- area optimization /
- combinatorial optimization /
- artificial bee colony algorithm /
- bacterial foraging algorithm /
- fixed polarity Reed-Muller logic circuit

HTML全文

图 1 ABC算法流程

Figure 1. Flow of artificial bee colony algorithm

下载: 全尺寸图片幻灯片

图 2 SMABC算法流程

Figure 2. Flow of SMABC algorithm

下载: 全尺寸图片幻灯片

图 3 引领蜂的趋化觅食行为

Figure 3. Chemotactic search of leader bee

下载: 全尺寸图片幻灯片

图 4 本文方法流程

Figure 4. Flow of proposed method

下载: 全尺寸图片幻灯片

图 5 某5变量FPRM表达式的电路网络

Figure 5. Circuit network of a 5-variable FPRM expression

下载: 全尺寸图片幻灯片

图 6 4种算法的最小面积收敛曲线

Figure 6. Convergence curves of minimum area of four algorithms

下载: 全尺寸图片幻灯片

表 1 3种优化算法的参数设置

Table 1. Parameters of three optimization algorithms

算法	${L}_{{\rm{c}}}$	${L}_{{\rm{s}}}$	$ {\alpha }_{1} $	$ {\alpha }_{2} $	Limit	交叉率	变异率	加速因子$ {C}_{1} $	加速因子 $ {C}_{2} $	惯性权重
SMABC	3	3	1	0.05	7
GA						0.7	0.03
PSO								2	2	0.3

下载: 导出CSV

表 2 4种算法的电路面积优化实验结果

Table 2. Experimental results of circuits area optimization based on four algorithms

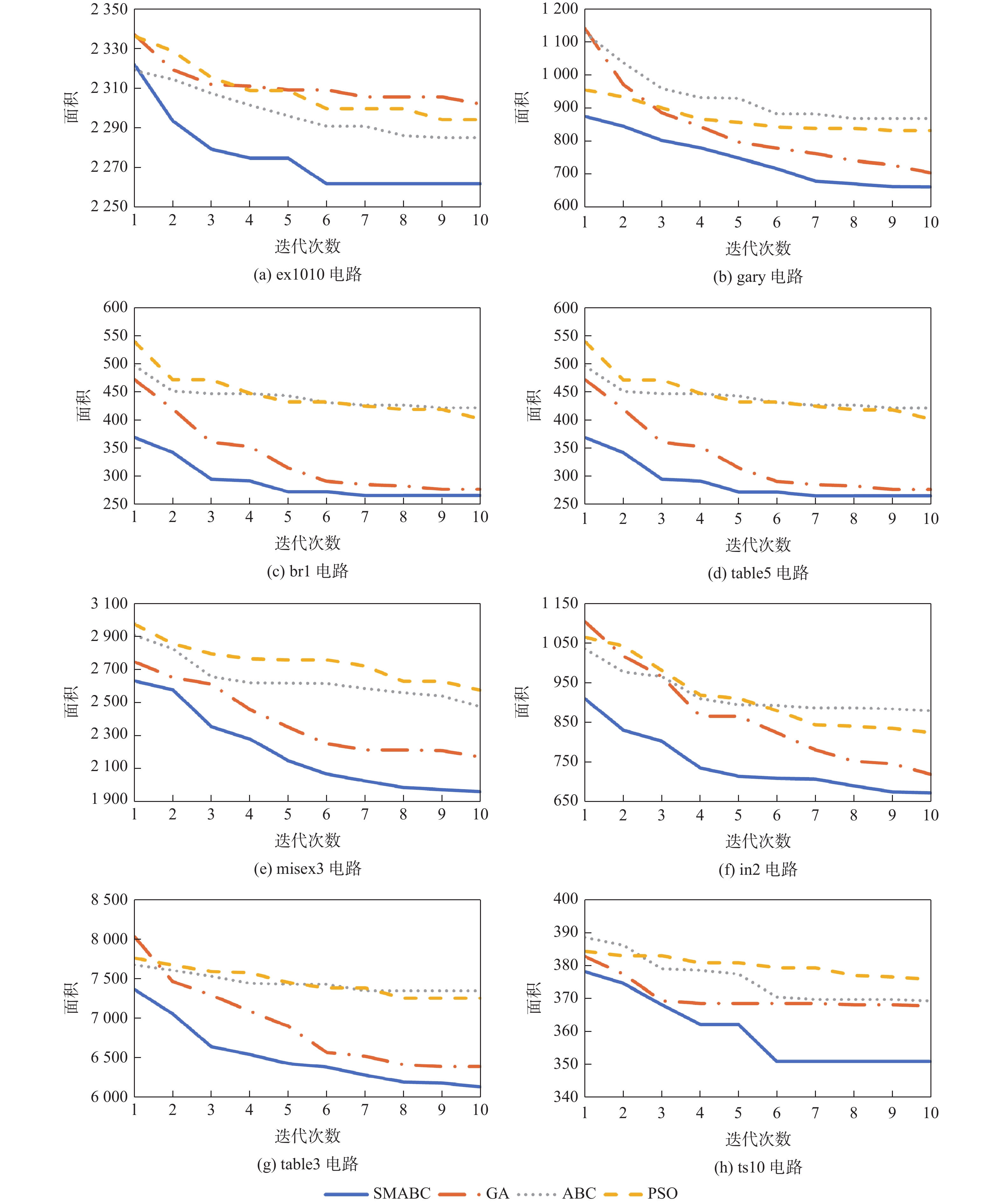
电路	输入位数	$A_{\mathrm{P}\mathrm{S}\mathrm{O} }$	$A_{\mathrm{G}\mathrm{A} }$	$A_{\mathrm{A}\mathrm{B}\mathrm{C} }$	$A_{\mathrm{S}\mathrm{M}\mathrm{A}\mathrm{B}\mathrm{C} }$	$A_{ {\mathrm{s}\mathrm{a}\mathrm{v}\mathrm{e}1} }$/%	$A_{ {\mathrm{s}\mathrm{a}\mathrm{v}\mathrm{e}2} }$/%	$A_{ {\mathrm{s}\mathrm{a}\mathrm{v}\mathrm{e}3} }$/%
rd84	8	56.20	55.60	55.00	55.00	2.18	1.09	0
ex1010	10	2292.20	2295.00	2276.35	2260.95	1.38	1.51	0.68
br1	12	388.20	277.40	411.30	266.00	45.94	4.29	54.62
br2	12	175.55	185.50	160.80	134.00	31.01	38.43	20.00
misex3	14	2381.60	2351.40	2402.35	1954.55	21.85	20.30	22.91
table3	14	7248.30	6154.95	7190.50	6059.55	19.62	1.57	18.66
gary	15	774.05	681.00	811.65	649.00	19.27	4.93	25.06
in0	15	789.00	682.00	924.30	649.00	21.58	5.08	42.42
table5	17	312.65	257.40	319.05	266.00	22.61	0.94	25.12
t2	17	85.70	82.10	89.30	80.00	7.12	2.63	11.63
in2	19	766.30	674.50	816.25	659.50	16.19	2.27	23.77
ts10	22	372.80	366.80	359.80	351.00	6.21	4.50	2.51

下载: 导出CSV

参考文献(22)

[1]	ZHAO B Y, BAI S Q, CONNOR S, et al. Physics-based circuit modeling methodology for system power integrity analysis and design[J]. IEEE Transactions on Electromagnetic Compatibility, 2020, 62(4): 1266-1277. doi: 10.1109/TEMC.2019.2927742
[2]	ŠTEVEK J, KVASNICA M, FIKAR M, et al. A parametric programming approach to automated integrated circuit design[J]. IEEE Transactions on Control Systems Technology, 2018, 26(4): 1180-1191. doi: 10.1109/TCST.2017.2716378
[3]	CARVALHO C, NEUMANN V G L. The next-to-minimal weights of binary projective reed-muller codes[J]. IEEE Transactions on Information Theory, 2016, 62(11): 6300-6303. doi: 10.1109/TIT.2016.2611527
[4]	HE Z X, XIAO L M, GU F, et al. An efficient and fast polarity optimization approach for mixed polarity Reed-Muller logic circuits[J]. Frontiers of Computer Science, 2017, 11(4): 728-742. doi: 10.1007/s11704-016-5259-2
[5]	DAS A, PRADHAN S N. Design time temperature reduction in mixed polarity dual Reed-Muller network: A NSGA-II based approach[J]. Advances in Electrical and Computer Engineering, 2020, 20(1): 99-104. doi: 10.4316/AECE.2020.01013
[6]	HE Z X, WU X Q, WANG C, et al. Delay optimization for ternary fixed polarity Reed-Muller circuits based on multilevel adaptive quantum genetic algorithm[J]. International Journal of Intelligent Systems, 2021, 36(10): 5981-6006. doi: 10.1002/int.22538
[7]	HE Z X, XIAO L M, HUO Z S, et al. Fast minimization of fixed polarity Reed-Muller expressions[J]. IEEE Access, 2019, 7: 24843-24851. doi: 10.1109/ACCESS.2019.2899035
[8]	FU Q, WANG P J, TONG N, et al. Multi-constrained polarity optimization of large-scale FPRM circuits based on multi-objective discrete particle swarm optimization[J]. Journal of Electronics & Information Technology, 2017, 39(3): 717-723.
[9]	WANG M B, WANG P J, FU Q, et al. Delay and area optimization for FPRM circuits based on MSPSO algorithm[C]// 2017 IEEE 12th International Conference on ASIC (ASICON). Piscataway: IEEE Press, 2018: 379-382.
[10]	CHEN Z W, ZHANG H H, WANG P J. Area optimization for FPRM circuit based on BDD[C]//2018 14th IEEE International Conference on Solid-State and Integrated Circuit Technology (ICSICT). Piscataway: IEEE Press, 2018: 1-3.
[11]	王稼磊, 张会红, 汪鹏君, 等. 基于参数自适应布谷鸟算法的RM电路面积优化[J]. 计算机应用研究, 2018, 35(9): 2689-2691. doi: 10.3969/j.issn.1001-3695.2018.09.029 WANG J L, ZHANG H H, WANG P J, et al. RM circuit area optimization based on cuckoo search with adaptive parameters[J]. Application Research of Computers, 2018, 35(9): 2689-2691(in Chinese). doi: 10.3969/j.issn.1001-3695.2018.09.029
[12]	汪鹏君, 汪迪生, 蒋志迪, 等. 基于 PSGA 算法的 ISFPRM 电路面积与功耗优化[J]. 电子学报, 2013, 41(8): 1542-1548. doi: 10.3969/j.issn.0372-2112.2013.08.014 WANG P J, WANG D S, JIANG Z D, et al. Area and power optimization of ISFPRM circuits based on PSGA algorithm[J]. Acta Electronica Sinica, 2013, 41(8): 1542-1548(in Chinese). doi: 10.3969/j.issn.0372-2112.2013.08.014
[13]	KARABOGA D. An idea based on honey bee swarm for numerical optimization: TR06[R]. Kayseri: Erciyes University, 2005.
[14]	ZHANG J R, TANG H M, TANNANT D D, et al. Combined forecasting model with CEEMD-LCSS reconstruction and the ABC-SVR method for landslide displacement prediction[J]. Journal of Cleaner Production, 2021, 293: 126205. doi: 10.1016/j.jclepro.2021.126205
[15]	BINGUL Z, KARAHAN O. Comparison of PID and FOPID controllers tuned by PSO and ABC algorithms for unstable and integrating systems with time delay[J]. Optimal Control Applications and Methods, 2018, 39(4): 1431-1450. doi: 10.1002/oca.2419
[16]	MOHAMAD E T, LI D Y, MURLIDHAR B R, et al. The effects of ABC, ICA, and PSO optimization techniques on prediction of ripping production[J]. Engineering with Computers, 2020, 36(4): 1355-1370. doi: 10.1007/s00366-019-00770-9
[17]	ASLAN S. A comparative study between artificial bee colony (ABC) algorithm and its variants on big data optimization[J]. Memetic Computing, 2020, 12(2): 129-150. doi: 10.1007/s12293-020-00298-2
[18]	BRINDHA D, NAGARAJAN N. An efficient automatic segmentation of spinal cord in MRI images using interactive random walker (RW) with artificial bee colony (ABC) algorithm[J]. Multimedia Tools and Applications, 2020, 79(5): 3623-3644.
[19]	BANHARNSAKUN A. Feature point matching based on ABC-NCC algorithm[J]. Evolving Systems, 2018, 9(1): 71-80. doi: 10.1007/s12530-017-9183-y
[20]	TOKTAS A, USTUN D. A triple-objective optimization scheme using butterfly-integrated ABC algorithm for design of multilayer RAM[J]. IEEE Transactions on Antennas and Propagation, 2020, 68(7): 5602-5612. doi: 10.1109/TAP.2020.2981728
[21]	PANG B H, TENG Z J, SUN H Y, et al. A malicious node detection strategy based on fuzzy trust model and the ABC algorithm in wireless sensor network[J]. IEEE Wireless Communications Letters, 2021, 10(8): 1613-1617. doi: 10.1109/LWC.2021.3070630
[22]	YAN Q Z, ZHOU Z R, WU M B, et al. A simplified analytical algorithm in ABC coordinate for the three-Level SVPWM[J]. IEEE Transactions on Power Electronics, 2021, 36(4): 3622-3627. doi: 10.1109/TPEL.2020.3027742