基于Safe-PPO算法的安全优先路径规划方法

别桐; 朱晓庆; 付煜; 李晓理; 阮晓钢; 王全民

doi:10.13700/j.bh.1001-5965.2021.0580

基于Safe-PPO算法的安全优先路径规划方法

doi: 10.13700/j.bh.1001-5965.2021.0580

别桐^{1, 2},
朱晓庆^{1, 2, ,},
付煜³,
李晓理¹,
阮晓钢^{1, 2},
王全民³

1.
北京工业大学信息学部人工智能与自动化学院，北京 100124
2.
北京工业大学计算智能与智能系统北京市重点实验室，北京 100124
3.
北京工业大学信息学部计算机学院，北京 100124

基金项目: 国家自然科学基金(61773027,62103009)；北京市自然科学基金(4202005)

详细信息

通讯作者:
E-mail：president2zhu@qq.com

中图分类号: TP242.6
计量
- 文章访问数: 258
- HTML全文浏览量: 57
- PDF下载量: 54
- 被引次数: 0
出版历程
- 收稿日期: 2021-09-28
- 录用日期: 2021-12-06
- 网络出版日期: 2022-03-03
- 整期出版日期: 2023-08-31

Safety priority path planning method based on Safe-PPO algorithm

BIE Tong^{1, 2},
ZHU Xiaoqing^{1, 2
, ,},
FU Yu³,
LI Xiaoli¹,
RUAN Xiaogang^{1, 2},
WANG Quanmin³

1.
School of Artificial Intelligence and Automation，Faulty of Information Technology，Beijing University of Technology，Beijing 100124，China
2.
Beijing Key Laboratory of Computational Intelligence and Intelligent System，Beijing University of Technology，Beijing 100124，China
3.
School of Computer Science，Faulty of Information Technology，Beijing University of Technology，Beijing 100124，China

Funds: National Natural Science Foundation of China (61773027,62103009); Natural Science Foundation of Beijing (4202005)

More Information

Corresponding author: E-mail：president2zhu@qq.com

摘要

摘要:
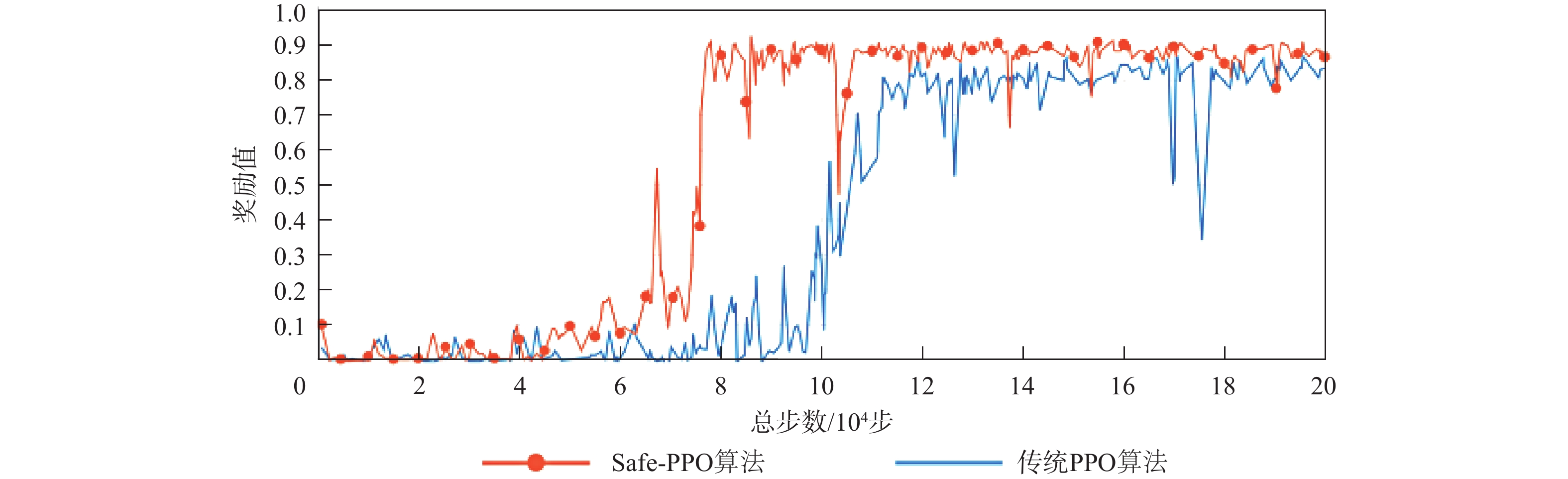
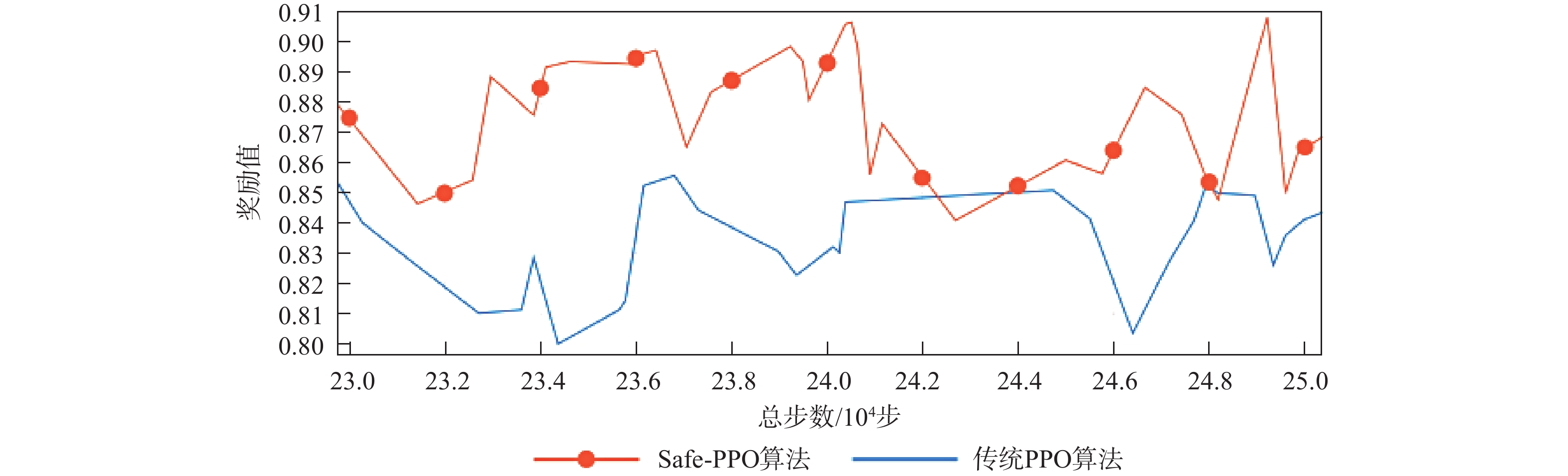
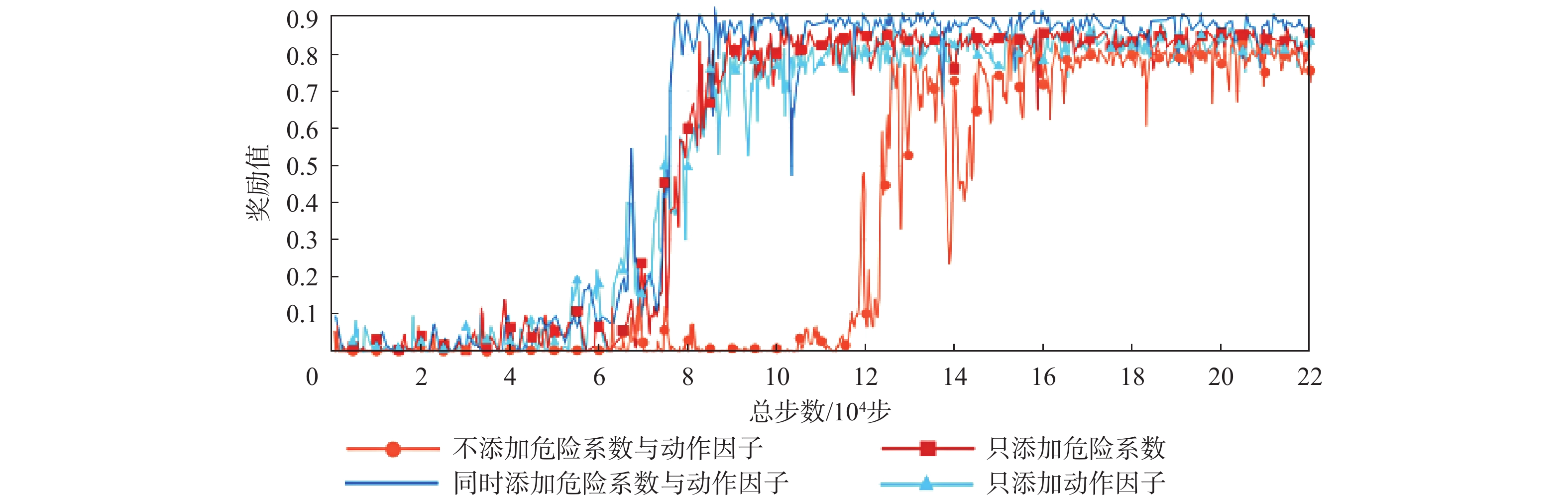
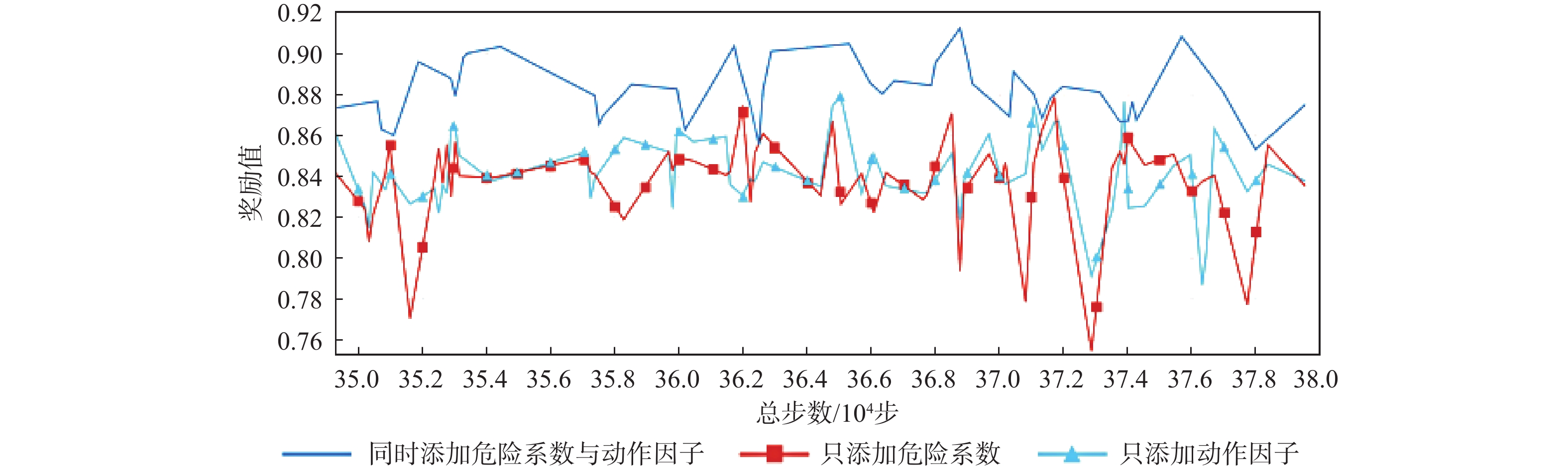
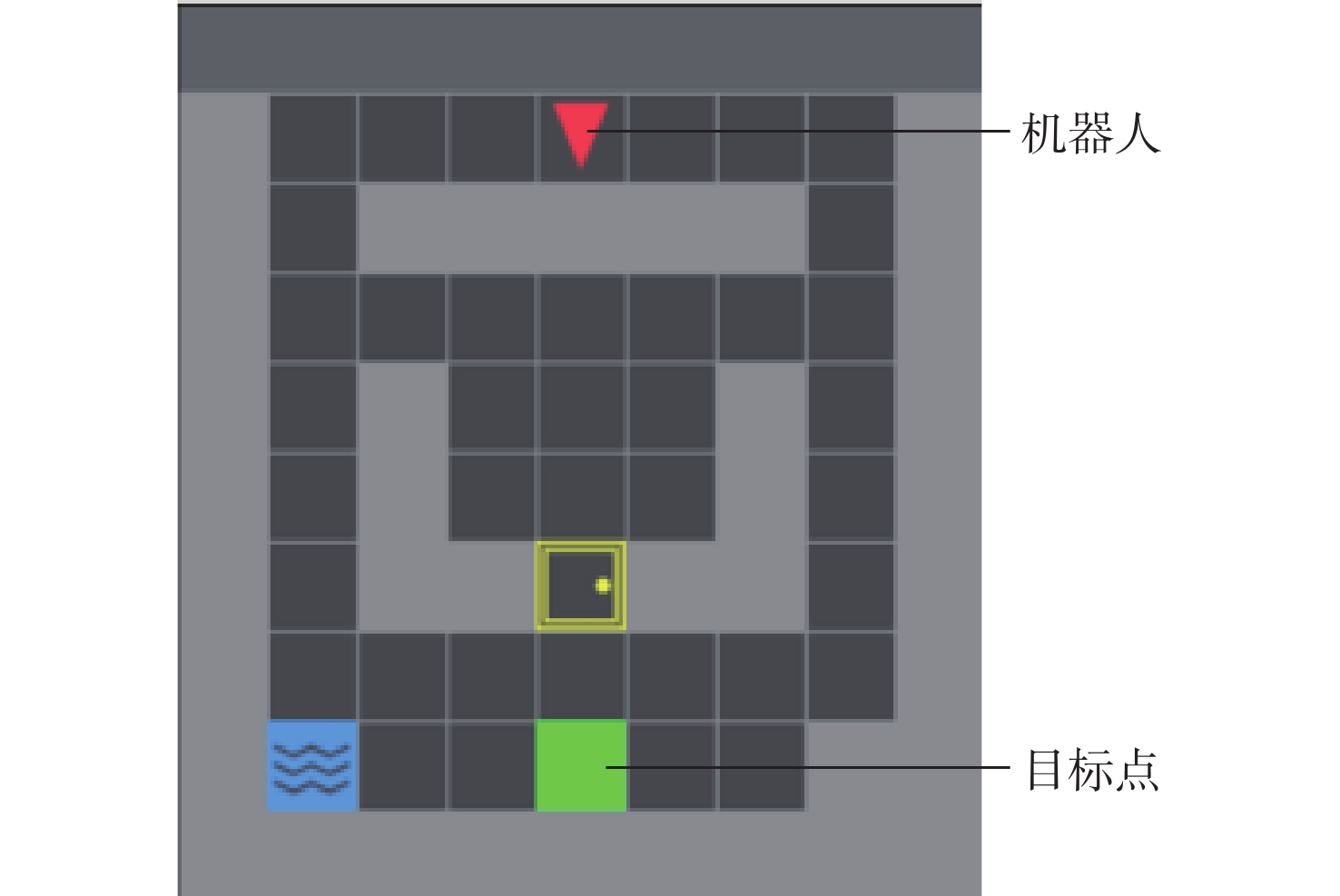
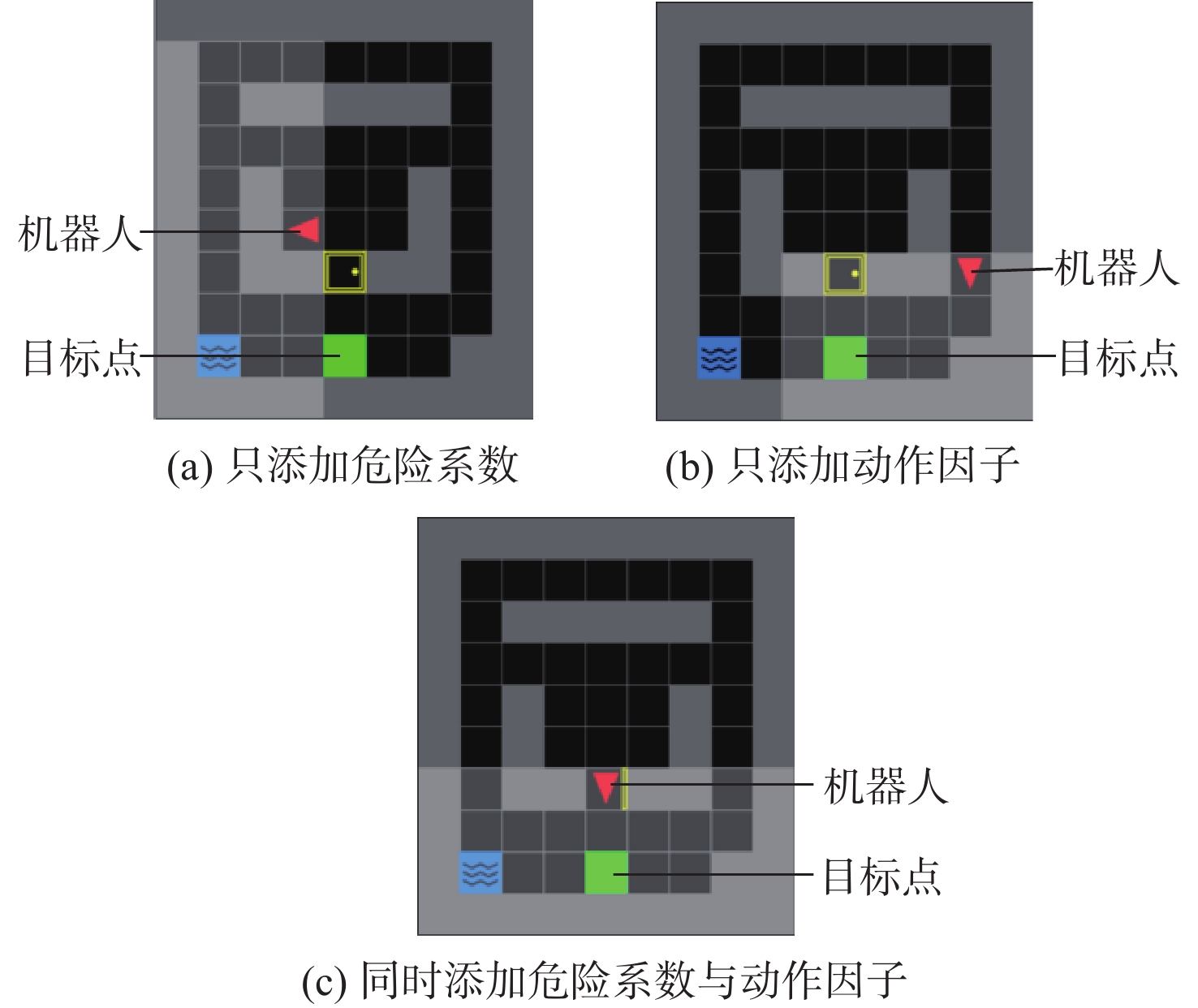
现有的路径规划算法对路径规划过程中的路径安全性问题考虑较少，并且传统的近端策略优化(PPO)算法存在一定的方差适应性问题。为解决这些问题，提出一种融合进化策略思想和安全奖励函数的安全近端策略优化(Safe-PPO)算法，所提算法以安全优先进行路径规划。采用协方差自适应调整的进化策略( CMA-ES)的思想对PPO算法进行改进，并引入危险系数与动作因子来评估路径的安全性。使用二维栅格地图进行仿真实验，采用传统的PPO算法和Safe-PPO算法进行对比；采用六足机器人在搭建的场景中进行实物实验。仿真实验结果表明：所提算法在安全优先导向的路径规划方面具有合理性与可行性：在训练时Safe-PPO算法相比传统的PPO算法收敛速度提升了18%，获得的奖励提升了5.3%；在测试时采用融合危险系数与动作因子的方案能使机器人学会选择更加安全的道路而非直观上最快速的道路。实物实验结果表明：机器人可以在现实环境中选择更加安全的路径到达目标点。
- 机器人导航 /
- 路径规划 /
- 深度强化学习 /
- 近端策略优化 /
- 安全路径选择
Abstract:
The existing path planning algorithms seldom consider the problem of security, and the traditional proximal policy optimization(PPO) algorithm has a variance adaptability problem. To solve these problems, the Safe-PPO algorithm combining evolutionary strategy and safety reward function was proposed. The algorithm is safety-oriented for path planning. CMA-ES was used to improve the PPO algorithm. The hazard coefficient and movement coefficient were introduced to evaluate the safety of the path. Used a grid map for simulation experiments, and compared the traditional PPO algorithm with the Safe-PPO algorithm; The hexapod robot was used to carry out the physical experiment in the constructed scene. The simulation results show that the Safe-PPO algorithm is reasonable and feasible in safety-oriented path planning. When compared to the conventional PPO algorithm, the Safe-PPO algorithm increased the rate of convergence during training by 18% and the incentive received by 5.3%. Using the algorithm that combined the Hazard coefficient and movement coefficient during testing enabled the robot to learn to choose the safer path rather than the fastest one. The outcomes of the physical testing demonstrated that the robot could select a more secure route to the objective in the created setting.
- robot navigation /
- path planning /
- deep reinforcement learning /
- proximal policy optimization /
- safe path selection

HTML全文

图 1 本文算法流程

Figure 1. Flow of the proposed algorithm

下载: 全尺寸图片幻灯片

图 2 实验环境示意图

Figure 2. Schematic diagram of experimental environment

下载: 全尺寸图片幻灯片

图 3 危险空间示意图

Figure 3. Hazard space diagram

下载: 全尺寸图片幻灯片

图 4 危险系数问题示意图

Figure 4. Diagram of hazard coefficient

下载: 全尺寸图片幻灯片

图 5 动作因子问题示意图

Figure 5. Diagram of movement coefficient

下载: 全尺寸图片幻灯片

图 6 通道编号示意图

Figure 6. Diagram of channel number

下载: 全尺寸图片幻灯片

图 7 使用传统PPO算法与Safe-PPO算法训练效果对比

Figure 7. Comparison of training effects between traditional PPO and Safe-PPO algorithm

下载: 全尺寸图片幻灯片

图 8 局部放大图

Figure 8. A partial enlargement

下载: 全尺寸图片幻灯片

图 9 测试训练收敛后的机器人

Figure 9. Test the robot after training convergence

下载: 全尺寸图片幻灯片

图 10 机器人随机选择通道1或通道2

Figure 10. The robot randomly selects channel 1 or channel 2

下载: 全尺寸图片幻灯片

图 11 调整机器人初始位置的影响

Figure 11. The effect of adjusting initial position of robot

下载: 全尺寸图片幻灯片

图 12 增加危险系数后机器人放弃通道3并改选通道4

Figure 12. The robot gave up channel 3 and changed to channel 4 when hazard coefficient was increased

下载: 全尺寸图片幻灯片

图 13 100次测试的结果示意图

Figure 13. Schematic of results of 100 tests

下载: 全尺寸图片幻灯片

图 14 4组实验的训练所获奖励

Figure 14. The training rewards of four groups of experiments

下载: 全尺寸图片幻灯片

图 15 3种策略训练所获奖励局部放大图

Figure 15. A partial enlargement of rewards obtained from three strategy training

下载: 全尺寸图片幻灯片

图 16 复杂度提高后的实验环境

Figure 16. The experimental environment with increased complexity

下载: 全尺寸图片幻灯片

图 17 3种方案的测试效果对比

Figure 17. Comparison of test results of three schemes

下载: 全尺寸图片幻灯片

图 18 直线通道实验环境

Figure 18. Linear channel experimental environment

下载: 全尺寸图片幻灯片

图 19 直线通道实验过程

Figure 19. Linear channel experimental procedure

下载: 全尺寸图片幻灯片

图 20 通道选取实验环境

Figure 20. Channel selection experimental environment

下载: 全尺寸图片幻灯片

图 21 通道选取实验过程

Figure 21. Channel selection experimental procedure

下载: 全尺寸图片幻灯片

图 22 迷宫实验环境

Figure 22. Labyrinth experimental environment

下载: 全尺寸图片幻灯片

图 23 迷宫实验过程

Figure 23. Labyrinth experimental procedure

下载: 全尺寸图片幻灯片

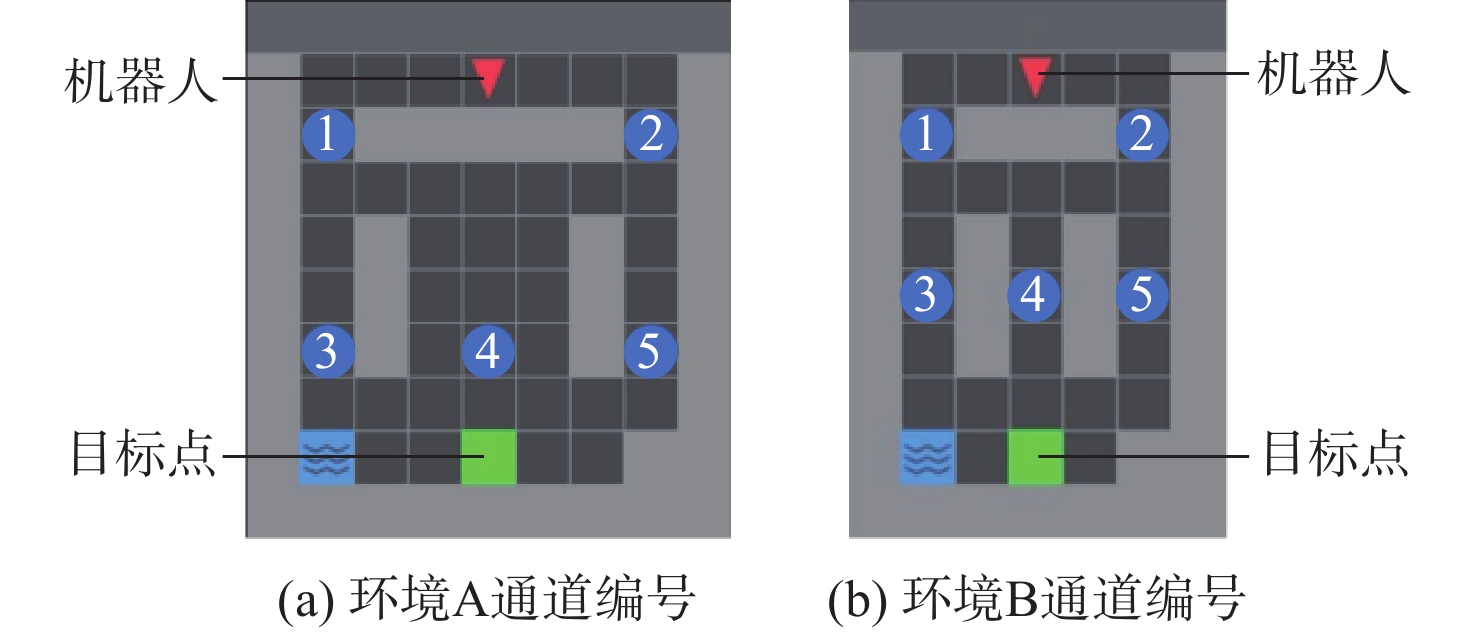
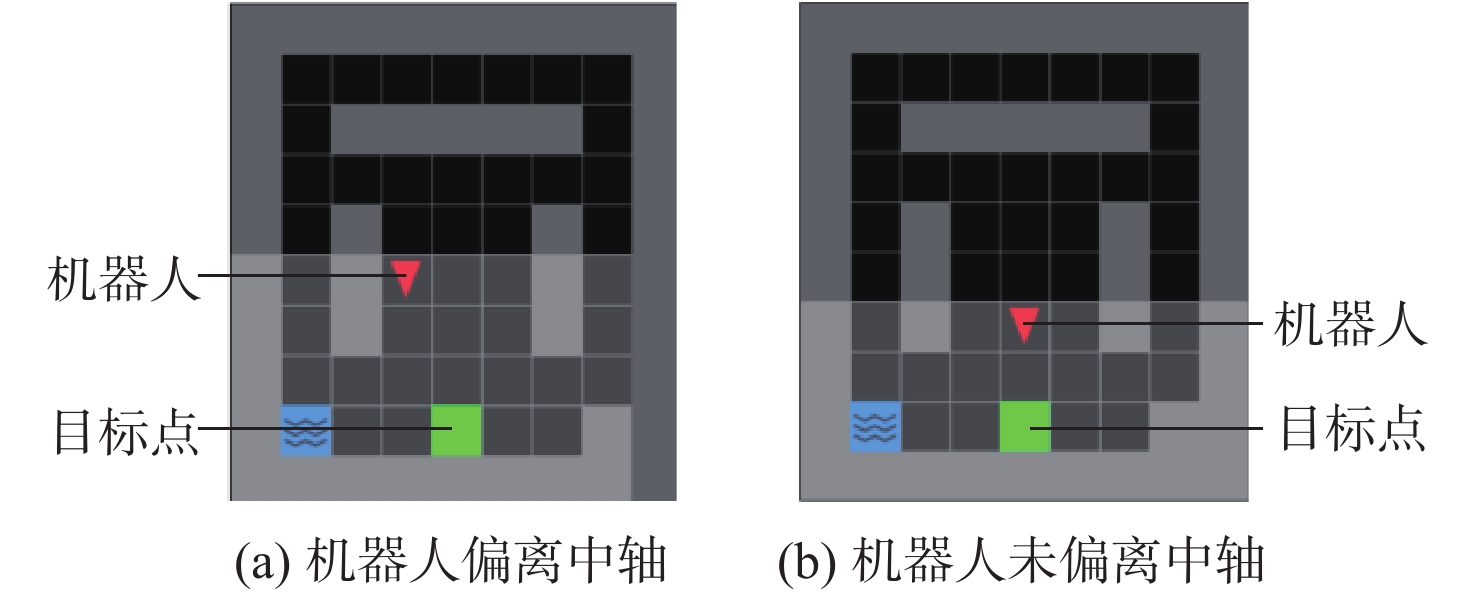
表 1 传统PPO算法与Safe-PPO算法的中轴偏离测试结果

Table 1. Center line deviation test of traditional PPO algorithm and Safe-PPO algorithm

算法 (4, 4)偏离 (4, 5)偏离 (4, 6)偏离无偏离

Safe-PPO 3 5 1 91
传统PPO 18 31 24 27

下载: 导出CSV

参考文献(25)

[1]	魏彤, 龙琛. 基于改进遗传算法的移动机器人路径规划[J]. 北京航空航天大学学报, 2020, 46(4): 703-711. doi: 10.13700/j.bh.1001-5965.2019.0298 WEI T, LONG C. Path planning for mobile robot based on improved genetic algorithm[J]. Journal of Beijing University of Aeronautics and Astronautics, 2020, 46(4): 703-711(in Chinese). doi: 10.13700/j.bh.1001-5965.2019.0298
[2]	XU Y R, LIU R. Path planning for mobile articulated robots based on the improved A* algorithm[J]. International Journal of Advanced Robotic Systems, 2017, 14(4): 1-10.
[3]	MAJUMDER S, PRASAD M S. Three dimensional D* algorithm for incremental path planning in uncooperative environment[C]//2016 3rd International Conference on Signal Processing and Integrated Networks. Piscataway: IEEE Press, 2016: 431-435.
[4]	MASHAYEKHI R, IDRIS M Y I, ANISI M H, et al. Hybrid RRT: A semi-dual-tree RRT-based motion planner[J]. IEEE Access, 2020, 8: 18658-18668. doi: 10.1109/ACCESS.2020.2968471
[5]	LIU J H, YANG J G, LIU H P, et al. An improved ant colony algorithm for robot path planning[J]. Soft Computing, 2017, 21(19): 5829-5839. doi: 10.1007/s00500-016-2161-7
[6]	董豪, 杨静, 李少波, 等. 基于深度强化学习的机器人运动控制研究进展[J]. 控制与决策, 2022, 37(2): 278-292. DONG H, YANG J, LI S B, et al. Research progress of robot motion control based on deep reinforcement learning[J]. Control and Decision, 2022, 37(2): 278-292(in Chinese).
[7]	VOLODYMYR M, KORAY K, DAVID S, et al. Playing atari with deep reinforcement learning[EB/OL]. (2013-12-19)[2021-09-01].https://arxiv.org/pdf/1312.5602.pdf.
[8]	GU S, TIMOTHY L, ILYA S, et al. Continuous deep Q-learning with model-based acceleration[C]//33rd International Conference on Machine Learning. New York: International Machine Learning Society, 2016: 2829-2838.
[9]	JOHN S, SERGEY L, PHILIPP M, et al. Trust region policy optimization[C]//32th International Conference on Machine Learning. Lille: International Machine Learning Society, 2015: 1889-1897.
[10]	SCHULMAN J, WOLSKI F, DHARIWAL P, et al. Proximal policy optimization algorithms[EB/OL]. (2017-08-28)[2020-09-01].https://arxiv.org/abs/1707.06347.
[11]	MNIH V, ADRI`AP B, MEHDI M, et al. Asynchronous methods for deep reinforcement learning[C]//33rd International Conference on Machine Learning. New York: International Machine Learning Society, 2016: 1928-1937.
[12]	多南讯, 吕强, 林辉灿, 等. 迈进高维连续空间: 深度强化学习在机器人领域中的应用[J]. 机器人, 2019, 41(2): 276-288. DUO N X, LV Q, LIN H C, et al. Step into high-dimensional and continuous action space: A survey on applications of deep reinforcement learning to robotics[J]. Robot, 2019, 41(2): 276-288(in Chinese).
[13]	沈鹏. 自主车辆复杂环境下安全导航方法研究[D]. 淄博: 山东理工大学, 2019: 36-49. SHEN P. Research on safe navigation method of autonomous vehicles in complex environment[D]. Zibo: Shandong University of Technology, 2019: 36-49(in Chinese).
[14]	邵旭阳. 家庭环境下面向高效与安全导航的二维物品语义地图构建[D]. 济南: 山东大学, 2021: 65-81. SHAO X Y. Construction of two-dimensional object semantic map for efficient and safe navigation in home environment[D]. Jinan: Shandong University, 2021: 65-81(in Chinese).
[15]	ESHGHI M, SCHMIDTKE H R. An approach for safer navigation under severe hurricane damage[J]. Journal of Reliable Intelligent Environments, 2018, 4(3): 161-185. doi: 10.1007/s40860-018-0066-1
[16]	HEESS N, TB D, SRIRAM S, et al. Emergence of locomotion behaviours in rich environments[EB/OL]. (2017-7-10)[2021-9-1].https://arxiv.org/abs/1707.02286.
[17]	HAN S, ZHOU W B, LÜ S, et al. Regularly updated deterministic policy gradient algorithm[EB/OL]. (2020-7-1)[2021-9-1].https://arxiv.org/abs/2007.00169.
[18]	WU J T, LI H Y. Deep ensemble reinforcement learning with multiple deep deterministic policy gradient algorithm[J]. Mathematical Problems in Engineering, 2020, 2020: 1-12.
[19]	HANSEN N. The CMA evolution strategy: A comparing review[C]//Towards a New Evolutionary Computation. Berlin: Springer, 2007: 75-102.
[20]	LOSHCHILOV I, GLASMACHERS T, BEYER H G. Large scale black-box optimization by limited-memory matrix adaptation[J]. IEEE Transactions on Evolutionary Computation, 2019, 23(2): 353-358. doi: 10.1109/TEVC.2018.2855049
[21]	DE BOER P T, KROESE D P, MANNOR S, et al. A tutorial on the cross-entropy method[J]. Annals of Operations Research, 2005, 134(1): 19-67. doi: 10.1007/s10479-005-5724-z
[22]	LARRAÑAGA P, LOZANO J A. Estimation of distribution algorithms: A new tool for evolutionary computation[M]. Boston: Kluwer Academic Publishers, 2002.
[23]	HANSEN N. The CMA evolution strategy: A tutorial[EB/OL]. (2016-4-4)[2021-9-1].https://arxiv.org/abs/1604.00772.
[24]	PENG X B, KUMAR A, ZHANG G, et al. Advantage-weighted regression: Simple and scalable off-policy reinforcement learning[J/OL]. Machine Learning, 2019, (2019-10-7)[2021-9-1].https://arxiv.org/abs/1910.00177. DOI: 10.48550/arXiv.1910.00177.
[25]	JOHN S, PHILIPP M, SERGEY L, et al. High-dimensional continuous control using generalized advantage estimation[J/OL]. Computer Science, 2015, (2018-10-20)[2021-9-1].https://arxiv.org/abs/1506.02438. DOI: 10.48550/arXiv.1506.02438.