高马赫数空腔非定常流动机理

张培红; 程晓辉; 陈洪杨; 贾洪印; 罗磊; 唐银

doi:10.13700/j.bh.1001-5965.2021.0609

高马赫数空腔非定常流动机理

doi: 10.13700/j.bh.1001-5965.2021.0609

1.
中国空气动力研究与发展中心计算空气动力研究所，绵阳 621000
2.
航天时代飞鸿技术有限公司，北京 100094

基金项目: 国家数值风洞工程项目

详细信息

通讯作者:
E-mail：rorzey@buaa.edu.cn

中图分类号: V221⁺.3；O355
计量
- 文章访问数: 356
- HTML全文浏览量: 48
- PDF下载量: 27
- 被引次数: 0
出版历程
- 收稿日期: 2021-10-15
- 录用日期: 2022-01-17
- 网络出版日期: 2022-03-10
- 整期出版日期: 2023-08-31

Unsteady flow mechanism of high Mach number cavity

1.
Computational Aerodynamic Institute of China Aerodynamic Research & Development Center，Mianyang 621000，China
2.
Aerospace Times FeiHong Technology Company Limited，Beijing 100094，China

Funds: National Numerical Windtunnel Project

More Information

Corresponding author: E-mail：rorzey@buaa.edu.cnu.cn

摘要

摘要:
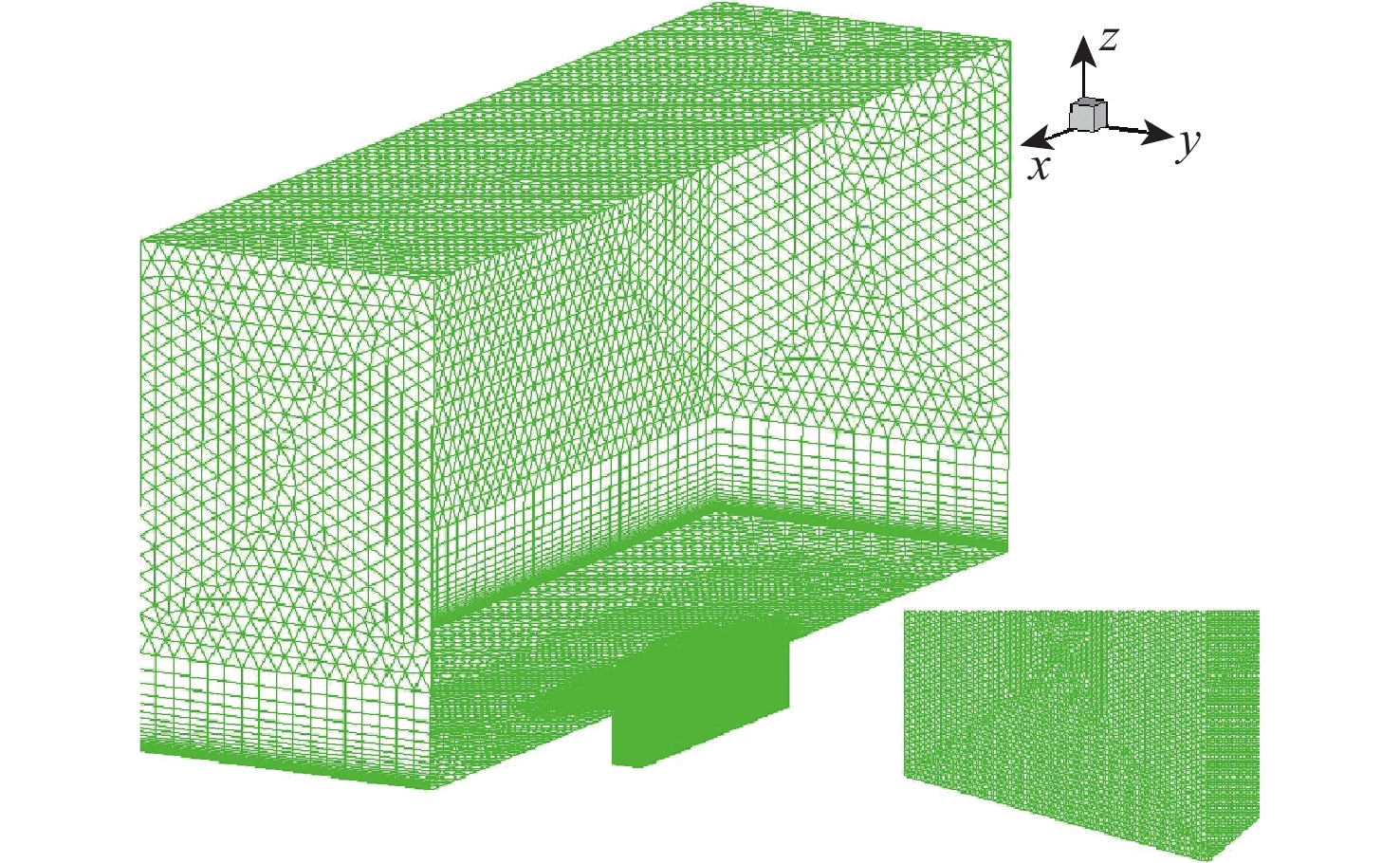
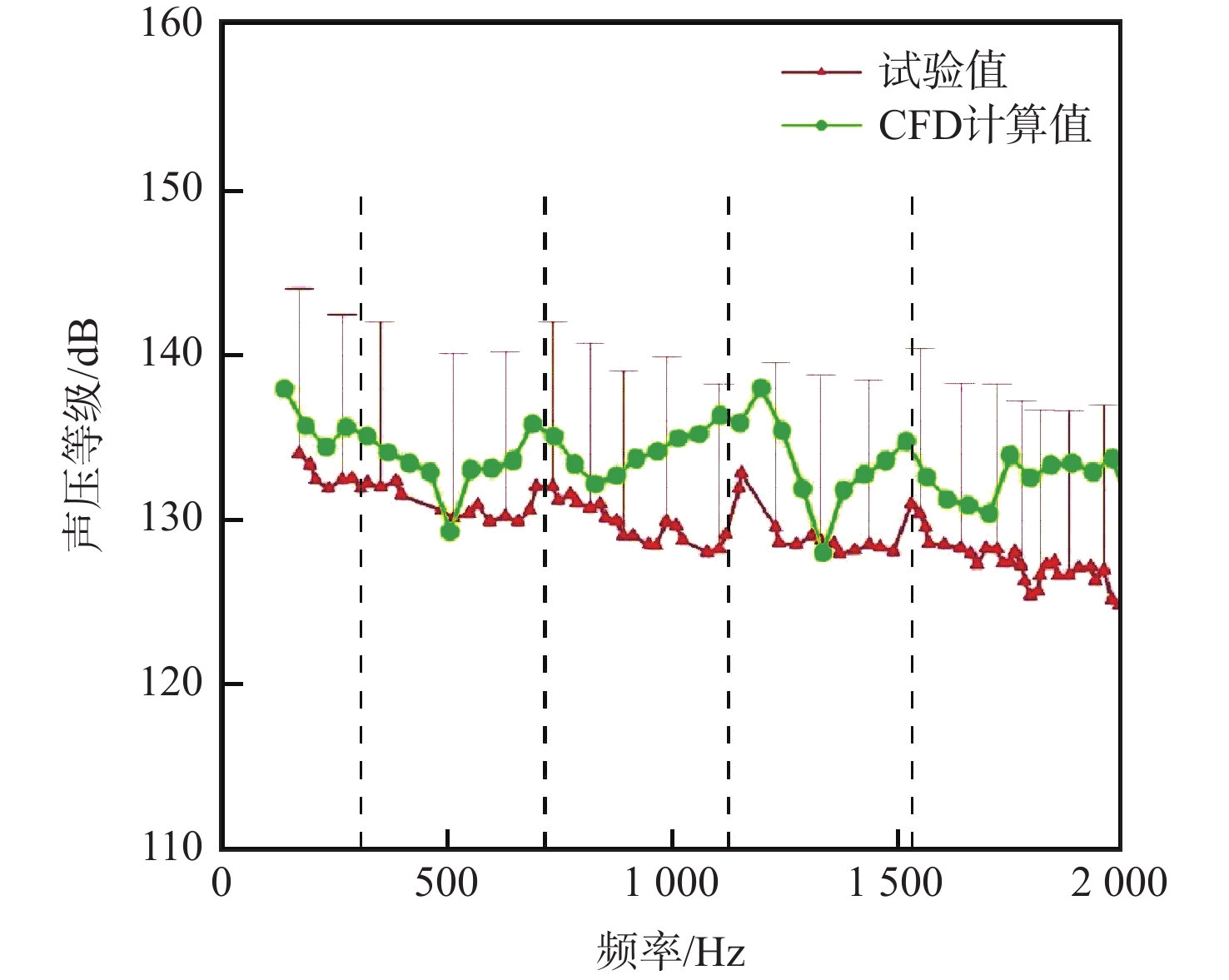
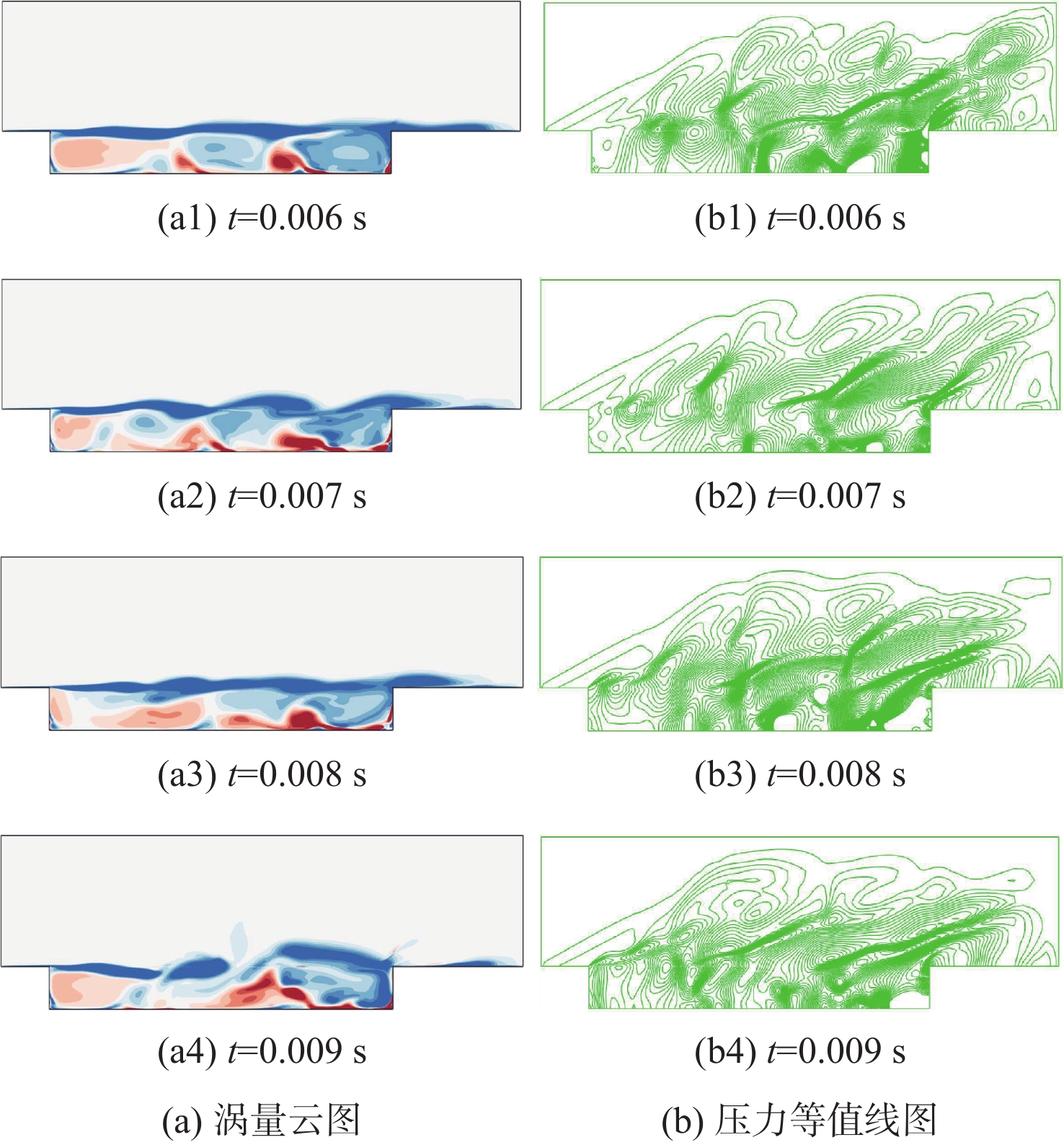
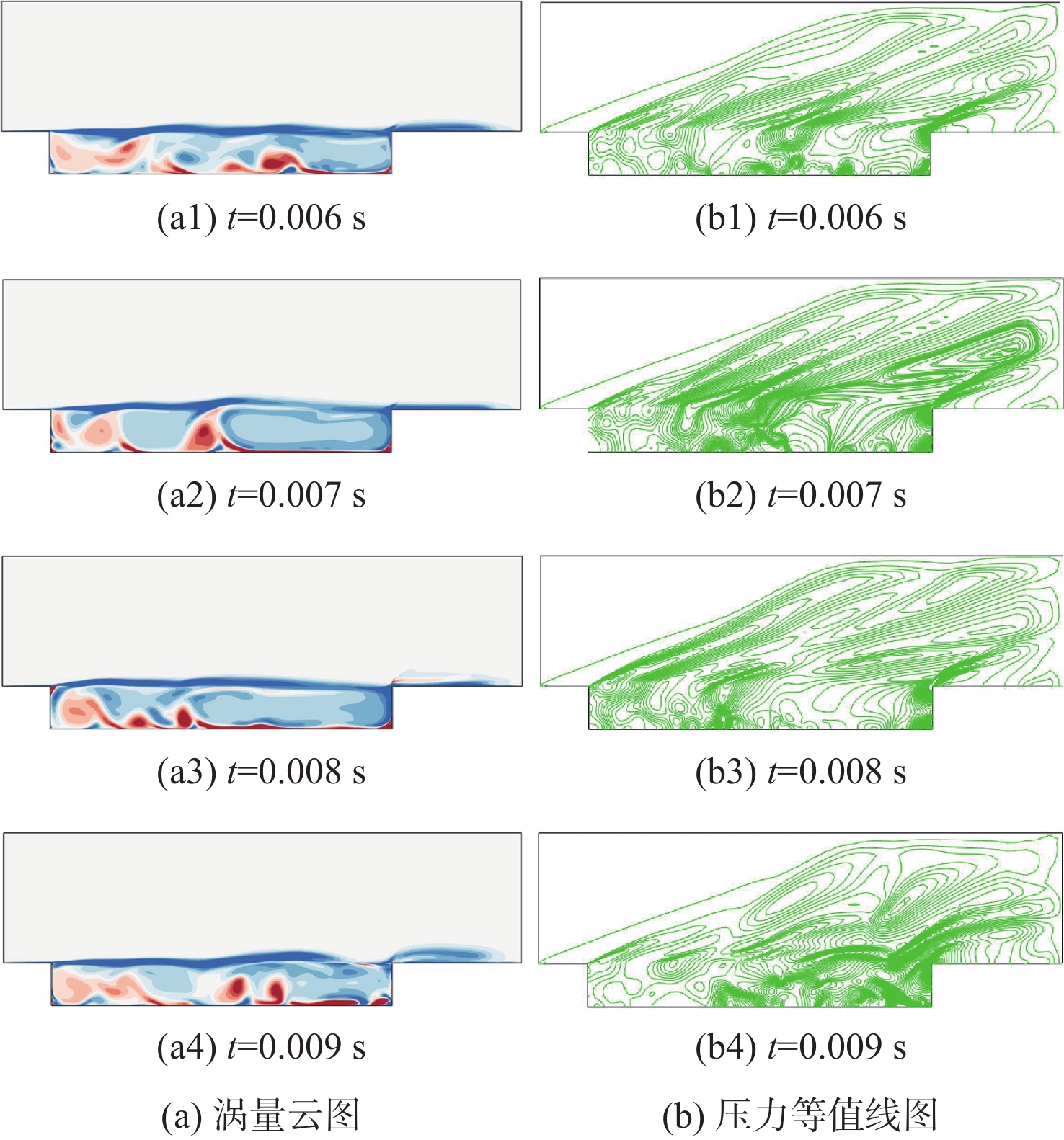
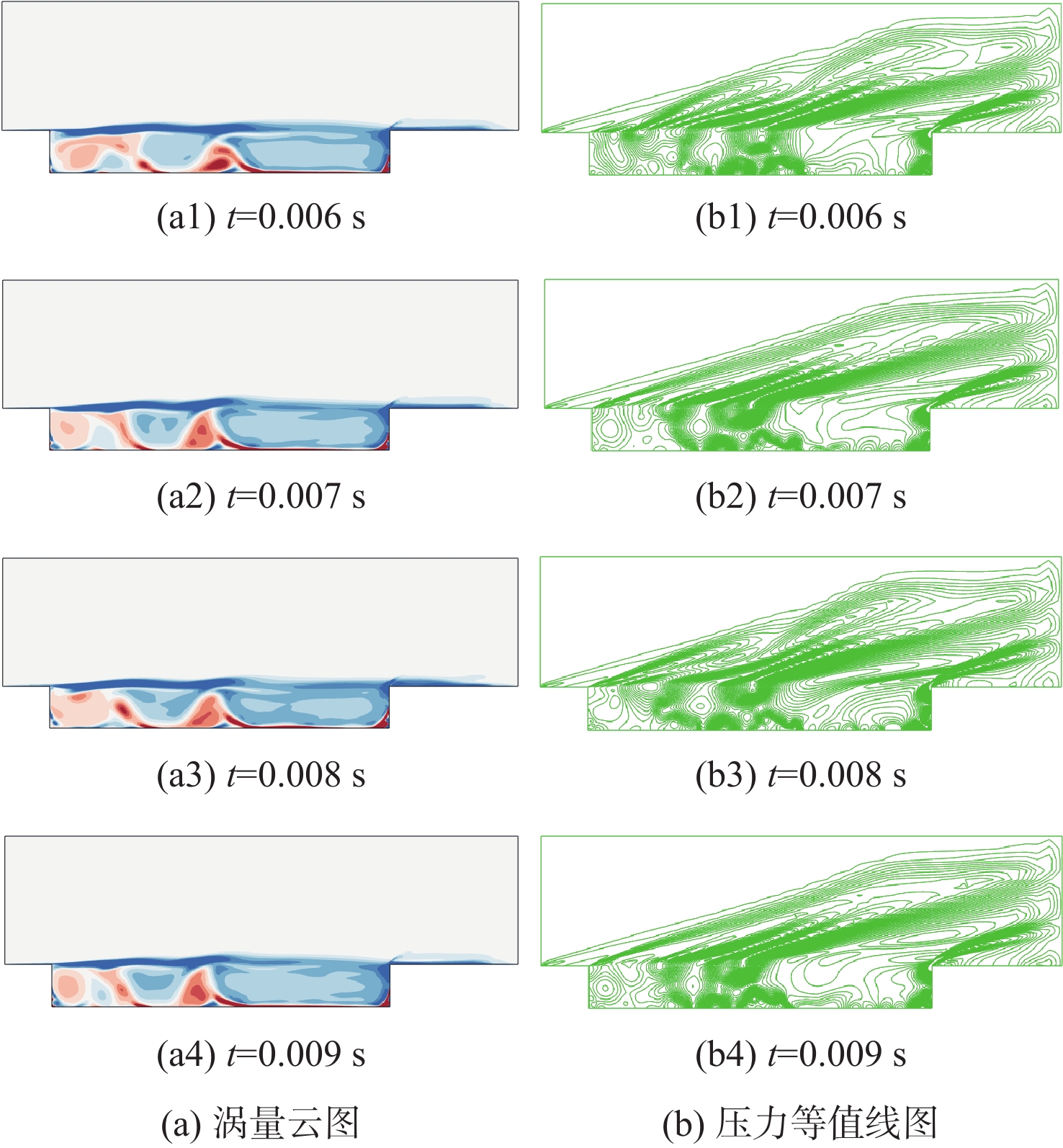
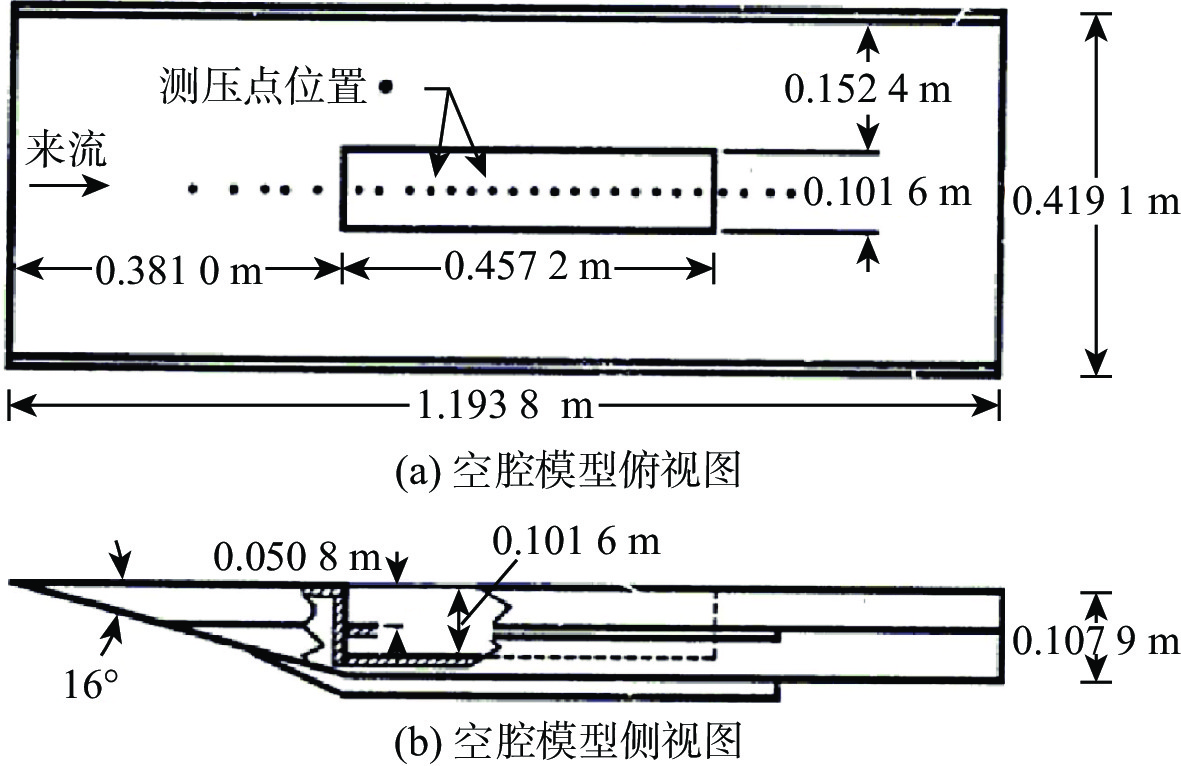
空腔流动广泛存在于飞行器中，内埋弹舱流动是最典型的空腔流动之一。空腔流动结构复杂，并且由于剪切层、涡和激波的相互作用，会产生强烈的压力脉动。针对高马赫数空腔强剪切、强激波的流动特点，提出基于非结构混合网格的中心型和迎风型格式混合方法，通过高马赫数空腔标模算例验证，计算得到空腔1阶、2阶主频与试验数据相比误差不超过5%，空腔噪声强度与试验数据相比误差不超过10 dB，验证了所提方法的可靠性。采用数值模拟方法，开展高马赫数（大于2）空腔流动的脉动特性研究，分析了不同马赫数对空腔声压级的影响，讨论不同马赫数下空腔脉动的产生的声学机制。研究表明：在高马赫数条件下，剪切层动力学与空腔声学的耦合减小，随马赫数增加，空腔振荡的物理机制由Rossiter模型的旋涡声学共振机制转变为闭箱声学机制。
- 空腔流动 /
- 脉动特性 /
- 声压等级 /
- 数值模拟 /
- 空腔噪声
Abstract:
The cavity flow widely exists in aircraft, and the flow in embedded weapon bay is one of the most typical cavity flows. The cavity flow has a complex structure and generates strong pressure fluctuations due to the interaction of shear layers, vortices, and shock waves. Using the unstructured hybrid mesh, a hybrid algorithm of central and upwind schemes is developed that focuses on the properties of high Mach number cavity flow. The cavity first-order and second-order dominant frequencies are calculated and verified by the numerical example of the high Mach number cavity standard model, with an error of no more than 5% compared with the experiment data. The cavity noise intensity has an error of no more than 10 dB compared with the experiment data, which verified the reliability of the method. The studies on the fluctuation characteristics of high Mach number (Ma> 2) cavity flow has been carried out with the numerical simulation method. The impact of various Mach numbers on the cavity's sound pressure level was examined, and it was also described how the cavity fluctuates acoustically at various Mach numbers. It is shown that the coupling between shear layer dynamics and cavity acoustics decreases at high Mach number conditions, and the physical mechanism of cavity oscillation changes from the vortex acoustic resonance mechanism of the Rossiter model to the closed-box acoustic mechanism as the Mach number increases.
- cavity flow /
- fluctuation characteristics /
- sound pressure level /
- numerical simulation /
- cavity noise

HTML全文

图 1 空腔标模试验模型

Figure 1. Test model of cavity standard model

下载: 全尺寸图片幻灯片

图 2 空腔标模网格

Figure 2. Grid of cavity standard model

下载: 全尺寸图片幻灯片

图 3 空腔后壁面上监控点K的位置

Figure 3. Location of pressure orifice K on the rear wall of cavity

下载: 全尺寸图片幻灯片

图 4 监控点K处CFD计算得到的空腔声压等级与试验比较(Ma = 3.51)

Figure 4. Comparison of CFD calculation with test results of SPL for monitoring point K (Ma = 3.51)

下载: 全尺寸图片幻灯片

图 5 Ma = 2.0时，L/D = 8空腔不同时刻涡量云图和压力等值线图

Figure 5. Instantaneous vorticity contours and pressure contour plots at different times for L/D = 8 cavity at Ma = 2.0

下载: 全尺寸图片幻灯片

图 6 Ma = 3.0时，L/D = 8空腔不同时刻涡量云图和压力等值线图

Figure 6. Instantaneous vorticity contours and pressure contour plots at different times for L/D = 8 cavity at Ma = 3.0

下载: 全尺寸图片幻灯片

图 7 Ma = 4.0时，L/D = 8空腔不同时刻涡量云图和压力等值线图

Figure 7. Instantaneous vorticity contours and pressure contour plots at different times for L/D = 8 cavity at Ma = 4.0

下载: 全尺寸图片幻灯片

图 8 Ma =2.0, 3.0, 4.0时，L/D = 8空腔后壁面y/D = 0.75处监控点A的频谱图

Figure 8. Frequency specturum of monitoring point A at y/D = 0.75 for the rear wall of L/D = 8 cavity at Ma = 2.0, 3.0, 4.0

下载: 全尺寸图片幻灯片

图 9 CFD计算得到的斯特劳哈尔数同Rossiter声学模型和闭箱声学模型预测值比较

Figure 9. Comparison of Strouhal number of CFD calculation with predicted values of Rossiter’s equation and closed-box acoustic model

下载: 全尺寸图片幻灯片

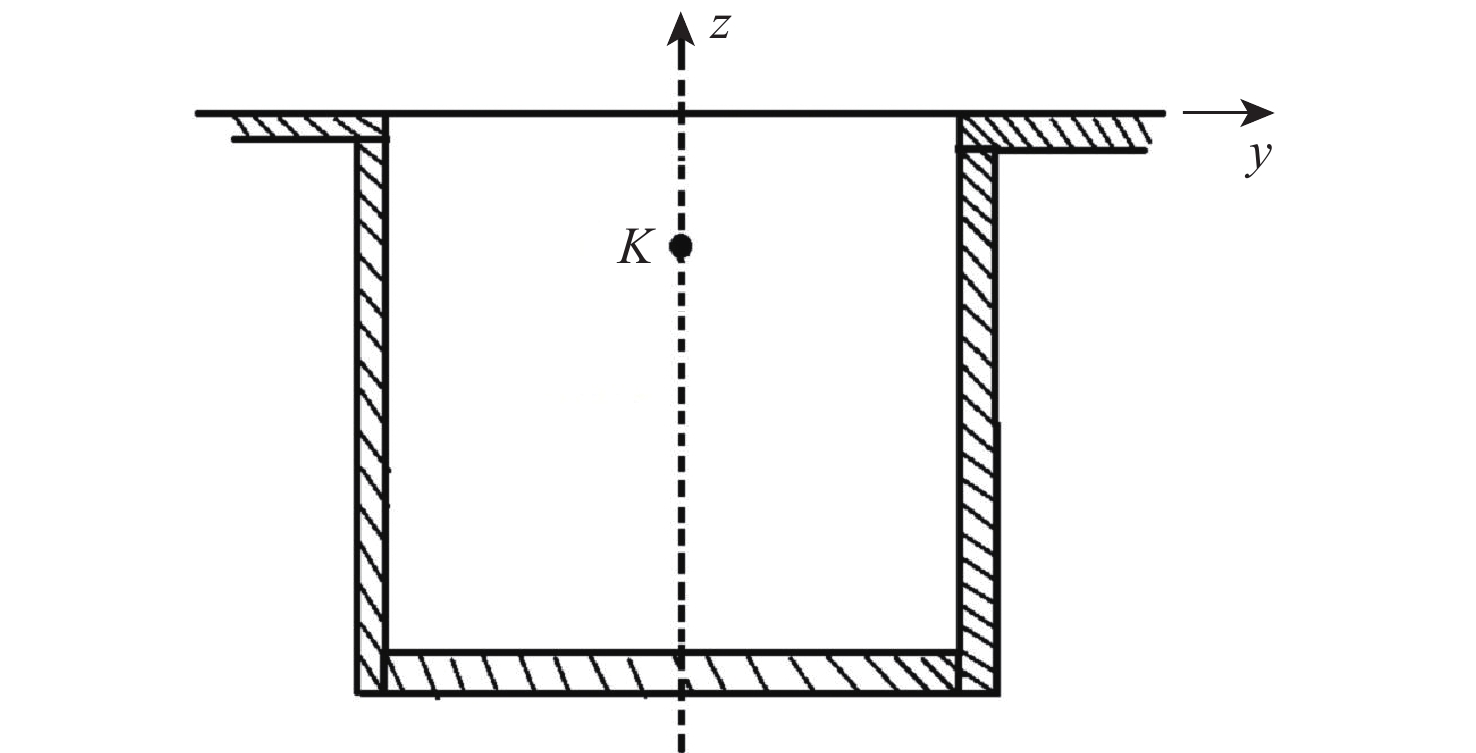
表 1 CFD计算得到的监控点K不同模态频率、幅值与试验值比较

Table 1. Comparison of different frequencies and amplitudes of CFD calculation with text results for monitoring point K

模态	SPL频率/Hz		SPL幅值/dB		频率误差/%	幅值误差/%
模态	试验值	计算值	试验值	计算值	频率误差/%	幅值误差/%
1阶模态	287	275	132.5	135.6	4.18	3.1
2阶模态	695	689	132.1	135.8	0.86	3.7
3阶模态	1152	1195	132.8	138	3.73	5.2
4阶模态	1527	1516	131	134.7	0.72	3.7

下载: 导出CSV

表 2 CFD计算得到的全局声压等级与试验值比较

Table 2. Comparison CFD calculation with text results of OASPL

数据类型	试验值/dB	计算值/dB	误差/dB
OASPL	151.94	154.79	2.85

下载: 导出CSV

表 3 CFD计算、Rossiter声学模型和闭箱声学模型得到的$ fL/{U_\infty } $

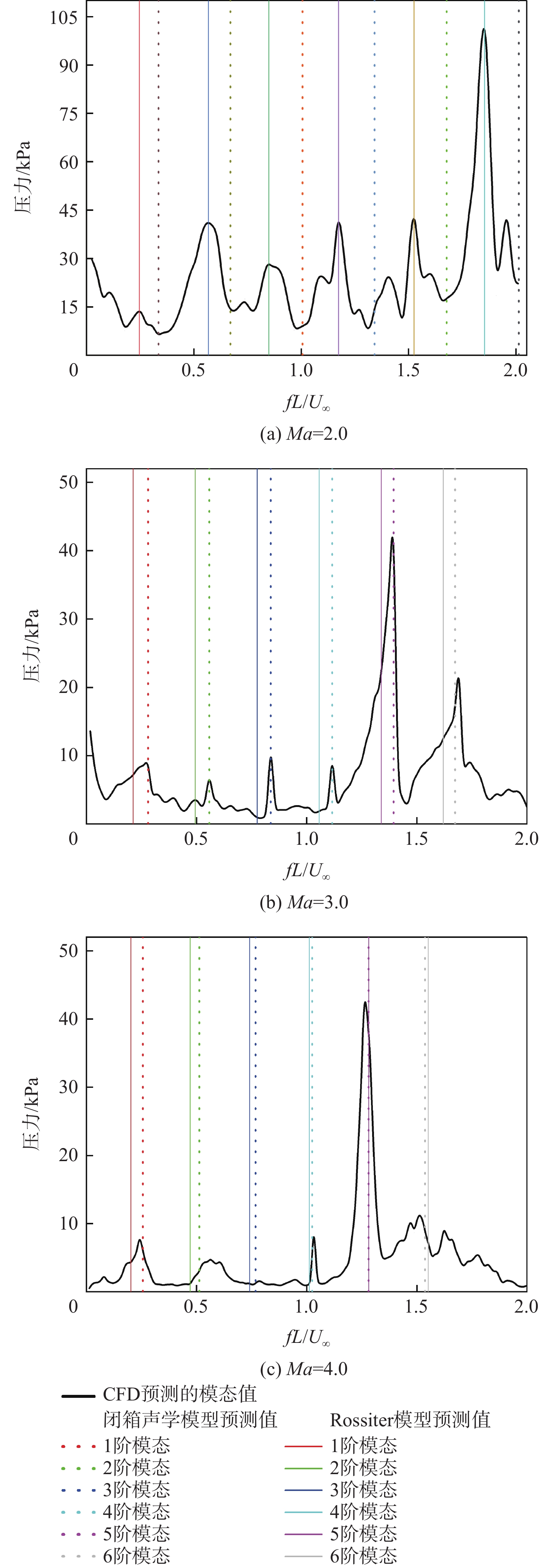
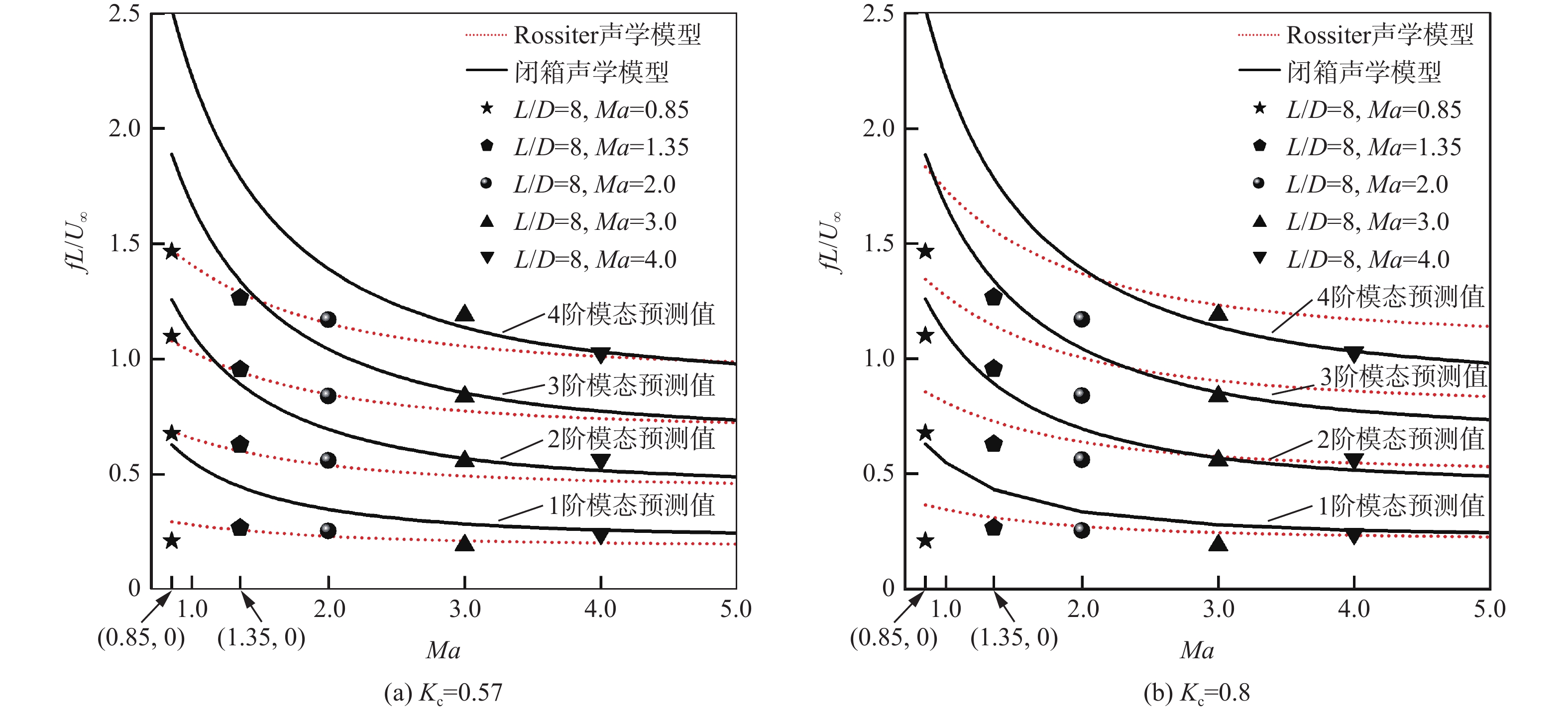
Table 3. Strouhal Number of CFD calculation with predicted values of Rossiter’s equation and closed-box acoustic model

Ma	1阶模态			2阶模态			3阶模态			4阶模态
Ma	CFD 计算值	Rossiter 声学模型	闭箱声学模型	CFD 计算值	Rossiter 声学模型	闭箱声学模型	CFD 计算值	Rossiter 声学模型	闭箱声学模型	CFD 计算值	Rossiter 声学模型	闭箱声学模型
0.85	0.211 76	0.294 24	0.629 31	0.677 84	0.686 57	1.258 61	1.099 90	1.078 89	1.887 91	1.465 66	1.471 21	2.517 21
1.35	0.267 60	0.257 72	0.432 64	0.628 80	0.601 36	0.865 27	0.955 50	0.944 99	1.297 91	1.266 66	1.288 62	1.730 55
2.0	0.254 48	0.231 12	0.335 41	0.559 85	0.539 27	0.670 82	0.839 77	0.847 43	1.006 23	1.170 59	1.155 59	1.341 64
3.0	0.191 76	0.211 43	0.278 89	0.557 84	0.493 34	0.557 77	0.836 76	0.775 25	0.836 66	1.192 52	1.057 16	1.115 55
4.0	0.241 26	0.202 36	0.256 17	0.562 93	0.472 18	0.512 35		0.742 33	0.768 52	1.025 99	1.011 82	1.024 70

下载: 导出CSV

参考文献(25)

[1]	LAWSON S J, BARAKOS G N. Review of numerical simulations for high-speed, turbulent cavity flows[J]. Progress in Aerospace Sciences, 2011, 47(3): 186-216. doi: 10.1016/j.paerosci.2010.11.002
[2]	欧阳绍修, 刘学强, 张宝兵. DES方法模拟空腔流动及噪声分析[J]. 南京航空航天大学学报, 2012, 44(6): 792-796. OUYANG S X, LIU X Q, ZHANG B B. Cavity flow simulation and noise analysis using DES method[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2012, 44(6): 792-796(in Chinese).
[3]	KRISGNAMUTY K. Acoustic radiation from two-dimensional rectangular cutouts in aerodynamic: NACATN-3487[R]. Washington, D. C. : NASA, 1955.
[4]	ROSHKO A. Some measurements of flow in a rectangular cut-out: NACA TN3488[R]. Washington, D. C. : NASA, 1955.
[5]	MAULL D J, EAST L F. Three-dimensional flow in cavities[J]. Journal of Fluid Mechanics, 1963, 16: 620-632. doi: 10.1017/S0022112063001014
[6]	ROSSITER J E. Wind tunnel experiments on the flow over rectangular cavities at subsonic and transonic speeds[J]. Royal Aircraft Establishment Technical Report, 1964, 3438: 8-12.
[7]	HELLER H H, BLISS D B. Aerodynamically induced pressure oscillations in cavities, physical mechanisms and suppression concepts: TR-74-133 [R]. Ohio: AFFDL, 1975.
[8]	RAMAN G, ENVIA E, BENCIC T. Tone noise and nearfield pressure produced by jet-cavity interaction[C]// Proceedings of the 37th Aerospace Sciences Meeting and Exhibit. Reston: AIAA, 1999.
[9]	UKEILEY L, MURRAY N. Velocity and surface pressure measurements in an open cavity[J]. Experiments in Fluids, 2005, 38(5): 656-671. doi: 10.1007/s00348-005-0948-x
[10]	MURRAY R, ELLIOTT G. The compressible shear layer over a two-dimensional cavity[C]// Proceedings of the 36th AIAA Aerospace Sciences Meeting and Exhibit. Reston: AIAA, 1998.
[11]	KAUFMAN L G, MACIULAITIS A, CLARK R L. Mach 0.6 to 3.0 flows over rectangular cavities: AFWAL TR-82-3112 [R]. Wright-Patterson: Airforce Wright Aeronautical Laborattories, 1983.
[12]	ZHANG X, RONA A, EDWARDS J A. An observation of pressure waves around a shallow cavity[J]. Journal of Sound and Vibration, 1998, 214(4): 771-778. doi: 10.1006/jsvi.1998.1635
[13]	RIZZETTA D P, VISBAL M R. Large-eddy simulation of supersonic cavity flow fields including flow control[J]. AIAA Journal, 2003, 41(8): 1452-1462. doi: 10.2514/2.2128
[14]	CHANG K, CONSTANTINESCU G, PARK S O. Analysis of the flow and mass transfer processes for the incompressible flow past an open cavity with a laminar and a fully turbulent incoming boundary layer[J]. Journal of Fluid Mechanics, 2006, 561: 113. doi: 10.1017/S0022112006000735
[15]	PENG S H, LEICHER S. DES and hybrid RANS–LES modelling of unsteady pressure oscillations and flow features in a rectangular cavity[C]//Advances in Hybrid RANS-LES Modelling, Notes on Numerical Fluid Mechanics and Multidisciplinary Design. Berlin: Springer, 2008: 132-141.
[16]	HAMED A, BASU D, DAS K. Detached eddy simulations of supersonic flow over cavity[C]// Proceedings of the 41st Aerospace Sciences Meeting and Exhibit. Reston: AIAA, 2003.
[17]	刘俊, 杨党国, 王显圣, 等. 湍流边界层厚度对三维空腔流动的影响[J]. 航空学报, 2016, 37(2): 475-483. LIU J, YANG D G, WANG X S, et al. Effect of turbulent boundary layer thickness on a three-dimensional cavity flow[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(2): 475-483(in Chinese).
[18]	马小亮, 杨国伟. 凹腔非定常特性的数值模拟[J]. 计算物理, 2010, 27(3): 375-380. MA X L, YANG G W. Simulation of unsteady cavity flow[J]. Chinese Journal of Computational Physics, 2010, 27(3): 375-380(in Chinese).
[19]	司海青, 王同光. 边界条件对三维空腔流动振荡的影响[J]. 南京航空航天大学学报, 2006, 38(5): 595-599. SI H Q, WANG T G. Influence of boundary condition on 3-D cavity flow-induced oscillations[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2006, 38(5): 595-599(in Chinese).
[20]	王一丁, 郭亮, 童明波, 等. 高速飞行器空腔脉动压力主动控制与非线性数值模拟[J]. 航空学报, 2015, 36(1): 213-222. WANG Y D, GUO L, TONG M B, et al. Active control and nonlinear numerical simulation for oscillating pressure of high-speed aircraft cavity[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(1): 213-222(in Chinese).
[21]	STRELETS M. Detached eddy simulation of massively separated flows[C]// Proceedings of the 39th Aerospace Sciences Meeting and Exhibit. Reston: AIAA, 2001.
[22]	肖志祥, 罗堃宇, 刘健. 宽速域RANS-LES混合方法的发展及应用[J]. 空气动力学学报, 2017, 35(3): 338-353. XIAO Z X, LUO K Y, LIU J. Developments and applications of hybrid RANS-LES methods for wide-speed-range flows[J]. Acta Aerodynamica Sinica, 2017, 35(3): 338-353(in Chinese).
[23]	肖志祥, 崔文瑶, 刘健, 等. 新一代战斗机非定常流动数值研究综述[J]. 航空学报, 2020, 41(6): 523451. XIAO Z X, CUI W Y, LIU J, et al. Review of numerical research on unsteady flows of the new generation fighters[J]. Acta Aeronautica et Astronautica Sinica, 2020, 41(6): 523451(in Chinese).
[24]	TRAVIN A K, SHUR M L, SPALART P R, et al. Improvement of delayed detached-eddy simulation for LES with wall modeling[C]//European Conference on Computational Fluid Dynamics. Delft: TU Delft, 2006: 32-410.
[25]	BAUER R C, DIX R E. Engineering model of unsteady flow in a cavity: AEDC-TR-91-17 [R]. Arnold : Arnold Engineering Development Center, 1991.