基于应变的几何非线性梁建模与分析

许秋怡; 孟杨; 李书

doi:10.13700/j.bh.1001-5965.2021.0627

基于应变的几何非线性梁建模与分析

doi: 10.13700/j.bh.1001-5965.2021.0627

北京航空航天大学航空科学与工程学院，北京 100191

详细信息

通讯作者:
E-mail：summy@buaa.edu.cn

中图分类号: V214.3
计量
- 文章访问数: 163
- HTML全文浏览量: 47
- PDF下载量: 34
- 被引次数: 0
出版历程
- 收稿日期: 2021-10-22
- 录用日期: 2021-11-26
- 网络出版日期: 2021-12-30
- 整期出版日期: 2023-08-31

Strain-based geometrically nonlinear beam modeling and analysis

School of Aeronautic Science and Engineering, Beihang University, Beijing 100191, China

More Information

Corresponding author: E-mail: summy@buaa.edu.cn

摘要

摘要:
柔性机翼在气动载荷作用下产生较大变形，几何非线性因素不容忽视。利用机翼柔性特点，通常采用梁模型进行结构建模。从几何精确梁理论出发，结合Hamilton原理推导了几何非线性梁的动力学平衡方程。不同于经典的位移基有限元，采用梁广义应变作为插值变量，得到广义质量阵、广义阻尼阵、刚度阵及载荷列向量，建立非线性应变梁模型。结合Newmark数值算法和牛顿-拉夫森（Newdon-Raphson）迭代法建立了动力学方程求解算法。针对典型算例，开展静、动力学分析，并分别与有限元软件的仿真结果进行对比。结果表明：在相当计算精度下，所建模型收敛特性更好。为进一步验证所建模型在工程实际应用中的精度和有效性，开展针对典型大展弦比机翼的地面静力试验。试验表明：仿真结果与激光位移计和光纤传感设备测得的变形值具有较高的一致性，验证了所建模型具有较高精度。
- 几何非线性 /
- 应变 /
- 梁 /
- 结构动力学 /
- 有限元
Abstract:
Under the action of aerodynamic forces, flexible wings undergo large deformations, for which geometric nonlinearity cannot be ignored. By taking advantage of their slenderness, flexible wings can be modeled as beams. This paper developed the dynamic equilibrium equations of nonlinear beams based on the geometrically exact beam theory and Hamilton principle. Different from the classical displacement-based finite element, this work took the generalized strains as interpolated variables and obtained the generalized mass matrix, damping matrix, stiffness matrix and force vectors, based on which a strain-based nonlinear beam model was proposed. The nonlinear dynamic equations were then solved by Newmark method combined with Newton-Raphson iterations with typical examples investigated from both static and dynamic perspectives. Next, the results were compared with those calculated by finite-element software, which proved that the strain-based beam model has better convergence with the comparable accuracy. The method was further verified by static ground tests of a large-aspect-ratio wing model, during which laser displacement sensor and fiber optic sensing technology were utilized to measure the structural deformation. The excellent agreement between numerical results calculated by the proposed method and the test results further validated the accuracy of the strain-based formulation.
- geometric nonlinearity /
- strain /
- beam /
- structural dynamics /
- finite-element method

HTML全文

图 1 梁空间构形示意图

Figure 1. Kinematic dagram of beam spaxial configuration

下载: 全尺寸图片幻灯片

图 2 单元划分示意图

Figure 2. Illustration of elements

下载: 全尺寸图片幻灯片

图 3 悬臂梁模型示意图

Figure 3. Illustration of cantilevered beam

下载: 全尺寸图片幻灯片

图 4 悬臂梁受端部弯矩作用变形图

Figure 4. Deformation of cantilever beam subjected to tip moment

下载: 全尺寸图片幻灯片

图 5 梁端部位移随载荷大小变化

Figure 5. Tip displacements with respect to force magnitudes

下载: 全尺寸图片幻灯片

图 6 Nastran非线性静力学迭代

Figure 6. Nonlinear static iterations in Nastran

下载: 全尺寸图片幻灯片

图 7 本文模型非线性静力学求解迭代收敛曲线

Figure 7. Iterative curve for solving nonlinear statics of proposed model

下载: 全尺寸图片幻灯片

图 8 悬臂梁在定向载荷和随动载荷作用下的变形

Figure 8. Deformation of cantilevered beam subjected to dead force and follower force

下载: 全尺寸图片幻灯片

图 9 端部定向正弦载荷作用下位移响应

Figure 9. Responses of tip displacement subject to sinusoidal dead force

下载: 全尺寸图片幻灯片

图 10 端部随动正弦载荷作用下位移响应

Figure 10. Responses of tip displacement subject to sinusoidal follower force

下载: 全尺寸图片幻灯片

图 11 用于地面试验的机翼模型图

Figure 11. Wing model used in ground test

下载: 全尺寸图片幻灯片

图 12 地面静力试验示意图

Figure 12. Diagram of ground static tests

下载: 全尺寸图片幻灯片

图 13 光纤光栅传感器黏贴示意图

Figure 13. Installation of fiber grating sensors

下载: 全尺寸图片幻灯片

图 14 机翼主梁表面弯曲应变

Figure 14. Bending strains on beam surface at different positions

下载: 全尺寸图片幻灯片

图 15 自重作用下机翼垂向变形

Figure 15. Vertical displacements of wing under gravity

下载: 全尺寸图片幻灯片

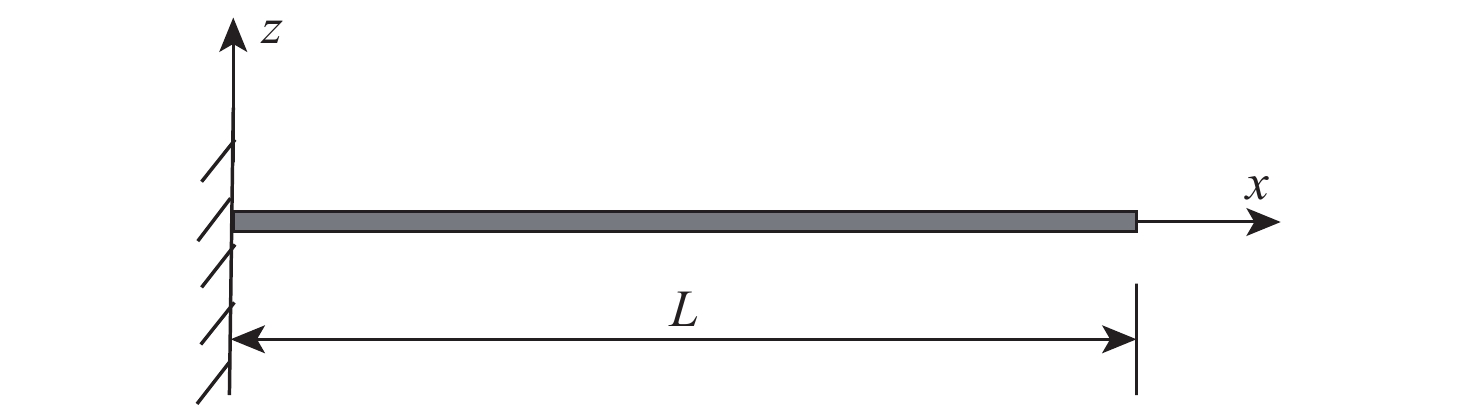
表 1 悬臂梁模型物理属性

Table 1. Properties of cantilevered beam

参数	数值
长度L/m	1.00
弹性模量E/GPa	210
剪切模量G/GPa	84.2
横截面宽度b/mm	35
横截面高度h/mm	1.5
密度$\rho $/(kg·m⁻³)	$7.75 \times {10^3}$
扭转惯量${I_x}$/(kg·m)	$5.37 \times {10^{ - 9}}$
面外弯曲惯量${I_y}$/(kg·m)	$9.84 \times {10^{ - 12}}$
面内弯曲惯量${I_{\textit{z}}}$/(kg·m)	$5.36 \times {10^{ - 9}}$

下载: 导出CSV

表 2 不同端部载荷作用下端部垂向位移

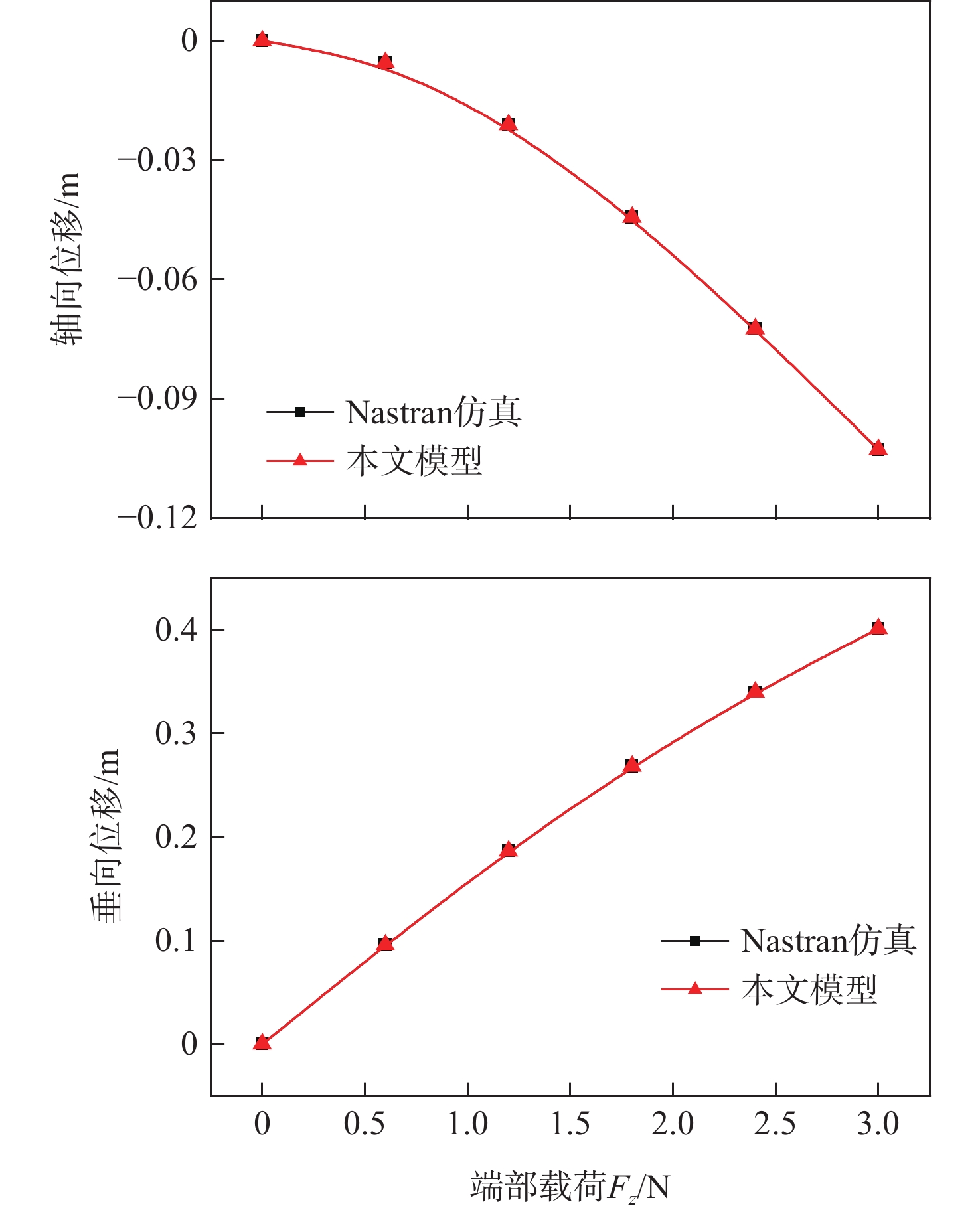
Table 2. Tip vertical displacements with respect to different tip forces

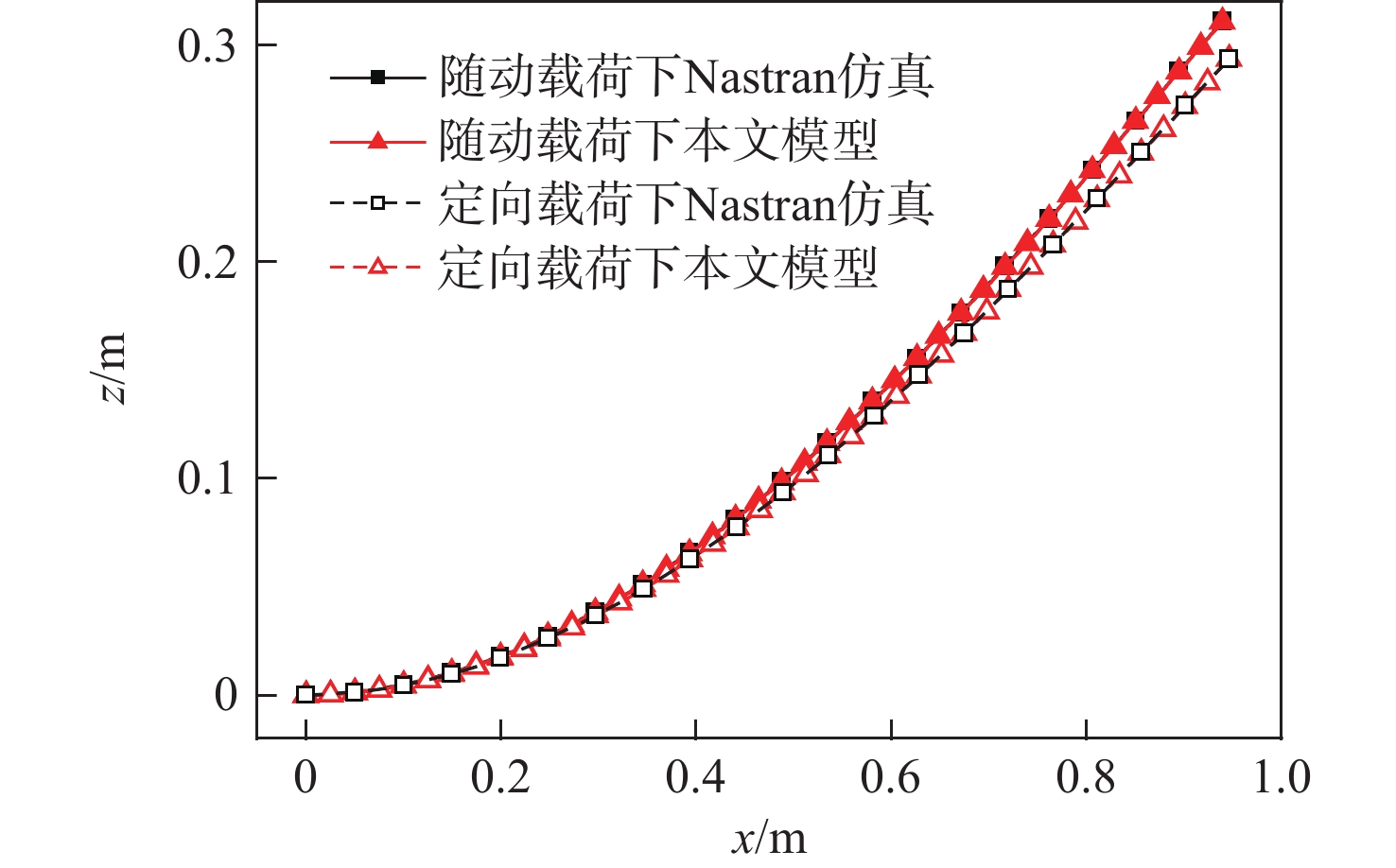
端部载荷/N	端部垂向位移/m		相对误差/%
端部载荷/N	Nastran仿真	本文模型	相对误差/%
0.6	0.09584	0.09578	−0.063
1.2	0.18655	0.18643	−0.064
1.8	0.26852	0.26836	−0.060
2.4	0.34020	0.33999	−0.062
3.0	0.40165	0.40140	−0.062

下载: 导出CSV

表 3 不同端部载荷作用下端部轴向位移

Table 3. Tip axial displacements with respect to different tip forces

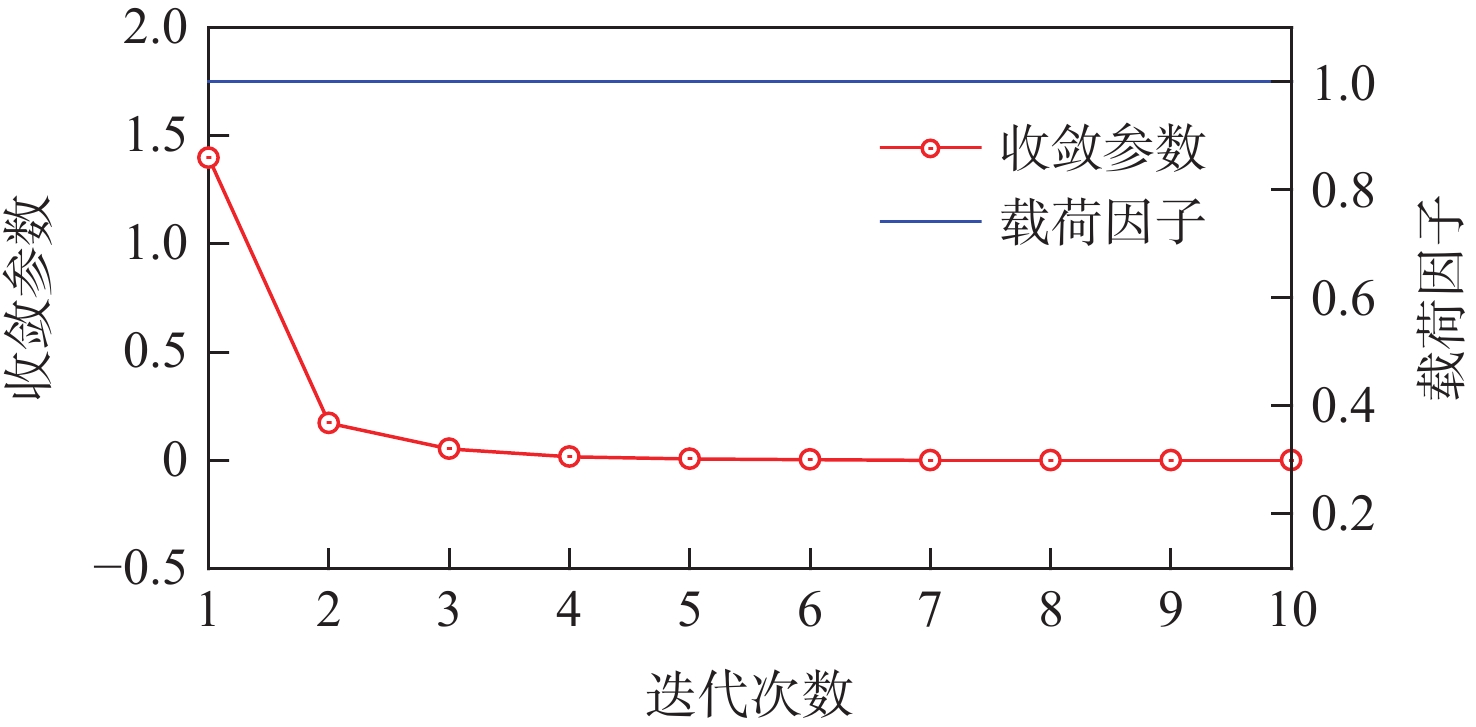
端部载荷/N	端部轴向位移/m		相对误差/%
端部载荷/N	Nastran仿真	本文模型	相对误差/%
0.6	−0.005525	−0.005523	−0.040
1.2	−0.021120	−0.021110	−0.047
1.8	−0.044360	−0.044340	−0.045
2.4	−0.072380	−0.072350	−0.041
3.0	−0.102720	−0.102670	−0.049

下载: 导出CSV

表 4 本文模型各迭代步端部垂向位移

Table 4. Tip vertical displacements of each iteration step in proposed model

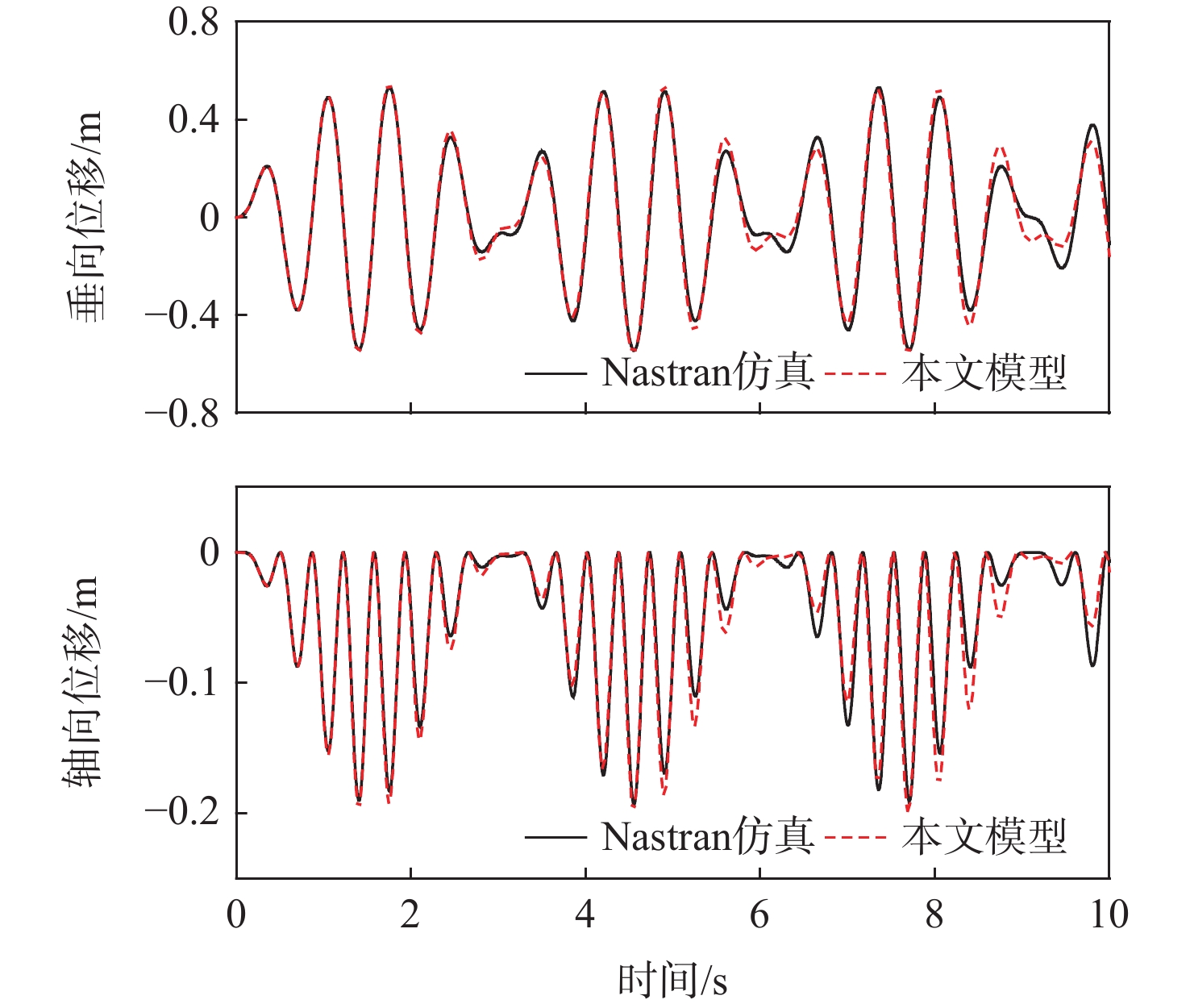
迭代次数	端部垂向位移/m
1	0.447575
2	0.386251
3	0.405881
4	0.400023
5	0.401817
6	0.401272
7	0.401438
8	0.401388
9	0.401403
10	0.401398

下载: 导出CSV

表 5 机翼模型主要参数

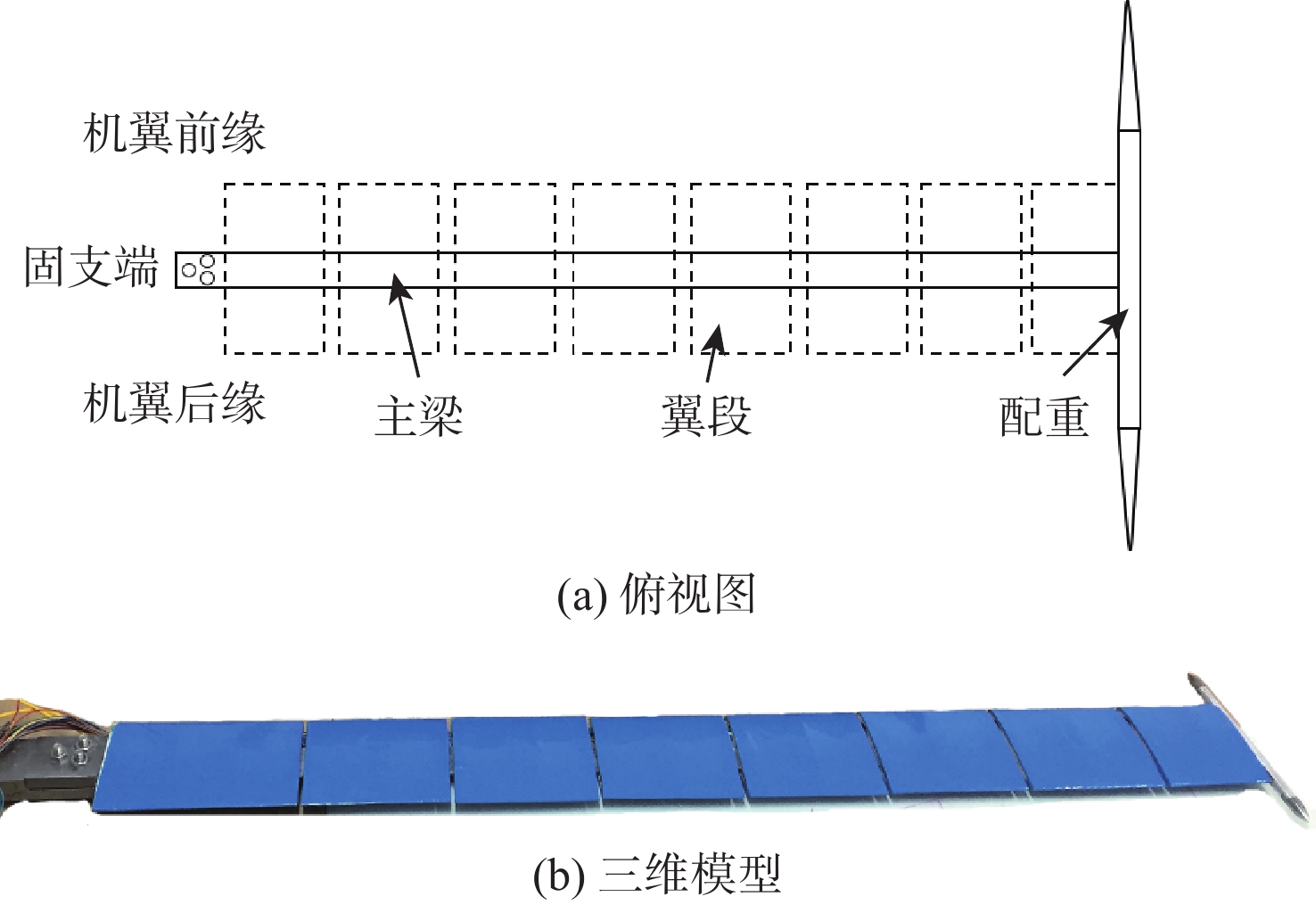
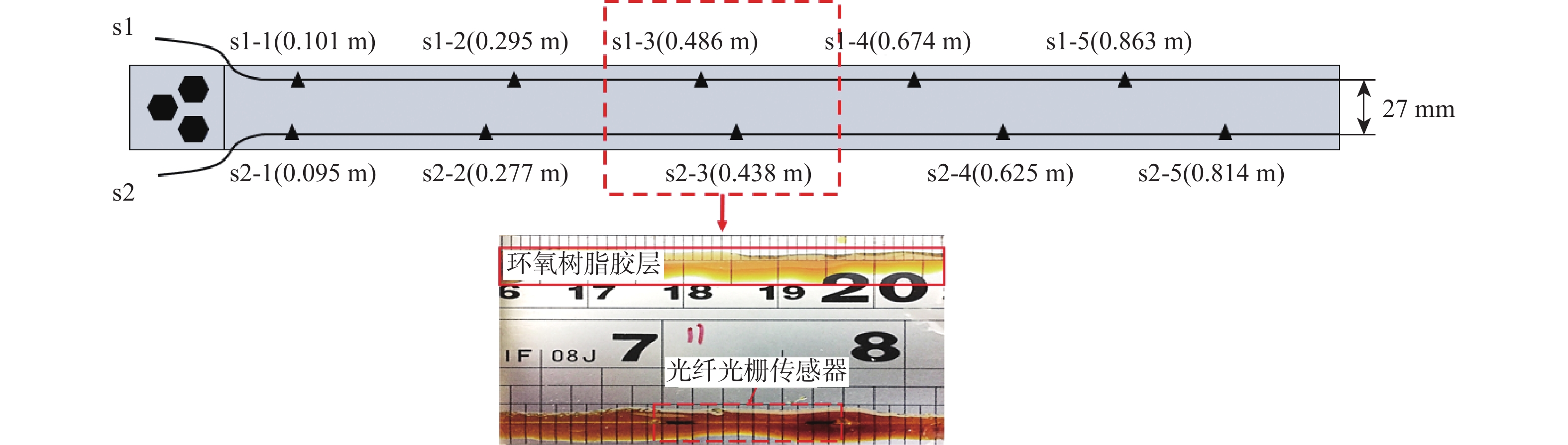
Table 5. Main parameters of wing model

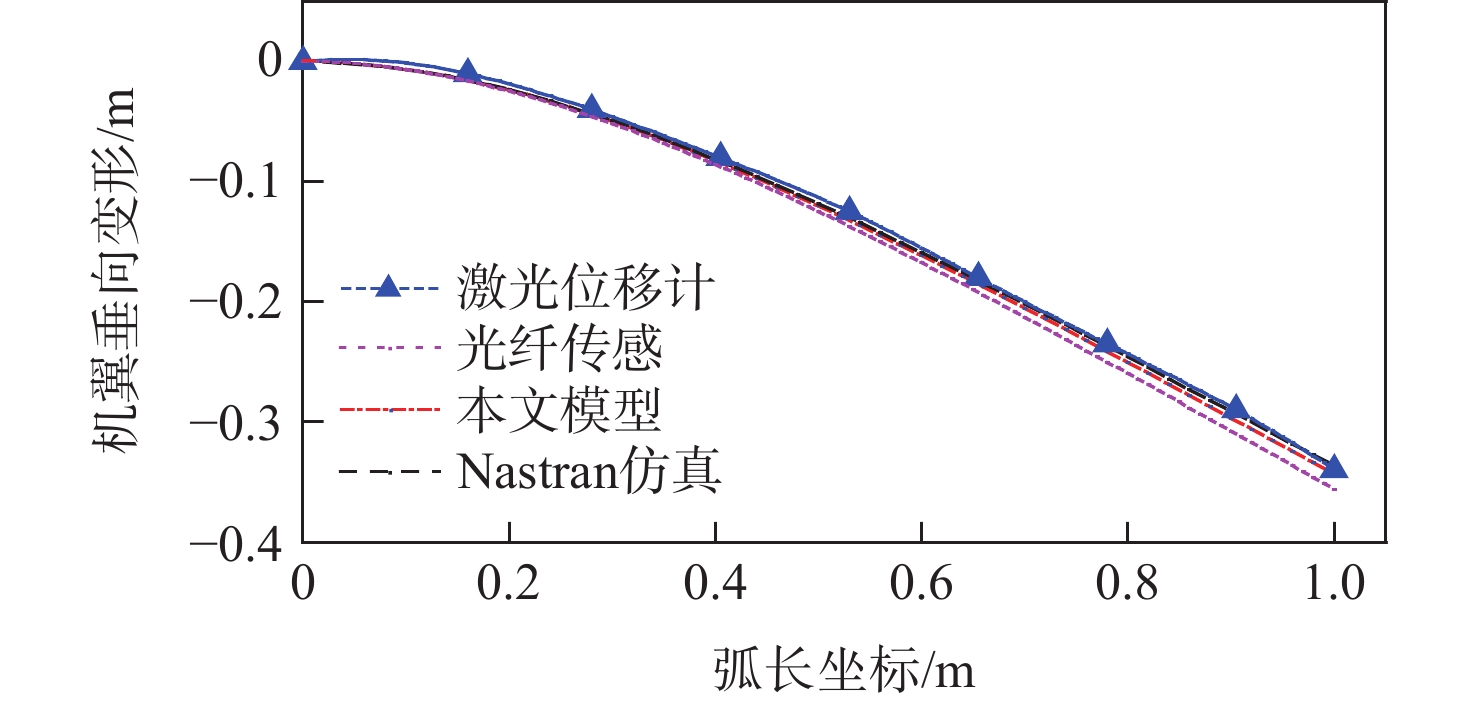
机翼展长/m	机翼弦长/m	机翼总质量/kg
1.0	0.01	0.672

下载: 导出CSV

表 6 不同展向位置机翼垂向变形

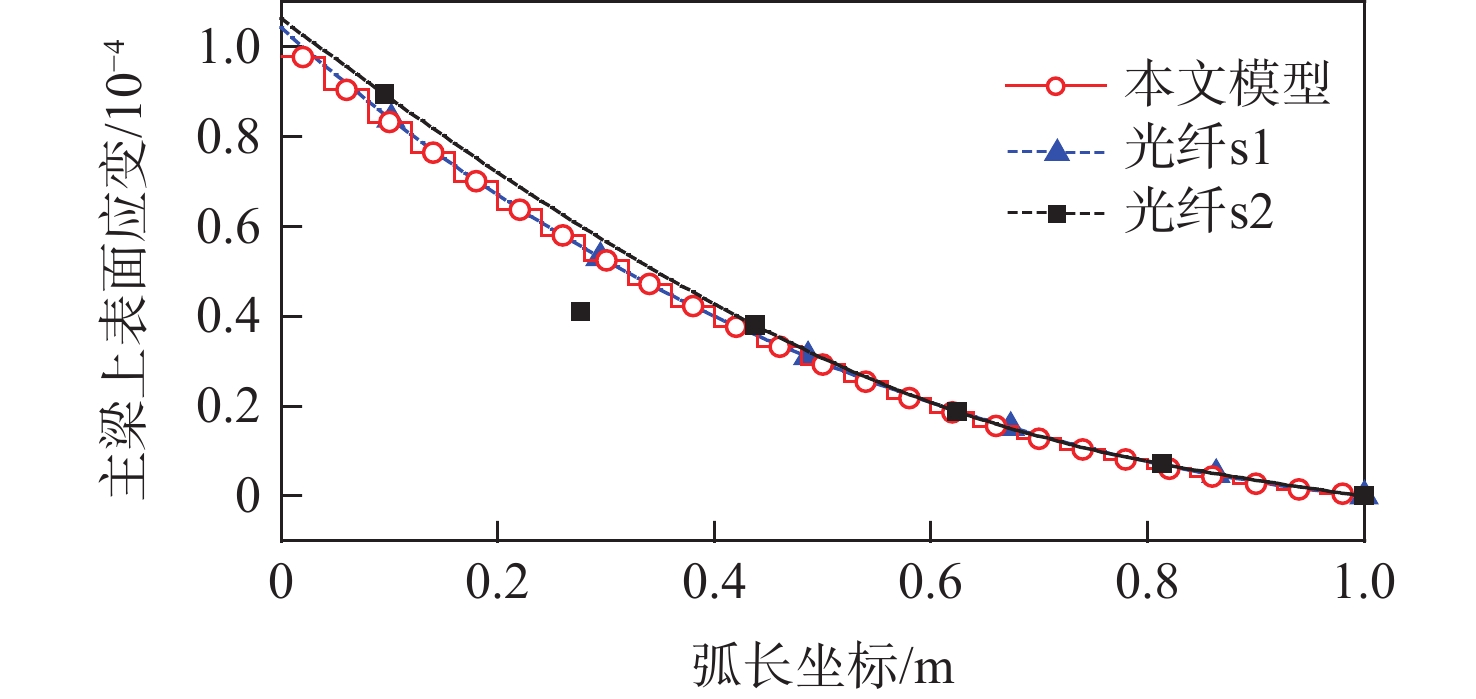
Table 6. Vertical displacements at different positions

展向位置/m	试验值/m			垂向变形${{\textit{z}}_2}$/m	${{\textit{z}}_2} - {{\textit{z}}_1} $的相对误差/%
展向位置/m	激光位移计	光纤传感	平均值${{\textit{z}}_1}$	垂向变形${{\textit{z}}_2}$/m	${{\textit{z}}_2} - {{\textit{z}}_1} $的相对误差/%
0.2	−0.01851	−0.02457	−0.02154	−0.02364	−0.21
0.4	−0.07833	−0.08559	−0.08196	−0.08243	−0.05
0.6	−0.15509	−0.16753	−0.16131	−0.16149	−0.02
0.8	−0.24355	−0.25978	−0.25167	−0.25058	0.11
1.0	−0.34	−0.35587	−0.34794	−0.34323	0.47

下载: 导出CSV

参考文献(19)

[1]	谢长川, 吴志刚, 杨超. 大展弦比柔性机翼的气动弹性分析[J]. 北京航空航天大学学报, 2003, 29(12): 1087-1090. doi: 10.3969/j.issn.1001-5965.2003.12.007 XIE C C, WU Z G, YANG C. Aeroelastic analysis of flexible large aspect ratio wing[J]. Journal of Beijing University of Aeronautics and Astronautics, 2003, 29(12): 1087-1090(in Chinese). doi: 10.3969/j.issn.1001-5965.2003.12.007
[2]	FUNG Y C, TONG P. Classical and computational solid mechanics[M]. Singapore: World Scientific, 2001.
[3]	朱菊芬, 周承芳, 吕和祥. 一般杆系结构的非线性数值分析[J]. 应用数学和力学, 1987, 8(12): 1099-1109. ZHU J F, ZHOU C F, LYU H X. The nonlinear numerical analysis method for frames[J]. Applied Mathematics and Mechanics, 1987, 8(12): 1099-1109(in Chinese).
[4]	LOVE A E H. A treatise on the mathematical theory of elasticity[M]. 4th ed. New York: Dover, 1944.
[5]	REISSNER E. On one-dimensional large-displacement finite-strain beam theory[J]. Studies in Applied Mathematics, 1973, 52(2): 87-95. doi: 10.1002/sapm197352287
[6]	SIMO J C. A finite strain beam formulation. The three-dimensional dynamic problem. Part I[J]. Computer Methods in Applied Mechanics and Engineering, 1985, 49(1): 55-70. doi: 10.1016/0045-7825(85)90050-7
[7]	SIMO J C, VU-QUOC L. A three-dimensional finite-strain rod model. part II: Computational aspects[J]. Computer Methods in Applied Mechanics and Engineering, 1986, 58(1): 79-116. doi: 10.1016/0045-7825(86)90079-4
[8]	IURA M, ATLURI S N. On a consistent theory, and variational formulation of finitely stretched and rotated 3-D space-curved beams[J]. Computational Mechanics, 1988, 4(2): 73-88. doi: 10.1007/BF00282411
[9]	DANIELSON D A, HODGES D H. Nonlinear beam kinematics by decomposition of the rotation tensor[J]. Journal of Applied Mechanics, 1987, 54(2): 258-262. doi: 10.1115/1.3173004
[10]	CRISFIELD M A, JELENIĆ G. Objectivity of strain measures in the geometrically exact three-dimensional beam theory and its finite-element implementation[J]. Proceedings of the Royal Society of London Series A:Mathematical, Physical and Engineering Sciences, 1999, 455(1983): 1125-1147. doi: 10.1098/rspa.1999.0352
[11]	ZHONG P N, HUANG G J, YANG G W. Frame-invariance in finite element formulations of geometrically exact rods[J]. Applied Mathematics and Mechanics, 2016, 37(12): 1669-1688. doi: 10.1007/s10483-016-2147-8
[12]	SIMO J C, TARNOW N, DOBLARE M. Non-linear dynamics of three-dimensional rods: Exact energy and momentum conserving algorithms[J]. International Journal for Numerical Methods in Engineering, 1995, 38(9): 1431-1473. doi: 10.1002/nme.1620380903
[13]	ZUPAN D, SAJE M. Finite-element formulation of geometrically exact three-dimensional beam theories based on interpolation of strain measures[J]. Computer Methods in Applied Mechanics and Engineering, 2003, 192(49-50): 5209-5248. doi: 10.1016/j.cma.2003.07.008
[14]	ČEŠAREK P, SAJE M, ZUPAN D. Kinematically exact curved and twisted strain-based beam[J]. International Journal of Solids and Structures, 2012, 49(13): 1802-1817. doi: 10.1016/j.ijsolstr.2012.03.033
[15]	SU W H, CESNIK C E S. Strain-based geometrically nonlinear beam formulation for modeling very flexible aircraft[J]. International Journal of Solids and Structures, 2011, 48(16-17): 2349-2360. doi: 10.1016/j.ijsolstr.2011.04.012
[16]	MENG Y, WAN Z Q, XIE C C, et al. Time-domain nonlinear aeroelastic analysis and wind tunnel test of a flexible wing using strain-based beam formulation[J]. Chinese Journal of Aeronautics, 2021, 34(1): 380-396. doi: 10.1016/j.cja.2020.07.027
[17]	MENG Y, XIE C C, WAN Z Q. Strain-based shape prediction for flexible beam-like structures[C]//Proceedings of the AIAA Scitech 2019 Forum. Reston: AIAA, 2019.
[18]	肖业伦. 航空航天器运动的建模飞行动力学的理论基础[M]. 北京: 北京航空航天大学出版社, 2003: 6-17. XIAO Y L. Modeling of aerospace vehicle motion: Theoretical basis of flight dynamics[M]. Beijing: Beihang University Press, 2003: 6-17 (in Chinese).
[19]	MENG Y, XIE C C, WAN Z Q. Deformed wing shape prediction using fiber optic strain data[C]//International Forum on Aeroelasticity and Structural Dynamics 2017. Como: IFASD, 2017.