高级搜索

留言板

尊敬的读者、作者、审稿人, 关于本刊的投稿、审稿、编辑和出版的任何问题, 您可以本页添加留言。我们将尽快给您答复。谢谢您的支持!

姓名
邮箱
手机号码
标题
留言内容
验证码

基于混合策略的麻雀搜索算法改进及应用

宋立钦,  陈文杰,  陈伟海,  林岩,  孙先涛

downloadPDF
文章导航 > 北京航空航天大学学报  > 2023 >  49(8): 2187-2199.
宋立钦，陈文杰，陈伟海，等. 基于混合策略的麻雀搜索算法改进及应用[J]. 北京航空航天大学学报，2023，49（8）：2187-2199 doi: 10.13700/j.bh.1001-5965.2021.0629
引用本文: 宋立钦，陈文杰，陈伟海，等. 基于混合策略的麻雀搜索算法改进及应用[J]. 北京航空航天大学学报，2023，49（8）：2187-2199 doi: 10.13700/j.bh.1001-5965.2021.0629
shu
SONG L Q，CHEN W J，CHEN W H，et al. Improvement and application of hybrid strategy-based sparrow search algorithm[J]. Journal of Beijing University of Aeronautics and Astronautics，2023，49（8）：2187-2199 （in Chinese） doi: 10.13700/j.bh.1001-5965.2021.0629
Citation: SONG L Q，CHEN W J，CHEN W H，et al. Improvement and application of hybrid strategy-based sparrow search algorithm[J]. Journal of Beijing University of Aeronautics and Astronautics，2023，49（8）：2187-2199 （in Chinese） doi: 10.13700/j.bh.1001-5965.2021.0629
shu

基于混合策略的麻雀搜索算法改进及应用

doi: 10.13700/j.bh.1001-5965.2021.0629
  • 1.

    安徽大学 电气工程与自动化学院，合肥 230601

  • 2.

    北京航空航天大学 自动化科学与电气工程学院，北京 100191

基金项目: 国家自然科学基金(51975002)
详细信息
    通讯作者:

    E-mail：wjchen@ahu.edu.cn

  • 中图分类号: TP301.6

Improvement and application of hybrid strategy-based sparrow search algorithm

  • 1.

    School of Electrical Engineering and Automation，Anhui University，Hefei 230601，China

  • 2.

    School of Automation Science and Electrical Engineering，Beihang University，Beijing 100191，China

Funds: National Natural Science Foundation of China (51975002)
More Information

    摘要
  • 摘要:

    针对麻雀搜索算法(SSA)搜索精度不高、全局搜索能力不强、收敛速度慢和易于陷入局部最优等问题，提出了一种基于混合策略的麻雀搜索算法(HSSA)。采用改进的Circle混沌映射初始化种群，提高种群多样性；结合樽海鞘群算法改进发现者的搜索公式，提高算法迭代前期的全局搜索能力和范围；在加入者的搜索公式中引入自适应步长因子，提高算法的局部搜索能力和收敛速度；通过镜像选择机制，提升每次迭代后的个体质量，提高算法的寻优精度和寻优速度；在位置更新处加入模拟退火机制，帮助算法跳出局部最优。利用8种测试函数进行测试，结果表明，改进算法比SSA有更好的寻优性能。将改进前后算法与极限学习机结合进行实验，人体表面肌电信号数据集的分类预测精度从80.17%提高到90.87%，证实了改进算法的可行性和良好性能。

     

    Abstract:

    Aiming at solving the problems in the original sparrow search algorithm (SSA), such as low search accuracy, weak global search ability, slow convergence speed and easy tendency to fall into local optimum, a hybrid strategy-based sparrow search algorithm (HSSA) is proposed. First, an improved Circle chaotic map was used to initialize the population and increase the diversity of the population. Then, the salp swarm algorithm was integrated into the search formula of the discoverers to enhance its global search ability and scope in the early stage of iteration, and an adaptive step size factor was introduced into the search formula of the participants to improve the local search ability and convergence speed of the algorithm. Next, the mirror selection mechanism was applied to boost the individual quality after each iteration, thereby improving the search accuracy and speed of the algorithm. Finally, a simulated annealing mechanism was added to the location update, thus enabling the algorithm effectively to jump out of local optimum. The test results of eight functions show that the HSSA has better optimization performance than SSA. By combining the improved algorithm and the extreme learning machine, the classification and prediction accuracy of human surface electromyogram signal data increased from 80.17% to 90.87%, which proves the feasibility and good performance of the improved algorithm.

     

    • HTML全文

  • 图 1  Circle混沌映射分布

    Figure 1.  Distribution of Circle chaotic mapping

    下载: 全尺寸图片 幻灯片

    图 2  改进Circle混沌映射分布

    Figure 2.  Distribution of improved Circle chaotic mapping

    下载: 全尺寸图片 幻灯片

    图 3  Circle混沌映射分布直方图

    Figure 3.  Distribution histogram of Circle chaotic mapping

    下载: 全尺寸图片 幻灯片

    图 4  改进Circle混沌映射分布直方图

    Figure 4.  Distribution histogram of improved Circle chaotic mapping

    下载: 全尺寸图片 幻灯片

    图 5  改进前发现者位置更新

    Figure 5.  Location update of discoverer before improvement

    下载: 全尺寸图片 幻灯片

    图 6  改进后发现者位置更新

    Figure 6.  Location update of discoverer after improvement

    下载: 全尺寸图片 幻灯片

    图 7  镜像选择前种群个体位置

    Figure 7.  Individual position of population before mirror selection

    下载: 全尺寸图片 幻灯片

    图 8  镜像选择后种群个体位置

    Figure 8.  Individual position of population after mirror selection

    下载: 全尺寸图片 幻灯片

    图 9  函数收敛曲线

    Figure 9.  Function convergence curves

    下载: 全尺寸图片 幻灯片

    图 10  分类预测结果

    Figure 10.  Classification and prediction results

    下载: 全尺寸图片 幻灯片

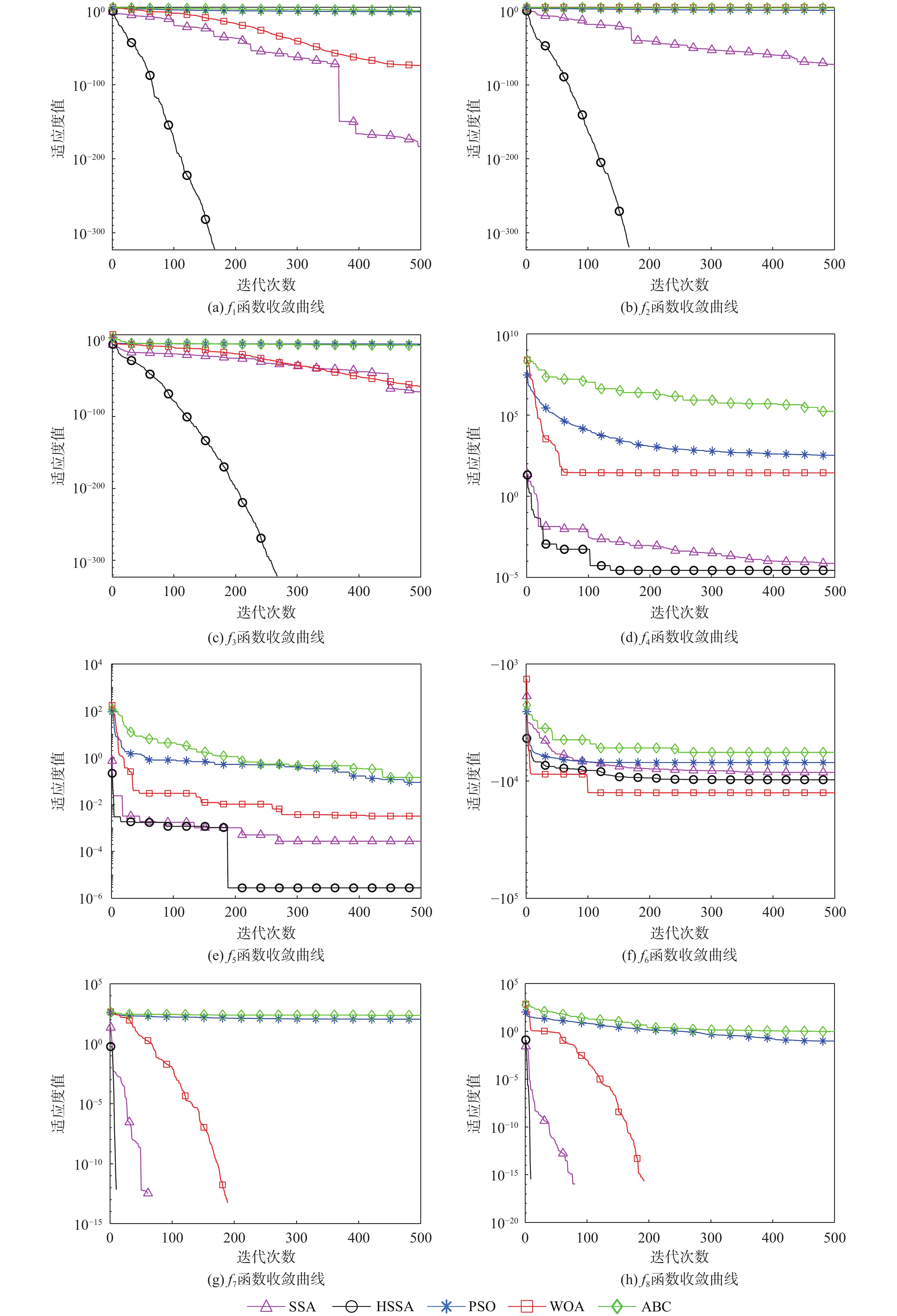
    表  1  基准测试函数

    Table  1.   Benchmark function

    函数公式维度搜索范围最优值
    Sphere${f_1}(x) = \displaystyle\sum\limits_{i = 1}^n {x_i^2}$30[−100,100]0
    Schwefel 1.2${f_2}(x) = {\displaystyle\sum\limits_{i = 1}^n {\left(\displaystyle\sum\limits_{j = 1}^i {x_j}\right) } ^2}$30[−100,100]0
    Schwefel 2.22${f_3}(x) = \displaystyle\sum\limits_{i = 1}^n {\left| { {x_i} } \right|} + \displaystyle\prod\limits_{i = 1}^n {\left| { {x_i} } \right|}$30[−10,10]0
    Rosenbrock${f_4}(x) = \displaystyle\sum\limits_{i = 1}^{n - 1} {[100{ {({x_{i + 1} } - x_i^2)}^2} + { {({x_i} - 1)}^2}]}$30[−30,30]0
    Quartic${f_5}(x) = \displaystyle\sum\limits_{i = 1}^n {ix_i^4} + {\text{random} }[0,1)$30[−1.28,1.28]0
    Schwefel 2.26${f_6}(x) = \displaystyle\sum\limits_{i = 1}^n - {x_i}\sin \left(\sqrt {\left| { {x_i} } \right|} \right)$30[−500,500]−418.9829D
    Rastrigin${f_7}(x) = \displaystyle\sum\limits_{i = 1}^n {[x_i^2} - 10\cos (2{\text{π}} {x_i}) + 10]$30[−5.12,5.12]0
    Griewank${f_8}(x) = \dfrac{1}{ {4\;000} }\displaystyle\sum\limits_{i = 1}^n x_i^2 - \displaystyle\prod\limits_{i = 1}^n \cos \left(\frac{ { {x_i} } }{ {\sqrt i } } \right) + 1$30[−600,600]0
    下载: 导出CSV

    表  2  算法参数设置

    Table  2.   Algorithm parameter setting

    算法参数设置
    PSOw=0.9,${b_1}$=1.49445,${b_2}$=1.49445
    WOAa∈[0,2],并从2线性下降
    ABClimit=round(0.6dim·SN),α=1
    SSANPD=0.2Npop,NSD=0.2Npop,NST=0.8
    HSSANPD=0.2Npop,NSD=0.2Npop,NST=0.8
    　注：w为速度惯帧因子，b1为自我学习因子，b2为群体学习因子，a为系数向量参数，α为加速系数最大值，NPD为发现群体数量，NSD为警戒者群体数量，Npop为麻雀种群总体数量，NST为安全值。
    下载: 导出CSV

    表  3  不同算法性能比较

    Table  3.   Different algorithm performance comparison

    算法f1最优值f1平均值f1标准差f2最优值f2平均值f2标准差
    30维度80维度30维度80维度30维度80维度30维度80维度30维度80维度30维度80维度
    PSO7.8266×10−21.2812×101.7368×10−12.4010×105.7849×10−26.51491.0177×102.5212×1032.3679×104.7073×1031.1637×101.8037×103
    WOA2.1712×10−872.5127×10−832.7104×10−738.0992×10−737.5627×10−732.9123×10−731.4619×1043.0385×1054.4221×1046.3370×1051.4604×1041.4869×105
    ABC1.01033.3429×1043.04944.1617×1041.21614.2347×1032.3674×1042.2500×1053.3160×1042.8599×1054.3822×1032.4257×104
    SSA03.4278×10−2857.5229×10−647.1855×10−624.1205×10−633.9356×10−61004.5283×10−532.6559×10−501.8261×10−521.1838×10−49
    HSSA000000000000
    算法f3最优值f3平均值f3标准差f4最优值f4平均值f4标准差
    30维度80维度30维度80维度30维度80维度30维度80维度30维度80维度30维度80维度
    PSO1.54523.4350×107.63697.1998×105.05404.4183×103.6179×103.2169×1031.9818×1021.0255×1041.4541×1027.8634×103
    WOA4.8362×10−605.7468×10−588.9308×10−528.7071×10−502.6744×10−513.2665×10−492.7245×107.7556×102.8045×107.8265×104.3436×10−12.5962×10−1
    ABC7.7434×10−21.8097×1021.7277×10−12.5012×1066.7687×10−26.1799×1063.5734×1041.2974×1071.1895×1051.9164×1078.3608×1042.6806×106
    SSA002.2314×10−347.4340×10−341.2221×10−332.9924×10−332.7287×10−71.2367×10−61.2243×10−44.0708×10−42.7915×10−49.8010×10−4
    HSSA0000003.0903×10−91.3311×10−91.8279×10−59.5380×10−52.8747×10−51.8788×10−4
    算法f5最优值f5平均值f5标准差f6最优值f6平均值f6标准差
    30维度80维度30维度80维度30维度80维度30维度80维度30维度80维度30维度80维度
    PSO1.1184×10−21.7785×10−22.4244×10−11.4840×106.7847×10−13.2151×10−8.0468×103−2.1345×104−6.9903×103−1.8001×1046.8632×1021.5812×103
    WOA6.3498×10−51.6010×10−43.1861×10−35.5515×10−33.4663×10−36.8377×10−3−1.2569×104−3.3513×104−1.0796×104−2.7519×1041.6727×1044.4798×103
    ABC6.6656×10−27.9981×102.4620×10−11.8093×1026.5205×10−23.9405×10−6.1723×103−1.0288×104−5.0231×103−8.4095×1033.8759×1027.5729×102
    SSA2.9224×10−57.4100×10−56.8172×10−46.3589×10−45.2774×10−45.4482×10−4−8.9290×103−2.1726×104−7.8563×103−1.9349×1046.2220×1021.3935×103
    HSSA1.6312×10−61.1632×10−67.2701×10−58.0308×10−56.0700×10−56.6827×10−5−1.1463×104−2.6134×104−8.6946×103−2.3089×1049.4777×1022.0416×103
    算法f7最优值f7平均值f7标准差f8最优值f8平均值f8标准差
    30维度80维度30维度80维度30维度80维度30维度80维度30维度80维度30维度80维度
    PSO4.6017×102.9785×1027.4888×103.6656×1022.0656×104.3011×103.0326×10−21.95141.2749×10−16.99886.3700×10−23.0342
    WOA0001.1369×10−1504.5768×10−15006.5410×10−38.9356×10−33.5826×10−24.8943×10−2
    ABC1.9322×1026.4124×1028.3605×1022.3044×1021.3884×104.1130×106.5856×10−12.9809×1029.8984×10−13.5744×1027.4134×10−23.5119×10
    SSA000000000000
    HSSA000000000000
    下载: 导出CSV

    表  4  Wilcoxon秩和检验P值

    Table  4.   P values for Wilcoxon rank-sum test

    函数解维度为30时解维度为80时
    PSOWOAABCSSAPSOWOAABCSSA
    ${f_1}$1.2118×10−121.2118×10−121.2118×10−121.2118×10−121.2118×10−121.2118×10−121.2118×10−121.2118×10−12
    ${f_2}$1.2118×10−121.2118×10−121.2118×10−121.2118×10−121.2118×10−121.2118×10−121.2118×10−121.2118×10−12
    ${f_3}$1.2118×10−121.2118×10−121.2118×10−121.2118×10−121.2118×10−121.2118×10−121.2118×10−121.2118×10−12
    ${f_4}$3.0199×10−113.0199×10−113.0199×10−114.0772×10−113.0199×10−113.0199×10−113.0199×10−116.0658×10−11
    $ {f_5} $3.0199×10−113.0199×10−113.0199×10−113.0199×10−113.0199×10−113.0199×10−113.0199×10−113.0199×10−11
    ${f_6}$3.0199×10−113.0199×10−113.0199×10−117.3891×10−113.3384×10−113.0199×10−113.0199×10−115.5329×10−8
    ${f_7}$1.2118×10−123.2801×10−71.2118×10−12−1.2118×10−121.4000×10−41.2118×10−12−
    ${f_8}$1.2118×10−121.9457×10−91.2118×10−12−1.2118×10−121.4552×10−41.2118×10−12−
    下载: 导出CSV

    表  5  不同改进SSA算法性能比较

    Table  5.   Performance comparison of different improved SSA

    算法f1f2f3f4
    最优值平均值标准差最优值平均值标准差最优值平均值标准差最优值平均值标准差
    ISSA01.13×10−814.42×10−8106.28×10−931.49×10−9209.25×10−493.20×10−487.85×10−79.16×10−61.44×10−5
    HSSA0000000003.17×10−114.37×10−66.98×10−6
    算法f5f6f7f8
    最优值平均值标准差最优值平均值标准差最优值平均值标准差最优值平均值标准差
    ISSA2.11×10−53.20×10−42.13×10−4−1.26×104−1.26×104 2.70×10−1000000
    HSSA2.26×10−65.04×10−54.45×10−5−1.14×104−8.87×1037.01×102000000
    下载: 导出CSV

    表  6  不同改进策略性能比较

    Table  6.   Performance comparison of different improvement strategies

    算法f1f2
    最优值平均值标准差最优值平均值标准差
    SSA07.5229×10−644.1205×10−6304.5283×10−531.8261×10−52
    FSSA000000
    JSSA01.0968×10−696.0072×10−691.8655×10−2325.6152×10−733.0754×10−72
    ZSSA01.2469×10−756.8296×10−7507.1562×10−613.9196×10−62
    MSSA02.1033×10−741.1520×10−7303.6053×10−531.9747×10−52
    HSSA000000
    算法f3f4
    最优值平均值标准差最优值平均值标准差
    SSA02.2314×10−341.2221×10−332.7287×10−71.2243×10−42.7915×10−4
    FSSA0006.6257×10−82.2162×10−44.1812×10−4
    JSSA4.0143×10−2059.6876×10−355.2114×10−334.4375×10−81.1542×10−42.3480×10−4
    ZSSA01.3695×10−367.5600×10−363.8087×10−81.5027×10−53.7874×10−5
    MSSA01.2196×10−396.6790×10−393.2697×10−87.8910×10−51.5986×10−4
    HSSA0003.0903×10−91.8279×10−52.8747×10−5
    算法f5f6
    最优值平均值标准差最优值平均值标准差
    SSA2.9224×10−56.8172×10−45.2774×10−4−8.9290×103−7.8563×1036.2220×102
    FSSA1.6271×10−52.4741×10−42.2118×10−4−1.0214×104−8.5659×1037.7704×102
    JSSA1.7568×10−54.3131×10−44.5376×10−4−1.0555×104−8.6250×1036.1708×102
    ZSSA8.6875×10−63.0508×10−43.1683×10−4−9.5045×103−8.4983×1038.1482×102
    MSSA4.3844×10−64.1541×10−44.2651×10−4−9.7063×103−8.4040×1037.8980×102
    HSSA1.6312×10−67.2701×10−56.0701×10−5−1.1463×104−8.6946×1039.4777×102
    算法f7f8
    最优值平均值标准差最优值平均值标准差
    SSA000000
    FSSA000000
    JSSA000000
    ZSSA000000
    MSSA000000
    HSSA000000
    下载: 导出CSV

    表  7  动作类别标签

    Table  7.   Label of action category

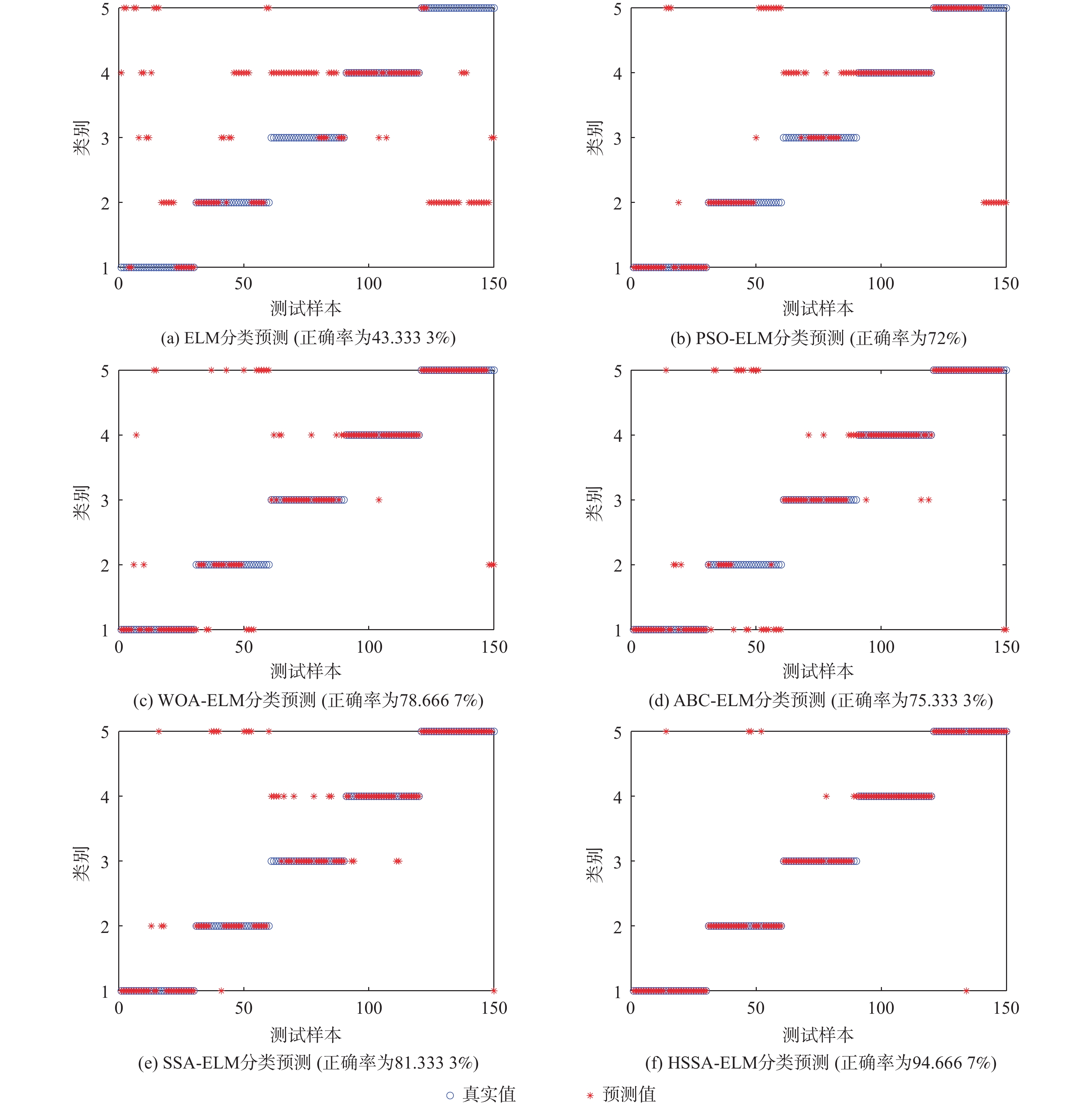
    类别标签人体动作
    1跳跃
    2跑步
    3下蹲
    4站立
    5行走
    下载: 导出CSV

    表  8  算法分类预测精度比较

    Table  8.   Comparison of classification and prediction accuracy of algorithms %

    算法类别最优预测精度平均预测精度
    ELM54.6742.67
    PSO-ELM78.0070.89
    WOA-ELM82.3377.56
    ABC-ELM76.6772.42
    SSA-ELM84.0080.17
    HSSA-ELM96.0090.87
    下载: 导出CSV
    • 参考文献(28)
  • [1] XUE J K, SHEN B. A novel swarm intelligence optimization approach: Sparrow search algorithm[J]. Systems Science & Control Engineering, 2020, 8(1): 22-34.
    [2] WANG D S, TAN D P, LIU L. Particle swarm optimization algorithm: An overview[J]. Soft Computing, 2018, 22(2): 387-408. doi: 10.1007/s00500-016-2474-6
    [3] KARABOGA D, OZTURK C. A novel clustering approach: Artificial bee colony (ABC) algorithm[J]. Applied Soft Computing, 2011, 11(1): 652-657. doi: 10.1016/j.asoc.2009.12.025
    [4] 吕鑫, 慕晓冬, 张钧. 基于改进麻雀搜索算法的多阈值图像分割[J]. 系统工程与电子技术, 2021, 43(2): 318-327. doi: 10.12305/j.issn.1001-506X.2021.02.05

    LV X, MU X D, ZHANG J. Multi-threshold image segmentation based on improved sparrow search algorithm[J]. Systems Engineering and Electronics, 2021, 43(2): 318-327(in Chinese). doi: 10.12305/j.issn.1001-506X.2021.02.05
    [5] 汤安迪, 韩统, 徐登武, 等. 基于混沌麻雀搜索算法的无人机航迹规划方法[J]. 计算机应用, 2021, 41(7): 2128-2136.

    TANG A D, HAN T, XU D W, et al. Path planning method of unmanned aerial vehicle based on chaos sparrow search algorithm[J]. Journal of Computer Applications, 2021, 41(7): 2128-2136(in Chinese).
    [6] 黄敬宇. 融合t分布和Tent混沌映射的麻雀搜索算法研究[D]. 兰州: 兰州大学, 2021.

    HUANG J Y. Research on sparrow search algorithm based on fusion of t distribution and tent chaotic mapping[D]. Lanzhou: Lanzhou University, 2021(in Chinese).
    [7] 徐健, 陈倩倩, 刘秀平. 基于交叉运算的人工蜂群优化BP神经网络的脑电信号分类[J]. 激光与光电子学进展, 2020, 57(21): 244-253.

    XU J, CHEN Q Q, LIU X P. Classification of electroencephalography based on BP neural network optimized by crossover operation of artificial bee colonies[J]. Laser & Optoelectronics Progress, 2020, 57(21): 244-253(in Chinese).
    [8] 刘栋, 魏霞, 王维庆, 等. 基于SSA-ELM的短期风电功率预测[J]. 智慧电力, 2021, 49(6): 53-59.

    LIU D, WEI X, WANG W Q, et al. Short-term wind power prediction based on SSA-ELM[J]. Smart Power, 2021, 49(6): 53-59(in Chinese).
    [9] 蒋艳会, 李峰. 基于混沌粒子群算法的多阈值图像分割[J]. 计算机工程与应用, 2010, 46(10): 175-176. doi: 10.3778/j.issn.1002-8331.2010.10.055

    JIANG Y H, LI F. Multi-threshold method of image segmentation based on chaotic particle swarm optimization algorithm[J]. Computer Engineering and Applications, 2010, 46(10): 175-176(in Chinese). doi: 10.3778/j.issn.1002-8331.2010.10.055
    [10] HUANG G B, WANG D H, LAN Y. Extreme learning machines: a survey[J]. International Journal of Machine Learning and Cybernetics, 2011, 2(2): 107-122. doi: 10.1007/s13042-011-0019-y
    [11] 吕鑫, 慕晓冬, 张钧, 等. 混沌麻雀搜索优化算法[J]. 北京航空航天大学学报, 2021, 47(8): 1712-1720.

    LYU X, MU X D, ZHANG J, et al. Chaos sparrow search optimization algorithm[J]. Journal of Beijing University of Aeronautics and Astronautics, 2021, 47(8): 1712-1720(in Chinese).
    [12] HERBADJI D, DEROUICHE N, BELMEGUENAI A, et al. A tweakable image encryption algorithm using an improved logistic chaotic map[J]. Traitement Du Signal, 2019, 36(5): 407-417. doi: 10.18280/ts.360505
    [13] ARORA S, ANAND P. Chaotic grasshopper optimization algorithm for global optimization[J]. Neural Computing and Applications, 2019, 31(8): 4385-4405. doi: 10.1007/s00521-018-3343-2
    [14] 张达敏, 徐航, 王依柔, 等. 嵌入Circle映射和逐维小孔成像反向学习的鲸鱼优化算法[J]. 控制与决策, 2021, 36(5): 1173-1180.

    ZHANG D M, XU H, WANG Y R, et al. Whale optimization algorithm for embedded Circle mapping and onedimensional oppositional learning based small hole imaging[J]. Control and Decision, 2021, 36(5): 1173-1180(in Chinese).
    [15] MIRJALILI S, GANDOMI A H, MIRJALILI S Z, et al. Salp swarm algorithm: A bio-inspired optimizer for engineering design problems[J]. Advances in Engineering Software, 2017, 114: 163-191. doi: 10.1016/j.advengsoft.2017.07.002
    [16] LI J N, LE M L. Improved whale optimization algorithm based on mirror selection[J]. Transactions of Nanjing University of Aeronautics and Astronautics, 2020, 37(S): 115-123.
    [17] TIZHOOSH H R. Opposition-based learning: a new scheme for machine intelligence[C]//International Conference on Computational Intelligence for Modelling, Control and Automation and International Conference on Intelligent Agents, Web Technologies and Internet Commerce (CIMCA-IAWTIC’06). Piscataway: IEEE Press, 2006: 695-701.
    [18] SUMAN B, KUMAR P. A survey of simulated annealing as a tool for single and multiobjective optimization[J]. Journal of the Operational Research Society, 2006, 57(10): 1143-1160. doi: 10.1057/palgrave.jors.2602068
    [19] SHADRAVAN S, NAJI H R, BARDSIRI V K. The sailfish optimizer: A novel nature-inspired metaheuristic algorithm for solving constrained engineering optimization problems[J]. Engineering Applications of Artificial Intelligence, 2019, 80: 20-34. doi: 10.1016/j.engappai.2019.01.001
    [20] MIRJALILI S, LEWIS A. The whale optimization algorithm[J]. Advances in Engineering Software, 2016, 95: 51-67. doi: 10.1016/j.advengsoft.2016.01.008
    [21] 黄海燕, 彭虎, 邓长寿, 等. 均匀局部搜索和高斯变异的布谷鸟搜索算法[J]. 小型微型计算机系统, 2018, 39(7): 1451-1458. doi: 10.3969/j.issn.1000-1220.2018.07.015

    HUANG H Y, PENG H, DENG C S, et al. Cuckoo search algorithm of uniform local search and Gauss mutation[J]. Journal of Chinese Computer Systems, 2018, 39(7): 1451-1458(in Chinese). doi: 10.3969/j.issn.1000-1220.2018.07.015
    [22] 付华, 刘昊. 多策略融合的改进麻雀搜索算法及其应用[J]. 控制与决策, 2022, 37(1): 87-96. doi: 10.13195/j.kzyjc.2021.0582

    FU H, LIU H. Improved sparrow search algorithm with multi-strategy integration and its application[J]. Control and Decision, 2022, 37(1): 87-96(in Chinese). doi: 10.13195/j.kzyjc.2021.0582
    [23] 刘小娟, 王联国. 一种基于差分进化的正弦余弦算法[J]. 工程科学学报, 2020, 42(12): 1674-1684.

    LIU X J, WANG L G. A sine cosine algorithm based on differential evolution[J]. Chinese Journal of Engineering, 2020, 42(12): 1674-1684(in Chinese).
    [24] 唐延强, 李成海, 宋亚飞, 等. 自适应变异麻雀搜索优化算法[J]. 北京航空航天大学学报, 2023, 49(3): 681-692. doi: 10.13700/j.bh.1001-5965.2021.0282

    TANG Y Q, LI C H, SOMG Y F, et al. Adaptive mutation sparrow search optimization algorithm[J]. Journal of Beijing University of Aeronautics and Astronautics, 2023, 49(3): 681-692(in Chinese). doi: 10.13700/j.bh.1001-5965.2021.0282
    [25] 毛清华, 张强. 融合柯西变异和反向学习的改进麻雀算法[J]. 计算机科学与探索, 2021, 15(6): 1155-1164. doi: 10.3778/j.issn.1673-9418.2010032

    MAO Q H, ZHANG Q. Improved sparrow algorithm combining Cauchy mutation and opposition-based learning[J]. Journal of Frontiers of Computer Science and Technology, 2021, 15(6): 1155-1164(in Chinese). doi: 10.3778/j.issn.1673-9418.2010032
    [26] 张强, 李盼池, 王梅. 基于自适应进化策略的人工蜂群优化算法[J]. 电子科技大学学报, 2019, 48(4): 560-566. doi: 10.3969/j.issn.1001-0548.2019.04.013

    ZHANG Q, LI P C, WANG M. Artificial bee colony optimization algorithm based on adaptive evolution strategy[J]. Journal of University of Electronic Science and Technology of China, 2019, 48(4): 560-566(in Chinese). doi: 10.3969/j.issn.1001-0548.2019.04.013
    [27] 佟丽娜, 侯增广, 彭亮, 等. 基于多路sEMG时序分析的人体运动模式识别方法[J]. 自动化学报, 2014, 40(5): 810-821.

    TONG L N, HOU Z G, PENG L, et al. Multi-channel sEMG time series analysis based human motion recognition method[J]. Acta Automatica Sinica, 2014, 40(5): 810-821(in Chinese).
    [28] 刘冰, 李宁, 于鹏, 等. 上肢康复外骨骼机器人控制方法进展研究[J]. 电子科技大学学报, 2020, 49(5): 643-651. doi: 10.12178/1001-0548.2020212

    LIU B, LI N, YU P, et al. Research on the control methods of upper limb rehabilitation exoskeleton robot[J]. Journal of University of Electronic Science and Technology of China, 2020, 49(5): 643-651(in Chinese). doi: 10.12178/1001-0548.2020212
    • 相关文章
    • 施引文献
  • 资源附件(0)
  • 加载中
WeChat 点击查看大图
图(10) / 表(8)
计量
  • 文章访问数:  412
  • HTML全文浏览量:  39
  • PDF下载量:  47
  • 被引次数: 0
出版历程
  • 收稿日期:  2021-10-23
  • 录用日期:  2021-12-10
  • 网络出版日期:  2022-01-25
  • 整期出版日期:  2023-08-31

目录

    /

    返回文章
    返回
    常见问答

    版权所有 © 《北京航空航天大学学报》编辑部

    通讯地址：北京市海淀区学院路37号 《北京航空航天大学学报》编辑部　 邮编：100191 邮箱：jbuaa@buaa.edu.cn

    本系统由 北京仁和汇智信息技术有限公司 开发    百度统计