-
摘要:
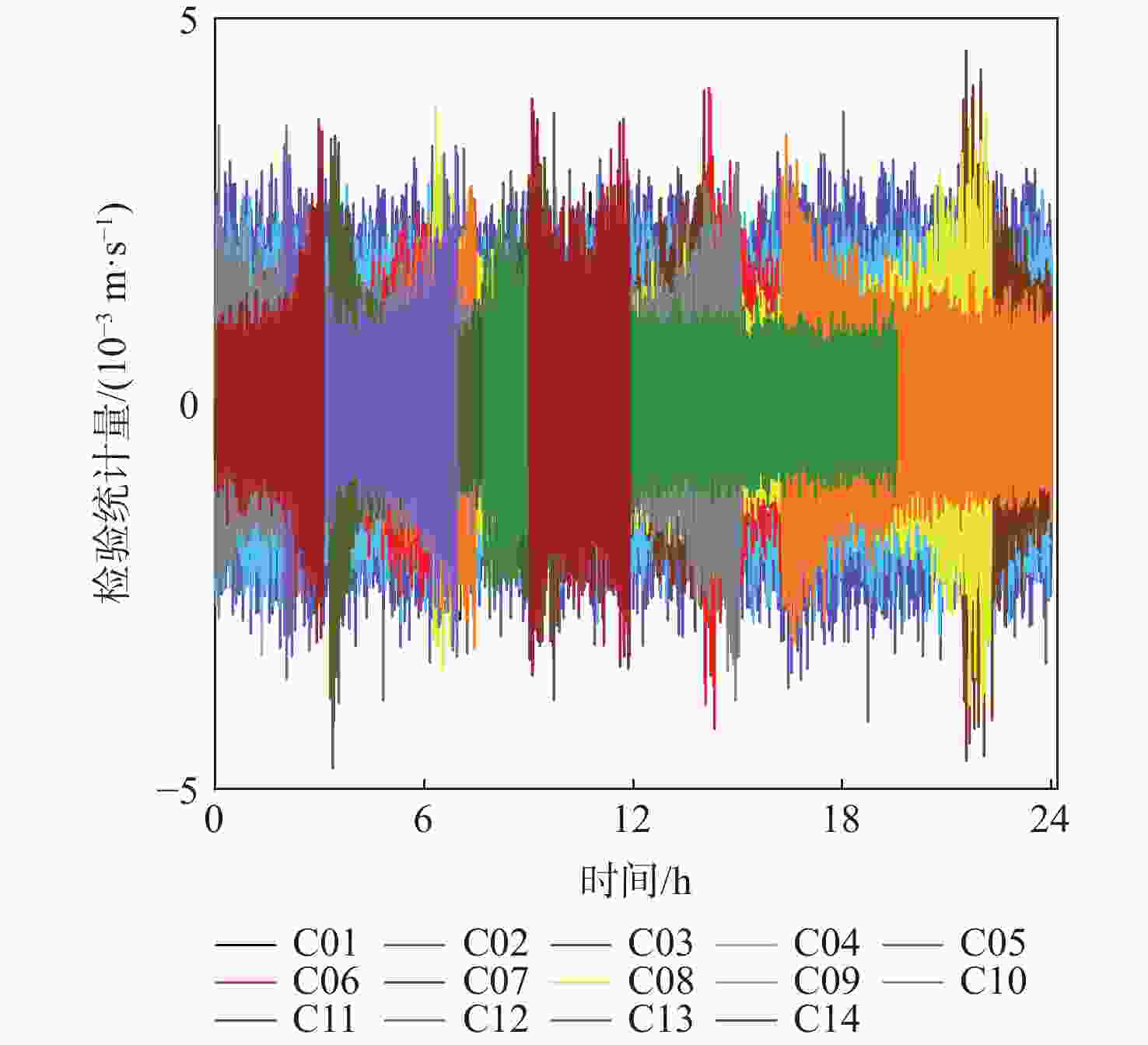
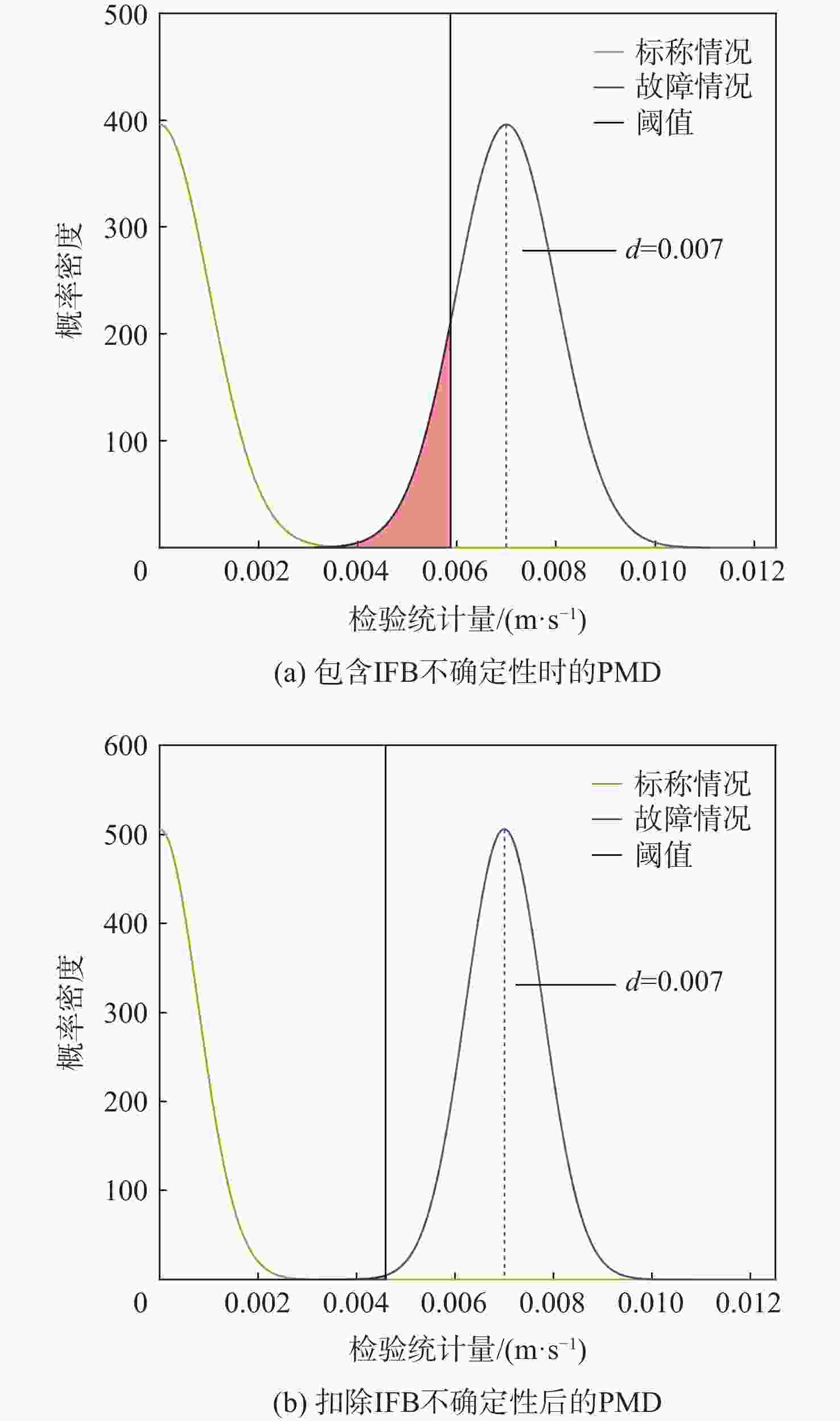
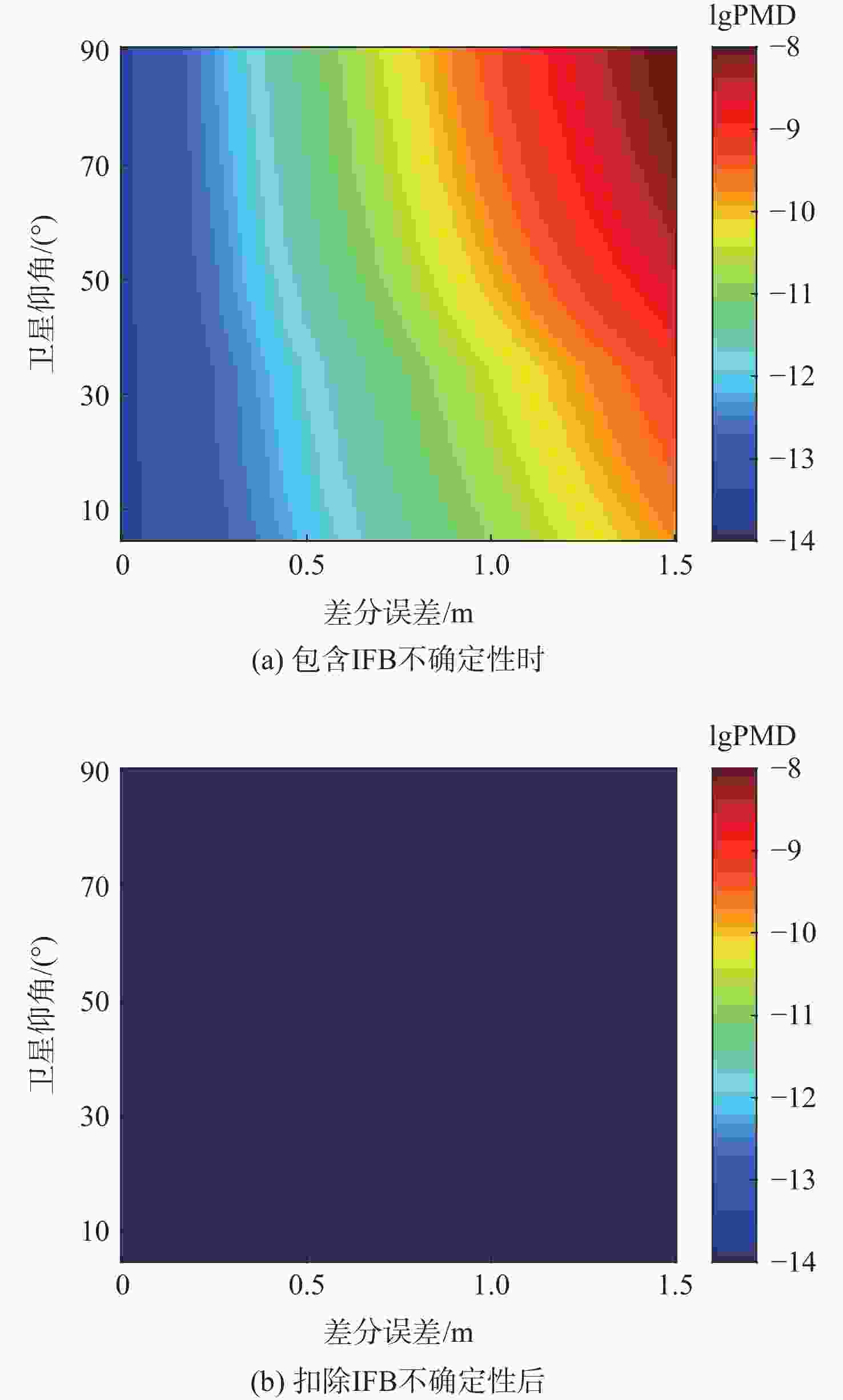
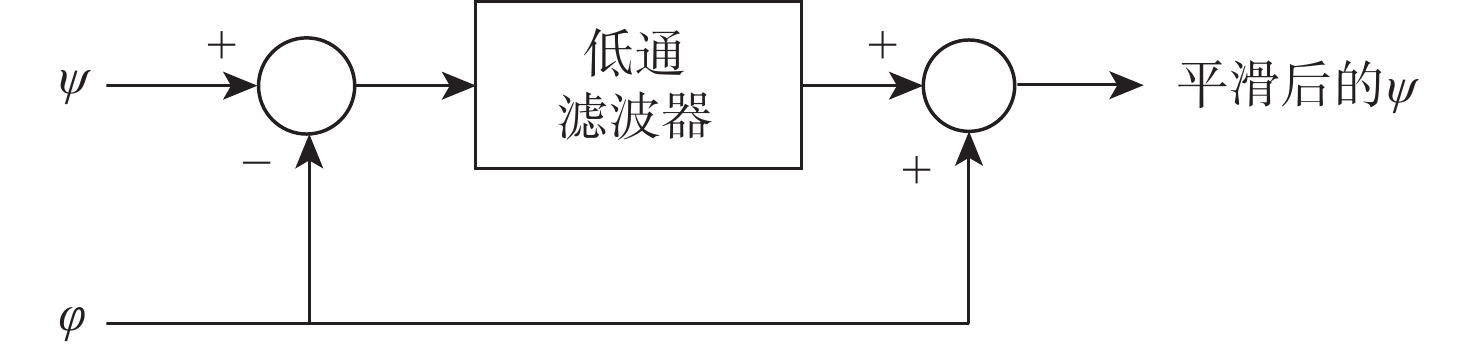
码载分歧（CCD）监测器是卫星导航地基增强系统（GBAS）引入的完好性监测器之一，用于监测码伪距与载波相位观测值之间的不一致性。双频平滑技术的引入改变了CCD监测器的检验统计量等参数，进而影响了监测性能。针对双频GBAS中存在的频间偏差（IFB），基于北斗双频观测数据，分析IFB不确定性对于双频码载分歧监测性能的影响。研究结果表明:在IFB不确定性的影响下，监测器的阈值增大了26.1%，导致其在发生CCD故障情况下的漏检率显著增大，最小可检测故障值增大了26.9%，监测器的灵敏度降低；最坏情况下系统完好性损失概率从低于10−14增大到接近10−8，同时机载端为满足漏检率性能安全要求所引入的延迟值更大，导致CCD监测器的故障响应变慢，双频GBAS的完好性受到影响。
Abstract:Code carrier divergence (CCD) monitor is one of the integrity monitors introduced by ground-based augmentation systems (GBAS), which is used to monitor the inconsistency between code pseudorange and carrier phase observations. Dual-frequency smoothing technology changes the test statistics and other parameters of CCD monitor, which affect the monitoring performance. Considering the inter-frequency bias (IFB) introduced in dual-frequency GBAS, the impact of IFB uncertainty on the dual-frequency CCD monitoring is analyzed based on the dual-frequency observation data of BDS B1I and B3I signals. The results show that under the influence of IFB uncertainty, the threshold of the monitor increases by 26.1%, resulting in a significant increase of the probability of missed detection (PMD) in the case of CCD fault. And the minimum detectable fault increases by 26.9%, which means a decrease in the sensitivity of the monitor. Meanwhile, the probability of the loss of integrity in the worst case increases from less than 10−14 to nearly 10−8, and the delay introduced by the airborne to meet the PMD requirement is larger, resulting in a slower response of CCD monitor and impacts the integrity of dual-frequency GBAS.
-
图 10 监测器性能安全验证（${\mathit{t}}_{{{\rm{delay}}}}$=0）
Figure 10. Monitor performance safety verification (${\mathit{t}}_{\rm{delay}}$=0)
图 11 监测器性能安全验证（${\mathit{t}}_{\rm{delay}}$=50 s）
Figure 11. Monitor performance safety verification (${\mathit{t}}_{\rm{delay}}$=50 s)
表 1 监测阈值比较
Table 1. Comparison of monitoring threshold
仿真试验场景 原始标准差/
(10−4 m·s−1)包络标准差/
(10−4 m·s−1)阈值/
(10−4 m·s−1)包含IFB不确定性 6.22 10 58 扣除IFB不确定性 4.17 7.88 46 
下载: 导出CSV
表 2 不同监测阈值对应的漏检率对比
Table 2. Comparison of PMD related to different monitoring thresholds
监测阈值/(m·s−1) ${\mathrm{P}\mathrm{M}\mathrm{D}}_{1} $ ${\mathrm{P}\mathrm{M}\mathrm{D}}_{2} $ 7×10−5 11.68 0.12 8×10−5 1.39 7.99×10−4 9×10−7 6.87 1.18×10−4 1×10−7 1.33 3.62×10−7 1.1×10−10 9.96 2.29×10−8
下载: 导出CSV
表 3 CCD故障误差分析的仿真条件
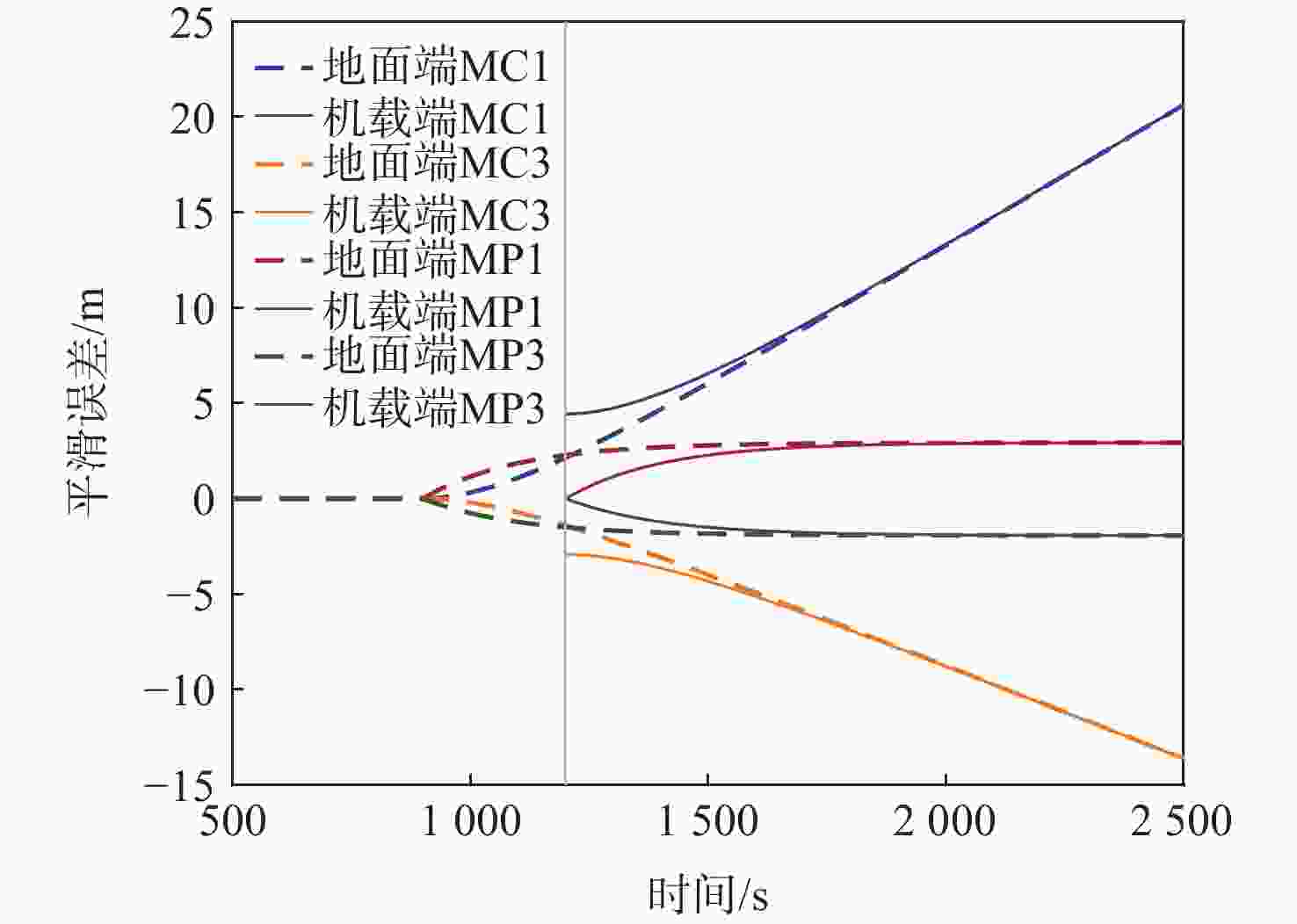
Table 3. Simulation conditions of CCD fault error analysis
参数 数值 CCD监测器滤波时间常数$ {\tau }_{\mathrm{m}} $/s 30 Hatch滤波的时间常数$ \tau $/s 100 CCD故障发生的时刻$ {t}_{\mathrm{f}} $/s 450 地面双频CCD监测器初始化时刻$ {t}_{\mathrm{g},0} $/s 0 机载双频CCD监测器初始化时刻$ {t}_{\mathrm{a},0} $/s 600 从机载滤波器初始化到将测量值
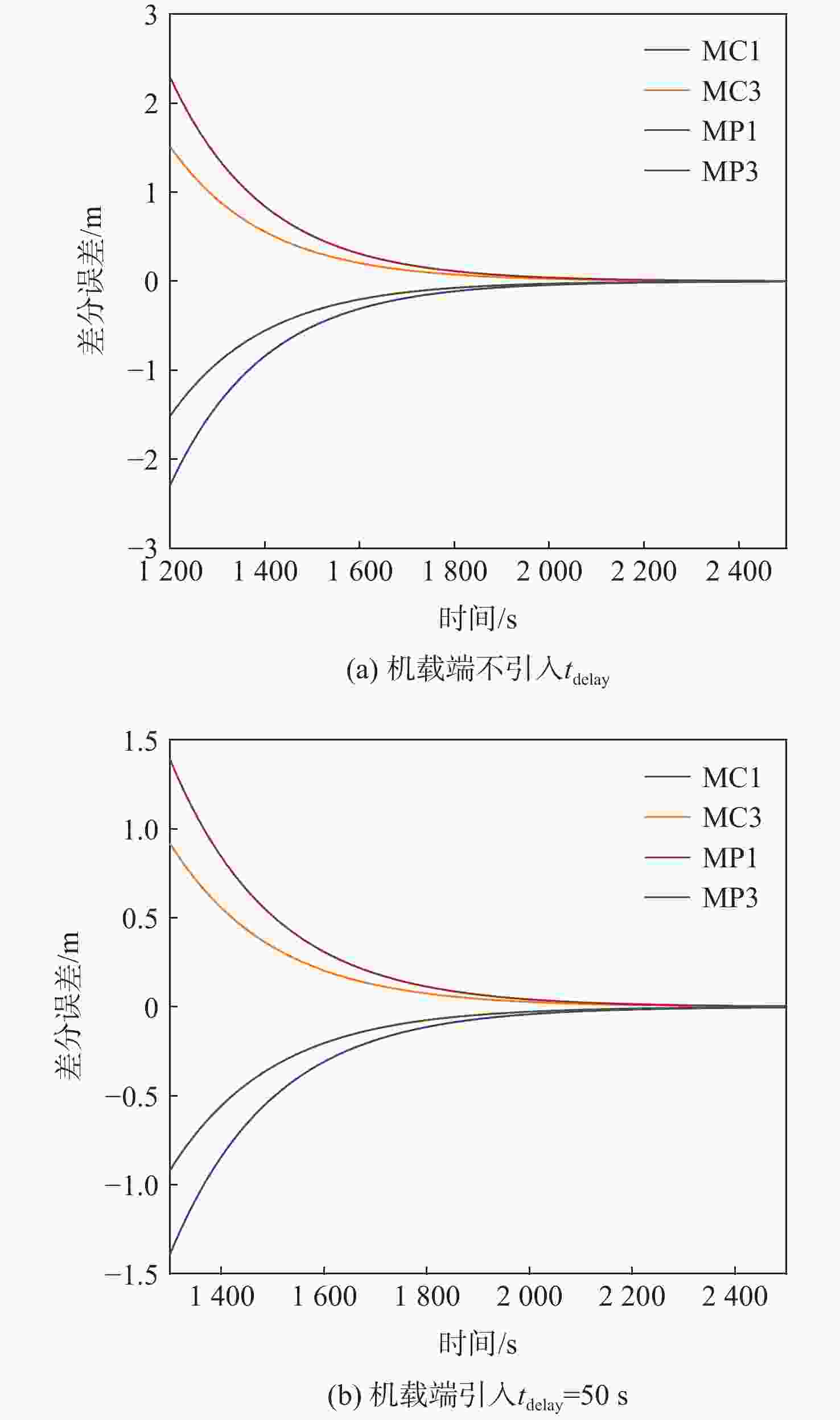
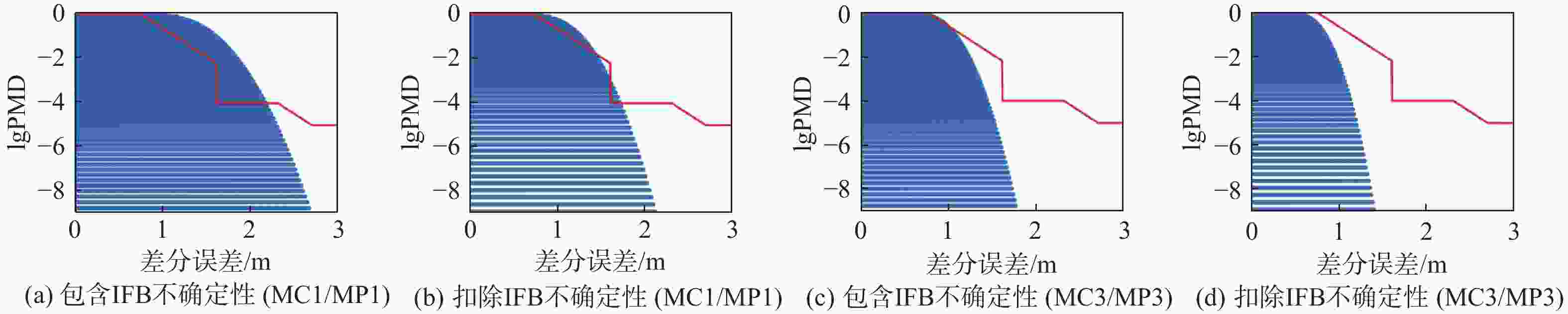
应用于定位解的时间延迟$ {t}_{\mathrm{d}\mathrm{e}\mathrm{l}\mathrm{a}\mathrm{y}} $/s0, 50 地面端延迟$ {\tau }_{\mathrm{G}} $/s 1.5 数据及完好性信息的更新率$ {f}_{\mathrm{C}} $/Hz 2 仿真时间$ t $/s [0∶0.5∶1800] 故障$ d $/( m·s−1) 0.001
下载: 导出CSV
表 4 为满足PMD要求在机载端引入的最小$ {\mathit{t}}_{\mathbf{d}\mathbf{e}\mathbf{l}\mathbf{a}\mathbf{y}} $值
Table 4. Minimum $ {\mathit{t}}_{\mathbf{d}\mathbf{e}\mathbf{l}\mathbf{a}\mathbf{y}} $ introduced in airborn to meet PMD requirements
故障模式 包含IFB不确定性/s 扣除IFB不确定性/s MC1 (MP1) 50 22 MC3 (MP3) 6 0
下载: 导出CSV
-
[1] 谢钢. GPS原理与接收机设计[M]. 北京: 电子工业出版社, 2017.XIE G. Principles of GPS and receiver design[M]. Beijing: Publishing House of Electronics Industry, 2017 (in Chinese). [2] Radio Technical Commission for Aeronautics (RTCA) Special Committee 159 (SC-159). Minimum operational performance standards for GPS local area augmentation system airborne equipment: DO-253C[S]. Washington, D. C. : RTCA, 2008. [3] Radio Technical Commission for Aeronautics (RTCA) Special Committee 159 (SC-159). Minimum operational performance standards for GPS local area augmentation system airborne Equipment: DO-253D[S]. Washington, D. C. : RTCA, 2017. [4] International Civil Aviation Organization (ICAO) Navigation Systems Panel (NSP). GBAS CAT II/III development baseline SARPs[S]. Montreal: ICAO, 2010. [5] XIE G. Optimal on-airport monitoring of the integrity of GPS-based landing systems[D]. Stanford: Stanford University, 2004. [6] SIMILI D V, PERVAN B. Code-carrier divergence monitoring for the GPS local area augmentation system[C]// 2006 IEEE/ION Position, Location, and Navigation Symposium. Piscataway: IEEE Press, 2006. [7] European Organization for Civil Aviation Equipment (EUROCAE). Minimum operational performance specification for global navigation satellite ground based augmentation system ground equipment to support category I operations: ED-114A[S]. SaintDenis: EUROCAE, 2013. [8] KONNO H. Dual-frequency smoothing for CAT III LAAS performance assessment considering ionosphere anomalies[C]//Proceedings of the 20th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS 2007). Fort Worth: The Institute of Navigation, 2007: 424-437. [9] SUNG Y T, LIN Y W, YEH S J, et al. A dual-frequency ground based augmentation system prototype for GPS and BDS[C]// Proceedings of the 32nd International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS 2019). Fort Worth: The Institute of Navigation, 2019: 628-636. [10] CIRCIU M S, MEURER M, FELUX M, et al. Evaluation of GPS L5 and Galileo E1 and E5a performance for future multifrequency and multiconstellation GBAS[J]. Navigation, 2017, 64(1): 149-163. doi: 10.1002/navi.181 [11] FELUX M, CIRCIU M, BELABBAS B, et al. Concept for a dual frequency dual constellation GBAS[C]// Proceedings of the 28th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS 2015). Fort Worth: The Institute of Navigation, 2015: 1519-1525. [12] KONNO H, PULLEN S, RIFE J, et al. Ionosphere monitoring methodology for hybrid dual-frequency LAAS[C]// Proceedings of the 19th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS 2006). Fort Worth: The Institute of Navigation, 2006: 409-424. [13] KONNO H, PULLEN S, RIFE J, et al. Evaluation of two types of dual-frequency differential GPS techniques under anomalous ionosphere conditions[C]// Proceedings of the 2006 National Technical Meeting of the Institute of Navigation. Fort Worth: The Institute of Navigation, 2006: 735-747. [14] JIANG Y P, MILNER C, MACABIAU C. Code carrier divergence monitoring for dual-frequency GBAS[J]. GPS Solutions, 2017, 21(2): 769-781. doi: 10.1007/s10291-016-0567-4 [15] BAO Y D, LI J, LIU H N. Extraction and analysis of DCB daily variation based on single station dual-frequency observations[C]//Proceedings of the 9th China Satellite Navigation Academic Annual Conference. Berlin: Springer, 2018. [16] MA G, MARUYAMA T. Derivation of TEC and estimation of instrumental biases from GEONET in Japan[J]. Annales Geophysicae, 2003, 21(10): 2083-2093. doi: 10.5194/angeo-21-2083-2003 [17] HOLASCHUTZ D, BISHOP R H, HARRIS R B, et al. Inter-frequency bias estimation for the GPS monitor station network[C]// International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS 2008). Savannah: The Institute of Navigation, 2008: 2405-2415. [18] LI Z S, YUAN Y B, LI H, et al. Two-step method for the determination of the differential code biases of COMPASS satellites[J]. Journal of Geodesy, 2012, 86(11): 1059-1076. doi: 10.1007/s00190-012-0565-4 [19] LIU Y H, LI X H, ZHANG H J, et al. Calculation and accuracy evaluation of TGD from IFB for BDS[J]. GPS Solutions, 2016, 20(3): 461-471. doi: 10.1007/s10291-015-0454-4 [20] MURPHY T, GEREN P, PANKASKIE T. GPS antenna group delay variation induced errors in a GNSS based precision approach and landing systems[C]// 20th International Technical Meeting of the Satellite Division. Fort Worth: The Institute of Navigation, 2007: 2974-2989. [21] BEER S, WANNINGER L, HEBELBANTH A. Estimation of absolute GNSS satellite antenna group delay variations based on those of absolute receiver antenna group delays[J]. GPS Solutions, 2021, 25(3): 1-10. [22] THOMAS Z. A new evaluation of maximum allowable errors and missed detection probabilities for LAAS ranging source monitors[C]// Proceedings of the 58th Annual Meeting of The Institute of Navigation and CIGTF 21st Guidance Test Symposium (2002). Fort Worth: The Institute of Navigation, 2002: 187-194. -
下载:
点击查看大图
计量
- 文章访问数: 791
- HTML全文浏览量: 48
- PDF下载量: 9
- 被引次数: 0
