Non-probabilistic reliability analysis method for propellent tank with crack defect
-
摘要:
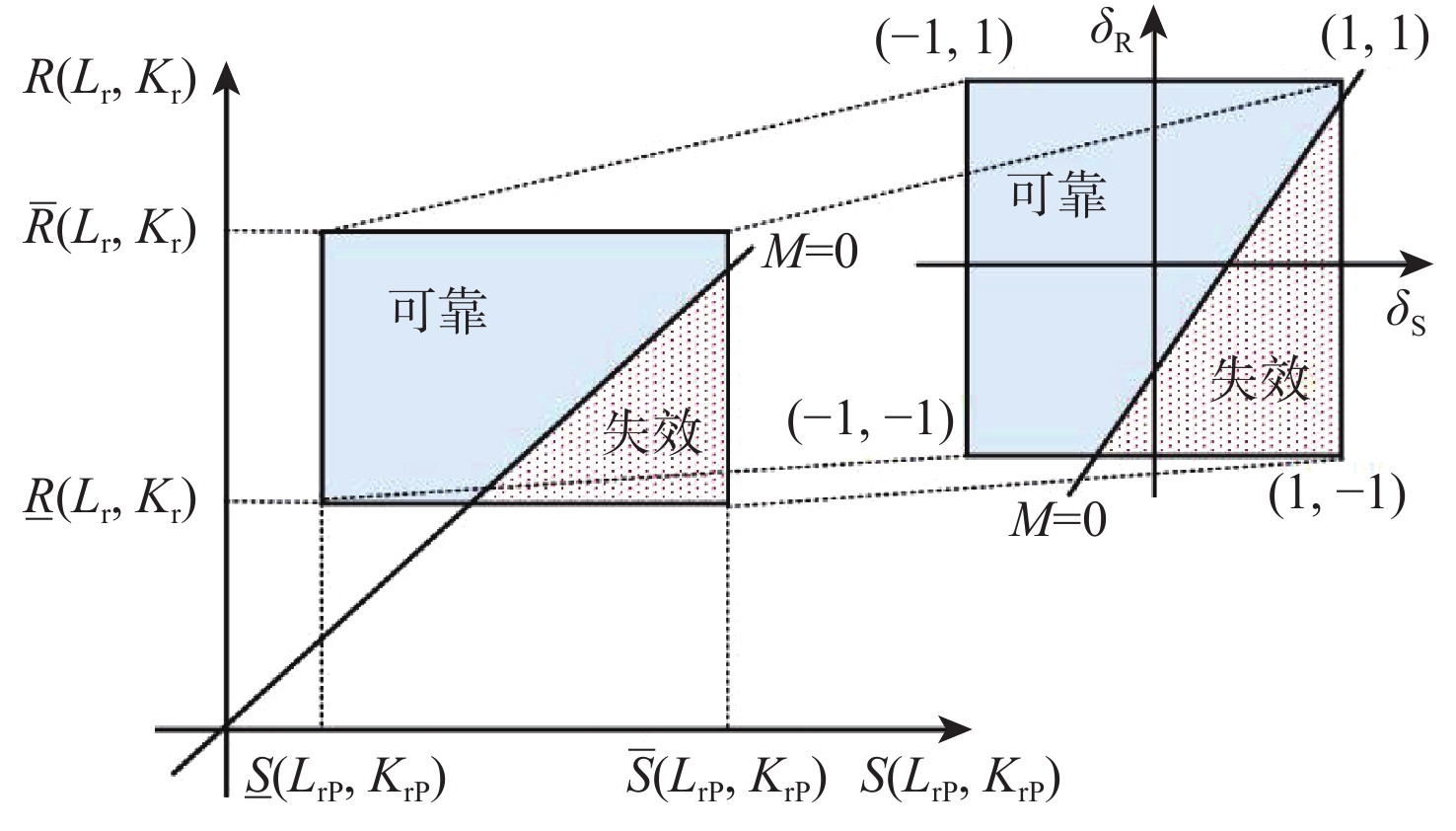
在推进剂储罐服役期内，准确地对裂纹缺陷进行分析，掌握储罐存在裂纹缺陷情况下的可靠状态，既可保证发射场的安全，亦可有效避免不必要的恐慌，为应急预案的制定提供参考。基于区间理论与失效评定图理论，提出一种非概率失效评定图（NFAD）可靠性分析方法。有效解决了工程实际中难以准确获得失效评定点与失效评定曲线情况下，推进剂储罐裂纹缺陷的可靠性分析问题。结合实例参数对所提方法进行验证，结果表明：无需精确失效评定图与失效评定曲线，所提方法可对储罐裂纹缺陷的任意状态进行分析，并可以充分考虑分析中的不确定性，将传统失效评定图方法失效或可靠的二元逻辑状态细化为3种情况，可靠性指标为0表示失效状态，可靠性指标大于0小于1表示可靠度，可靠性指标大于等于1表示安全裕度。
Abstract:During the service period of the propellant tank, the accurate analysis of its crack defects and reliable state with crack defects can not only guarantee the safety of the launch site, but also effectively avoid unnecessary panic, providing a reference for emergency plan formulation. Based on interval theory and failure assessment diagram theory, a non-probabilistic failure assessment diagram (NFAD) is proposed. The reliability analysis of the crack defect of propellant tanks can be effectively conducted when it is difficult to accurately obtain the failure evaluation point and curve in engineering practice. The proposed method is verified with the example parameters. The results show that this method can analyze any state of tank crack defects without accurate failure assessment point and curve, fully considering the uncertainty in the analysis. The binary logic states of failure or reliability of the traditional failure assessment chart method are divided into three cases with he reliability index is equal to 0, the reliability index is greater than 0 and less than 1, and the reliability index is greater than or equal to 1, represent the failure state, reliability degree and safety margin respectively.
-
图 2 非概率失效评定图区间变量转换
Figure 2. Interval variable conversion of non-probabilistic failure assessment diagram
表 1 示例参数
Table 1. Sample parameters
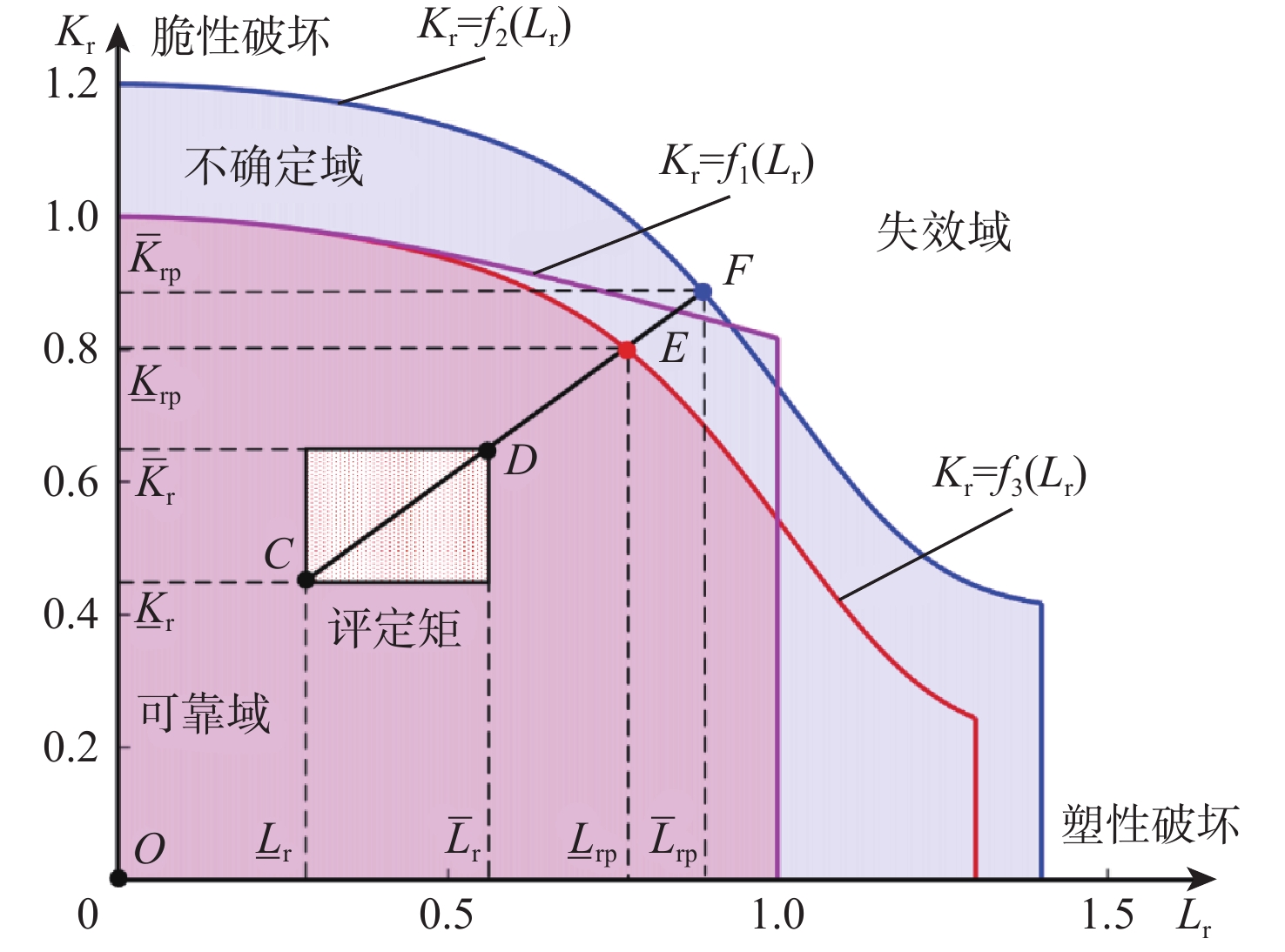
MPa 序号 $\underline K _{\text{r} }$ ${\overline K_{\text{r} } }$ $\underline {L} _{\text{r} }$ ${\overline L_{\text{r} } }$ 1 0.5 0.6 0.6 0.7 2 0.5 0.7 0.6 0.7 3 0.6 0.7 0.7 0.8 4 0.6 0.8 0.7 0.8 5 0.7 0.8 0.8 0.9 6 0.7 0.9 0.8 0.9 7 0.8 0.9 0.9 1.0 8 0.8 1.0 0.9 1.0 9 0.9 1.0 1.0 1.1 10 0.9 1.1 1.0 1.1 
下载: 导出CSV
表 2 可靠性分析结果
Table 2. Reliability analysis results
示例 ${\eta _{\rm{d} } }$ 状态 $f_{{\rm{s}}1}$ 状态 $f_{{\rm{s}}2}$ 状态 $f_{{\rm{s}}3}$ 状态 $f_{{\rm{s}}4}$ 状态 1 1.21 可靠 1.21 可靠 1.38 可靠 1.44 可靠 1.64 可靠 2 1.12 可靠 1.12 可靠 1.22 可靠 1.44 可靠 1.64 可靠 3 1.05 可靠 1.05 可靠 1.19 可靠 1.21 可靠 1.38 可靠 4 0.98 非完全可靠 失效 1.07 可靠 1.21 可靠 1.38 可靠 5 0.65 非完全可靠 失效 1.04 可靠 1.05 可靠 1.18 可靠 6 0.05 非完全可靠 失效 失效 1.05 可靠 1.18 可靠 7 0 失效 失效 失效 失效 1.04 可靠 8 0 失效 失效 失效 失效 1.04 可靠 9 0 失效 失效 失效 失效 失效 10 0 失效 失效 失效 失效 失效 注：fs1，fs2，fs3，fs4分别为$\left(\overline L_{\mathrm{r} }, \overline{K}_{\mathrm{r} }\right)$, $ f_{1}\left(L_{\mathrm{r}}\right) $；$\left(\overline L_{\mathrm{r} }, \overline {K}_{\mathrm{r} }\right)$,$ f_{2}\left(L_{\mathrm{r}}\right) $；$\left(\underline{L}_{{\rm{r}}}, \underline{K}_{{\rm{r}}}\right)$,$ f_{1}\left(L_{\mathrm{r}}\right) $；$\left(\underline{L}_{{\rm{r}}}, \underline{K}_{{\rm{r}}}\right)$,$ f_{2}\left(L_{\mathrm{r}}\right) $传统失效评定图方法的可靠性指标。
下载: 导出CSV
表 3 某型推进剂储罐应力参数
Table 3. Stress parameters of a certain propellant tank
$\sigma _{\text{m}}^{\text{c}}$ $\sigma _{\text{m}}^{\text{r}}$ $\sigma _{\text{s}}^{\text{c}}$ $\sigma _{\text{s}}^{\text{r}}$ $\sigma _{\text{d}}^{\text{c}}$ $\sigma _{\text{d}}^{\text{r}}$ 101.469 30.147 300 15 30.147 3.015
下载: 导出CSV
-
[1] BANNISTER A C, RUIZ OCEJO J, GUTIERREZ-SOLANA F. Implications of the yield stress/tensile stress ratio to the SINTAP failure assessment diagrams for homogeneous materials[J]. Engineering Fracture Mechanics, 2000, 67(6): 547-562. doi: 10.1016/S0013-7944(00)00073-4 [2] British Energy Generation Limited. Assessment of the integrity of structures containing defects : R6 Revision 4[S]. Gloucester: British Energy Generation Limited, 2001. [3] British Standards Institute. Guide on methods for assessing the acceptability of flaws in metallic structures: BS 7910[S]. London: BSI Standards Limited, 2013. [4] American Petroleum Institute and American Society of Mechanical Engineers. Fitness-for-service: API 579-1/ASME FFS-1[S]. Washington, D.C. : API Publishing Services, 2016. [5] 国家市场监督管理总局, 国家标准化管理委员会. 在用含缺陷压力容器安全评定: GB/T 19624—2019[S]. 北京: 中国标准出版社, 2019.State Administration for Market Regulation, Standardization Administration of the People's Republic of China. Safety assessment of in-service pressure vessels containing defects: GB/T 19624—2019[S]. Beijing: Standards Press of China, 2019 (in Chinese). [6] WEI S J, TOMAC I. Numerical evaluation of failure assessment diagram (FAD) for hydraulic fracture propagation in sandstone[J]. Engineering Fracture Mechanics, 2022, 263: 108311. doi: 10.1016/j.engfracmech.2022.108311 [7] RADU D, SEDMAK A, BĂNCILĂ R. Determining the crack acceptability in the welded joints of a wind loaded cylindrical steel shell structure[J]. Engineering Failure Analysis, 2018, 91: 341-353. doi: 10.1016/j.engfailanal.2018.04.032 [8] AINSWORTH R A, GINTALAS M, SAHU M K, et al. Application of failure assessment diagram methods to cracked straight pipes and elbows[J]. International Journal of Pressure Vessels and Piping, 2016, 148: 26-35. doi: 10.1016/j.ijpvp.2016.10.005 [9] KINGKLANG S, DAODON W, UTHAISANGSUK V. Failure investigation of liquefied petroleum gas cylinder using FAD and XFEM[J]. International Journal of Pressure Vessels and Piping, 2019, 171: 69-78. doi: 10.1016/j.ijpvp.2019.02.007 [10] ANDREWS R, COSHAM A, MACDONALD K. Application of BS 7910 to high pressure pipelines[J]. International Journal of Pressure Vessels and Piping, 2018, 168: 148-155. doi: 10.1016/j.ijpvp.2018.09.008 [11] CHOCAT R, BEAUCAIRE P, DEBEUGNY L, et al. Damage tolerance reliability analysis combining Kriging regression and support vector machine classification[J]. Engineering Fracture Mechanics, 2019, 216: 106514. doi: 10.1016/j.engfracmech.2019.106514 [12] PLUVINAGE G, BOULEDROUA O, HADJ MELIANI M, et al. Corrosion defect analysis using domain failure assessment diagram[J]. International Journal of Pressure Vessels and Piping, 2018, 165: 126-134. doi: 10.1016/j.ijpvp.2018.06.005 [13] XIAO Q D, LIU Y H, DAI Y W. Developments of strain-based failure assessment diagram applications: Measuring reference strain by displacement and a modified assessment method[J]. International Journal of Mechanical Sciences, 2018, 140: 27-36. doi: 10.1016/j.ijmecsci.2018.02.045 [14] ROTH S, KUNA M. Prediction of size-dependent fatigue failure modes by means of a cyclic cohesive zone model[J]. International Journal of Fatigue, 2017, 100: 58-67. doi: 10.1016/j.ijfatigue.2017.01.044 [15] RADU V, ROTH M. Probabilistic fracture mechanics applied for DHC assessment in the cool-down transients for CANDU pressure tubes[J]. Nuclear Engineering and Design, 2012, 253: 211-218. doi: 10.1016/j.nucengdes.2012.08.036 [16] BOULEDROUA O, ZELMATI D, HASSANI M. Inspections, statistical and reliability assessment study of corroded pipeline[J]. Engineering Failure Analysis, 2019, 100: 1-10. doi: 10.1016/j.engfailanal.2019.02.012 [17] JIN H J, WU S J. Effect of plasticity constraint on structural integrity assessment of pressure vessel welds[J]. International Journal of Pressure Vessels and Piping, 2015, 134: 72-81. doi: 10.1016/j.ijpvp.2015.09.001 [18] BERGANT M A, YAWNY A A, PEREZ IPIÑA J E. A comparison of failure assessment diagram options for Inconel 690 and Incoloy 800 nuclear steam generators tubes[J]. Annals of Nuclear Energy, 2020, 140: 107310. doi: 10.1016/j.anucene.2020.107310 [19] FUENTES J D, CICERO S, IBÁÑEZ-GUTIÉRREZ F T, et al. On the use of British standard 7910 option1 failure assessment diagram to non-metallic materials[J]. Fatigue & Fracture of Engineering Materials & Structures, 2018, 41(1): 146-158. -
下载:
点击查看大图
计量
- 文章访问数: 118
- HTML全文浏览量: 39
- PDF下载量: 13
- 被引次数: 0
