基于直角网格伴随自适应的声爆预测

朱震浩; 肖天航; 徐雅楠; 邓双厚; 张珍铭; 余雄庆

doi:10.13700/j.bh.1001-5965.2021.0689

基于直角网格伴随自适应的声爆预测

doi: 10.13700/j.bh.1001-5965.2021.0689

1.
南京航空航天大学航空学院，南京 210016
2.
上海机电工程研究所，上海 201109

基金项目: 国家自然科学基金(11672133)；陕西省自然科学基础研究计划(2021JQ-078)；航空科学基金(F2021110)；航天进入减速与着陆技术实验室开放基金(EDL19092111)

详细信息

通讯作者:
E-mail：xthang@nuaa.edu.cn

中图分类号: V221⁺.3；TB553
计量
- 文章访问数: 132
- HTML全文浏览量: 273
- PDF下载量: 12
- 被引次数: 0
出版历程
- 收稿日期: 2021-11-16
- 录用日期: 2022-01-05
- 网络出版日期: 2022-01-25
- 整期出版日期: 2023-10-01

Adjoint-based adaptive Cartesian mesh refinement for sonic boom prediction

1.
College of Aerospace Engineering，Nanjing University of Aeronautics and Astronautics，Nanjing 210016，China
2.
Shanghai Electro-Mechanical Engineering Institute，Shanghai 201109，China

Funds: National Natural Science Foundation of China (11672133); National Science Foundation of Shanxi Province (2021JQ-078); Aeronautical Science Foundation of China (F2021110); Open Foundations of EDL Laboratory (EDL19092111)

More Information

Corresponding author: E-mail：xthang@nuaa.edu.cn

摘要

摘要:
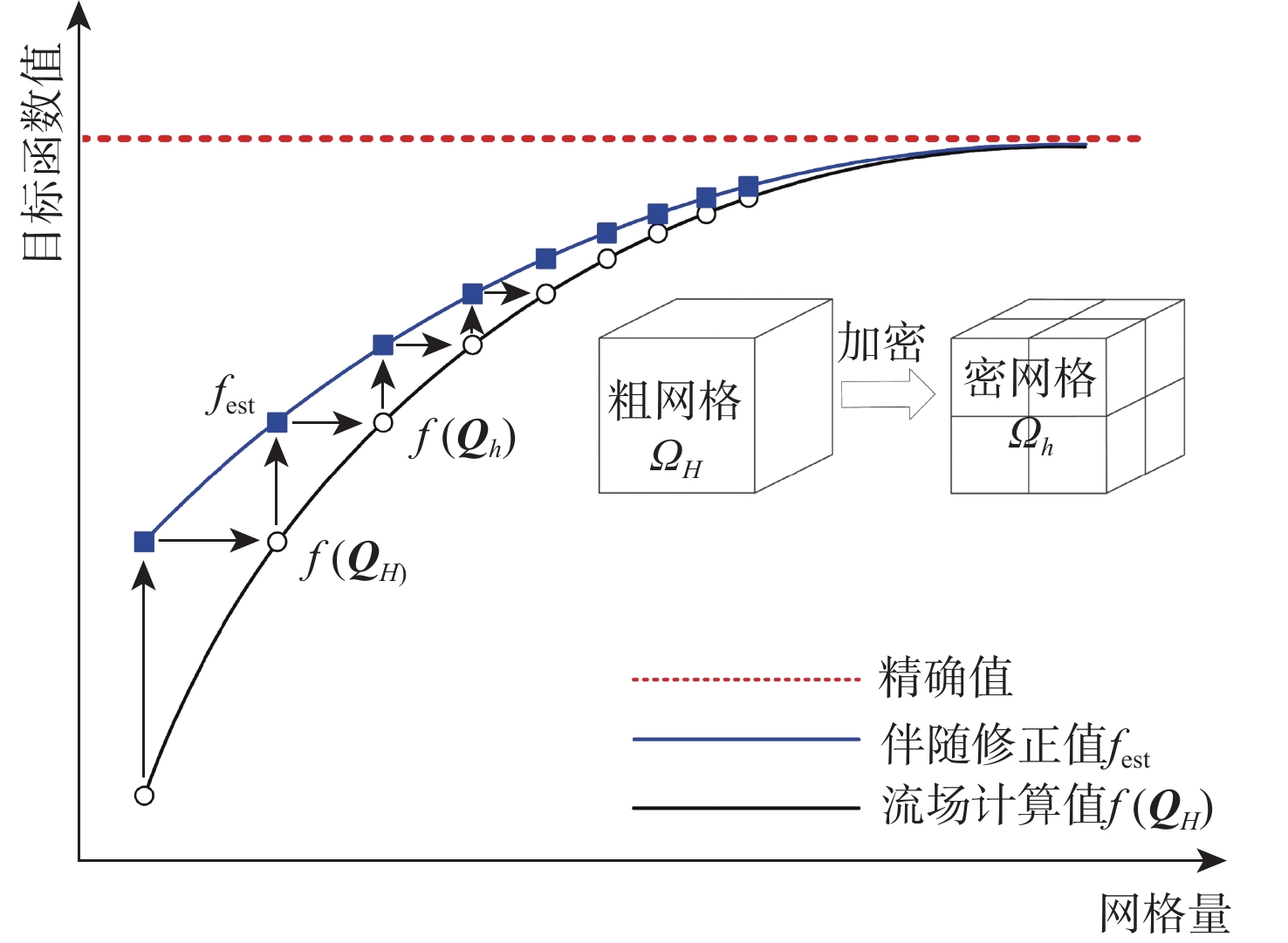
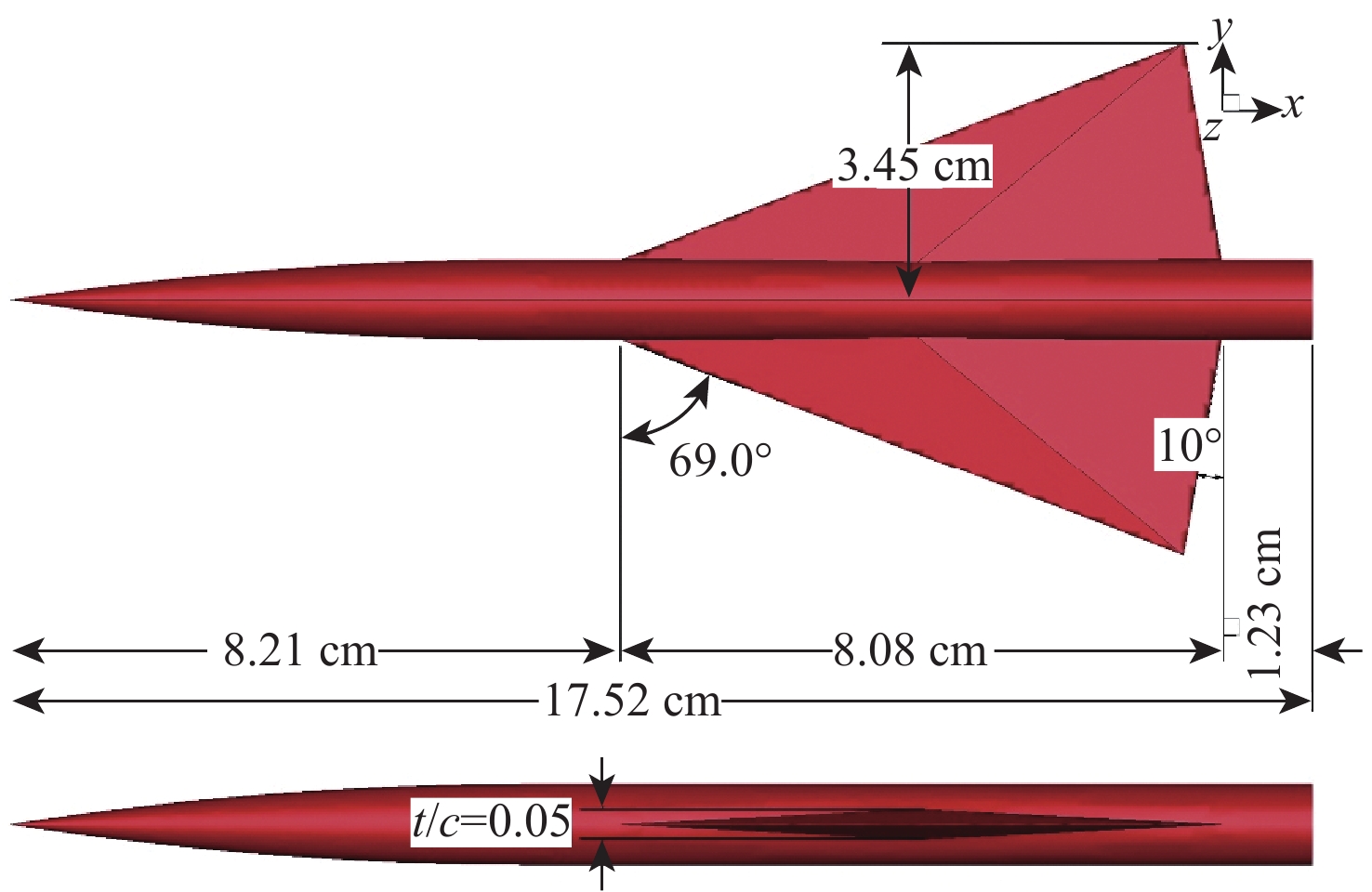
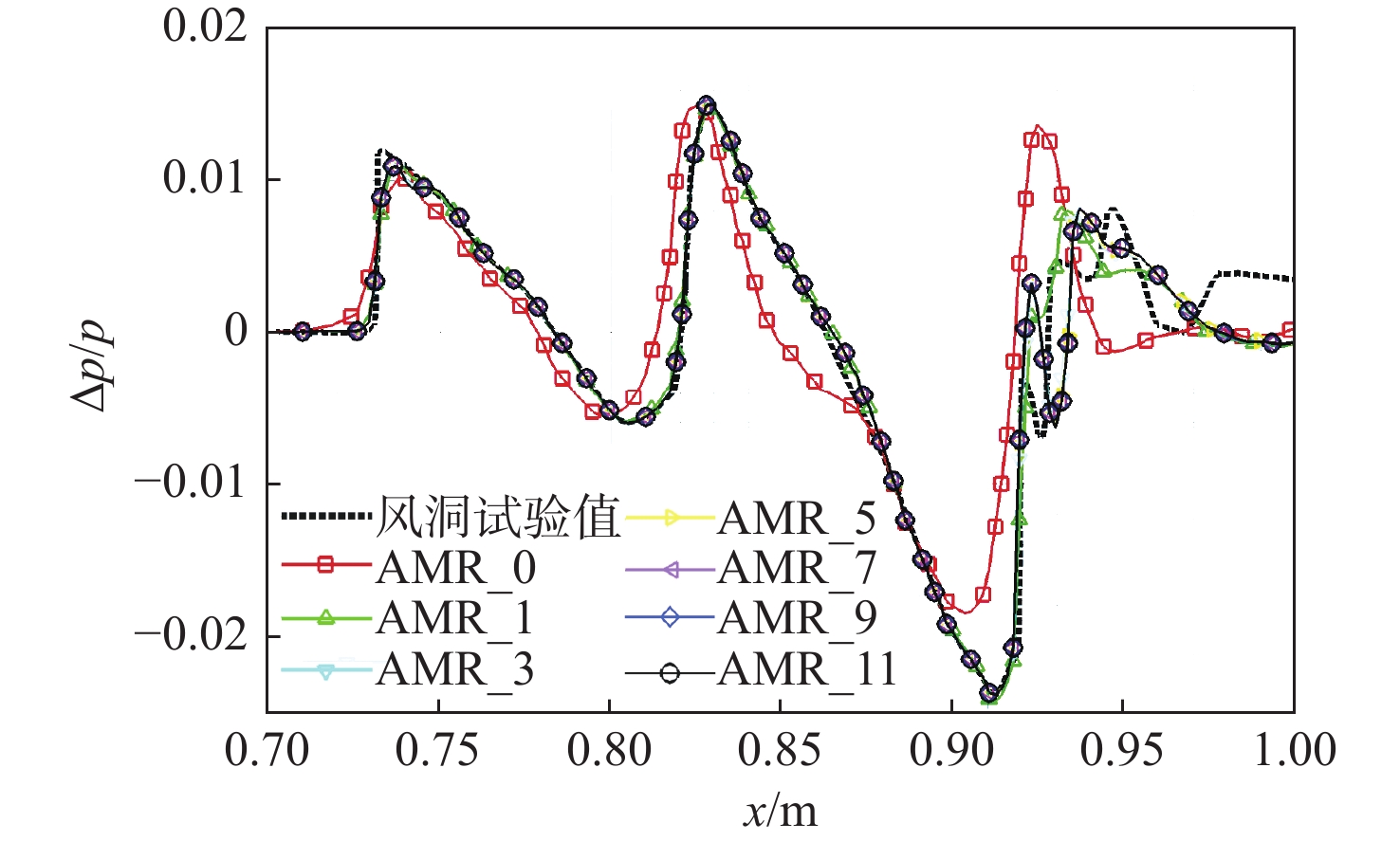
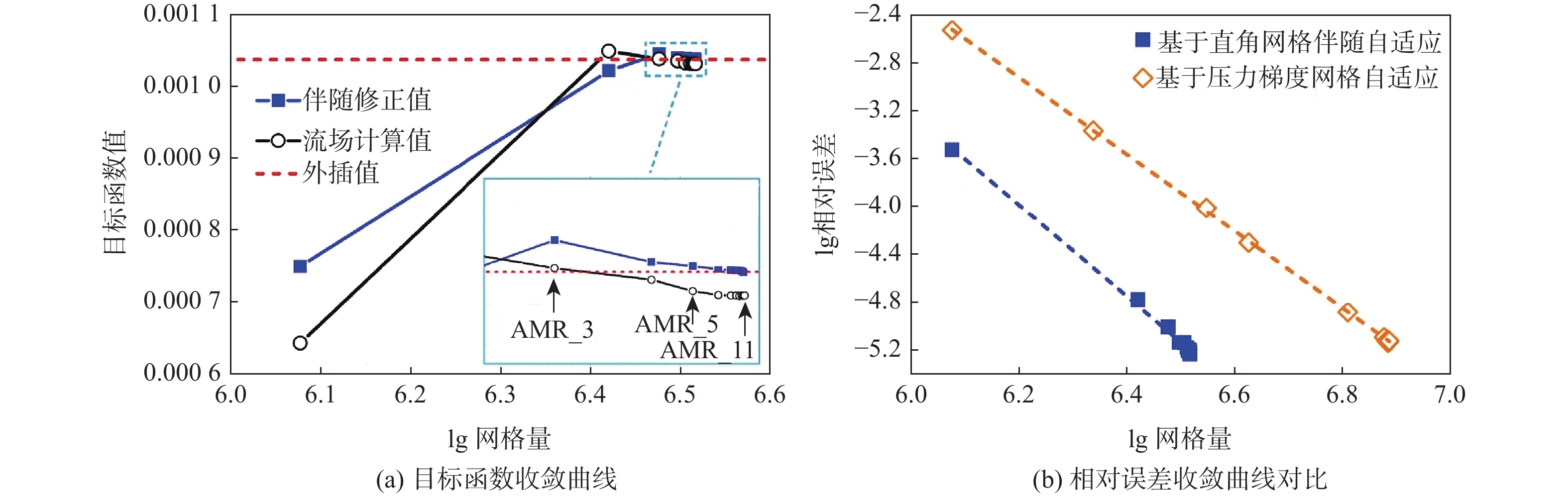
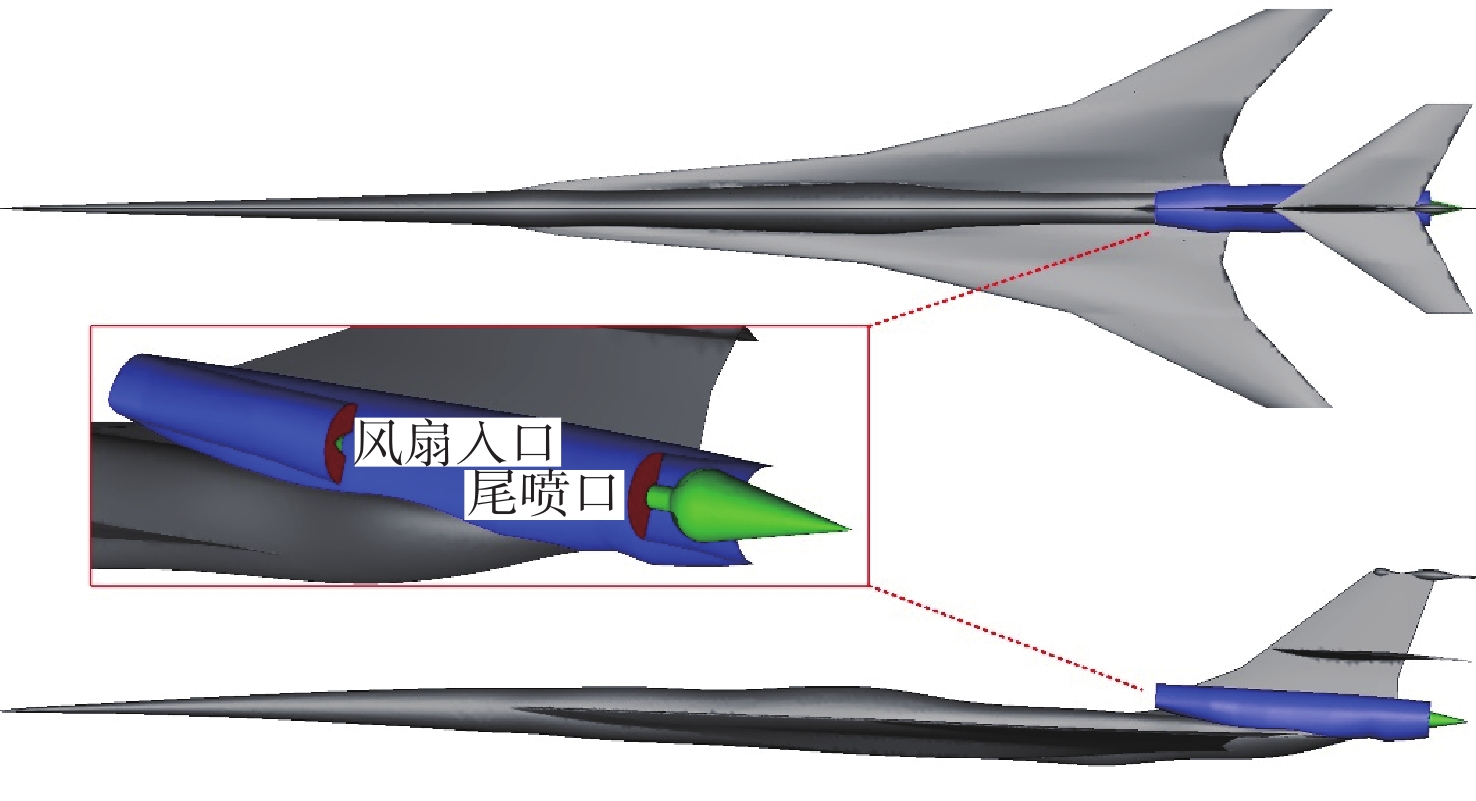
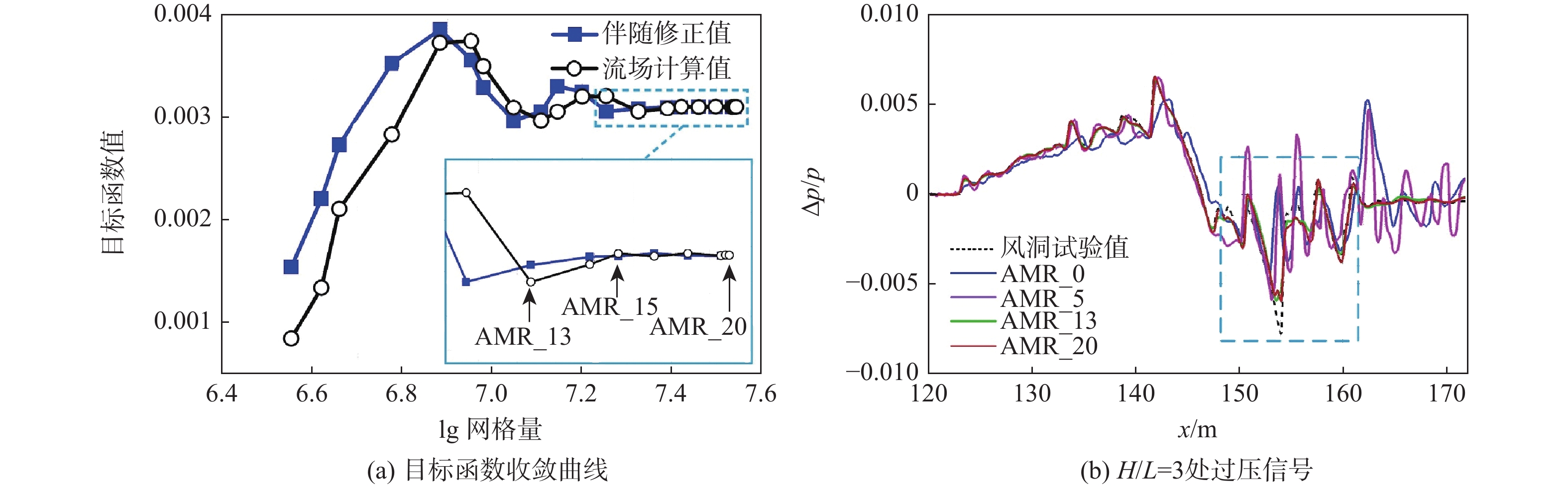
声爆预测是超声速民机设计关键技术之一，近场过压信号的精确计算是声爆预测的基础和重要环节。针对超声速民机声爆预测问题，发展了基于直角网格伴随自适应的超声速近场求解方法。运用有限体积法求解流体控制方程，以指定近场位置过压值平方的积分作为目标函数，通过求解离散伴随方程获得目标函数对流场残差的敏感度，评估和修正目标函数全局误差，并驱动网格自适应加密，通过局部加密逐渐减小各个网格单元的剩余误差，提高目标函数的计算精度。选取69°后掠三角翼翼身组合体和美国国家航空航天局（NASA）的C25D超声速民机模型进行算例验证并与试验数据对比，结果表明：与流场特征自适应网格方法相比，所提方法能够以更少的网格量，更精确地捕捉流场中的激波和膨胀波，得到更精确的近场过压信号分布，是一种可用于声爆预测的高精度、高效率的超声速近场求解方法。
- 超声速民机 /
- 声爆预测 /
- 伴随 /
- 误差估计 /
- 网格自适应 /
- 直角网格
Abstract:
In view of the sonic boom prediction for supersonic transport, this paper develops a numerical method for supersonic near-field based on a finite volume scheme and an adjoint-based Cartesian adaptive mesh refinement for the governing equations. By solving the adjoint equation on an embedded-boundary Cartesian mesh, it can be determined that how sensitive the chosen output functional is to the residual of the discretized Euler equations, such as the surface integral of the related pressure signatures. Then, the computed adjoint variables render a correction term to improve the accuracy of the function on the coarse mesh and direct estimation of the remaining error to form an error estimate and a localized refinement parameter, according to which the Cartesian grid cells are locally refined subsequently. As a result, local mesh refinement steadily reduces each cell’s remaining error, improving the output function’s computational correctness. The 69° delta wing-body and NASA C25D configuration with powered nacelle are employed as validation cases where the computed results are compared with the documented experimental tests. Results show that compared with feature-based mesh refinement, the present adjoint-based refinement method captures the shock and expansion waves and the near-field pressure signatures with higher accuracy at a less computational cost, indicating its effectiveness and efficiency for sonic boom prediction.
- supersonic transport /
- sonic boom prediction /
- adjoint /
- error estimate /
- adaptive mesh refinement /
- Cartesian mesh

HTML全文

图 1 直角网格伴随自适应过程目标函数变化曲线

Figure 1. Functional convergence for adjoint-based adaptive Cartesian mesh refinement

下载: 全尺寸图片幻灯片

图 2 69°后掠三角翼翼身组合体(Model 4)模型几何外形^[32]

Figure 2. Geometry of 69° Delta Wing-Body (Model 4)^[32]

下载: 全尺寸图片幻灯片

图 3 4种不同网格划分策略的对称面网格及过压值云图

Figure 3. Final meshes generated by four strategies and corresponding over-pressure contours at symmetry plane

下载: 全尺寸图片幻灯片

图 4 H/L=3.1处4种网格及风洞试验得到的过压信号对比

Figure 4. Comparison of pressure signatures obtained from numerical simulations of four different grids and wind tunnel tests at H/L=3.1

下载: 全尺寸图片幻灯片

图 5 不同自适应次数得到的H/L=3.1处过压信号

Figure 5. Pressure signatures at H/L=3.1 measured after different refinement times

下载: 全尺寸图片幻灯片

图 6 H/L=3.1处目标函数收敛曲线和直角网格伴随自适应与压力梯度自适应的误差收敛对比

Figure 6. Functional convergence using adjoint-based Cartesian mesh refinement and comparison of relative error for adjoint-based and pressure gradient-based mesh refinement at H/L=3.1

下载: 全尺寸图片幻灯片

图 7 带动力短舱的C25D几何外形^[34-35]

Figure 7. Geometry of C25D configuration with powered nacelle^[34-35]

下载: 全尺寸图片幻灯片

图 8 C25D模型初始网格与最终的自适应网格示意及各自计算结果

Figure 8. The initial and final refined mesh for C25D model as well as the corresponding results

下载: 全尺寸图片幻灯片

图 9 目标函数收敛曲线及不同自适应次数得到的H/L=3处的过压信号

Figure 9. Functional convergence and pressure signatures at H/L=3 measured after different refinement times

下载: 全尺寸图片幻灯片

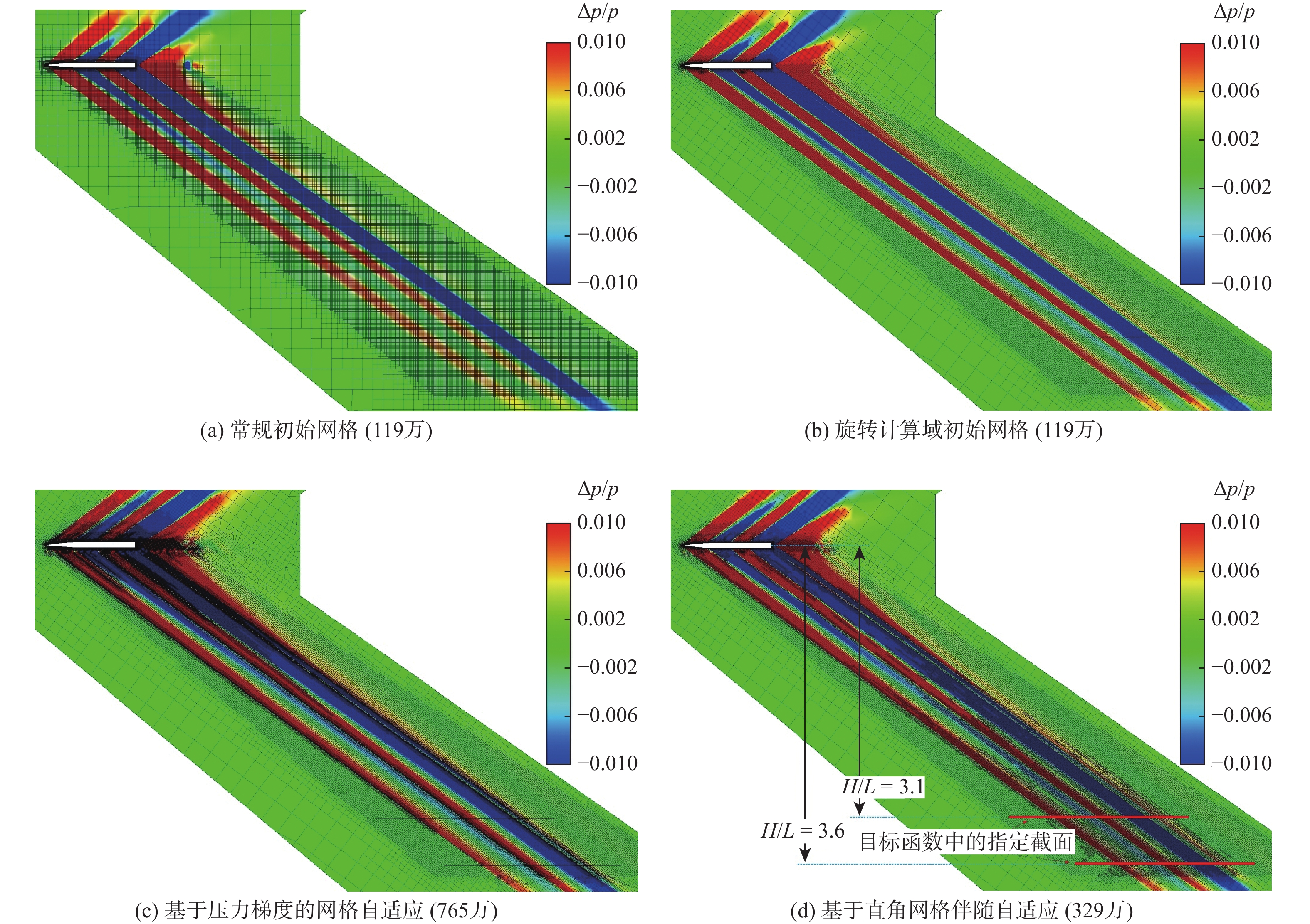
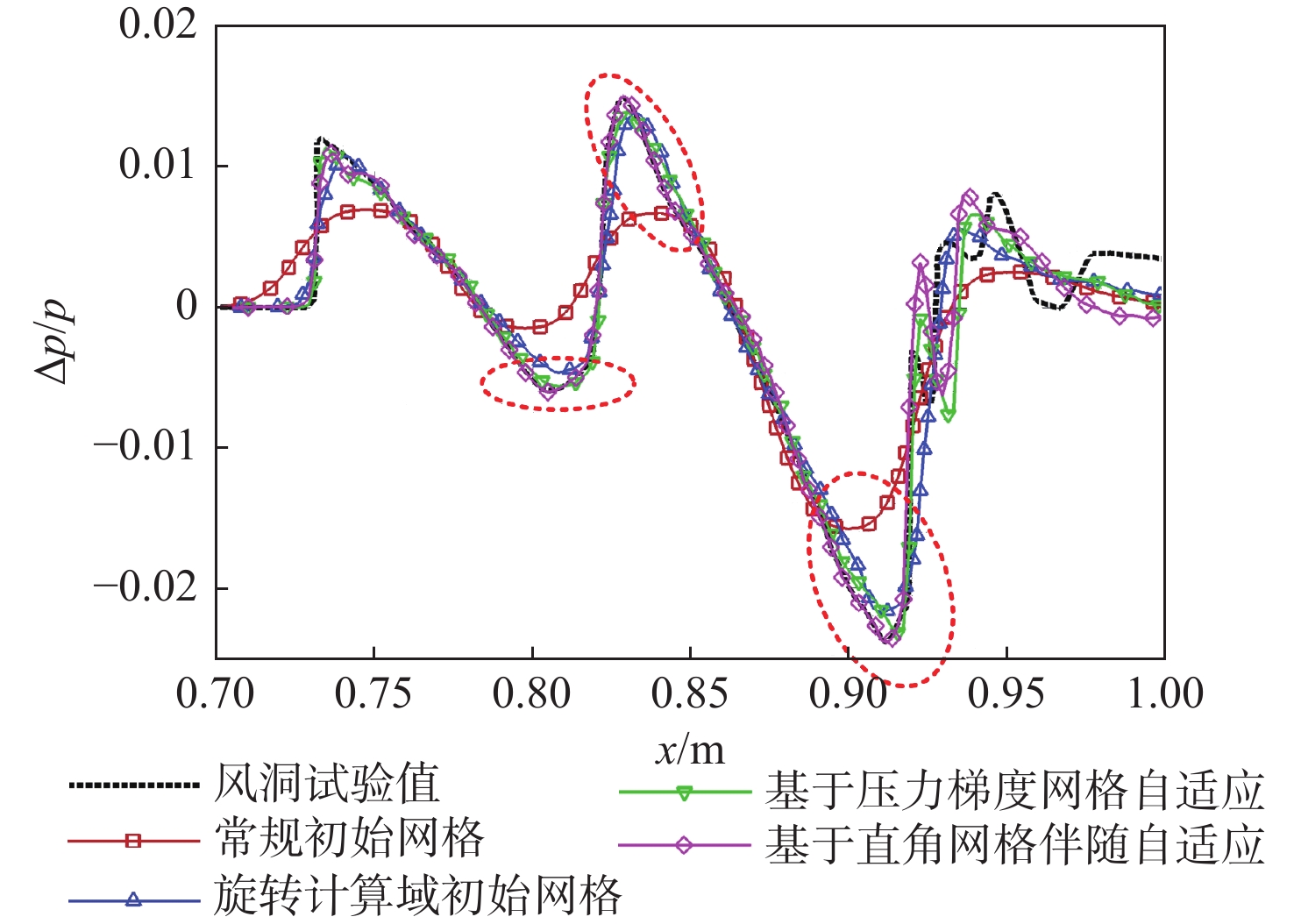
表 1 4种网格最终网格量、计算精度和计算耗时明细

Table 1. Comparison of final grid size, computational accuracy and cost for four grid strategies

网格	网格量/10⁴	计算精度	计算耗时/h
常规初始网格	119	很差	2
旋转计算域初始网格	119	一般	2
基于压力梯度网格自适应	765	较精确	28
基于直角网格伴随自适应	329	更精确	12 (6)

下载: 导出CSV

参考文献(35)

[1]	朱自强, 兰世隆. 超声速民机和降低音爆研究[J]. 航空学报, 2015, 36(8): 2507-2528. ZHU Z Q, LAN S L. Study of supersonic commercial transport and reduction of sonic boom[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(8): 2507-2528(in Chinese).
[2]	韩忠华, 乔建领, 丁玉临, 等. 新一代环保型超声速客机气动相关关键技术与研究进展[J]. 空气动力学学报, 2019, 37(4): 620-635. doi: 10.7638/kqdlxxb-2018.0288 HAN Z H, QIAO J L, DING Y L, et al. Key technologies for next-generation environmentally-friendly supersonic transport aircraft: A review of recent progress[J]. Acta Aerodynamica Sinica, 2019, 37(4): 620-635(in Chinese). doi: 10.7638/kqdlxxb-2018.0288
[3]	钱战森, 韩忠华. 声爆研究的现状与挑战[J]. 空气动力学学报, 2019, 37(4): 601-619. doi: 10.7638/kqdlxxb-2019.0054 QIAN Z S, HAN Z H. Progress and challenges of sonic boom research[J]. Acta Aerodynamica Sinica, 2019, 37(4): 601-619(in Chinese). doi: 10.7638/kqdlxxb-2019.0054
[4]	SMITH H. A review of supersonic business jet design Issues[J]. The Aeronautical Journal, 2007, 111(1126): 761-776. doi: 10.1017/S0001924000001883
[5]	SUN Y C, SMITH H. Review and prospect of supersonic business jet design[J]. Progress in Aerospace Sciences, 2017, 90: 12-38. doi: 10.1016/j.paerosci.2016.12.003
[6]	钱战森, 刘中臣, 冷岩, 等. OS-X0试验飞行器声爆特性飞行测量与数值模拟分析[J]. 空气动力学学报, 2019, 37(4): 675-682. doi: 10.7638/kqdlxxb-2018.0276 QIAN Z S, LIU Z C, LENG Y, et al. Flight measurement and numerical simulation of sonic boom signature of OS-X0 experimental aircraft[J]. Acta Aerodynamica Sinica, 2019, 37(4): 675-682(in Chinese). doi: 10.7638/kqdlxxb-2018.0276
[7]	王刚, 马博平, 雷知锦, 等. 典型标模音爆的数值预测与分析[J]. 航空学报, 2018, 39(1): 121458. WANG G, MA B P, LEI Z J, et al. Simulation and analysis for sonic boom on several benchmark cases[J]. Acta Aeronautica et Astronautica Sinica, 2018, 39(1): 121458(in Chinese).
[8]	冯晓强, 李占科, 宋笔锋. 超音速客机音爆问题初步研究[J]. 飞行力学, 2010, 28(6): 21-23. doi: 10.13645/j.cnki.f.d.2010.06.005 FENG X Q, LI Z K, SONG B F. Preliminary analysis on the sonic boom of supersonic aircraft[J]. Flight Dynamics, 2010, 28(6): 21-23(in Chinese). doi: 10.13645/j.cnki.f.d.2010.06.005
[9]	兰世隆. 超声速民机声爆理论、预测和最小化方法概述[J]. 空气动力学学报, 2019, 37(4): 646-654. doi: 10.7638/kqdlxxb-2018.0294 LAN S L. Overview of sonic boom theory, prediction and minimization methods for supersonic civil aircraft[J]. Acta Aerodynamica Sinica, 2019, 37(4): 646-654(in Chinese). doi: 10.7638/kqdlxxb-2018.0294
[10]	PLOTKIN K J. Review of sonic boom theory[C]//12th Aeroacoustic Conference. Reston: AIAA, 1989: 1105.
[11]	MAGLIERI D J, BOBBITT P J, PLOTKIN K J, et al. Sonic boom: Six decades of research[M]. Hampton: Langley Research Center, 2014.
[12]	PLOTKIN K J. State of the art of sonic boom modeling[J]. The Journal of the Acoustical Society of America, 2002, 111(1): 530-536. doi: 10.1121/1.1379075
[13]	HAERING E, MURRAY J, PURIFOY D, et al. Airborne shaped sonic boom demonstration pressure measurements with computational fluid dynamics comparisons[C]//Proceedings of the 43rd AIAA Aerospace Sciences Meeting and Exhibit. Reston: AIAA, 2005: 9.
[14]	MEREDITH K, DAHLIN J, GRAHAM D, et al. Computational fluid dynamics comparison and flight test measurement of F-5E off-body pressures[C]//Proceedings of the 43rd AIAA Aerospace Sciences Meeting and Exhibit. Reston: AIAA, 2005: 6.
[15]	CASTNER R. Analysis of exhaust plume effects on sonic boom for a 59-degree wing body model[C]//Proceedings of the 49th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition. Reston: AIAA, 2011: 917.
[16]	KIRZ J. DLR TAU simulations for the third AIAA sonic boom prediction workshop near-field cases[C]//Proceedings of the AIAA Scitech 2021 Forum. Reston: AIAA, 2021: 472.
[17]	PARK M A, CAMPBELL R L, ELMILIGUI A A, et al. Specialized CFD grid generation methods for near-field sonic boom prediction[C]//Proceedings of the 52nd Aerospace Sciences Meeting. Reston: AIAA, 2014: 115.
[18]	ISHIKAWA H, MAKINO Y, ITO T, et al. Sonic boom prediction using multi-block structured grids CFD code considering jet-on effects[C]//Proceedings of the 27th AIAA Applied Aerodynamics Conference. Reston: AIAA, 2009: 3508.
[19]	CLIFF S E, THOMAS S D. Euler/experiment correlations of sonic boom pressure signatures[J]. Journal of Aircraft, 1993, 30(5): 669-675. doi: 10.2514/3.46396
[20]	LYU F X, XIAO T H, YU X Q. A fast and automatic full-potential finite volume solver on Cartesian grids for unconventional configurations[J]. Chinese Journal of Aeronautics, 2017, 30(3): 951-963. doi: 10.1016/j.cja.2017.03.001
[21]	吕凡熹, 肖天航, 余雄庆. 基于自适应直角网格的二维全速势方程有限体积解法[J]. 计算力学学报, 2016, 33(3): 424-430. LYU F X, XIAO T H, YU X Q. A finite volume method for 2D Full-Potential equation on adaptive Cartesian grids[J]. Chinese Journal of Computational Mechanics, 2016, 33(3): 424-430(in Chinese).
[22]	吕凡熹, 李正洲, 邓经枢, 等. 面向飞行器概念设计的全速域气动分析工具[J]. 空气动力学学报, 2017, 35(5): 625-632. LYU F X, LI Z Z, DENG J S, et al. An aerodynamic analysis tool for aircraft conceptual design at full speed range[J]. Acta Aerodynamica Sinica, 2017, 35(5): 625-632(in Chinese).
[23]	NAYANI S. Evaluation of grid modification methods for on-and off-track sonic boom analysis[C]//Proceedings of the 51st AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition. Reston: AIAA, 2013: 798.
[24]	CLIFF S E, THOMAS S D, MCMULLEN M S, et al. Assessment of unstructured Euler methods for sonic boom pressure signatures using grid refinement and domain rotation methods: TM-2008-214568[R]. Washington, D.C.: NASA, 2008.
[25]	OZCER I, KANDIL O. Fun3D/OptiGRID coupling for unstructured grid adaptation for sonic boom problems[C]//Proceedings of the 46th AIAA Aerospace Sciences Meeting and Exhibit. Reston: AIAA, 2008: 61.
[26]	VENDITTI D A, DARMOFAL D L. Grid adaptation for functional outputs: Application to two-dimensional inviscid flows[J]. Journal of Computational Physics, 2002, 176(1): 40-69. doi: 10.1006/jcph.2001.6967
[27]	JONES W, NIELSEN E, PARK M. Validation of 3D adjoint based error estimation and mesh adaptation for sonic boom prediction[C]//Proceedings of the 44th AIAA Aerospace Sciences Meeting and Exhibit. Reston: AIAA, 2006: 1150.
[28]	NEMEC M, AFTOSMIS M, WINTZER M. Adjoint-based adaptive mesh refinement for complex geometries[C]//Proceedings of the 46th AIAA Aerospace Sciences Meeting and Exhibit. Reston: AIAA, 2008: 725.
[29]	WINTZER M, NEMEC M, AFTOSMIS M. Adjoint-based adaptive mesh refinement for sonic boom prediction[C]//Proceedings of the 26th AIAA Applied Aerodynamics Conference. Reston: AIAA, 2008: 6593.
[30]	NEMEC M, RODRIGUEZ D L, AFTOSMIS M J. Adjoint-based mesh adaptation and shape optimization for simulations with propulsion[C]//Proceedings of the AIAA Aviation 2019 Forum. Reston: AIAA, 2019: 3488.
[31]	XIAO T H, QIN N, LUO D M, et al. Deformable overset grid for multibody unsteady flow simulation[J]. AIAA Journal, 2016, 54(8): 2392-2406. doi: 10.2514/1.J054861
[32]	HUNTON L W, HICKS R M, MENDOZA J P. Some effects of wing planform on sonic boom: TN D-7160[R]. Washington, D.C.: NASA, 1973.
[33]	CELIK I, KARATEKIN O. Numerical experiments on application of Richardson extrapolation with nonuniform grids[J]. Journal of Fluids Engineering, 1997, 119(3): 584-590. doi: 10.1115/1.2819284
[34]	ORDAZ I, WINTZER M, RALLABHANDI S K. Full-carpet design of a low-boom demonstrator concept[C]//Proceedings of the 33rd AIAA Applied Aerodynamics Conference. Reston: AIAA, 2015: 2261.
[35]	WINTZER M, ORDAZ I. Under-track CFD-based shape optimization for a low-boom demonstrator concept[C]//Proceedings of the 33rd AIAA Applied Aerodynamics Conference. Reston: AIAA, 2015: 2260.