A mesh parameterization method and life reliability-based optimization for turbine blade
-
摘要:
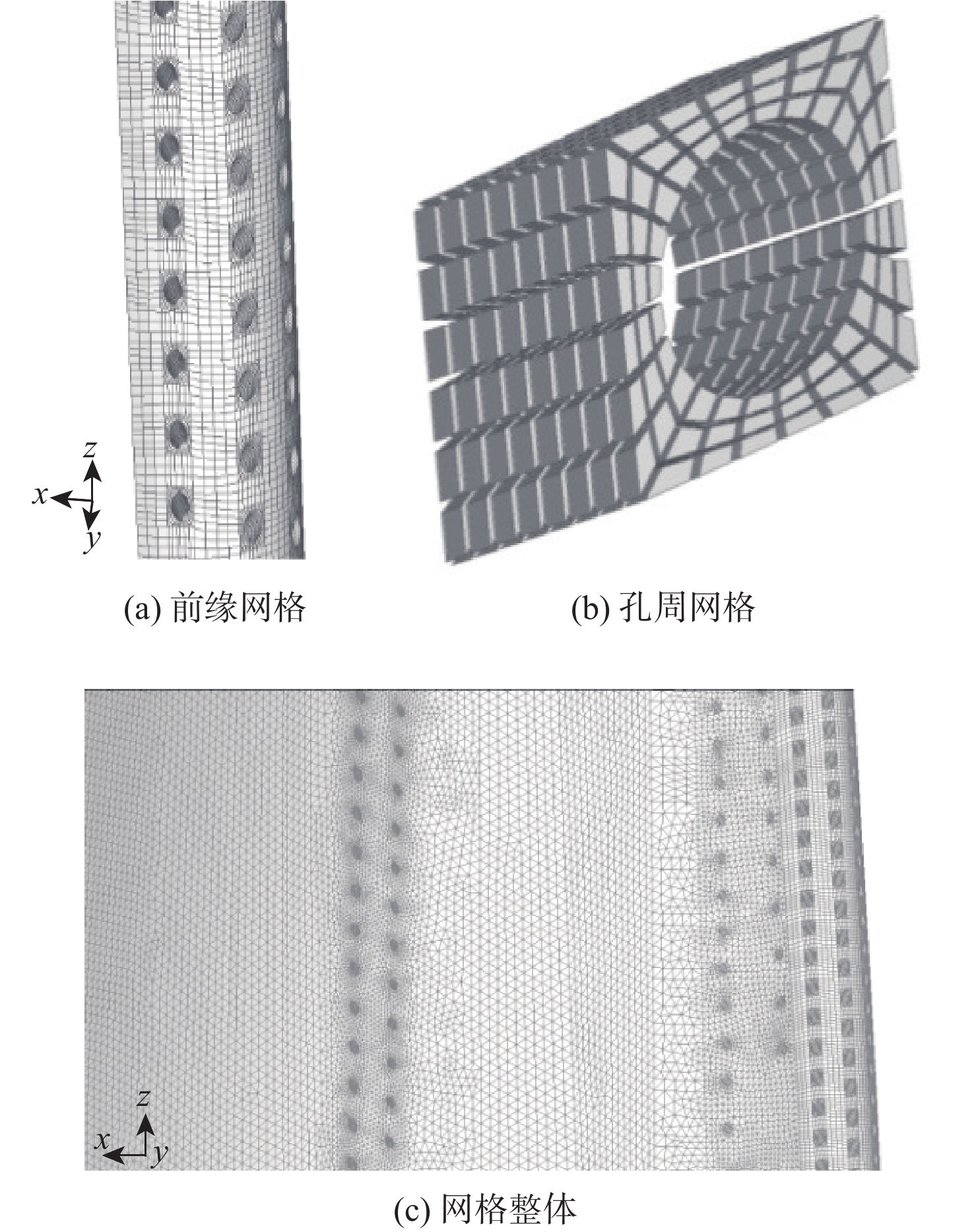
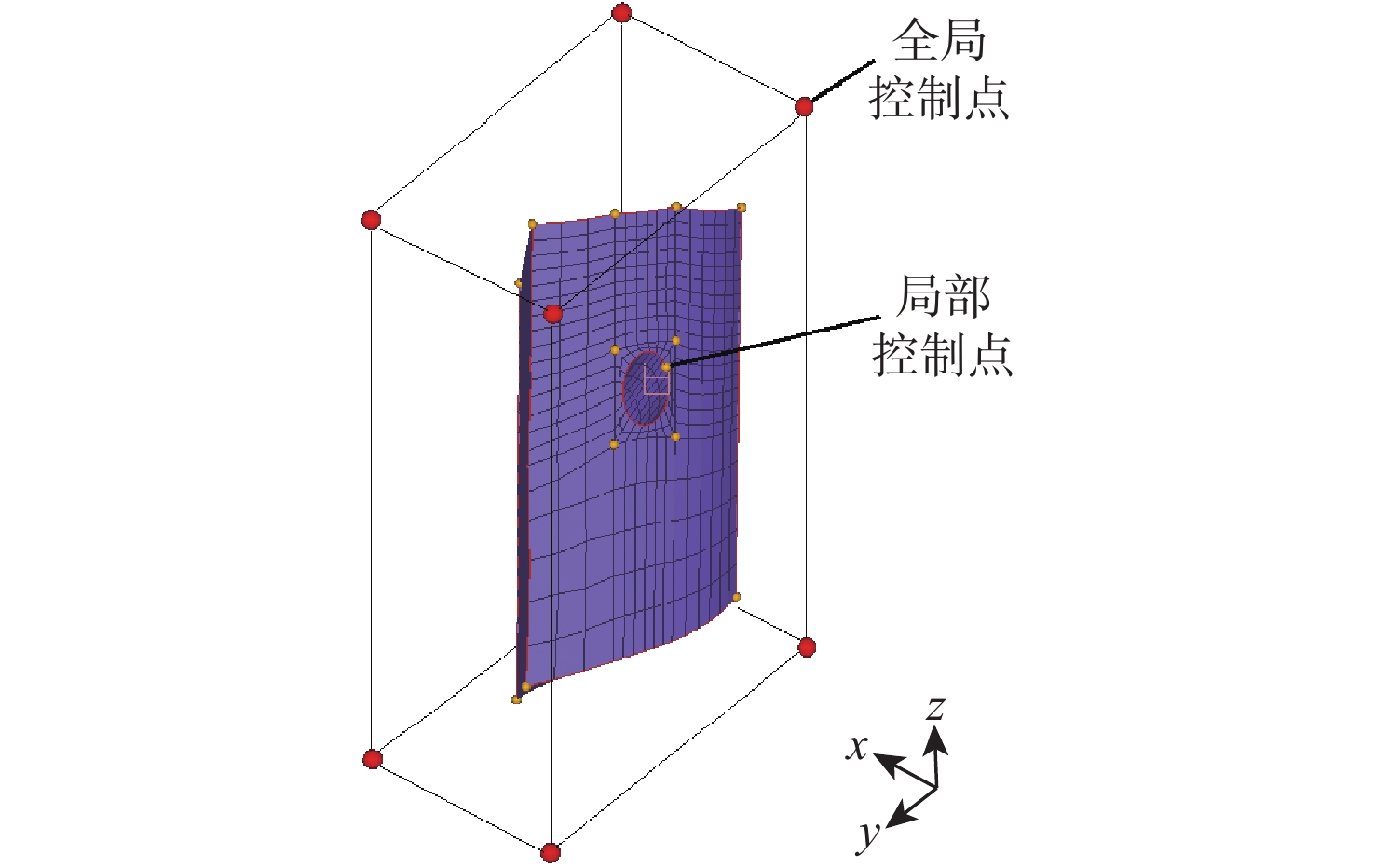
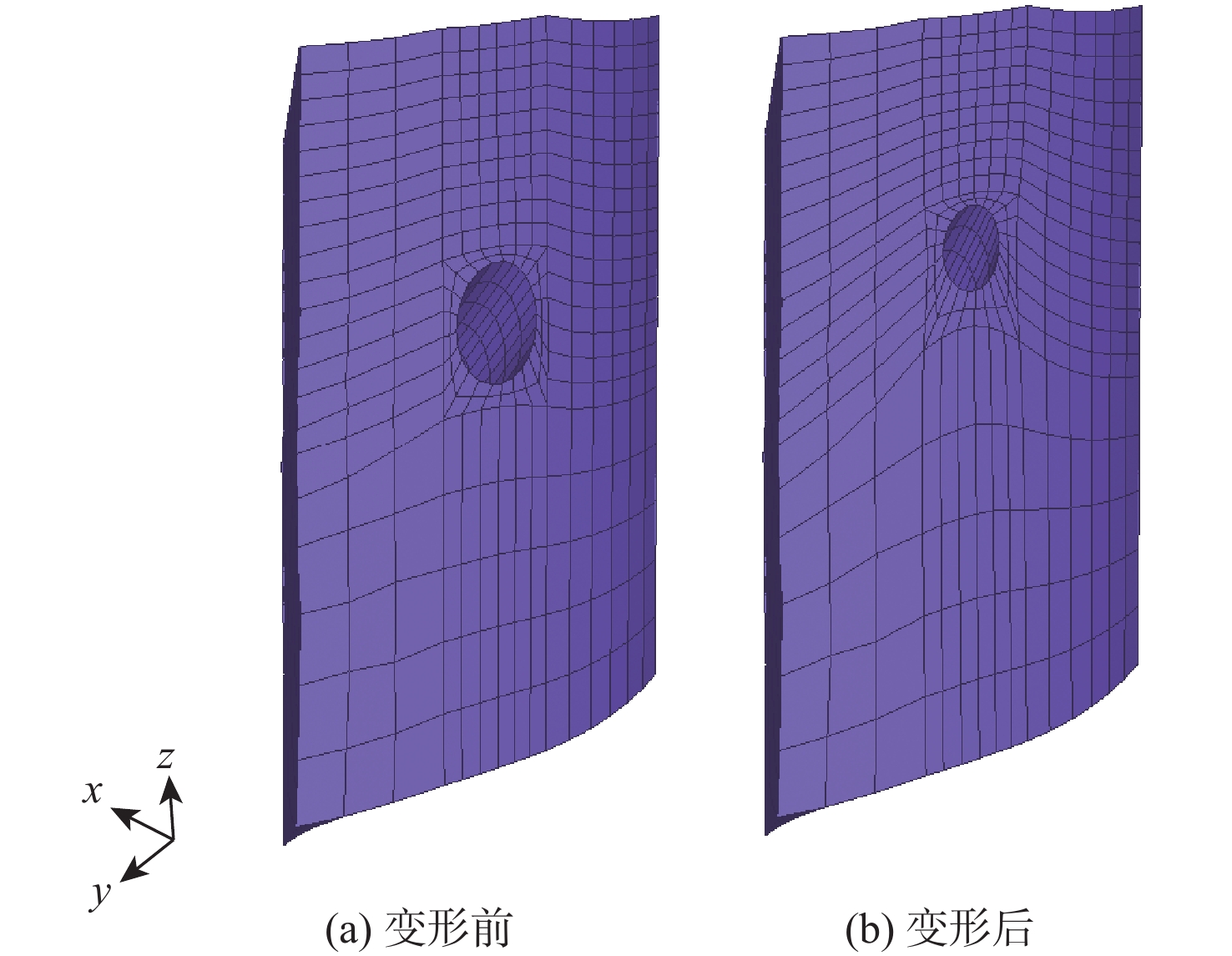
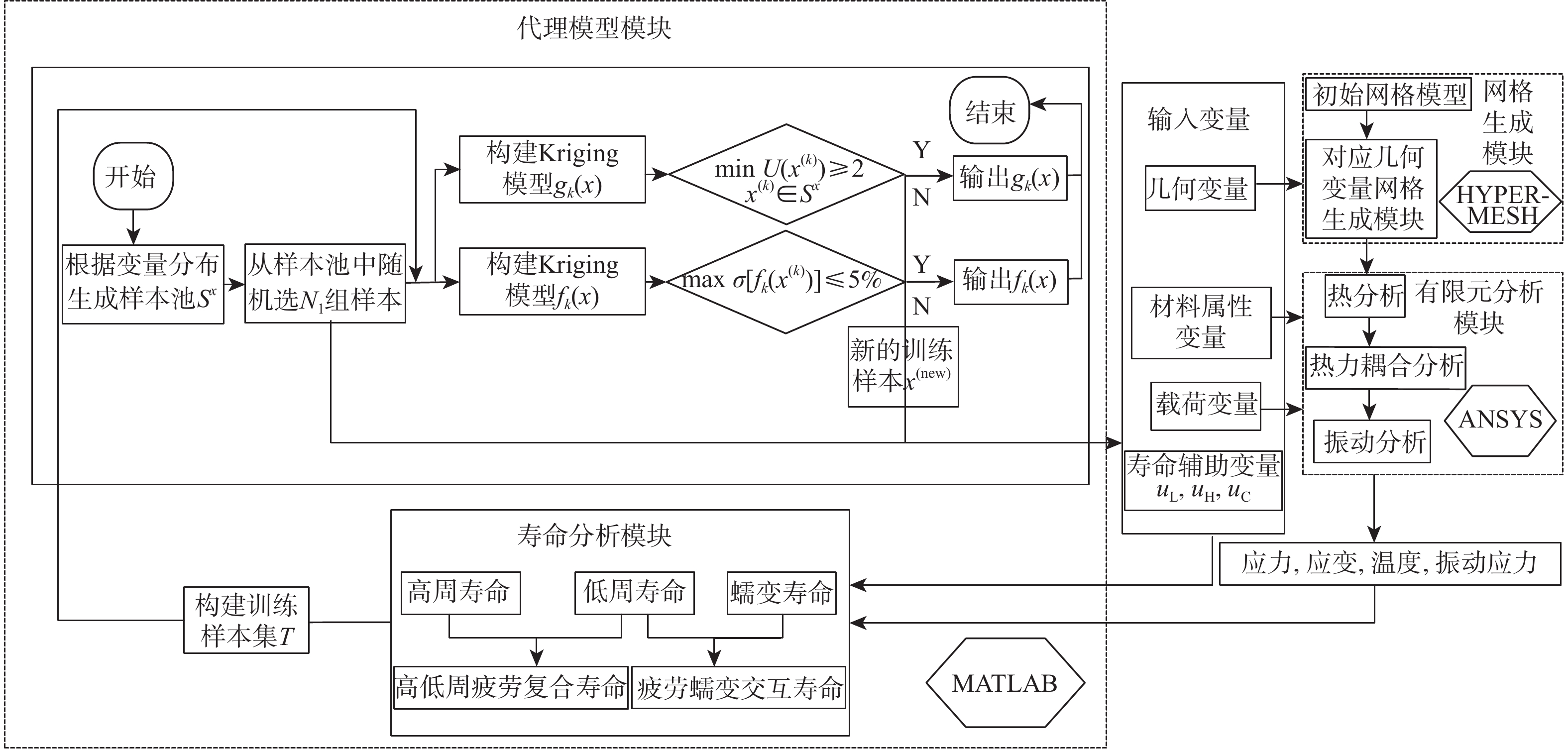
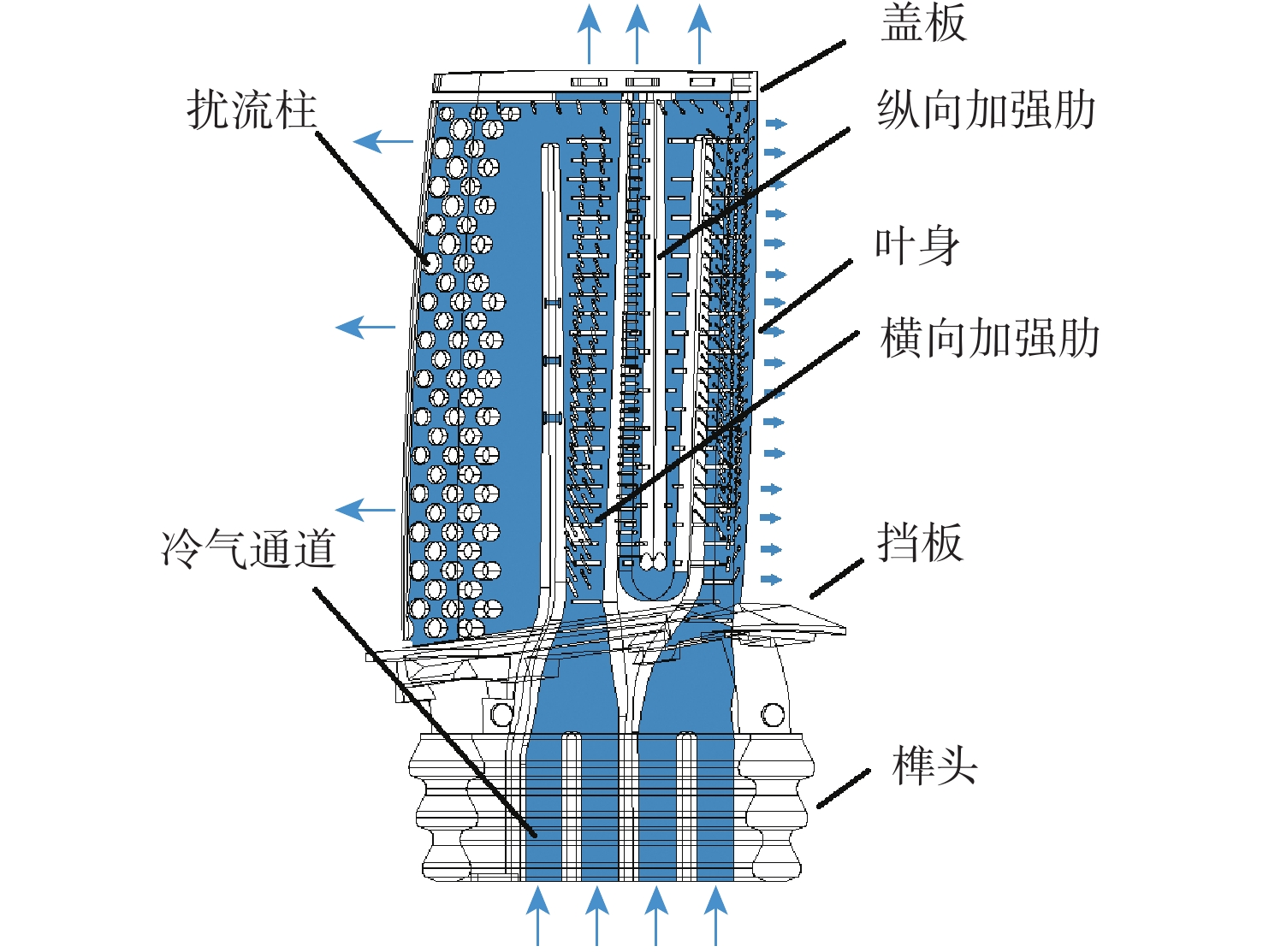
涡轮叶片的寿命可靠性优化对保障发动机安全，提高发动机使用寿命具有重要意义。传统的确定性优化由于没有考虑不确定性因素的影响，其结果往往导致结构可靠性低，严重威胁发动机的安全。针对复杂的含气膜孔几何变量的涡轮叶片几何构型，提出局部参数化网格变形方法，在关注的叶片前缘部分采用六面体网格，并利用局部网格变形法实现其参数化变形，其他部分采用四面体网格，以缩短其网格划分时间，提高其网格划分效率。所提方法实现了不确定条件下的含气膜孔几何变量涡轮叶片的寿命可靠性优化，在满足可靠性约束和几何约束的条件下，使得涡轮叶片基于不确定性的寿命均值提高了18.36%。
Abstract:The optimization of the life reliability of turbine blades is of great significance for the safety and service life improvement of aeroengines. The traditional deterministic optimization method does not consider the influence of uncertain factors, which tends to cause low structural reliability, seriously threatening the safety of the aeroengine. Thus, this paper focuses on the life reliability-based optimization of the turbine blade in uncertain environments. A local mesh deformation method is proposed for the turbine blade with geometric variables of the film hole to realize mesh parameterization. Based on the proposed method, the life reliability-based optimization of the turbine blade with film hole geometric variables is achieved under uncertain conditions. With satisfying reliability constraints and geometric constraints, the average lifetime value of turbine blades based on uncertainty is increased by 18.36%.
-
图 8 最大工作状态叶身温度分布
Figure 8. Temperature distribution of turbine blade in the maximum working condition
图 10 寿命可靠性设计优化的流程图
Figure 10. Flow chart of life reliability-based design optimization
图 11 完全解耦法建立代理模型的流程图
Figure 11. Flow chart of the surrogate model using full decoupling method
表 1 ANSYS软件网格质量检查结果
Table 1. Results of mesh quality check from ANSYS software
检查指标 网格数量 占比/%
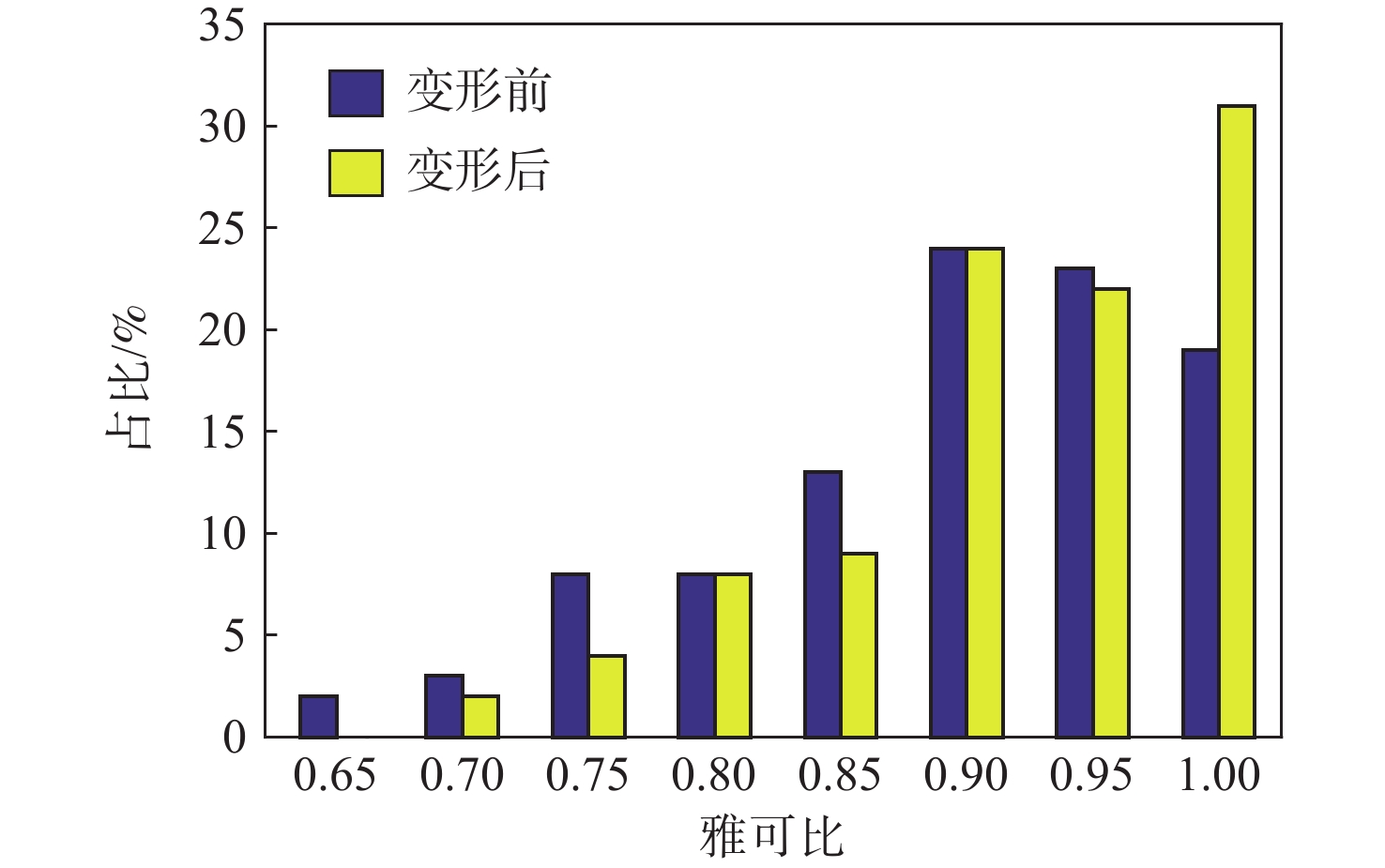
（低质量+畸形）检查总数 低质量 畸形 长宽比 2 283 364 24 0 0 平行偏差 188 393 10 0 0.01 最大角度 2 283 364 201 0 0.01 雅可比 2 283 364 0 0 0 翘曲因子 188 393 0 0 0 合计 2 283 364 235 0 0.01 
下载: 导出CSV
表 2 DZ125合金的材料属性
Table 2. Material properties of DZ125 alloy
温度T/℃ 弹性模量$E/{\text{GPa}} $ 泊松比$\nu $ 剪切模量$ G/{\text{GPa}} $ 线膨胀系数$ \alpha $/℃−1 横向 纵向 横向 纵向 横向 纵向 横向 纵向 20 176.5 127.0 0.26 0.410 70.0 107.0 12.27 12.45 500 161.5 112.5 0.27 0.410 63.5 101.5 13.03 13.26 600 151.5 108.5 0.27 0.415 59.5 97.5 13.39 13.53 700 145.5 104.5 0.29 0.430 56.5 92.5 13.91 14.04 800 139.5 102.0 0.29 0.430 52.5 90.5 14.43 14.55 900 135.0 97.0 0.3 0.435 52.0 89.0 14.96 15.06 1000 123.0 89.0 0.31 0.450 46.5 72.5 15.84 16.02
下载: 导出CSV
温度T/℃ 密度ρ/（kg·m−3） 热导率$\lambda $/(W·(m·℃)−1) 屈服强度$\sigma_{0.2}/{\rm{MPa}} $ 拉伸极限$\sigma_{b}/{\rm{MPa}} $ 横向 纵向 横向 纵向 20 8570 840 985 1090 1320 500 14.99 600 16.79 700 17.96 775 930 975 1220 800 19.63 785 933 933 1130 900 19.51 665 580 808 850 1000 19.43 420 395 560 575 注：下标b表示抗拉强度。
下载: 导出CSV
表 3 发动机典型循环载荷谱
Table 3. Typical cycle load spectrum of the aeroengine
工作循环 工作转速/
(r·min−1)每900 h
循环次数每周运行
时间/min启动-最大-停车 0,21842,0 1014 53.25 慢车-最大-慢车 11125,21842,11125 1190 3.80 巡航-最大-巡航 13357,21842,13357 1053 0.33
下载: 导出CSV
表 4 叶片校核点处的热力耦合分析响应
Table 4. Thermal-mechanical response at the check point of the turbine blade
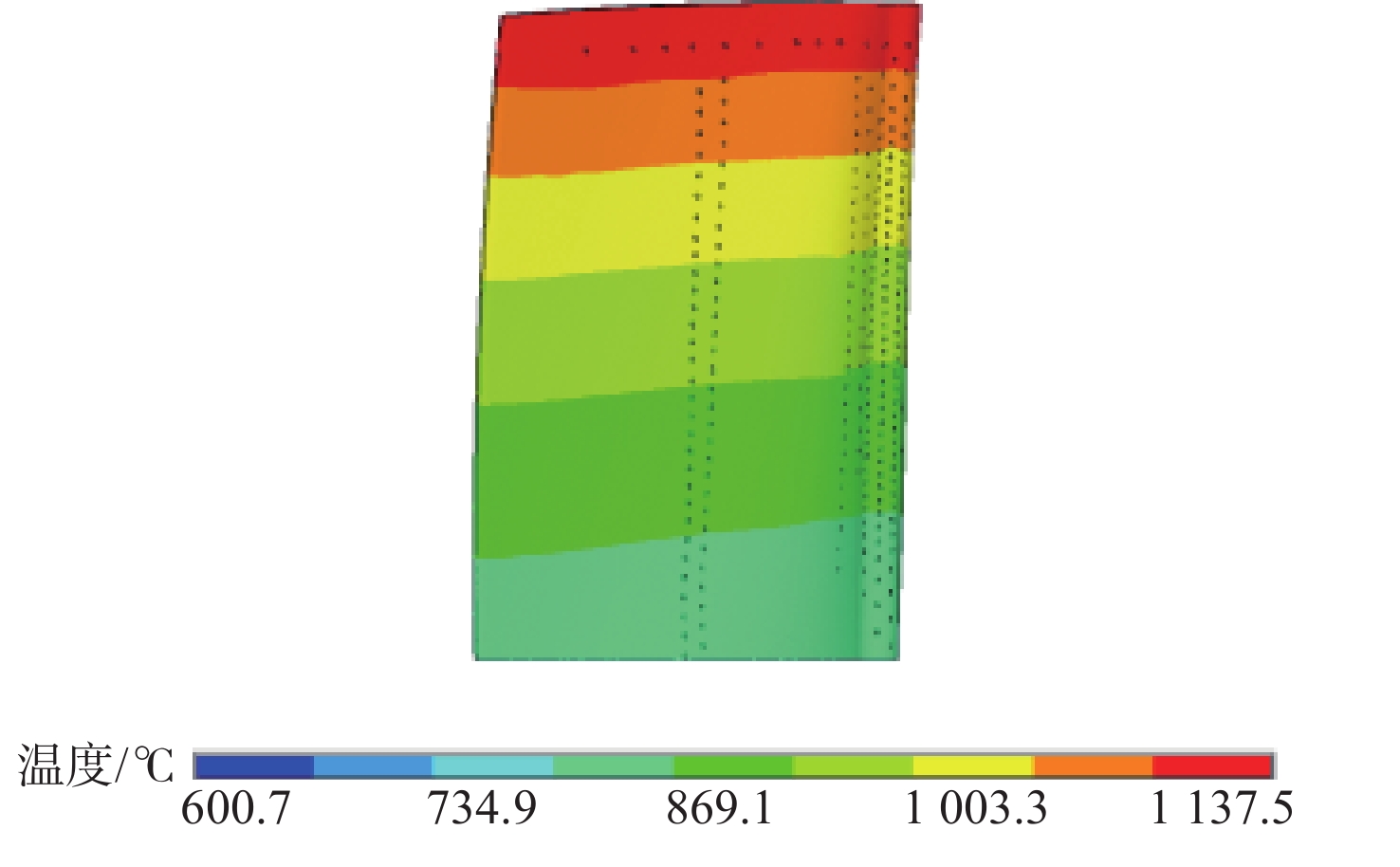
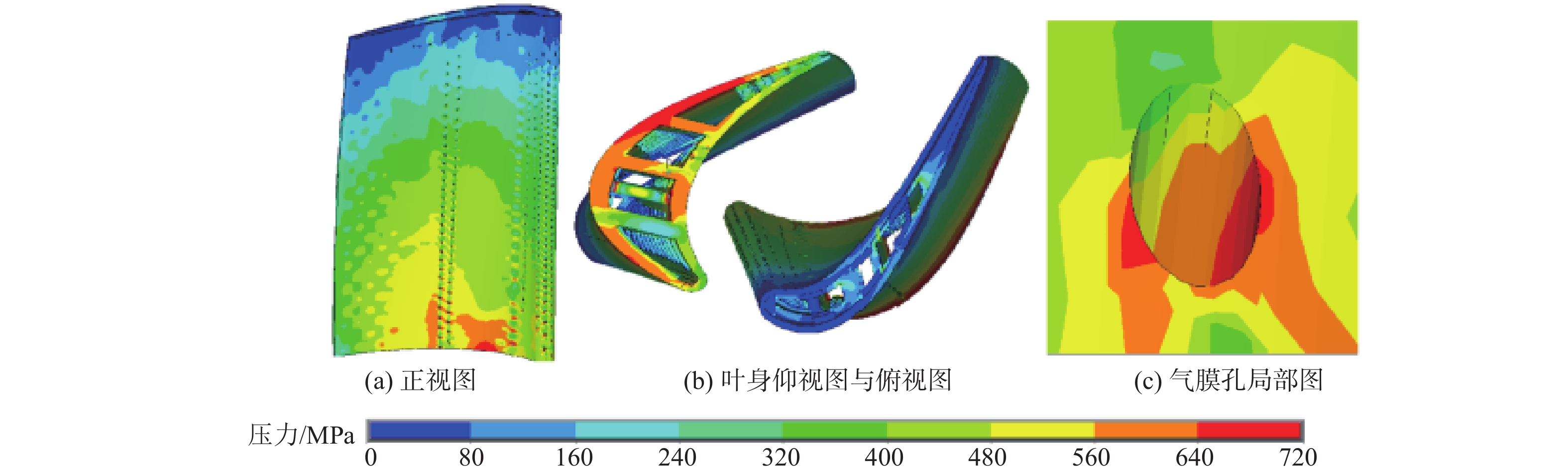
工作状态 转速/(r·min−1) 温度T/℃ 最大等效应力 $ \sigma {\text{/MPa}} $ 总应变$ \varepsilon $ 最大状态 21 842 817.307 5 796.075 2 0.0111 慢车状态 11 125 659.808 7 352.165 4 0.002 7 巡航状态 13 357 663.506 6 461.846 8 0.003 6
下载: 导出CSV
表 5 叶片校核点处的振动响应
Table 5. Vibration response at the check point of the turbine blade
工作状态 转速/(r·min−1) 激振频率/Hz 最大等效振动应力$ \sigma {\text{/MPa}} $ 最大状态 21 842 5096.466 7 178.324 1 慢车状态 11 125 2595.833 3 15.3682 巡航状态 13 357 3116.633 3 17.1643
下载: 导出CSV
表 6 涡轮叶片寿命可靠性优化结果
Table 6. Life reliability-based optimization results for turbine blade
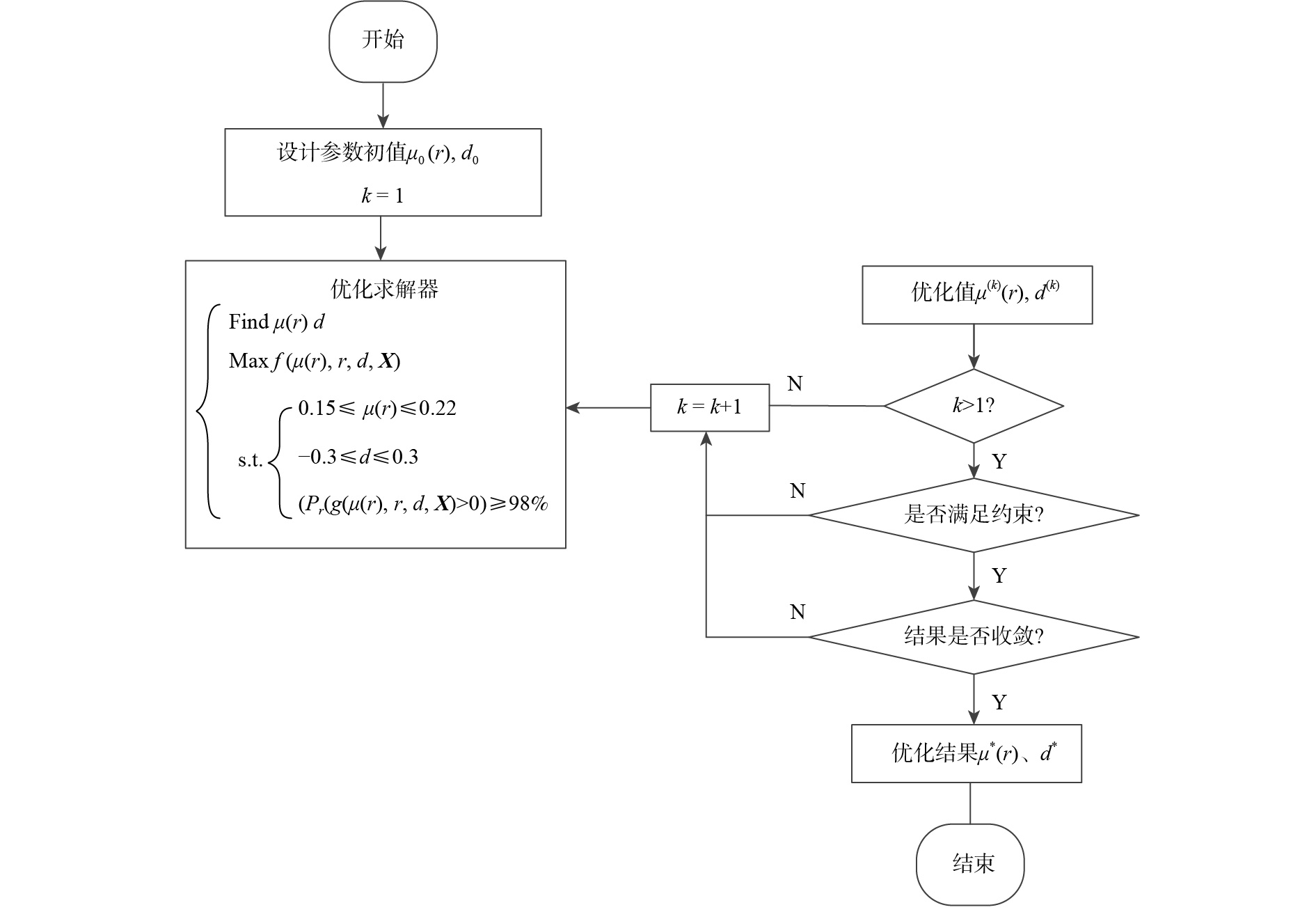
类型 $r$/mm $d$/mm $ \mu \left( N \right) $ 初值 0.215 0 13081 优化值 0.214 −0.199 15483
下载: 导出CSV
-
[1] 赵福星, 李伟. 国产涡喷发动机叶片断裂故障排故实践[C]//航空发动机叶片故障及预防研讨会论文集, 2005: 144-148.ZHAO F X, LI W. Practice on fracture failure troubleshooting for domestic turbojet engine blades[C]//Proceedings of Aeroengine Blade Failure and Prevention Seminar, 2005: 144-148(in Chinese). [2] 王卫国. 轮盘低循环疲劳寿命预测模型和试验评估方法研究[D]. 南京: 南京航空航天大学, 2006.WANG W G. Research on prediction model for disc LCF life and experiment assessment methodology[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2006 (in Chinese). [3] SOKOLOWSKI D E. Toward improved durability in advanced aircraft engine hot sections[C]//Proceedings of the Thirty-third ASME International Gas Turbine and Aeroengine Congress and Exposition. New York: ASME, 1988 [4] JUVINALL R C. Engineering considerations of stress, strain, and strength[M]. New York: McGraw-Hill, 1967. [5] LEWIS B L, BECKWITH L R. A unified approach to turbine blade life prediction[C]//SAE Technical Paper Series. Warrendale: SAE International, 1982. [6] 段巍, 安利强, 徐飞. 基于随机有限元——一次二阶矩法的汽轮机叶片可靠度计算[J]. 华北电力大学学报, 2004, 31(3): 104-107.DUAN W, AN L Q, XU F. Reliability calculation of steam turbine blade based on SFEM and mean-variance method[J]. Journal of North China Electric Power University, 2004, 31(3): 104-107(in Chinese). [7] 段巍, 王璋奇. 基于响应面方法的汽轮机叶片静动频概率设计及敏感性分析[J]. 中国电机工程学报, 2007, 27(20): 12-17.DUAN W, WANG Z Q. Probability design of static frequency and dynamic frequency for steam turbine blade and sensitivity analysis based on the response surface method[J]. Proceedings of the CSEE, 2007, 27(20): 12-17(in Chinese). [8] 费成巍, 白广忱. 航空发动机涡轮叶片径向变形的概率分析[J]. 航空发动机, 2012, 38(1): 17-20.FEI C W, BAI G C. Probabilistic analysis of turbine blade radial deformation for aeroengine[J]. Aeroengine, 2012, 38(1): 17-20(in Chinese). [9] 周平, 白广忱. 基于神经网络与果蝇优化算法的涡轮叶片低循环疲劳寿命健壮性设计[J]. 航空动力学报, 2013, 28(5): 1013-1018.ZHOU P, BAI G C. Robust design of turbine-blade low cycle fatigue life based on neural networks and fruit fly optimization algorithm[J]. Journal of Aerospace Power, 2013, 28(5): 1013-1018(in Chinese). [10] 李磊, 李宏林, 杨子龙, 等. 基于网格参数化变形的单级涡轮多学科可靠性设计优化[J]. 航空动力学报, 2019, 34(8): 1764-1772.LI L, LI H L, YANG Z L, et al. Reliability based multidisciplinary design optimization of single turbine stage based on parameterized mesh deformation[J]. Journal of Aerospace Power, 2019, 34(8): 1764-1772(in Chinese). [11] TRUONG A H, OLDFIELD C A, ZINGG D W. Mesh movement for a discrete-adjoint newton-krylov algorithm for aerodynamic optimization[J]. AIAA Journal, 2008, 46(7): 1695-1704. doi: 10.2514/1.33836 [12] 周正贵. 高亚声速压气机叶片优化设计[J]. 推进技术, 2004, 25(1): 58-61.ZHOU Z G. Optimization of high subsonic axial compressor blades[J]. Journal of Propulsion Technology, 2004, 25(1): 58-61(in Chinese). [13] 李立州, 王婧超, 韩永志, 等. 基于网格变形技术的涡轮叶片变形传递[J]. 航空动力学报, 2007, 22(12): 2101-2104.LI L Z, WANG J C, HAN Y Z, et al. Displacement transfer with the mesh deformation method in multidisciplinary optimization of turbine blades[J]. Journal of Aerospace Power, 2007, 22(12): 2101-2104(in Chinese). [14] 史振. 燃气涡轮叶片复合冷却结构参数化设计与数值研究[D]. 哈尔滨: 哈尔滨工业大学, 2015.SHI Z. Parametric design and numerical research of gas turbine cooling structure[D]. Harbin: Harbin Institute of Technology, 2015 (in Chinese). [15] 杨帆. 基于网格参数化的涡轮冷却叶片可靠性多学科设计优化[D]. 西安: 西北工业大学, 2016.YANG F. Multidisciplinary design optimization of turbine cooling blade reliability based on grid parameterization[D]. Xi’an: Northwestern Polytechnical University, 2016 (in Chinese). [16] 岳孟赫, 刘勇, 刘闯, 等. 涡轮冷却叶片参数化造型与网格自动生成[J]. 航空发动机, 2017, 43(6): 15-20.YUE M H, LIU Y, LIU C, et al. Parameterized molding design and grid auto-generation for cooling turbine blade[J]. Aeroengine, 2017, 43(6): 15-20(in Chinese). [17] 凌春燕, 吕震宙, 员婉莹. 失效概率函数求解的高效算法[J]. 国防科技大学学报, 2018, 40(3): 159-167.LING C Y, LYU Z Z, YUAN W Y. Efficient method for failure probability function[J]. Journal of National University of Defense Technology, 2018, 40(3): 159-167(in Chinese). [18] ECHARD B, GAYTON N, LEMAIRE M. AK-MCS: An active learning reliability method combining kriging and monte carlo simulation[J]. Structural Safety, 2011, 33(2): 145-154. doi: 10.1016/j.strusafe.2011.01.002 -
下载:
点击查看大图
计量
- 文章访问数: 293
- HTML全文浏览量: 19
- PDF下载量: 31
- 被引次数: 0
