-
摘要:
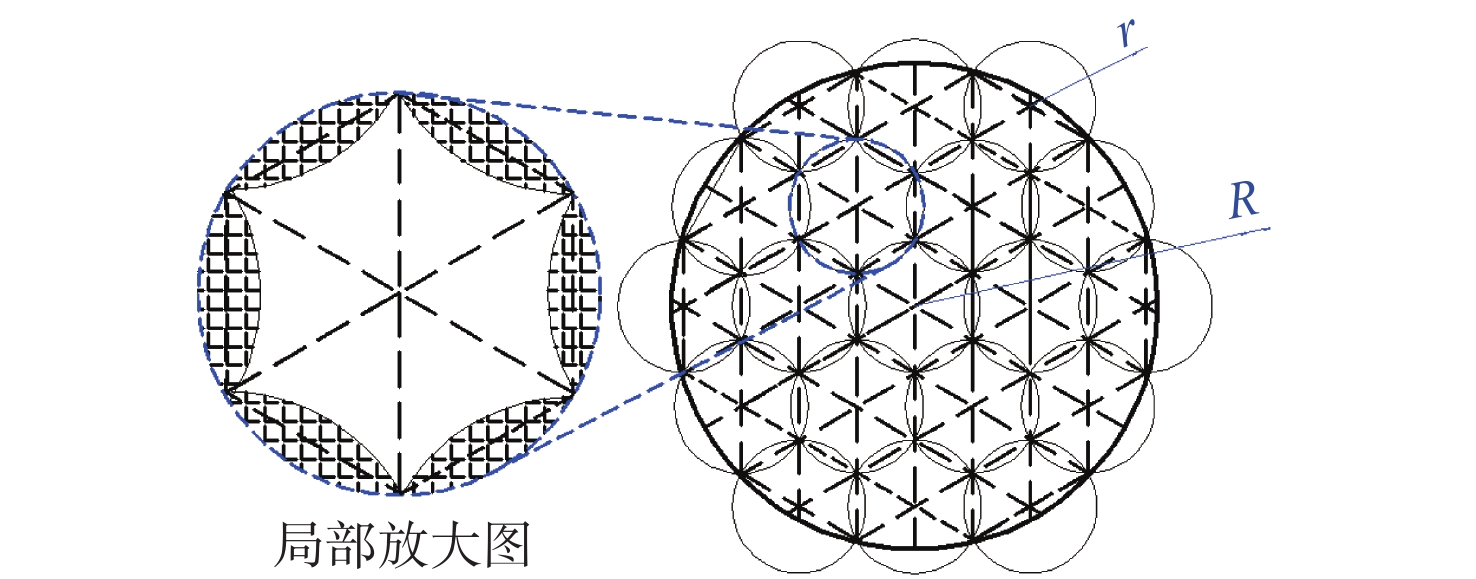
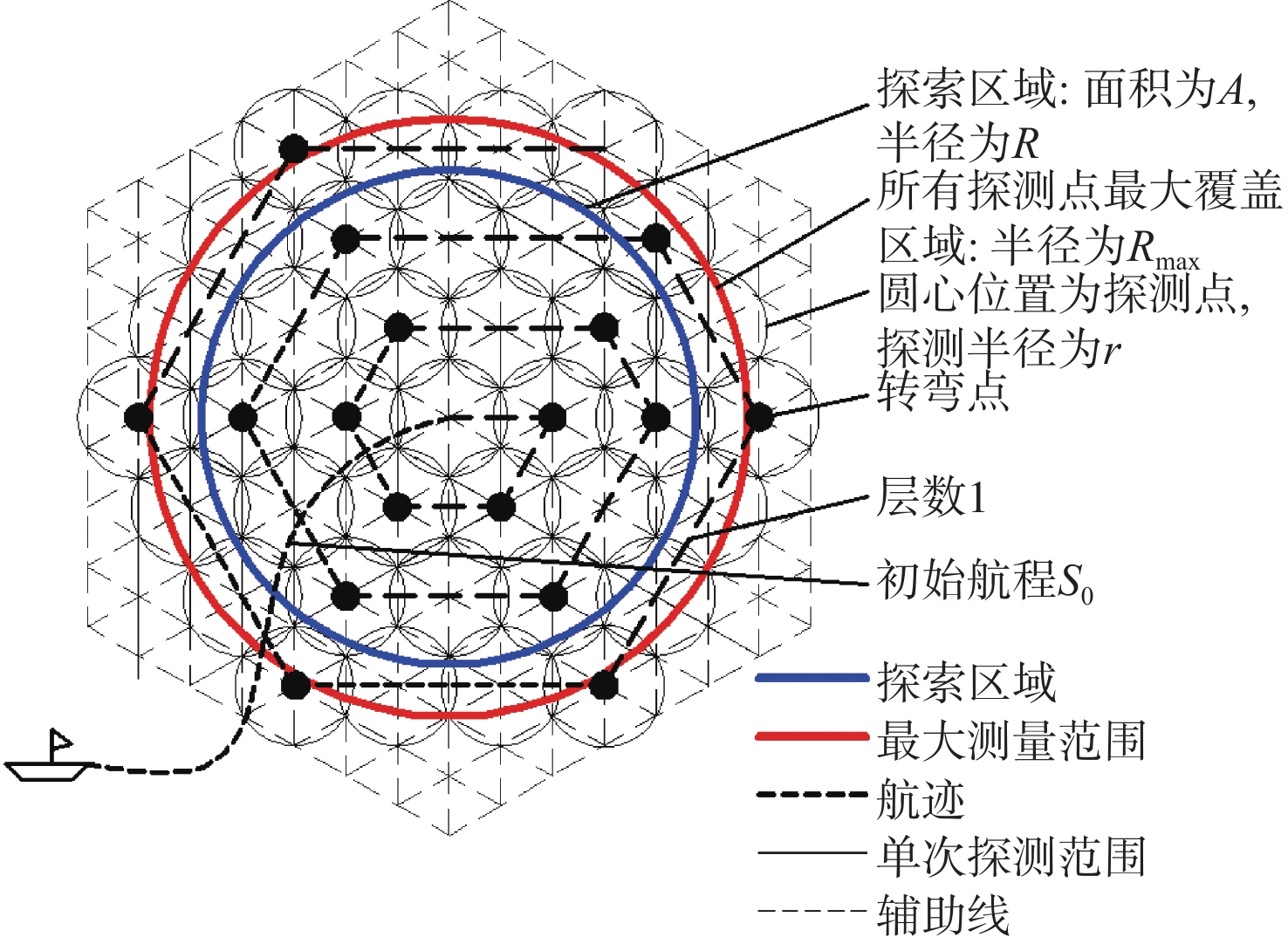
海上搜索、航空反潜等海上活动经常需要对目标海域进行全面搜索，在研究扩展方形搜索方法的缺点后，提出采用基于蜂窝结构的扩展六边形搜索方法。从理论上分析2种方法的搜索效率、探测次数、所需航程和重复搜索面积等内容；证明了当目标搜索区域半径大于某值时，所提方法明显优于扩展方形搜索方法，并给出了该值的计算方法。通过仿真验证了理论分析的正确性，为海上搜索任务提供了更为高效的搜寻方法，同时为无人化自动搜索提供理论基础和参考依据。
Abstract:Maritime search, aviation anti-submarine, and other maritime activities often need to comprehensively search the target sea area. After studying the shortcomings of the expanding square search method, an expanding hexagon search method based on the cellular structure is proposed. A theoretical analysis of the two approaches’ search effectiveness, detection times, needed range, and repeated search area is done. It is proved that when the radius of the target search area is greater than a certain value, the expanding hexagon search method is obviously better than the expanding square, and the calculation method of the value is given. The correctness of the theoretical analysis is verified by simulation.This results in a more effective search strategy for marine search jobs as well as a theoretical foundation and reference point for future unmanned automatic search.
-
图 9 ${\varDelta }_{\Delta t}$的取值范围
Figure 9. Range of values of $ {\varDelta }_{\Delta t} $
图 10 ${t}_{m}、{t}_{s}、{t}_{{\textit{z}}}$对$ \Delta t $影响
Figure 10. Effect of ${t}_{m}、{t}_{s}、{t}_{{\textit{z}}}$ on $ \Delta t $
表 1 本文方法主要参数规律
Table 1. Main parameters of proposed method
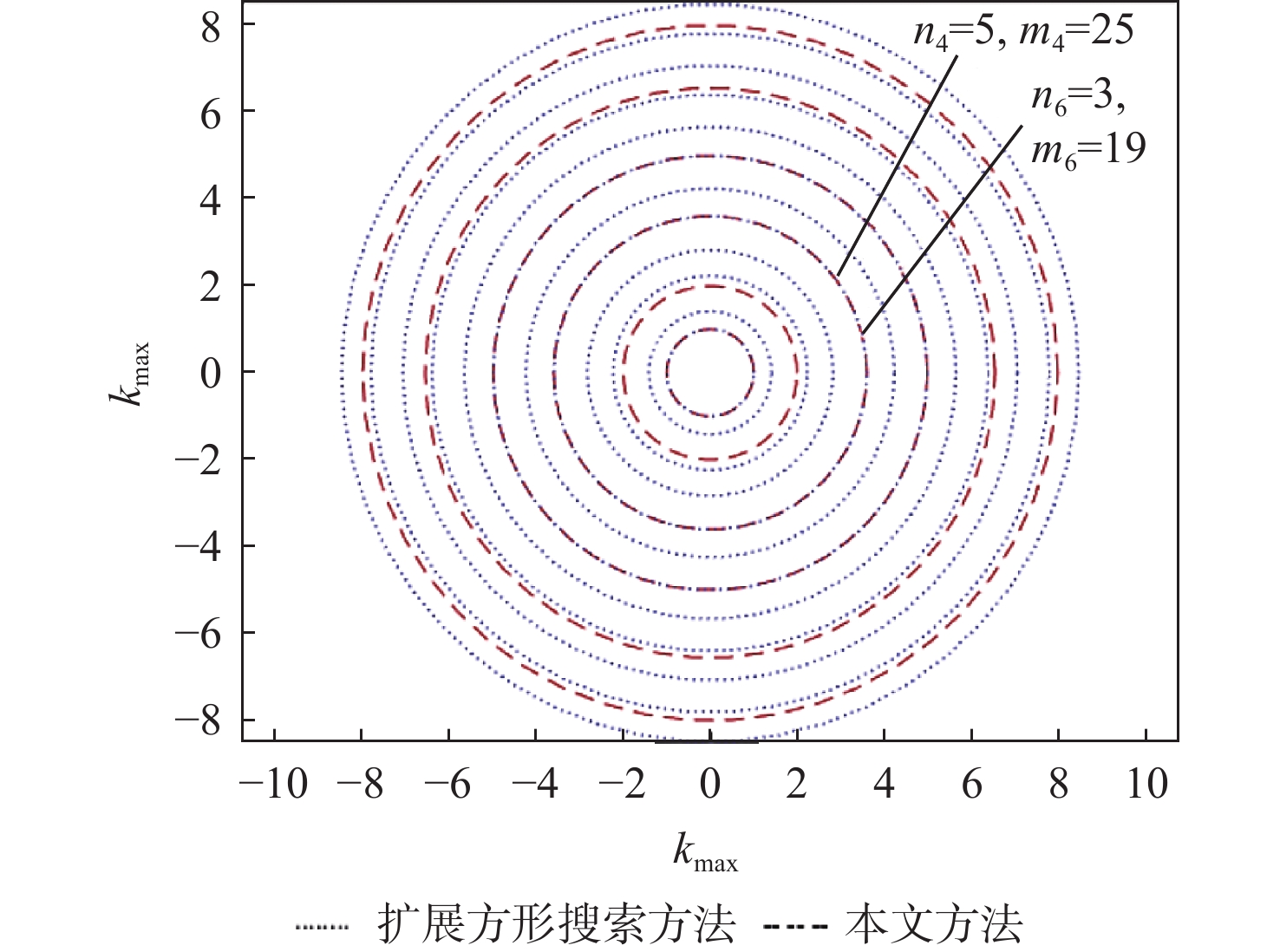
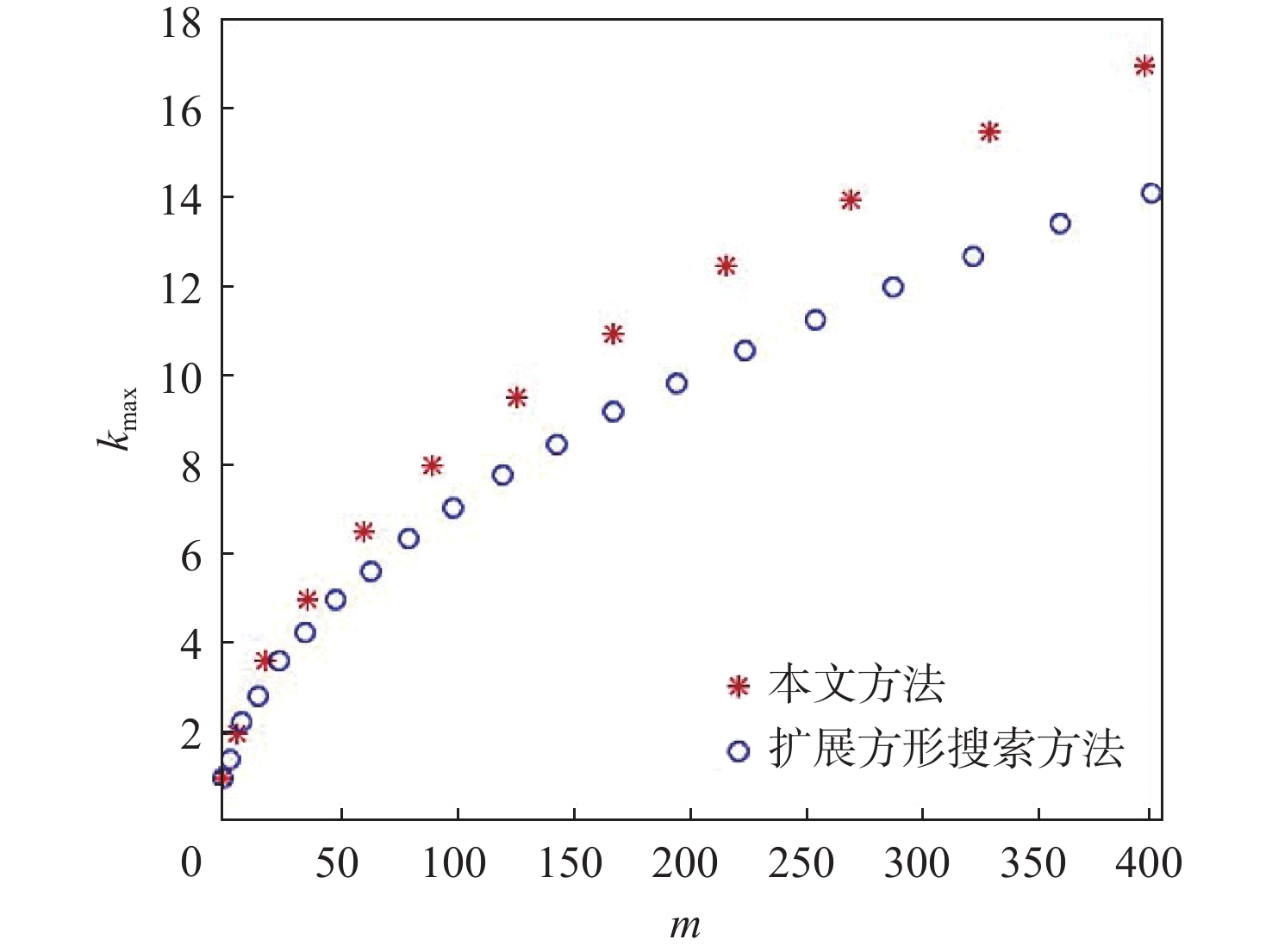
层数l 探测次数m 航程s 转弯次数z 1 1 $ {s}_{0} $ 0 2 7 $ {s}_{0}+6\sqrt{3}r $ 5 3 19 $ {s}_{0}+18\sqrt{3}r $ 11 $\vdots$ $\vdots$ $\vdots$ $\vdots$ $ {n}_{6} $ $ 3{{n}_{6}}^{2}-3{n}_{6}+1 $ $ {s}_{0}+3\sqrt{3}({{n}_{6}}^{2}-{n}_{6})r $ $ 6\left({n}_{6}-1\right)-1 $ 
下载: 导出CSV
表 2 扩展方形搜索方法主要参数规律
Table 2. Extended square search method main parameter law
层数l 探测次数m 航程s 转弯次数z 1 1 $ {s}_{0} $ 0 2 4 $ {s}_{0}+3\sqrt{2}r $ 2 3 9 $ {s}_{0}+8\sqrt{2}r $ 4 $\vdots$ $\vdots$ $\vdots$ $\vdots$ $ {n}_{4} $ $ {{n}_{4}}^{2} $ $ {s}_{0}+\sqrt{2}({{n}_{4}}^{2}-1)r $ $ 2\left({n}_{4}-1\right) $
下载: 导出CSV
表 3 动态目标搜索效能对比
Table 3. Dynamic target search performance comparison
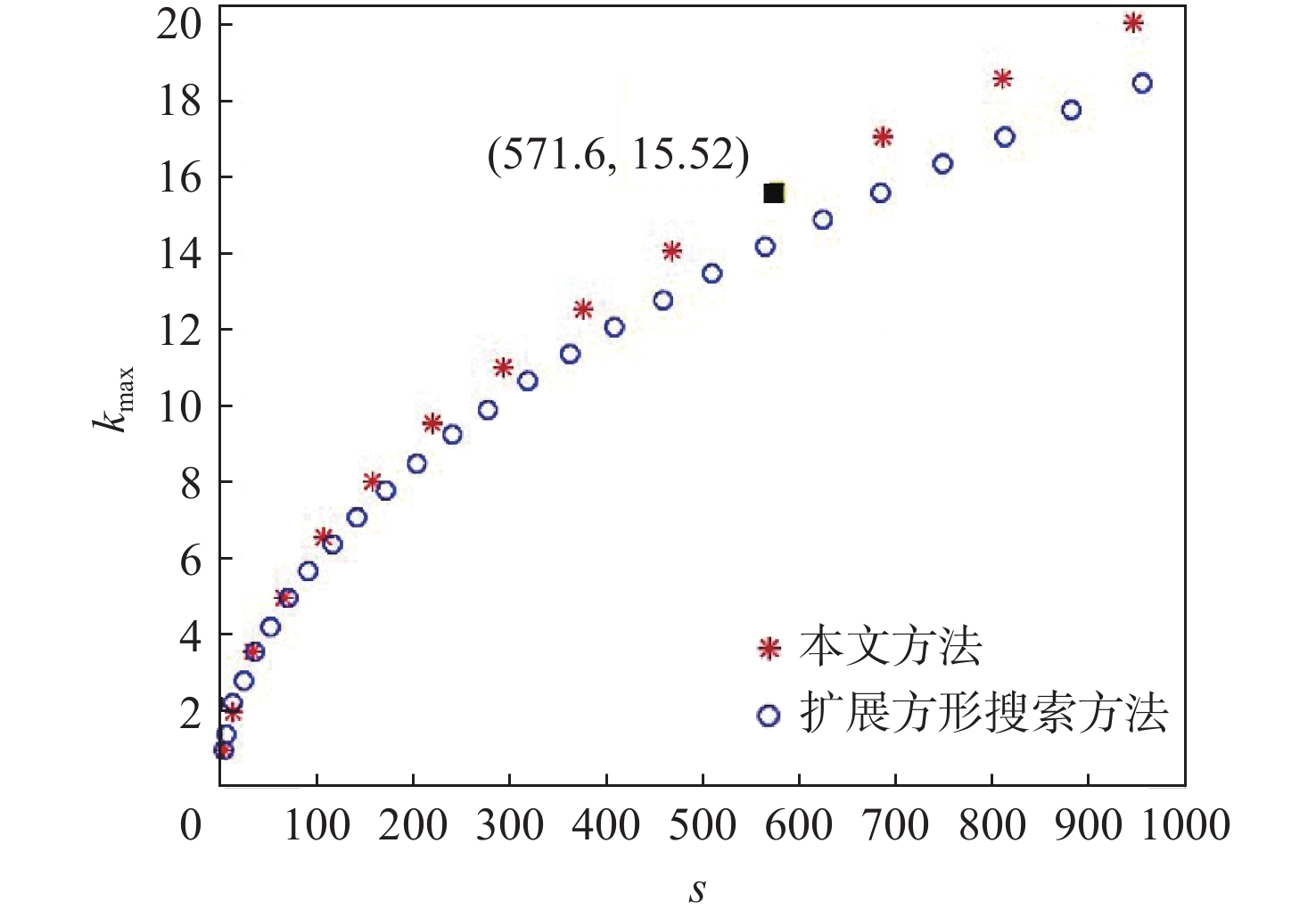
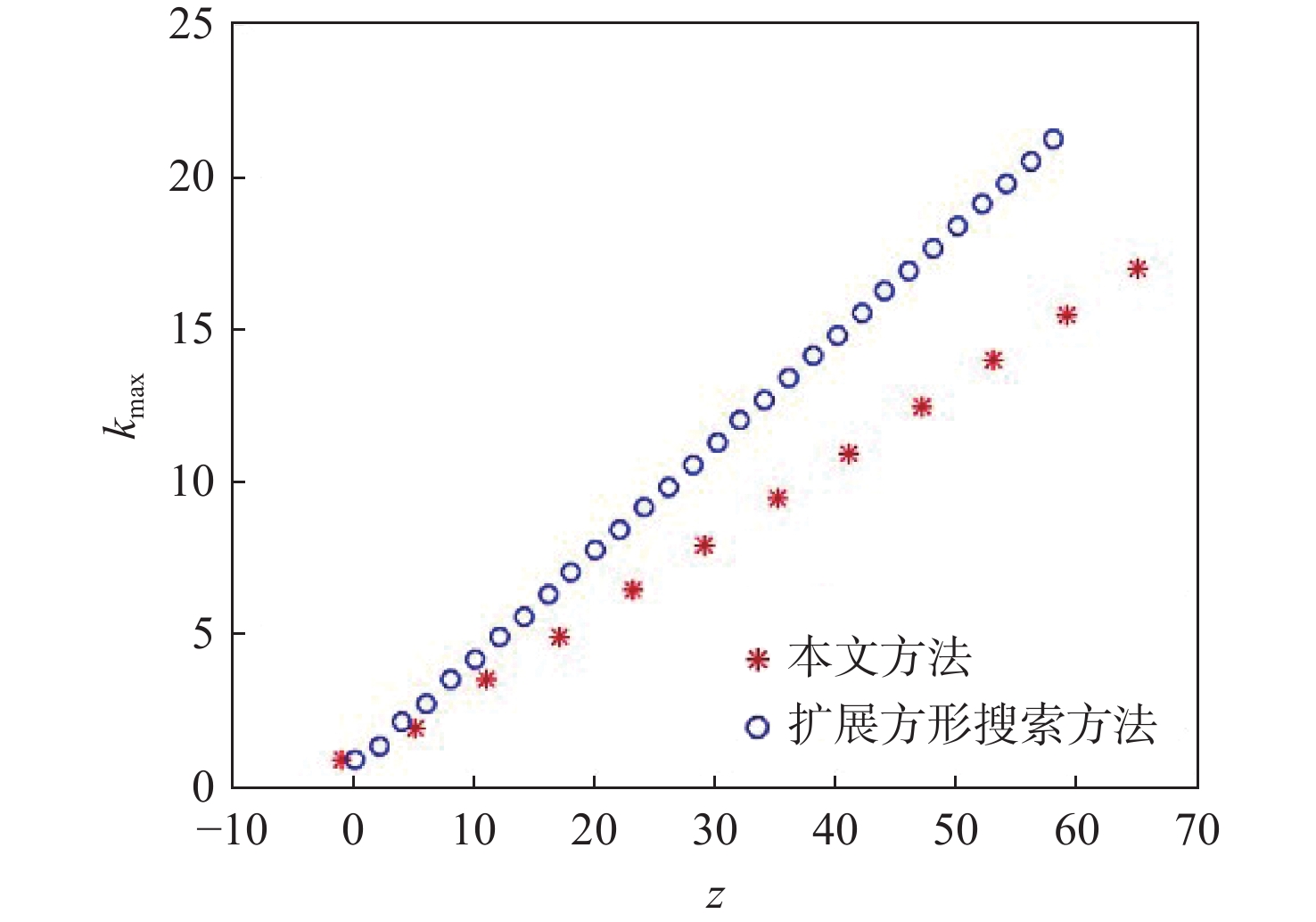
方法 平均探测次数/次 平均探测时间/h 平均航程/km 本文方法 14.74 2.77 88.15 扩展方形搜索方法 18.70 3.44 92.70
下载: 导出CSV
表 4 静态目标搜索效能对比
Table 4. Static target search performance comparison
方法 平均探测次数/次 平均搜索时间/h 平均航程/km 本文方法 9.73 6.14 42.02 扩展方形搜索方法 11.53 6.99 41.36
下载: 导出CSV
-
[1] 吴芳, 吴铭, 杨日杰. 反潜机吊放声纳扩展螺旋线形搜潜建模[J]. 北京航空航天大学学报, 2011, 37(9): 1137-1141.WU F, WU M, YANG R J. Building extended spirality searching model of dipping sonar of anti-submarine airplane[J]. Journal of Beijing University of Aeronautics and Astronautics, 2011, 37(9): 1137-1141(in Chinese). [2] SMITH T J. Two evaluative models for a family of submarine versus submarine expanding square search plans[D]. Monterey: Naval Postgraduate School Monterey CA, 1973. [3] 张发强, 孙建华. 舰载直升机在护航编队中对海盗目标预警的使用研究[J]. 舰船电子工程, 2010, 30(11): 7-9.ZHANG F Q, SUN J H. Research on the service that the ship-board aircraft searching the viking targets in the escort formation[J]. Ship Electronic Engineering, 2010, 30(11): 7-9(in Chinese). [4] 艾兵, 杨睿. 直升机海上搜索航路辅助规划算法[J]. 电光与控制, 2017, 24(11): 91-94.AI B, YANG R. An algorithm of auxiliary route planning for helicopter marine search[J]. Electronics Optics & Control, 2017, 24(11): 91-94(in Chinese). [5] 中国海上搜救中心. 国家海上搜救手册[M]. 大连: 大连海事大学出版社, 2011.CHINA MRCC, National maritime SAR manual of China [M]. Dalian: Dalian Maritime University Press, 2011 (in Chinese). [6] IMO/ICAO. International aeronautical and maritime search and rescue manual—Volume III mobile facilities: Doc 9731-3 [S]. London/Montreal : IMO/ICAO, 2003. [7] KASYK L, PLESKACZ K, BUGAJSKI G. An analysis of discrepancies in search areas in a diagram of an expanding square search[J]. Zeszyty Naukowe Akademii Morskiej w Szczecinie, 2016, 45(117): 94-98. [8] LIANG X D, LI L Y, WU J G, et al. Mobile robot path planning based on adaptive bacterial foraging algorithm[J]. Journal of Central South University, 2013, 20(12): 3391-3400. doi: 10.1007/s11771-013-1864-5 [9] SILJANDER M, VENÄLÄINEN E, GOERLANDT F, et al. GIS-based cost distance modelling to support strategic maritime search and rescue planning: A feasibility study[J]. Applied Geography, 2015, 57: 54-70. doi: 10.1016/j.apgeog.2014.12.013 [10] YANG T T, JIANG Z, SUN R J, et al. Maritime search and rescue based on group mobile computing for unmanned aerial vehicles and unmanned surface vehicles[J]. IEEE Transactions on Industrial Informatics, 2020, 16(12): 7700-7708. doi: 10.1109/TII.2020.2974047 [11] MATOS A, MARTINS A, DIAS A, et al. Multiple robot operations for maritime search and rescue in euRathlon 2015 competition[C]// OCEANS 2016 - Shanghai. Piscataway: IEEE Press, 2016: 1-7. [12] AGBISSOH OTOTE D, LI B S, AI B, et al. A decision-making algorithm for maritime search and rescue plan[J]. Sustainability, 2019, 11(7): 2084. doi: 10.3390/su11072084 [13] AKBARI A, PELOT R, EISELT H A. A modular capacitated multi-objective model for locating maritime search and rescue vessels[J]. Annals of Operations Research, 2018, 267(1-2): 3-28. doi: 10.1007/s10479-017-2593-1 [14] 孙明太, 王涛, 赵绪明. 反潜直升机吊声搜潜效能的建模仿真[J]. 火力与指挥控制, 2005, 30(3): 33-36.SUN M T, WANG T, ZHAO X M. Modeling and simulation the efficiency of the dipping sonar on the antisubmarine helicopter[J]. Fire Control & Command Control, 2005, 30(3): 33-36(in Chinese). [15] 邱平. 海上最佳搜寻区域与搜寻方法的研究[D]. 大连: 大连海事大学, 2006.QIU P. A numerical study on the optimal search area and search patterns over sea[D]. Dalian: Dalian Maritime University, 2006 (in Chinese). [16] AKBARI A, EISELT H A, PELOT R. A maritime search and rescue location analysis considering multiple criteria, with simulated demand[J]. INFOR:Information Systems and Operational Research, 2018, 56(1): 92-114. doi: 10.1080/03155986.2017.1334322 [17] KERSHNER R. The number of circles covering a set[J]. American Journal of Mathematics, 1939, 61(3): 665. doi: 10.2307/2371320 [18] ONGGO B S, KARATAS M. Test-driven simulation modelling: A case study using agent-based maritime search-operation simulation[J]. European Journal of Operational Research, 2016, 254(2): 517-531. doi: 10.1016/j.ejor.2016.03.050 -
下载:
点击查看大图
计量
- 文章访问数: 82
- HTML全文浏览量: 8
- PDF下载量: 8
- 被引次数: 0
