-
摘要:
柱塞泵摩擦副多场耦合建模及求解是柱塞泵失效机理研究及可靠性提升的基础，针对双斜式柱塞泵球面配流副多场耦合模型求解难的问题，提出油膜厚度场-压力场-温度场动态耦合模型及求解方法。在球面配流副受力分析的基础上结合雷诺方程和能量方程建立球面配流副油膜厚度场-压力场-温度场耦合模型；基于有限差分法和牛顿迭代法求解动态耦合模型，温度场、压力场、厚度场间相互耦合变化；通过仿真求解，与现有模型进行对比，结果相近且更符合实际，验证了所提模型及求解方法的有效性。
-
关键词:
- 双斜式柱塞泵 /
- 球面配流副 /
- 厚度场-压力场-温度场耦合模型 /
- 有限差分法 /
- 牛顿迭代法
Abstract:The multi-field coupling modeling and solution of the friction pair of the piston pump is the basis for the study of the failure mechanism of the piston pump and the improvement of its reliability. To resolve the difficulty, in solving the multi-field coupling model of the spherical port pair of the double-oblique-type axial piston pump, a dynamic coupling model of oil film thickness field-pressure field-temperature field and its solution method are proposed. First, based on the force analysis of the spherical port pair, the Reynolds equation and the energy equation are combined to establish a coupling model of the thickness field-pressure field-temperature field of the spherical port pair. Secondly, the dynamic coupling model is solved based on the finite difference method. Finally, the simulation is compared with the existing model to verify the effectiveness of the proposed model and solution method.
-
轴向柱塞泵具有高效率和高功重比的优势[1]，在军工[2]、船舶[3]、工程机械[4]等领域得到了广泛的应用。其中高压大流量柱塞泵作为机械设备的关键基础件，在机电设备制造业受到格外重视。摩擦副是高压大流量柱塞泵的薄弱环节之一[5]，有必要研究其多场耦合模型及求解方法，为高压大流量柱塞泵失效机理的研究和可靠性提升奠定基础[6]。
通常，高压大流量柱塞泵为改善摩擦副的受力形式，其结构与传统的柱塞与转轴平行的柱塞泵不同，其柱塞与转轴有一定的倾斜角度，且配流副为球面。此类轴向柱塞泵简称双斜式柱塞泵[7-8]。这种形式具有结构紧凑、体积小、承载面积大、受力状况好、抗倾覆力矩能力强等优点，国内外众多学者对其开展了大量的研究。文献[9-11]基于雷诺平均 Navier-Stokes方程对球面配流副的压力场进行了积分计算，考虑了球坐标系中与z轴夹角方向的压力场变化，未考虑在xy平面投影与x轴夹角方向的压力场变化。李小金等[12]建立基于球面坐标系的贴体坐标系，并基于贴体坐标系建立球面配流副的雷诺方程，利用有限差分法求解雷诺方程，得到球面配流副的二维稳态压力场，但并未考虑温度场对油液黏度及压力场的影响。Deng等[13-14]对回程盘的球轴承副进行球面雷诺方程压力场分析，并对柱塞泵泄漏量及磨损量进行研究，同样未考虑温度场对油液黏度的影响。
在柱塞泵运转过程中，温度直接影响油液黏度，进而影响摩擦副中压力场和油膜厚度场的分布。因此，为分析柱塞泵性能，有必要建立考虑厚度场-压力场-温度场的动态耦合模型。但是，高压大流量柱塞泵特殊的球面配流副结构使得多场耦合模型的建立及求解变得困难，有必要进行深入研究。
综上，以双斜式柱塞泵为研究对象，在考虑温度对油液黏度的影响、金属表面热变形和底面流体压力引起的弹性变形的基础上，建立球面配流副油膜厚度场-压力场-温度场动态耦合模型[15-16]，基于有限差分法求解微分方程的数值解，最后通过仿真方法验证提出的多场耦合模型的有效性和正确性。
1. 柱塞受力分析
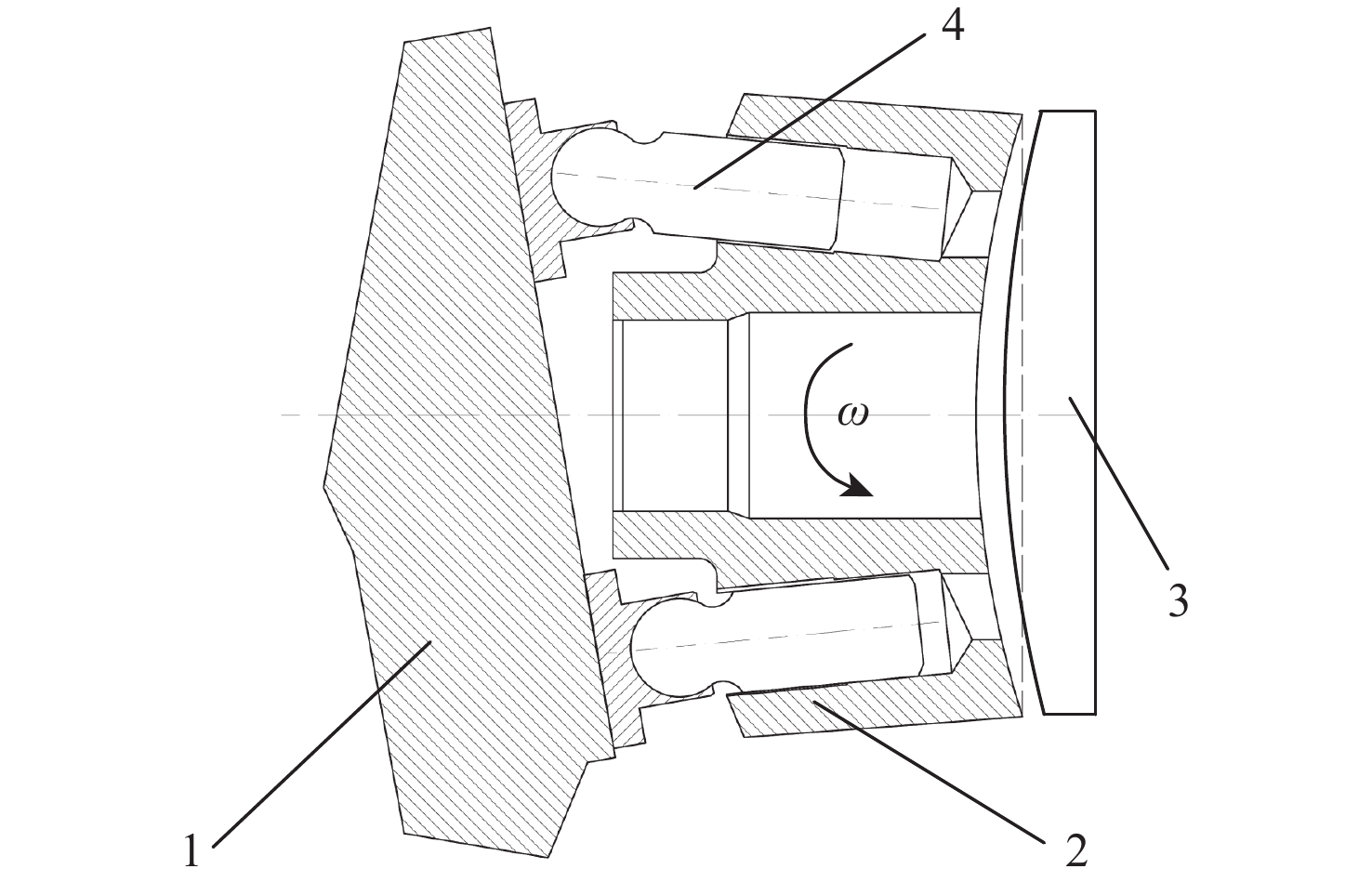
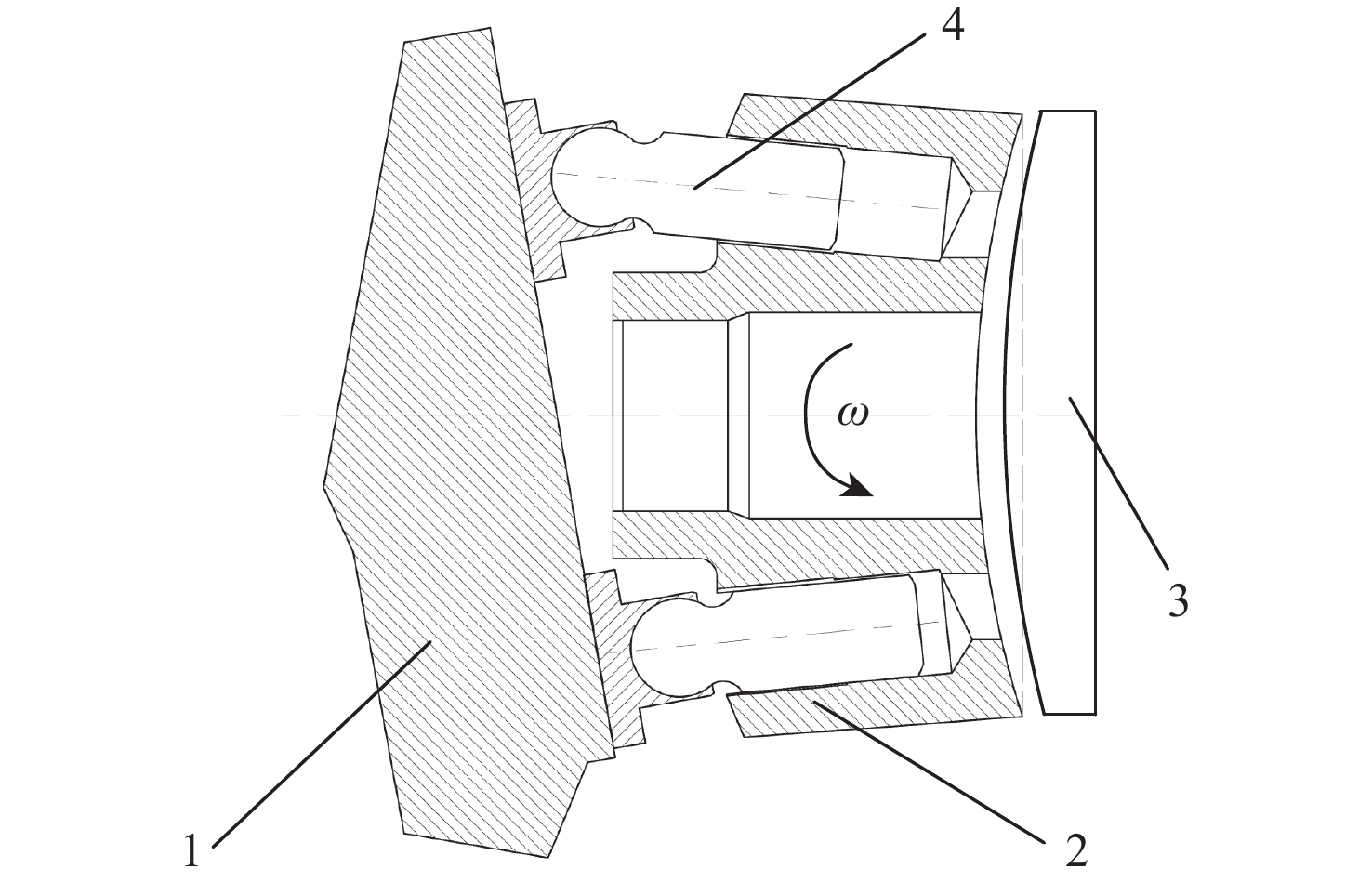
双斜式柱塞泵结构如图1所示，总柱塞个数为9。当主轴按图示逆时针方向以角速度ω转动时，位于上死点的柱塞随缸体转动，在斜盘面作用下，位于图1纸面外的柱塞向下死点运动，当柱塞头部转过角度φ=180°时，达到下死点并从下死点向上死点运动(见图1纸面内的柱塞)。
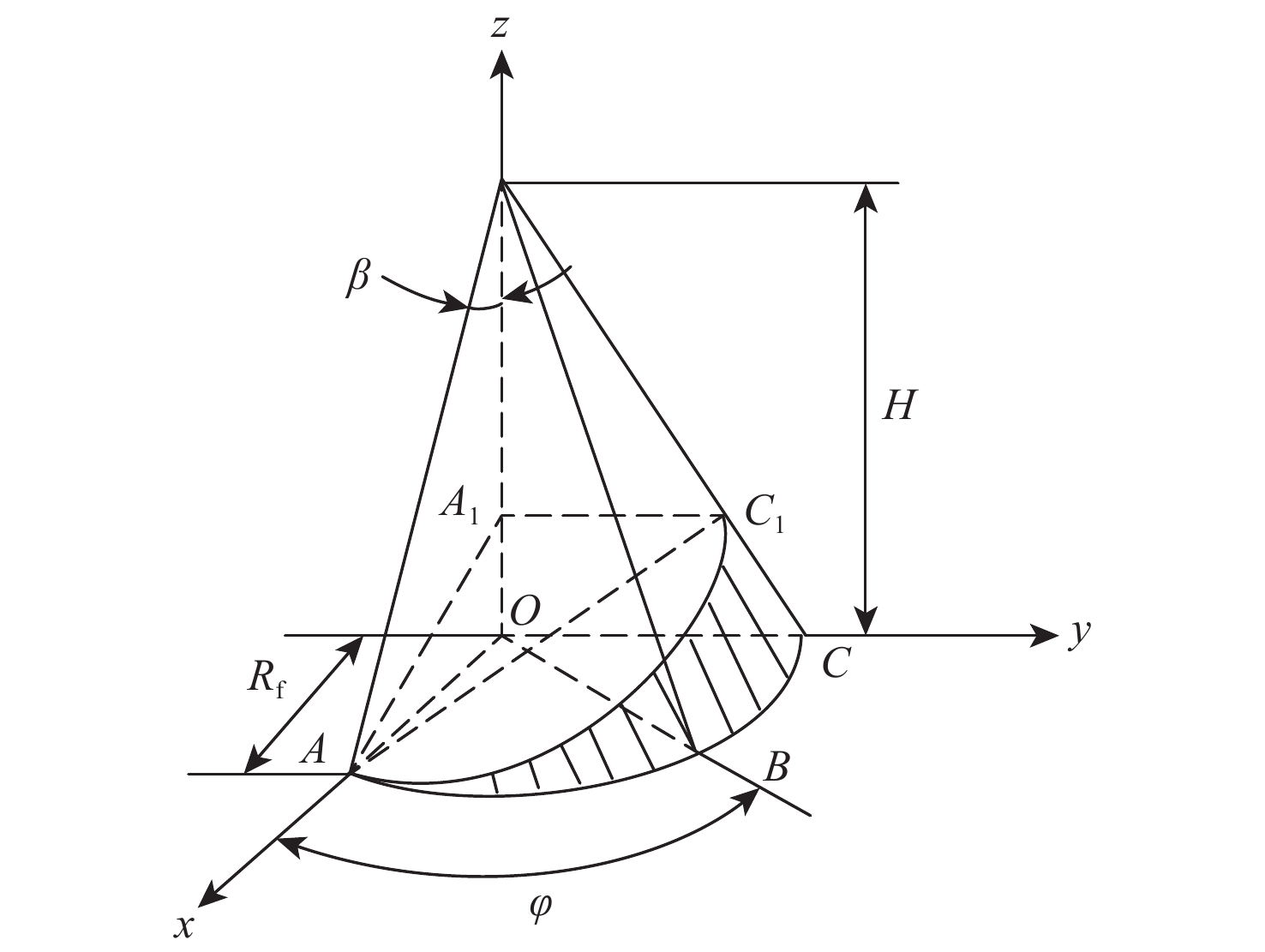
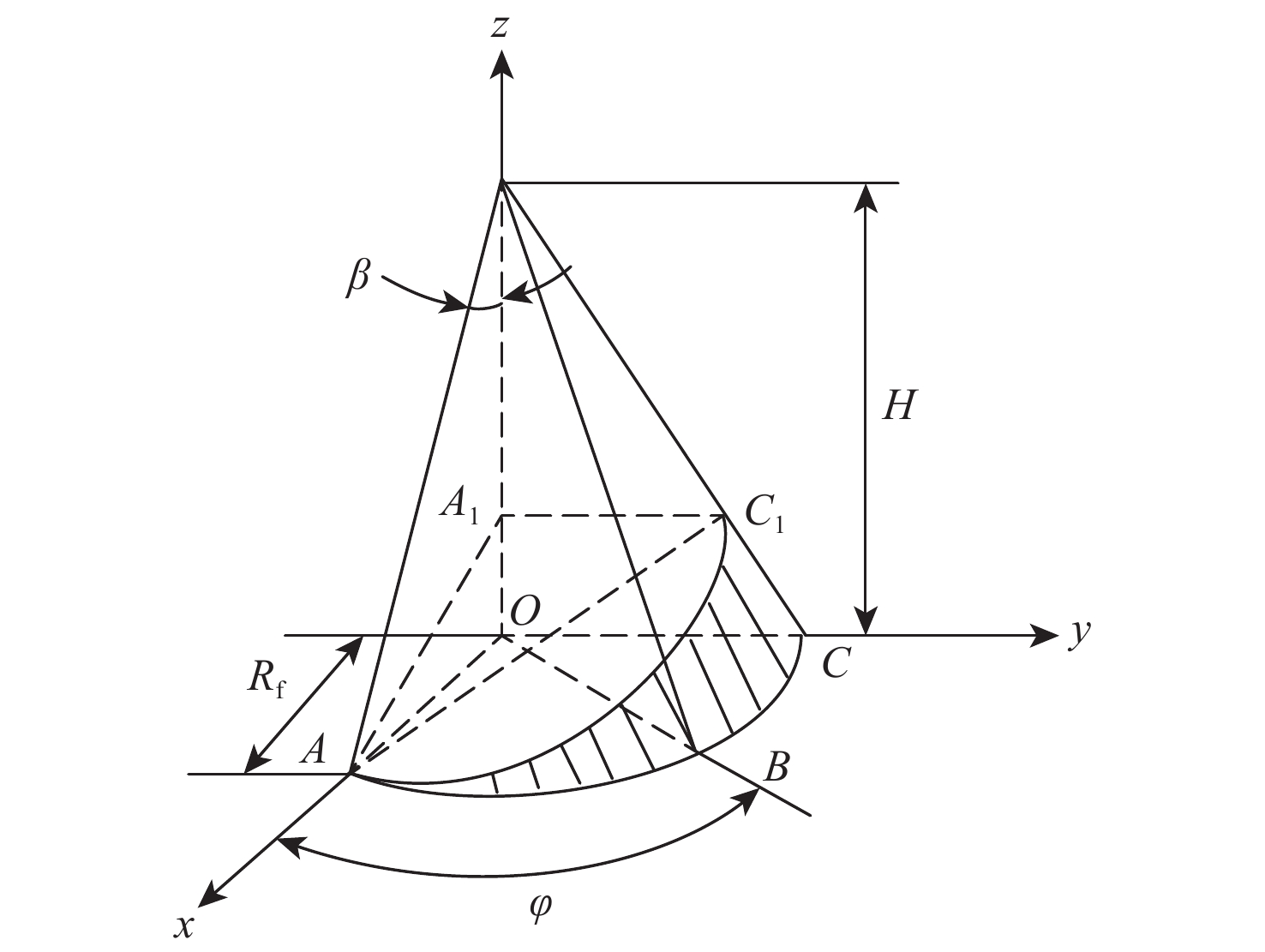
图 1 双斜式柱塞泵结构1-斜盘 2-缸体 3-配油盘 4-柱塞Figure 1. Structure of double-oblique-type axial piston pump由几何关系知，柱塞头部的运动轨迹位于斜盘平面与柱塞轴线所在圆锥曲面的交线上。如图2所示，建立柱塞Oxyz坐标系[17]，z轴为转轴所在直线，H为圆锥高度，Rf为圆锥底面半径，即上死点到缸体轴线距离，φ为柱塞头部转过角度，β为柱塞倾角，平面AA1C1为斜盘所在平面，∠A1AO=γ为斜盘倾角。
经简单地分析可得，柱塞行程为AC1，其在缸体内的位移方程为
S(φ)=Rftanγ(1−cosφ)cosβ(1−k1cosφ) (1) 式中：k1=tanγtanβ。
由式(1)可得柱塞速度为
v=Rfω(1−k1)tanγsinφcosβ(1−k1cosφ)2 (2) 则柱塞加速度为
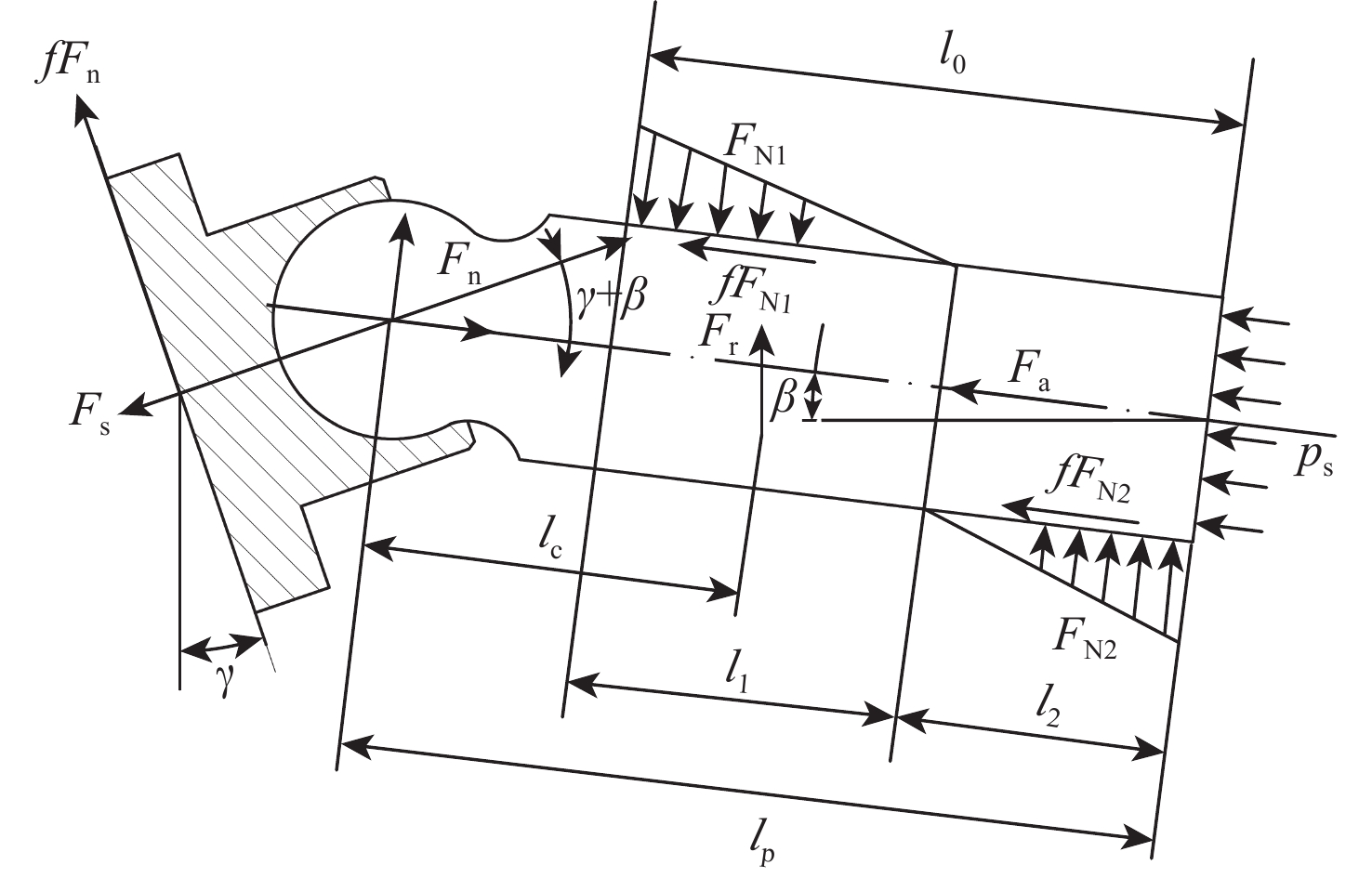
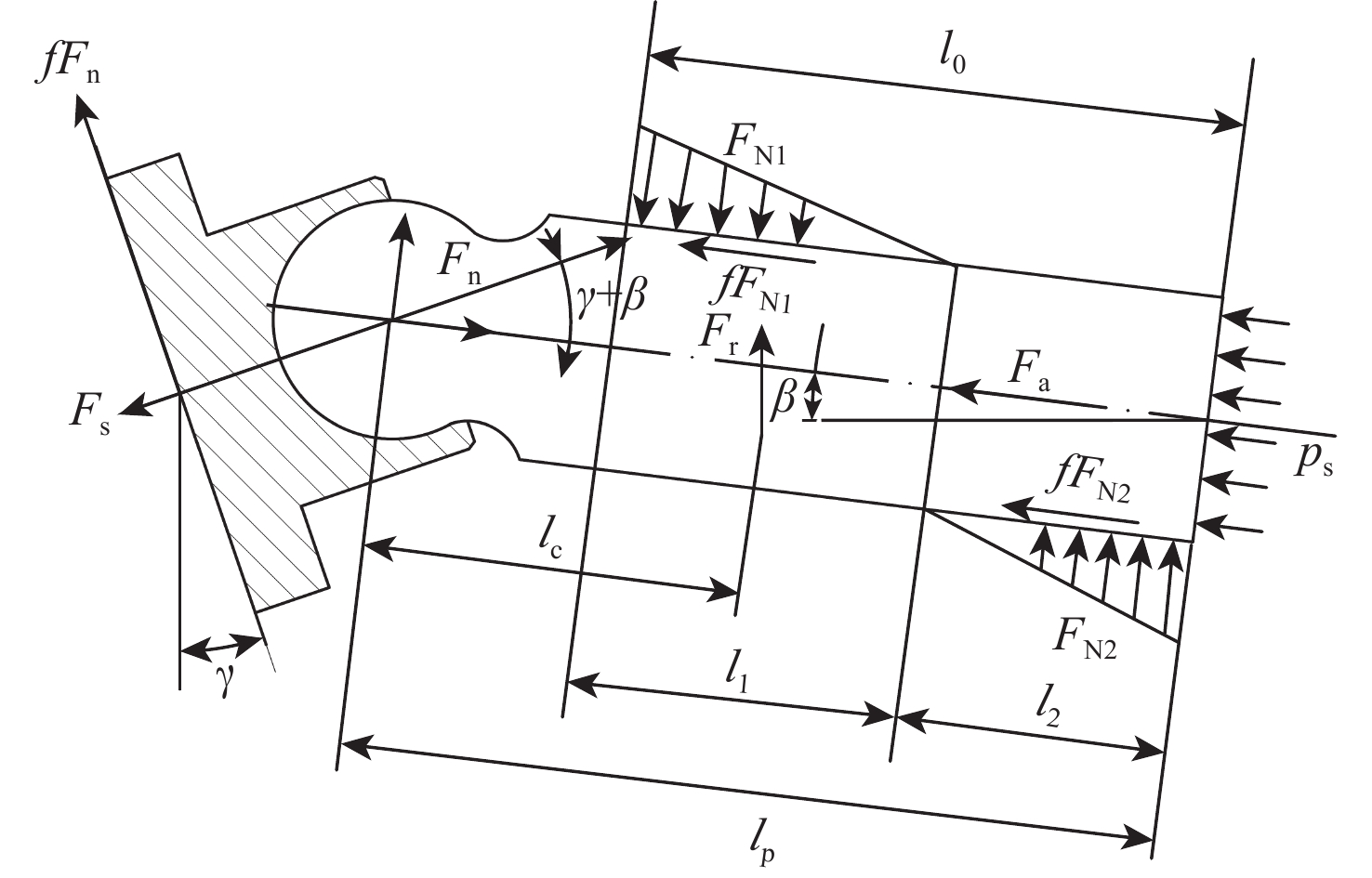
a=Rfω2(1−k1)tanγ[cosφ(1−k1cosφ)−2k1sin2φ]cosβ(1−k1cosφ)3 (3) 对单个柱塞进行受力分析，受力图如图3所示。柱塞底部液压力为
Fp=πd24ps (4) 式中：d为柱塞直径；ps为柱塞腔吸排油压力。
柱塞滑靴组件往复运动惯性力为
Fa=mpsa (5) 式中：mps为柱塞滑靴总质量；a为柱塞加速度。
柱塞圆周运动离心力为
Fr=mps(Rf−lcsinβ)ω2 (6) 式中：lc为柱塞球头中心到柱塞副质心距离。
斜盘对滑靴组件的作用力为
Fn=π 2⋅R21−R22ln(R1/R2)pr (7) 式中:R1、R2为滑靴底面密封带内外半径；pr为滑靴底面油室压力。
回程弹簧力Fs及缸体对柱塞的支撑力FN1、FN2设为未知量，则支撑面所受摩擦力可表示为fFn、fFN1、fFN2，其中f=0.008～0.08。
基于图3所示受力分析，建立与柱塞轴线平行方向的力平衡方程为
(Fn−Fs)sin(γ+β)+Frcosβ+FN2−FN1−fFncos(γ+β)=0 (8) 与柱塞轴线垂直方向的力平衡方程为
(Fn−Fs)cos(γ+β)−Frsinβ−Ff2sign(v)−Ff1sign(v)−Fp+Fa+fFnsin(γ+β)=0 (9) 柱塞球头的力矩平衡方程为
Ff1d2sign(v)+lcFrcosβ+FN2(lp−l2/4)−FN1(lp−l0+l1/4)−Ff2d2sign(v)+fFn(lplung−lp)cos(γ+β)=0 (10) 式中：lplung为柱塞位于下死点处柱塞底部与坐标平面距离；lp为柱塞球头中心到柱塞底部的距离；l0为柱塞留缸长度；l1、l2为柱塞所受支撑力与缸体接触长度。
联立式(8)~式(10)可解得单个柱塞在运动过程中所受的力，由此根据力的相互作用可得柱塞对缸体反作用力。
2. 缸体受力分析
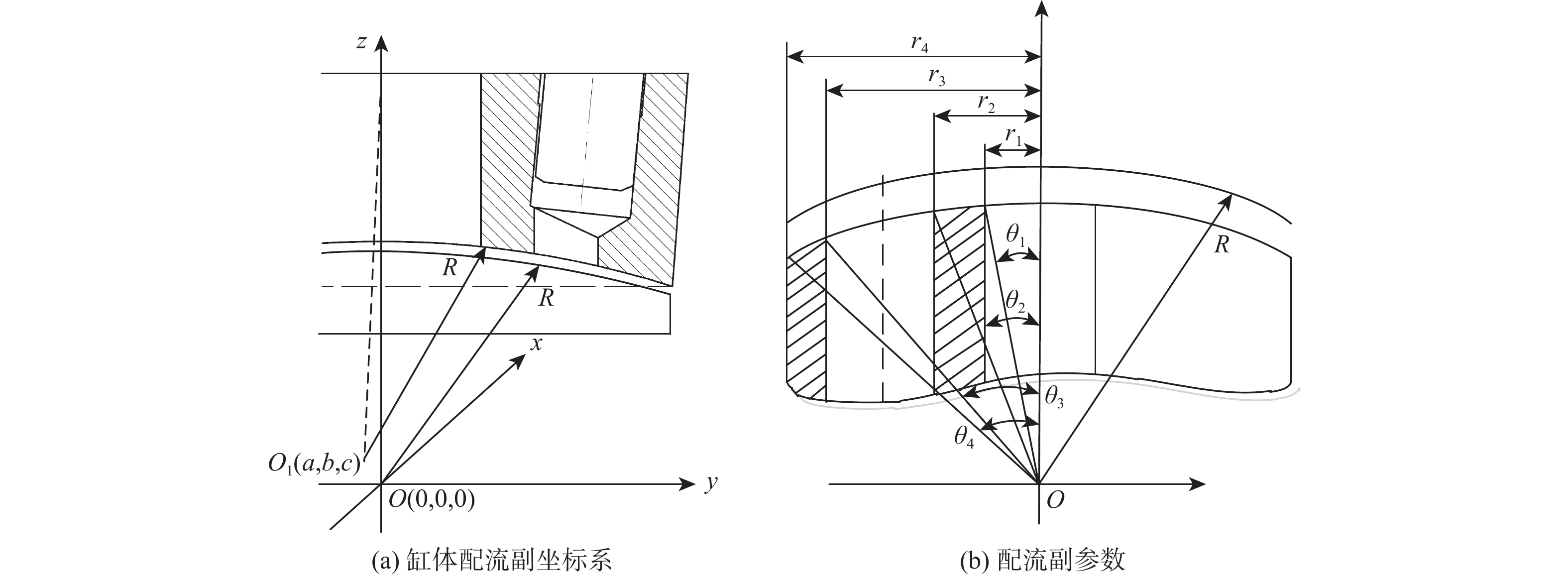
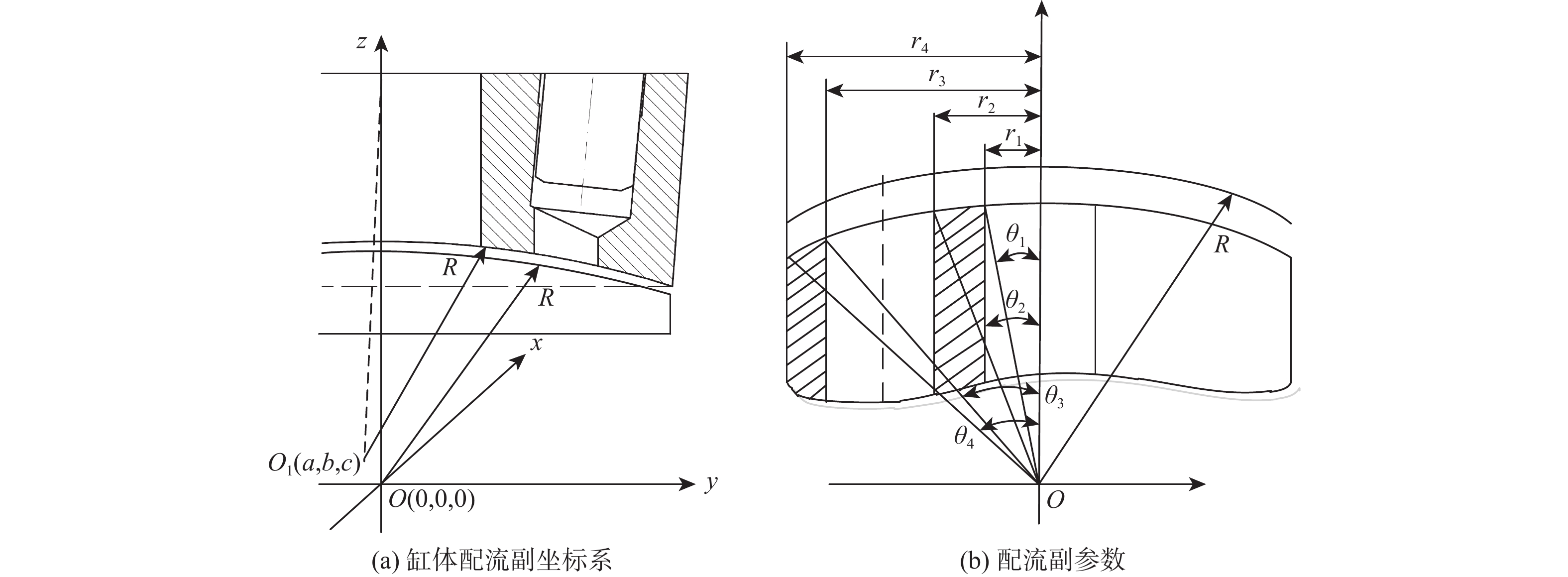
图4为缸体配流副坐标系及其参数，对缸体配流副建立如图4（a）所示的坐标系，其中，上半部分为柱塞泵缸体结构，下半部分为柱塞泵配流盘结构，两者有相同的曲率半径R。定义球面坐标系，配流盘球心为O（0，0，0），缸体球心为O1（a，b，c）。测量配流副各参数如图4（b）所示，其中r1、r2、r3、r4分别表示配流副内外密封带的内外半径，θ1、θ2、θ3、θ4分别表示配流副内外密封带的内外圈边缘与缸体轴线的夹角。
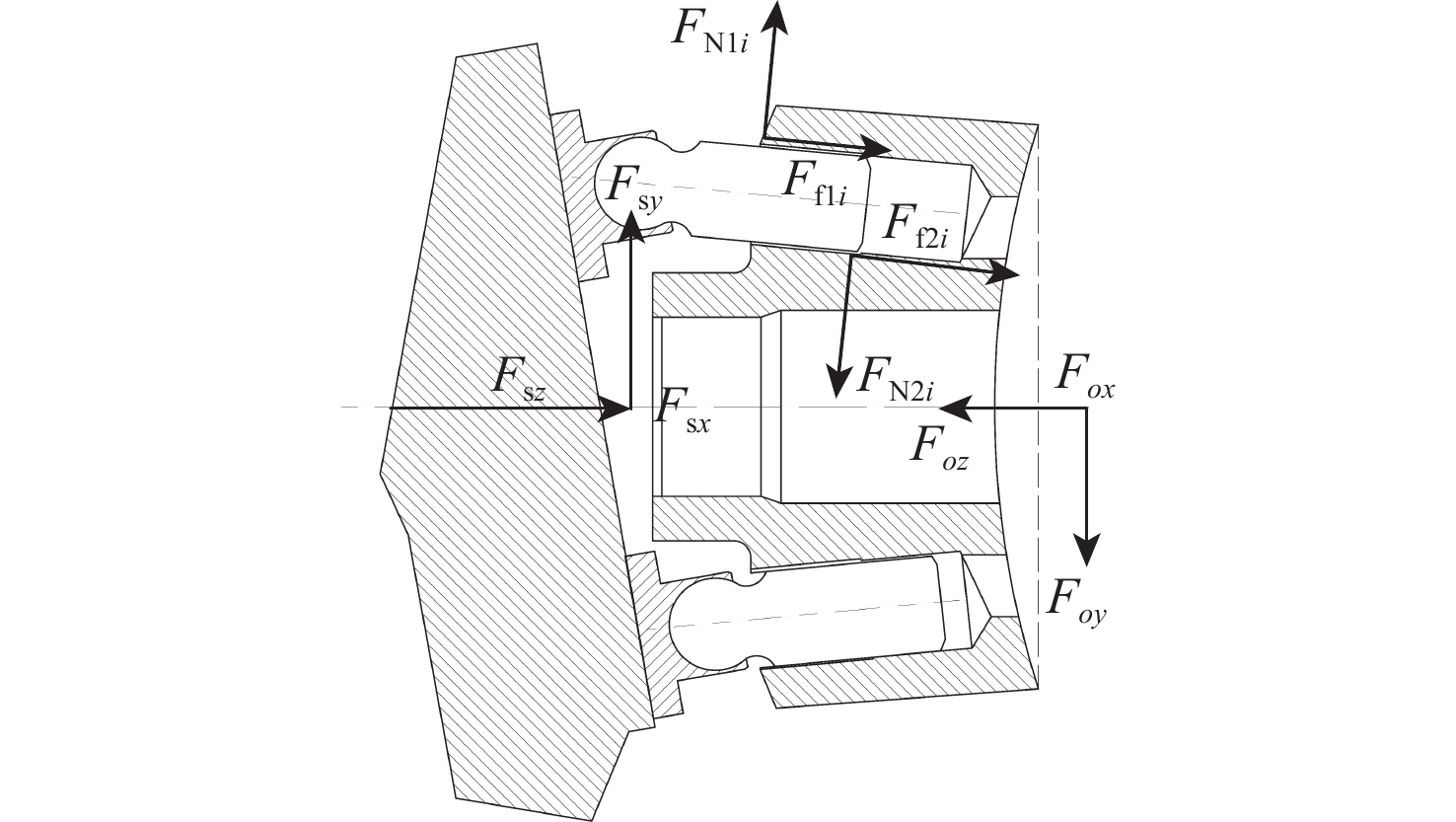
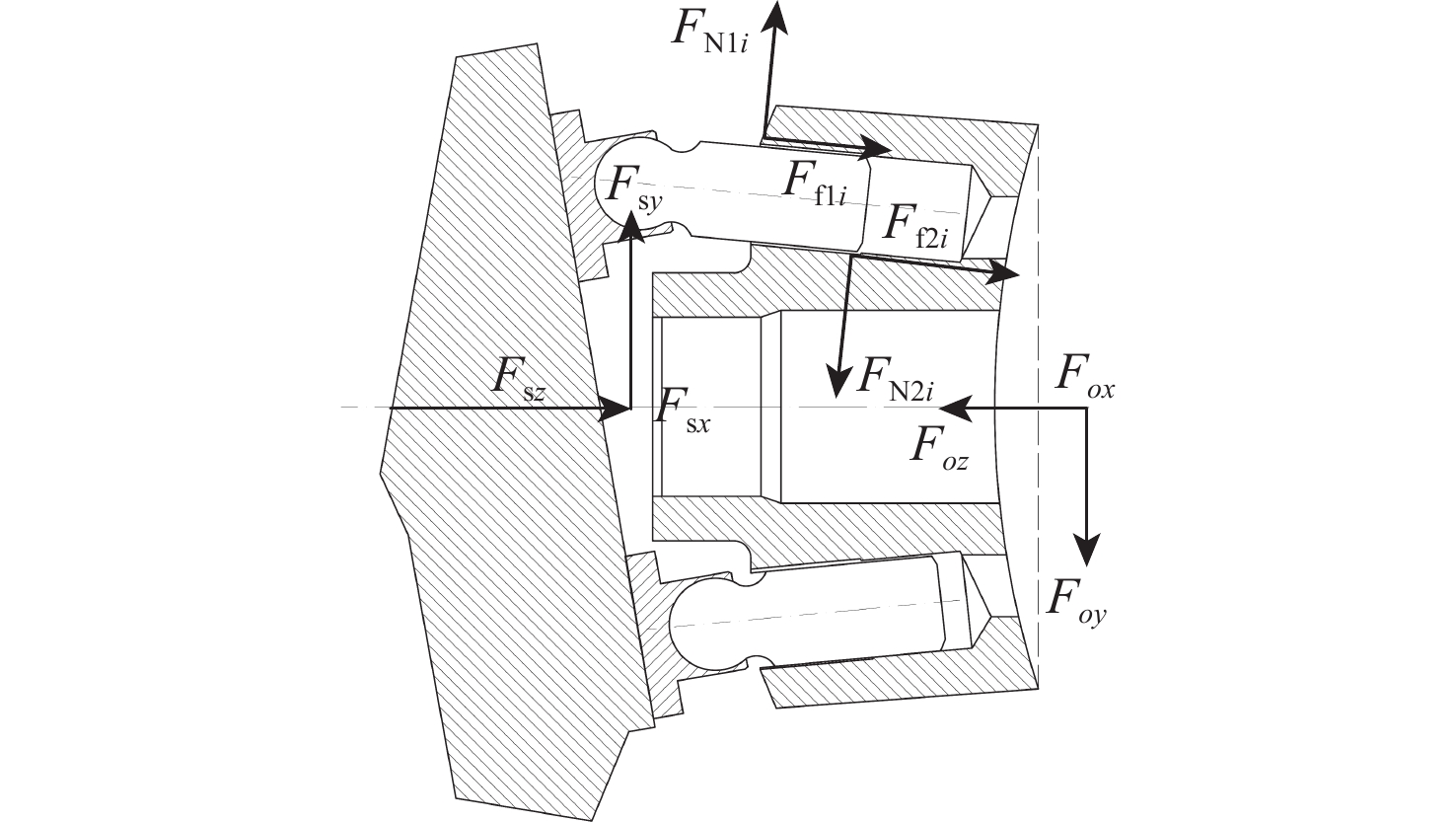
图 4 缸体配流副坐标系及其参数Figure 4. Coordinate system and parameters of cylinder distribution pair对缸体进行受力分析，如图5所示，缸体受到的力有9个柱塞分别对缸体施加的压力FN1i、FN2i；9个柱塞分别对缸体施加的摩擦力Ff1i、Ff2i；缸体所受预压紧力Fsx、Fsy、Fsz及配流副油膜对缸体的支撑力和9个柱塞腔中油液分别对缸体施加的压力。
配流副油膜对缸体的支撑力为
{Fox=∬ (11) 式中：p\left( {\theta ,\varphi } \right)为配流副油膜压力场分布。
每个柱塞腔中油液对缸体施加的压力为
{F_{{\text{p}}i}} = {p_{{\text{s}}i}}{A_i} (12) 式中：{p_{{\text{s}}i}} = \dfrac{{{p_{\text{h}}} - {p_{\rm{l}}}}}{2}\sin \left( {\varphi + \dfrac{{2{\text{π}}}}{9}i} \right) + \dfrac{{{p_{\text{h}}} + {p_{\rm{l}}}}}{2}为柱塞腔油液压力，采用正弦形式拟合高压区与低压区，{p_{\text{h}}}为柱塞泵高压区压力，{p_{\rm{l}}}为柱塞泵低压区压力；{A_i}为对应柱塞腔面积。
由于式(12)中采用的是正弦方式拟合高低压区油液压力，而不是采用突变形式，可以通过严格的数学推导证明，9个柱塞腔油液对缸体施加的总压力保持恒定，因此，总压力与柱塞倾角的正余弦乘积也保持恒定，即柱塞腔油液对缸体施加的三轴压力保持恒定。
基于图5所示受力分析，建立缸体三轴的力平衡方程为
\left\{ \begin{aligned} &\sum\limits_{i = 1}^9 {\left[ {\left( {{F_{{\text{N}}1i}} - {F_{{\text{N}}2i}}} \right)\cos \beta \cos {\varphi _i} - {F_{{\text{p}}i}}\sin \beta \cos {\varphi _i} - } \right.} \\ &\quad\quad\left. {\left( {{F_{{\rm{f}}1i}} + {F_{{\rm{f}}2i}}} \right)\sin \beta \cos {\varphi _i}{\text{sign}}\left( {{v_i}} \right)} \right] = {F_{{{o}}x}} + {F_{{\text{s}}x}} \\ &\sum\limits_{i = 1}^9 {\left[ {\left( {{F_{{\text{N}}1i}} - {F_{{\text{N}}2i}}} \right)\cos \beta \sin {\varphi _i} - {F_{{\text{p}}i}}\sin \beta \sin {\varphi _i} - } \right.} \\ &\quad\quad\left. {\left( {{F_{{\rm{f}}1i}} + {F_{{\rm{f}}2i}}} \right)\sin \beta \sin {\varphi _i}{\text{sign}}\left( {{v_i}} \right)} \right] = {F_{{{o}}y}} + {F_{{\text{s}}y}} \\ &\sum\limits_{i = 1}^9 {\left[ {\left( {{F_{{\text{N}}1i}} + {F_{{\text{N}}2i}}} \right)\sin \beta + {F_{{\text{p}}i}}\cos \beta + } \right.} \\ &\quad\quad \left. {\left( {{F_{{\rm{f}}1i}} + {F_{{\rm{f}}2i}}} \right)\cos \beta {\text{sign}}\left( {{v_i}} \right)} \right] = {F_{{{o}}{\textit{z}}}} + {F_{{\text{s}}{\textit{z}}}} \\ \end{aligned} \right. (13) 3. 球面配流副多场耦合模型
综合考虑配流副油膜厚度场、压力场和温度场的耦合作用。球面坐标系下，配流副任意点油膜的厚度h\left( {\theta ,\varphi } \right)，压力p\left( {\theta ,\varphi } \right)和黏度\mu \left( {\theta ,\varphi } \right)都是变量\theta、\varphi 的函数。由此建立球面坐标系下配流副油膜的雷诺方程为
\begin{gathered} \frac{{\partial} }{{\partial \varphi }}\left( {\frac{{{h^3}}}{\mu }\cdot\frac{{\partial p}}{{\partial \varphi }}} \right) + \sin \theta \frac{\partial }{{\partial \theta }}\left( {\frac{{h^3}{\sin \theta }}{\mu }\cdot\frac{{\partial p}}{{\partial \theta }}} \right) = \\ \quad\quad 6\omega {r^2}{\sin ^2}\theta \frac{{\partial h}}{{\partial \varphi }} + 12{r^2}{\sin ^2}\theta \frac{{\partial h }}{{\partial t}} \\ \end{gathered} (14) 式(14)可整理为
\begin{split} &\frac{{h}^{3}}{\mu }\cdot\frac{{\partial }^{2}p}{\partial {\varphi }^{2}}+\frac{{{h}^{3}\mathrm{sin}}^{2}\theta }{\mu }\cdot\frac{{\partial }^{2}p}{\partial {\theta }^{2}}+\left(\frac{3{h}^{2}}{\mu }\cdot\frac{\partial h}{\partial \varphi }-\frac{{h}^{3}}{{\mu }^{2}}\cdot\frac{\partial \mu }{\partial \varphi }\right)\frac{\partial p}{\partial \varphi }+\\ &\quad\quad \mathrm{sin}\;\theta \left(\frac{3{h}^{2}\mathrm{sin}\;\theta }{\mu }\cdot\frac{\partial h}{\partial \theta }-\frac{{h}^{3}\mathrm{sin}\;\theta }{{\mu }^{2}}\cdot\frac{\partial \mu }{\partial \theta }+\frac{{h}^{3}}{\mu }\mathrm{cos}\;\theta \right)\frac{\partial p}{\partial \theta }=\\ &\quad\quad 6\omega {R}^{2}\mathrm{sin}\;\theta \frac{\partial h}{\partial \varphi }+12{R}^{2}{\mathrm{sin}}^{2}\theta \frac{\partial h}{\partial t}\end{split} (15) 其边界条件为
\left\{ \begin{aligned} &p({\theta }_{1},\varphi )=p({\theta }_{4},\varphi )=0,p({\theta }_{2},\varphi )=p({\theta }_{3},\varphi )={p}_{{\rm{s}}}\\& p(\theta ,0)=p(\theta ,2{\text{π}}),{\dfrac{\partial p}{\partial \varphi }\Bigg|}_{(\theta ,0)}={\dfrac{\partial p}{\partial \varphi }\Bigg|}_{(\theta ,2{\text{π}} )}\end{aligned}\right. 利用有限差分法对式(15)中偏微分进行逼近，对2个密封带分别进行网格划分，当网格点不在边界时，有
\left\{ \begin{aligned} & {\frac{{\partial {p_{i,j}}}}{{\partial \theta }} = \frac{{{p_{i + 1,j}} - {p_{i - 1,j}}}}{{2{{\Delta }}\theta }}} \\ & {\frac{{\partial {p_{i,j}}}}{{\partial \varphi }} = \frac{{{p_{i,j + 1}} - {p_{i,j - 1}}}}{{2{{\Delta }}\varphi }}} \end{aligned} \right. (16) 当网格处于边界时，采用单向差分或者后向差分，则压力分布的二阶偏导为
\left\{ \begin{aligned} &\frac{{{\partial ^2}{p_{i,j}}}}{{\partial {\theta ^2}}} = \left[{{\left( {\dfrac{{\partial {p_{i + \Delta \theta ,j}}}}{{\partial \theta }}} \right) - \left( {\dfrac{{\partial {p_{i - \Delta \theta ,j}}}}{{\partial \theta }}} \right)}}\right]\Big/{{{{\Delta }}\theta }} = \\ &\quad\quad \left( {{\dfrac{{{p_{i + 1,j}} - {p_{i,j}}}}{{{{\Delta }}\theta }} - \dfrac{{{p_{i,j}}- {p_{i - 1,j}}}}{{{t{\Delta }}\theta }}}} \right) \Big/ {{{{\Delta }}\theta }} = \frac{{{p_{i + 1,j}} + {p_{i - 1,j}} - 2{p_{i,j}}}}{{{{\Delta }}{\theta ^2}}} \\ & \frac{{{\partial ^2}{p_{i,j}}}}{{\partial {\varphi ^2}}} = \left[{{\left( {\dfrac{{\partial {p_{i,j + \Delta r}}}}{{\partial \varphi }}} \right) - \left( {\dfrac{{\partial {p_{i,j - \Delta r}}}}{{\partial \varphi }}} \right)}}\right]\Big/{{{{\Delta }}\varphi }} = \\ &\quad\quad \left( {{\dfrac{{{p_{i,j + 1}} - {p_{i,j}}}}{{{{\Delta }}\varphi }} - \dfrac{{{p_{i,j}} - {p_{i,j - 1}}}}{{{{\Delta }}\varphi }}}} \right) \Big/ {{{{\Delta }}\varphi }} = \dfrac{{{p_{i,j + 1}} + {p_{i,j - 1}} - 2{p_{i,j}}}}{{{{\Delta }}{\varphi ^2}}} \end{aligned} \right. (17) 考虑黏温效应和黏压效应，配流副油膜油液的动力黏度受到温度和压力的影响：
\mu = {\mu _0}\exp \left[ {{\alpha _p}p - {\alpha _T}\left( {T - {T_0}} \right)} \right] (18) 式中：\mu 为油液动力黏度修正值；p为配流副油膜压力场分布；{T_0}为参考温度，一般为20℃；T为配流副油膜温度场分布；{\mu _0}为p=0，T={T_0}时油液的动力黏度；{\alpha _p}为黏压系数；{\alpha _T}为黏温系数。
相比于\theta 、\varphi方向的热传导，r方向的热传导可以忽略。油膜温度场分布可以由下面的能量方程求出：
\begin{split} & {c_p}\rho \omega \frac{{\partial T}}{{\partial \varphi }} = \lambda \left( {\frac{1}{{{R^2}{{\sin }^2}\theta }}\cdot\frac{{{\partial ^2}T}}{{\partial {\varphi ^2}}} + } \right. \\ &\quad\quad\left. {\frac{1}{{{R^2}}}\cdot\frac{{{\partial ^2}T}}{{\partial {\theta ^2}}} + \frac{{\cos \theta }}{{{R^2}\sin \theta }}\cdot\frac{{\partial T}}{{\partial \theta }}} \right) + \mu {\omega ^2} \\ \end{split} (19) 式中：{c_p}为油液比热容；\rho 为油液密度。
与球面坐标雷诺方程求解类似，球面坐标能量方程整理后可利用差商代替偏导数，从而推导出有限个离散点迭代关系的线性方程组。求解出线性方程组的数值解，可用来近似逼近偏微分方程的解，利用牛顿迭代法求解足够精确的数值解。
根据图4所示坐标系，建立配流副油膜厚度场模型。配流盘球心位于原点，则其球面方程为
{x^2} + {y^2} + {z^2} = {R^2} (20) 可定义从原点O穿过配流盘球面点到达缸体球面点的距离为油膜厚度，也可定义z坐标的差值为油膜厚度[18]，为计算简便，选择定义2个球面z坐标的差值为油膜厚度，则配流副任意一点的油膜厚度可表示为
\begin{split} &h\left( {\theta ,\varphi } \right) = \sqrt {{R^2} - {{\left( {{x_0} - a} \right)}^2} - {{\left( {{y_0} - b} \right)}^2}} \;+\; c\;-\\ & \quad\sqrt {{R^2} - {x_0}^2 + {y_0}^2} = \sqrt {{R^2} - {k_a}^2 - {k_b}^2} + \\ & \quad c - R\cos \theta \\ \end{split} (21) 式中：{k}_{a}=R\mathrm{sin} \;\theta\mathrm{cos} \;\varphi -a；{k}_{b}=R\mathrm{sin} \;\theta \mathrm{sin} \;\varphi -b。
则膜厚对\theta 、\varphi 、t的变化率分别为
\left\{ \begin{aligned} &{\frac{{\partial h}}{{\partial \theta }} = \frac{{ - {k_a}R\cos \varphi \cos \theta - {k_b}R\sin \varphi \cos \theta }}{{\sqrt {{R^2} - {k_a}^2 - {k_b}^2} }} + R\sin \theta } \\ &{\frac{{\partial h}}{{\partial \varphi }} = \frac{{{k_a}R\sin \theta \sin \varphi - {k_b}R\sin \theta \cos \varphi }}{{\sqrt {{R^2} - {k_a}^2 - {k_b}^2} }}} \\ &{\frac{{\partial h}}{{\partial t}} = \frac{{{k_a}\dot a + {k_b}\dot b}}{{\sqrt {{R^2} - {k_a}^2 - {k_b}^2} }} + \dot c} \end{aligned} \right. (22) 为了精确估计油膜厚度，需要考虑金属表面热变形对上式厚度模型进行修正，修正公式可以表示为
h\left( {\theta ,\varphi } \right) = {h_0}\left( {\theta ,\varphi } \right) + \Delta {h_T} + \Delta {h_p} (23) 式中：h\left( {\theta ,\varphi } \right)为油膜厚度修正模型输出的配流副油膜厚度场；{h_0}\left( {\theta ,\varphi } \right)为油膜厚度模型输出的配流副油膜厚度场；\Delta {h_T}为金属表面热变形；\Delta {h_p}为底面流体压力引起的弹性形变。两者变形的计算公式为
\left\{ \begin{aligned} & {{{\Delta }}{h_T} = {a_T}{{\Delta }}T(r,\theta ){l_{{\text{valve}}}}} \\ & {{{\Delta }}{h_p} = {l_{{\text{valve}}}} {p_{i,j}}/{E_{\text{v}}} + {l_{{\text{cy}}}} {p_{i,j}}/{E_{{\text{cy}}}}} \end{aligned} \right. (24) 式中：{a_T}为材料的线膨胀系数；\Delta T\left( {\theta ,\varphi } \right)为该点温度与基础温度的差值；{l_{{\text{valve}}}}为该点配流盘厚度；{E_{\text{v}}}为配流盘材料的弹性模量；{E_{{\text{cy}}}}为缸体材料的弹性模量；{l_{{\text{cy}}}}为该点缸体厚度；p\left( {i,j} \right)为节点（i，j）的压力。
4. 求解算法及结果分析
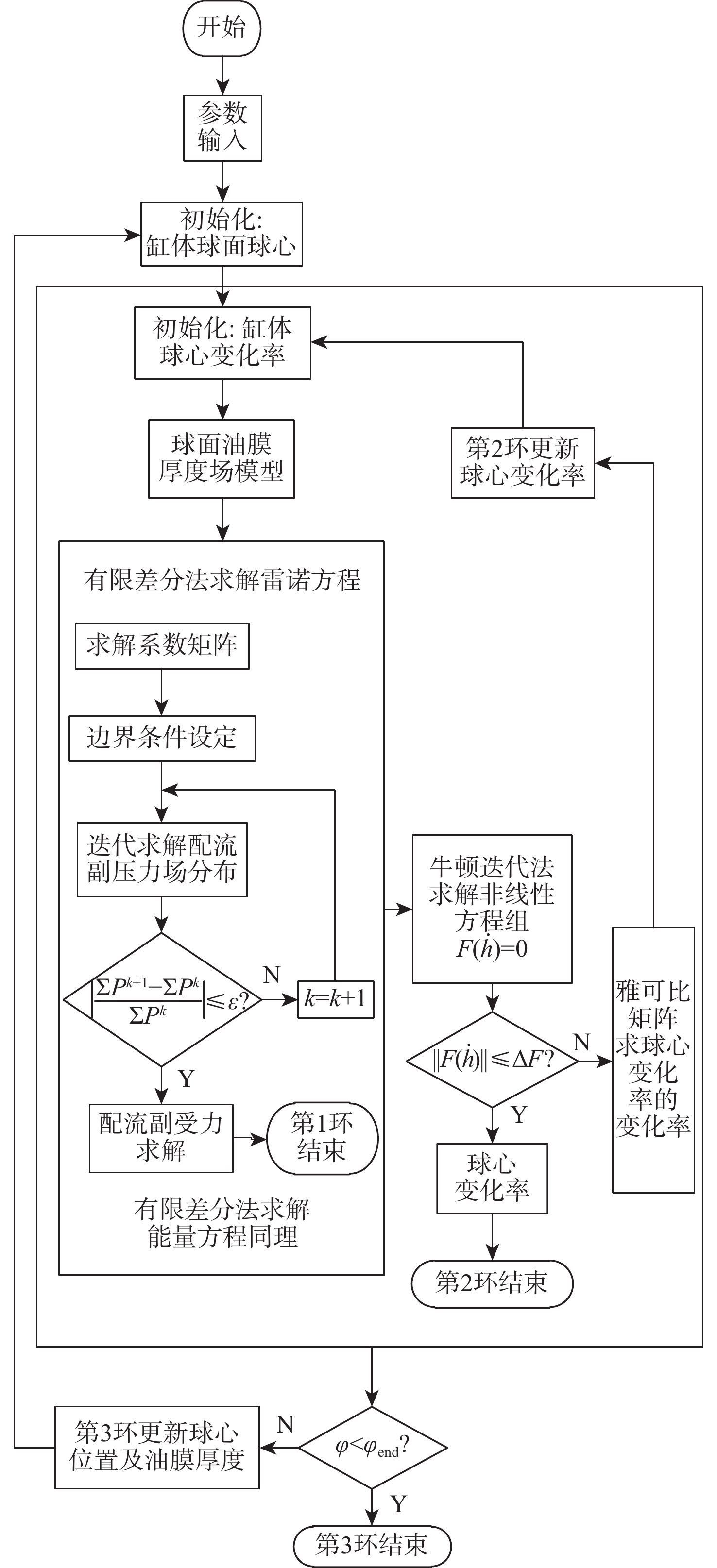
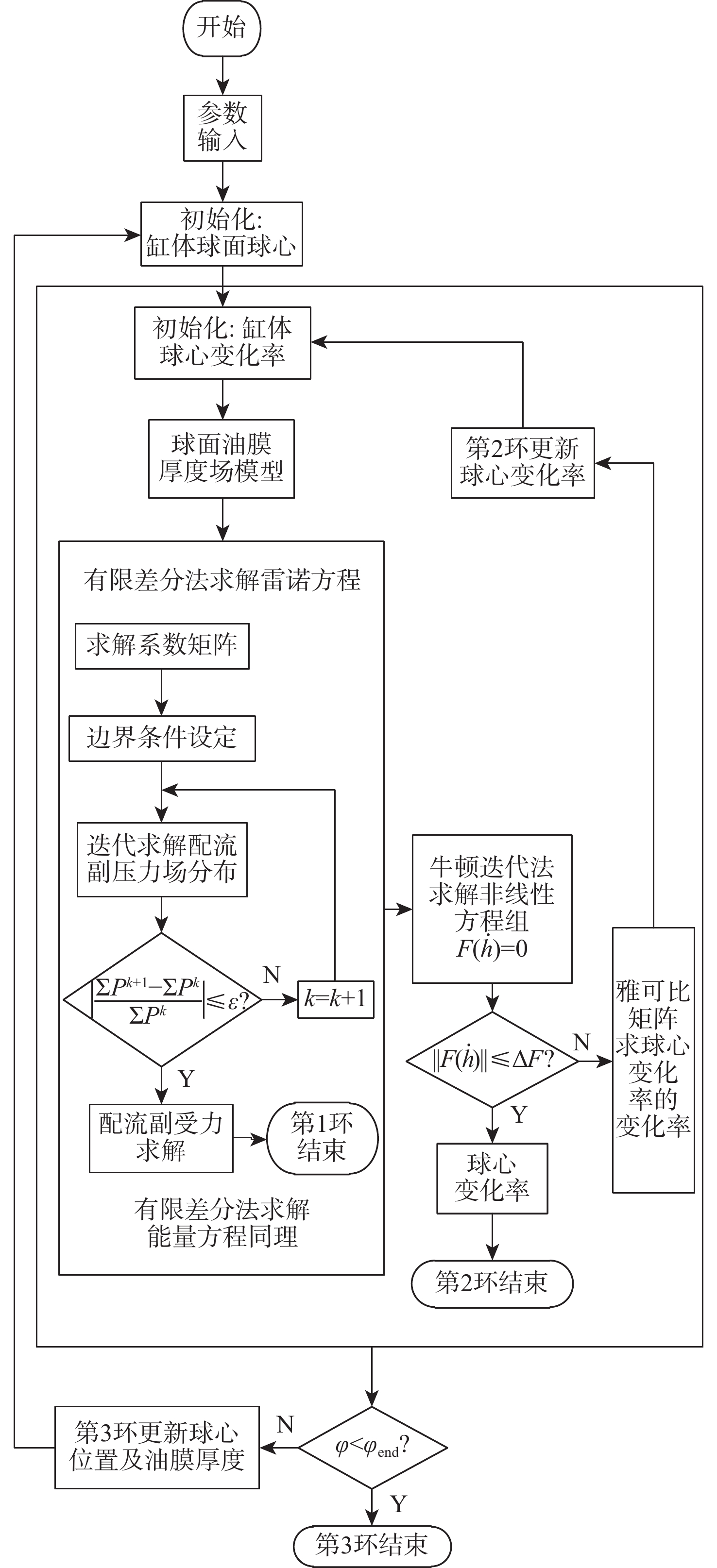
基于上述分析，在MATLAB中利用相应算法实现多场耦合模型求解，共包括3层循环：最内环有限差分法求解球面坐标系下雷诺方程和能量方程， 得到的结果如厚度场、压力场、温度场等代入第2环中，通过牛顿迭代法求解非线性方程组，判断收敛后由此求得缸体球心变化率，最外环是配流副在旋转过程中进行缸体球心更新和配流副油膜厚度更新。多场耦合模型求解算法流程如图6所示。
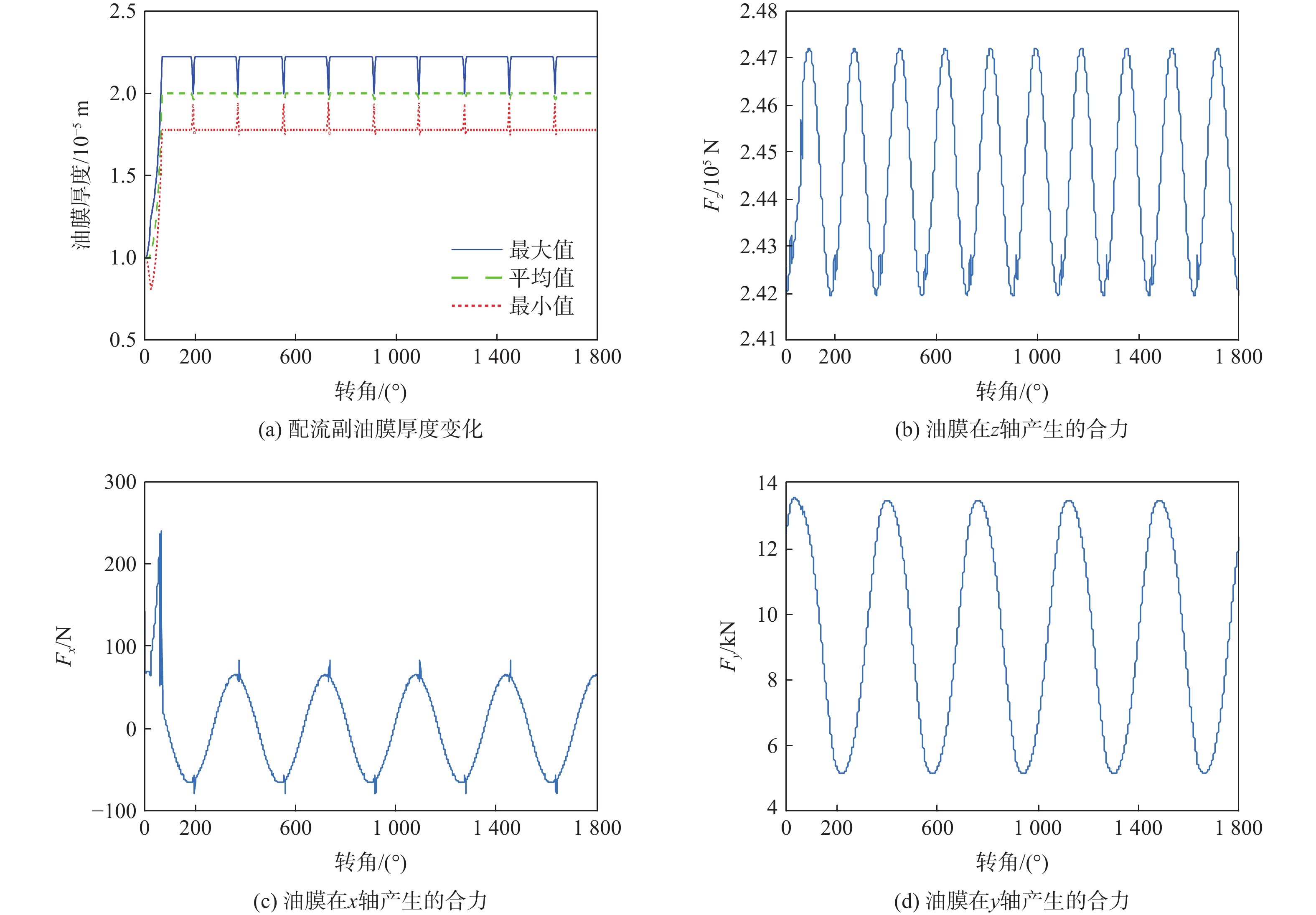
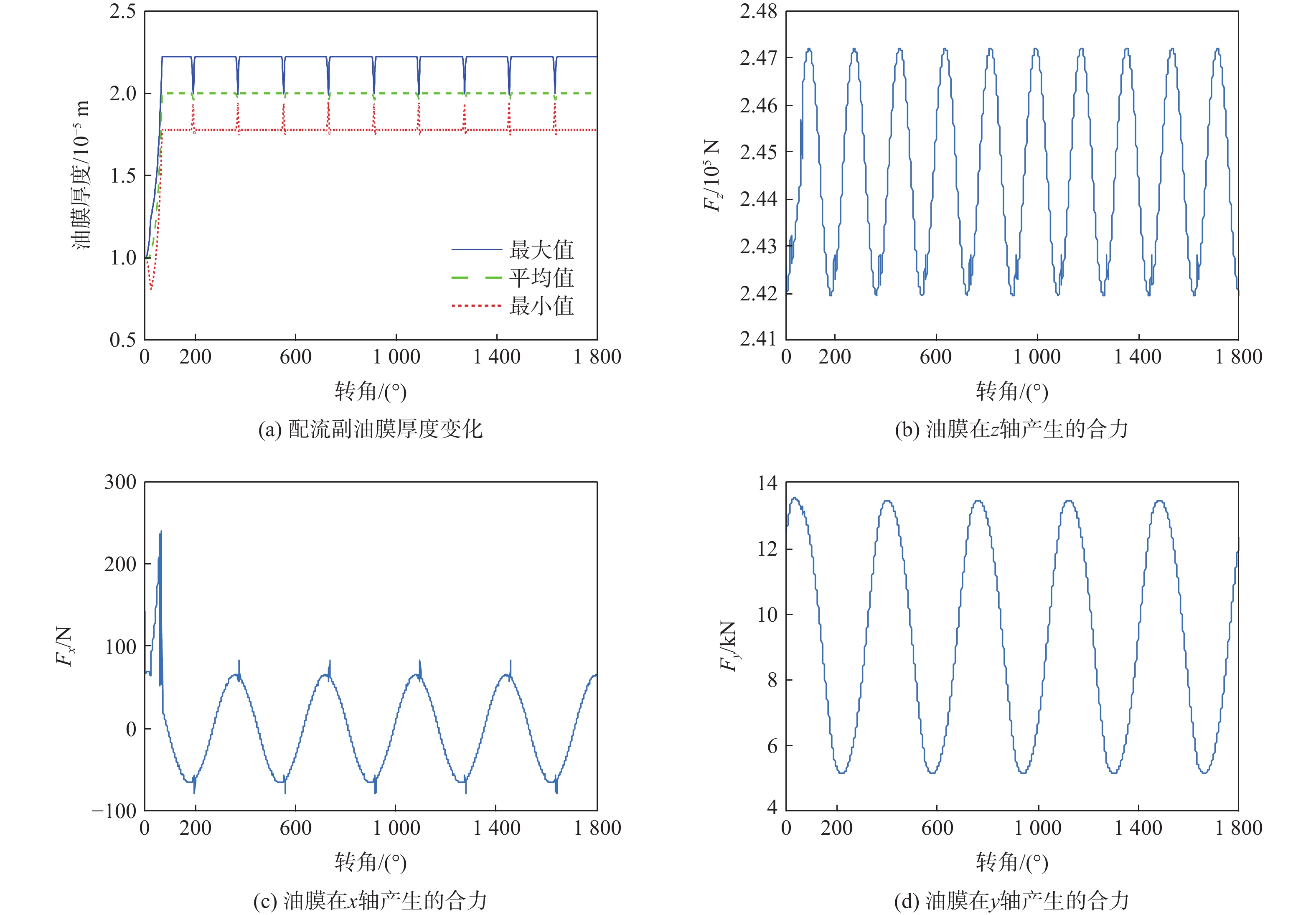
图 6 配流副油膜动态耦合模型仿真计算流程Figure 6. Simulation calculation process of oil film dynamic coupling model of distribution pair为验证提出的球面配流副油膜耦合模型，对某型号双斜式柱塞泵进行建模仿真，代入测得的数据，如表1所示。运行后得到的油膜厚度和三轴力动态变化曲线如图7所示。
表 1 仿真数据Table 1. Simulation data参数 数值 转速/({\rm{r}}\cdot{\rm{ min}}^{-1}) 1500 高压区压强{p_{\text{h}}}/MPa 30 低压区压强 {p_{\rm{l}}} /MPa 3 柱塞倾角\beta /(°) 5 斜盘倾角\gamma /(°) 15 配流盘曲率半径R/mm 58.9 圆锥半径{R_{\text{f}}}/mm 103.8 柱塞直径d/mm 45 柱塞滑靴总质量{m_{{\text{ps}}}}/g 1970 柱塞球头到柱塞副距离/mm 48.52 滑靴密封带内外半径/mm 25，20.9 黏压系数{\alpha _p} 1.8 \times {10^{ - 8}} 黏温系数{\alpha _T} 0.03 油液比热{c_p}/(J·(kg·℃)−1) 1 884 油液密度\rho /({\text{kg}} \cdot {{\text{m}}^ - }^{\text{3}}) 850 
图 7 配流副油膜厚度、合力变化曲线Figure 7. Curves of oil film thickness and resultant force of distribution pair运行程序5个周期，得到缸体与配流盘之间的油膜动态变化规律如图7所示。由于柱塞腔油液在每个角度对缸体的三轴压力恒定，因此，油膜的厚度在稳定后变化不大。从图7中可以看出，程序在运行90°后，配流盘每旋转1周，油膜呈周期性地变化规律，其中，x轴方向受力接近于0，z轴受力最大，这与实际情况相符合，同时也表明从程序运行90°往后，模型已经基本收敛。
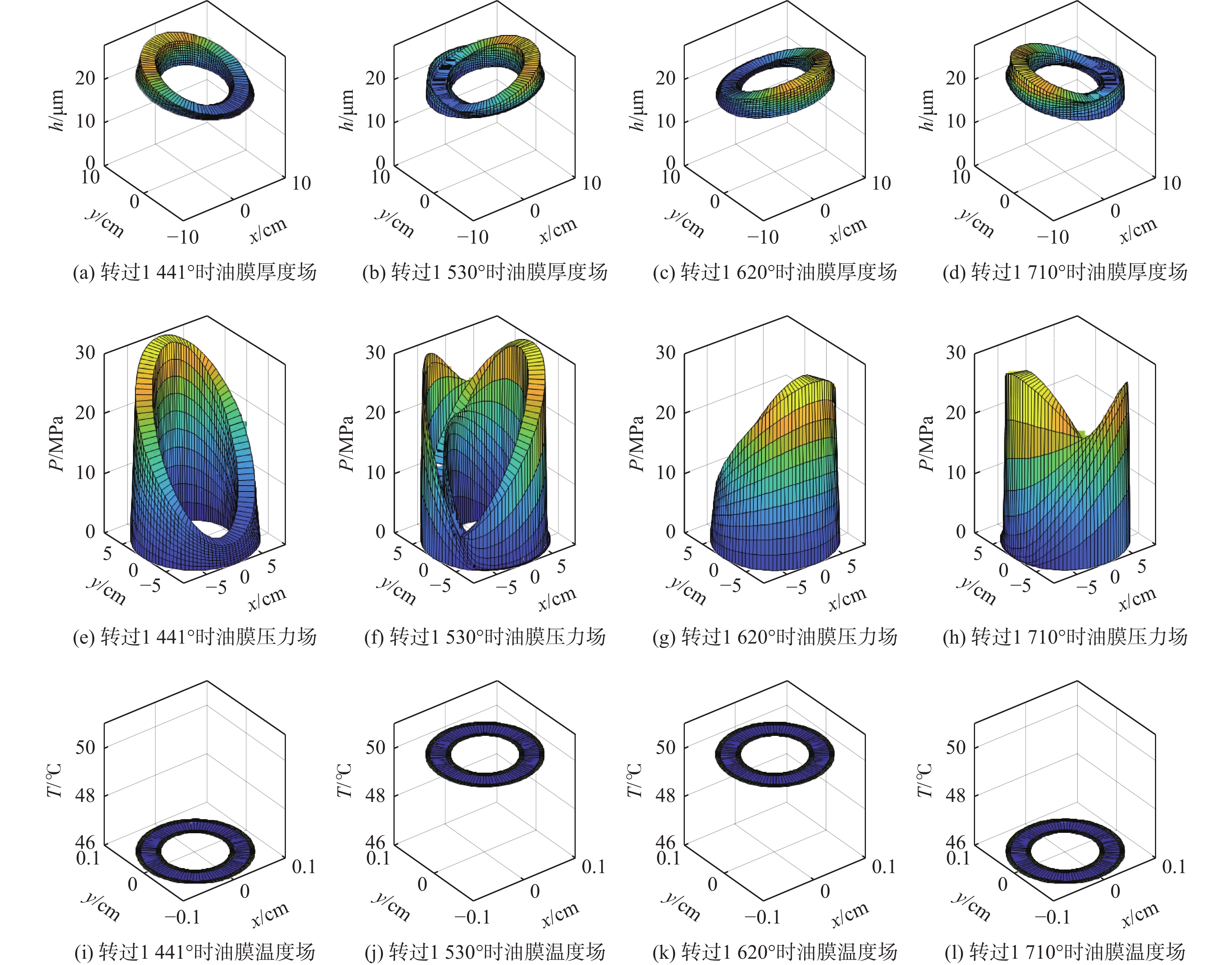
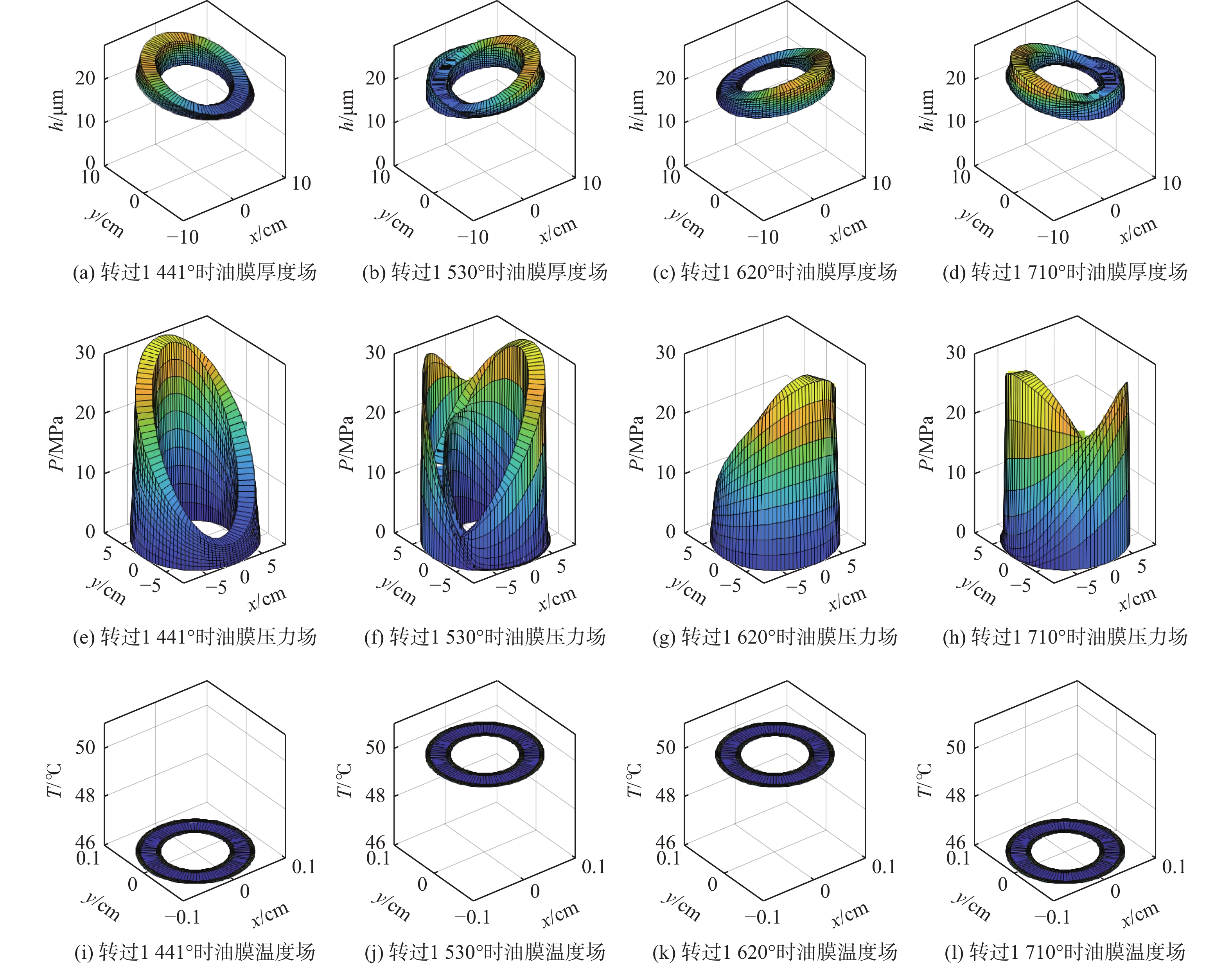
为了油膜特性的分析精度，取程序运行第5个周期的仿真结果作为油膜特性分析依据。根据图7结果当缸体逆时针旋转时，相当于配流盘带着高低压区在缸体上顺时针旋转，在第5圈时，配流盘和缸体之间油膜厚度场、压力场及温度场的动态变化如图8所示。图8中，每一列表示在相应转角处的各个场，第1行表示厚度场，第2行为压力场，第3行为温度场。油膜厚度场始终呈现球面坐标下的圆环形分布，由于缸体在旋转过程中的球心变化，导致球面环形油膜一边高一边低，但始终保持着形状，且压力高的一侧由于金属受压力作用导致的弹性变形较大因此油膜厚度也较大，压力小的一侧由于金属受压力作用导致的弹性变形较小，因此油膜厚度也较小，这点在转角为1530°和1710°处尤为明显。在这2处，配流副油膜压力场产生畸变，某些角度密封带压力比对应的进出油腔压力大得多，此时对应的油膜厚度也大，因此，认为是金属变形导致的油膜厚度变大。对于配流副油膜压力场分布，由于在封油带采用正弦拟合高低压区压强，因此，封油带呈现较为规则的环形，而在密封带，压力有时会比封油带高，有时又会比封油带低。
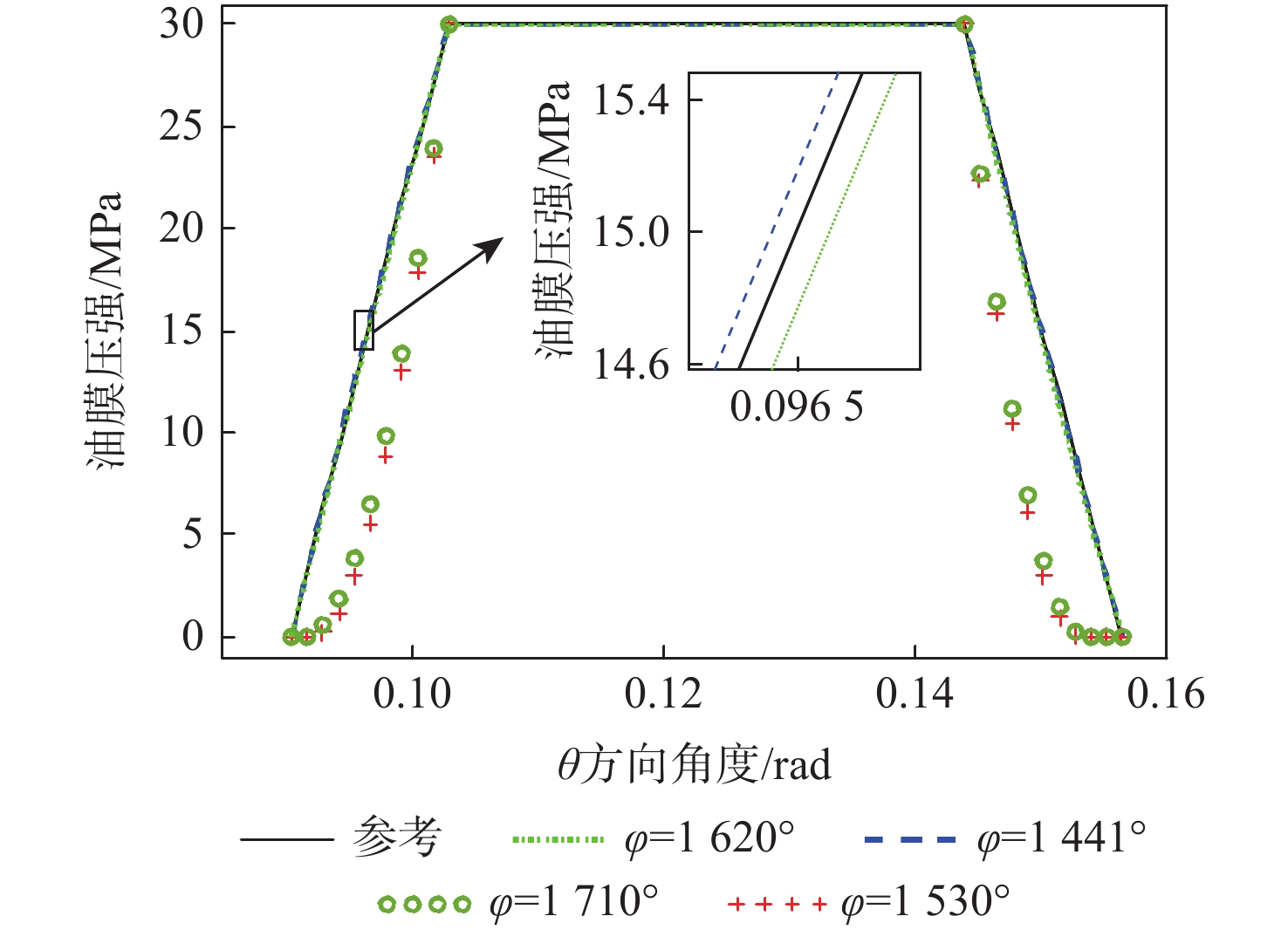
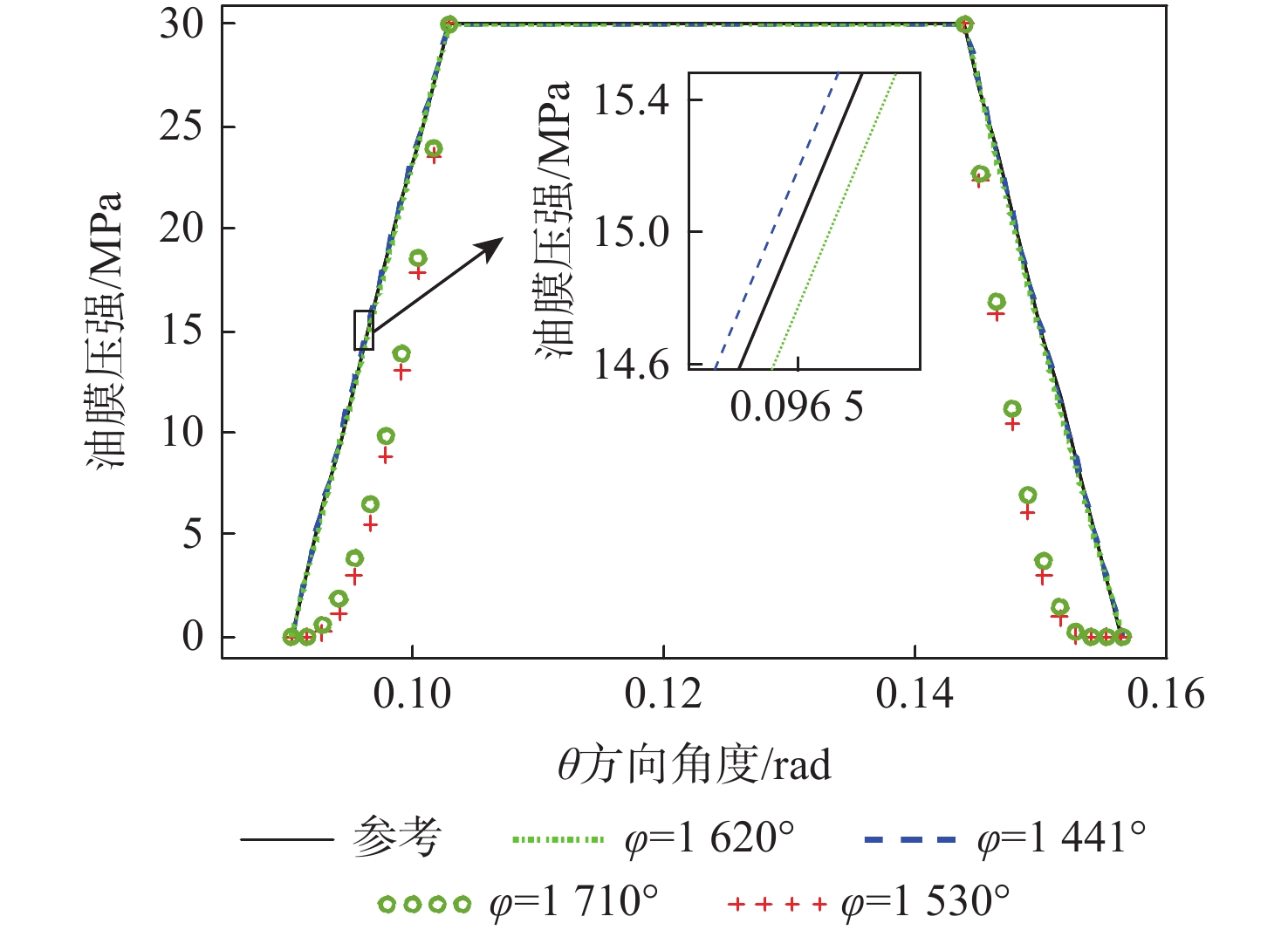
图 8 配流副油膜厚度场、压力场和温度场分布Figure 8. Distribution of oil film thickness field, pressure field and temperature field of distribution pair文献[9]在研究球面配流副油膜时未考虑周向压力场变化，只考虑径向压力场变化，认为高压区范围中不同周向角度的压力场变化曲线保持一致，将其作为参考，与本文所述多场耦合数值求解方法不同转角结果压强最大处进行对比，结果如图9所示。
图 9 不同转角压力分布比较Figure 9. Comparison of pressure distribution at different rotation angles从图9中可以看出，参考压力分布在内外密封带均成线性分布，本文所述多场耦合数值求解方法在第5周期的不同转角处压力最大处压力场分布不同，当转角在0和{\text{π}}附近时，压力分布与参考分布接近，当转角在{\text{π}}/2和3{\text{π}}/2处时，压力分布变化较大，但整体趋势一致，同时此处压力场导致的各向压力均为最大或最小。文献[9]求出的参考压力分布与基于牛顿迭代法和有限差分法求解雷诺方程和能量方程计算出的最高压处压力分布极为接近，但未考虑周向压力场变化，认为高压区范围中不同周向角度的压力场变化曲线保持一致，而所述数值求解方法压力分布在周向会有变化。
5. 结 论
1） 综合考虑球面配流副间隙的油膜和缸体、柱塞对球面配流副的作用，考虑温度对油液黏度的影响、金属表面热变形和底面流体压力引起的弹性变形，使压力场建模和求解更加精确，为双斜式柱塞泵的理论研究提供基础。
2） 采用正弦拟合排油区和吸油区的压力分布，导致计算的压力场分布和各方向的力呈规律性变化，若采用其他方式表述吸排油区压力分布，计算结果会有略微变化。
3） 基于牛顿迭代法和有限差分法求解雷诺方程和能量方程，求解结果与参考结果在最高压处数值极为接近，表明本文提出的球面配流副油膜厚度场-压力场-温度场耦合模型正确、可行，但本文结果在周向存在变化，与实际更为符合。
-
图 1 双斜式柱塞泵结构
1-斜盘 2-缸体 3-配油盘 4-柱塞
Figure 1. Structure of double-oblique-type axial piston pump
图 4 缸体配流副坐标系及其参数
Figure 4. Coordinate system and parameters of cylinder distribution pair
图 6 配流副油膜动态耦合模型仿真计算流程
Figure 6. Simulation calculation process of oil film dynamic coupling model of distribution pair
图 7 配流副油膜厚度、合力变化曲线
Figure 7. Curves of oil film thickness and resultant force of distribution pair
图 8 配流副油膜厚度场、压力场和温度场分布
Figure 8. Distribution of oil film thickness field, pressure field and temperature field of distribution pair
图 9 不同转角压力分布比较
Figure 9. Comparison of pressure distribution at different rotation angles
表 1 仿真数据
Table 1. Simulation data
参数 数值 转速/({\rm{r}}\cdot{\rm{ min}}^{-1}) 1500 高压区压强{p_{\text{h}}}/MPa 30 低压区压强 {p_{\rm{l}}} /MPa 3 柱塞倾角\beta /(°) 5 斜盘倾角\gamma /(°) 15 配流盘曲率半径R/mm 58.9 圆锥半径{R_{\text{f}}}/mm 103.8 柱塞直径d/mm 45 柱塞滑靴总质量{m_{{\text{ps}}}}/g 1970 柱塞球头到柱塞副距离/mm 48.52 滑靴密封带内外半径/mm 25，20.9 黏压系数{\alpha _p} 1.8 \times {10^{ - 8}} 黏温系数{\alpha _T} 0.03 油液比热{c_p}/(J·(kg·℃)−1) 1 884 油液密度\rho /({\text{kg}} \cdot {{\text{m}}^ - }^{\text{3}}) 850 
下载: 导出CSV
-
[1] CHAO Q, ZHANG J H, XU B, et al. Test rigs and experimental studies of the slipper bearing in axial piston pumps: A review[J]. Measurement, 2019, 132: 135-149. doi: 10.1016/j.measurement.2018.09.027 [2] GAO K, FU Y L, ZHAO J G, et al. Thermal analysis and simulation for EHA hydraulic piston pump[C]//Proceedings of 2021 Chinese Intelligent Systems Conference. Berlin: Springer, 2022: 874-883. [3] RHAKASYWI D, MARASABESSY A, HATUWE M R, et al. Safety factor of pump vibrations on ships based on the natural frequency of pump vibrations according to ISO 10816-3 [J]. Safety, 2020, 43(7): 180-192. [4] DESHMUKH S, RAINA A K, MURTHY V M S R, et al. Roadheader—A comprehensive review[J]. Tunnelling and Underground Space Technology, 2020, 95: 103148. doi: 10.1016/j.tust.2019.103148 [5] WU H C, ZHAO L M, NI S L, et al. Study on friction performance and mechanism of slipper pair under different paired materials in high-pressure axial piston pump[J]. Friction, 2020, 8(5): 957-969. doi: 10.1007/s40544-019-0314-2 [6] JI Z L. Research on thermal-fluid-structure coupling of valve plate pair in an axial piston pump with high pressure and high speed[J]. Industrial Lubrication and Tribology, 2018, 70(6): 1137-1144. doi: 10.1108/ILT-04-2017-0102 [7] 卿绿军, 陈万强, 李祥阳, 等. 工作参数对斜柱塞轴向柱塞泵流量特性的影响[J]. 液压气动与密封, 2017, 37(9): 51-55.QING L J, CHEN W Q, LI X Y, et al. Influence of operating parameters on the flow characteristics for axial piston pump with conical barrel[J]. Hydraulics Pneumatics & Seals, 2017, 37(9): 51-55(in Chinese). [8] 薛亚峰. 轴向柱塞变量泵平面与球面配流副磨损量的对比分析[J]. 矿山机械, 2016, 44(2): 93-96.XUE Y F. Comparative analysis on abrasion loss of planar and spherical port pair of axial piston variable pump[J]. Mining & Processing Equipment, 2016, 44(2): 93-96(in Chinese). [9] 李小宁, 毕诸明. 球面配流副的力学模型研究[J]. 机床与液压, 1996, 24(1): 9-13.LI X N, BI Z M. Study of mechanical model of spherical port plate[J]. Machine Tool & Hydraulics, 1996, 24(1): 9-13(in Chinese). [10] 王伟. 轴向柱塞泵球面配流副理论研究[D]. 淮南: 安徽理工大学, 2009.WANG W. Axial piston pump with flow spherical vice theoretical research[D]. Huainan: Anhui University of Science & Technology, 2009 (in Chinese). [11] 李传奇. 双斜式轴向柱塞泵的理论基础研究[D]. 淮南: 安徽理工大学, 2009.LI C Q. Theoretical fundamental research of the double-oblique-type axial piston pump[D]. Huainan: Anhui University of Science & Technology, 2009 (in Chinese). [12] 李小金, 苑士华, 胡纪滨. 球面配流副二维稳态压力场的数值求解方法研究[J]. 中国机械工程, 2010, 21(2): 150-154.LI X J, YUAN S H, HU J B. Numerical solution for two-dimensional steady-state pressure distribution on spherical port plate of axial piston machines[J]. China Mechanical Engineering, 2010, 21(2): 150-154(in Chinese). [13] DENG H S, WANG L, GUO Y C, et al. Analysis of the hydrodynamic lubrication characteristics of the external return spherical bearing pair of an axial piston pump/motor[J]. Mathematical Problems in Engineering, 2020, 2020: 1-14. [14] DENG H S, HU C, WANG Q C, et al. Friction and wear analysis of the external return spherical bearing pair of axial piston pump/motor[J]. Mechanics & Industry, 2020, 21(1): 104. [15] SHI C, WANG S P, WANG X J, et al. Dynamic lubrication model for slipper/swashplate of high-speed electro-hydrostatic actuator pump[C]//2017 12th IEEE Conference on Industrial Electronics and Applications (ICIEA). Piscataway: IEEE Press, 2018: 642-647. [16] SHI C, WANG S P, WANG X J, et al. Variable load failure mechanism for high-speed load sensing electro-hydrostatic actuator pump of aircraft[J]. Chinese Journal of Aeronautics, 2018, 31(5): 949-964. doi: 10.1016/j.cja.2018.01.005 [17] 许贤良, 刘利国. A4V柱塞泵运动方程研究[J]. 煤矿机械, 2001, 22(7): 19-21.XU X L, LIU L G. Research on movement equation of A4V piston pump[J]. Coal Mine Machinery, 2001, 22(7): 19-21(in Chinese). [18] 向伦凯, 周燕飞. 球面配流副油膜的几何成型计算[J]. 机械设计与制造工程, 2016, 45(9): 21-24.XIANG L K, ZHOU Y F. Geometric shape calculation of the oil film in the spherical port plate pair[J]. Machine Design and Manufacturing Engineering, 2016, 45(9): 21-24(in Chinese). 期刊类型引用(2)
1. 黄振羽，袁振，甘甜. 基于响应面法的斜轴马达配流盘形变分析与配流副结构优化. 润滑与密封. 2025(04): 176-183 . 
百度学术2. 夏毅敏，李正辉，谭顺辉，刘伟，夏士奇. 固-液-温耦合作用下油液特性对大排量柱塞泵流量脉动的影响. 华南理工大学学报(自然科学版). 2023(09): 44-55 . 百度学术其他类型引用(3)
-
下载:
下载:
百度学术
点击查看大图
计量
- 文章访问数: 235
- HTML全文浏览量: 79
- PDF下载量: 28
- 被引次数: 5
