基于改进雷达图法的群智能算法综合性能评估

程宝鹏; 方洋旺; 彭维仕; 杜泽弘

doi:10.13700/j.bh.1001-5965.2021.0726

基于改进雷达图法的群智能算法综合性能评估

doi: 10.13700/j.bh.1001-5965.2021.0726

程宝鹏¹,
方洋旺^{1, 2, ,},
彭维仕³,
杜泽弘⁴

1.
西安邮电大学计算机学院，西安 710121
2.
西北工业大学无人系统技术研究院，西安 710072
3.
武警工程大学装备管理与保障学院，西安 710086
4.
上海机电工程研究所，上海 201109

基金项目: 国家自然科学基金(71801222,61973253)

详细信息

通讯作者:
E-mail：17792018598@163.com

中图分类号: TP302.7
计量
- 文章访问数: 142
- HTML全文浏览量: 18
- PDF下载量: 8
- 被引次数: 0
出版历程
- 收稿日期: 2021-12-02
- 录用日期: 2022-01-17
- 网络出版日期: 2022-02-15
- 整期出版日期: 2023-10-31

Comprehensive performance evaluation of swarm intelligence algorithms based on improved radar graph method

1.
School of Computer Science & Technology，Xi’an University of Posts & Telecommunications，Xi’an 710121，China
2.
Unmanned System Research Institute，Northwestern Polytechnical University，Xi’an 710072，China
3.
School of Equipment Management and Support，People Armed Police Engineering University，Xi’an 710086，China
4.
Shanghai Electro-Mechanical Engineering Institute，Shanghai 201109，China

Funds: National Natural Science Foundation of China (71801222,61973253)

More Information

Corresponding author: E-mail：17792018598@163.com

摘要

摘要:
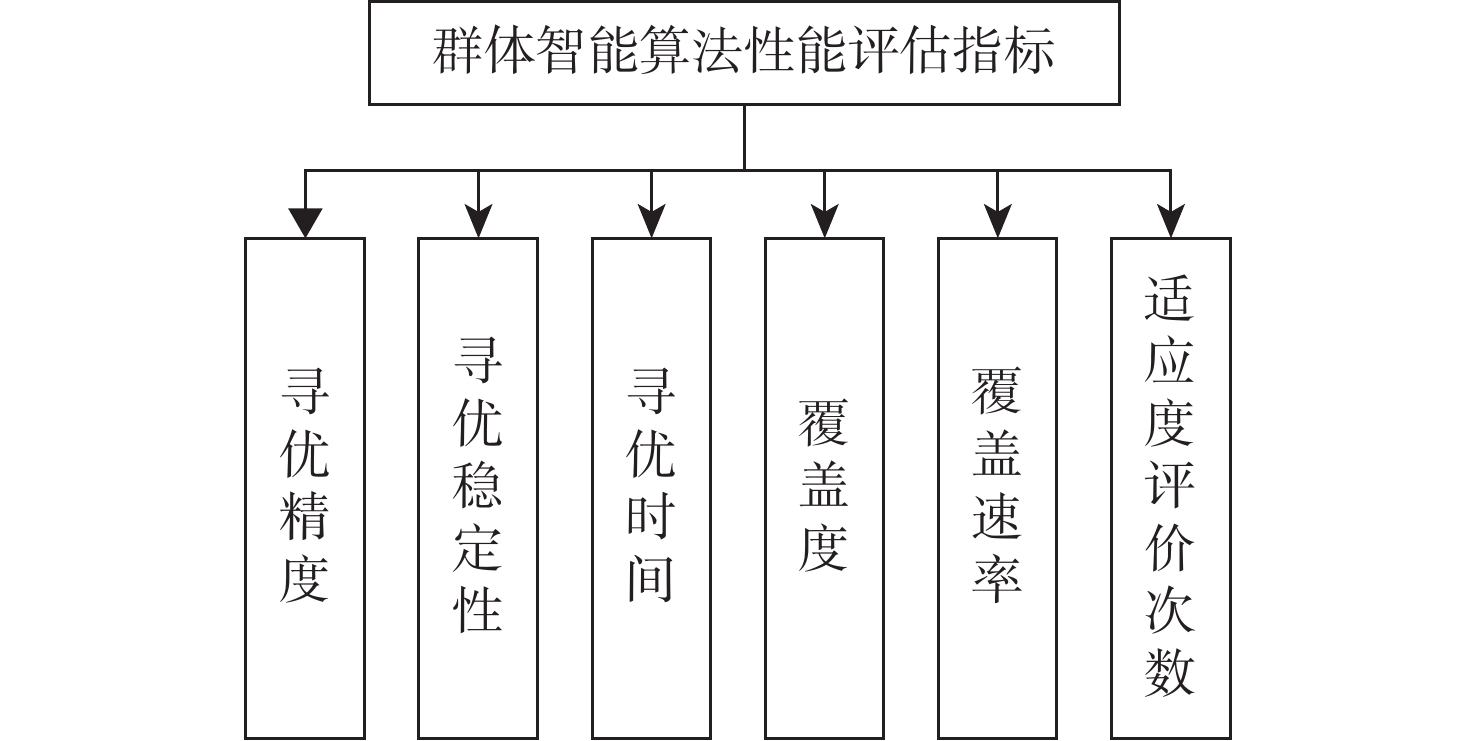
为解决传统性能评估方法无法准确评估群智能算法性能的问题，提出一种基于改进雷达图法的群智能算法综合性能评估方法。建立适应度评价次数、寻优时间、寻优稳定性、寻优精度、覆盖度、覆盖速率6种群体智能算法性能评估指标模型。在典型测试函数上，基于上述6种指标，通过改进雷达图法分析3种常用群智能算法的综合性能。仿真结果表明：所提方法能够全面客观的反映群智能算法的综合性能，为群智能算法的性能分析、优化和决策提供理论依据。
- 群智能算法 /
- 函数优化 /
- 雷达图法 /
- 覆盖度 /
- 覆盖速率 /
- 综合性能评估
Abstract:
In order to solve the problem that traditional performance evaluation methods cannot accurately evaluate the performance of swarm intelligence algorithms, a comprehensive performance evaluation method for swarm intelligence algorithms based on the improved radar graph method was proposed. Six performance evaluation index models for swarm intelligence algorithm were established, including fitness evaluation time, optimization time, optimization stability, optimization accuracy, coverage, and coverage rate. The improved radar graph method was utilized to examine the complete performance of three widely-known swarm intelligence algorithms based on the aforementioned six indicators using common test functions. The simulation results show that the comprehensive proposed method of swarm intelligence algorithm based on the improved radar graph can reflect the comprehensive performance of swarm intelligence algorithm comprehensively and objectively, and provide theoretical basis for the performance analysis, optimization, and decision-making of swarm intelligence algorithm.
- swarm intelligence algorithms /
- function optimization /
- radar graph method /
- coverage /
- coverage rate /
- comprehensive performance evaluation

HTML全文

图 1 群智能算法性能评估指标体系

Figure 1. Performance evaluation indicators system of swarm intelligence algorithms

下载: 全尺寸图片幻灯片

图 2 粒子寻优过程

Figure 2. Optimization process of particles

下载: 全尺寸图片幻灯片

图 3 粒子位置所在维度

Figure 3. Dimension of particles position

下载: 全尺寸图片幻灯片

图 4 粒子迭代过程

Figure 4. Iteration process of particles

下载: 全尺寸图片幻灯片

图 5 群智能算法综合性能评估雷达图

Figure 5. Radar graph of comprehensive performance evaluation of swarm intelligence algorithm

下载: 全尺寸图片幻灯片

图 6 改进的群智能算法综合性能评估雷达图

Figure 6. Improved radar graph of comprehensive performance evaluation of swarm intelligence algorithm

下载: 全尺寸图片幻灯片

图 7 算法在Griewank函数下的改进雷达图(等权)

Figure 7. Improved radar graph of algorithms under Griewank functions(same weight)

下载: 全尺寸图片幻灯片

图 8 算法在Griewank函数下的改进雷达图(不等权)

Figure 8. Improved radar graph of algorithms under Griewank function(unequal weight)

下载: 全尺寸图片幻灯片

表 1 单峰测试函数

Table 1. Single peak test functions

函数名	函数表达式	定义域	最优值	维度
Rotated Hyper-Ellipsoid	$f(x) = \displaystyle \sum\limits_{i = 1}^d {\displaystyle \sum\limits_{j = 1}^d {x_j^2} }$	[−65.536,65.536]	0	2, 10
Sum Squares	$f(x) = \displaystyle \sum\limits_{i = 1}^d {ix_i^2}$	[−10,10]	0	2, 10

下载: 导出CSV

表 2 多峰测试函数

Table 2. Multimodal peak test functions

函数名	函数表达式	定义域	最优值	维度
Bohachevsky	$f(x)=x_{1}^{2}+2 x_{2}^{2}-0.3 \cos \left(3 {\text{π}} x_{1}\right)-0.4 \cos \left(4 {\text{π}} x_{2}\right)+0.7$	[−100,100]	0	2
Levy	$f(x)=\sin ^{2}\left(3 {\text{π}} x_{1}\right)+\left(x_{1}-1\right)^{2}\left[1+\sin ^{2}\left(3 {\text{π}} x_{2}\right)\right]+\left(x_{2}-1\right)^{2}\left[1+\sin ^{2}\left(2 {\text{π}} x_{2}\right)\right]$	[−10, 10]	0	2
Rastrigin	$f(x) = 10d + \displaystyle \sum\limits_{i = 1}^d {[x_i^2 - 10\cos (2{\text{π} } {x_i})]}$	[−5.12,5.12]	0	10
Griewank	$f(x)=1+\displaystyle\sum\limits_{i=1}^d\dfrac{x_i^2}{4\;000}+\displaystyle\prod_{i=1}^d{\rm{cos} }\left(\dfrac{x_i}{\sqrt i}\right)$	[−600,600]	0	10

下载: 导出CSV

表 3 算法初始化参数

Table 3. Initial parameters of algorithms

算法	参数	初始值
ACO	$\rho $	0.8
	$ \alpha $	1
	$\beta $	5
BA	$A_{\rm{l}}$	0.6
	$r$	0.7
	$ \alpha ' $	0.9
	$\gamma $	0.9
PSO	$w$	0.5
	${c_1}$	1.5
	${c_2}$	1.5

下载: 导出CSV

表 4 参考值$\theta $

Table 4. Reference value $\theta $

函数名	维度	$\theta $ 值
Rotated Hyper-Ellipsoid	2	$1.334 \times {10^{ - 2}}$
Rotated Hyper-Ellipsoid	10	$5.911 \times {10^3}$
Sum Squares	2	$5.148 \times {10^{ - 5}}$
Sum Squares	10	$ 1.930 $
Bohachevsky	2	$1.013$
Levy	2	$2.124 \times {10^{ - 2}}$
Rastrigin	10	$4.380 \times {10^1}$
Griewank	10	$1.438 \times {10^{ - 4}}$

下载: 导出CSV

表 5 算法在二维测试函数下的指标值

Table 5. Indexes value of algorithms in 2D test functions

函数名	算法	适应度评价次数	寻优时间/s	寻优精度	寻优覆盖度	寻优覆盖速率	寻优稳定性
Rotated Hyper-Ellipsoid	BA	328	0.586	$6.715 \times {10^{ - 5}}$	$4.387 \times {10^{ - 5}}$	$2.816 \times {10^{ - 3}}$	$6.154 \times {10^{ - 5}}$
	PSO	828	0.454	$2.503 \times {10^{ - 139}}$	$3.750 \times {10^{ - 4}}$	$1.450 \times {10^{ - 2}}$	$1.367 \times {10^{ - 138}}$
	ACO	18990	0.346	$1.334 \times {10^{ - 2}}$	$4.603 \times {10^{ - 3}}$	$1.980 \times {10^{ - 1}}$	$4.830 \times {10^{ - 2}}$
Sum Squares	BA	27316	0.434	$5.148 \times {10^{ - 5}}$	$1.460 \times {10^{ - 3}}$	$4.992 \times {10^{ - 3}}$	$5.968 \times {10^{ - 5}}$
	PSO	2410	0.360	$1.947 \times {10^{ - 141}}$	$6.650 \times {10^{ - 3}}$	$8.384 \times {10^{ - 3}}$	$7.816 \times {10^{ - 141}}$
	ACO	8553	0.279	$1.040 \times {10^{ - 6}}$	$6.082 \times {10^{ - 2}}$	$8.055 \times {10^{ - 2}}$	$1.098 \times {10^{ - 6}}$
Bohachevsky	BA	160	0.562	$8.651 \times {10^{ - 4}}$	$2.190 \times {10^{ - 5}}$	$ 5.945 \times {10^{ - 3}} $	$8.183 \times {10^{ - 4}}$
	PSO	593	0.400	0	$2.196 \times {10^{ - 4}}$	$1.844 \times {10^{ - 2}}$	0
	ACO	33098	0.267	$1.013$	$2.176 \times {10^{ - 3}}$	$1.876 \times {10^{ - 1}}$	$4.822 \times {10^{ - 1}}$
Levy	BA	871	0.554	$4.403 \times {10^{ - 4}}$	$1.438 \times {10^{ - 3}}$	$4.360 \times {10^{ - 3}}$	$3.271 \times {10^{ - 4}}$
	PSO	991	0.388	$1.350 \times {10^{ - 31}}$	$6.961 \times {10^{ - 3}}$	$8.877 \times {10^{ - 3}}$	$6.681 \times {10^{ - 47}}$
	ACO	23073	0.317	$2.124 \times {10^{ - 2}}$	$1.952 \times {10^{ - 2}}$	$1.804 \times {10^{ - 2}}$	$5.152 \times {10^{ - 2}}$

下载: 导出CSV

表 6 算法在十维测试函数下的指标值

Table 6. Indexes value of algorithms in 10D test functions

函数名	算法	适应度评价次数	寻优时间 /s	寻优精度	寻优覆盖度	寻优覆盖速率	寻优稳定性
Rotated Hyper-Ellipsoid	BA	333	0.917	$1.800$	$1.669 \times {10^{ - 29}}$	$2.601 \times {10^{ - 2}}$	$5.087 \times {10^{ - 1}}$
	PSO	398	0.661	$1.165 \times {10^{ - 8}}$	$8.895 \times {10^{ - 29}}$	$3.073 \times {10^{ - 2}}$	$3.186 \times {10^{ - 8}}$
	ACO	41691	0.625	$5.911 \times {10^3}$	$7.666 \times {10^{ - 28}}$	$2.344 \times {10^{ - 1}}$	$1.844 \times {10^3}$
Sum Squares	BA	37333	0.534	$1.930$	$8.529 \times {10^{ - 22}}$	$9.957 \times {10^{ - 3}}$	$3.968 \times {10^{ - 1}}$
	PSO	2393	0.393	$1.742 \times {10^{ - 9}}$	$8.865 \times {10^{ - 21}}$	$5.294 \times {10^{ - 2}}$	$5.503 \times {10^{ - 9}}$
	ACO	29673	0.251	$6.049 \times {10^{ - 2}}$	$1.184 \times {10^{ - 19}}$	$2.421 \times {10^{ - 1}}$	$9.447 \times {10^{ - 2}}$
Rastrigin	BA	32080	0.622	$ 4.380 \times {10^1} $	$4.830 \times {10^{ - 19}}$	$8.789 \times {10^{ - 3}}$	$1.077 \times {10^1}$
	PSO	1230	0.404	$8.099$	$4.427 \times {10^{ - 18}}$	$1.678 \times {10^{ - 2}}$	$7.158$
	ACO	4321	0.301	$2.304 \times {10^1}$	$1.037 \times {10^{ - 17}}$	$2.536 \times {10^{ - 2}}$	$3.946$
Griewank	BA	36911	1.111	$1.438 \times {10^{ - 4}}$	$8.799 \times {10^{ - 22}}$	$1.216 \times {10^{ - 2}}$	$3.058 \times {10^{ - 5}}$
	PSO	3123	0.898	$8.293 \times {10^{ - 12}}$	$9.019 \times {10^{ - 21}}$	$4.856 \times {10^{ - 2}}$	$2.771 \times {10^{ - 11}}$
	ACO	31561	0.709	$3.754 \times {10^{ - 6}}$	$1.162 \times {10^{ - 19}}$	$2.376 \times {10^{ - 1}}$	$1.481 \times {10^{ - 6}}$

下载: 导出CSV

表 7 算法在二维测试函数上综合指标值

Table 7. Comprehensive indexes value of algorithms in 2D test functions

函数名	PSO	ACO	BA
Rotated Hyper-Ellipsoid	0.5753	0.4917	0.3690
Sum Squares	0.5968	0.4828	0.1281
Bohachevsky	0.5673	0.4522	0.3729
Levy	0.6096	0.3335	0.2734

下载: 导出CSV

表 8 算法在十维测试函数上综合指标值

Table 8. Comprehensive indexes value of algorithms in 10D test functions

函数名	PSO	ACO	BA
Rotated Hyper-Ellipsoid	0.5874	0.3824	0.2494
Sum Squares	0.5960	0.4221	0.0769
Rastrigin	0.6130	0.5257	0.3218
Griewank	0.5975	0.4262	0.1126

下载: 导出CSV

参考文献(24)

[1]	KAUR K, KUMAR Y. Swarm intelligence and its applications towards various computing: A systematic review[C]//2020 International Conference on Intelligent Engineering and Management. Piscataway: IEEE Press, 2020: 57-62.
[2]	BREZOČNIK L, FISTER I, PODGORELEC V. Swarm intelligence algorithms for feature selection: A review[J]. Applied Sciences, 2018, 8(9): 1521. doi: 10.3390/app8091521
[3]	DANESH M, SHIRGAHI H. A novel hybrid knowledge of firefly and pso swarm intelligence algorithms for efficient data clustering[J]. Journal of Intelligent & Fuzzy Systems, 2017, 33(6): 3529-3538.
[4]	CHAI X Q. Task scheduling based on swarm intelligence algorithms in high performance computing environment[J]. Journal of Ambient Intelligence and Humanized Computing, 2020: 1-9.
[5]	LIN N, TANG J C, LI X W, et al. A novel improved bat algorithm in UAV path planning[J]. Computers, Materials & Continua, 2019, 61(1): 323-344.
[6]	GAN C, CAO W H, WU M, et al. A new bat algorithm based on iterative local search and stochastic inertia weight[J]. Expert Systems with Applications, 2018, 104: 202-212. doi: 10.1016/j.eswa.2018.03.015
[7]	AHMED A M, RASHID T A, SAEED S A M. Cat swarm optimization algorithm: A survey and performance evaluation[J]. Computational Intelligence and Neuroscience, 2020, 2020: 1-20.
[8]	REVATHI K, KRISHNAMOORTHY N. The performance analysis of swallow swarm optimization algorithm[C]//2015 2nd International Conference on Electronics and Communication Systems. Piscataway: IEEE Press, 2015: 558-562.
[9]	李雅丽, 王淑琴, 陈倩茹, 等. 若干新型群智能优化算法的对比研究[J]. 计算机工程与应用, 2020, 56(22): 1-12. LI Y L, WANG S Q, CHEN Q R, et al. Comparative study of several new swarm intelligence optimization algorithms[J]. Computer Engineering and Applications, 2020, 56(22): 1-12(in Chinese).
[10]	张九龙, 王晓峰, 芦磊, 等. 若干新型智能优化算法对比分析研究[J]. 计算机科学与探索, 2022, 16(1): 88-105. doi: 10.3778/j.issn.1673-9418.2107028 ZHANG J L, WANG X F, LU L, et al. Analysis and research of several new intelligent optimization algorithms[J]. Journal of Frontiers of Computer Science and Technology, 2022, 16(1): 88-105(in Chinese). doi: 10.3778/j.issn.1673-9418.2107028
[11]	孙雅薇, 田建宇, 梁炜, 等. 基于雷达图法的通信网络效能可视化建模[J]. 计算机仿真, 2019, 36(10): 1-5. doi: 10.3969/j.issn.1006-9348.2019.10.001 SUN Y W, TIAN J Y, LIANG W, et al. Visual modeling of communication network effectiveness based on radar chart[J]. Computer Simulation, 2019, 36(10): 1-5(in Chinese). doi: 10.3969/j.issn.1006-9348.2019.10.001
[12]	陈勇, 陈潇凯, 李志远, 等. 具有评价结果唯一性特征的雷达图综合评价法[J]. 北京理工大学学报, 2010, 30(12): 1409-1412. CHEN Y, CHEN X K, LI Z Y, et al. Method of radar chart comprehensive evaluation with uniqueness feature[J]. Transactions of Beijing Institute of Technology, 2010, 30(12): 1409-1412(in Chinese).
[13]	李青, 战仁军, 彭维仕. 基于雷达图的防暴武器系统作战效能评估方法[J]. 火力与指挥控制, 2020, 45(8): 186-190. LI Q, ZHAN R J, PENG W S. Operational effectiveness evaluation method of riot weapon systems[J]. Fire Control & Command Control, 2020, 45(8): 186-190(in Chinese).
[14]	程志友, 朱唯韦, 陶青, 等. 基于改进雷达图的配电系统电能质量评估方法[J]. 电测与仪表, 2019, 56(14): 34 -39. CHENG Z Y, ZHU W W, TAO Q, et al. Power quality evaluation method of distribution system based on improved radar chart[J]. Electrical Measurement & Instrumentation, 2019, 56(14): 34 -39(in Chinese).
[15]	DORIGO M, MANIEZZO V, COLORNI A. Ant system: Optimization by a colony of cooperating agents[J]. IEEE Transactions on Systems, Man, and Cybernetics Part B, Cybernetics: A Publication of the IEEE Systems, Man, and Cybernetics Society, 1996, 26(1): 29-41. doi: 10.1109/3477.484436
[16]	YANG X S, HE X S. Bat algorithm: Literature review and applications[J]. International Journal of Bio-Inspired Computation, 2013, 5(3): 141. doi: 10.1504/IJBIC.2013.055093
[17]	KENNEDY J. Particle swarm optimization[C]//Encyclopedia of Machine Learning and Data Mining. Berlin: Springer, 2017: 967-972.
[18]	Dan Simon. 进化优化算法: 基于仿生和种群的计算机智能方法[M]. 陈曦译. 北京: 清华大学出版社, 2018: 455-457. DAN S. Evolutionary optimization algorithms: Biologically inspired and population-based approaches to computer intelligence[M]. Chen Xi translated. Beijing: Tsinghua University Press, 2018: 455-457(in Chinese).
[19]	陈一昭, 姜麟. 蚁群算法参数分析[J]. 科学技术与工程, 2011, 11(36): 9080-9084. CHEN Y Z, JIANG L. Parametric study of ant colony optimization[J]. Science Technology and Engineering, 2011, 11(36): 9080-9084(in Chinese).
[20]	包子阳, 余继周, 杨杉. 智能优化算法及其MATLAB实例[M]. 第2版. 北京: 电子工业出版社, 2018: 95-97. BAO Z Y, YU J Z, YANG S. Intelligent optimization algorithm and its MATLAB example[M]. 2nd ed. Beijing: Publishing House of Electronics Industry, 2018: 95-97 (in Chinese).
[21]	YANG X S. A new metaheuristic bat-inspired algorithm[C]//Nature Inspired Cooperative Strategies for Optimization (NICSO 2010). Berlin: Springer, 2010: 65-74.
[22]	CLERC M. The swarm and the queen: Towards a deterministic and adaptive particle swarm optimization[C]//Proceedings of the 1999 Congress on Evolutionary Computation-CEC99. Piscataway: IEEE Press, 2002: 1951-1957.
[23]	杨博雯, 钱伟懿. 粒子群优化算法中惯性权重改进策略综述[J]. 渤海大学学报(自然科学版), 2019, 40(3): 274-288. YANG B W, QIAN W Y. Summary on improved inertia weight strategies for particle swarm optimization algorithm[J]. Journal of Bohai University (Natural Science Edition), 2019, 40(3): 274-288(in Chinese).
[24]	王凌峰, 姚依楠. 主观线性加权评价问题的新方法: 中位数层次分析法[J]. 系统科学学报, 2018, 26(1): 96-99. WANG L F, YAO Y N. A new method for subjective linear weighted evaluation: The median analytic hierarchy process[J]. Chinese Journal of Systems Science, 2018, 26(1): 96-99(in Chinese).