基于佳点集的改进麻雀搜索算法

闫少强; 杨萍; 朱东林; 吴丰轩; 阎哲

doi:10.13700/j.bh.1001-5965.2021.0730

基于佳点集的改进麻雀搜索算法

doi: 10.13700/j.bh.1001-5965.2021.0730

1.
火箭军工程大学基础部，西安 710025
2.
江西理工大学信息工程学院，赣州 341000

基金项目: 国家自然科学基金(61703411)

详细信息

通讯作者:
E-mail：yyp_ing@163.com

中图分类号: TP301.6
计量
- 文章访问数: 207
- HTML全文浏览量: 19
- PDF下载量: 37
- 被引次数: 0
出版历程
- 收稿日期: 2021-12-03
- 录用日期: 2022-01-25
- 网络出版日期: 2022-01-29
- 整期出版日期: 2023-10-31

Improved sparrow search algorithm based on good point set

1.
School of Combat Support，Rocket Military Engineering University，Xi’an 710025，China
2.
School of Information Engineering，Jiangxi University of Technology，Ganzhou 341000，China

Funds: National Natural Science Foundation of China (61703411)

More Information

Corresponding author: E-mail：yyp_ing@163.com

摘要

摘要:
为改善麻雀搜索算法（SSA）初始种群质量和稳定性差，易陷入局部最优的缺点，提出一种基于佳点集的改进麻雀搜索算法(GSSA)。加入佳点集使初始种群更加均匀，提升了种群多样性；结合SSA算法特点引入改进的迭代局部搜索，在不降低原算法收敛速度快的基础上，使算法的搜索能力更加灵活；在算法中加入逐维透镜成像反向学习机制，减少各个维度间的干扰，帮助算法跳出局部最优并加速收敛。经12个测试函数仿真实验，并借助Wilcoxon秩和检验、平均误差M等证明了GSSA在寻优精度和稳定性等寻优性能都有较大的提升，且收敛速度更快。
- 麻雀搜索算法 /
- 优化算法 /
- 佳点集 /
- 迭代局部搜索 /
- 逐维透镜反向学习
Abstract:
An enhanced sparrow search algorithm based on a good point set (GSSA) is developed to address the sparrow search algorithm (SSA) weak starting population quality, instability, and susceptibility to local optimization. Firstly, adding a good point set makes the initial population more uniform and improves the population diversity. Second, while retaining the benefits of the original algorithm’s quick convergence speed, an enhanced iterative local search is merged with the features of the SSA algorithm to increase the search capabilities of the latter. Finally, a dimension by dimension lens imaging reverse learning mechanism is added to the algorithm to reduce the interference between various dimensions, help the algorithm jump out of local optimization and accelerate convergence. Through 12 test function simulation experiments, with the help of the Wilcoxon rank sum test and mean error M, it is proved that GSSA has greatly improved the optimization performance such as optimization accuracy and stability, and the convergence speed is faster.
- sparrow search algorithm /
- optimization algorithm /
- good point set /
- iterative local search /
- dimension by dimension lens reverse learning

HTML全文

图 1 佳点集分布

Figure 1. Distribution of good point sets

下载: 全尺寸图片幻灯片

图 2 改进的迭代局部搜索原理

Figure 2. Improved iterative local search principle

下载: 全尺寸图片幻灯片

图 3 透镜反向学习原理

Figure 3. Principle of len reverse learning

下载: 全尺寸图片幻灯片

图 4 各改进策略结果对比

Figure 4. Comparison of improvement strategies

下载: 全尺寸图片幻灯片

图 5 各算法的平均收敛曲线

Figure 5. Average convergences curves of test function

下载: 全尺寸图片幻灯片

图 6 测试函数排序雷达图

Figure 6. Radar diagram of test function sorting

下载: 全尺寸图片幻灯片

表 1 参数设置

Table 1. Parameter settings

算法	a	b	n	S	P_D	D_S	k
GWO	2→0
WOA		1
MWOA			12000
SSA				0.8	0.2	0.2
CSSA				0.8	0.2	0.2
GSSA				0.8	0.2	0.2	12000

下载: 导出CSV

表 2 测试函数

Table 2. Test function

函数	维度	搜索区域	理论值
${F_1}\left( x \right) =\displaystyle\sum \limits_{i = 1}^n x_i^2$	30	[−100,100]	0
${F_2}\left( x \right) = \displaystyle\sum \limits_{i = 1}^n \left\| { {x_i} } \right\| + \displaystyle\prod \limits_{i = 1}^n \left\| { {x_i} } \right\|$	30	[−100,100]	0
${F_3}\left( x \right) = {\max _i}\left\{ {\left\| {{x_i}} \right\|,1 \leqslant i \leqslant n} \right\}$	30	[−100,100]	0
${F_4}\left( x \right) = \displaystyle\sum \limits_{i = 1}^{n - 1} \left[ {100{ {({x_{i + 1} } - x_i^2)}^2} + { {({x_i} - 1)}^2} } \right]$	30	[−30,30]	0
${F_5}\left( x \right) = \displaystyle\sum \limits_{i = 1}^n {\left( {\left[ { {x_i} + 0.5} \right]} \right)^2}$	30	[−100,100]	0
${F_6}\left( x \right) = \displaystyle\sum \limits_{i = 1}^n - {x_i}\sin \left( {\sqrt {\left\| { {x_i} } \right\|} } \right)$	30	[−500,500]	−12569.4
${F_7}\left( x \right) = \dfrac{1}{ {4\;000} }\displaystyle\sum \limits_{i = 1}^n x_i^2 - \displaystyle\prod \limits_{i = 1}^n \cos \left( {\frac{ { {x_i} } }{ {\sqrt i } } } \right) + 1$	30	[−600,600]	0
$\begin{array}{l} {F_8}\left( x \right) = \dfrac{ {\text{π} } }{n}\Biggr\{ {10{\text{sin} }\left( { {\text{π} }{y_1} } \right) + \displaystyle\sum \limits_{i = 1}^{n - 1} { {\left( { {y_i} - 1} \right)}^2} } \;\cdot \\ \qquad{\left[ {1 + 10{\text{si} }{ {\text{n} }^2}\left( { {\text{π} }{y_{i + 1} } } \right)} \right] + } \\ \qquad{ { {\left( { {y_n} - 1} \right)}^2} } \Biggr\} + \displaystyle\sum \limits_{i = 1}^n u\left( { {x_i},10,100,4} \right) \\ \qquad{y_i} = 1 + \dfrac{ { {x_i} + 1} }{4} \\\end{array}$	30	[−50,50]	0
$\begin{gathered} {F_9}\left( x \right) = 0.1\Biggr\{ { {\sin }^2}\left( {3{\text{π} }{x_1} } \right) + \displaystyle\sum \limits_{i = 1}^n { {\left( { {x_i} - 1} \right)}^2} \;\cdot \\ \qquad{\left[ {1 + { {\sin }^2}\left( {3{\text{π} }{x_i} + 1} \right)} \right] + } \\ \qquad { {\text{ } }{ {\left( { {x_n} - 1} \right)}^2}\left[ {1 + { {\sin }^2}\left( {2{\text{π} }{x_n} } \right)} \right]} \Biggr\} + \\ \qquad \displaystyle\sum \limits_{i = 1}^n u\left( { {x_i},5,100,4} \right) \\ \end{gathered}$	30	[−50,50]	0
${F_{10} }\left( x \right) = {\left( {\dfrac{1}{ {500} } + \displaystyle\sum \limits_{j = 1}^{25} {1}\Bigg/\Bigg({ {j + \displaystyle\sum \limits_{i = 1}^2 { {\left( { {x_i} - {a_{ij} } } \right)}^6} } }\Bigg) } \right)^{-1 } }$	2	[−65.536, 65.536]	0.998
${F_{11} }\left( x \right) = \displaystyle\sum \limits_{i = 1}^{11} {\left( { {a_i} - \frac{ { {x_1}\left( {b_i^2 + {b_1}{x_2} } \right)} }{ {b_i^2 + {b_1}{x_3} + {x_4} } } } \right)^2}$	4	[−5,5]	0.0003
${F_{12} }\left( x \right) = \displaystyle\sum \limits_{i = 1}^{10} {\left[ {\left( {{\boldsymbol{X}} - {a_i} } \right){ {\left( {{\boldsymbol{X}} - {a_i} } \right)}^{\rm{T} } } + {c_i} } \right]^{ - 1} }$	4	[0,10]	−10.5364

下载: 导出CSV

表 3 测试函数结果对比

Table 3. Comparison of test function results

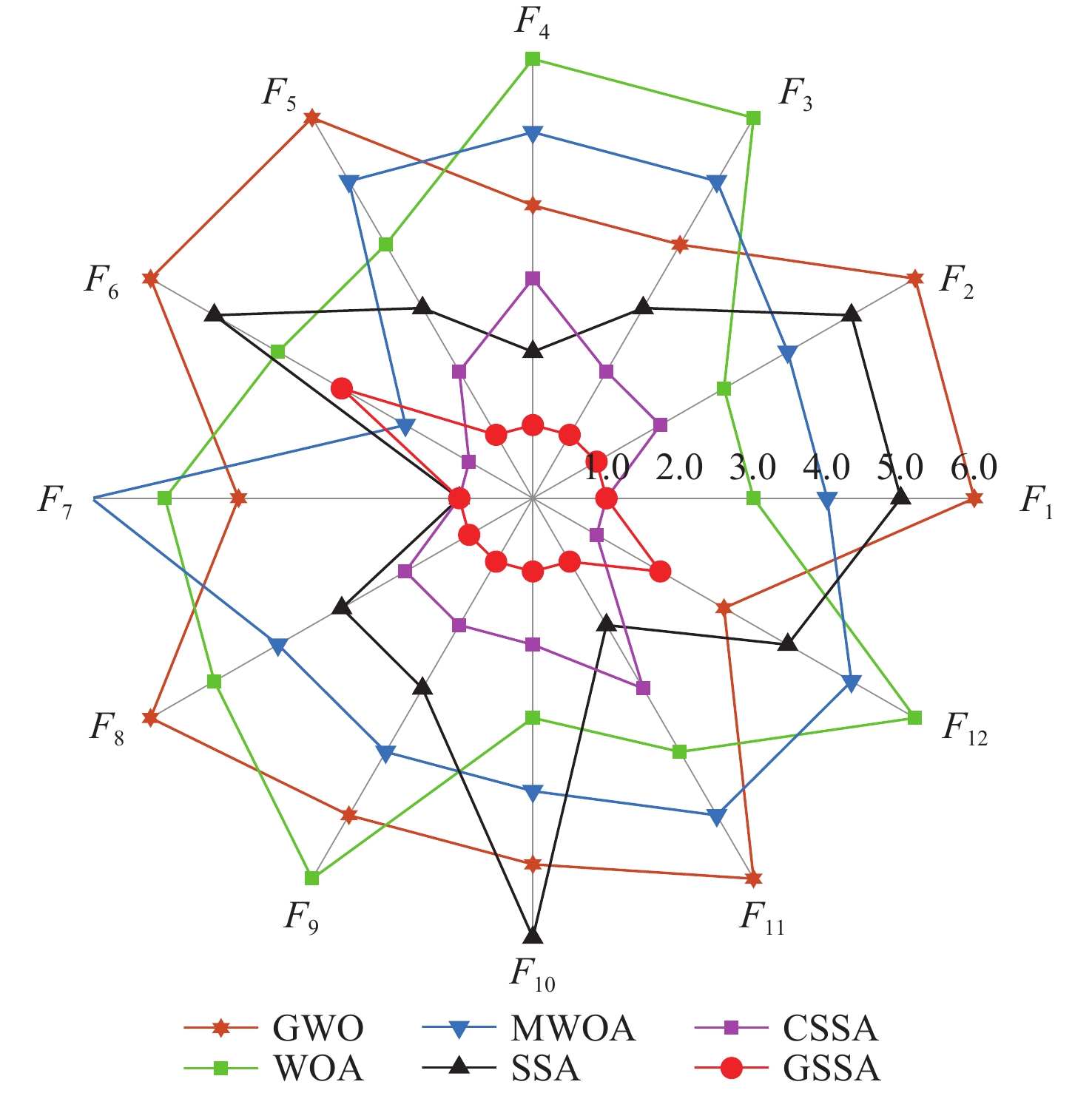
函数	算法	最优值	最差值	均值	标准差	排名	函数	算法	最优值	最差值	均值	标准差	排名
F₁	GWO	1.75×10⁻²⁷	2.34×10⁻²⁵	3.31×10⁻²⁶	5.42×10⁻²⁶	6	F₇	GWO	0	3.17×10⁻²	4.59×10⁻³	9.70×10⁻³	4
	WOA	2.18×10⁻⁸⁷	5.74×10⁻⁷³	2.62×10⁻⁷⁴	1.05×10⁻⁷³	3		WOA	0	1.48×10⁻¹	4.93×10⁻³	2.70×10⁻²	5
	MWOA	3.13×10⁻⁸³	3.65×10⁻⁷¹	1.33×10⁻⁷²	6.66×10⁻⁷²	4		MWOA	0	1.64×10⁻¹	5.48×10⁻³	3.00×10⁻²	6
	SSA	0	5.91×10⁻⁶³	1.97×10⁻⁶⁴	1.08×10⁻⁶³	5		SSA	0	0	0	0	1
	CSSA	0	0	0	0	1		CSSA	0	0	0	0	1
	GSSA	0	0	0	0	1		GSSA	0	0	0	0	1
F₂	GWO	1.33×10⁻¹⁶	2.07×10⁻¹⁵	7.21×10⁻¹⁶	4.63×10⁻¹⁶	6	F₈	GWO	5.13×10⁻⁷	1.14×10⁻¹	3.90×10⁻²	2.17×10⁻²	6
	WOA	2.65×10⁻⁵⁷	2.69×10⁻⁴⁹	9.79×10⁻⁵¹	4.90×10⁻⁵⁰	3		WOA	3.55×10⁻³	9.25×10⁻²	2.40×10⁻²	1.86×10⁻²	5
	MWOA	1.06×10⁻⁵⁶	1.57×10⁻⁴⁸	9.36×10⁻⁵⁰	3.45×10⁻⁴⁹	4		MWOA	6.06×10⁻³	6.53×10⁻²	2.25×10⁻²	1.45×10⁻²	4
	SSA	0	9.86×10⁻³⁷	5.16×10⁻³⁸	1.91×10⁻³⁷	5		SSA	1.57×10⁻³²	4.18×10⁻⁸	2.15×10⁻⁹	8.19×10⁻⁹	3
	CSSA	0	3.51×10⁻²⁸⁷	1.17×10⁻²⁸⁸	0	2		CSSA	3.01×10⁻¹⁴	3.32×10⁻⁹	2.70×10⁻¹⁰	6.03×10⁻¹⁰	2
	GSSA	0	0	0	0	1		GSSA	1.57×10⁻³²	1.04×10⁻¹⁴	3.92×10⁻¹⁶	1.90×10⁻¹⁵	1
F₃	GWO	5.77×10⁻⁸	3.64×10⁻⁶	7.30×10⁻⁷	8.46×10⁻⁷	4	F₉	GWO	1.01×10⁻¹	9.71×10⁻¹	5.42×10⁻¹	1.99×10⁻¹	5
	WOA	4.37	90.3	47.4	26.1	6		WOA	1.26×10⁻¹	1.11	5.50×10⁻¹	2.96×10⁻¹	6
	MWOA	1.63	85.0	43.4	25.0	5		MWOA	8.24×10⁻²	9.67×10⁻¹	5.37×10⁻¹	2.11×10⁻¹	4
	SSA	0	8.18×10⁻²⁸	2.73×10⁻²⁹	1.49×10⁻²⁸	3		SSA	1.35×10⁻³²	1.89×10⁻⁷	1.42×10⁻⁸	3.90×10⁻⁸	3
	CSSA	0	1.10×10⁻²⁹⁷	4.27×10⁻²⁹⁹	0	2		CSSA	1.62×10⁻¹¹	5.14×10⁻⁸	3.14×10⁻⁹	9.25×10⁻⁹	2
	GSSA	0	0	0	0	1		GSSA	1.35×10⁻³²	1.23×10⁻¹⁴	6.19×10⁻¹⁶	2.29×10⁻¹⁵	1
F₄	GWO	26.1	28.5	27.2	7.68×10⁻¹	4	F₁₀	GWO	9.98×10⁻¹	12.7	3.62	3.36	5
	WOA	27.2	28.8	28.3	4.77×10⁻¹	6		WOA	9.98×10⁻¹	10.8	3.22	3.52	3
	MWOA	27.0	28.8	28.0	5.22×10⁻¹	5		MWOA	9.98×10⁻¹	10.8¹	3.61	3.81	4
	SSA	0	1.37×10⁻⁴	9.74×10⁻⁶	2.75×10⁻⁵	2		SSA	9.98×10⁻¹	12.7	9.53	4.83	6
	CSSA	8.00×10⁻⁹	4.20×10⁻⁴	4.53×10⁻⁵	1.07×10⁻⁴	3		CSSA	9.98×10⁻¹	2.98	1.26	6.86×10⁻¹	2
	GSSA	0	8.16×10⁻¹⁶	2.72×10⁻¹⁷	1.49×10⁻¹⁶	1		GSSA	9.98×10⁻¹	9.98×10⁻¹	9.98×10⁻¹	1.21×10⁻¹⁴	1
F₅	GWO	2.34×10⁻¹	1.67	7.61×10⁻¹	4.05×10⁻¹	6	F₁₁	GWO	3.08×10⁻⁴	2.04×10⁻²	1.77×10⁻³	5.06×10⁻³	6
	WOA	9.41×10⁻²	1.18	3.99×10⁻¹	2.27×10⁻¹	4		WOA	3.29×10⁻⁴	2.24×10⁻³	6.62×10⁻⁴	4.24×10⁻⁴	4
	MWOA	5.41×10⁻²	8.77×10⁻¹	4.07×10⁻¹	2.21×10⁻¹	5		MWOA	3.07×10⁻⁴	2.25×10⁻³	6.73×10⁻⁴	4.85×10⁻⁴	5
	SSA	0	1.85×10⁻⁷	2.61×10⁻⁸	4.61×10⁻⁸	3		SSA	3.07×10⁻⁴	3.30×10⁻⁴	3.08×10⁻⁴	4.14×10⁻⁶	2
	CSSA	5.28×10⁻¹²	6.86×10⁻⁸	6.71×10⁻⁹	1.45×10⁻⁸	2		CSSA	3.07×10⁻⁴	1.22×10⁻³	3.42×10⁻⁴	1.68×10⁻⁴	3
	GSSA	0	3.57×10⁻¹⁶	1.37×10⁻¹⁷	6.55×10⁻¹⁷	1		GSSA	3.08×10⁻⁴	3.08×10⁻⁴	3.08×10⁻⁴	2.68×10⁻¹⁵	1
F₆	GWO	−7.20×10³	−2.66×10³	−5.94×10³	−1.19×10³	6	F₁₂	GWO	−10.5	−5.13	−10.4	9.87×10⁻¹	3
	WOA	−1.26×10⁴	−6.67×10³	−1.01×10⁴	−1.92×10³	4		WOA	−10.5	−1.68	−7.03	3.45	6
	MWOA	−1.26×10⁴	−8.51×10³	−1.09×10⁴	−1.57×10³	2		MWOA	−10.5	−1.86	−7.15	3.25	5
	SSA	−1.26×10⁴	−6.50×10³	−9.28×10³	−2.06×10³	5		SSA	−10.5	−5.13	−9.99	1.65	4
	CSSA	−1.26×10⁴	−8.66×10³	−1.10×10⁴	−1.11×10³	1		CSSA	−10.5	−10.5	−10.5	1.44×10⁻¹⁵	1
	GSSA	−1.16×10⁺⁰⁴	−8.64×10⁺⁰³	−1.06×10⁴	−5.11×10²	3		GSSA	−10.5	−10.5	−10.5	1.95×10⁻⁵	2

下载: 导出CSV

表 4 测试函数Wilcoxon秩和检验的p值

Table 4. p-value of Wilcoxon rank sum test of test function

函数	GWO	WOA	MWOA	SSA	CSSA
F₁	1.21×10⁻¹²	1.21×10⁻¹²	1.21×10⁻¹²	6.25×10⁻¹⁰	Na
F₂	1.21×10⁻¹²	1.21×10⁻¹²	1.21×10⁻¹²	4.57×10⁻¹²	8.87×10⁻⁷
F₃	1.21×10⁻¹²	1.21×10⁻¹²	1.21×10⁻¹²	4.57×10⁻¹²	1.37×10⁻³
F₄	3.00×10⁻¹¹	3.00×10⁻¹¹	3.00×10⁻¹¹	5.87×10⁻⁰⁷	3.00×10⁻¹¹
F₅	3.01×10⁻¹¹	3.01×10⁻¹¹	3.01×10⁻¹¹	4.81×10⁻¹⁰	3.01×10⁻¹¹
F₆	2.75×10⁻¹¹	2.51×10⁻¹	6.30×10⁻²	1.11×10⁻²	4.47×10⁻²
F₇	1.10×10⁻²	1.61×10⁻¹	3.34×10⁻¹	Na	Na
F₈	3.02×10⁻¹¹	3.02×10⁻¹¹	3.02×10⁻¹¹	2.36×10⁻⁴	3.02×10⁻¹¹
F₉	3.02×10⁻¹¹	3.02×10⁻¹¹	3.02×10⁻¹¹	8.14×10⁻⁷	3.02×10⁻¹¹
F₁₀	8.54×10⁻¹¹	1.79×10⁻¹¹	1.79×10⁻¹¹	1.59×10⁻⁹	2.13×10⁻¹
F₁₁	8.48×10⁻⁹	3.02×10⁻¹¹	5.57×10⁻¹⁰	8.48×10⁻⁹	8.48×10⁻⁹
F₁₂	7.13×10⁻⁸	2.69×10⁻¹¹	2.69×10⁻¹¹	3.47×10⁻¹	1.10×10⁻¹¹

下载: 导出CSV

表 5 各算法M排名

Table 5. Algorithm M ranking

算法	M	排名
GWO	555.28	6
WOA	210.07	5
MWOA	143.85	3
SSA	174.49	4
CSSA	129.61	2
GSSA	68.02	1

下载: 导出CSV

参考文献(16)

[1]	XUE J K, SHEN B. A novel swarm intelligence optimization approach: sparrow search algorithm[J]. Systems Science & Control Engineering, 2020, 8(1): 22-34.
[2]	李雅丽, 王淑琴, 陈倩茹, 等. 若干新型群智能优化算法的对比研究[J]. 计算机工程与应用, 2020, 56(22): 1-12. LI Y L, WANG S Q, CHEN Q R, et al. Comparative study of several new swarm intelligence optimization algorithms[J]. Computer Engineering and Applications, 2020, 56(22): 1-12(in Chinese).
[3]	吕鑫, 慕晓冬, 张钧. 基于改进麻雀搜索算法的多阈值图像分割[J]. 系统工程与电子技术, 2021, 43(2): 318-327. LYU X, MU X D, ZHANG J. Multi-threshold image segmentation based on improved sparrow search algorithm[J]. Systems Engineering and Electronics, 2021, 43(2): 318-327(in Chinese).
[4]	吕鑫, 慕晓冬, 张钧, 等. 混沌麻雀搜索优化算法[J]. 北京航空航天大学学报, 2021, 47(8): 1712-1720. LYU X, MU X D, ZHANG J, et al. Chaos sparrow search optimization algorithm[J]. Journal of Beijing University of Aeronautics and Astronautics, 2021, 47(8): 1712-1720(in Chinese).
[5]	汤安迪, 韩统, 徐登武, 等. 基于混沌麻雀搜索算法的无人机航迹规划方法[J]. 计算机应用, 2021, 41(7): 2128-2136. TANG A D, HAN T, XU D W, et al. Path planning method of unmanned aerial vehicle based on chaos sparrow search algorithm[J]. Journal of Computer Applications, 2021, 41(7): 2128-2136(in Chinese).
[6]	陈义雄, 梁昔明, 黄亚飞. 基于佳点集构造的改进量子粒子群优化算法[J]. 中南大学学报(自然科学版), 2013, 44(4): 1409-1414. CHEN Y X, LIANG X M, HUANG Y F. Improved quantum particle swarm optimization based on good-point set[J]. Journal of Central South University (Science and Technology), 2013, 44(4): 1409-1414(in Chinese).
[7]	张达敏, 徐航, 王依柔, 等. 嵌入Circle映射和逐维小孔成像反向学习的鲸鱼优化算法[J]. 控制与决策, 2021, 36(5): 1173-1180. ZHANG D M, XU H, WANG Y R, et al. Whale optimization algorithm for embedded Circle mapping and onedimensional oppositional learning based small hole imaging[J]. Control and Decision, 2021, 36(5): 1173-1180(in Chinese).
[8]	华罗庚, 王元. 数论在近代分析中的应用[M]. 北京: 科学出版社, 1978: 1-99. HUA L G, WANG Y. Application of number theory in modern analysis [M]. Beijing: Science Press, 1978: 1-99(in Chinese).
[9]	GAN C, CAO W H, WU M, et al. A new bat algorithm based on iterative local search and stochastic inertia weight[J]. Expert Systems with Applications, 2018, 104: 202-212. doi: 10.1016/j.eswa.2018.03.015
[10]	YANG X S. A new metaheuristic bat-inspired algorithm[C]//Nature Inspired Cooperative Strategies for Optimization (NICSO 2010). Berlin: Springer, 2010: 65-74.
[11]	MOLINA D, LATORRE A, HERRERA F. SHADE with iterative local search for large-scale global optimization[C]// 2018 IEEE Congress on Evolutionary Computation (CEC). Piscataway: IEEE Press, 2018: 1-8.
[12]	XIA X W, LIU J N, LI Y X. Particle swarm optimization algorithm with reverse-learning and local-learning behavior[J]. Journal of Software, 2014, 9(2): 350-357.
[13]	何杰光, 彭志平, 崔得龙, 等. 一种多反向学习的教与学优化算法[J]. 工程科学与技术, 2019, 51(6): 159-167. HE J G, PENG Z P, CUI D L, et al. Multi-opposition teaching-learning-based optimization[J]. Advanced Engineering Sciences, 2019, 51(6): 159-167(in Chinese).
[14]	RAHNAMAYAN S, TIZHOOSH H R, SALAMA M M A. Opposition-based differential evolution[J]. IEEE Transactions on Evolutionary Computation, 2008, 12(1): 64-79. doi: 10.1109/TEVC.2007.894200
[15]	龙文, 伍铁斌, 唐明珠, 等. 基于透镜成像学习策略的灰狼优化算法[J]. 自动化学报, 2020, 46(10): 2148-2164. LONG W, WU T B, TANG M Z, et al. Grey wolf optimizer algorithm based on lens imaging learning strategy[J]. Acta Automatica Sinica, 2020, 46(10): 2148-2164(in Chinese).
[16]	OUYANG C T, ZHU D L, QIU Y X. Lens learning sparrow search algorithm[J]. Mathematical Problems in Engineering, 2021, 2021: 1-17.