-
摘要:
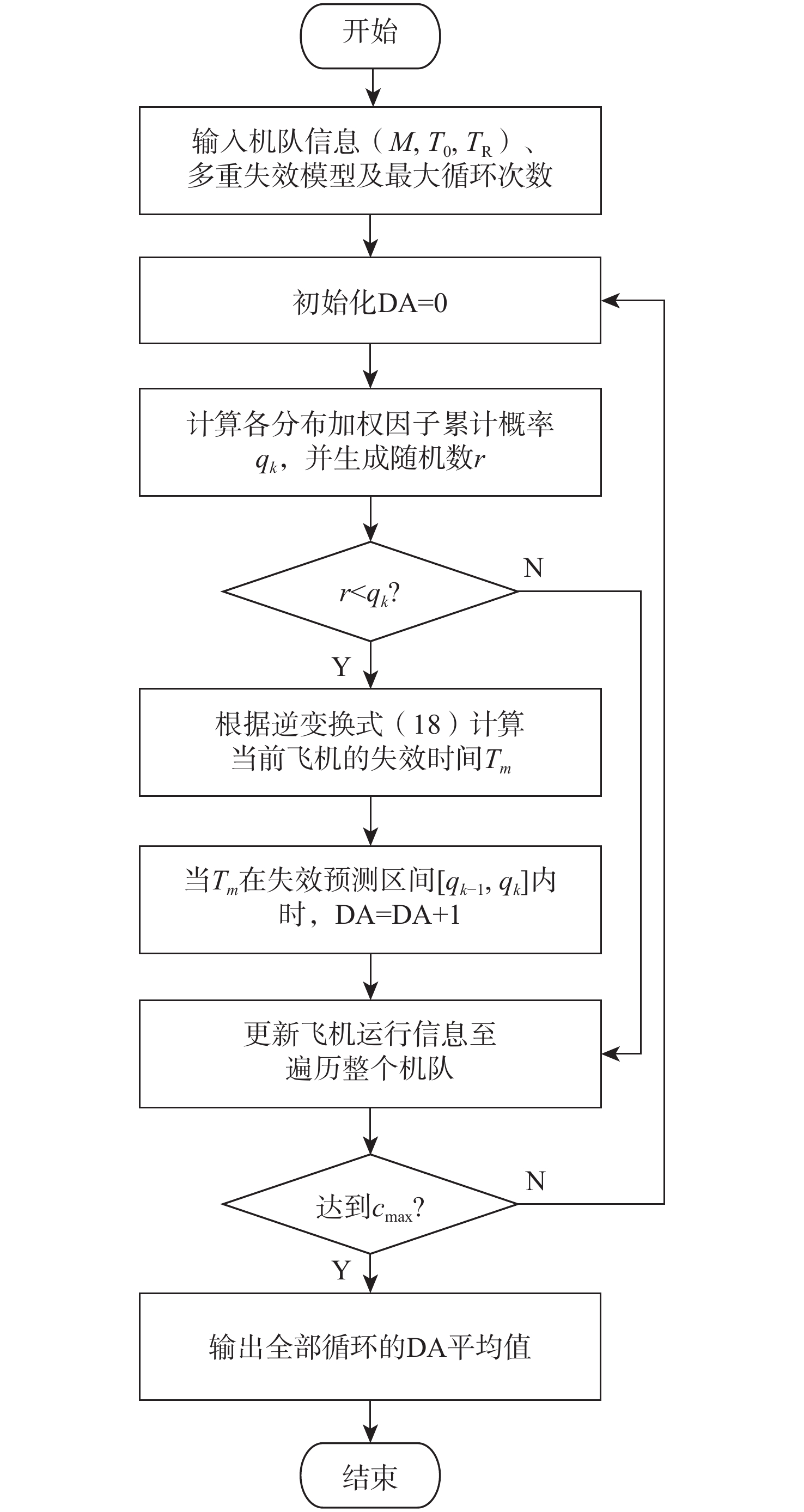
针对民用飞机部件具有多重失效的特点，提出一种面向多重耗损失效模式的运行风险评估方法。以机队运行失效数据为样本，构建基于混合威布尔分布的多重失效模型，提出基于期望最大（EM）算法的混合威布尔分布参数估计方法，并利用粒子群优化（PSO）算法对EM算法进行优化，提高了参数估计精度；以基于混合威布尔分布的多重失效模型为基础，利用蒙特卡罗仿真的方法提出多重失效模式影响下的机队缺陷飞机数量（DA）预测算法；构建贝叶斯网络模型以分析初因事件发生条件下的不安全后果发生概率（CP），并结合由历史运营经验得到的死亡率（IR）和未检出率（ND），计算总体未纠正机队风险（
R T）。实例表明：所提风险评估方法可以直接应用于多重失效模式导致的机队风险评估，所提模型参数估计方法相比极大似然估计和最小二乘估计方法，均方根误差分别降低了80.6%和85.7%。Abstract:An operation risk assessment method is proposed for aircraft components with multiple wear-out failure modes. A multiple failure model is constructed using the fleet operating failure data samples and the mixed Weibull distribution. And the parameter estimation method of the mixed Weibull distribution is proposed based on the expectation maximization (EM) algorithm, which has been optimized by using the particle swarm optimization (PSO) algorithm to improve the accuracy of the parameter estimation. In terms of the mixed Weibull distribution-based reliability model, the calculating method for the number of defect airplanes (DA), which is caused by the multiple failure modes, is given via the Monte Carlo simulation method. To determine the Conditional Probability (CP) of dangerous consequences emerging from a certain initial situation, the Bayesian network (BN) is designed. Finally, the total uncorrected fleet risk (
R T) is calculated in terms of the injury ratio (IR), the Not Detected probability (ND), the DA value, and the CP value. A case study shows that the proposed risk assessment method can be directly applied in the evaluation of fleet risks caused by multiple failure modes.Furthermore, the root mean squared error of the suggested parameter estimation approach has been decreased by 85.7% and 80.6%, respectively, when compared to the maximum likelihood estimation (MLE) and the least-squares estimation (LSE). -
图 1 基于PSO-EM算法的混合威布尔分布参数估计方法
Figure 1. Parameter estimation method of mixed Weibull distribution based on PSO-EM algorithm
图 5 机队裂纹失效概率密度函数拟合结果
Figure 5. Fitting results of probability density function for fleet crack failure
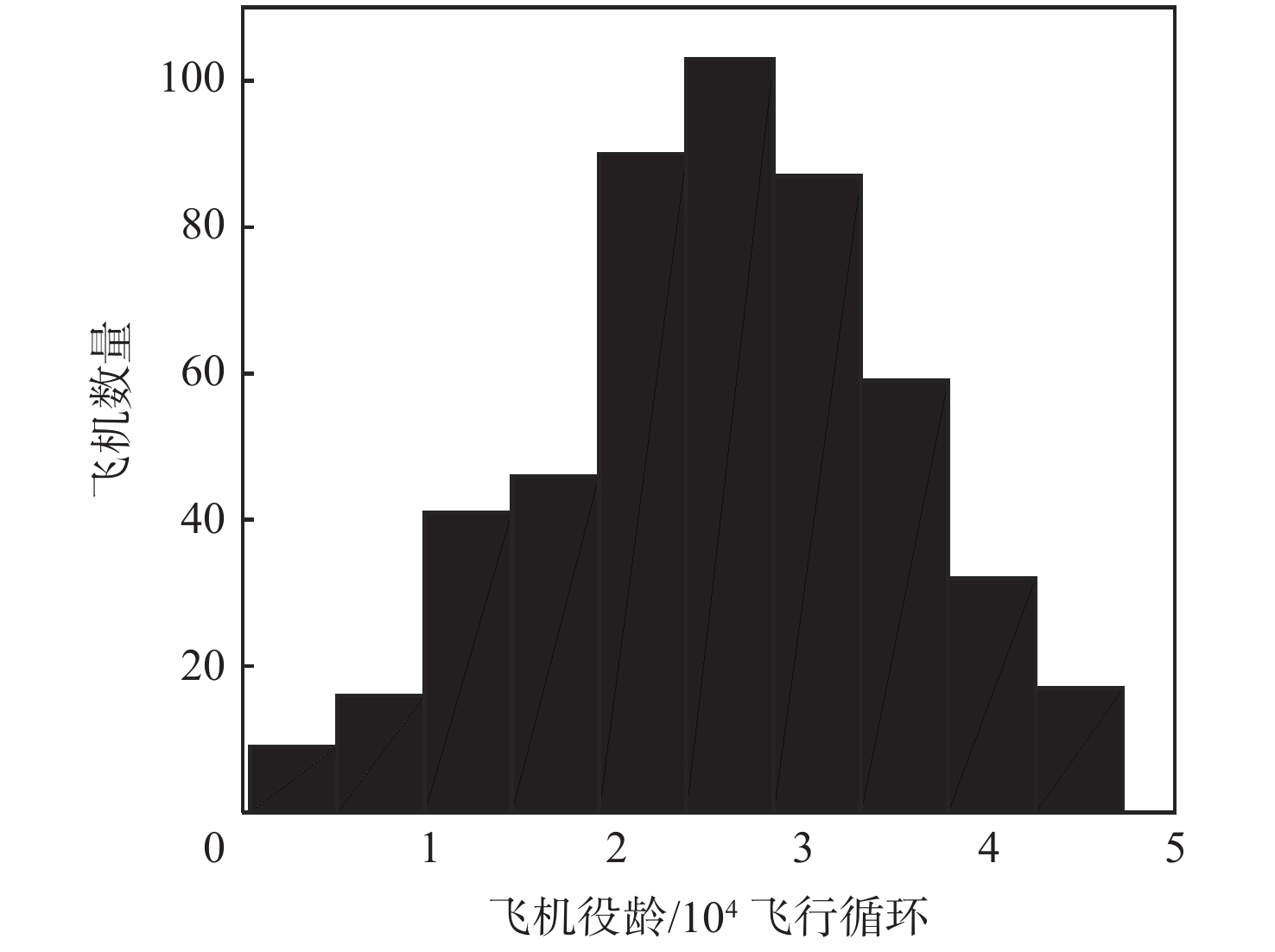
表 1 机队运行寿命数据
Table 1. Fleet operational failure data
序号 时间/
飞行循环序号 时间/
飞行循环序号 时间/
飞行循环序号 时间/
飞行循环1 1410 6 6202 11 10978 16 18196 2 2786 7 6750 12 14660 17 18558 3 5145 8 7253 13 15110 18 19636 4 5877 9 9753 14 15559 19 23603 5 6086 10 9944 15 17527 20 23924 
下载: 导出CSV
表 2 模型参数初值及边界值
Table 2. Initial values and boundary values of model parameters
模型参数 ${ \pi _1}$ ${ \pi _2}$ $ {\alpha _1} $ $ {\alpha _2} $ 初值 0.35 0.65 5876.1 17526.4 边界下限 0.1 0.5 5288 15773 边界上限 0.5 0.8 6464 19279
下载: 导出CSV
表 3 多重失效模型参数估计结果
Table 3. Parameters’ estimation results of multiple failure model
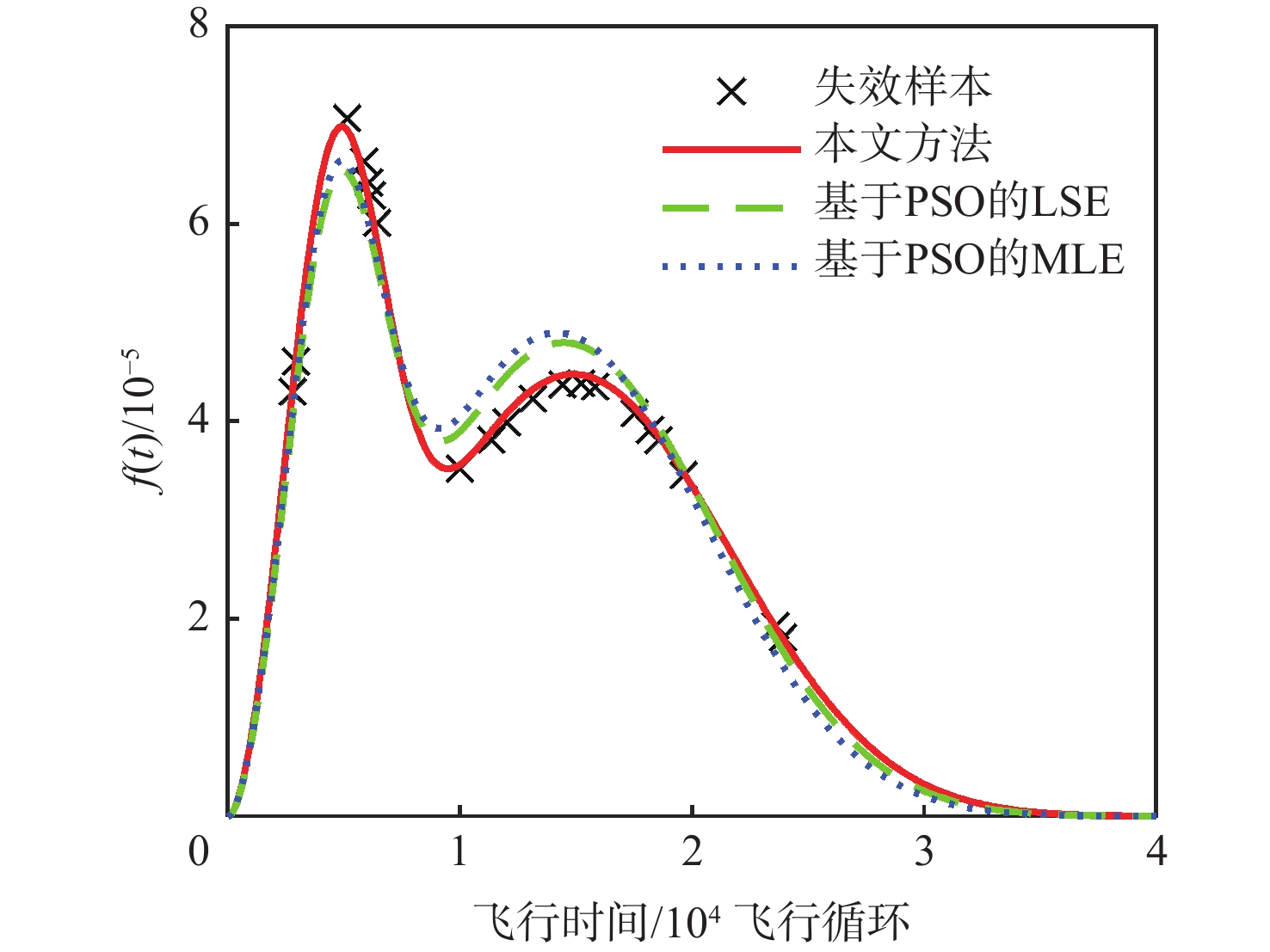
估计方法 ${ \pi_1}$ ${ \pi_2}$ $ {\alpha _1} $ $ {\alpha _2} $ δRMSE 本文方法 0.29 0.71 5412.7 17468.1 0.0024 基于PSO
的LSE0.26 0.74 5384.5 16991.7 0.0126 基于PSO
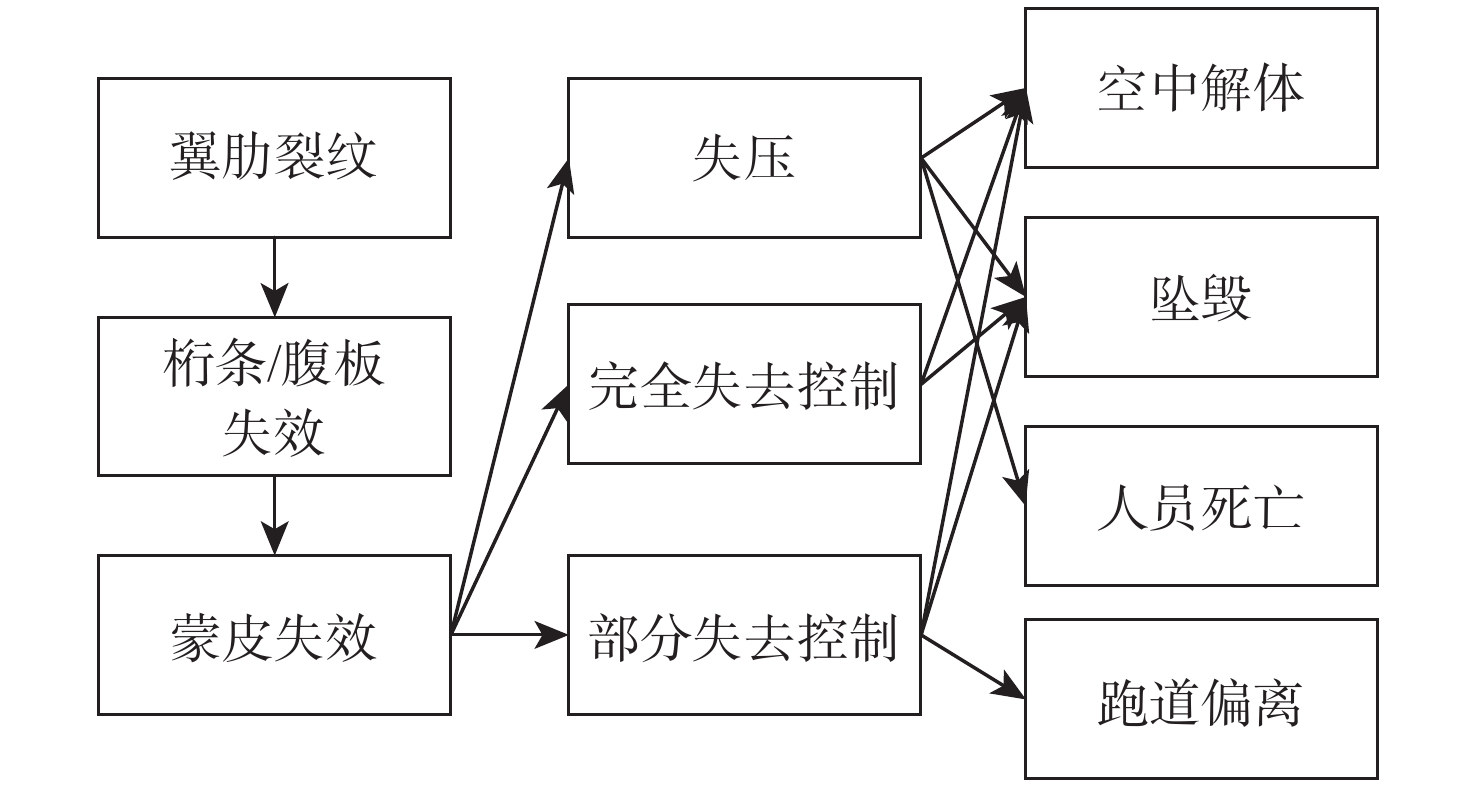
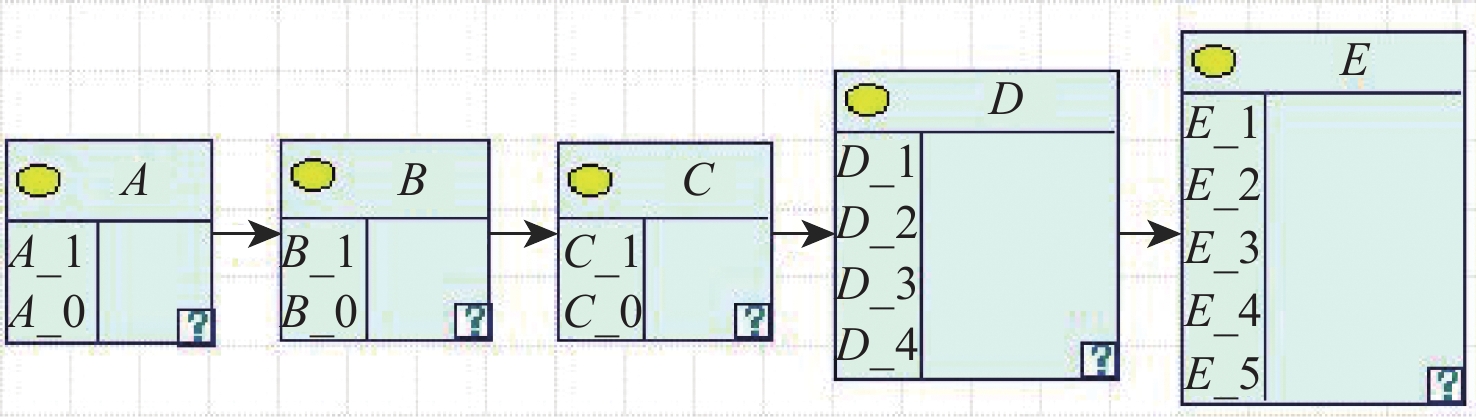
的MLE0.26 0.74 5339.9 16645.8 0.0168
下载: 导出CSV
表 4 BN节点信息
Table 4. Node information in BN
节点 事件 状态 A 翼肋裂纹 1 0 B 桁条/腹板失效 1 0 C 蒙皮失效 1 0 D 失压 1 完全失去控制 2 部分失去控制 3 无影响 4 E 空中解体 1 坠毁 2 人员死亡 3 跑道偏离 4 无影响 5
下载: 导出CSV
表 5 节点D条件概率
Table 5. Conditional probability of node D
C $P\left( {D = 1\left| C \right.} \right)$ $P\left( {D = 2\left| C \right.} \right)$ $P\left( {D = 3\left| C \right.} \right)$ $P\left( {D = 4\left| C \right.} \right)$ 1 0.5 0.001 0.05 0.449 0 0 0 0 1
下载: 导出CSV
表 6 节点E条件概率
Table 6. Conditional probability of node E
D $P\left( {E = 1\left| D \right.} \right)$ $P\left( {E = 2\left| D \right.} \right)$ $P\left( {E = 3\left| D \right.} \right)$ $P\left( {E = 4\left| D \right.} \right)$ $P\left( {E = 5\left| D \right.} \right)$ 1 0.001 0.005 0.01 0 0.984 2 0.5 0.5 0 0 0 3 0.001 0.01 0 0.1 0.889 4 0 0 0 0 1
下载: 导出CSV
表 7 四种不安全后果的死亡率
Table 7. The injury ratio of four unsafe outcomes
不安全后果 死亡率 人员死亡 0.001 跑道偏离 0.03 坠毁 0.98 空中解体 1
下载: 导出CSV
-
[1] SHAKIR H M, IQBAL B. Application of Lean principles and software solutions for maintenance records in continuing airworthiness management organisations[J]. The Aeronautical Journal, 2018, 122(1254): 1263-1274. doi: 10.1017/aer.2018.65 [2] SENOL M B. Evaluation and prioritization of technical and operational airworthiness factors for flight safety[J]. Aircraft Engineering and Aerospace Technology, 2020, 92(7): 1049-1061. doi: 10.1108/AEAT-03-2020-0058 [3] ARNALDO V R M, GÓMEZ C V F, PEREZ S L, et al. Prediction of aircraft safety incidents using Bayesian inference and hierarchical structures[J]. Safety Science, 2018, 104: 216-230. doi: 10.1016/j.ssci.2018.01.008 [4] TORREGOSA R F, HU W. Probabilistic risk analysis of fracture of aircraft structures using a Bayesian approach to update the distribution of the equivalent initial flaw sizes[J]. Fatigue & Fracture of Engineering Materials & Structures, 2013, 36(11): 1092-1101. [5] ZHOU D, ZHUANG X, ZUO H F. A novel three-parameter weibull distribution parameter estimation using chaos simulated annealing particle swarm optimization in civil aircraft risk assessment[J]. Arabian Journal for Science and Engineering, 2021, 46(9): 8311-8328. doi: 10.1007/s13369-021-05467-0 [6] BANGHART M, BIAN L K, STRAWDERMAN L, et al. Risk assessment on the EA-6B aircraft utilizing Bayesian networks[J]. Quality Engineering, 2017, 29(3): 499-511. doi: 10.1080/08982112.2017.1319957 [7] HOSKOVA M, ZIEJA M, WOCH M, et al. A method to evaluate an aircraft operational risk[C]//Safety and Reliability – Safe Societies in a Changing World. London: CRC Press, 2018: 1441-1446. [8] WANG W, ZHANG T W, WANG L. Markov chain-based flight operations risk analysis[C]// 2017 13th International Conference on Natural Computation, Fuzzy Systems and Knowledge Discovery (ICNC-FSKD). Piscataway: IEEE Press, 2018: 2441-2445. [9] Transport Airplane Directorate. Transport airplane risk assessment methodology handbook: PS- ANM-25-05[S]. Washington, D. C. : Federal Aviation Administration, 2011. [10] VIOLETTE M G, SAFARIAN P, HAN N, et al. Transport airplane risk analysis[J]. Journal of Aircraft, 2015, 52(2): 395-402. doi: 10.2514/1.C032663 [11] 张子文, 陆中. 基于蒙特卡洛仿真的运输类飞机耗损失效风险评估[J]. 航空计算技术, 2020, 50(3): 35-39.ZHANG Z W, LU Z. Risk assessment of transport aircraft based on Monte Carlo simulation targeted on wear-out failure[J]. Aeronautical Computing Technique, 2020, 50(3): 35-39(in Chinese). [12] 郭媛媛, 孙有朝, 李龙彪. 基于蒙特卡罗方法的民用飞机故障风险评估方法[J]. 航空学报, 2017, 38(10): 221126.GUO Y Y, SUN Y C, LI L B. Failure risk assessment method of civil aircraft based on Monte Carlo method[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(10): 221126(in Chinese). [13] BIAN T A, ZHENG H Y, YIN L K, et al. Failure mode and effects analysis based on D numbers and TOPSIS[J]. Quality and Reliability Engineering International, 2018, 34(4): 501-515. doi: 10.1002/qre.2268 [14] FATTAHI R, TAVAKKOLI-MOGHADDAM R, KHALILZADEH M, et al. A novel FMEA model based on fuzzy multiple-criteria decision-making methods for risk assessment[J]. Journal of Enterprise Information Management, 2020, 33(5): 881-904. doi: 10.1108/JEIM-09-2019-0282 [15] HE L L, LU Z Z, LI X Y. Failure-mode importance measures in structural system with multiple failure modes and its estimation using copula[J]. Reliability Engineering & System Safety, 2018, 174: 53-59. [16] XU M, DROGUETT E L, LINS I D, et al. On the q-Weibull distribution for reliability applications: An adaptive hybrid artificial bee colony algorithm for parameter estimation[J]. Reliability Engineering & System Safety, 2017, 158: 93-105. [17] PRATAVIERA F, ORTEGA E M M, CORDEIRO G M, et al. A new generalized odd log-logistic flexible Weibull regression model with applications in repairable systems[J]. Reliability Engineering & System Safety, 2018, 176: 13-26. [18] MAZZEO D, OLIVETI G, LABONIA E. Estimation of wind speed probability density function using a mixture of two truncated normal distributions[J]. Renewable Energy, 2018, 115: 1260-1280. doi: 10.1016/j.renene.2017.09.043 [19] LU Z, DONG L, ZHOU J. Nonlinear least squares estimation for parameters of mixed weibull distributions by using particle swarm optimization[J]. IEEE Access, 2019, 7: 60545-60554. doi: 10.1109/ACCESS.2019.2915279 [20] FLORENCE D, PATRICK P. Bayesian estimation of Weibull mixture in heavily censored data setting[J]. Reliability Engineering & System Safety, 2018, 180: 453-462. [21] TZOREFF E, WEISS A J. Expectation-maximization algorithm for direct position determination[J]. Signal Processing, 2017, 133: 32-39. doi: 10.1016/j.sigpro.2016.10.015 [22] ABUALIGAH L M, KHADER A T. Unsupervised text feature selection technique based on hybrid particle swarm optimization algorithm with genetic operators for the text clustering[J]. The Journal of Supercomputing, 2017, 73(11): 4773-4795. doi: 10.1007/s11227-017-2046-2 [23] MORADI P, GHOLAMPOUR M. A hybrid particle swarm optimization for feature subset selection by integrating a novel local search strategy[J]. Applied Soft Computing, 2016, 43: 117-130. doi: 10.1016/j.asoc.2016.01.044 [24] GORDAN B, ARMAGHANI D J, HAJIHASSANI M, et al. Prediction of seismic slope stability through combination of particle swarm optimization and neural network[J]. Engineering with Computers, 2016, 32(1): 85-97. doi: 10.1007/s00366-015-0400-7 [25] XU S W, WU Y, WANG X F, et al. Indoor 3D visible light positioning system based on adaptive parameter particle swarm optimisation[J]. IET Communications, 2020, 14(20): 3707-3714. doi: 10.1049/iet-com.2019.1141 [26] 赵洪利, 刘宇文. 基于蒙特卡罗模拟的航空发动机故障风险预测[J]. 北京航空航天大学学报, 2015, 41(3): 545-550.ZHAO H L, LIU Y W. Forecasting for aero-engine failure risk based on Monte Carlo simulation[J]. Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(3): 545-550(in Chinese). [27] CHEN X G. A novel reliability estimation method of complex network based on Monte Carlo[J]. Cluster Computing, 2017, 20(2): 1063-1073. doi: 10.1007/s10586-017-0826-3 [28] URGUN D, SINGH C. A hybrid Monte Carlo simulation and multi label classification method for composite system reliability evaluation[J]. IEEE Transactions on Power Systems, 2019, 34(2): 908-917. doi: 10.1109/TPWRS.2018.2878535 [29] DINIS D, BARBOSA-POVOA A, TEIXEIRA A P. Valuing data in aircraft maintenance through big data analytics: A probabilistic approach for capacity planning using Bayesian networks[J]. Computers & Industrial Engineering, 2019, 128: 920-936. [30] 于劲松, 沈琳, 唐荻音, 等. 基于贝叶斯网络的故障诊断系统性能评价[J]. 北京航空航天大学学报, 2016, 42(1): 35-40.YU J S, SHEN L, TANG D Y, et al. Performance evaluation of fault diagnosis system based on Bayesian network[J]. Journal of Beijing University of Aeronautics and Astronautics, 2016, 42(1): 35-40(in Chinese). [31] FEROZE N, ASLAM M. Approximate Bayesian analysis of doubly censored samples from mixture of two Weibull distributions[J]. Communications in Statistics-Theory and Methods, 2019, 48(11): 2862-2878. doi: 10.1080/03610926.2018.1473430 [32] QAZI A, DICKSON A, QUIGLEY J, et al. Supply chain risk network management: A Bayesian belief network and expected utility based approach for managing supply chain risks[J]. International Journal of Production Economics, 2018, 196: 24-42. doi: 10.1016/j.ijpe.2017.11.008 -
下载:
点击查看大图
计量
- 文章访问数: 135
- HTML全文浏览量: 39
- PDF下载量: 7
- 被引次数: 0
