Nonlinear spatial K-means clustering algorithm for detection of zero-speed interval in inertial pedestrian navigation
-
摘要:
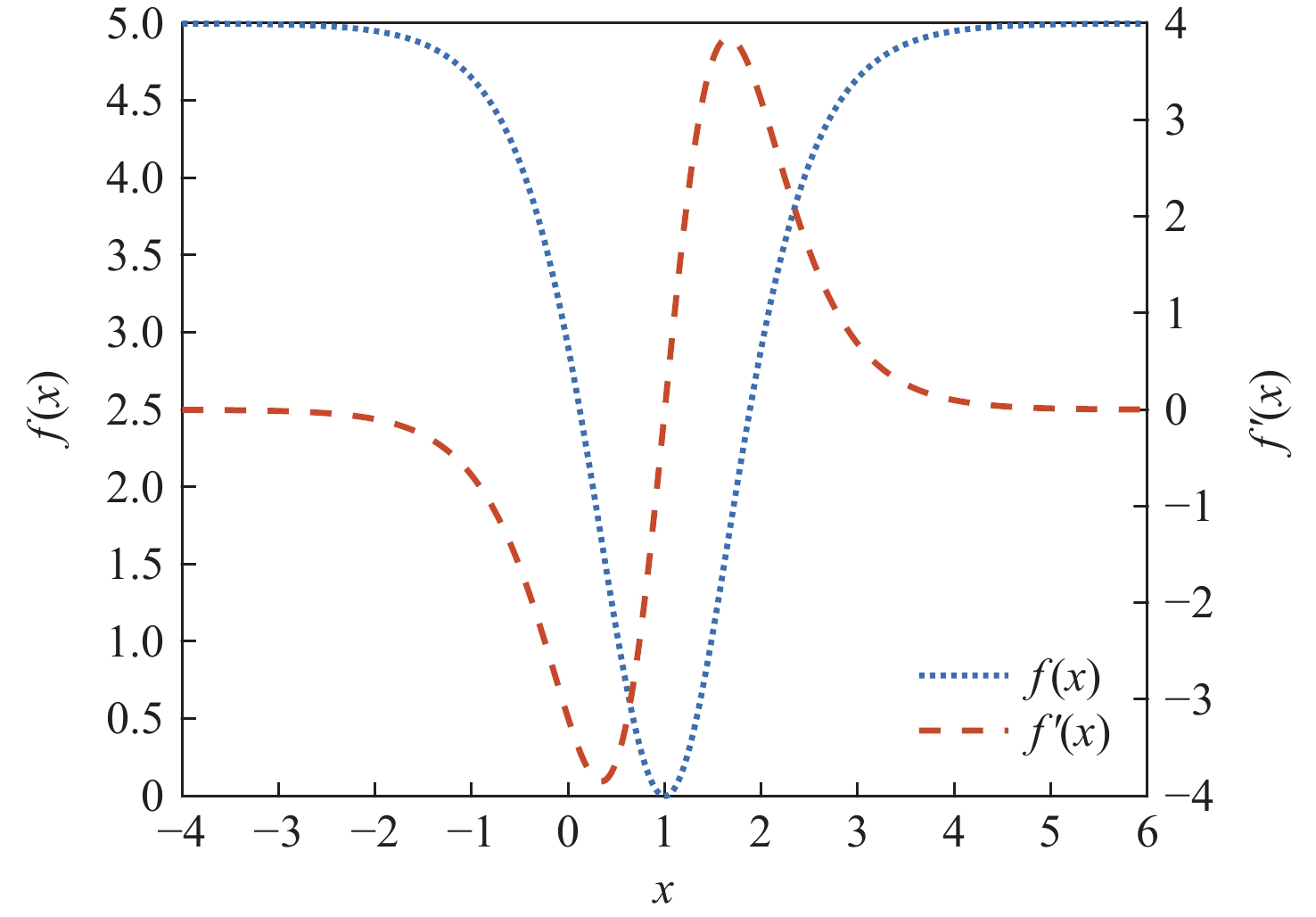
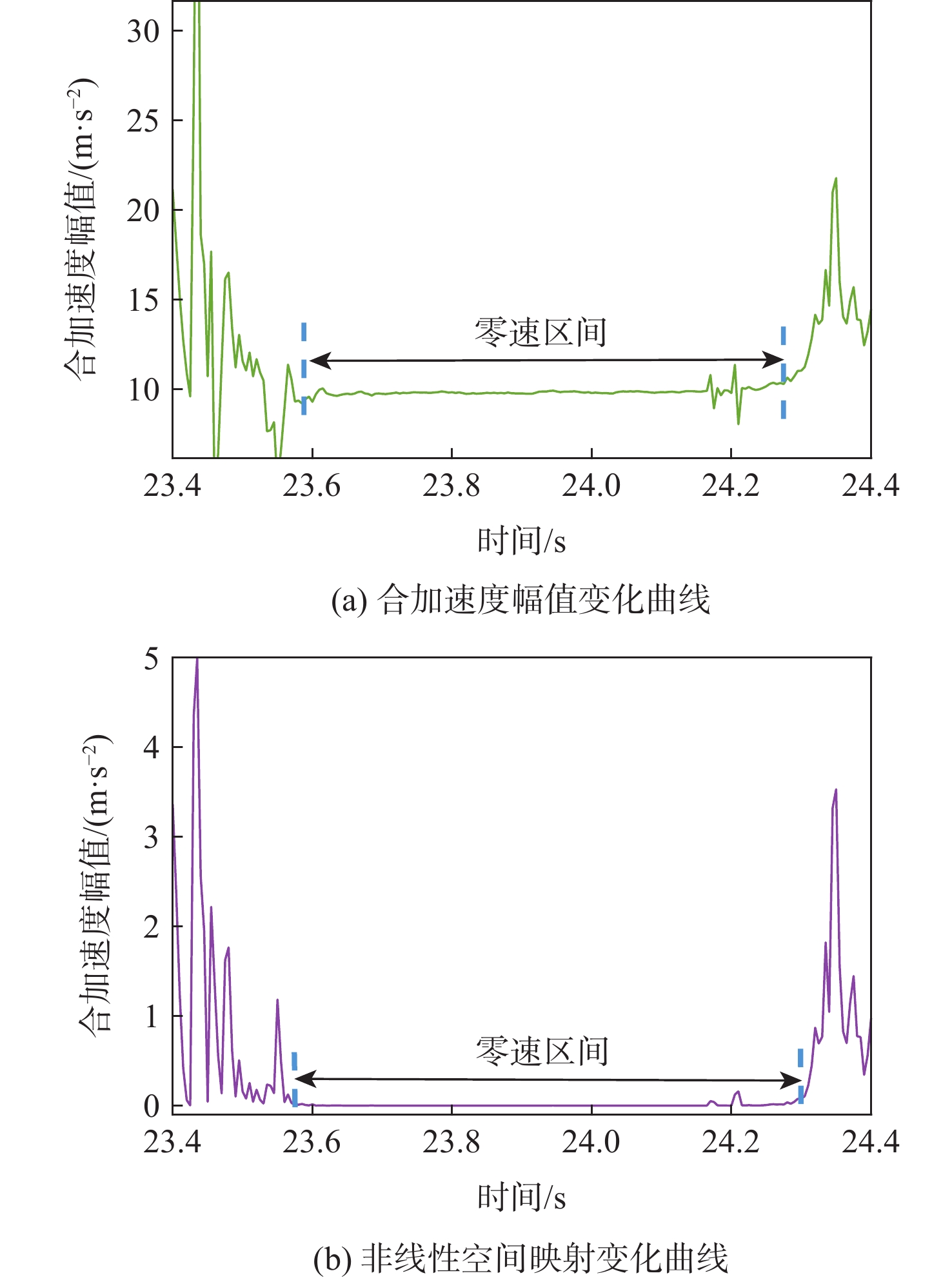
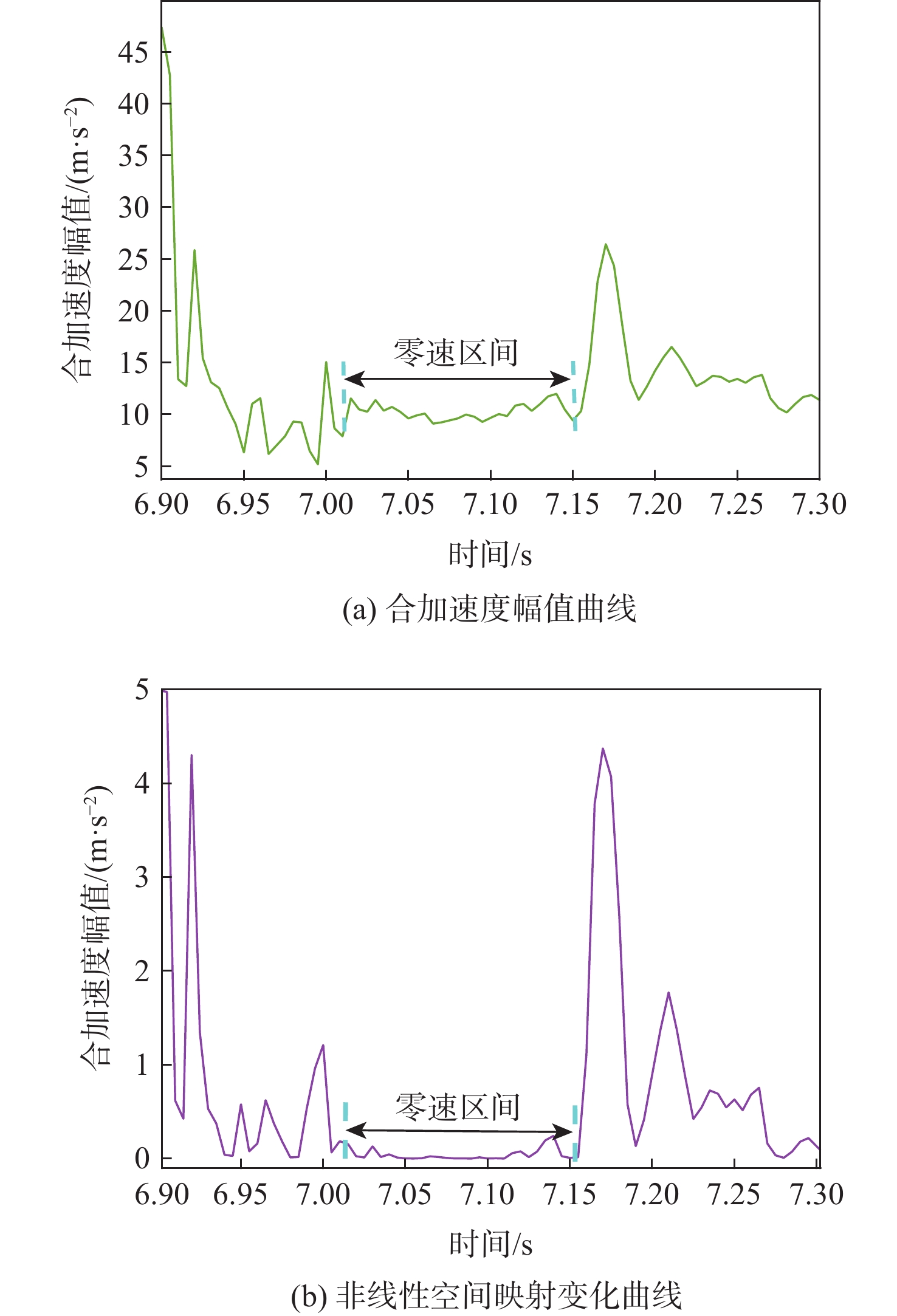
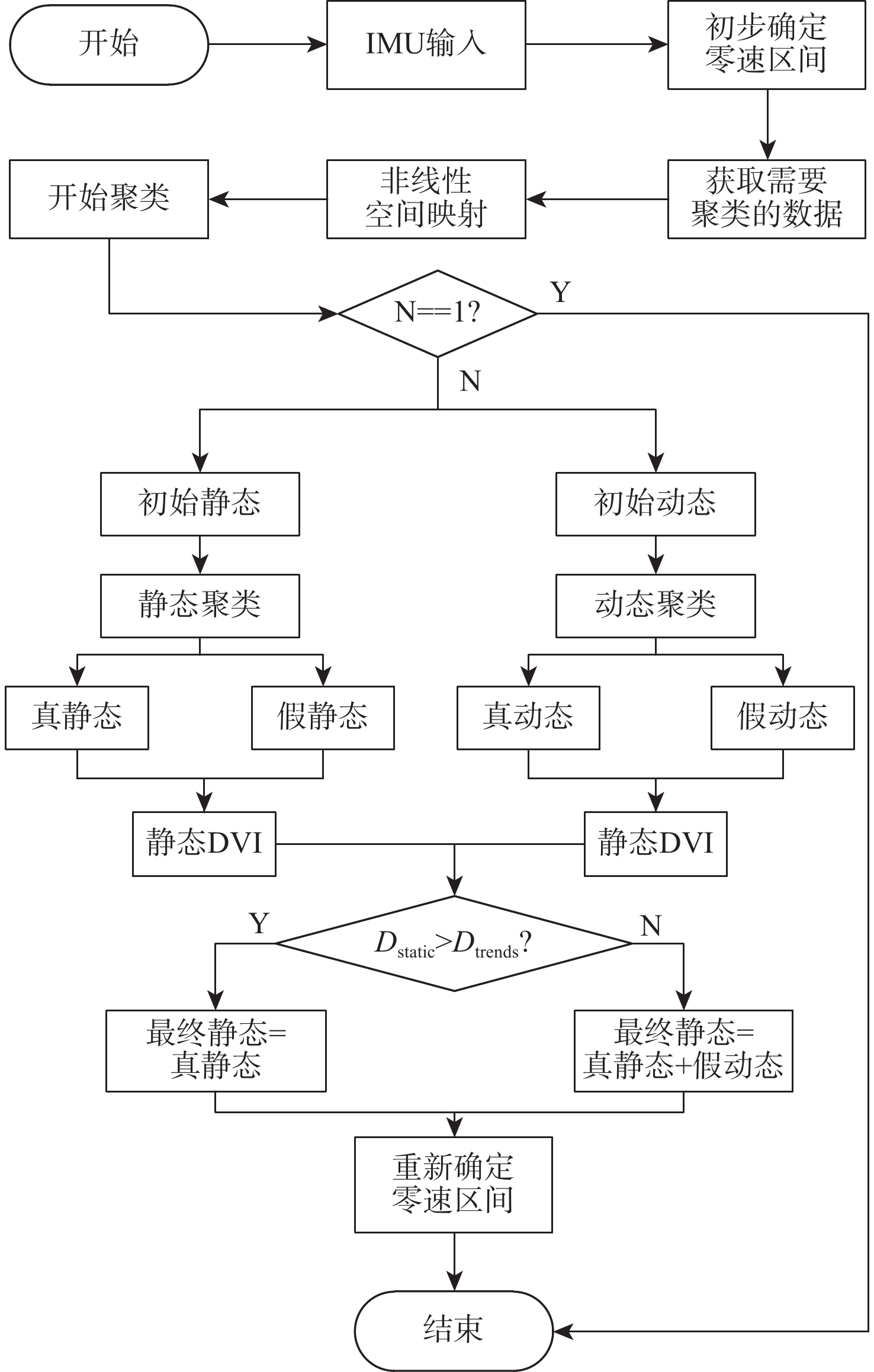
惯性行人导航系统中，零速区间检测的准确性直接关系着基于零速修正（ZUPT）的行人导航精度。为此，设计了一种基于非线性空间映射与K-means聚类算法结合的零速区间检测算法。通过经典零速区间检测算法广义似然比检测（GLRT）确定初始零速区间；选取零速区间与非零速区间交界处的加速度数据，将合加速度幅值作为变量，映射到设计的非线性空间中，放大数据差异；利用K-means聚类算法对映射后的数据进行聚类，经过去噪声处理后确定出更精准的零速区间；通过惯性行人导航系统实验验证非线性空间K-means聚类零速区间检测算法的有效性。实验表明，所提出的惯性行人导航零速区间检测的非线性空间K-means聚类算法相比于GLRT算法和基于K-means聚类的零速区间检测算法，定位精度显著提高，并在匀速行走、变速行走和长距离长航时行走3种运动模式下进行了实验验证；相比基于K-means聚类的零速区间检测算法，减小了计算量。所提算法能够自适应不同的运动状态，无需随时调整阈值，且理论上可以优化任意传统零速区间检测算法，具有良好的工程应用价值。
Abstract:The accuracy of zero-speed zone recognition in the inertial pedestrian navigation system is directly correlated with the accuracy of pedestrian navigation based on the zero velocity update (ZUPT). This paper designs a zero-speed interval detection algorithm based on the combination of nonlinear space mapping and a K-means clustering algorithm. Firstly, the initial zero speed interval is determined by the classical zero speed detection algorithm generalized likelihood ratio test (GLRT); then select the acceleration data at the junction of the zero-speed interval and the non-zero-speed interval, and use the resultant acceleration amplitude as a variable to map to the designed In the nonlinear space, enlarge the data difference; then use the K-means clustering algorithm to cluster the mapped data, and determine the more accurate zero-speed interval after de-noising processing; finally,verify the effectiveness of nonlinearity spatial K-means clustering zero-speed interval detection algorithm through the inertial pedestrian navigation system experiment. Experiments show that the positioning accuracy of the nonlinear spatial K-means clustering algorithm for zero speed interval detection of inertial pedestrian navigation proposed in this paper is significantly improved compared with the GLRT algorithm and zero speed detection algorithm based on K-means clustering, and is verified by experiments in three motion modes: constant speed walking, variable speed walking and long-distance and long-time walking. In addition, compared with the zero speed detection algorithm based on K-means clustering, the amount of calculation is reduced. The zero speed interval detection algorithm can adapt to different motion states without adjusting the threshold at any time, and can theoretically optimize any traditional zero speed interval detection algorithm, which has good engineering application value.
-
图 3 行走情况下的合加速度幅值和非线性空间映射变化曲线
Figure 3. Acceleration amplitude and nonlinear spatial mapping in case of walking
图 4 慢跑情况下的合加速度幅值和非线性空间映射变化曲线
Figure 4. Acceleration amplitude and nonlinear spatial mapping in case of jogging
图 6 MIMU惯性传感器安装位置及行人导航系统构成
Figure 6. Installation position of MIMU inertial sensor and composition of pedestrian navigation system
图 9 匀速行走状态下实验路径对比
Figure 9. Path comparison of experiments under constant speed walking
图 12 长距离长航时运动状态下的实验的路径对比
Figure 12. Path comparison of experiments under long-distance and long endurance motion
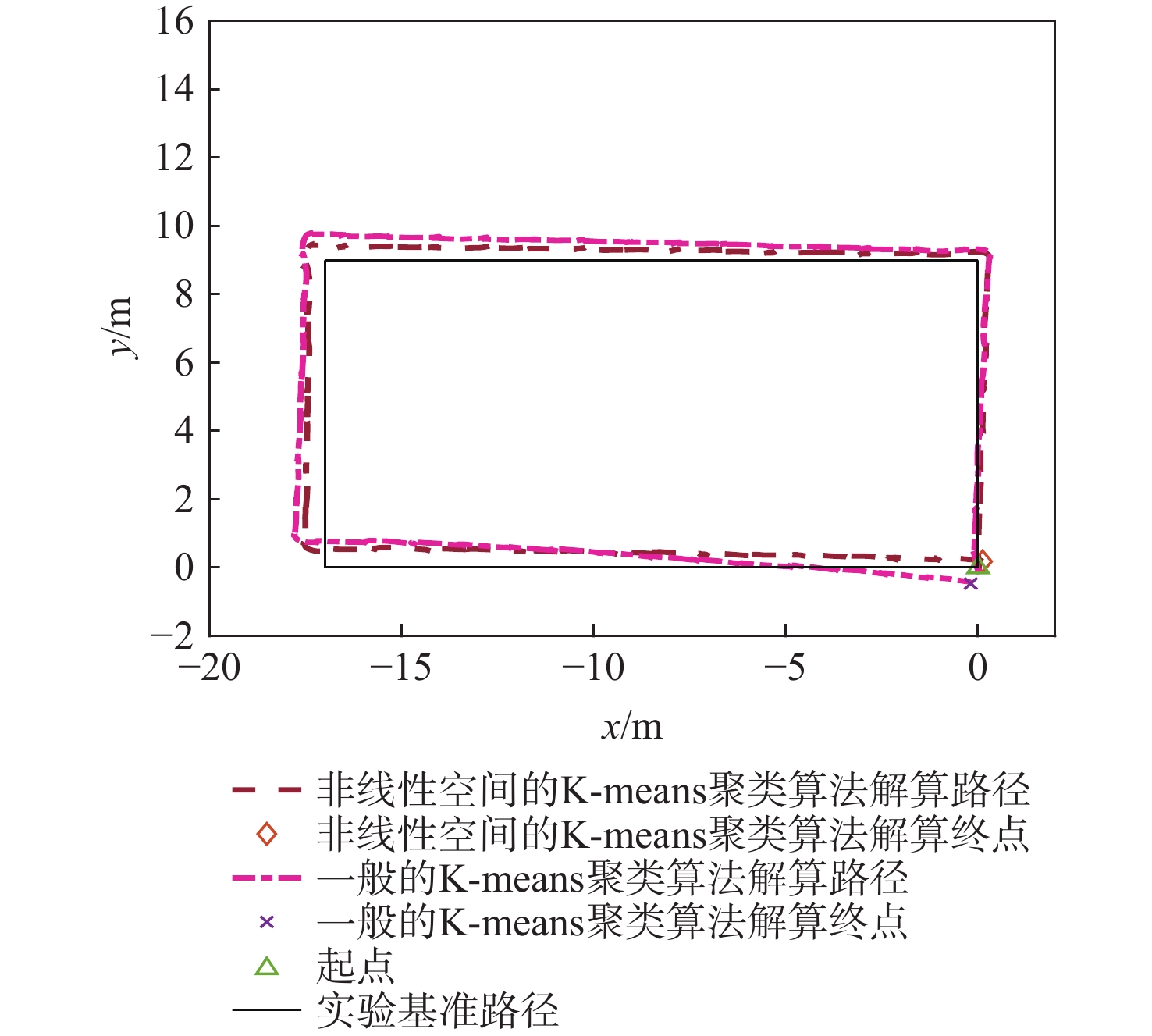
表 1 不同算法平均DVI指数
Table 1. Average DVI indexs of different algorithms
序号 一般的K-means
聚类算法非线性空间的
K-means聚类算法1 0.2594 0.8157 2 0.2728 0.5789 3 0.3080 0.5340 4 0.3044 0.5387 5 0.2605 0.5319 
下载: 导出CSV
表 2 3种算法运行时间结果
Table 2. Runtime results of three kinds of algorithms
序号 T1/s T2/s T3/s 1 143.781 5.293 298.862 2 46.623 3.998 100.997 3 125.138 5.521 247.865 4 125.862 7.401 254.176
下载: 导出CSV
表 3 匀速行走状态下3种算法位置误差与导航轨迹误差
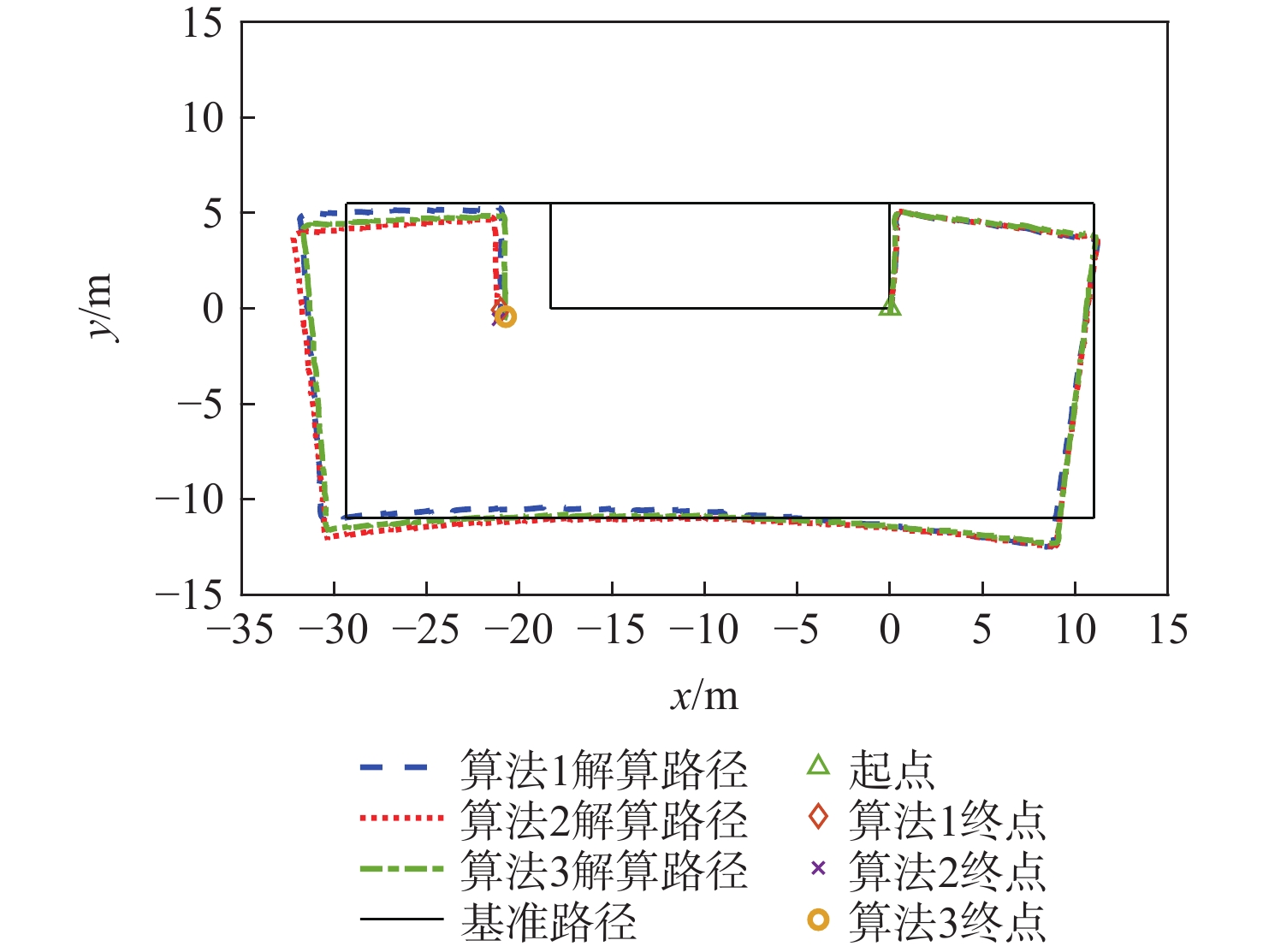
Table 3. Position error and navigation track error of three kinds of algorithm in uniform walking state
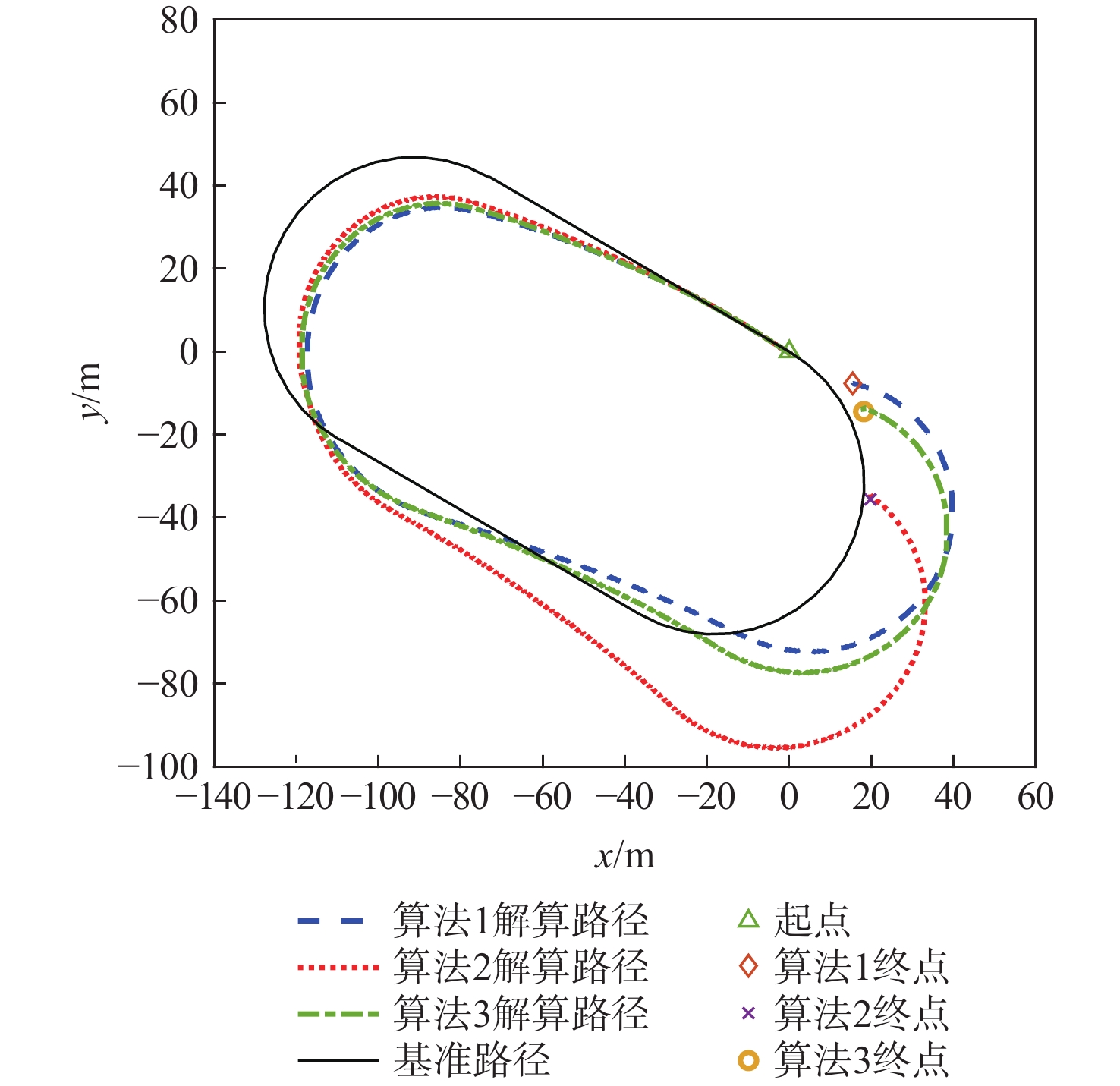
m 算法 参考点坐标 对应点坐标 $\Delta r$ $\Delta R$ $\Delta S$ 算法1 (0,5.5) (0.31,5.07) 0.53 1.59 0.58 (11,5.5) （11.05,3.94） 1.56 (11,−11) (9.17,−11.94) 2.05 (−29.32,−11) (−30.27,−11.02) 0.95 (−29.32,5.5) (−31.08,4.95) 1.84 (−18.32,5.5) (−20.40,5.11) 2.12 (−18.32,0) (−20.47,−0.07) 2.08 算法2 (0,5.5) (0.24,5.27) 0.33 2.07 0.99 (11,5.5) (11.05,3.93) 1.57 (11,−11) (9.16,−12.09) 2.14 (−29.32,−11) (−30.30,−11.87) 1.31 (−29.32,5.5) (−32.03,3.70) 3.25 (−18.32,5.5) (−21.15,4.22) 3.11 (−18.32,0) (−21.03,−0.68) 2.79 算法3 (0,5.5) (0.34,4.92) 0.67 1.97 0.73 (11,5.5) (10.52,3.73) 1.83 (11,−11) (9.01,−12.26) 2.36 (−29.32,−11) (−30.32,−11.61) 1.17 (−29.32,5.5) (−31.69,4.09) 2.76 (−18.32,5.5) (−20.83,4.81) 2.60 (−18.32,0) (−20.73,−0.42) 2.45
下载: 导出CSV
表 4 3种算法位置误差与导航轨迹误差
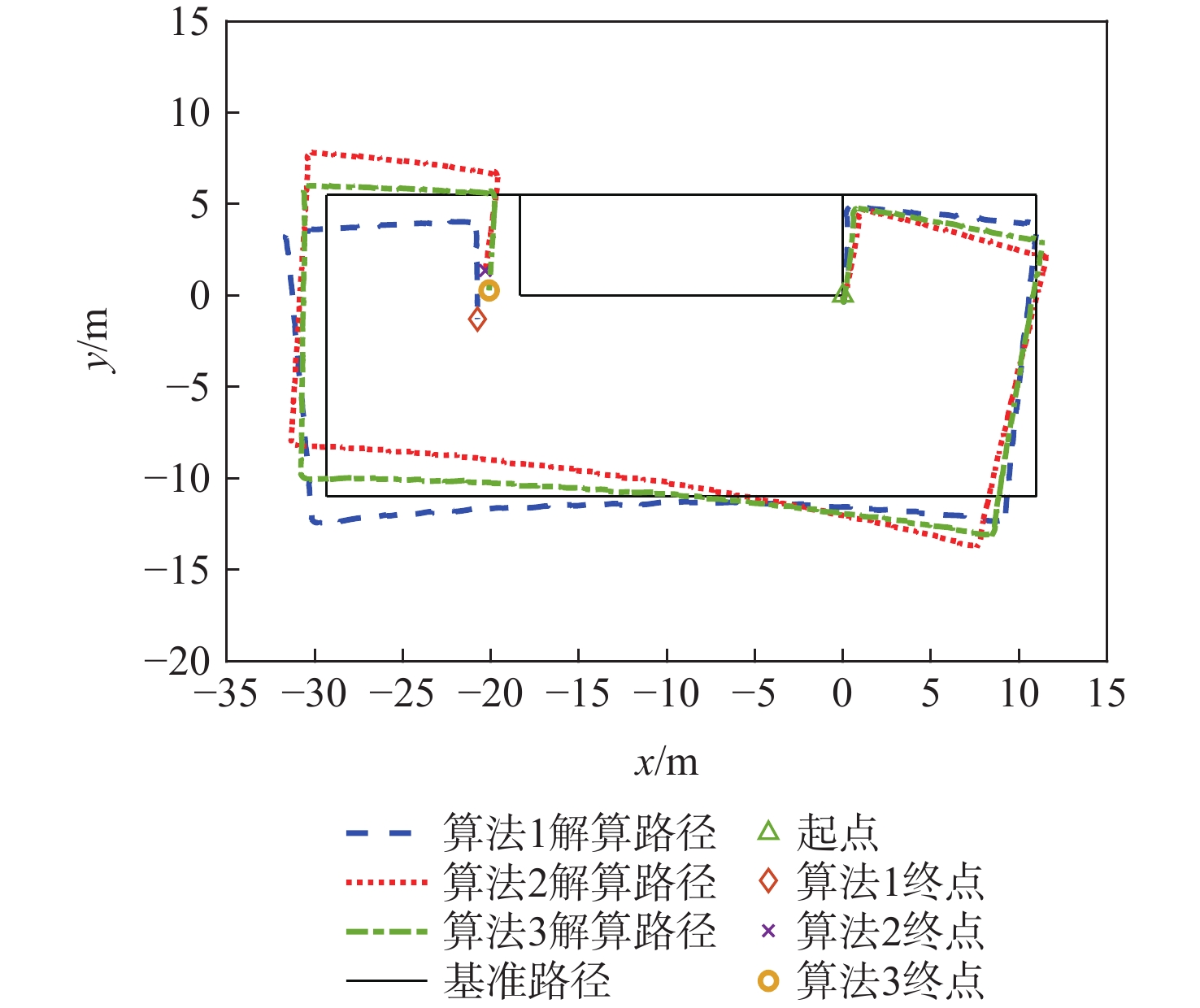
Table 4. Position error and navigation track error of three kinds of algorithm
m 算法 参考点坐标 对应点坐标 $\Delta r$ $\Delta R$ $\Delta S$ 算法1 (0,5.5) (0.31,5.07) 1.00 1.73 0.63 (11,5.5) (11.05,3.94) 2.30 (11,−11) (9.17,−11.94) 2.87 (−29.32,−11) (−30.27,−11.02) 1.74 (−29.32,5.5) (−31.08,4.95) 1.18 (−18.32,5.5) (−20.40,5.11) 1.16 (−18.32,0) (−20.47,−0.07) 1.85 算法2 (0,5.5) (0.24,5.27) 1.35 2.77 1.03 (11,5.5) (11.05,3.93) 3.57 (11,−11) (9.16,−12.09) 4.34 (−29.32,−11) (−30.30,−11.87) 3.66 (−29.32,5.5) (−32.03,3.70) 2.45 (−18.32,5.5) (−21.15,4.22) 1.63 (−18.32,0) (−21.03,−0.68) 2.42 算法3 (0,5.5) (0.34,4.92) 1.06 1.89 0.71 (11,5.5) (10.52,3.73) 2.54 (11,−11) (9.01,−12.26) 3.29 (−29.32,−11) (−30.32,−11.61) 1.69 (−29.32,5.5) (−31.69,4.09) 1.34 (−18.32,5.5) (−20.83,4.81) 1.53 (−18.32,0) (−20.73,−0.42) 1.80
下载: 导出CSV
-
[1] 裴凌, 刘东辉, 钱久超. 室内定位技术与应用综述[J]. 导航定位与授时, 2017, 4(18): 1-10. doi: 10.19306/j.cnki.2095-8110.2017.03.001PEI L, LIU D H, QIAN J C. A survey of indoor positioning technology and application[J]. Navigation Positioning and Timing, 2017, 4(18): 1-10(in Chinese). doi: 10.19306/j.cnki.2095-8110.2017.03.001 [2] MINNE K, MACOIR N, ROSSEY J, et al. Experimental evaluation of UWB indoor positioning for indoor track cycling[J]. Sensors, 2019, 19(9): 2041. doi: 10.3390/s19092041 [3] XU H, DING Y, LI P, et al. An RFID indoor positioning algorithm based on Bayesian probability and K-nearest neighbor[J]. Sensors, 2017, 17(8): 1806. doi: 10.3390/s17081806 [4] LIU F, LIU J, YIN Y, et al. Survey on WiFi-based indoor positioning techniques[J]. IET Communications, 2020, 14(9): 1372-1383. doi: 10.1049/iet-com.2019.1059 [5] OU C W, CHAO C J, CHANG F S, et al. A ZigBee position technique for indoor localization based on proximity learning[C]//Proceedings of the 2017 IEEE International Conference on Mechatronics and Automation. Piscataway: IEEE Press, 2017: 875-880. [6] 潘献飞, 穆华, 胡小平. 单兵自主导航技术发展综述[J]. 导航定位与授时, 2018, 5(1): 1-11. doi: 10.19306/j.cnki.2095-8110.2018.01.001PAN X F, MU H, HU X P. A survey of the development of autonomous navigation technology for individual soldier[J]. Navigation Positioning and Timing, 2018, 5(1): 1-11(in Chinese). doi: 10.19306/j.cnki.2095-8110.2018.01.001 [7] ELWELL J. Inertial navigation for the urban warrior[C]//Proceedings of the Society of Photo-Optical Instrumentation Engineers. Bellingham: SPIE, 1999, 3709: 196-204. [8] MA M, SONG Q, GU Y, et al. An adaptive zero velocity detection algorithm based on multi-sensor fusion for a pedestrian navigation system[J]. Sensors, 2018, 18(10): 3261. doi: 10.3390/s18103261 [9] WANG Y S, SHKEL A M. Adaptive threshold for zero-velocity detector in ZUPT-aided pedestrian inertial navigation[J]. IEEE Sensors Letters, 2019, 3(11): 1-4. [10] 王凯龙. GNSS和IMU的室内外行人无缝导航方法研究[D]. 南昌: 南昌大学, 2018.WANG K L. The method research of indoor and outdoor pedestrians seamless navigation based on GNSS and IMU[D]. Nanchang: Nanchang University, 2018(in Chinese). [11] SUN W, DING W, YAN H F, et al. Zero velocity interval detection based on a continuous hidden Markov model in micro inertial pedestrian navigation[J]. Measurement Science and Technology, 2018, 29(6): 065103. doi: 10.1088/1361-6501/aab59d [12] 戴洪德, 李松林, 周绍磊, 等. 基于伪标准差和N-P准则的行人导航零速检测[J]. 中国惯性技术学报, 2018, 26(6): 701-707. doi: 10.13695/j.cnki.12-1222/o3.2018.06.001DAI H D, LI S L, ZHOU S L, et al. Pedestrian navigation zero-velocity detection based on pseudo-standard deviation and N-P criterion[J]. Journal of Chinese Inertial Technology, 2018, 26(6): 701-707(in Chinese). doi: 10.13695/j.cnki.12-1222/o3.2018.06.001 [13] WAGSTAFF B, KELLY J. LSTM-based zero-velocity detection for robust inertial navigation[C]//Proceedings of the 2018 International Conference on Indoor Positioning and Indoor Navigation. Piscataway: IEEE Press, 2018: 1-8. [14] SKOG I, HANDEL P, NILSSON J O, et al. Zero-velocity detection—An algorithm evaluation.[J]. IEEE Transactions on Biomedical Engineering, 2010, 57(11): 2657-2666. doi: 10.1109/TBME.2010.2060723 [15] WAHLSTRÖM J, SKOG I, GUSTAFSSON F, et al. Zero-velocity detection—A Bayesian approach to adaptive thresholding[J]. IEEE Sensors Letters, 2019, 3(6): 1-4. [16] 孙伟, 宋如意, 丁伟. 步态特征提取的K均值聚类自适应判别[J]. 测绘科学, 2019, 44(12): 29-34. doi: 10.16251/j.cnki.1009-2307.2019.12.005SUN W, SONG R Y, DING W. Adaptive gait features discrimination based on K means clustering[J]. Science of Surveying and Mapping, 2019, 44(12): 29-34(in Chinese). doi: 10.16251/j.cnki.1009-2307.2019.12.005 [17] LI Y, WANG J J. A pedestrian navigation system based on low cost IMU[J]. Journal of Navigation, 2014, 67(6): 929-949. doi: 10.1017/S0373463314000344 [18] WANG Z L, ZHAO H Y, QIU S, et al. Stance-phase detection for ZUPT-aided foot-mounted pedestrian navigation system[J]. IEEE-ASME Transactions on Mechatronics, 2015, 20(6): 3170-3181. doi: 10.1109/TMECH.2015.2430357 [19] FAHAD A, ALSHATRI N, TARI Z, et al. A survey of clustering algorithms for big data: Taxonomy and empirical analysis[J]. IEEE Transactions on Emerging Topics in Computing, 2014, 2(3): 267-279. doi: 10.1109/TETC.2014.2330519 -
下载:
点击查看大图
计量
- 文章访问数: 557
- HTML全文浏览量: 41
- PDF下载量: 11
- 被引次数: 0
