-
摘要:
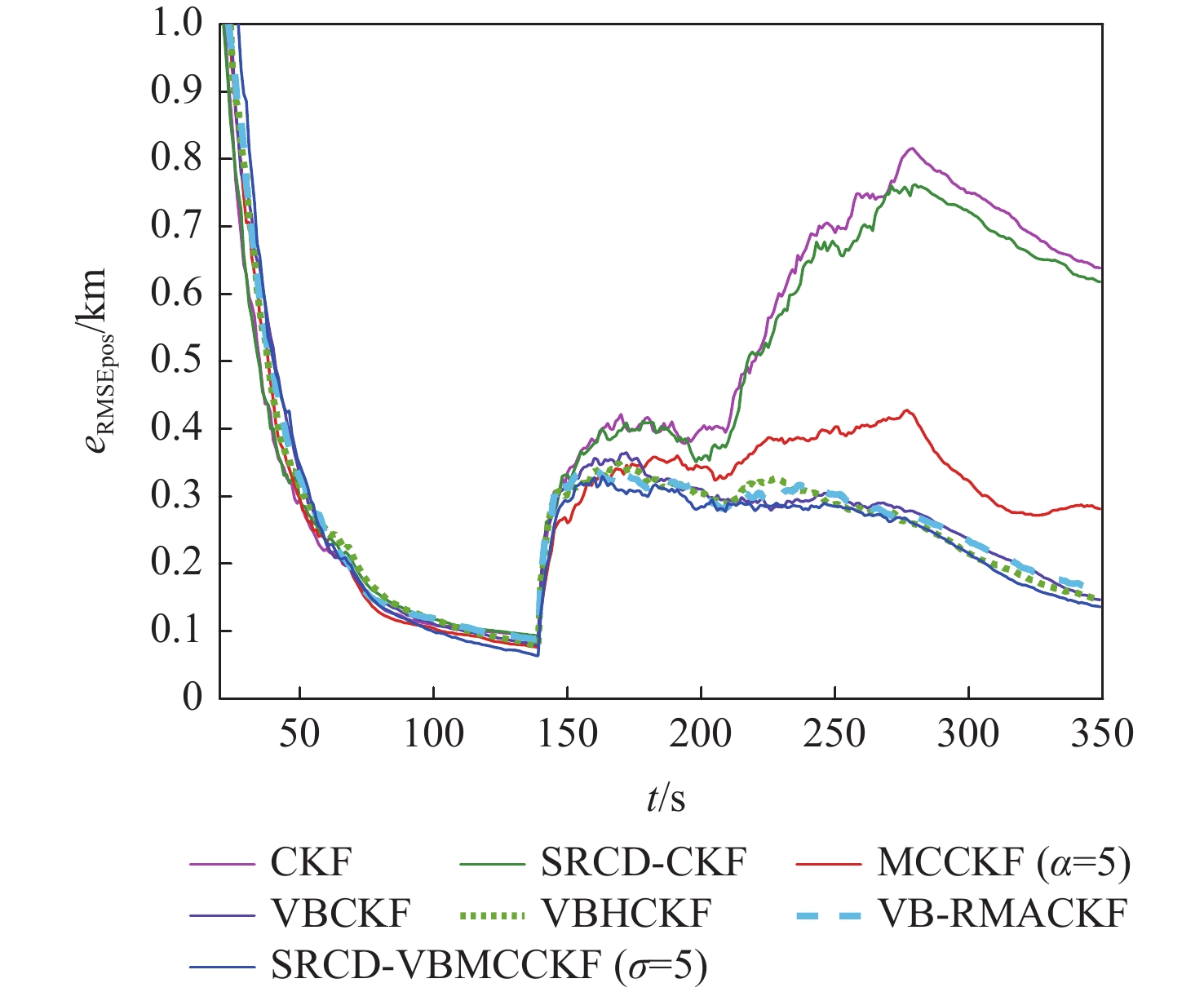
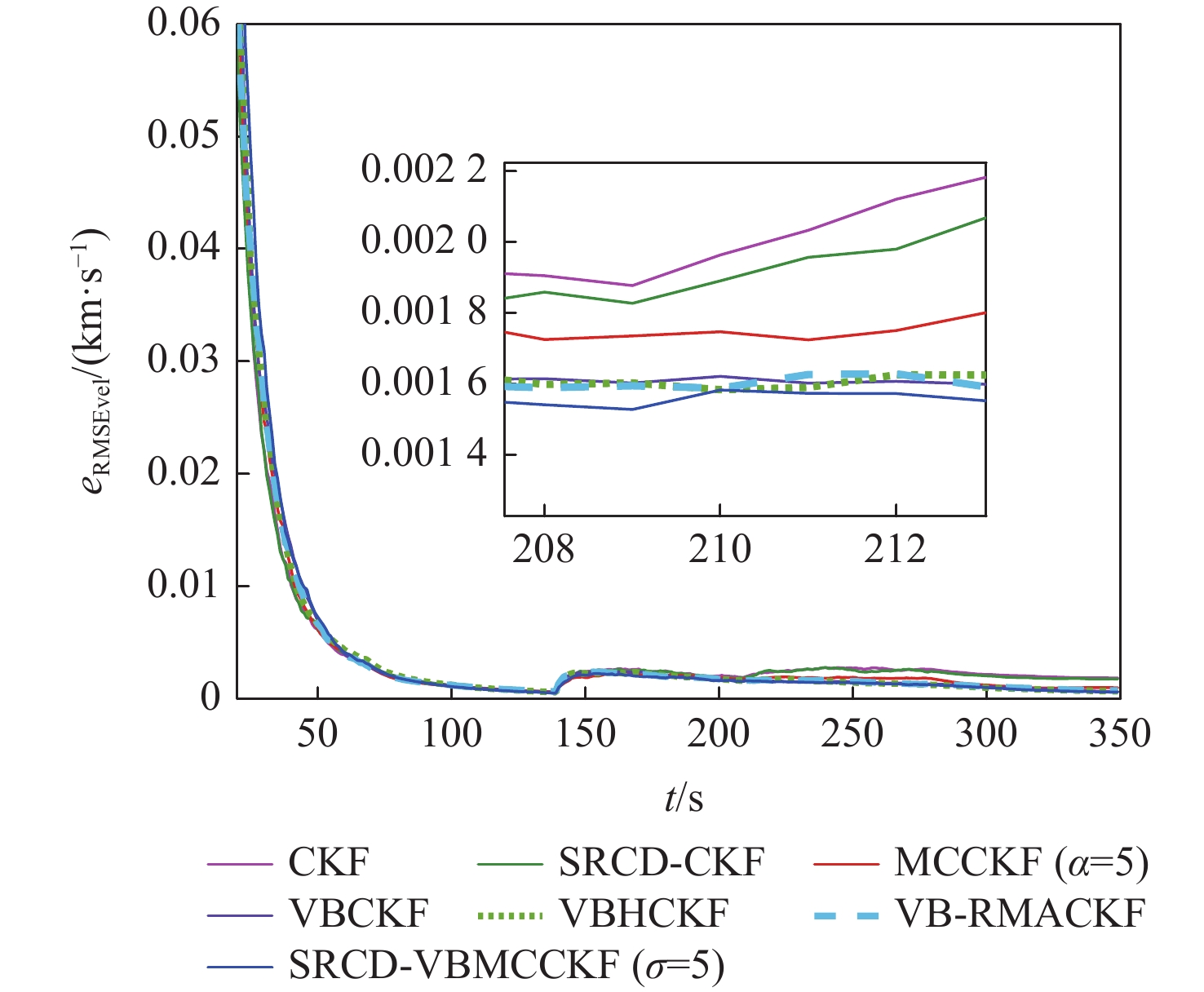
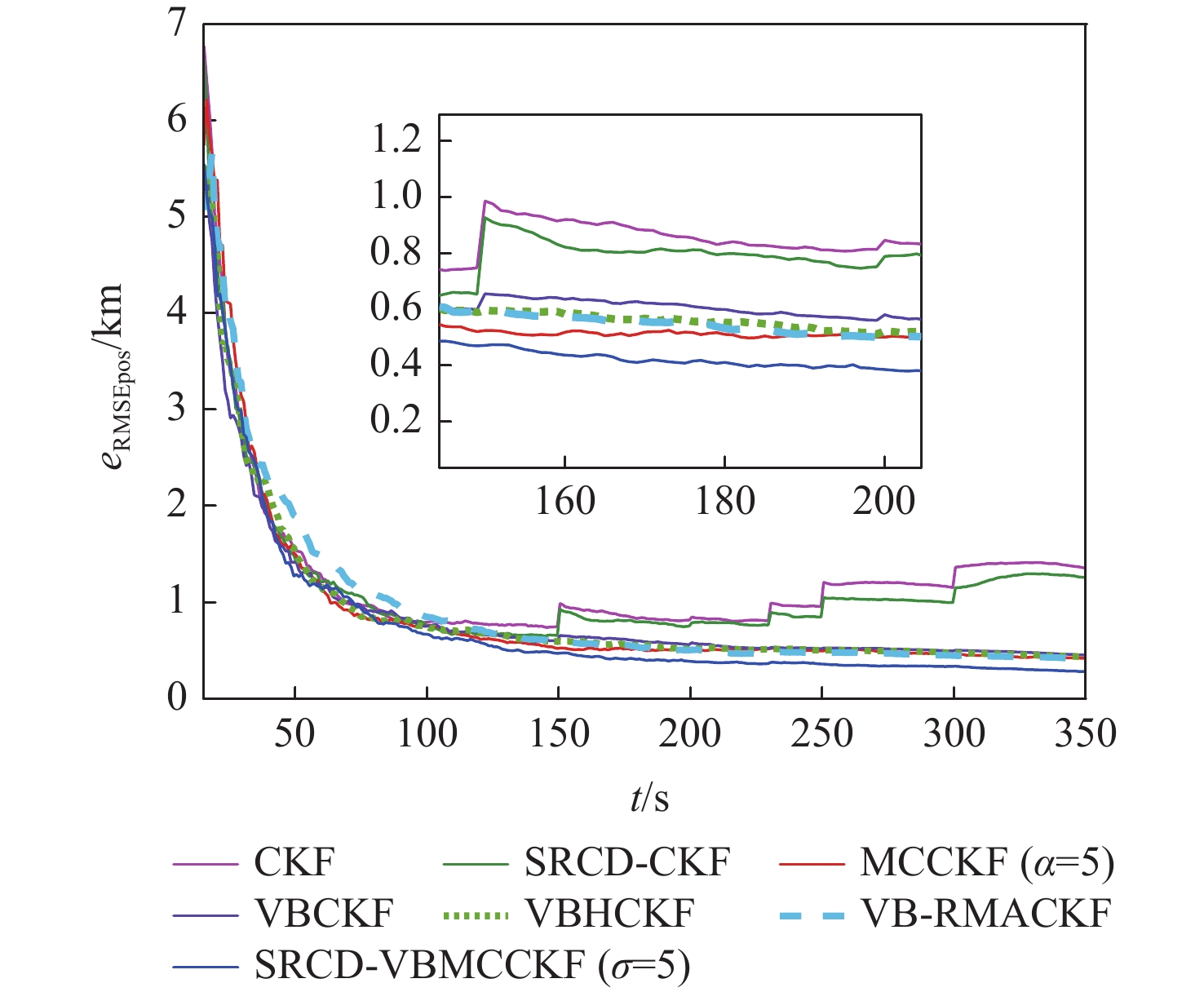
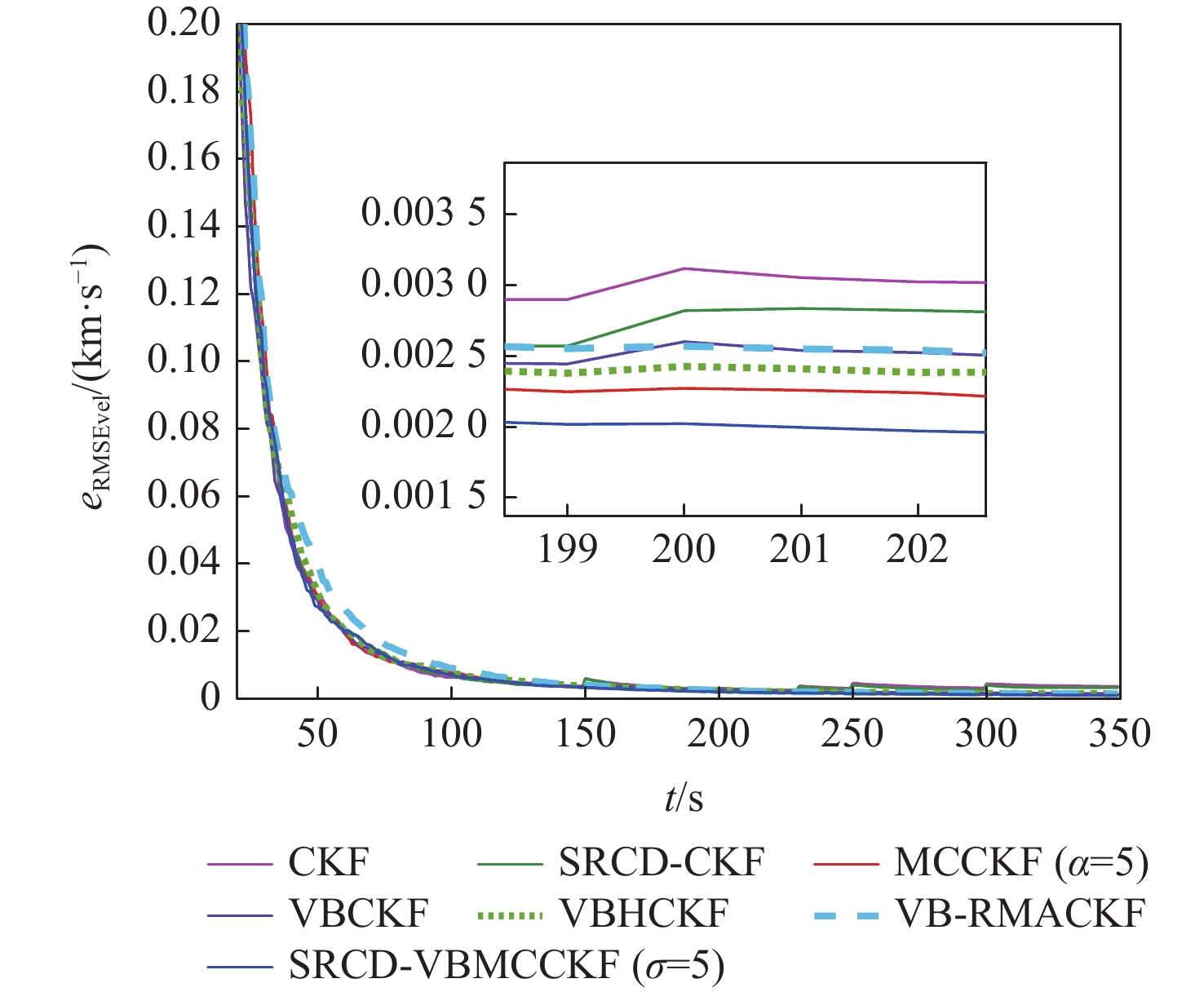
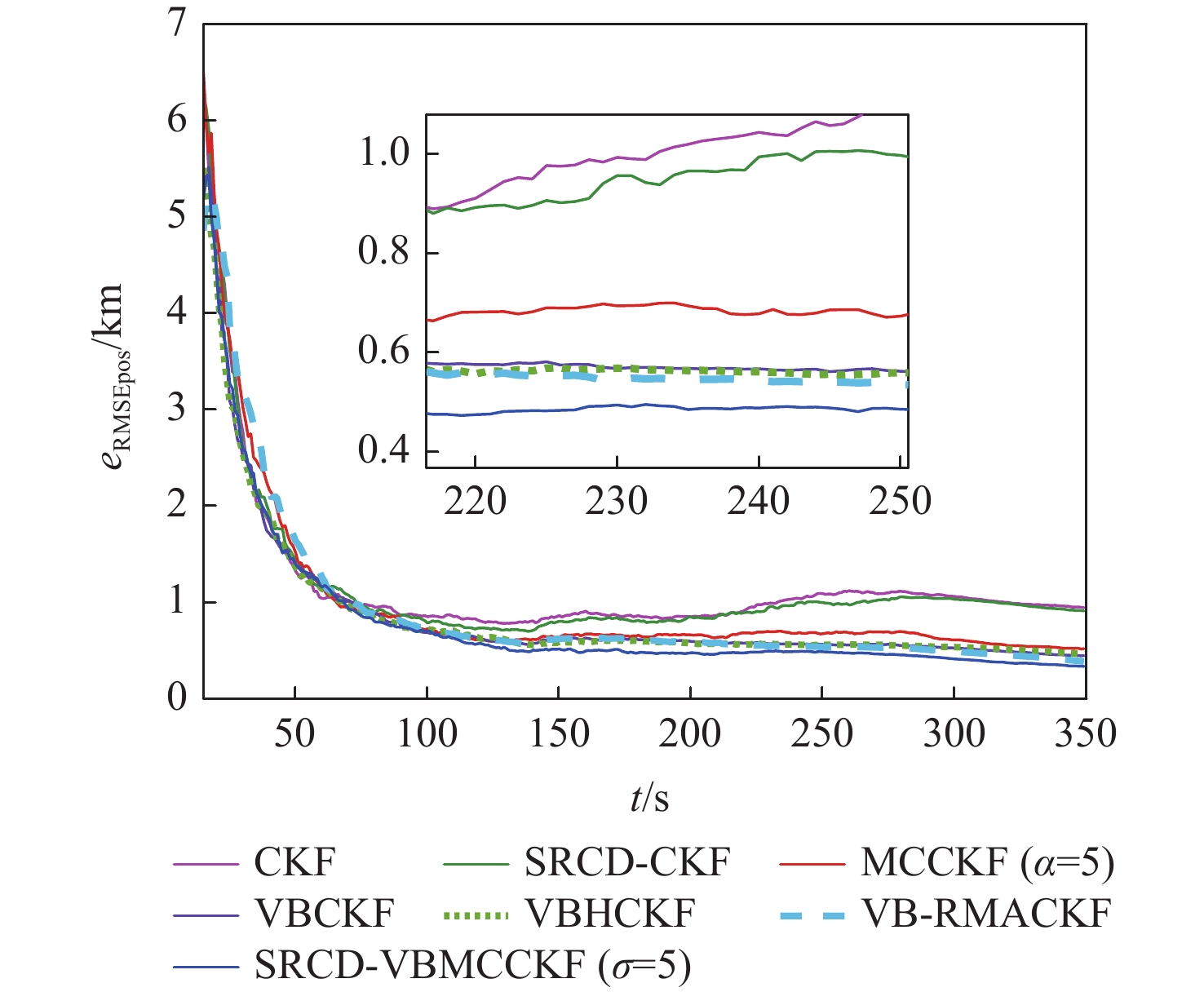
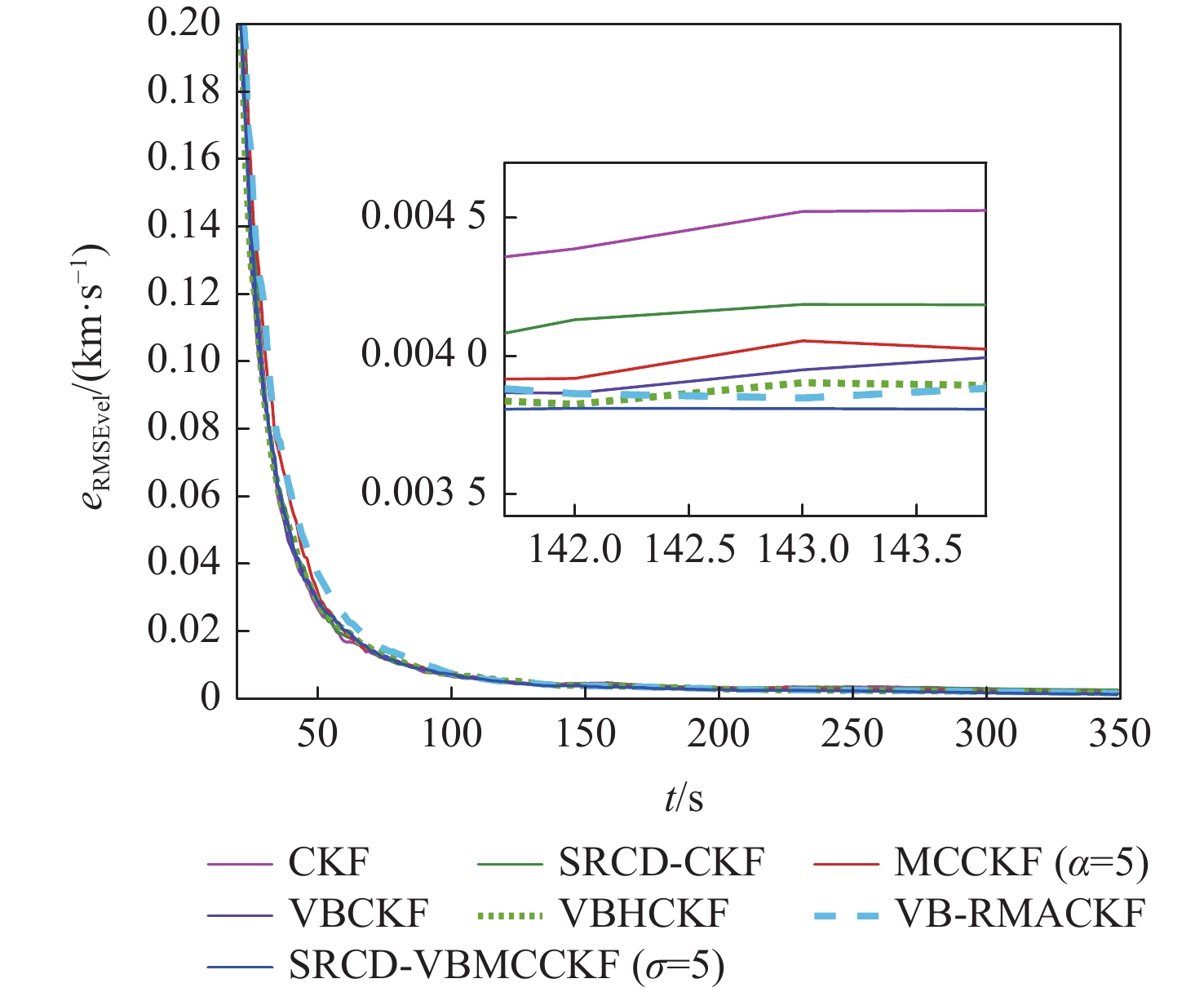
针对纯方位目标跟踪中测量噪声协方差未知和非高斯测量噪声突变问题，提出了一种平方根连续-离散变分贝叶斯最大相关熵容积卡尔曼滤波（SRCD-VBMCCKF）算法。将目标跟踪模型建立为连续状态空间-离散测量空间模型，提高了目标跟踪的解算精度；由变分贝叶斯准则对未知的时变测量噪声进行估计，提升了算法的自适应性；考虑到测量中出现的非高斯突变噪声，由最大相关熵准则构建抗差因子，进一步增强了算法对异常测量值的鲁棒能力。仿真结果表明：所提算法能够对测量中的未知时变噪声和非高斯重尾突变噪声有效抑制，且相比于传统滤波算法，所提算法兼具自适应性和鲁棒性。
Abstract:To address the problems of unknown covariance of measurement noise and non-Gaussian mutation measurement noise in bearings-only target tracking, a square-root continuous-discrete variational Bayesian maximum correntropy cubature Kalman filter (SRCD-VBMCCKF) algorithm is proposed. Firstly, the target tracking model is established as a continuous state space-discrete measurement space model, which improves the accuracy of target tracking; secondly, the unknown time-varying measurement noise is estimated by the variational Bayes criterion, which improves the adaptability of the algorithm; finally, considering the non-Gaussian mutation noise in the measurement, the robustness factor is constructed by the maximum correntropy criterion, which further enhances the algorithm’s robustness to abnormal measurements. The simulation results show that the proposed algorithm can effectively suppress the unknown time-varying noise and non-Gaussian heavy-tail mutation noise in the measurement. Compared with the traditional filtering algorithm, the proposed algorithm is both adaptive and robust.
-
图 2 未知时变噪声下各算法的${e_{{\text{RMSEpos}}}}$
Figure 2. ${e_{{\text{RMSEpos}}}}$ of each algorithm under unknown time-varying noise
图 3 未知时变噪声下各算法的${e_{{\text{RMSEvel}}}}$
Figure 3. ${e_{{\text{RMSEvel}}}}$ of each algorithm under unknown time-varying noise
图 4 非高斯突变噪声下各算法的${e_{{\text{RMSEpos}}}}$
Figure 4. ${e_{{\text{RMSEpos}}}}$ of each algorithm under non-Gaussian outlier noise
图 5 非高斯突变噪声下各算法的${e_{{\text{RMSEvel}}}}$
Figure 5. ${e_{{\text{RMSEvel}}}}$ of each algorithm under non-Gaussian outlier noise
图 6 叠加噪声下各算法的${e_{{\text{RMSEpos}}}}$
Figure 6. ${e_{{\text{RMSEpos}}}}$ of each algorithm under superimposed noise
图 7 叠加噪声下各算法的${e_{{\text{RMSEvel}}}}$
Figure 7. ${e_{{\text{RMSEvel}}}}$ of each algorithm under superimposed noise
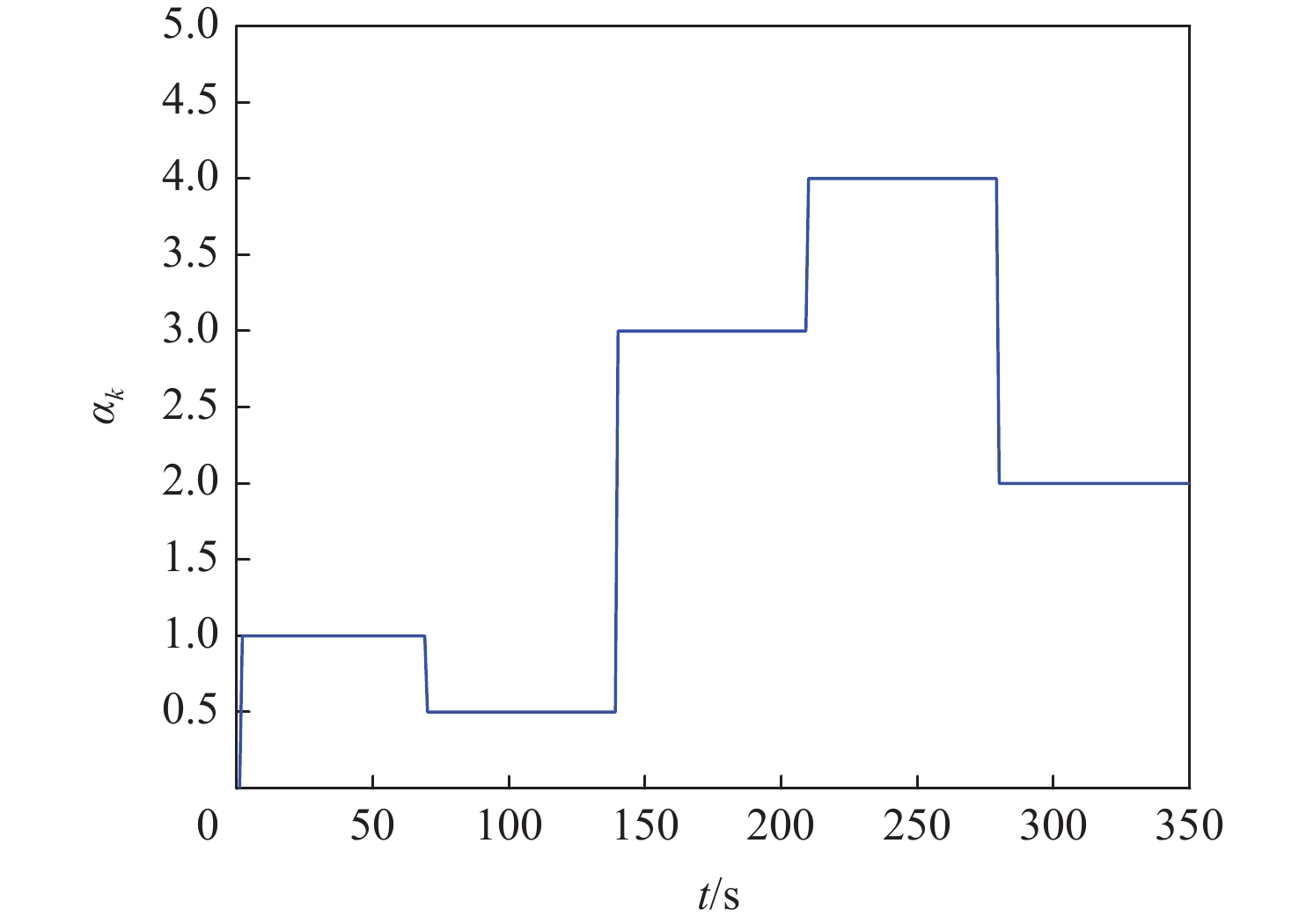
表 1 异常突变值设置点
Table 1. Set points of outliers
时间/s 测量噪声 150 10$ \boldsymbol{R}_k $ 200 5$ \boldsymbol{R}_k $ 230 15$ \boldsymbol{R}_k $ 250 20$ \boldsymbol{R}_k $ 300 30$ \boldsymbol{R}_k $ 
下载: 导出CSV
-
[1] 刘玉双, 赵剡, 吴发林. 基于外定界椭球集员估计的纯方位目标跟踪[J]. 北京航空航天大学学报, 2017, 43(3): 497-505. doi: 10.13700/j.bh.1001-5965.2016.0196LIU Y S, ZHAO Y, WU F L. Bearing-only target tracking based on ellipsoidal outer-bounding set-membership estimation[J]. Journal of Beijing University of Aeronautics and Astronautics, 2017, 43(3): 497-505(in Chinese). doi: 10.13700/j.bh.1001-5965.2016.0196 [2] HE R K, CHEN S X, WU H, et al. Adaptive covariance feedback cubature Kalman filtering for continuous-discrete bearings-only tracking system[J]. IEEE Access, 2018, 7: 2686-2694. [3] ARASARATNAM I, HAYKIN S R, HURD T R. Cubature Kalman filtering for continuous-discrete systems: Theory and simulations[J]. IEEE Transactions on Signal Processing, 2010, 58(10): 4977-4993. doi: 10.1109/TSP.2010.2056923 [4] CROUSE D F. Cubature Kalman filters for continuous-time dynamic models. Part Ⅱ: A solution based on moment matching[C]//Proceedings of the IEEE Radar Conference. Piscataway: IEEE Press, 2014: 194-199. [5] KULIKOVA M, KULIKOV G Y. NIRK-based accurate continuous-discrete extended Kalman filters for estimating continuous-time stochastic target tracking models[J]. Journal of Computational and Applied Mathematics, 2017, 316: 260-270. doi: 10.1016/j.cam.2016.08.036 [6] NARASIMHAPPA M, MAHINDRAKAR A D, GUIZILINI V C, et al. MEMS-based IMU drift minimization: Sage husa adaptive robust Kalman filtering[J]. IEEE Sensors Journal, 2020, 20(1): 250-260. doi: 10.1109/JSEN.2019.2941273 [7] SARKKA S, NUMMENMAA A. Recursive noise adaptive Kalman filtering by variational Bayesian approximations[J]. IEEE Transactions on Automatic Control, 2009, 54(3): 596-600. doi: 10.1109/TAC.2008.2008348 [8] SÄRKKÄ S, HARTIKAINEN J. Non-linear noise adaptive Kalman filtering via variational Bayes[C]//Proceedings of the IEEE International Workshop on Machine Learning for Signal Processing. Piscataway: IEEE Press, 2013: 1-6. [9] HUANG Y L, HANG Y G, WU Z M, et al. A novel adaptive Kalman filter with inaccurate process and measurement noise covariance matrices[J]. IEEE Transactions on Automatic Control, 2018, 63(2): 594-601. [10] CHANG G B, LIU M. M-estimator-based robust Kalman filter for systems with process modeling errors and rank deficient measurement models[J]. Nonlinear Dynamics, 2015, 80(3): 1431-1449. doi: 10.1007/s11071-015-1953-0 [11] HUANG W, SHAN H J, XU J S, et al. Robust variable kernel width for maximum correntropy criterion algorithm[J]. Signal Processing, 2021, 182: 107948. doi: 10.1016/j.sigpro.2020.107948 [12] LIU X, CHEN B D, XU B, et al. Maximum correntropy unscented filter[J]. International Journal of Systems Science, 2017, 48(8): 1607-1615. doi: 10.1080/00207721.2016.1277407 [13] 卢航, 郝顺义, 彭志颖, 等. 基于MCC的鲁棒高阶CKF在组合导航中的应用[J]. 计算机工程与应用, 2020, 56(1): 257-264. doi: 10.3778/j.issn.1002-8331.1809-0206LU H, HAO S Y, PENG Z Y, et al. Application of robust high-degree CKF based on MCC in integrated navigation[J]. Computer Engineering and Applications, 2020, 56(1): 257-264(in Chinese). doi: 10.3778/j.issn.1002-8331.1809-0206 [14] KULIKOV G Y, KULIKOVA M V. Accurate cubature and extended Kalman filtering methods for estimating continuous-time nonlinear stochastic systems with discrete measurements[J]. Applied Numerical Mathematics, 2017, 111: 260-275. doi: 10.1016/j.apnum.2016.09.015 [15] IZANLOO R, FAKOORIAN S A, YAZDI H S, et al. Kalman filtering based on the maximum correntropy criterion in the presence of non-Gaussian noise[C]//Proceedings of the Annual Conference on Information Science and Systems. Piscataway: IEEE Press, 2016: 500-505. [16] 张敬艳, 修建娟, 董凯. 噪声非高斯条件下基于最大相关熵准则的容积滤波算法[J]. 兵器装备工程学报, 2021, 42(8): 245-250. doi: 10.11809/bqzbgcxb2021.08.039ZHANG J Y, XIU J J, DONG K. Maximum correntropy cubature Kalman filter under non-Gaussian noise[J]. Journal of Ordnance Equipment Engineering, 2021, 42(8): 245-250(in Chinese). doi: 10.11809/bqzbgcxb2021.08.039 [17] WANG G Q, LI N, ZHANG Y G. Maximum correntropy unscented Kalman and information filters for non-Gaussian measurement noise[J]. Journal of the Franklin Institute, 2017, 354(18): 8659-8677. doi: 10.1016/j.jfranklin.2017.10.023 [18] ARASARATNAM I, HAYKIN S. Cubature Kalman filters[J]. IEEE Transactions on Automatic Control, 2009, 54(6): 1254-1269. doi: 10.1109/TAC.2009.2019800 [19] 彭美康, 郭蕴华, 汪敬东, 等. 基于鲁棒容积卡尔曼滤波的自适应目标跟踪算法[J]. 控制理论与应用, 2020, 37(4): 793-800.PENG M K, GUO Y H, WANG J D, et al. Adaptive target tracking algorithm based on robust cubature Kalman filter[J]. Control Theory & Applications, 2020, 37(4): 793-800(in Chinese). -
下载:
点击查看大图
计量
- 文章访问数: 675
- HTML全文浏览量: 54
- PDF下载量: 41
- 被引次数: 0
