-
摘要:
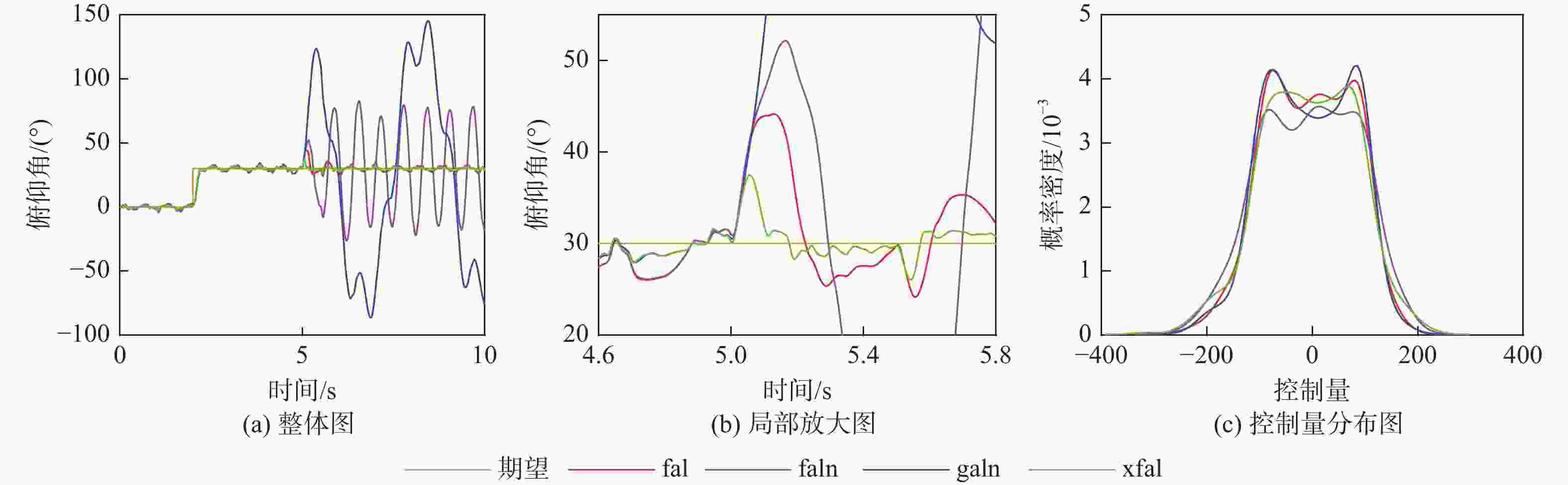
针对四旋翼无人机姿态自抗扰控制(ADRC)系统应对复杂干扰时,基于传统fal函数设计的扩张状态观测器(ESO)抗扰动能力不足、易产生抖振的问题,提出一种改进型ADRC并用于四旋翼姿态控制。基于正弦函数构建一种新型光滑非线性xfal函数以改进ESO,利用Lyapunov函数对改进ESO的稳定性进行证明。通过仿真平台,与其他ADRC进行比较。实验结果表明:改进型ADRC和标准ADRC相比,当四旋翼无人机不受干扰时,在其抖振区间内,俯仰角均方误差降低了约38.7%;当四旋翼无人机分别受到连续干扰、突发干扰、复杂干扰时,在各自计算区间内,俯仰角均方误差分别降低了约78.4%、80.2%、83.3%。因此,改进型ADRC在有效减小抖振的同时,还具备优良的抗干扰能力。
Abstract:An improved active disturbance rejection control (ADRC) was proposed for quadrotor attitude control to address the extended state observer (ESO) based on the traditional fal function's problems with easy chattering and insufficient anti-interference ability when responding to complex disturbances. A new smooth nonlinear xfal function was constructed based on the sine function to improve ESO. The stability of the improved ESO was proved by Lyapunov function. Finally, the improved ADRC was compared with other ADRCs through simulation platform. The results demonstrate that when compared to the standard ADRC, the mean square error of the pitch angle is reduced by approximately 38.7% in its chattering interval, and by approximately 78.4%, 80.2%, and 83.3% in their respective calculation intervals when the quadrotor was subjected to continuous interference, sudden interference, and complex interference, respectively. This indicates that the improved ADRC has excellent anti-interfere capabilities.
-
表 1 四旋翼无人机仿真参数
Table 1. Four-rotor UAV simulation parameters
参数 数值 质量m/kg 0.057 力臂d/m 0.059 转动惯量Ix/(kg·m2) 4.45×10−4 转动惯量Iy/(kg·m2) 4.29×10−4 转动惯量Iz/(kg·m2) 8.6×10−4 油门-拉力系数${C'_{{T} } }$/N 3.8×10−4 油门$\sigma $ 0~1000 表 2 TD和NLSEF参数
Table 2. TD and NLSEF parameters
类型 r h ${\alpha _1}$ ${\alpha _2}$ ${\beta _{01}}$ ${\beta _{02}}$ $\delta $ TD 800 0.005 NLSEF 0.75 0.75 80 4 0.005 表 3 ESO参数
Table 3. ESO parameters
参数 fal faln galn xfal b0 40 40 40 40 ${\alpha _1}$ 0.5 0.5 0.4 ${\alpha _2}$ 0.25 0.25 0.35 ${\beta _1}$ 180 180 180 180 ${\beta _2}$ 2160 2160 2160 2160 ${\beta _3}$ 24000 24000 24000 24000 h 0.005 0.005 0.005 0.005 $\delta $ 0.025 0.025 ${K_1}$ 3 ${K_2}$ 4 R1 2 R2 2 表 4 无人机在各个干扰下的均方误差
Table 4. Mean square error of UAV under various disturbances
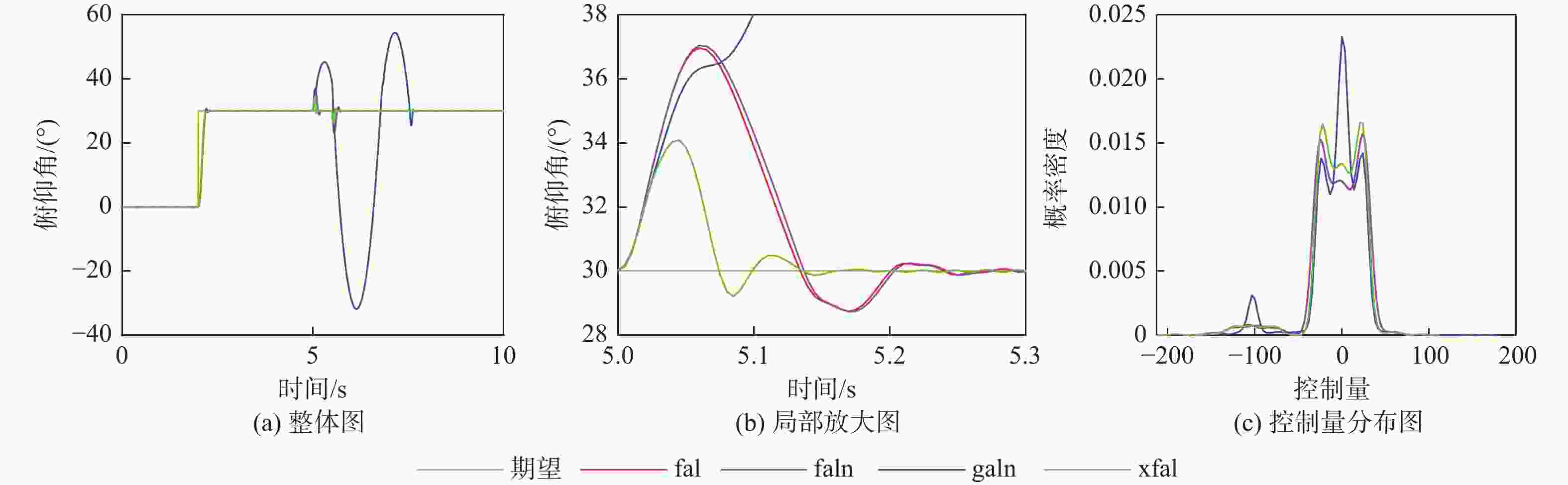
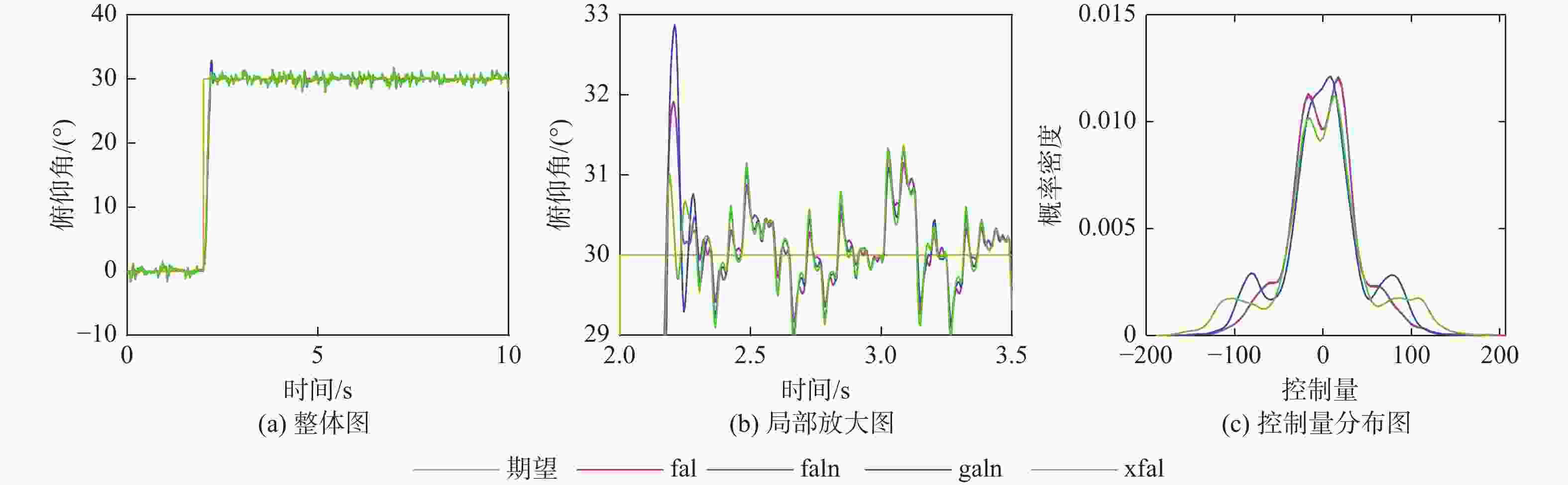
控制器 无干扰 正弦波 方波 白噪声 综合干扰 fal 0.00163 2.0968 6.9385 0.2621 7.1904 faln 0.00163 2.0968 7.2880 0.2574 * galn 0.00098 0.4564 * 0.2456 * xfal 0.00100 0.4542 1.3747 0.2910 1.1975 注:“*”表示失控,无均方差。 -
[1] 李俊芳, 李峰, 吉月辉, 等. 四旋翼无人机轨迹稳定跟踪控制[J]. 控制与决策, 2020, 35(2): 349-356. doi: 10.13195/j.kzyjc.2018.0639LI J F, LI F, JI Y H, et al. Trajectory stable tracking control of quadrotor UAV[J]. Control and Decision, 2020, 35(2): 349-356(in Chinese). doi: 10.13195/j.kzyjc.2018.0639 [2] PETRLÍK M, BÁČA T, HEŘT D, et al. A robust UAV system for operations in a constrained environment[J]. IEEE Robotics and Automation Letters, 2020, 5(2): 2169-2176. doi: 10.1109/LRA.2020.2970980 [3] ZHOU L H, ZHANG J Q, DOU J X, et al. A fuzzy adaptive backstepping control based on mass observer for trajectory tracking of a quadrotor UAV[J]. International Journal of Adaptive Control and Signal Processing, 2018, 32(12): 1675-1693. doi: 10.1002/acs.2937 [4] QI G Y, HUANG D H. Modeling and dynamical analysis of a small-scale unmanned helicopter[J]. Nonlinear Dynamics, 2019, 98(3): 2131-2145. doi: 10.1007/s11071-019-05313-x [5] JITHU G, JAYASREE P R. Quadrotor modelling and control[C]// 2016 International Conference on Electrical, Electronics, and Optimization Techniques (ICEEOT). Piscataway: IEEE Press, 2016: 1167-1172. [6] NGUYEN K D, HA C. Design of synchronization controller for the station-keeping hovering mode of quad-rotor unmanned aerial vehicles[J]. International Journal of Aeronautical and Space Sciences, 2019, 20(1): 228-237. doi: 10.1007/s42405-018-0115-2 [7] 华和安, 方勇纯, 钱辰, 等. 基于线性滤波器的四旋翼无人机强化学习控制策略[J]. 电子与信息学报, 2021, 43(12): 3407-3417. doi: 10.11999/JEIT210251HUA H A, FANG Y C, QIAN C, et al. Reinforcement learning control strategy of quadrotor unmanned aerial vehicles based on linear filter[J]. Journal of Electronics & Information Technology, 2021, 43(12): 3407-3417(in Chinese). doi: 10.11999/JEIT210251 [8] SAIF A W A, ALIYU A, AL DHAIFALLAH M, et al. Decentralized backstepping control of a quadrotor with tilted-rotor under wind gusts[J]. International Journal of Control, Automation and Systems, 2018, 16(5): 2458-2472. doi: 10.1007/s12555-017-0099-x [9] 张钊, 杨忠, 段雨潇, 等. 主动变形四旋翼自抗扰飞行控制方法[J]. 控制理论与应用, 2021, 38(4): 444-456. doi: 10.7641/CTA.2020.00344ZHANG Z, YANG Z, DUAN Y X, et al. Active disturbance rejection control method for actively deformable quadrotor[J]. Control Theory & Applications, 2021, 38(4): 444-456(in Chinese). doi: 10.7641/CTA.2020.00344 [10] 唐志勇, 马福源, 裴忠才. 四旋翼的改进PSO-RBF神经网络自适应滑模控制[J]. 北京航空航天大学学报, 2023, 49(7): 1563-1572. doi: 10.13700/j.bh.1001-5965.2021.0477TANG Z Y, MA F Y, PEI Z C. Improved PSO-RBF neural network adaptive sliding mode control for quadrotor systems[J]. Journal of Beijing University of Aeronautics and Astronautics, 2023, 49(7): 1563-1572(in Chinese). doi: 10.13700/j.bh.1001-5965.2021.0477 [11] 高俊山, 段立勇, 邓立为. 四旋翼无人机抗干扰轨迹跟踪控制[J]. 控制与决策, 2021, 36(2): 379-386. doi: 10.13195/j.kzyjc.2019.0875GAO J S, DUAN L Y, DENG L W. Anti-interference trajectory tracking control of quadrotor UAV[J]. Control and Decision, 2021, 36(2): 379-386(in Chinese). doi: 10.13195/j.kzyjc.2019.0875 [12] HAN J Q. From PID to active disturbance rejection control[J]. IEEE Transactions on Industrial Electronics, 2009, 56(3): 900-906. doi: 10.1109/TIE.2008.2011621 [13] 张勇, 陈增强, 张兴会, 等. 四旋翼无人机系统PD-ADRC串级控制[J]. 系统工程与电子技术, 2018, 40(9): 2055-2061. doi: 10.3969/j.issn.1001-506X.2018.09.23ZHANG Y, CHEN Z Q, ZHANG X H, et al. PD-ADRC cascade control for quadrotor system[J]. Systems Engineering and Electronics, 2018, 40(9): 2055-2061(in Chinese). doi: 10.3969/j.issn.1001-506X.2018.09.23 [14] 王术波, 韩宇, 陈建, 等. 基于ADRC迭代学习控制的四旋翼无人机姿态控制[J]. 航空学报, 2020, 41(12): 324112.WANG S B, HAN Y, CHEN J, et al. Active disturbance rejection control of UAV attitude based on iterative learning control[J]. Acta Aeronautica et Astronautica Sinica, 2020, 41(12): 324112(in Chinese). [15] 陈增强, 李毅, 孙明玮, 等. 四旋翼无人飞行器ADRC-GPC控制[J]. 哈尔滨工业大学学报, 2016, 48(9): 176-180. doi: 10.11918/j.issn.0367-6234.2016.09.030CHEN Z Q, LI Y, SUN M W, et al. ADRC-GPC control of a quad-rotor unmanned aerial vehicle[J]. Journal of Harbin Institute of Technology, 2016, 48(9): 176-180(in Chinese). doi: 10.11918/j.issn.0367-6234.2016.09.030 [16] 张勇, 陈增强, 张兴会, 等. 基于自抗扰的四旋翼无人机动态面姿态控制[J]. 吉林大学学报(工学版), 2019, 49(2): 562-569. doi: 10.13229/j.cnki.jdxbgxb20171241ZHANG Y, CHEN Z Q, ZHANG X H, et al. Dynamic surface attitude control of quad-rotor UAV based on ADRC[J]. Journal of Jilin University (Engineering and Technology Edition), 2019, 49(2): 562-569(in Chinese). doi: 10.13229/j.cnki.jdxbgxb20171241 [17] 石嘉, 裴忠才, 唐志勇, 等. 改进型自抗扰四旋翼无人机控制系统设计与实现[J]. 北京航空航天大学学报, 2021, 47(9): 1823-1831. doi: 10.13700/j.bh.1001-5965.2020.0333SHI J, PEI Z C, TANG Z Y, et al. Design and realization of an improved active disturbance rejection quadrotor UAV control system[J]. Journal of Beijing University of Aeronautics and Astronautics, 2021, 47(9): 1823-1831(in Chinese). doi: 10.13700/j.bh.1001-5965.2020.0333 [18] 陈志旺, 张子振, 曹玉洁. 自抗扰fal函数改进及在四旋翼姿态控制中的应用[J]. 控制与决策, 2018, 33(10): 1901-1907. doi: 10.13195/j.kzyjc.2017.0606CHEN Z W, ZHANG Z Z, CAO Y J. Fal function improvement of ADRC and its application in quadrotor aircraft attitude control[J]. Control and Decision, 2018, 33(10): 1901-1907(in Chinese). doi: 10.13195/j.kzyjc.2017.0606 [19] 杨文奇, 卢建华, 姜旭, 等. 基于改进ESO的四旋翼姿态自抗扰控制器设计[J]. 系统工程与电子技术, 2022, 44(12): 3792-3799. doi: 10.12305/j.issn.1001-506X.2022.12.24YANG W Q, LU J H, JIANG X, et al. Design of quadrotor attitude active disturbance rejection controller based on improved ESO[J]. Systems Engineering and Electronics, 2022, 44(12): 3792-3799(in Chinese). doi: 10.12305/j.issn.1001-506X.2022.12.24 [20] 杨盛毅, 唐胜景, 刘超, 等. 基于动力系统模型的四旋翼推力估计方法[J]. 北京理工大学学报, 2016, 36(6): 558-562. doi: 10.15918/j.tbit1001-0645.2016.06.002YANG S Y, TANG S J, LIU C, et al. Thrust estimation of quadrotor based on propulsion system model[J]. Transactions of Beijing Institute of Technology, 2016, 36(6): 558-562(in Chinese). doi: 10.15918/j.tbit1001-0645.2016.06.002 [21] 于洪国, 康忠健, 陈瑶. 基于双曲正切函数的二阶时变参数扩张状态观测器[J]. 控制理论与应用, 2016, 33(4): 530-534. doi: 10.7641/CTA.2016.50443YU H G, KANG Z J, CHEN Y. Time-varying parameter second-order extended state observer based on hyperbolic tangent function[J]. Control Theory & Applications, 2016, 33(4): 530-534(in Chinese). doi: 10.7641/CTA.2016.50443 [22] 周涛. 基于反双曲正弦函数的扩张状态观测器[J]. 控制与决策, 2015, 30(5): 943-946. doi: 10.13195/j.kzyjc.2014.0316ZHOU T. Extended state observer based on inverse hyperbolic sine function[J]. Control and Decision, 2015, 30(5): 943-946(in Chinese). doi: 10.13195/j.kzyjc.2014.0316 [23] ZHAO H X, CHEN S L, LI M. A sufficient condition for the stability of the third-order extended state observer[C]// Proceedings of the 32nd Chinese Control Conference. Piscataway: IEEE Press, 2013: 1526-1531. -






 下载:
下载: