-
摘要:
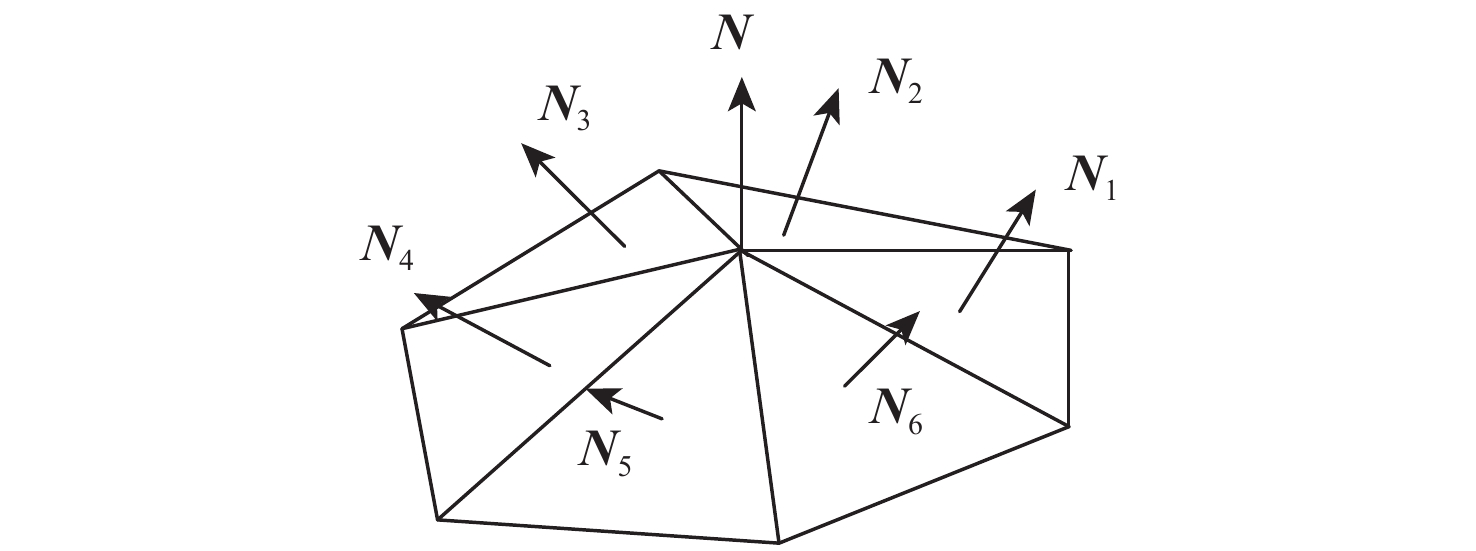
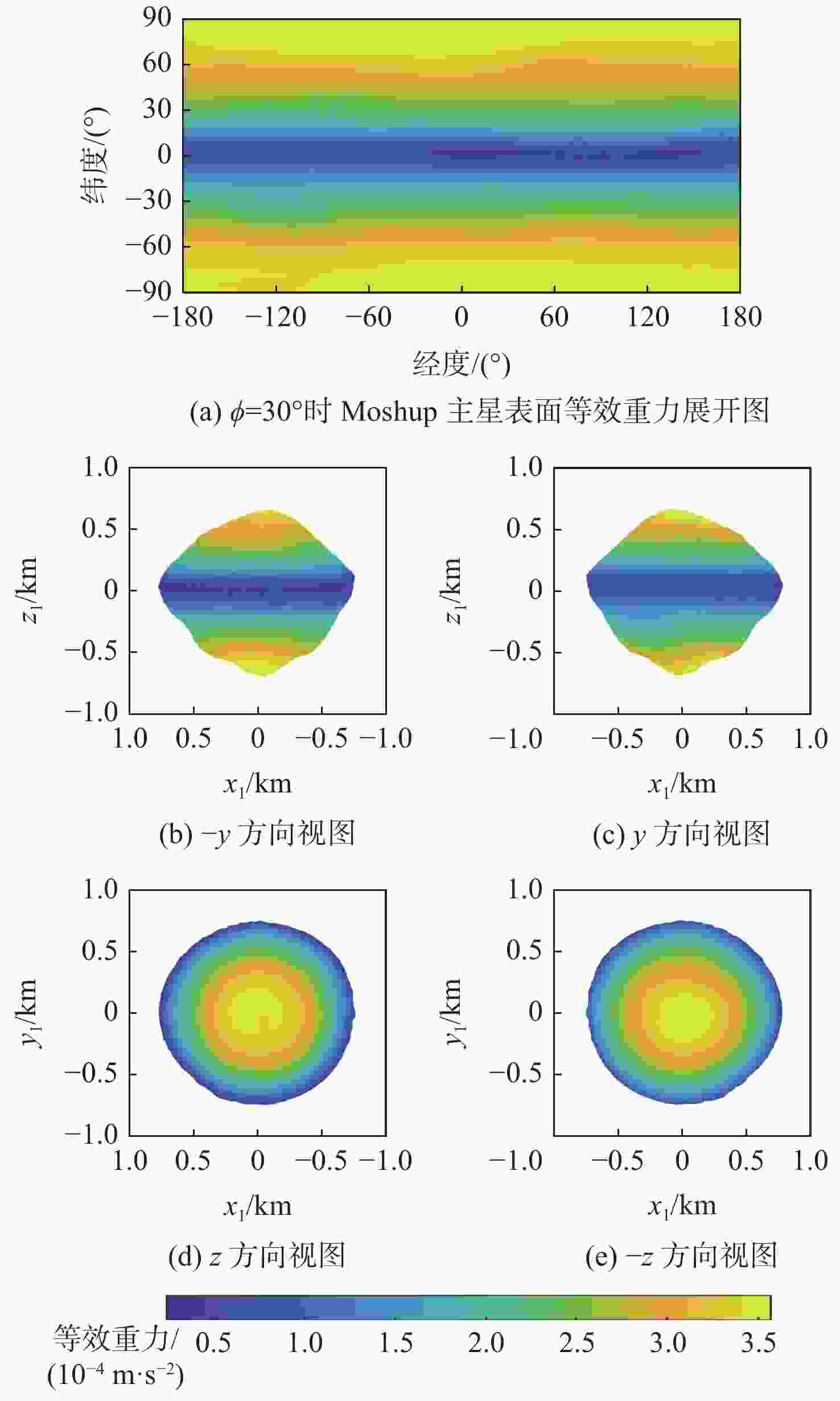
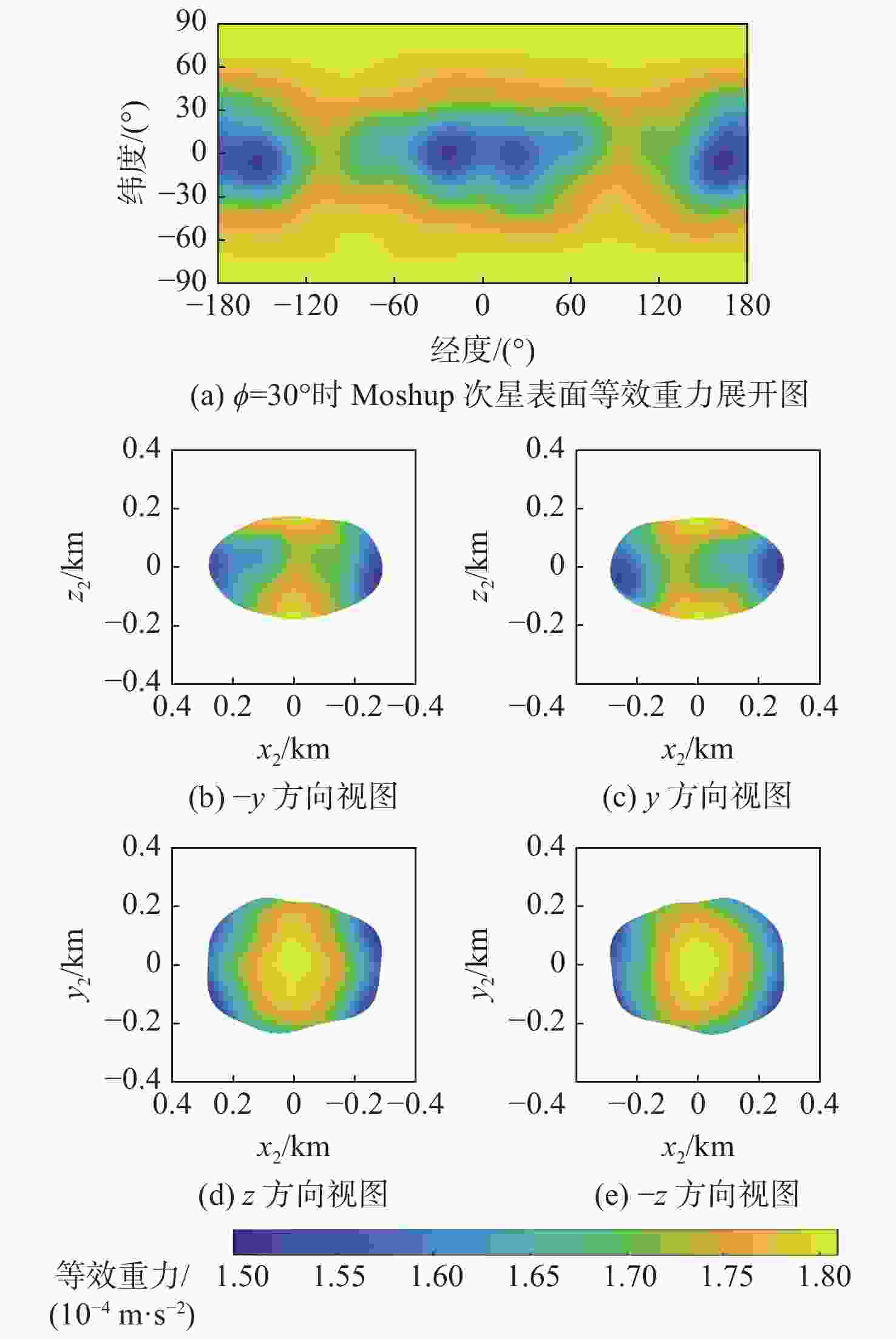
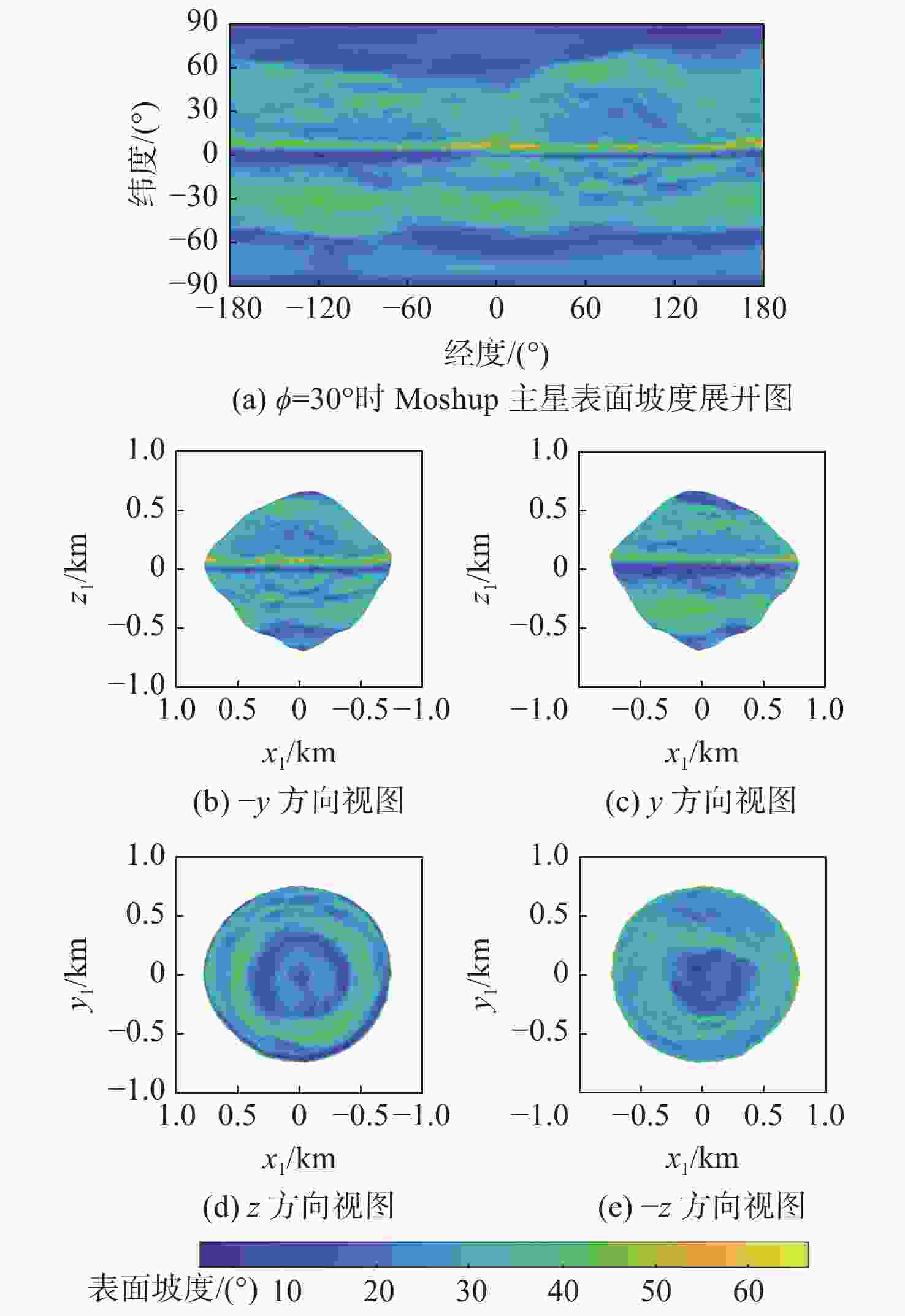
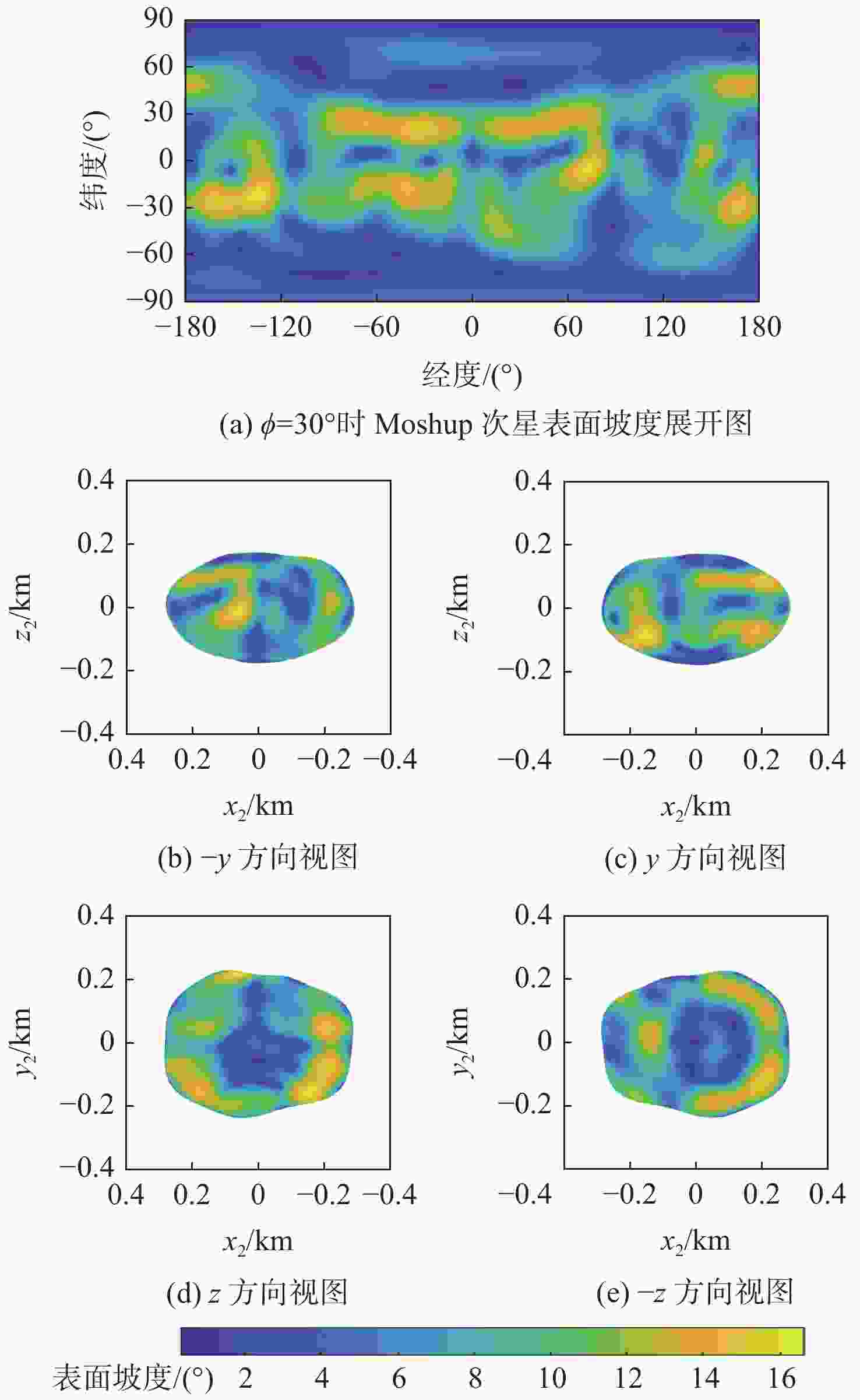
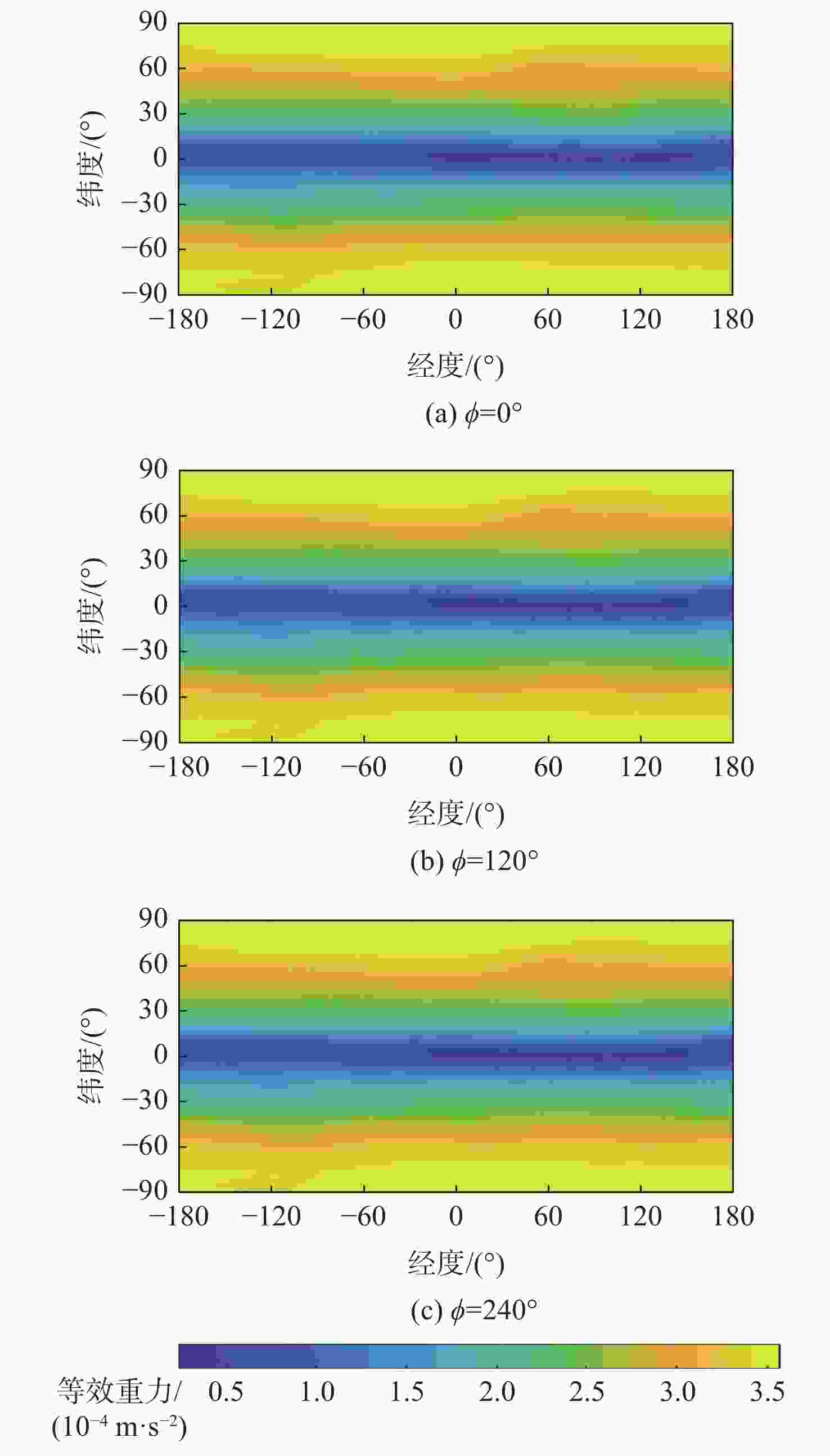
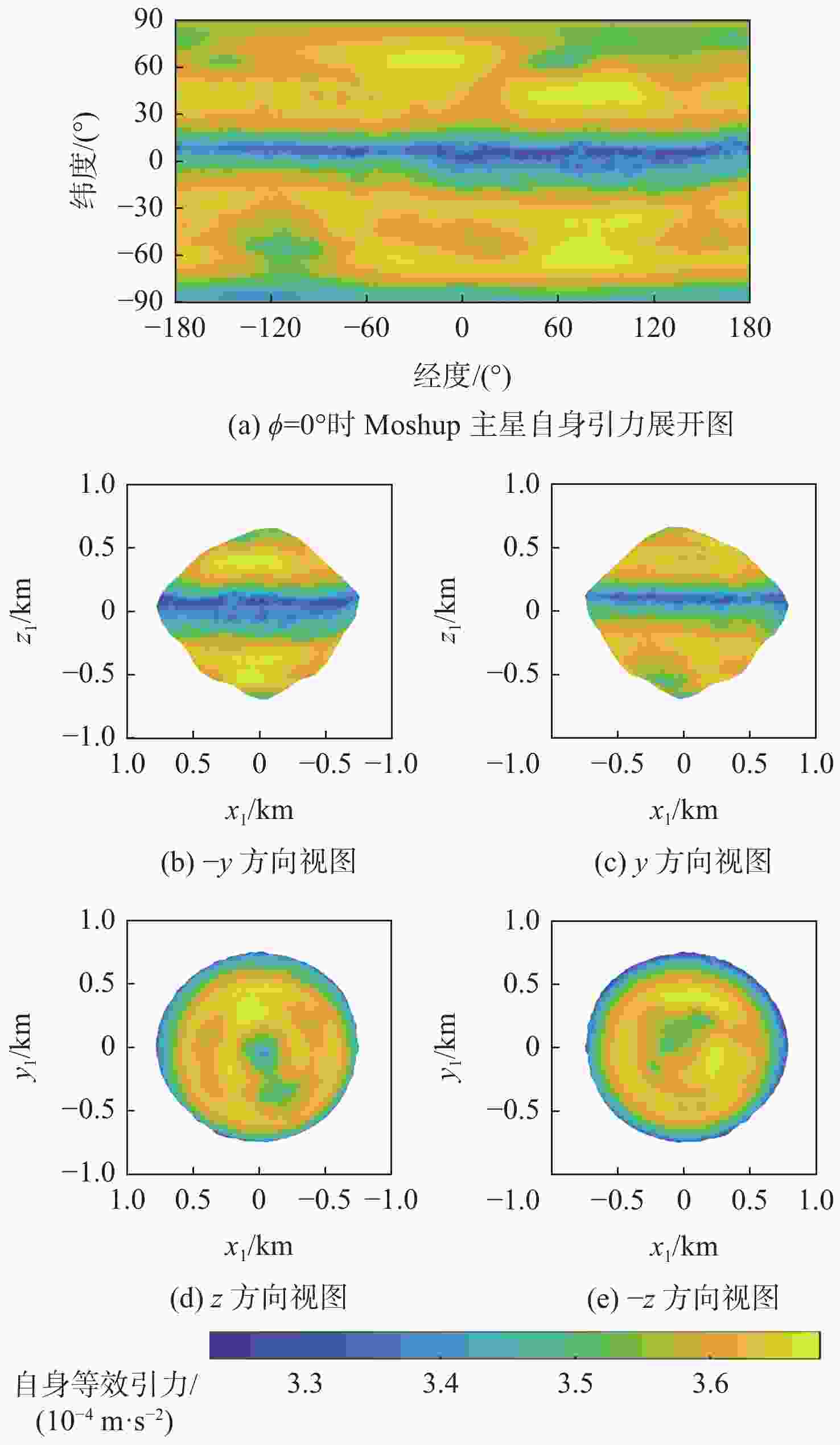
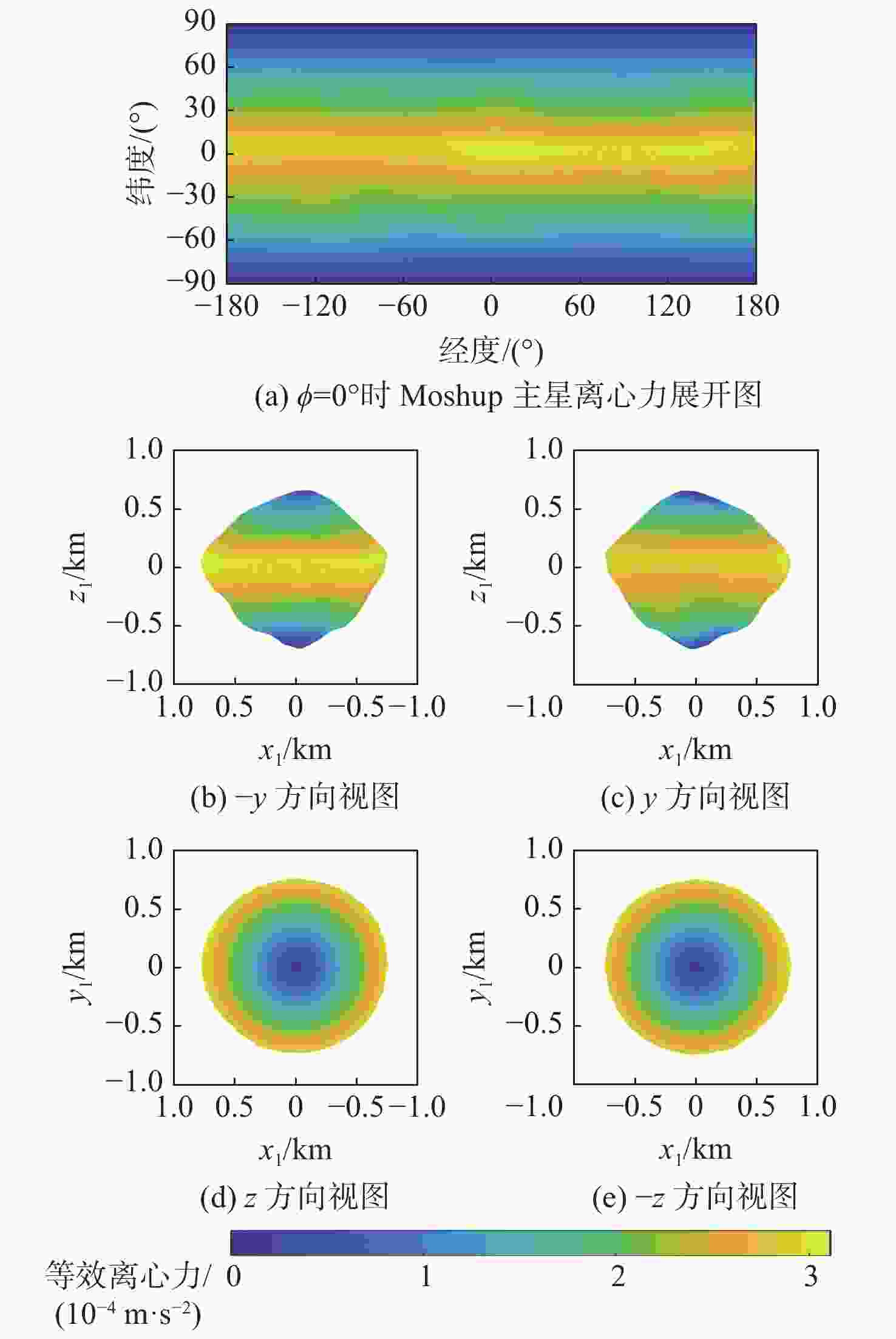
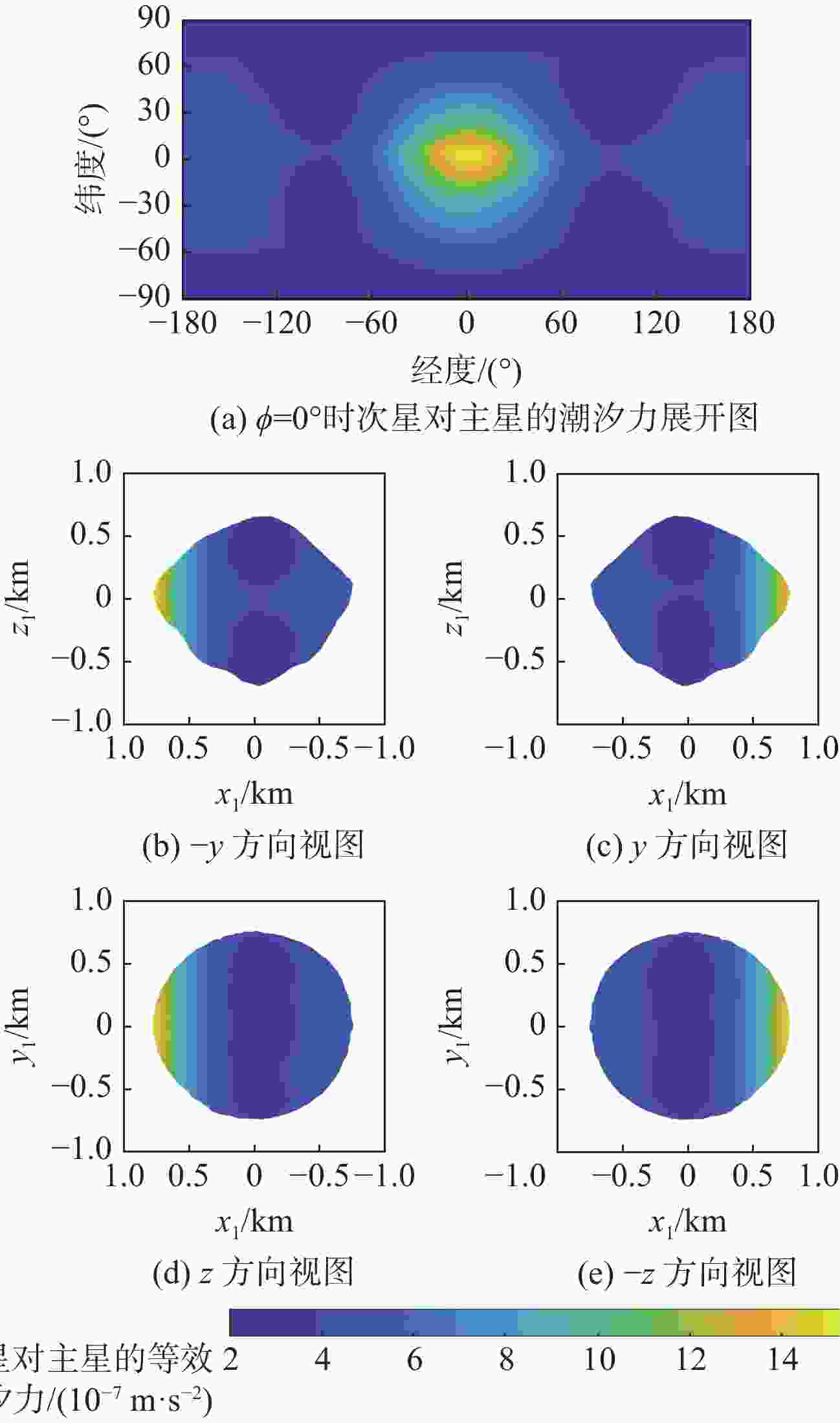
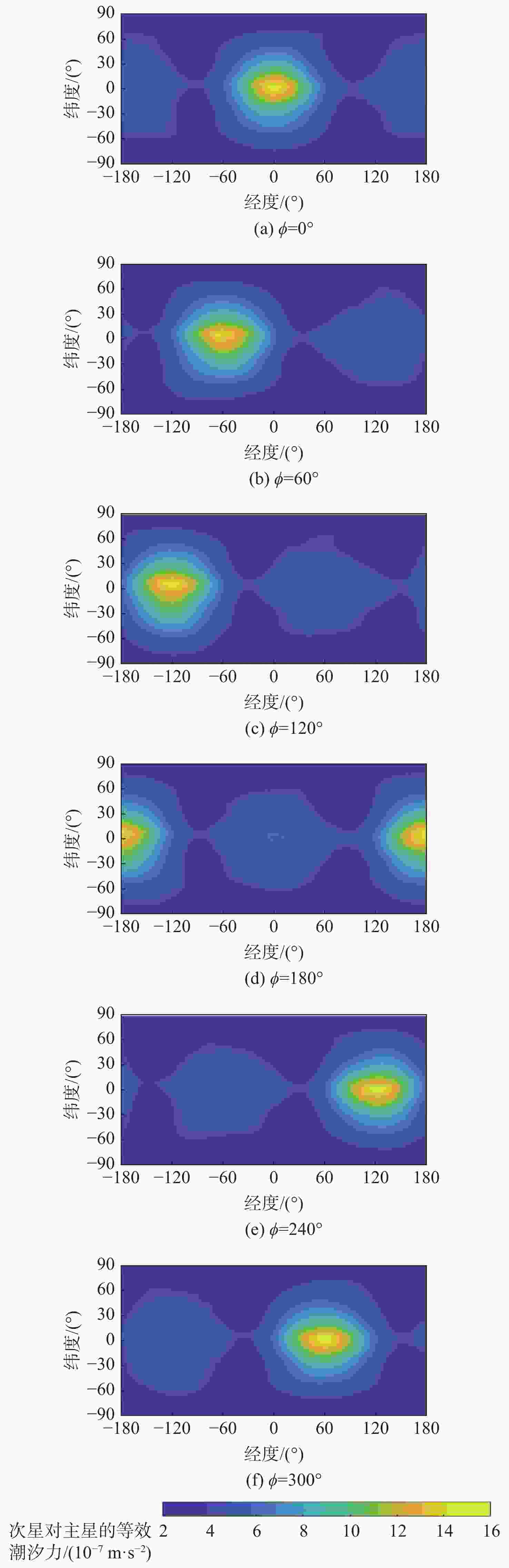
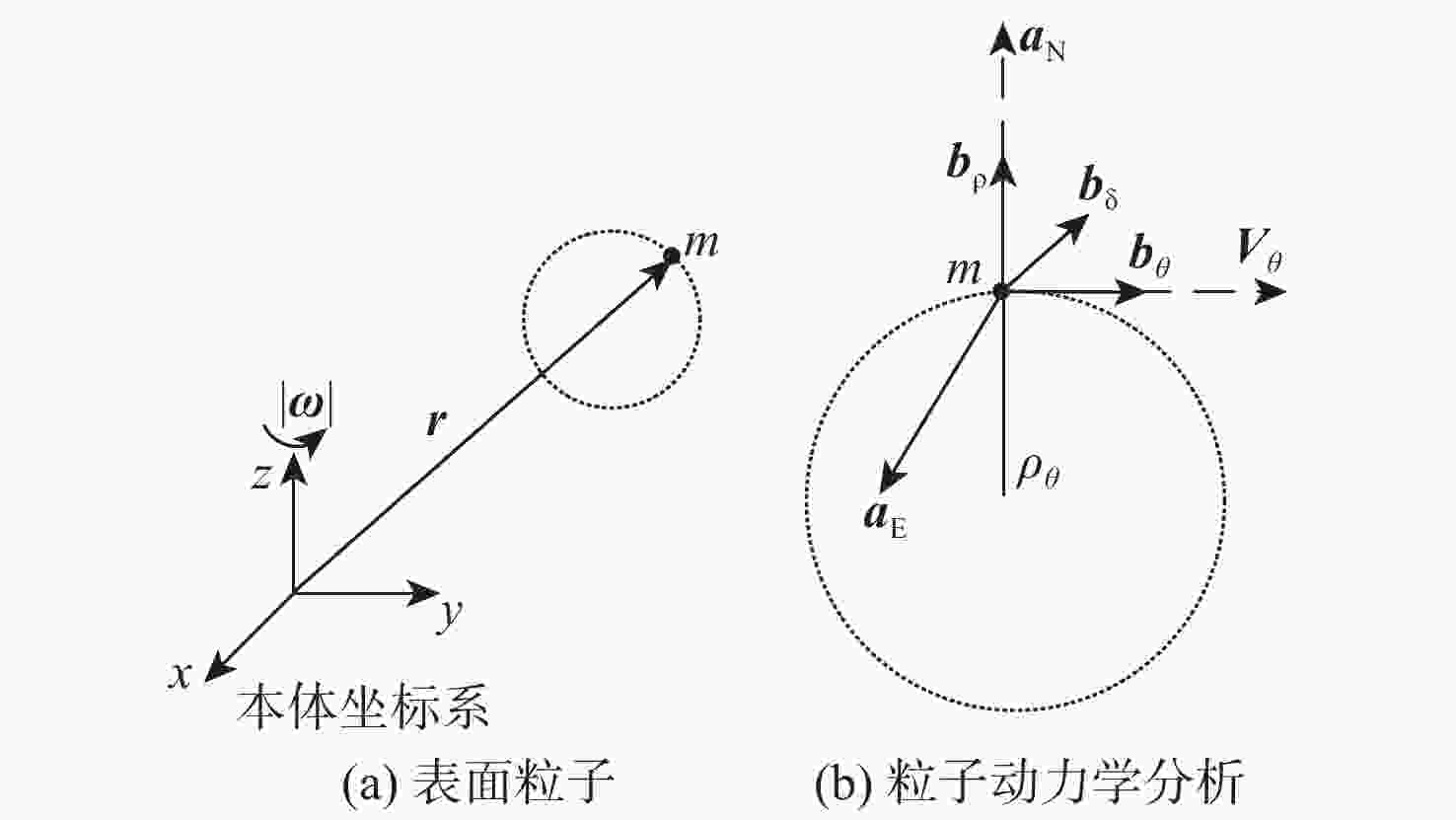
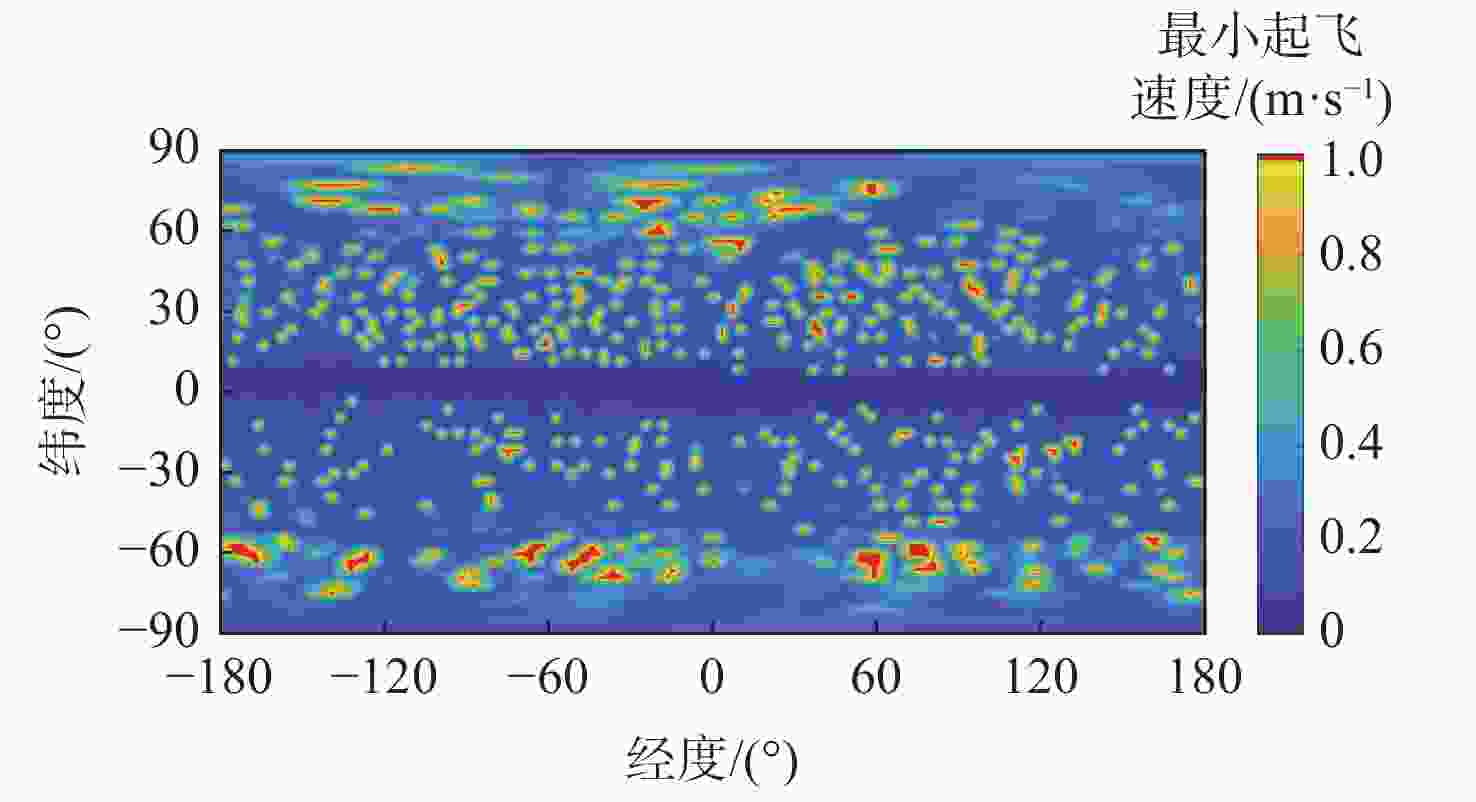
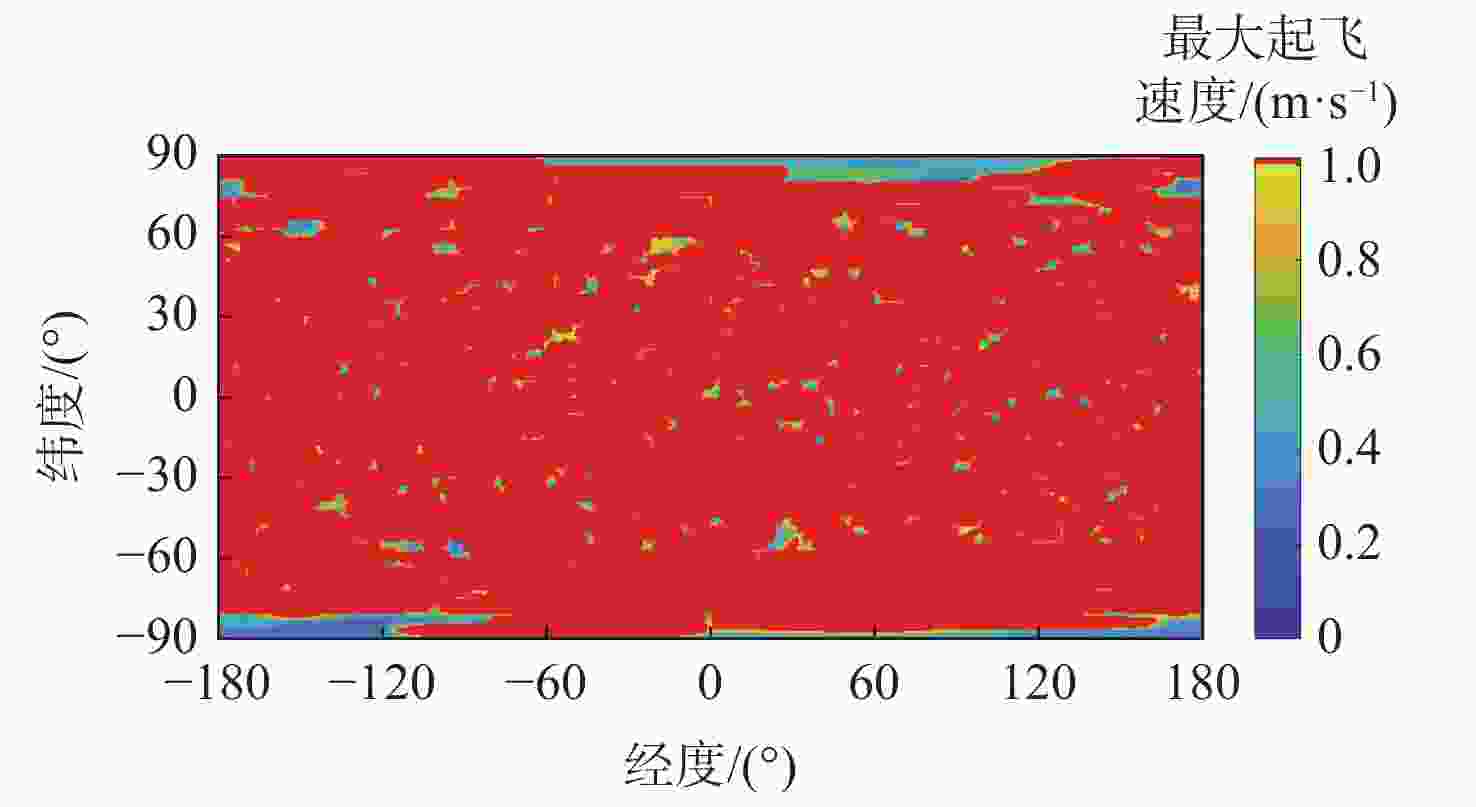
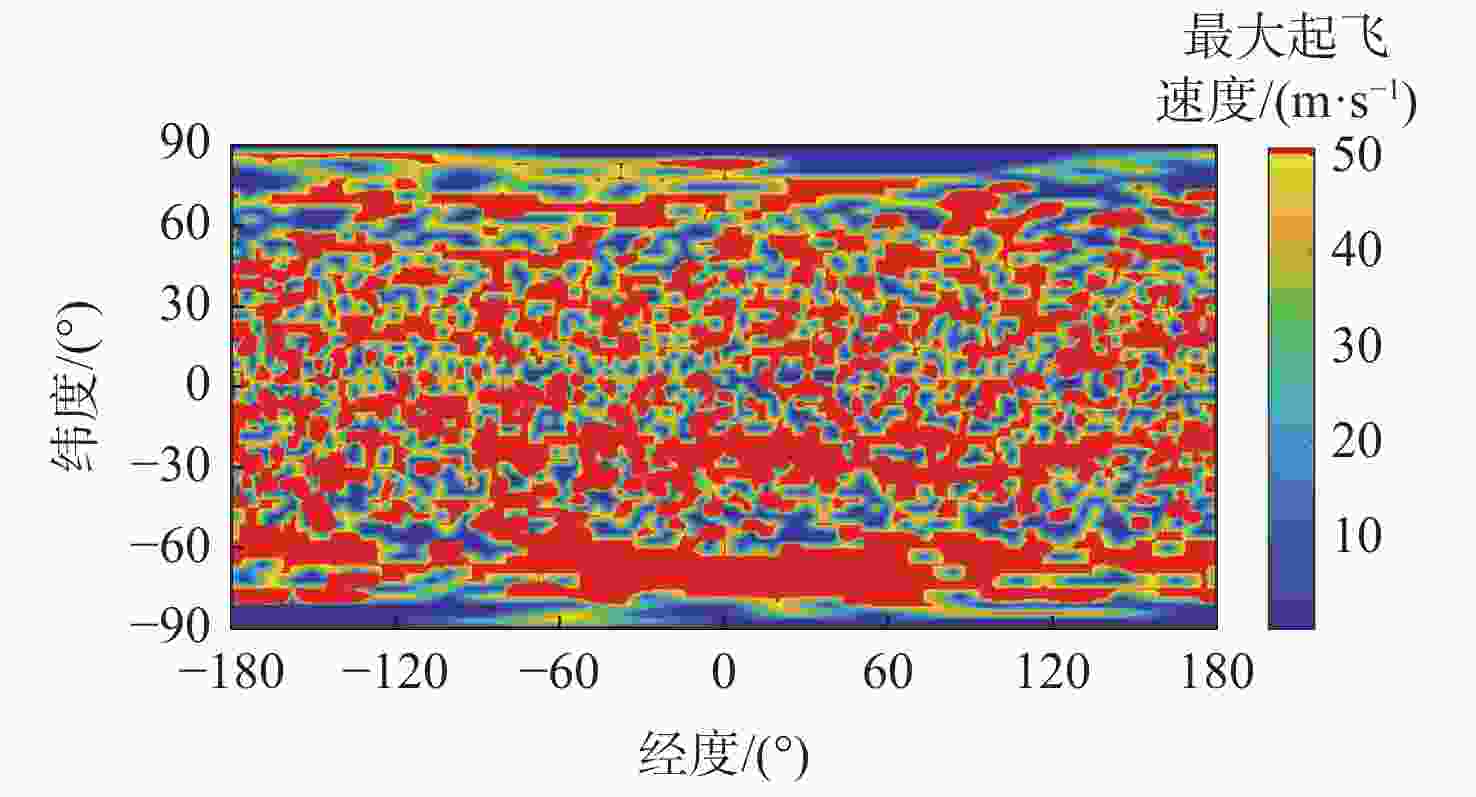
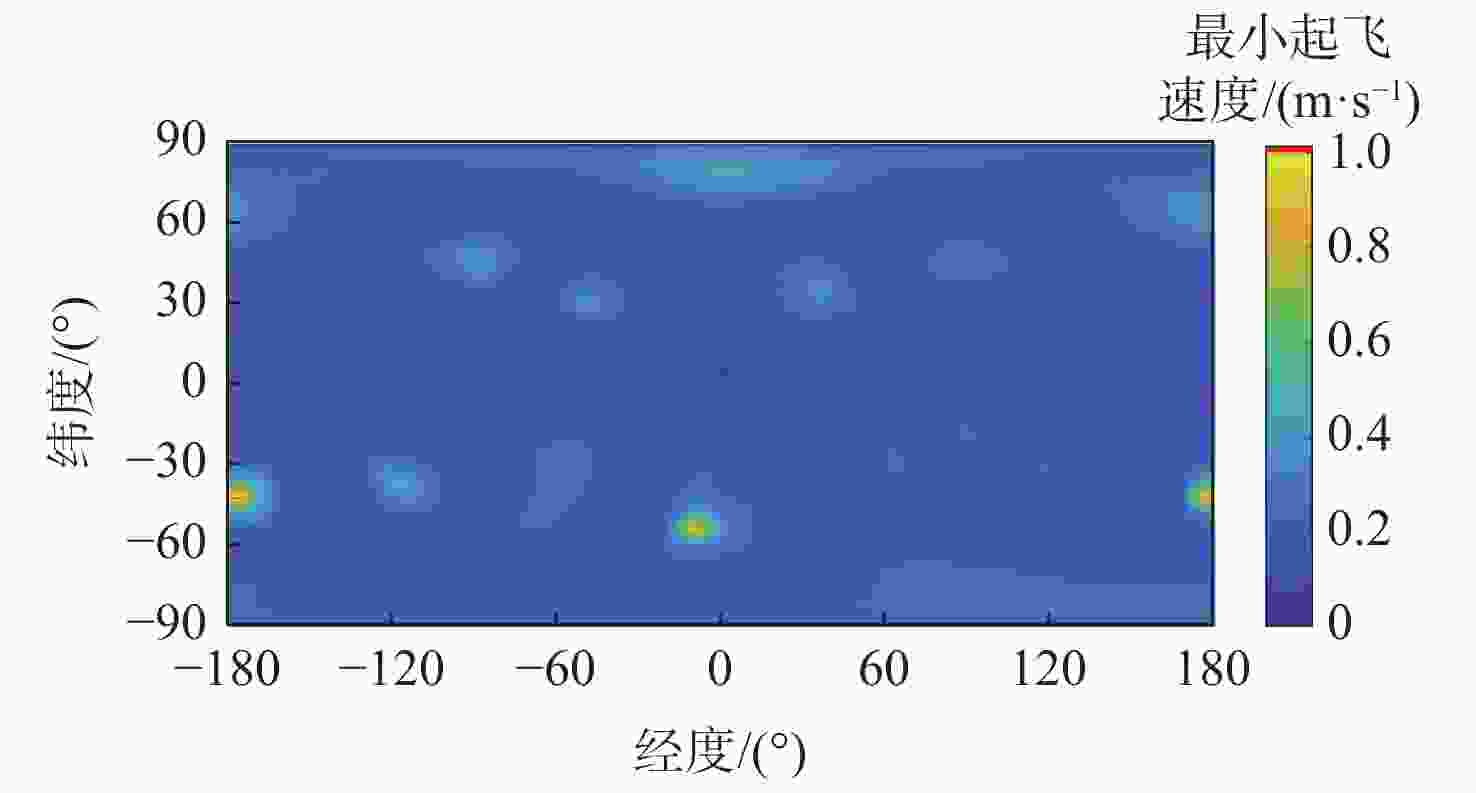
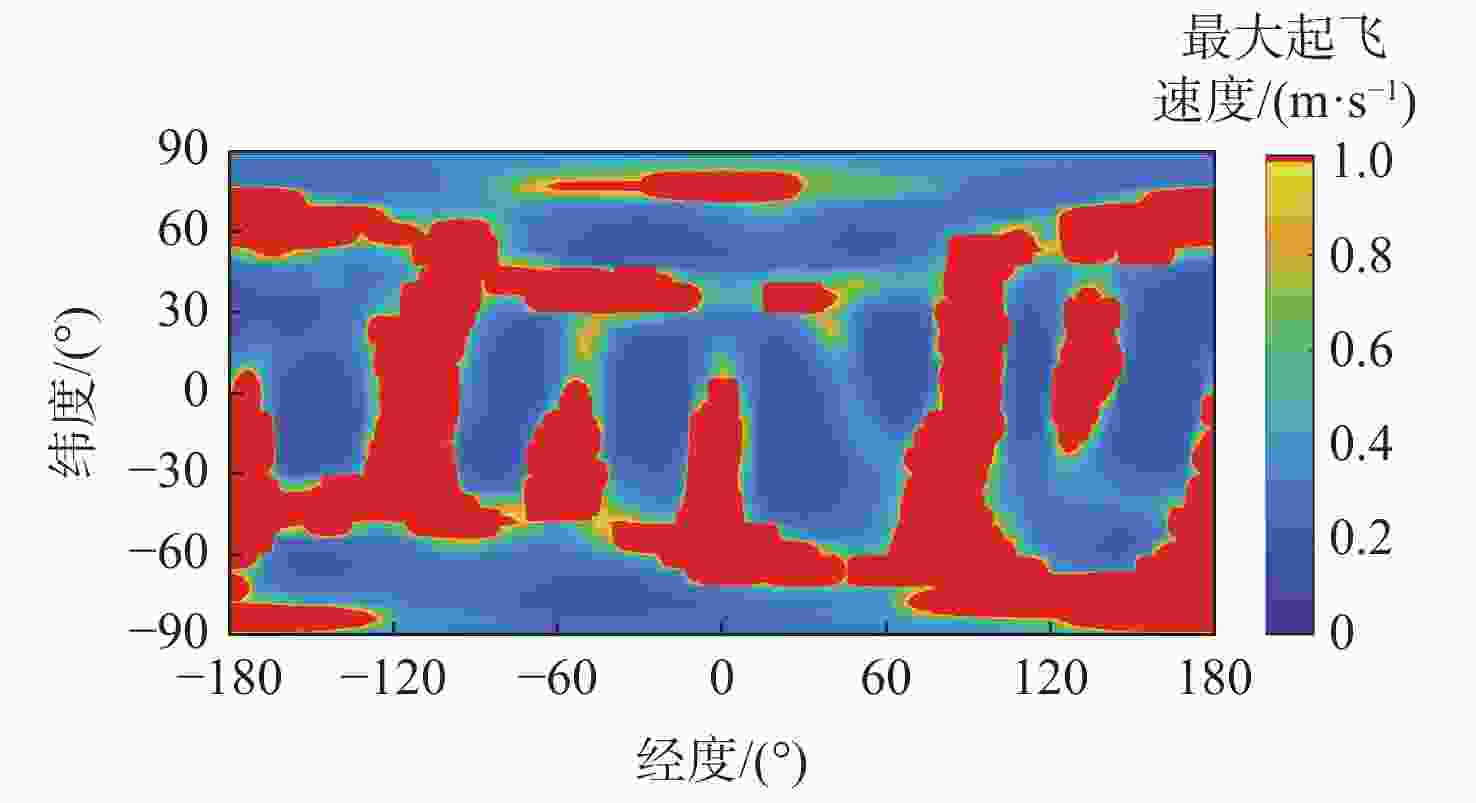
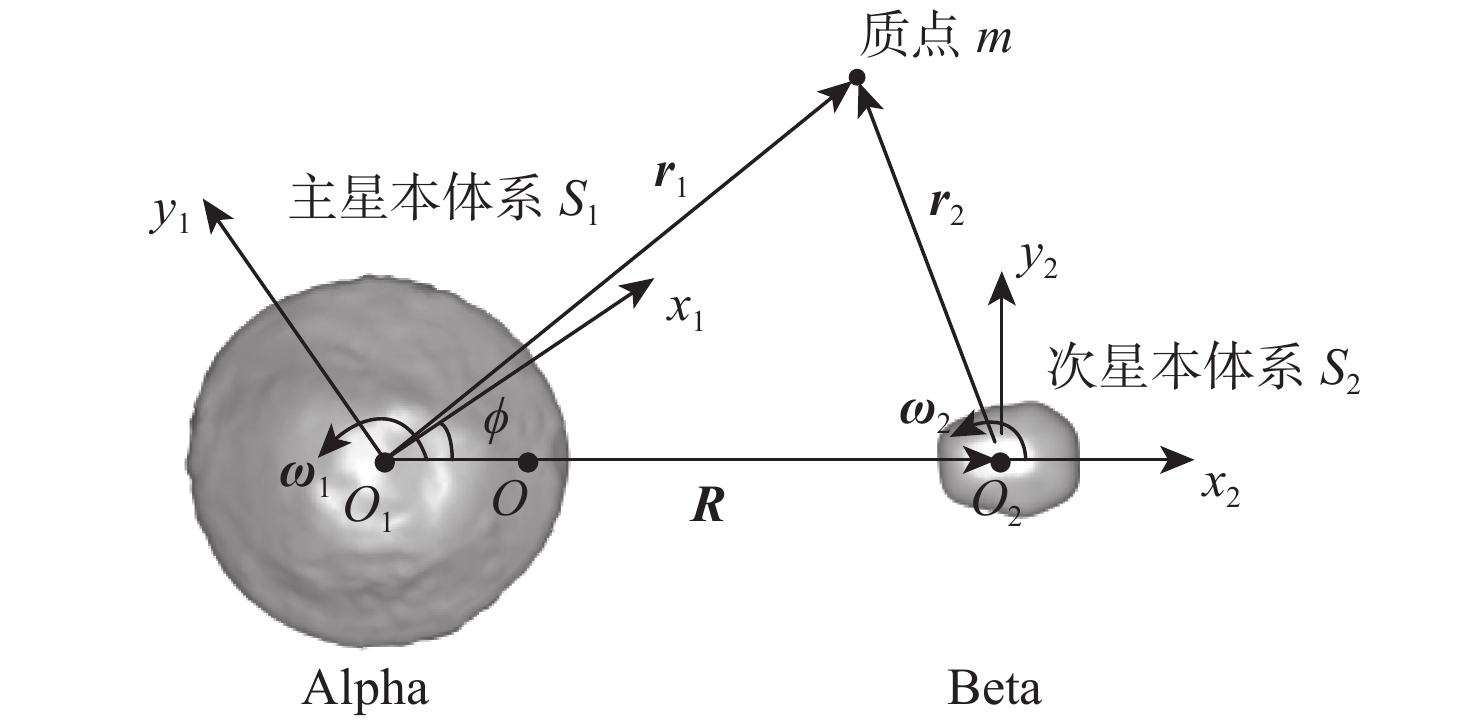
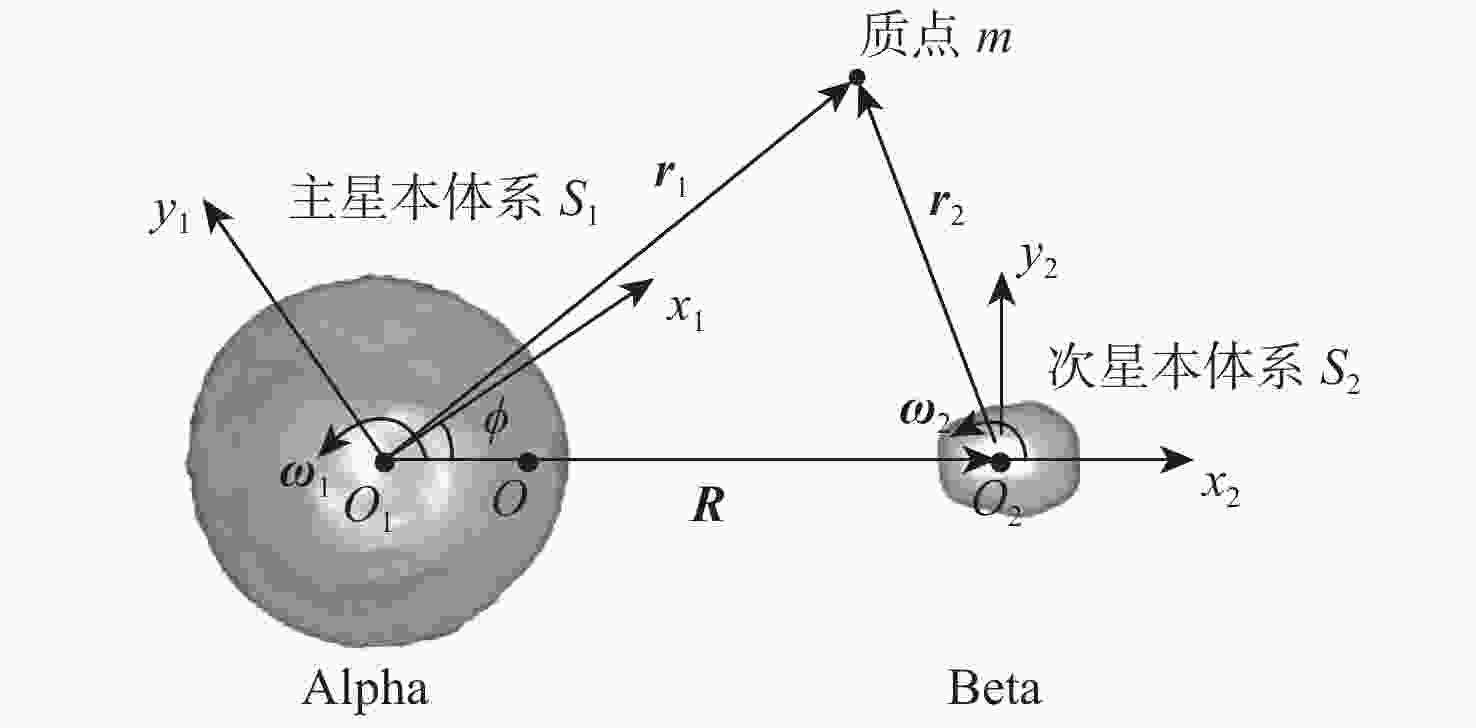
双小行星系统在太阳系中普遍存在，具有独特的探测价值，揭示其表面动力学环境是实现表面巡游探测的关键。相比于单小行星，双星系统成员间的摄动作用对表面动力学环境存在影响，需要加以专门的分析和研究。以近地双小行星系统(66391) Moshup为例，主、次星均采用多面体引力场模型，通过推导质点在主、次星表面附近的动力学方程，计算出主、次星的表面等效重力和表面坡度，以及表面各点处的最小和最大起飞速度，分析分布规律和成因，特别关注次星对高速旋转主星的周期性潮汐力的影响。在此研究结果的基础上，针对主星和次星分析适合探测器着陆和表面巡游的区域。结果表明：由于旋转离心力的影响，主、次星表面的等效重力分布有随纬度减小而降低的趋势，而坡度主要与局部地形相关，主星的北极高纬度区域和次星南北纬80°以上的区域坡度小，且等效重力较大，适合作为探测器的着陆点或开展表面巡游；次星潮汐力对主星表面重力存在周期性影响；主星表面大部分区域的最小起飞速度小于0.3 m/s，次星表面大部分区域的最小起飞速度在0.10～0.25 m/s之间。由于自转影响，主、次星的最小起飞速度方向几乎全部朝东。
Abstract:The binary asteroids are quite common in the solar system and are of unique scientific value. Studying the surface dynamical environment is the key to enabling surface roving exploration. The surface dynamical environment of the primary and secondary asteroid may be significantly affected by disturbances between them as compared to a single asteroid. In this study, the near-Earth binary asteroid system (66391) Moshup is taken as an example for the surface dynamical environment investigation. The polyhedral gravitational field models of the primary and secondary are adopted to establish the dynamical model of a point mass near the asteroid surface. The surface equivalent gravity and slope of the primary and secondary, as well as the minimum and maximum lift-off speeds, are calculated, and their distributions on the surface are analyzed. Much attention is focused on the periodical tidal effect of the secondary on the surface dynamical environment of the primary. Suitable areas on the primary and secondary for landing and roving are analyzed. Results show that the rotational centrifugal force causes the equivalent gravity to tend to decrease with latitude, and the slope is mostly dependent on the local terrain. The regions near the north pole of the primary and above the latitude of 80° of the secondary have small slopes and large equivalent gravity and are suitable for landing or roving. The tidal effect of the secondary has a periodic impact on the surface gravity of the primary. The minimum lift-off speeds in most areas of the primary surface are less than 0.3 m/s, while those in most areas of the secondary surface are between 0.10 m/s to 0.25 m/s. Due to the asteroid's rotation, almost all the directions of the minimum lift-off speeds are eastward.
-
图 11 次星对主星潮汐力的周期图像
Figure 11. Periodic image of tidal force of the secondary against primary asteroid
图 13 $\phi = 30^\circ $时主星表面最小起飞速度
Figure 13. Minimum lift-off velocity on primary asteroid surface when $\phi = 30^\circ $
图 14 $\phi = 30^\circ $时主星表面最大起飞速度
Figure 14. Maximum lift-off velocity on primary asteroid surface when $\phi = 30^\circ $
图 15 不可起飞速度为50 m/s时主星表面最大起飞速度
Figure 15. Maximum lift-off velocity on primary asteroid surface when upper limit lift-off velocity is 50 m/s
图 16 $\phi = 30^\circ $时次星表面最小起飞速度
Figure 16. Minimum lift-off velocity on secondary asteroid surface when $\phi = 30^\circ $
图 17 $\phi = 30^\circ $时次星表面最大起飞速度
Figure 17. Maximum lift-off velocity on secondary asteroid surface when $\phi = 30^\circ $
表 1 双小行星系统(66391) Moshup的基本参数
Table 1. Basic parameters of the binary asteroid (66391) Moshup
行星 质量/
(1012 kg)密度/
(kg·m−3)自转周期/h 尺寸/km 双星距离/km 主星 2.353 1970 2.7645 1.532×1.495×1.347 2.54 次星 0.135 2810 17.4223 0.571×0.463×0.349 2.54 
下载: 导出CSV
-
[1] MARGOT J L, NOLAN M C, BENNER L A M, et al. Binary asteroids in the near-Earth object population[J]. Science, 2002, 296(5572): 1445-1448. doi: 10.1126/science.1072094 [2] SHI Y, WANG Y, XU S J. Equilibrium points and associated periodic orbits in the gravity of binary asteroid systems: (66391) 1999 KW4 as an example[J]. Celestial Mechanics and Dynamical Astronomy, 2018, 130(4): 32-36. [3] WERNER R A. The gravitational potential of a homogeneous polyhedron or don’t cut corners[J]. Celestial Mechanics and Dynamical Astronomy, 1994, 59: 253-278. [4] 张振江, 崔祜涛, 任高峰. 不规则形状小行星引力环境建模及球谐系数求取方法[J]. 航天器环境工程, 2010, 27(3): 383-388. doi: 10.3969/j.issn.1673-1379.2010.03.024ZHANG Z J, CUI H T, REN G F. Modeling of gravitational environment of irregular shaped asteroids and methods for obtaining spherical harmonic coefficients[J]. Spacecraft Environment Engineering, 2010, 27(3): 383-388(in Chinese). doi: 10.3969/j.issn.1673-1379.2010.03.024 [5] LIANG C H, YUN Z. Methods for computing the gravitational potential of a small solar body[J]. Applied Mechanics and Materials, 2012, 241-244: 2787-2791. [6] SAWAI S, KAWAGUCHI J, OGASAWARA M, et al. Development of a target marker for landing on asteroids[J]. Journal of Spacecraft and Rockets, 2001, 38(4): 601-608. doi: 10.2514/2.3723 [7] LIU X D, BAOYIN H X, MA X R. Dynamics of surface motion on a rotating massive homogeneous body[J]. Science China Physics, Mechanics and Astronomy, 2013, 56(4): 818-829. doi: 10.1007/s11433-013-5044-2 [8] YU Y, BAOYIN H X. Modeling of migrating grains on asteroid’s surface[J]. Astrophysics and Space Science, 2015, 355(1): 43-56. doi: 10.1007/s10509-014-2140-3 [9] JIANG Y, ZHANG Y, BAOYIN H X. Surface motion relative to the irregular celestial bodies[J]. Planetary and Space Science, 2016, 127: 33-43. doi: 10.1016/j.pss.2016.04.007 [10] FERRARI F, TANGA P. The role of fragment shapes in the simulations of asteroids as gravitational aggregates[J]. Icarus, 2020, 350: 113871. doi: 10.1016/j.icarus.2020.113871 [11] LIU X W, YANG H W, LI S, et al. Lift-off velocity on the surface of a binary asteroid system[J]. Acta Astronautica, 2020, 170: 302-319. doi: 10.1016/j.actaastro.2020.02.006 [12] ZHANG Y L, LI J F, ZENG X Y. The dynamical environments analysis of surface particles for different shaped asteroids[J]. Advances in Space Research, 2021, 67(10): 3328-3342. doi: 10.1016/j.asr.2021.02.013 [13] WERNER R A, SCHEERES D J. Exterior gravitation of a polyhedron derived and compared with harmonic and mascon gravitation representations of asteroid 4769 Castalia[J]. Celestial Mechanics and Dynamical Astronomy, 1996, 65(3): 313-344. [14] VAN WAL S, SCHEERES D J. The lift-off velocity on the surface of an arbitrary body[J]. Celestial Mechanics and Dynamical Astronomy, 2016, 125(1): 1-31. doi: 10.1007/s10569-016-9671-6 [15] WANG Y, WU X J. Analysis of phobos’ dynamical environment considering effects of ephemerides and physical libration[J]. Monthly Notices of the Royal Astronomical Society, 2020, 497(1): 416-434. doi: 10.1093/mnras/staa1948 [16] HAMANN B. Curvature approximation for triangulated surfaces[C]//Proceedings of the Geometric Modelling. Berlin: Springer, 1993, 8: 139-153. -
下载:
点击查看大图
计量
- 文章访问数: 41
- HTML全文浏览量: 10
- PDF下载量: 4
- 被引次数: 0
