岸基BDS-R海面测高及其观测值加权方法

侯金华; 贺凯飞; 高凡; 储倜; 吴宇

doi:10.13700/j.bh.1001-5965.2022.0360

岸基BDS-R海面测高及其观测值加权方法

doi: 10.13700/j.bh.1001-5965.2022.0360

侯金华¹,
贺凯飞^1, ,,
高凡^{2, 3},
储倜¹,
吴宇¹

1.
中国石油大学（华东）海洋与空间信息学院，青岛 266580
2.
山东大学空间科学研究院，威海 264209
3.
山东大学空间科学与物理学院，威海 264209

基金项目: 国家自然科学基金(42174021)；山东省自然科学基金(ZR2021MD060)

详细信息

通讯作者:
E-mail：kfhe@upc.edu.cn

中图分类号: V221⁺.3；TB553
计量
- 文章访问数: 769
- HTML全文浏览量: 125
- PDF下载量: 17
- 被引次数: 0
出版历程
- 收稿日期: 2022-05-16
- 录用日期: 2022-08-29
- 网络出版日期: 2022-09-19
- 整期出版日期: 2024-03-27

Shore-based BDS-R sea surface altimetry and weighting method of its observed values

HOU Jinhua¹,
HE Kaifei^{1
, ,},
GAO Fan^{2, 3},
CHU Ti¹,
WU Yu¹

1.
College of Oceanography and Space Informatics，China University of Petroleum (East China)，Qingdao 266580，China
2.
Institute of Space Science，Shandong University，Weihai 264209，China
3.
School of Space Science and Physics，Shandong University，Weihai 264209，China

Funds: National Natural Science Foundation of China (42174021); Shandong Provincial Natural Science Foundation (ZR2021MD060)

More Information

Corresponding author: E-mail：kfhe@upc.edu.cn

摘要

摘要:
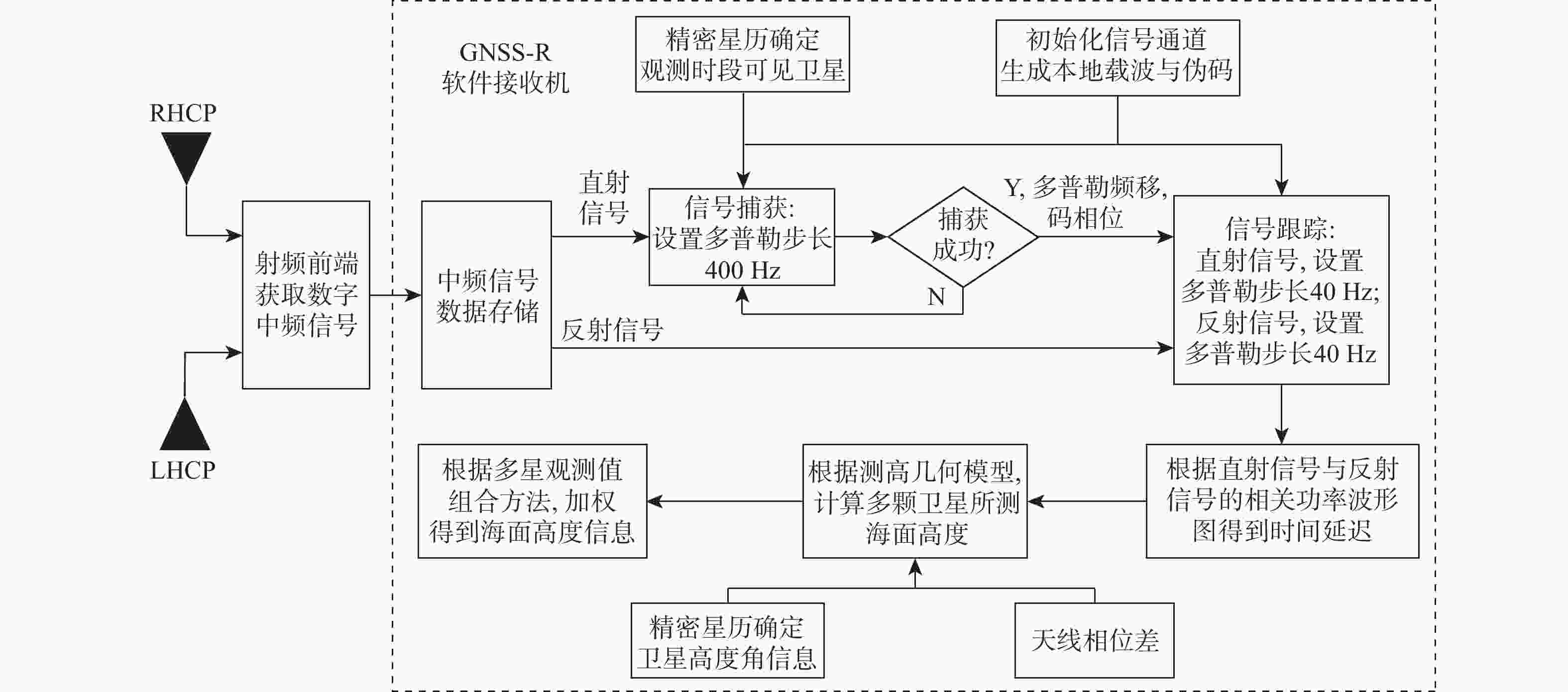
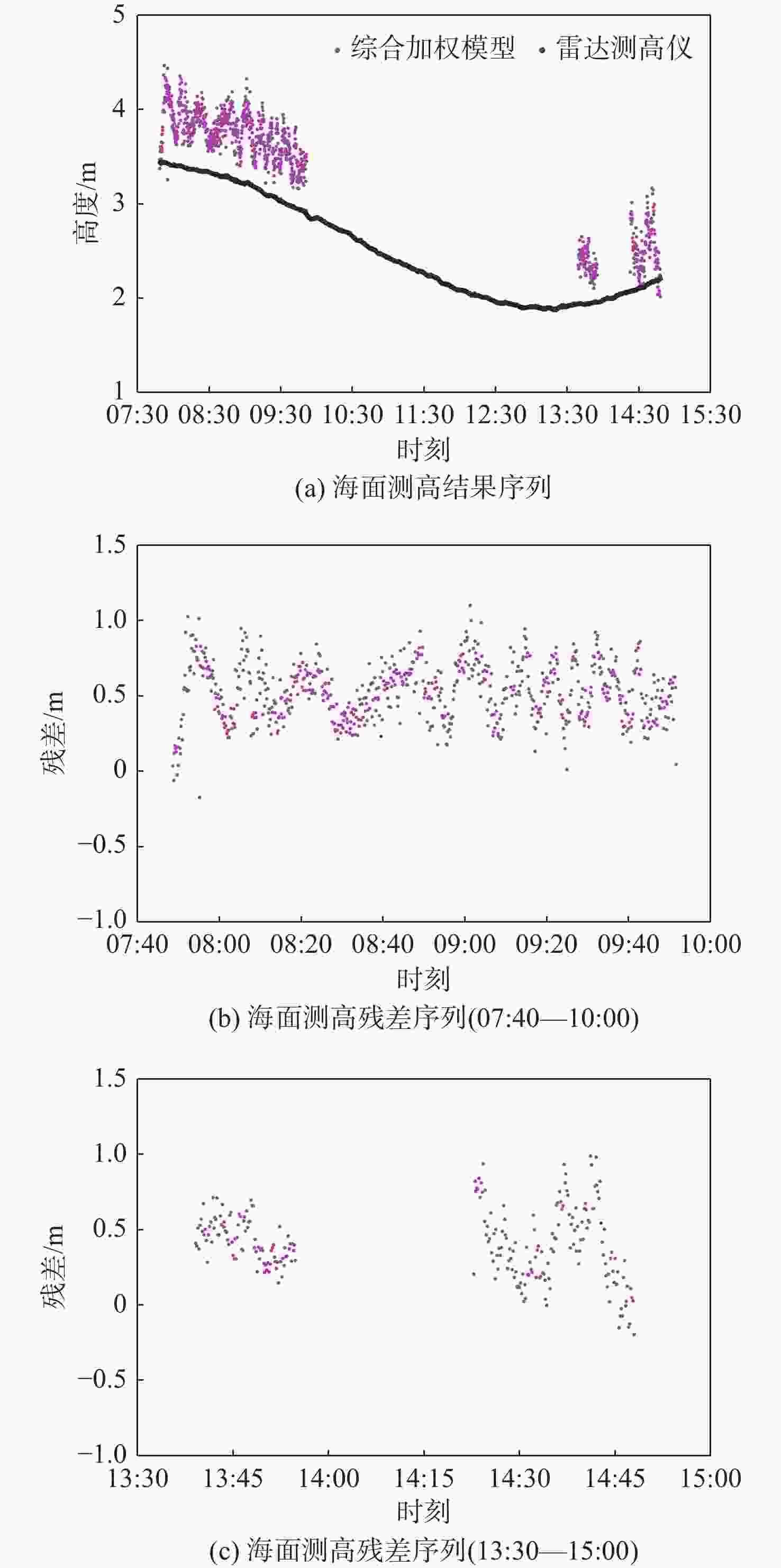
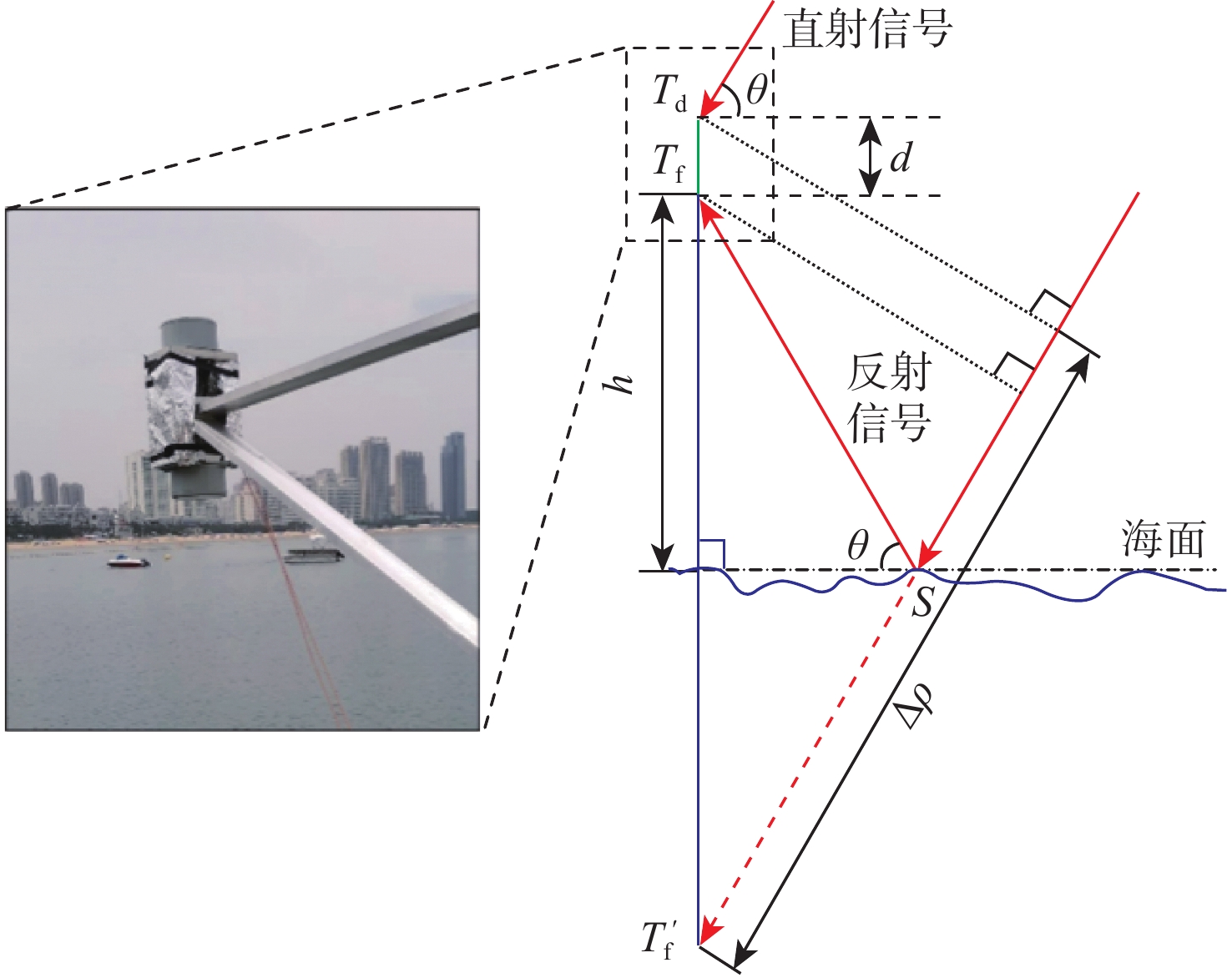
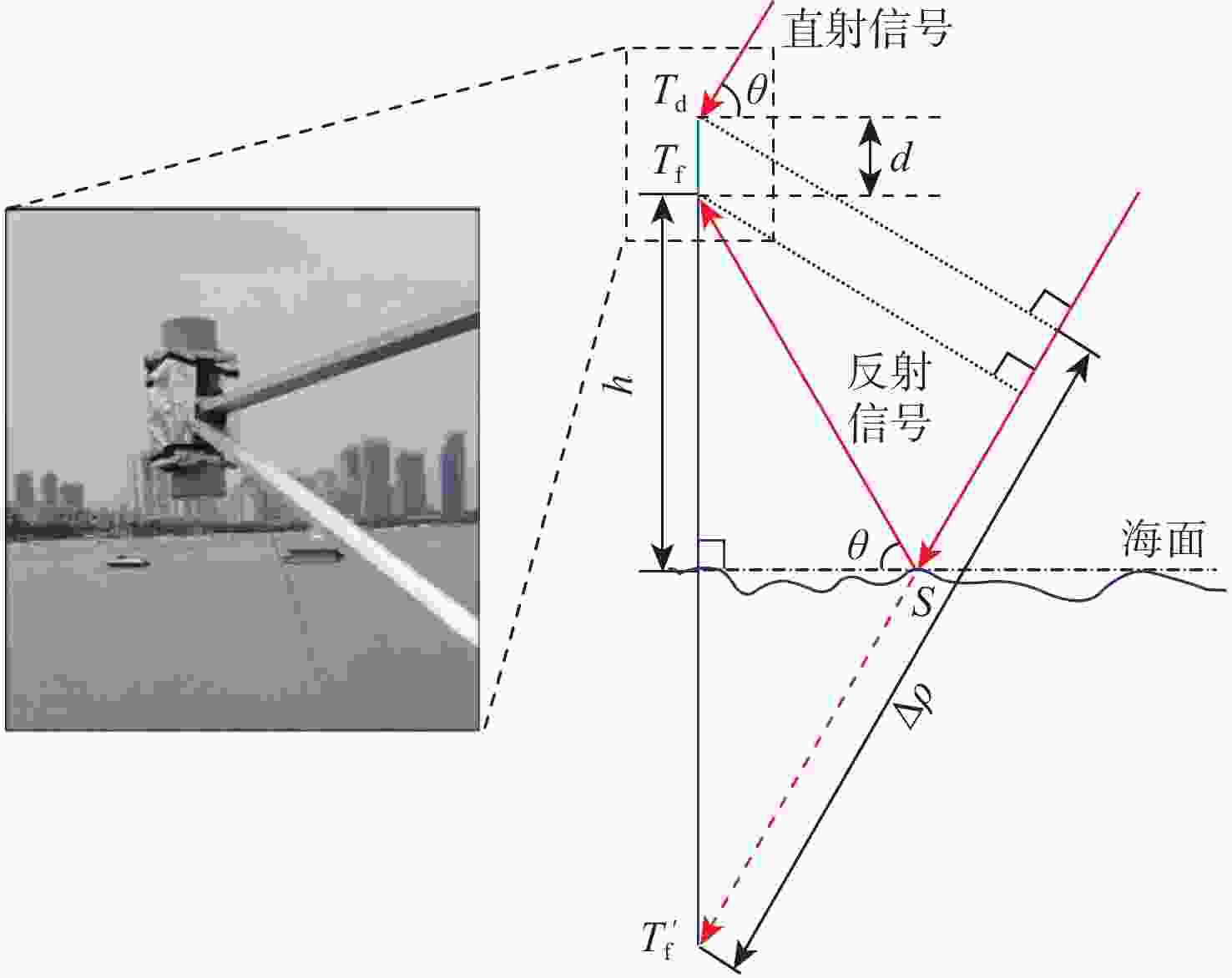
随着北斗三号卫星导航系统(BDS-3)的全球组网完成，其反射信号在全球导航卫星系统反射测量(GNSS-R) 海面测高领域的应用也更加广泛。为研究BDS-3 B1C反射信号码延迟海面测高性能，以及多星测高数据组合方法，进行了基于B1C码信号的双天线岸基北斗卫星导航系统反射测量(BDS-R)码延迟海面测高实验。利用自主研发的GNSS-R测高软件接收机对实验数据进行事后处理，将测高结果与岸基同步观测的雷达测高仪所测海面高度值进行对比分析，并基于反射信号信噪比(SNR)和卫星高度角加权的方法对多星测高观测值进行加权计算，评定BDS-R海面测高精度。结果表明：自主研发的GNSS-R测高软件接收机可用于海面测高，基于B1C码信号的BDS-R海面测高精度有达到分米级的可能性；根据10 s观测数据平滑可以得到，单颗卫星B1C码信号最优测高结果的均方根误差(RMSE)为0.634 m，平均绝对误差(MAE)为0.507 m，多星测高观测值加权组合最优结果的均方根误差为0.538 m，平均绝对误差为0.500 m，明显优于单星观测精度，最大可提升70%，最小可提升17%；针对同一信号多星GNSS-R测高数据加权方法，应用综合考虑卫星高度角和反射信号信噪比的加权模型优于其他加权模型，测高精度分别比信噪比分段模型、正弦函数模型、指数函数模型、等权模型提升9.4%、9.5%、20.5%、35.2%。
- B1C /
- 北斗卫星导航系统反射测量 /
- 软件接收机 /
- 海面测高 /
- 加权模型
Abstract:
With the completion of the global networking of BeiDou-3 satellite navigation system (BDS-3), its reflected signals are more and more widely used in the field of global navigation satellite system-reflectometry (GNSS-R) sea surface altimetry. A dual antenna coastal BDS-reflectometry (BDS-R) sea surface altimetry experiment based on BDS-3 B1C reflected signal code-level delay and the combination method of multi-satellite altimetry observations was carried out in order to investigate the performance of sea surface altimetry based on these two factors. The independently developed GNSS-R altimetry software receiver is used for post-processing of the experimental data, and the experimental results and the sea surface height of the shore-based synchronous observation radar altimeter were compared and analyzed to evaluate the accuracy of BDS-R sea surface altimetry. Additionally, the multi-satellite altimetry readings are combined using a weighted technique based on the signal-to-noise ratio (SNR) of the reflected signal and satellite elevation. The results show that the independently developed GNSS-R software receiver can be used for sea surface altimetry, and it is possible that the precision of BDS-R sea surface measurement based on B1C code can reach decimeter level. According to the result of moving averages with 10 s,the root mean square error (RMSE) and mean absolute error (MAE) of single satellite sea surface altimetry are 0.634 m and 0.507 m respectively, and the RMSE and MAE of the weighted combination of multi-satellite observations are 0.538 m and 0.500 m respectively. The observation accuracy of the latter is obviously better than that of the former, and the maximum and minimum observation accuracy can be improved by 70% and 17% respectively. The weighted model with thorough consideration of satellite elevation angle and reflected signal SNR is superior to other weighted models for the same signal multi-satellite GNSS-R altimetry data weighting method,and its measurement accuracy is improved by 9.4%, 9.5%, 20.5%, 35.2% compared with SNR segment model, sine function model, exponential function model, and equal weight model, respectively.
- B1C /
- BeiDou satellite navigation system-reflectometry /
- software receiver /
- sea surface altimetry /
- weighted model

HTML全文

图 1 双天线岸基BDS-R码延迟测高几何模型

Figure 1. Geometric model of dual antenna shore-based BDS-R code delay altimetry

下载: 全尺寸图片幻灯片

图 2 B1C码信号导频分量自相关函数

Figure 2. Autocorrelation function of B1C code signal pilot component

下载: 全尺寸图片幻灯片

图 3 GNSS-R软件接收机海面测高流程

Figure 3. Flow chart of GNSS-R software receiver sea surface altimetry

下载: 全尺寸图片幻灯片

图 4 实验场地与实验设备

Figure 4. Experimental site and equipments

下载: 全尺寸图片幻灯片

图 5 C25卫星反射信号信噪比与测高残差变化

Figure 5. Change of SNR and altimetry residual of C25 satellite reflection signal

下载: 全尺寸图片幻灯片

图 6 观测时段BDS-3可见卫星高度角与天顶轨迹（北京时间）

Figure 6. Elevation and zenith trajectory of BDS-3 visible satellite during observation period (UTC+8)

下载: 全尺寸图片幻灯片

图 7 海面测高原始观测值

Figure 7. Sea surface altimetry raw observations

下载: 全尺寸图片幻灯片

图 8 卫星高度角对测高结果的影响

Figure 8. Effect of satellite elevation on altimetry results

下载: 全尺寸图片幻灯片

图 9 单颗卫星海面测高10 s平滑结果及残差

Figure 9. 10 s smoothing results of single satellite observations sea surface altimetry and residuals

下载: 全尺寸图片幻灯片

图 10 多星原始观测值加权组合海面测高结果

Figure 10. Weighted combined sea surface altimetry results of multi-satellite raw observations

下载: 全尺寸图片幻灯片

图 11 多星观测值加权组合10 s平滑测高结果及残差

Figure 11. Weighted combined 10 s smoothed altimetry results and residuals of multi-satellite observations

下载: 全尺寸图片幻灯片

表 1 B1C码信号结构

Table 1. Signal structure of B1C code

信号分量	载波频率/MHz	调制方式		相位关系/(°)	功率比	符号速率/(symbol·s⁻¹)
数据分量	1575.42	正弦BOC(1,1)		0	1/4	100
导频分量	1575.42	QMBOC(6,1,4/33)	正弦BOC(1,1)	90	29/44	0
导频分量	1575.42	QMBOC(6,1,4/33)	正弦BOC(6,1)	0	1/11	0

下载: 导出CSV

表 2 B1C码信号测距码参数

Table 2. B1C code signal ranging code parameters

信号分量	主码码型	主码码长	主码周期/ms	子码码型	子码码长	子码周期/ms
数据分量	Weil码截短	10230	10
导频分量	Weil码截短	10230	10	Weil码截短	1800	18000

下载: 导出CSV

表 3 B1C码信号码延迟海面测高精度

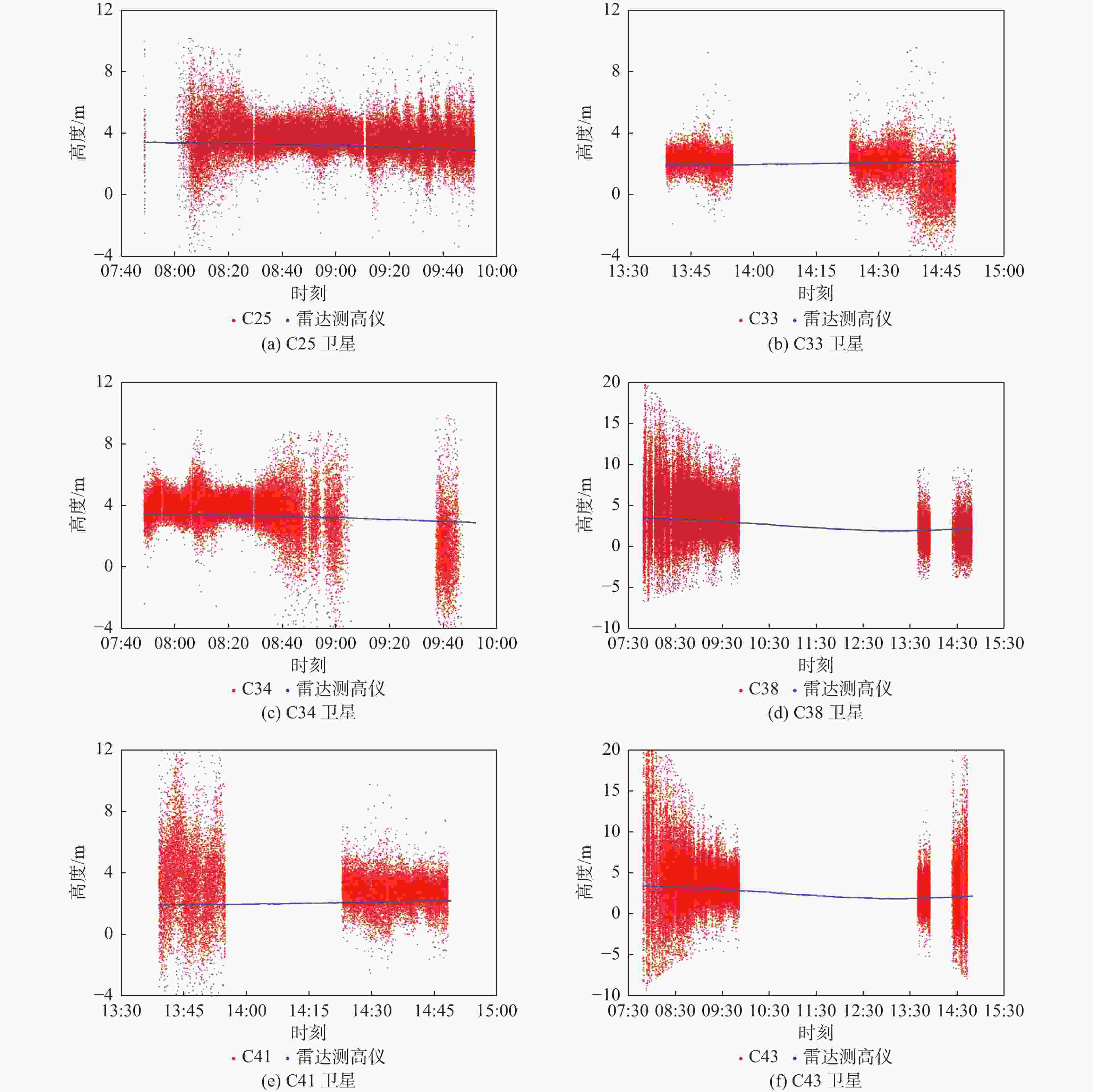
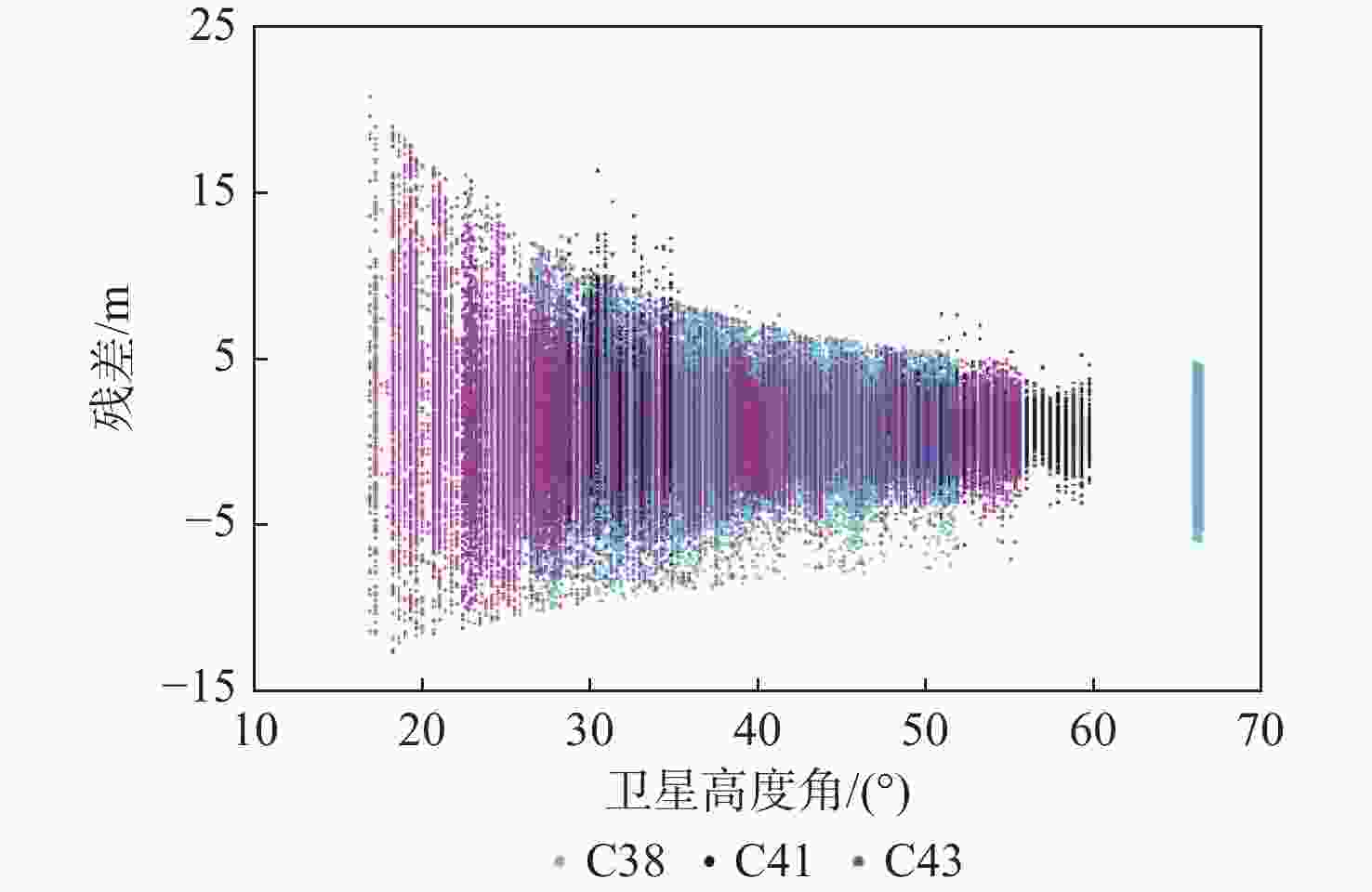
Table 3. Accuracy of code delay sea surface altimetry of B1C code signal

卫星编号	卫星轨道类型	均方根误差/m	标准差/m	平均绝对误差/m	最大误差/m	最小误差/m
C25	MEO	0.634	0.407	0.507	4.459	−0.848
C33	MEO	0.771	0.756	0.556	1.417	−2.181
C34	MEO	0.841	0.839	0.637	1.260	−6.710
C38	IGSO	1.097	0.921	0.863	7.104	−2.809
C41	MEO	1.216	0.692	1.004	3.923	−0.457
C43	MEO	1.446	1.166	1.027	8.603	−3.192

下载: 导出CSV

表 4 多星观测值加权组合海面测高精度

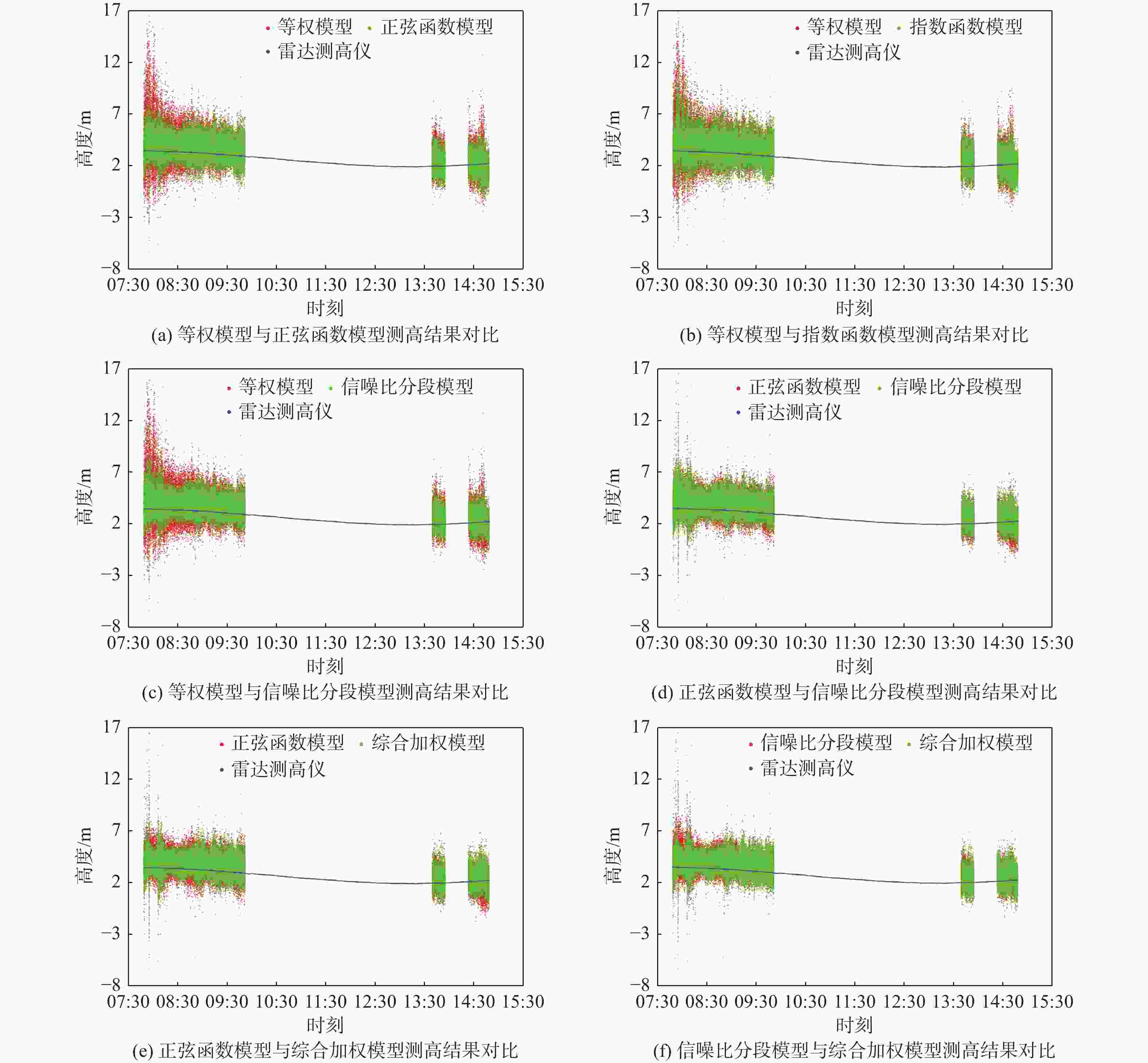
Table 4. Sea surface altimetry accuracy of weighted combination of multi-satellite observations

加权模型	均方根误差/m	标准差/m	平均绝对误差/m
等权模型	1.451	1.315	1.045
正弦函数模型	1.039	0.921	0.798
指数函数模型	1.183	1.075	0.867
信噪比分段模型	1.038	0.862	0.791
综合加权模型	0.940	0.785	0.716

下载: 导出CSV

表 5 单颗卫星测高与多星加权组合测高精度比较(07:40—10:00)

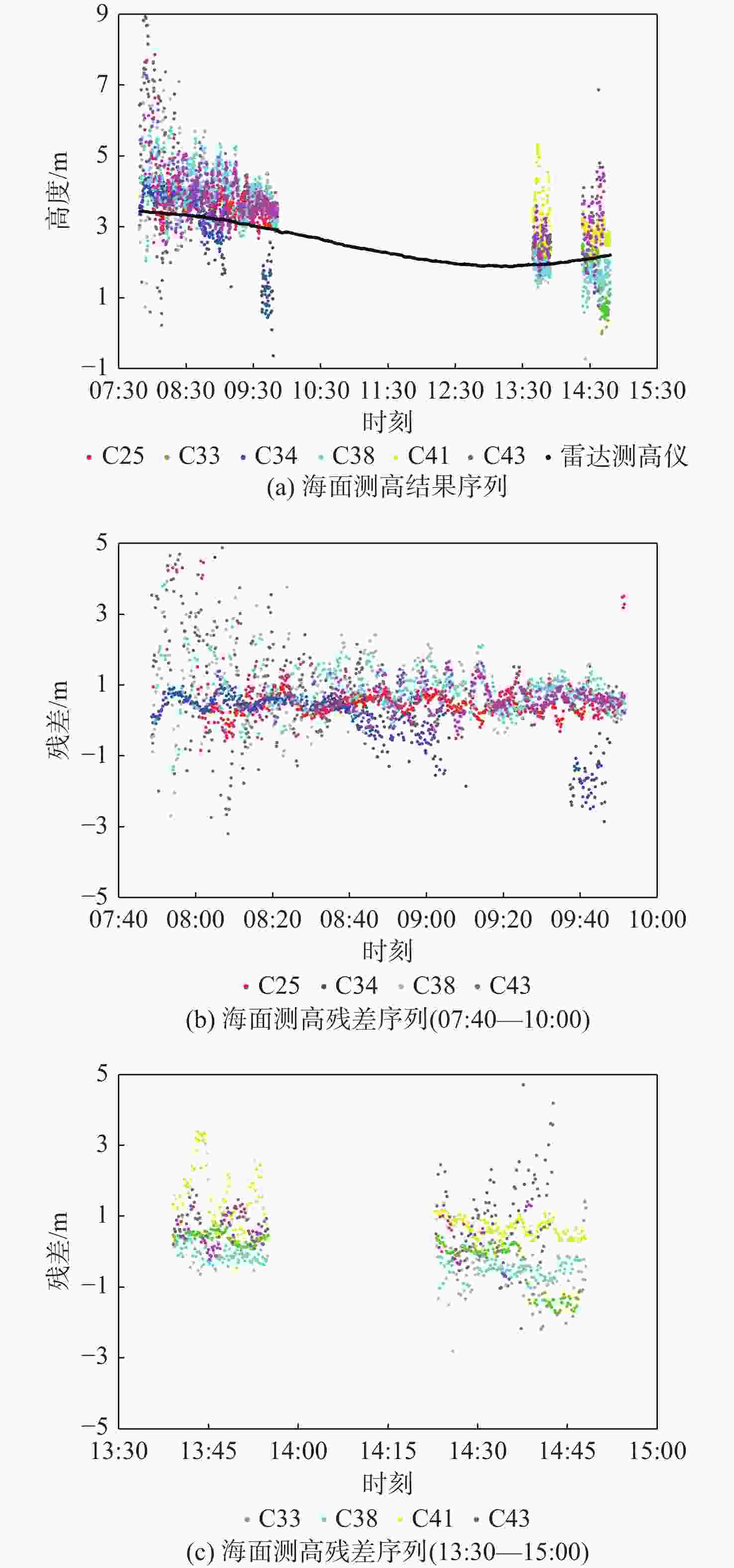
Table 5. Comparison of accuracy between single satellite altimetry and multi-satellite weighted combination altimetry (07:40—10:00)

观测类型		均方根误差/m	标准差/m	平均绝对误差/m	最大误差/m	最小误差/m
单星	C25	1.173	1.061	0.865	7.397	−7.419
	C34	1.368	1.344	0.976	6.901	−7.141
	C38	2.626	2.469	1.995	11.921	−10.218
	C43	2.875	2.785	1.937	20.766	−12.729
多星	正弦函数模型	1.092	0.919	0.839	20.766	−12.729
	信噪比分段模型	1.088	0.880	0.827	20.766	−12.729
	综合加权模型	0.971	0.796	0.733	20.766	−12.729

下载: 导出CSV

表 6 单颗卫星测高与多星加权组合测高精度比较(13:30—15:00)

Table 6. Comparison of accuracy between single satellite altimetry and multi-satellite weighted combination altimetry (13:30—15:00)

观测类型		均方根误差/m	标准差/m	平均绝对误差/m	最大误差/m	最小误差/m
单星	C33	1.219	1.209	0.862	7.407	−6.399
	C38	1.543	1.490	1.178	4.803	−6.039
	C41	2.063	1.814	1.453	16.332	−8.096
	C43	2.767	2.675	2.035	16.014	−10.001
多星	正弦函数模型	0.856	0.850	0.678	4.750	−3.852
	信噪比分段模型	0.873	0.778	0.686	4.744	−3.362
	综合加权模型	0.842	0.741	0.666	4.887	−3.522

下载: 导出CSV

参考文献(29)

[1]	LOWE S T, ZUFFADA C, CHAO Y, et al. 5-cm-precision aircraft ocean altimetry using GPS reflections[J]. Geophysical Research Letters, 2002, 29(10): 1375.
[2]	LOWE S T, ZUFFADA C, LABRECQUE J L, et al. An ocean-altimetry measurement using reflected GPS signals observed from a low-altitude aircraft[C]//Proceedings of the IEEE International Geoscience and Remote Sensing Symposiun. Piscataway: IEEE Press, 2000 : 2185-2187.
[3]	CLARIZIA M P, RUF C, CIPOLLINI P, et al. First spaceborne observation of sea surface height using GPS-reflectometry[J]. Geophysical Research Letters, 2016, 43(2): 767-774. doi: 10.1002/2015GL066624
[4]	MARTIN-NEIRA M, CAPARRINI M, FONT-ROSSELLO J, et al. The PARIS concept: An experimental demonstration of sea surface altimetry using GPS reflected signals[J]. IEEE Transactions on Geoscience and Remote Sensing, 2001, 39(1): 142-150. doi: 10.1109/36.898676
[5]	王鑫, 孙强, 张训械, 等. 中国首次岸基GNSS-R海洋遥感实验[J]. 科学通报, 2008, 53(5): 589-592. doi: 10.1360/csb2008-53-5-589 WANG X, SUN Q, ZHANG X X, et al. China’s first shore-based GNSS-R ocean remote sensing experiment[J]. Chinese Science Bulletin, 2008, 53(5): 589-592(in Chinese). doi: 10.1360/csb2008-53-5-589
[6]	陈世平, 方宗义, 林明森. 利用全球导航定位系统进行大气和海洋遥感[J]. 遥感技术与应用, 2005, 20(1): 30-37. CHEN S P, FANG Z Y, LIN M S. Remote sensing of atmosphere and oceanography using global navigation and positioning systems[J]. Remote Sensing Technology and Application, 2005, 20(1): 30-37(in Chinese).
[7]	JIN S, QIAN X, WU X. Sea level change from BeiDou navigation satellite system-reflectometry (BDS-R): First results and evaluation[J]. Global and Planetary Change, 2017, 149: 20-25. doi: 10.1016/j.gloplacha.2016.12.010
[8]	王泽明, 常亮, 冯贵平, 等. 自适应测站高的GNSS-R潮位监测研究[J]. 测绘科学, 2021, 46(8): 41-48. WANG Z M, CHANG L, FENG G P, et al. GNSS-R tide level monitoring based on adaptive station height[J]. Science of Surveying and Mapping, 2021, 46(8): 41-48(in Chinese).
[9]	MARTIN-NEIRA M. A passive reflectometry and interferometry system (PARIS): Application to ocean altimetry[J]. ESA Journal, 1993, 17(4): 331-355.
[10]	胡媛, 钟李程, 陈行杨, 等. GNSS-R信噪比信号在海面测高技术的研究综述[J]. 全球定位系统, 2021, 46(4): 1-7. HU Y, ZHONG L C, CHEN X Y, et al. A summary of research on GNSS-R signal-to-noise ratio signal height measurement technology on the sea[J]. GNSS World of China, 2021, 46(4): 1-7(in Chinese).
[11]	STRANDBERG J, HOBIGER T, HAAS R. Real-time sea-level monitoring using Kalman filtering of GNSS-R data[J]. GPS Solutions, 2019, 23(3): 61. doi: 10.1007/s10291-019-0851-1
[12]	RIUS A, CARDELLACH E, MARTIN-NEIRA M. Altimetric analysis of the sea-surface GPS-reflected signals[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(4): 2119-2127. doi: 10.1109/TGRS.2009.2036721
[13]	白伟华, 孙越强, 朱光武, 等. 利用岸基GNSS-R信号反演湖面高度[C]//第一届中国卫星导航学术年会. 北京: 中国科学院光电研究院, 2010: 1646-1652. BAI W H, SUN Y Q, ZHU G W, et al. Lake surface height retrieved using coastal GNSS-R signals[C]//Proceedings of the First China Satellite Navigation Conference. Beijing: Academy of Opto-Electronics, Chinese Academy of Sciences, 2010: 1646-1652(in Chinese).
[14]	SEMMLING M, BEYERLE G, BECKHEINRICH J, et al. Airborne GNSS reflectometry using crossover reference points for carrier phase altimetry[C]//Proceedings of the IEEE International Geoscience and Remote Sensing Symposium. Piscataway: IEEE Press, 2014: 3786-3789.
[15]	LESTARQUIT L, PEYREZABES M, DARROZES J, et al. Reflectometry with an open-source software GNSS receiver: Use case with carrier phase altimetry[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2016, 9(10): 4843-4853.
[16]	CARRENO-LUENGO H, CAMPS A, RAMOS-PEREZ I, et al. Experimental evaluation of GNSS-reflectometry altimetric precision using the P(Y) and C/A signals[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2014, 7(5): 1493-1500. doi: 10.1109/JSTARS.2014.2320298
[17]	胡媛, 陈行杨, 顾旺旺, 等. GNSS-R海面测高现状及其常用方法研究进展[J]. 全球定位系统, 2020, 45(3): 96-103. HU Y, CHEN X Y, GU W W, et al. Research of GNSS-R sea surface altimetry status and common methods[J]. GNSS World of China, 2020, 45(3): 96-103(in Chinese).
[18]	ZHANG Y, TIAN L, MENG W, et al. Feasibility of code-level altimetry using coastal BeiDou reflection (BeiDou-R) setups[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2015, 8(8): 4130-4140. doi: 10.1109/JSTARS.2015.2446684
[19]	GAO F, XU T, MENG X, et al. A coastal experiment for GNSS-R code-level altimetry using BDS-3 new civil signals[J]. Remote Sensing, 2021, 13(7): 1378. doi: 10.3390/rs13071378
[20]	王冬伟, 孙越强, 王先毅, 等. 使用BD-3 B2a反射信号测量水面高度[J]. 武汉大学学报·信息科学版, 2022, 47(11): 1878-1876. WANG D W, SUN Y Q, WANG X Y, et al. Water surface altimetry using BD-3 B2a reflected signal[J]. Geomatics and Information Science of Wuhan University, 2022, 47(11): 1878-1876(in Chinese).
[21]	GAO F, XU T, WANG N, et al. A shipborne experiment using a dual-antenna reflectometry system for GPS/BDS code delay measurements[J]. Journal of Geodesy, 2020, 94(9): 88. doi: 10.1007/s00190-020-01421-4
[22]	储倜, 贺凯飞, 高凡, 等. 基于QZSS L1信号的岸基GNSS-R码延迟海面测高[J]. 北京航空航天大学学报, 2022, 48(4): 691-697. CHU T, HE K F, GAO F, et al. Coastal GNSS-R ocean altimetry based on code delay of QZSS L1 signal[J]. Journal of Beijing University of Aeronautics and Astronautics, 2022, 48(4): 691-697(in Chinese).
[23]	樊梦文, 张波, 王峰. 基于半无码的P(Y)码自相关GNSS-R海面测高方法[J]. 北京航空航天大学学报, 2019, 45(2): 398-404. FAN M W, ZHANG B, WANG F. Semi-codeless based P(Y) code autocorrelation GNSS-R sea surface altimetry method[J]. Journal of Beijing University of Aeronautics and Astronautics, 2019, 45(2): 398-404(in Chinese).
[24]	WILLIAMS S, NIEVISNKI F G. Tropospheric delays in ground-based GNSS multipath reflectometry-Experimental evidence from coastal sites[J]. Journal of Geophysical Research Solid Earth, 2017, 122(3): 2310-2327. doi: 10.1002/2016JB013612
[25]	中国卫星导航系统管理办公室. 北斗卫星导航系统空间信号接口控制文件公开服务信号 B1C(1.0 版)[S]. 北京: 中国卫星导航系统管理办公室, 2017: 3-14. China Satellite Navigation Office. BeiDou navigation satellite system signal in space interface control document open service signal B1C (version 1.0) [S]. Beijing: China Satellite Navigation Office, 2017: 3-14(in Chinese).
[26]	戴吾蛟, 丁晓利, 朱建军. 基于观测值质量指标的GPS观测量随机模型分析[J]. 武汉大学学报·信息科学版, 2008, 33(7): 718-722. DAI W J, DING X L, ZHU J J. Comparing GPS stochastic models based on observation quality indices[J]. Geomatics and Information Science of Wuhan University, 2008, 33(7): 718-722(in Chinese).
[27]	刘成, 李芳. 不同卫星定位加权方法的比较与分析[J]. 测绘科学, 2018, 43(8): 39-44. LIU C, LI F. Comparison and analysis of different GNSS weighting methods[J]. Science of Surveying and Mapping, 2018, 43(8): 39-44(in Chinese).
[28]	刘若普, 翟传润, 战兴群. 基于分段信噪比加权的GPS定位方法[J]. 信息技术, 2008, 32(9): 17-20. LIU R P, ZHAI C R, ZHAN X Q. A method of GPS positioning based on piecewise and weighted signal-to-noise ratio[J]. Information Technology, 2008, 32(9): 17-20(in Chinese).
[29]	HAN S. Quality control issues relating to ambiguity resolution for real-time GPS kinematic positioning[J]. Journal of Geodesy, 1997, 71(6): 351-361. doi: 10.1007/s001900050103