-
摘要:
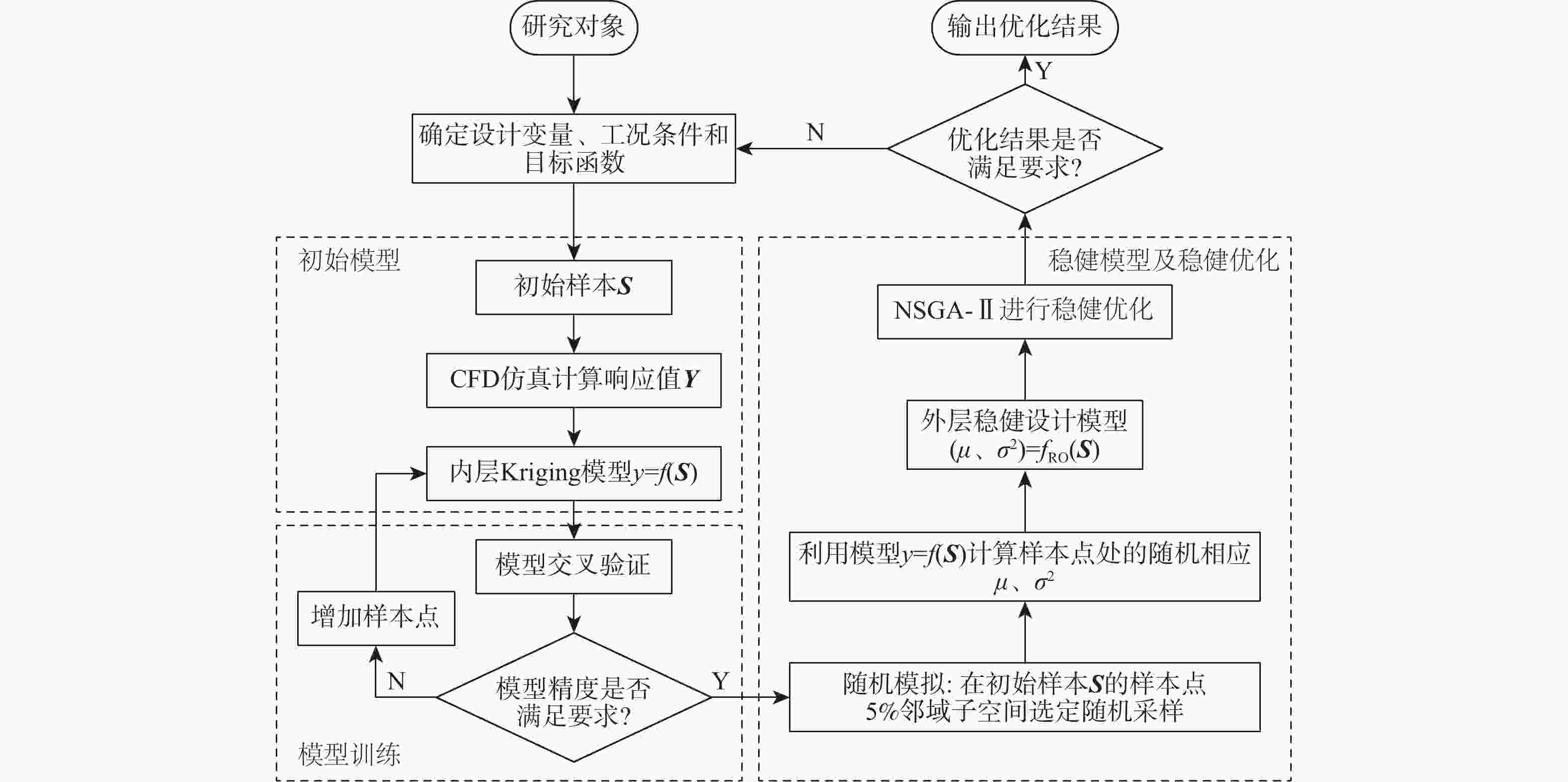
以油膜作为中间介质，对于高速旋转机械传动系统的可靠性、稳定性的提升有显著优势。而高速轴承-转子系统在加工制造和运行过程中，不可避免地存在影响系统承载性能的不确定性因素，影响油膜形状，导致承载性能发生变化，实际工作性能偏离设计目标。以高速动压油膜为研究对象，为掌握几何参数和转速对油膜承载性能波动的影响，进行稳健优化和分析，提取油膜性能稳健优化结果的特征区域。针对传动系统的不同需求，采用计算流体力学方法求解不同转速下的动压滑动轴承油膜压力场，进而求解其主要性能指标：承载力和摩擦功耗。建立研究目标的Kriging近似模型，并在样本点临近区域选择稳健目标计算的子空间，计算目标均值和方差。利用非支配排序遗传算法（NSGA-II）求解不同目标组合的Pareto最优解集。结合自组织映射图（SOM）方法进行相关性分析，提取设计目标与几何参数、转速之间的相关性特征，分析最优特征区域中偏心率对目标稳健性的影响，最终确定稳健性好的特征区域，并选择个别结果进行仿真计算验证。结果表明：所提出的最优性分析方法能够清晰展现出稳健最优性区域在设计空间中的分布情况，便于降低几何参数和转速的波动对油膜性能的影响；所提方法能提升优化设计结果的可实现性，有效促进理论设计与工程实际的衔接。
Abstract:Oil film, as the intermediate medium, offers substantial benefits for enhancing the stability and dependability of mechanical transmission systems with high rotation speeds. The high-speed bearing-rotor system is inevitably affected by environmental factors in manufacturing and operation. These factors affect the shape of the oil film, leading to changes in the performance of sliding bearing, and the actual working performance deviates from the design objectives. The high-speed dynamic pressure oil film was selected as the research object to grasp the influence of geometric parameters and rotation speeds on the fluctuation of oil film performance. Robust optimization and analysis were carried out and the robust optimization result of the oil film was extracted. The oil film pressure field of the hydrodynamic sliding bearing under various operating speeds is solved using the Computational Fluid Dynamics method in accordance with the various requirements of the transmission system. The performance properties: bearing capacity and friction power consumption are solved. The Kriging approximate model is established, and robust indices are calculated within the subspaces that are selected in the vicinity of the sample points. The non-dominated sorting genetic algorithm (NSGA-II) is used to solve the Pareto optimal solution of different objective combinations. The correlation analysis is carried out with the self-organizing maps (SOM), and the correlation characteristics between design objectives, geometric parameters, and rotation speeds are extracted. The robust optimal design is determined by analyzing the impact of the eccentricity on the robust indices in the optimized space. The results show that the proposed robust optimization method can clearly show the distribution of the robust optimality region in the design space and reduce the influence of geometrical parameters and rotation speeds on the oil film performance. The proposed method can improve the feasibility of design results and effectively promote the transition from a theoretical design to an engineering real-life practice.
-
Key words:
- robust design /
- Kriging model /
- Pareto front /
- self-organizing maps /
- slide bearing /
- optimality analysis
-
图 3 Pareto前沿及摩擦功耗−承载力满意度曲线
Figure 3. Pareto front and satisfactory curve of mean of friction power consumption and carrying capacity
图 4 承载力均值和摩擦功耗均值最优解集的四维数据折线图
Figure 4. 4D fold lines diagram of Pareto solutions of mean of friction power consumption and carrying capacity
图 5 承载力均值及其标准差最优解集的四维数据折线图
Figure 5. 4D fold lines diagram of Pareto solutions of mean and standard deviation of carrying capacity
图 6 摩擦功耗均值及其标准差最优解集的四维数据折线图
Figure 6. 4D fold lines diagram of Pareto solutions of the mean and standard deviation of friction power consumption
图 7 承载力标准差和摩擦功耗标准差最优解集的四维数据折线图
Figure 7. 4D fold lines diagram of Pareto solutions of standard deviation of friction power consumption and carrying capacity
图 8 4目标最优解集的六维数据折线图
Figure 8. 6D fold lines diagram of Pareto solutions of four objectives
图 9 六维数据SOM及最优设计结果
Figure 9. SOM visualization of 6D data and optimal design solutions
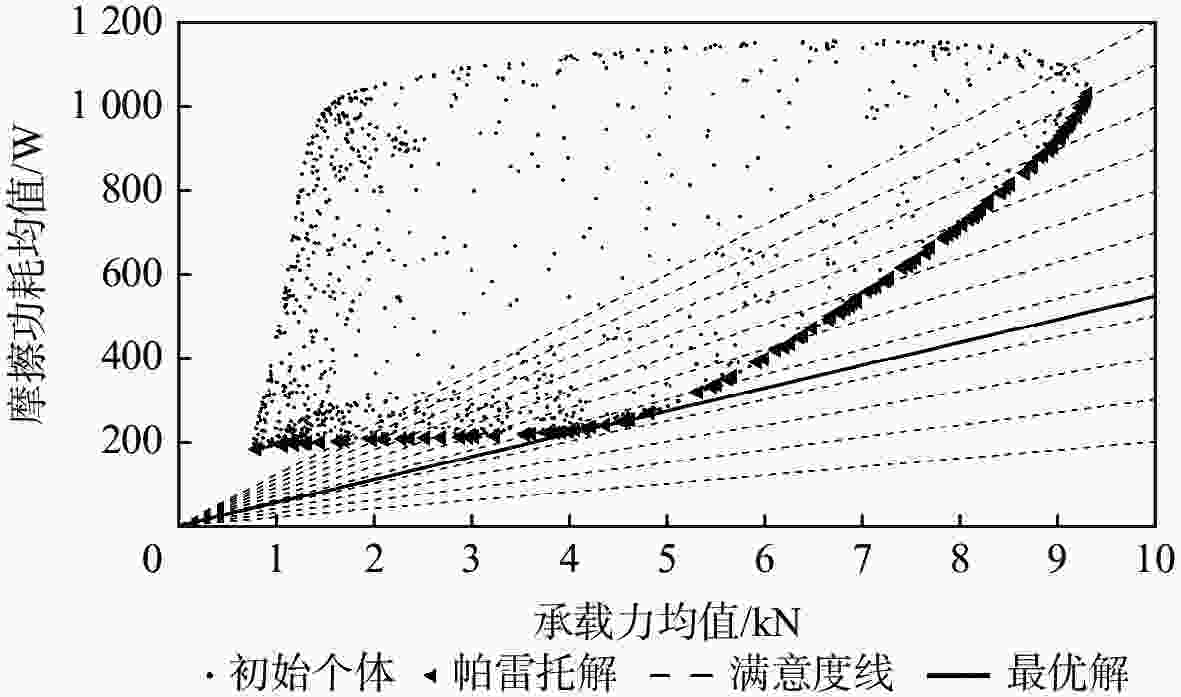
表 1 多目标优化结果
Table 1. Multi-objective optimization results
设计方案 偏心率ε 转速N/(r·min−1) Fr/N Hf/W Fr相对误差/% Hf相对误差/% 初始设计范围 [0.1,0.9] [103,104] 初始设计 0.50 5 500 2 444 486.3 优化“方案1” 0.79 3 051 4 209 218.7 5.6 21.3 方案1-CFD结果 0.79 3 051 3 985 180.2 优化“方案2” 0.67 3 045 3 257 195.1 1.3 9.8 方案2-CFD结果 0.67 3 045 3 300 177.8 注：滑动轴承轴颈直径为40 mm，半径间隙为0.05 mm。 
下载: 导出CSV
-
[1] 郭红, 岑少起, 张绍林. 圆柱、圆锥动静压滑动轴承设计 [M]. 郑州: 郑州大学出版社, 2013: 260-266.GUO H, CEN S Q, ZHANG S L. Design of cylindrical and conical hydrostatic sliding bearings[M]. Zhengzhou: Zhengzhou University Press, 2013: 260-266 (in Chinese). [2] 张直明. 滑动轴承的流体动力润滑理论 [M]. 北京: 高等教育出版社, 1986.ZHANG Z M. Hydrodynamic lubrication theory of sliding bearing [M]. Beijing: Higher Education Press, 1986 (in Chinese). [3] 孟凡明, 隆涛, 高贵响, 等. 气穴对滑动轴承摩擦学性能影响的CFD分析[J]. 重庆大学学报, 2013, 36(7): 6-11. doi: 10.11835/j.issn.1000-582X.2013.07.002MENG F M, LONG T, GAO G X, et al. Study on the effect of cavitation on tribological performances of sliding bearing by CFD method[J]. Journal of Chongqing University, 2013, 36(7): 6-11 (in Chinese). doi: 10.11835/j.issn.1000-582X.2013.07.002 [4] 张泽斌, 李永, 陈荣尚, 等. 含气率对润滑油黏度的影响[J]. 河南科技大学学报(自然科学版), 2019, 40(2): 23-27.ZHANG Z B, LI Y, CHEN R S, et al. Effect of void fraction on viscosity of lubricating oil[J]. Journal of Henan University of Science and Technology (Natural Science), 2019, 40(2): 23-27 (in Chinese). [5] 郭红, 夏伯乾, 孙一休. 径向动静压浮环轴承-转子系统稳定性分析[J]. 振动与冲击, 2017, 36(5): 7-11.GUO H, XIA B Q, SUN Y X. Stability analysis of a journal floating ring hybrid bearing-rotor system[J]. Journal of Vibration and Shock, 2017, 36(5): 7-11 (in Chinese). [6] GUO H, YANG S, ZHANG S L, et al. Influence of temperature-viscosity effect on ring-journal speed ratio and stability for a hydrodynamic floating ring bearing[J]. Industrial Lubrication and Tribology, 2019, 71(4): 540-547. doi: 10.1108/ILT-08-2018-0329 [7] 陈立周. 稳健设计 [M]. 北京: 机械工业出版社, 2000.CHEN L Z. Robust design [M]. Beijing: China Machine Press, 2000 (in Chinese). [8] LEARY S, BHASKAR A, KEANE A. Optimal orthogonal-array-based latin hypercubes[J]. Journal of Applied Statistics, 2003, 30(5): 585-598. doi: 10.1080/0266476032000053691 [9] 赵轲, 高正红, 黄江涛, 等. 基于PCE方法的翼型不确定性分析及稳健设计[J]. 力学学报, 2014, 46(1): 10-19.ZHAO K, GAO Z H, HUANG J T, et al. Uncertainty quantification and robust design of airfoil based on polynomial chaos technique[J]. Chinese Journal of Theoretical and Applied Mechanics, 2014, 46(1): 10-19 (in Chinese). [10] 赵轲. 基于CFD的复杂气动优化与稳健设计方法研究[D]. 西安: 西北工业大学, 2015.ZHAO K. Research on complex aerodynamic optimization and robust design method based on CFD[D]. Xi’an: Northwestern Polytechnical University, 2015 (in Chinese). [11] FANG K T, LIN D K J, WINKER P, et al. Uniform design: Theory and application[J]. Technometrics, 2000, 42(3): 237-248. doi: 10.1080/00401706.2000.10486045 [12] 尚宝平, 闫富宏, 刘高峰, 等. 基于近似模型的铣削工艺参数可靠性设计优化[J]. 中国机械工程, 2019, 30(4): 480-485. doi: 10.3969/j.issn.1004-132X.2019.04.015SHANG B P, YAN F H, LIU G F, et al. Reliability-based design optimization of milling process parameters using approximate model[J]. China Mechanical Engineering, 2019, 30(4): 480-485 (in Chinese). doi: 10.3969/j.issn.1004-132X.2019.04.015 [13] 蒋琛, 邱浩波, 高亮. 随机不确定性下的可靠性设计优化研究进展[J]. 中国机械工程, 2020, 31(2): 190-205. doi: 10.3969/j.issn.1004-132X.2020.02.005JIANG C, QIU H B, GAO L. Research Progressesin reliability-based design optimization under aleatory uncertainties[J]. China Mechanical Engineering, 2020, 31(2): 190-205 (in Chinese). doi: 10.3969/j.issn.1004-132X.2020.02.005 [14] ZHANG Z B, LI Y H. Exploration of anisotropic design space by using unified taylor-cokriging method[J]. Applied Mathematical Modelling, 2022, 110: 45-60. doi: 10.1016/j.apm.2022.05.033 [15] 李小刚, 程锦, 刘振宇, 等. 基于双层更新Kriging模型的机械结构动态特性稳健优化设计[J]. 机械工程学报, 2014, 50(3): 165-173. doi: 10.3901/JME.2014.03.165LI X G, CHENG J, LIU Z Y, et al. Robust optimization for dynamic characteristics of mechanical structures based on double renewal Kriging model[J]. Journal of Mechanical Engineering, 2014, 50(3): 165-173 (in Chinese). doi: 10.3901/JME.2014.03.165 [16] 张泽斌, 张鹏飞, 郭红, 等. Kriging序贯设计方法在滑动轴承优化中的应用[J]. 哈尔滨工业大学学报, 2019, 51(7): 178-183. doi: 10.11918/j.issn.0367-6234.201810147ZHANG Z B, ZHANG P F, GUO H, et al. Implementation of Kriging model based sequential design on the optimization of sliding bearing[J]. Journal of Harbin Institute of Technology, 2019, 51(7): 178-183 (in Chinese). doi: 10.11918/j.issn.0367-6234.201810147 [17] DEB K, AGRAWAL S, PRATAP A, et al. A fast elitist non-dominated sorting genetic algorithm for multi-objective optimization: NSGA-II [M]//Parallel Problem Solving from Nature PPSN VI. Berlin: Springer, 2000: 849-858. [18] LOPHAVEN S N, NIELSEN H B, SONDERGAARD J. DACE: A MATLAB kriging toolbox (version 2.0)[R]. Copenhagen: Technical University of Denmark, 2002. [19] HAN Z H, XU C Z, ZHANG L, et al. Efficient aerodynamic shape optimization using variable-fidelity surrogate models and multilevel computational grids[J]. Chinese Journal of Aeronautics, 2020, 33(1): 31-47. doi: 10.1016/j.cja.2019.05.001 [20] GEISSER S. Bayesian estimation in multivariate analysis[J]. The Annals of Mathematical Statistics, 1965, 36(1): 150-159. doi: 10.1214/aoms/1177700279 [21] 冯泽彪, 汪建均. 考虑模型响应不确定性的稳健参数设计[J]. 控制与决策, 2019, 34(2): 233-242.FENG Z B, WANG J J. Multi-response robust parameter design based on uncertainty of model response[J]. Control and Decision, 2019, 34(2): 233-242 (in Chinese). [22] 顾晓光, 马义中, 汪建均, 等. 多元质量特性的满意参数设计[J]. 控制与决策, 2014, 29(6): 1064-1070.GU X G, MA Y Z, WANG J J, et al. Satisfactory parameter design for multivariate quality characteristics[J]. Control and Decision, 2014, 29(6): 1064-1070 (in Chinese). [23] HWANG C L, YOON K. Methods for multiple attribute decision making[M]. Multiple Attribute Decision Making, Berlin: Springer, 1981: 58-191. [24] KOHONEN T. The self-organizing map[J]. Proceedings of the IEEE, 1990, 78(9): 1464-1480. doi: 10.1109/5.58325 [25] 张泽斌, 张鹏飞, 李瑞珍. 基于自组织映射的高维优化参变量相关性研究[J]. 西北工业大学学报, 2020, 38(3): 677-684. doi: 10.3969/j.issn.1000-2758.2020.03.028ZHANG Z B, ZHANG P F, LI R Z. SOM-based high-dimensional design spaces mapping for multi-objective optimization[J]. Journal of Northwestern Polytechnical University, 2020, 38(3): 677-684 (in Chinese). doi: 10.3969/j.issn.1000-2758.2020.03.028 -
下载:
点击查看大图
计量
- 文章访问数: 256
- HTML全文浏览量: 142
- PDF下载量: 11
- 被引次数: 0
