Low-energy transfer from Earth into DRO with hybrid gravity assist and numerical continuation
-
摘要:
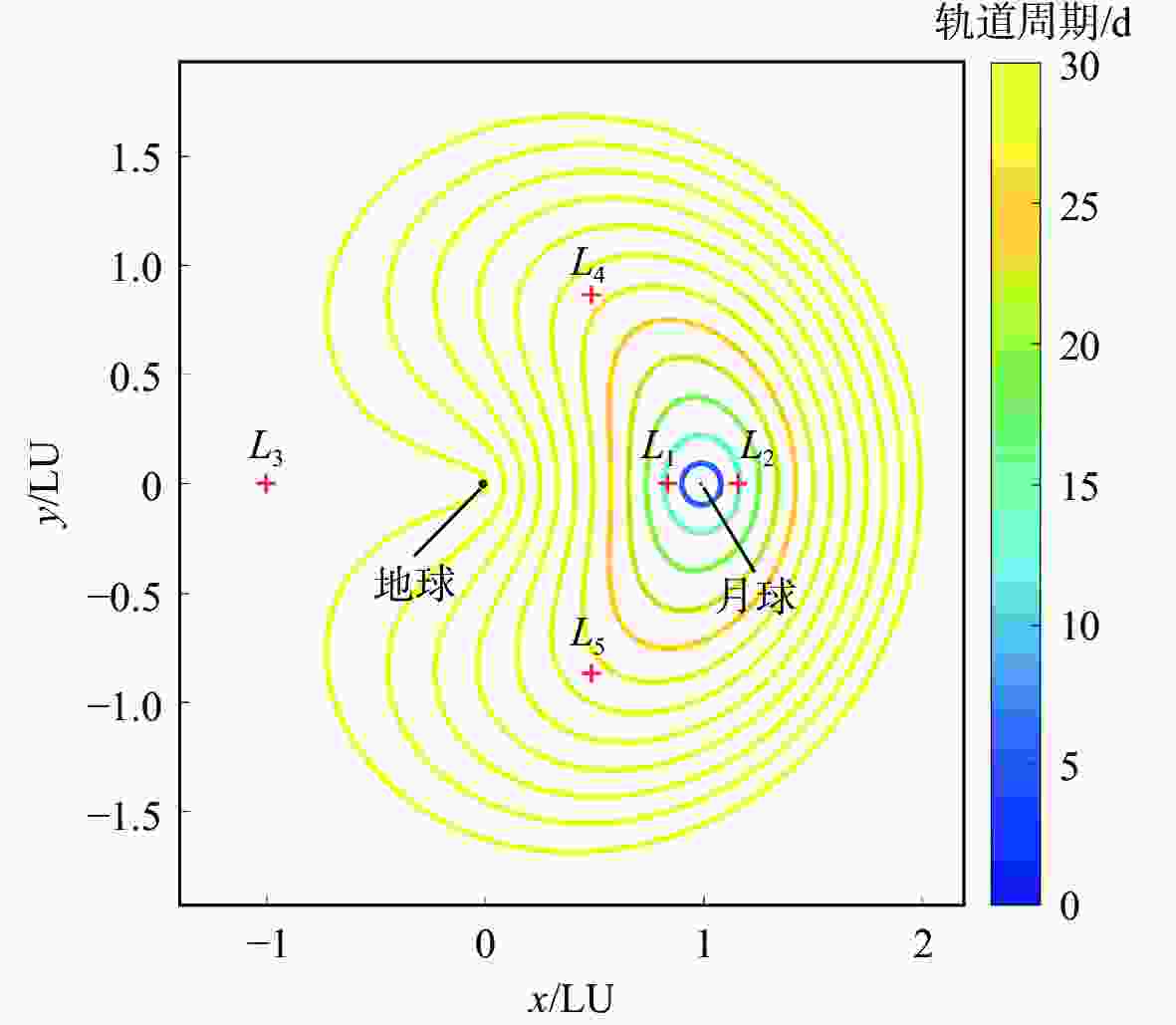
远距离逆行轨道(DRO)是地月空间中的一类周期轨道,这类轨道具有长期稳定、入轨能量低的特点,可作为未来载人月球和载人火星任务的中转站。对于地球至DRO的两脉冲入轨任务,采用日月综合借力(即同时使用弱稳定边界(WSB)和月球借力(LGA))可以最大化入轨质量,但是这类轨道对初值非常敏感。使用日月综合借力拓展DRO入轨脉冲包络,改进构造方法和提供解析梯度大幅提高多步打靶收敛率,提出2层伪弧长延拓方法进一步降低任务总脉冲。数值仿真采用共振比为2∶1的DRO,脉冲最低解采用“LGA+WSB+2LGA”的飞行模式,飞行时间为123天,近地轨道发射脉冲为3.125 km/s,DRO入轨脉冲仅为19.7 m/s。
Abstract:Distant retrograde orbits (DRO) are well-known trajectory types in cislunar space, such orbits have long-term stability and low insertion cost. In cislunar space, DRO are well-known trajectory types with minimal insertion costs and long-term stability. A cislunar station deployed on DRO might be expected to deliver a crew to the moon or Mars for exploration missions in the future. For low-energy transfer from Earth into DRO, the maximum delivery mass can be achieved by utilizing a weak stability boundary (WSB) and multiple lunar gravity assist (LGA) simultaneously, but this kind of transfer is very sensitive to initial values. A novel two-level pseudo-arc continuation method was proposed to explore local solution space, and this paper aims to improve both computational and transfer efficiency when leveraging hybrid gravity assist in cislunar space. Additionally, a modified problem description with an analytical gradient is used to improve multiple shooting efficiency under a bicircular restricted four-body problem. In the numerical simulation, the minimum cost solution shows “LGA+WSB+2LGA”, where the time of flight is 123 days, the LEO launching cost is 3.125 km/s and the 2:1 DRO insertion maneuver only needs 19.7 m/s.
-
表 1 有限差分和解析梯度的对比
Table 1. Comparison between finite difference and analytical gradient
名称 收敛数 收敛率/% 计算时间/s 有限差分 309 8.44 18.01 解析梯度 2361 64.54 20.24 表 2 数值延拓前后轨道对比
Table 2. Comparison of orbits before and after numerical continuation
任务名称 延拓前 延拓后 LEO发射时间/TU −31.944 945 682 3 −32.992 737 946 4 DRO入轨时间/TU −4.422 676 457 9 −4.699 448 716 6 LEO发射位置/LU [−0.025 926 418 9,
−0.010 152 072 7][−0.020 484 378 0,
−0.014 946 105 5]LEO发射速度/VU [6.340 104 171 1,
−8.603 190 754 6][9.288 605 287 2,
−5.179 229 375 6]DRO相位因子$\sigma $ 0.071 769 660 2 0.976 618 137 7 LEO发射脉冲/(km·s−1) 3.178 4 3.125 2 DRO入轨脉冲/(km·s−1) 0.040 9 0.019 7 任务总脉冲/(km·s−1) 3.219 4 3.144 9 任务总时间/d 119.669 9 123.022 4 表 3 3种任务场景对比
Table 3. Comparison between 3 mission scenarios
任务名称 发射脉冲/(km·s−1) 入轨脉冲/(km·s−1) 入轨质量/103 kg LEO至GEO 2.454 1.477 6.571 LEO至LLO
(综合借力)3.125 0.650 6.929 LEO至DRO
(综合借力)3.125 0.019 8.584 C1 数值仿真参数
C1. Numerical simulation parameters
名称 数值 太阳质量常数 μs/(km3·s−2) 132712440017.9870 地球质量常数 μe/(km3·s−2) 398600.4328969392 月球质量常数 μm/(km3·s−2) 4902.800582147764 重力加速度 g0/(m·s−2) 9.80665 地球平均半径 Re/km 6378.137 月球平均半径 Rm/km 1738 LEO地心距约束 r*leo/km 6578.137 月球影响球半径 rsoi,m/km 66100 归一化距离/LU 1 归一化时间/TU 1 归一化速度/VU 1 归一化地月质量参数 μ 0.012151 归一化太阳质量 ms 3.28901e5 归一化太阳距离 ρs 388.811 归一化太阳角速度 ωs −0.92519 多步打靶离散点 n 20 伪弧长延拓步长 Δs 0.1 DRO入轨太阳相位角 θs(τN) [0,2π) DRO入轨相位因子 σ [0,1) DRO入轨脉冲模 ΔV/(m·s−1) [10,100] DRO入轨脉冲方向角 φ/rad [0,2π) 2∶1共振DRO位置初值$r_{\mathrm{dro}}^0 $/LU [0.808936204186,0,] 2∶1共振DRO速度初值$v_{\mathrm{dro}}^0 $/VU [0,0.515632164331] 注:1 LU=384 400 km, 1 TU=4.348 113 05 d, 1 VU=1.023 232 81 km/s。 -
[1] WHITLEY R, MARTINEZ R. Options for staging orbits in cislunar space[C] //Proceedings of the IEEE Aerospace Conference. Piscataway: IEEE Press, 2016: 1-9. [2] 曾豪, 李朝玉, 彭坤, 等. 地月空间NRHO与DRO在月球探测中的应用研究[J]. 宇航学报, 2020, 41(7): 910-919.ZENG H, LI Z Y, PENG K, et al. Research on application of Earth-Moon NRHO and DRO for lunar exploration[J]. Journal of Astronautics, 2020, 41(7): 910-919 (in Chinese). [3] HÉNON M. Numerical exploration of the restricted problem[J]. Astronomy and Astrophysics, 1969(1): 223-238. [4] DEMEYER J, GURFIL P. Transfer to distant retrograde orbits using manifold theory[J]. Journal of Guidance, Control, and Dynamics, 2007, 30(5): 1261-1267. doi: 10.2514/1.24960 [5] MINGOTTI G, TOPPUTO F, BERNELLI-ZAZZERA F. Transfers to distant periodic orbits around the Moon via their invariant manifolds[J]. Acta Astronautica, 2012(79): 20-32. [6] BEZROUK C, PARKER J S. Long term evolution of distant retrograde orbits in the Earth-Moon system[J]. Astrophysics and Space Science, 2017, 362(9): 176. doi: 10.1007/s10509-017-3158-0 [7] LARA M. Design of distant retrograde orbits based on a higher order analytical solutiont[J]. Acta Astronautica, 2019(161): 562-578. [8] 吴小婧, 曾凌川, 巩应奎. DRO计算及其在地月系中的摄动力研究[J]. 北京航空航天大学学报, 2020, 46(5): 883-892.WU X J, ZENG L C, GONG Y K. DRO computation and its perturbative force in the Earth-Moon system[J]. Journal of Beijing University of Aeronautics and Astronautics, 2020, 46(5): 883-892 (in Chinese). [9] STRANGE N, LANDAU D, MCELRATH T, et al. Overview of mission design for NASA asteroid redirect robotic mission concept[C]//Proceedings of the 33rd International Electric Propulsion Conference. Washington, D. C. : NASA, 2013, 1-13. [10] DAWN T F, GUTKOWSKI J, BATCHA A, et al. Trajectory design considerations for exploration mission 1[C] // Proceedings of the Space Flight Mechanics Meeting. Reston: AIAA, 2018: 968. [11] CONTE D, DI CARLO M, HO K, et al. Earth-Mars transfers through Moon Distant Retrograde Orbits[J]. Acta Astronautica, 2018(143): 372-379. [12] WELCH C M, PARKER J S, BUXTON C. Mission considerations for transfers to a distant retrograde orbit[J]. The Journal of the Astronautical Sciences, 2015, 62(2): 101-124. doi: 10.1007/s40295-015-0039-z [13] CAPDEVILA L R, HOWELL K C. A transfer network linking Earth, Moon, and the triangular libration point regions in the Earth-Moon system[J]. Advances in Space Research, 2018, 62(7): 1826-1852. doi: 10.1016/j.asr.2018.06.045 [14] BELBRUNO E A, MILLER J K. Sun-perturbed Earth-to-moon transfers with ballistic capture[J]. Journal of Guidance Control Dynamics, 1993, 16(4): 770-775. doi: 10.2514/3.21079 [15] YAGASAKI K. Sun-perturbed Earth-to-Moon transfers with low energy and moderate flight time[J]. Celestial Mechanics and Dynamical Astronomy, 2004, 90(3): 197-212. [16] TOPPUTO F. On optimal two-impulse Earth-Moon transfers in a four-body model[J]. Celestial Mechanics and Dynamical Astronomy, 2013, 117(3): 279-313. doi: 10.1007/s10569-013-9513-8 [17] OSHIMA K, TOPPUTO F, YANAO T. Low-energy transfers to the Moon with long transfer time[J]. Celestial Mechanics and Dynamical Astronomy, 2019, 131(1): 4. doi: 10.1007/s10569-019-9883-7 [18] PARKER J S, ERSON R L. Low-energy lunar trajectory design[M]. Pasadena: John Wiley & Sons, 2014: 1-381. [19] ZHANG Z, HOU X. Transfer orbits to the Earth–Moon triangular libration points[J]. Advances in Space Research, 2015, 55(12): 2899-2913. doi: 10.1016/j.asr.2015.03.008 [20] PARRISH N L, KAYSER E, UDUPA S, et al. Survey of ballistic lunar transfers to near rectilinear halo orbit[C]//Proceedings of the AAS/AIAA Astrodynamics Specialist Conference. Reston:AIAA, 2019: 1-20. [21] XU M, XU S J. Exploration of distant retrograde orbits around Moon[J]. Acta Astronautica, 2009, 65(5-6): 853-860. doi: 10.1016/j.actaastro.2009.03.026 [22] TAN M H, ZHANG K, LV M B, et al. Transfer to long term distant retrograde orbits around the Moon[J]. Acta Astronautica, 2014(98): 50-63. [23] ZHANG R K, WANG Y, ZHANG C, et al. The transfers from lunar DROs to Earth orbits via optimization in the four body problem[J]. Astrophysics and Space Science, 2021, 366(6): 49. doi: 10.1007/s10509-021-03955-1 [24] SCHEUERLE S T, MCCARTHY B P, HOWELL K C. Construction of ballistic lunar transfers leveraging dynamical systems techniques[C]//Proceedings of the AAS/AIAA Astrodynamics Specialist Conference. Reston: AIAA, 2020: 1-20. -







 下载:
下载: