基于<i>ε-</i>level蝙蝠算法的无人机三维航迹规划

王福仪; 孟秀云; 张海阔

doi:10.13700/j.bh.1001-5965.2022.0502

基于ε-level蝙蝠算法的无人机三维航迹规划

doi: 10.13700/j.bh.1001-5965.2022.0502

北京理工大学宇航学院，北京 100081

详细信息

通讯作者:
E-mail：mengxy@bit.edu.cn

中图分类号: V249.122⁺.3；TP301.6
计量
- 文章访问数: 670
- HTML全文浏览量: 90
- PDF下载量: 13
- 被引次数: 0
出版历程
- 收稿日期: 2022-06-20
- 录用日期: 2022-08-12
- 网络出版日期: 2023-01-18
- 整期出版日期: 2024-05-29

UAV three-dimensional path planning based on ε-level bat algorithm

School of Aerospace Engineering，Beijing Institute of Technology，Beijing 100081，China

More Information

Corresponding author: E-mail：mengxy@bit.edu.cn

摘要

摘要:
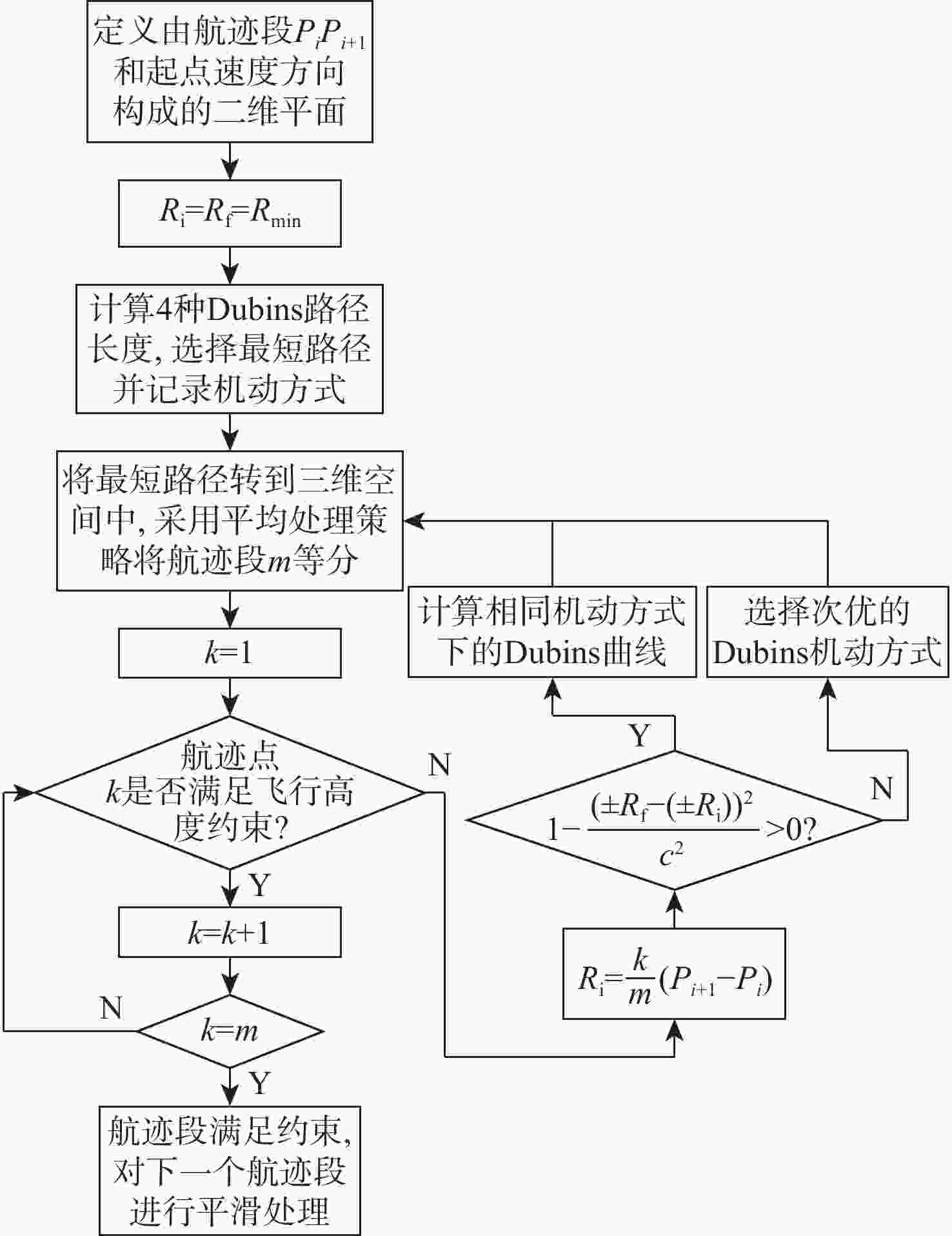
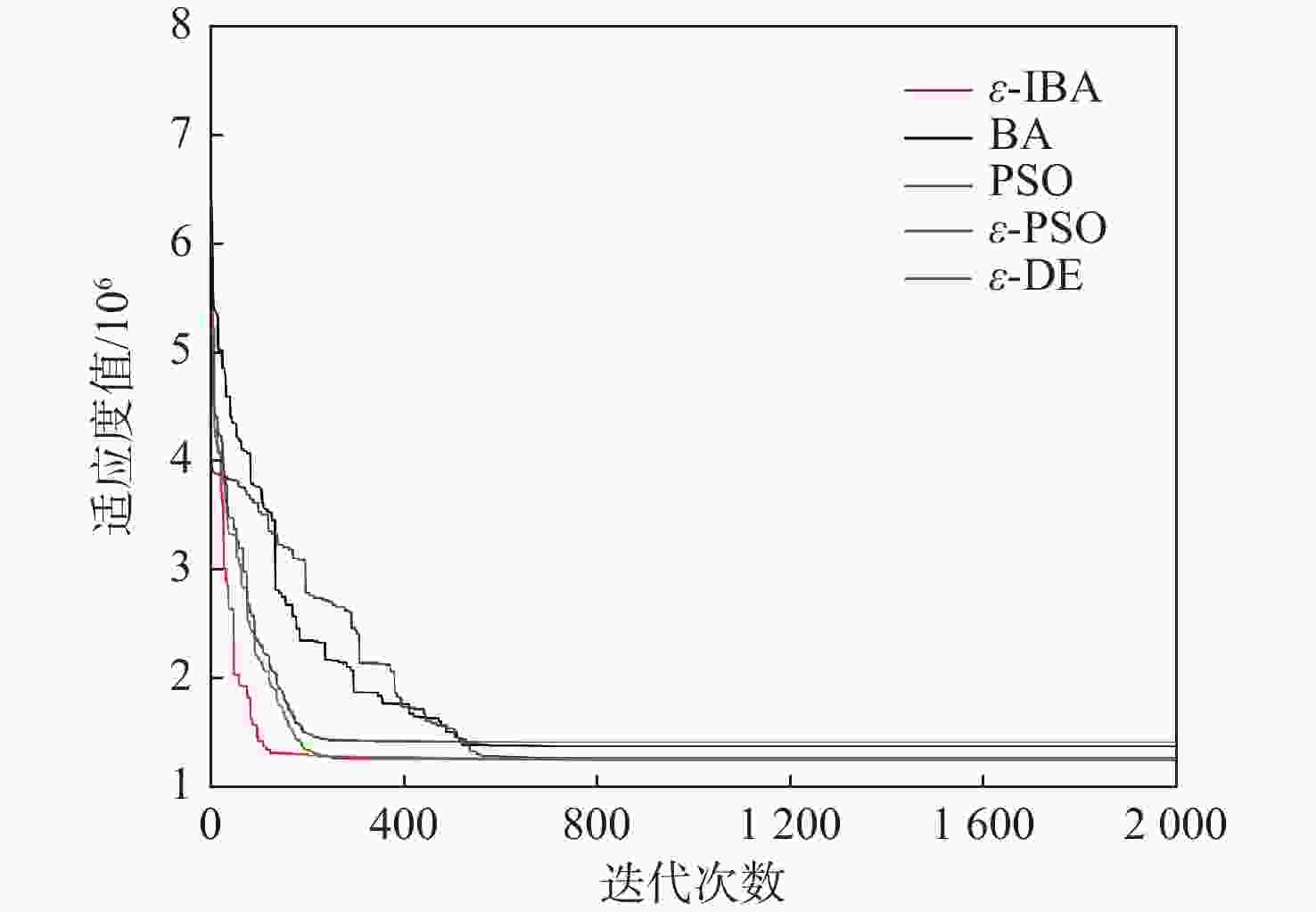
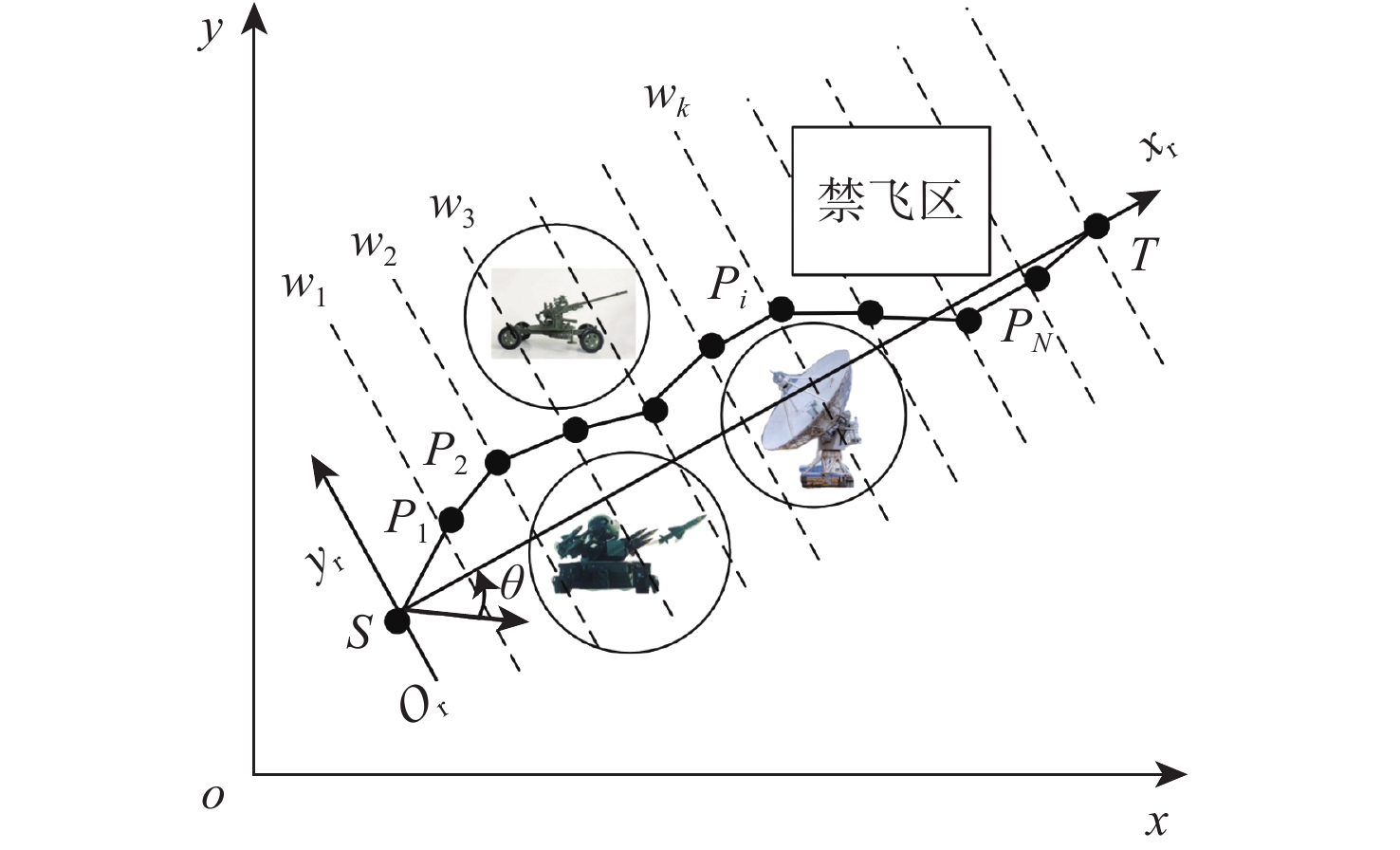
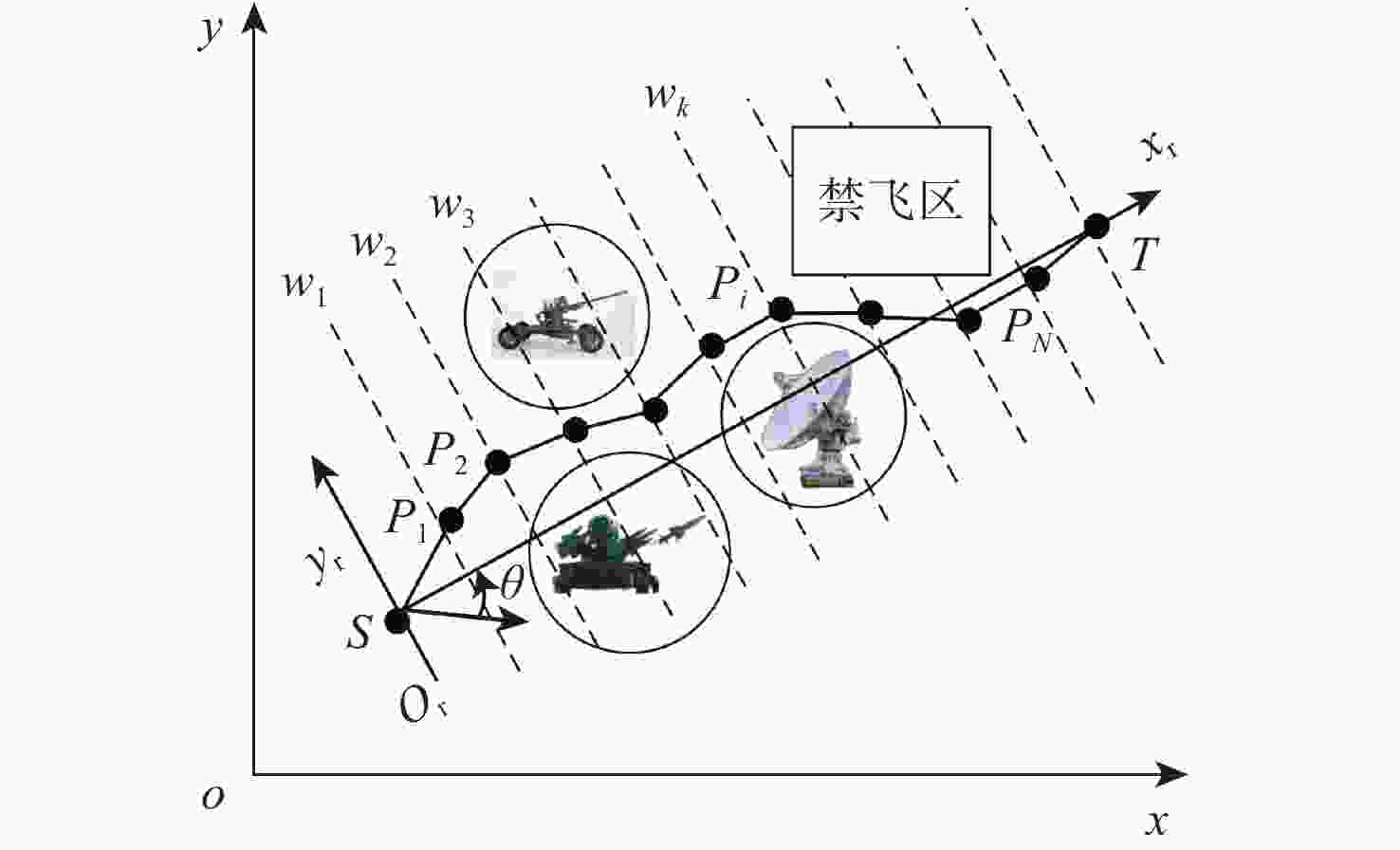
针对复杂地形环境、存在各种威胁和约束的无人机航迹规划问题，提出了一种基于ε-level改进蝙蝠算法的航迹规划算法。根据无人机目标函数和约束条件，建立无人机三维航迹规划模型；其次，针对蝙蝠算法处理高维带约束问题存在的早熟现象，设计了自适应权重系数和迭代阈值以平衡算法的探索能力和开发能力，并结合ε-level比较策略提高算法对非凸非线性约束优化问题的处理能力；设计了转弯半径可变的Dubins曲线用来对航迹进行平滑处理并解决2个航迹点连线贯穿地形的问题。通过仿真实验，并与蝙蝠算法、粒子群优化算法、ε-level粒子群优化算法和ε-level差分进化算法相比较，所提算法在开发能力、稳定性和成功率等方面都表现出较优的性能。
- 无人机航迹规划 /
- 蝙蝠算法 /
- 自适应权重系数 /
- ε-level比较策略 /
- Dubins平滑
Abstract:
To address the problem of complex terrain environment and various threats and constraints, this article proposes a path planning algorithm for UAV based on ε-level improved bat algorithm. First, according to the drone target function and constraints, a three-dimensional path planning model of the UAV is established. Second, in response to the precocious phenomenon in handling the high-dimensional constraints problem of the bat algorithm, the adaptive weight coefficient and iteration threshold are designed to balance the exploration and exploitation capabilities of bat algorithms. Furthermore, by integrating an ε-level comparative strategy, the algorithm's capability to handle issues of non-convex and non-linear constraints is enhanced. Additionally, a three-dimensional Dubins curve with variable turning radius is designed to smooth the path and solve the problem of penetrating the terrain of the two trails. Through simulation experiments and compared with BA, PSO, ε-PSO and ε-DE, the algorithm proposed in this paper shows superior performance in terms of exploitation ability, stability and success rate.
- UAV path planning /
- bat algorithm /
- adaptive weight coefficient /
- ε-level comparison strategy /
- Dubins smoothing

HTML全文

图 1 坐标转换

Figure 1. Coordinate conversion

下载: 全尺寸图片幻灯片

图 2 威胁代价计算

Figure 2. Calculation of threat cost

下载: 全尺寸图片幻灯片

图 3 $ r^{0}=0.5 $，$\gamma =0.3 $时发射率随迭代次数变化曲线

Figure 3. Emission rate changes with iterations when $r^{0}=0.5 $, $\gamma =0.3 $

下载: 全尺寸图片幻灯片

图 4 航迹贯穿地形

Figure 4. Track penetrates the terrain

下载: 全尺寸图片幻灯片

图 5 Dubins 曲线

Figure 5. Dubins curve

下载: 全尺寸图片幻灯片

图 6 三维 Dubins 曲线

Figure 6. Three -dimensional Dubins curve

下载: 全尺寸图片幻灯片

图 7 转弯半径可变的 Dubins 航迹平滑流程

Figure 7. Dubins track smoothing process with variable turning radius

下载: 全尺寸图片幻灯片

图 8 平滑后的航迹

Figure 8. Track after smooth

下载: 全尺寸图片幻灯片

图 9 不同算法得到的 UAV 航迹

Figure 9. UAV track obtained by different algorithms

下载: 全尺寸图片幻灯片

图 10 航迹剖面图

Figure 10. Track profile

下载: 全尺寸图片幻灯片

图 11 航迹代价收敛曲线

Figure 11. Convergence curves of path cost

下载: 全尺寸图片幻灯片

表 1 任务和威胁信息

Table 1. Task and threat information km

威胁类型	威胁范围
导弹	([190,180],90); ([650,460],80)
高射炮	([480,540],80); ([850,650],70)
雷达	([500,210],150); ([630,760],150)
禁飞区	([100,360],[380,600]); ([710,890],[170,370])

下载: 导出CSV

表 2 算法性能统计结果

Table 2. Algorithm performance statistics

算法	最优/10⁶	期望/10⁶	最差/10⁶	标准差/10⁵	成功率/%
$ \varepsilon \text{-} \mathrm{IBA} $	1.249	1.388	1.558	0.7850	98
BA	1.377	2.632	3.359	5.906	36
PSO	1.264	2.726	3.658	6.525	28
$ \varepsilon \text{-} {{\mathrm{PSO}} } $	1.260	1.523	1.869	1.583	64
$ \varepsilon \text{-} {{\mathrm{DE}}} $	1.412	1.755	2.039	2.329	54

下载: 导出CSV

参考文献(27)

[1]	SANTOSO F, GARRATT M, ANAVATTI S. State-of-the-art intelligent flight control systems in unmanned aerial vehicles[J]. IEEE Transactions on Automation Science and Engineering, 2018, 15(2): 613-627. doi: 10.1109/TASE.2017.2651109
[2]	ZHAO Y J, ZHENG Z, LIU Y. Survey on computational-intelligence-based UAV path planning[J]. Knowledge-Based Systems, 2018, 158: 54-64. doi: 10.1016/j.knosys.2018.05.033
[3]	LIU H, ZHANG N, LI Q. UAV path planning based on an improved ant colony algorithm[C]//Proceedings of 2021 4th International Conference on Intelligent Autonomous Systems (ICoIAS). Piscataway: IEEE Press, 2021: 357-360.
[4]	陈侠, 刘奎武, 毛海亮. 基于APF-RRT算法的无人机航迹规划[J]. 电光与控制, 2022, 29(5): 17-22. CHEN X, LIU K W, MAO H L. The path planning of UAV based on APF-RRT algorithm[J]. Electronics Optics & Control, 2022, 29(5): 17-22(in Chinese).
[5]	赵红超, 周洪庆, 王书湖. 无人机三维航迹规划的量子粒子群优化算法[J]. 航天控制, 2021, 39(1): 40-45. ZHAO H C, ZHOU H Q, WANG S H. Quantum particle swarm optimization algorithm of three-dimensional path planning of unmanned aerial vehicle[J]. Aerospace Control, 2021, 39(1): 40-45(in Chinese).
[6]	SHIVGAN R, DONG Z. Energy-efficient drone coverage path planning using genetic algorithm[C]//Proceedings of 2020 IEEE 21st International Conference on High Performance Switching and Routing (HPSR). Piscataway: IEEE Press, 2020: 1-6.
[7]	汤安迪, 韩统, 徐登武, 等. 混沌多精英鲸鱼优化算法[J]. 北京航空航天大学学报, 2021, 47(7): 1481-1494. TANG A D, HAN T, XU D W, et al. Chaotic multi-leader whale optimization algorithm[J]. Journal of Beijing University of Aeronautics and Astronautics, 2021, 47(7): 1481-1494(in Chinese).
[8]	GHAMBARI S, LEPAGNOT J, JOURDAN L, et al. UAV path planning in the presence of static and dynamic obstacles[C]//Proceedings of 2020 IEEE Symposium Series on Computational Intelligence (SSCI). Piscataway: IEEE Press, 2020, 465-472.
[9]	高阳阳, 余敏建, 韩其松, 等. 基于改进共生生物搜索算法的空战机动决策[J]. 北京航空航天大学学报, 2019, 45(3): 429-436. GAO Y Y, YU M J , HAN Q S, et al. Air combat maneuver decision-making based on improved symbiotic organisms search algorithm[J]. Journal of Beijing University of Aeronautics and Astronautics, 2019, 45(3): 429-436(in Chinese).
[10]	JAMSHIDI V, NEKOUKAR V, REFAN M H. Real time UAV path planning by parallel grey wolf optimization with align coefficient on CAN bus[J]. Cluster Computing-The Journal of Networks Software Tools and Applications, 2021, 24(3): 2495-2509.
[11]	YANG X. A new metaheuristic bat-inspired algorithm[C]//Proceedings of Nature Inspired Cooperative Strategies for Optimization(NICSO 2010). Berlin: Springer, 2010: 65-74.
[12]	GANDOMI A, YANG X. Chaotic bat algorithm[J]. Journal of Computational Science, 2014, 5(2): 224-232. doi: 10.1016/j.jocs.2013.10.002
[13]	LIU Q, WU L, XIAO W S, et al. A novel hybrid bat algorithm for solving continuous optimization problems[J]. Applied Soft Computing, 2018, 73: 67-82. doi: 10.1016/j.asoc.2018.08.012
[14]	RAUF H, MALIK S, SHOAIB U, et al. Adaptive inertia weight bat algorithm with sugeno-function fuzzy search[J]. Applied Soft Computing, 2020, 90: 106159. doi: 10.1016/j.asoc.2020.106159
[15]	LYU S L, LI Z, HUANG Y L, et al. Improved self-adaptive bat algorithm with step-control and mutation mechanisms[J]. Journal of Computational Science, 2019, 30: 65-78. doi: 10.1016/j.jocs.2018.11.002
[16]	YANG X, GANDOMI A. Bat algorithm: a novel approach for global engineering optimization[J]. Engineering Computations, 2012, 29(5): 464-483. doi: 10.1108/02644401211235834
[17]	OSABA E, YANG X, DIAZ F, et al. An improved discrete bat algorithm for symmetric and asymmetric traveling salesman problems[J]. Engineering Applications of Artificial Intelligence, 2016, 48: 59-71. doi: 10.1016/j.engappai.2015.10.006
[18]	TALBI N. Design of fuzzy controller rule base using bat algorithm[J]. Energy Procedia, 2019, 162: 241-250. doi: 10.1016/j.egypro.2019.04.026
[19]	HASANÇEBI O, TEKE T, PEKCAN O. A bat-inspired algorithm for structural optimization[J]. Computers & Structures, 2013, 128: 77-90.
[20]	WANG G G, CHU H C, SEYEDALI M. Three-dimensional path planning for UCAV using an improved bat algorithm[J]. Aerospace Science and Technology, 2016, 49: 231-238. doi: 10.1016/j.ast.2015.11.040
[21]	HOLUB J, FOO J, KILIVARAPU V, et al. Three dimensional multi-objective UAV path planning using digital pheromone particle swarm optimization[C]//Proceedings of 53rd AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference. Reston: AIAA, 2012: 1525. HOLUB J, FOO J, KILIVARAPU V, et al. Three dimensional multi-objective UAV path planning using digital pheromone particle swarm optimization[C]//Proceedings of 53rd AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference. Reston: AIAA, 2012: 1525.
[22]	DADGAR M, JAFARI S, HAMZEH A. A PSO-based multi-robot cooperation method for target searching in unknown environments[J]. Neurocomputing, 2016, 177: 62-74. doi: 10.1016/j.neucom.2015.11.007
[23]	TAKAHAMA T, SAKAI S. Constrained optimization by the ε constrained differential evolution with an archive and gradient-based mutation[C]//Proceedings of IEEE Congress on Evolutionary Computation. Piscataway: IEEE Press, 2010: 1-9.
[24]	TAKAHAMA T, SAKAI S. Solving constrained optimization problems by the ε constrained particle swarm optimizer with adaptive velocity limit control[C]//Proceedings of IEEE Conference on Cybernetics & Intelligent Systems. Piscataway: IEEE Press, 2006: 1-7. TAKAHAMA T, SAKAI S. Solving constrained optimization problems by the ε constrained particle swarm optimizer with adaptive velocity limit control[C]//Proceedings of IEEE Conference on Cybernetics & Intelligent Systems. Piscataway: IEEE Press, 2006: 1-7.
[25]	WANG L, LI P. An effective differential evolution with level comparison for constrained engineering design[J]. Structural and Multidisciplinary Optimization, 2010, 41(6): 947-963. doi: 10.1007/s00158-009-0454-5
[26]	ALLAIRE FCJ, TARBOUCHI M, LABONTÉ G, et al. Real-time UAV path-terrain collision evaluation on FPGA[C]//Proceedings of 2018 4th International Conference on Optimization and Applications (ICOA). Piscataway: IEEE Press, 2018: 1-5. ALLAIRE FCJ, TARBOUCHI M, LABONTÉ G, et al. Real-time UAV path-terrain collision evaluation on FPGA[C]//Proceedings of 2018 4th International Conference on Optimization and Applications (ICOA). Piscataway: IEEE Press, 2018: 1-5.
[27]	SHANMUGAVEL M, TSOURDOS A, ZBIKOWSKI R, et al. Path planning of multiple UAVs using dubins sets[C]//Proceedings of AIAA Guidance, Navigation, and Control Conference and Exhibit. Reston: AIAA, 2005: 5827. SHANMUGAVEL M, TSOURDOS A, ZBIKOWSKI R, et al. Path planning of multiple UAVs using dubins sets[C]//Proceedings of AIAA Guidance, Navigation, and Control Conference and Exhibit. Reston: AIAA, 2005: 5827.