基于改进Kinky Inference的输出调节自适应无拖曳控制

孙笑云; 沈强; 吴树范

doi:10.13700/j.bh.1001-5965.2022.0504

基于改进Kinky Inference的输出调节自适应无拖曳控制

doi: 10.13700/j.bh.1001-5965.2022.0504

孙笑云^{1, 2},
沈强^{1, 2, ,},
吴树范^{1, 2}

1.
上海市引力波探测前沿科学研究基地，上海 200240
2.
上海交通大学航空航天学院，上海 200240

基金项目: 科技部重点研发计划“引力波探测”重点专项课题(2020YFC2200800)；国家自然科学基金(62103275)；上海市自然科学基金面上项目(20ZR1427000)

详细信息

通讯作者:
E-mail：qiangshen@sjtu.edu.cn

中图分类号: V448.22.3
计量
- 文章访问数: 225
- HTML全文浏览量: 121
- PDF下载量: 6
- 被引次数: 0
出版历程
- 收稿日期: 2022-06-20
- 录用日期: 2022-07-22
- 网络出版日期: 2023-01-04
- 整期出版日期: 2024-05-29

Output regulation adaptive drag-free control with enhanced Kinky Inference

SUN Xiaoyun^{1, 2},
SHEN Qiang^{1, 2
, ,},
WU Shufan^{1, 2}

1.
Shanghai Frontiers Science Center of Gravitational Wave Detection，Shanghai 200240，China
2.
School of Aeronautics and Astronautics，Shanghai Jiao Tong University，Shanghai 200240，China

Funds: The key special topic of the Ministry of Science and Technology’s major research and development plan “Gravitational Wave Detection” (2020YFC2200800); National Natural Science Foundation of China (62103275); General Project of Shanghai Natural Science Foundation (20ZR1427000)

More Information

Corresponding author: E-mail：qiangshen@sjtu.edu.cn

摘要

摘要:
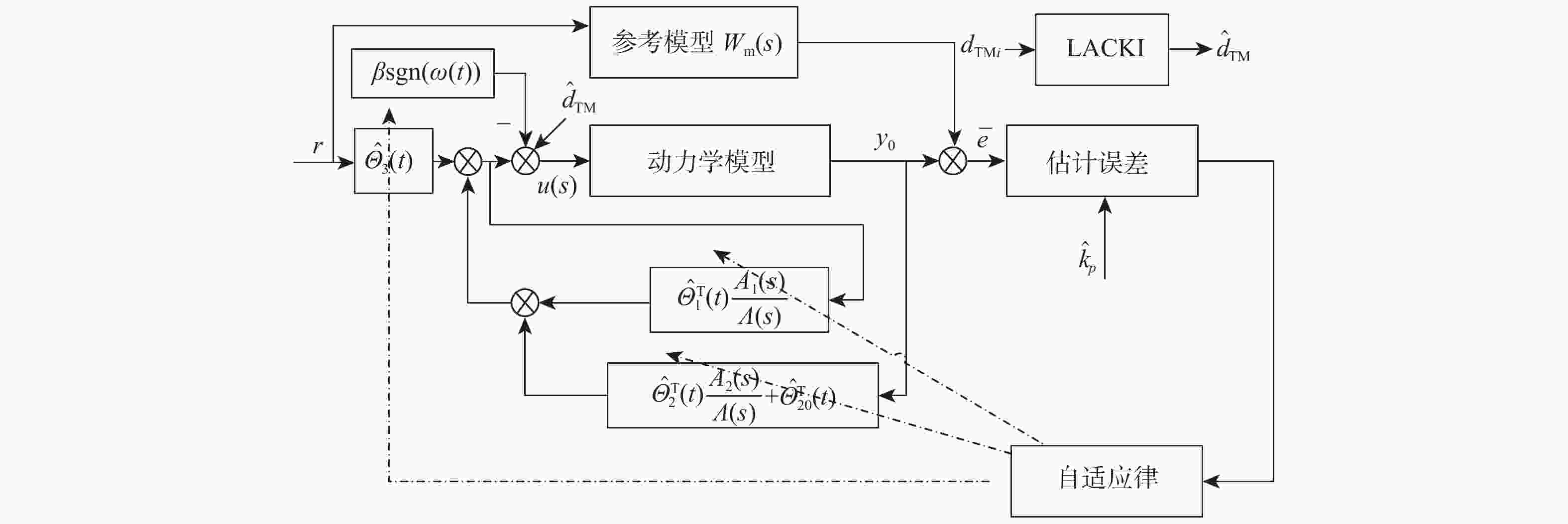
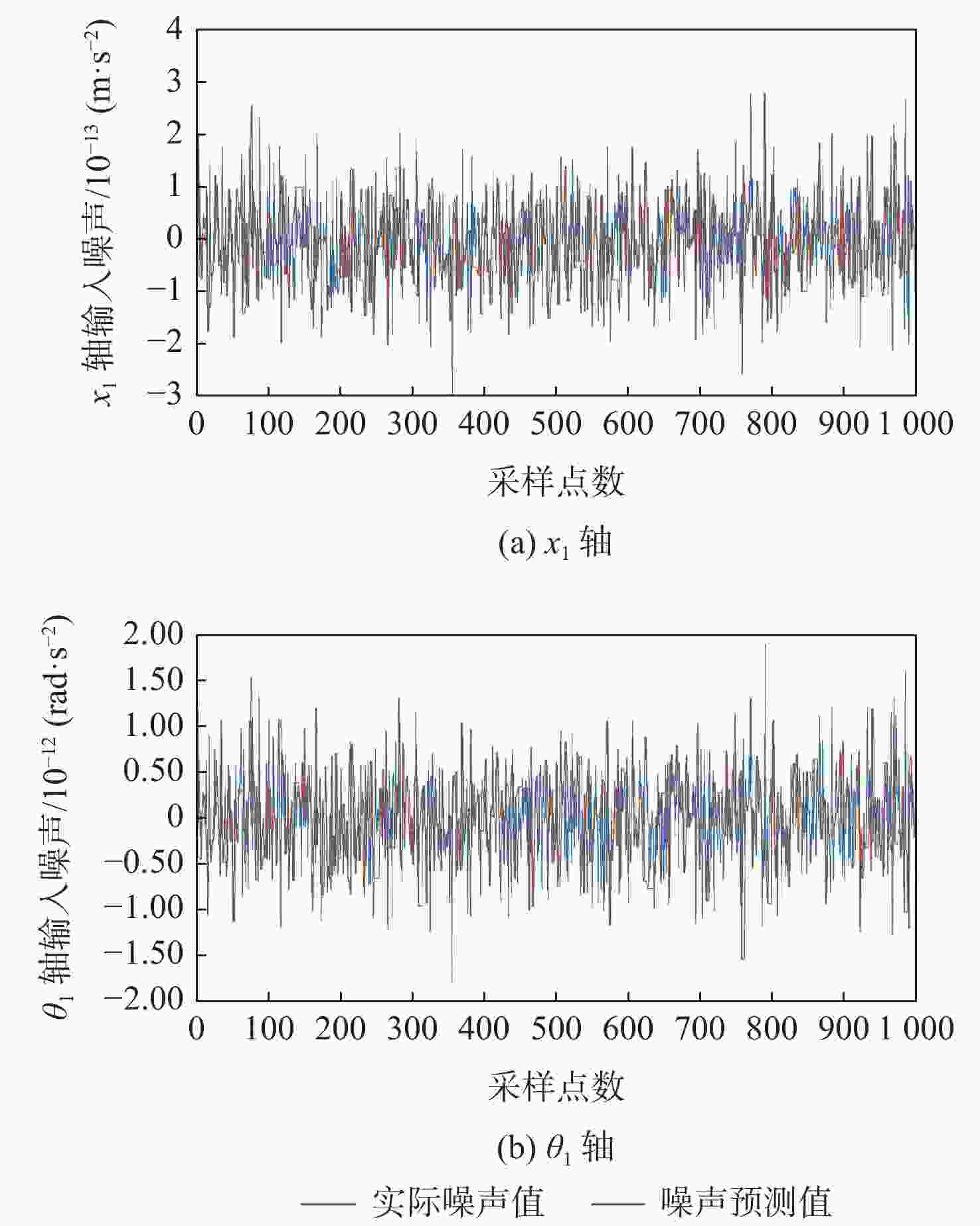
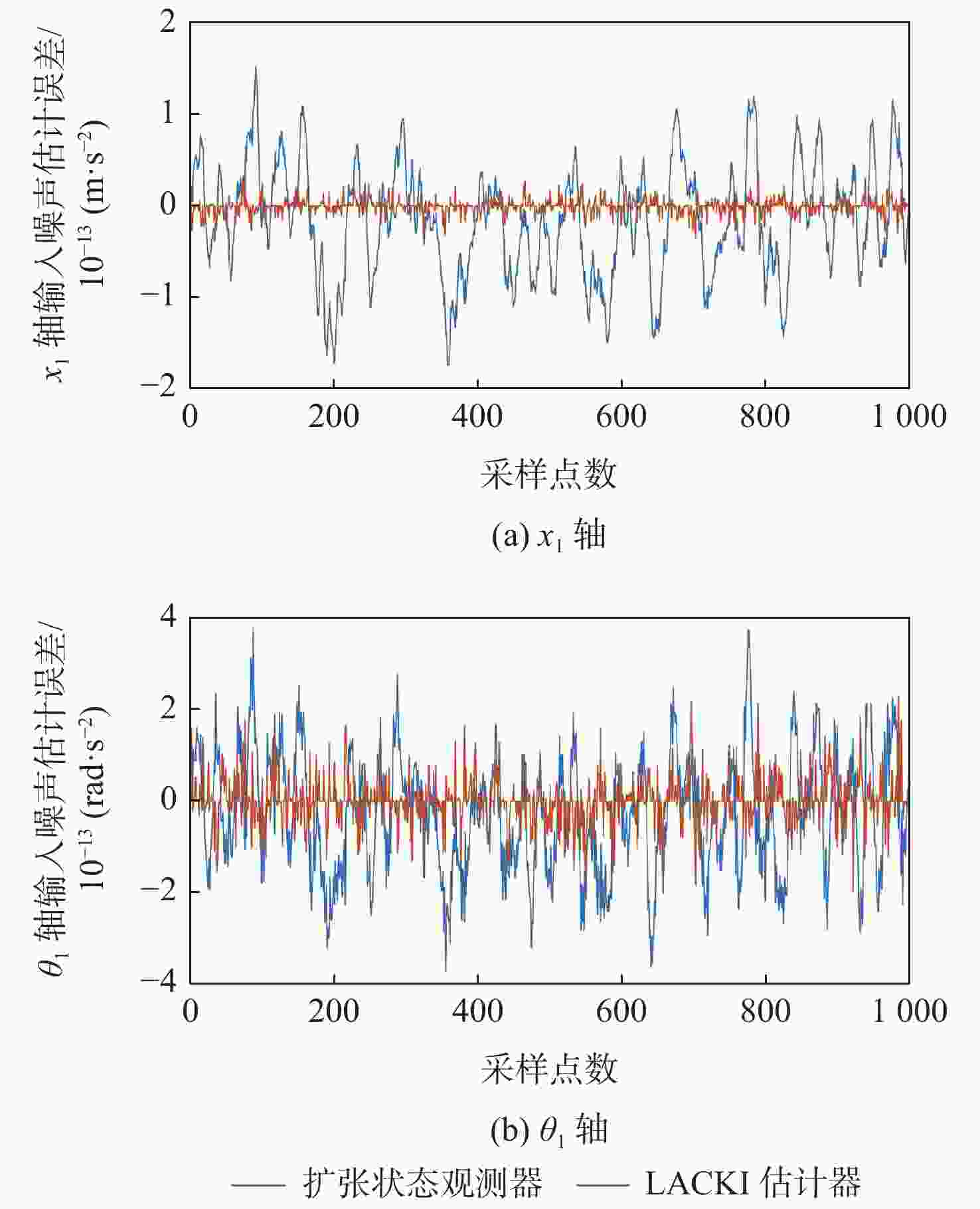
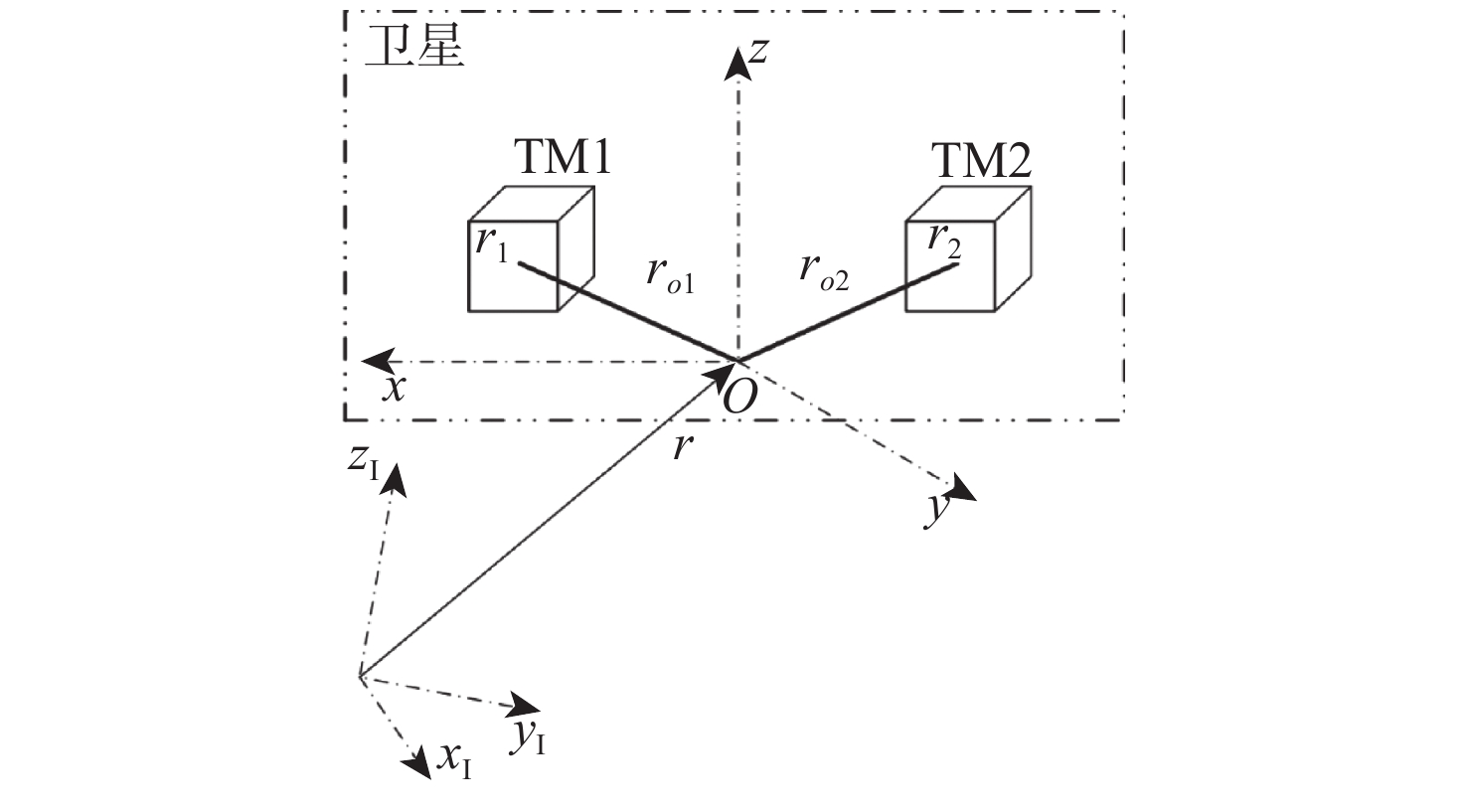
在空间引力波探测任务中，航天器内部检验质量因存在载荷硬件噪声、环境噪声及微推力器耦合噪声等复杂干扰，影响其无拖曳控制精度，难以实现超净、超稳控制需求。提出一种基于惰性适配Lipschitz常数Kinky Inference (LACKI)的航天器自适应无拖曳控制方法，运用监督学习规则实现先验知识不足、样本数据存在损坏时外界干扰的逼近和抑制，及基于输出调节的模型参考自适应控制（MRAC）方法实现检验质量精确的无拖曳控制。数值仿真验证了无拖曳控制中敏感轴平动和转动自由度的状态响应性能及LACKI规则针对外界干扰的估计效果，通过与常规线性控制方法的对比，验证了所提方法对于提高无拖曳控制精度的有效性。
- 监督学习 /
- Lipschitz估计 /
- 模型参考自适应控制 /
- 无拖曳控制 /
- 输出调节 /
- Kinky Inference
Abstract:
Achieving ultra-precision and ultra-stable requirements is challenging in the space gravitational wave detection mission due to complex disturbances present in the spacecraft's internal test masses, including load hardware noise, environmental noise, and micro-thrust coupling noise.These disturbances impact the accuracy of drag-free control. In this paper, an adaptive drag-free control method is proposed for spacecraft based on the lazily adapted Lipschitz constant Kinky Inference (LACKI) scheme. When there is not enough empirical data, the LACKI scheme is used to approximate disturbances and suppress non-Lipschitz components. The model reference adaptive control (MRAC), which is based on output regulation, is then used to precise the drag-free control of test masses. Numerical simulation verifies the state response performance of the translational and rotational degrees of freedom of sensitive axes and the estimation effect of the LACKI rule for random discontinuous disturbances, and the accuracy conclusion of the drag-free control loop is obtained.
- supervised learning /
- Lipschitz estimation /
- model reference adaptive control /
- drag-free control /
- output regulation /
- Kinky Inference

HTML全文

图 1 LISA Pathfinder航天器构型^[10]

Figure 1. LISA Pathfinder spacecraft configuration^[10]

下载: 全尺寸图片幻灯片

图 2 控制结构

Figure 2. Control structure

下载: 全尺寸图片幻灯片

图 3 LACKI规则下各自由度输入噪声估计

Figure 3. Input noise observation for each degree of freedom under LACKI rule

下载: 全尺寸图片幻灯片

图 4 LACKI-MRAC方案下增量学习性能

Figure 4. Supervised learning performance under LACKI-MRAC scheme

下载: 全尺寸图片幻灯片

图 5 不同方案下噪声估计误差对比

Figure 5. Noise estimation error comparison of various schemes

下载: 全尺寸图片幻灯片

图 6 LACKI-MRAC方案与QFT方案位移响应对比

Figure 6. Displacement response comparison between LACKI-MRAC scheme and QFT scheme

下载: 全尺寸图片幻灯片

参考文献(20)

[1]	FICHTER W, GATH P, VITALE S, et al. LISA Pathfinder drag-free control and system implications[J]. Classical and Quantum Gravity, 2005, 22(10): S139-S148. doi: 10.1088/0264-9381/22/10/002
[2]	MOBLEY F, FOUNTAIN G, SADILEK A, et al. Electromagnetic suspension for the tip-II satellite[J]. IEEE Transactions on Magnetics, 1975, 11(6): 1712-1716. doi: 10.1109/TMAG.1975.1058972
[3]	WU S F, FERTIN D. Spacecraft drag-free attitude control system design with quantitative feedback theory[J]. Acta Astronautica, 2008, 62(12): 668-682. doi: 10.1016/j.actaastro.2008.01.038
[4]	LIAN X B, ZHANG J X, LU L, et al. Frequency separation control for drag-free satellite with frequency-domain constraints[J]. IEEE Transactions on Aerospace and Electronic Systems, 2021, 57(6): 4085-4096. doi: 10.1109/TAES.2021.3088456
[5]	马浩君, 韩鹏, 高东, 等. 深空双质量块无拖曳卫星H_∞鲁棒控制器设计[J]. 哈尔滨工业大学学报, 2021, 53(2): 1-13. MA H J, HAN P, GAO D, et al. H_∞robust controller design for deep space drag-free satellite with two test masses[J]. Journal of Harbin Institute of Technology, 2021, 53(2): 1-13 (in Chinese).
[6]	张锦绣, 董晓光, 曹喜滨. 基于无速度测量的无拖曳卫星自适应控制方法[J]. 宇航学报, 2014, 35(4): 447-453. ZHANG J X, DONG X G, CAO X B. An adaptive controller for drag-free satellites without velocity measurement[J]. Journal of Astronautics, 2014, 35(4): 447-453 (in Chinese).
[7]	胡明, 李洪银, 周泽兵. 无拖曳控制技术及其应用[J]. 载人航天, 2013, 19(2): 61-69. HU M, LI H Y, ZHOU Z B. Drag-free control technology and its applications[J]. Manned Spaceflight, 2013, 19(2): 61-69 (in Chinese).
[8]	王玉爽. 无拖曳卫星控制方法研究[D]. 哈尔滨: 哈尔滨工业大学, 2011. WANG Y S. Research on control method of towless satellite[D]. Harbin: Harbin Institute of Technology, 2011 (in Chinese).
[9]	WANG X D, LONG J, ZHU Q, et al. Drag-free control for cold air thrusters based on variable universe adaptive fuzzy PID[C]// 2014 IEEE International Conference on Information and Automation (ICIA). Piscataway: IEEE Press, 2014: 159-163.
[10]	付海清, 吴树范, 刘梅林, 等. 基于干扰观测器的空间惯性传感器自适应控制[J]. 北京航空航天大学学报, 2023, 49(10): 2799-2806. FU H Q, WU S F, LIU M L, et al. Disturbance-observer based adaptive control for space inertial sensor[J]. Journal of Beijing University of Aeronautics and Astronautics, 2023, 49(10): 2799-2806 (in Chinese).
[11]	FAN H J, ZHAO X, WANG Y J, et al. Adaptive failure compensation control for LEO drag-free satellite with actuator failures and disturbances[C]// 2016 Chinese Control and Decision Conference (CCDC). Piscataway: IEEE Press, 2016: 1651-1656.
[12]	ZHAO X, FAN H J, WANG W. An adaptive compensation control scheme for LEO drag-free satellite under actuator failure[C]// 2016 35th Chinese Control Conference (CCC). Piscataway: IEEE Press, 2016: 813-818.
[13]	SUN X Y, SHEN Q, WU S F. Partial state feedback MRAC-based reconfigurable fault-tolerant control of drag-free satellite with bounded estimation error[J]. IEEE Transactions on Aerospace and Electronic Systems, 2023, 59(5): 6570-6586.
[14]	GUO J X, TAO G, LIU Y. A multivariable MRAC scheme with application to a nonlinear aircraft model[J]. Automatica, 2011, 47(4): 804-812. doi: 10.1016/j.automatica.2011.01.069
[15]	CALLIESS J P, ROBERTS S J, RASMUSSEN C E, et al. Lazily Adapted Constant Kinky Inference for nonparametric regression and model-reference adaptive control[J]. Automatica, 2020, 122: 109216. doi: 10.1016/j.automatica.2020.109216
[16]	JAN-PETER C. Conservative decision-making and inference in uncertain dynamical systems[D]. Oxford, UK: University of Oxford, 2014.
[17]	CALLIESS J P. Lipschitz optimisation for lipschitz interpolation[C]// 2017 American Control Conference (ACC). Piscataway: IEEE Press, 2017: 3141-3146.
[18]	MCNAMARA P, VITALE S, DANZMANN K. LISA pathfinder[J]. Classical and Quantum Gravity, 2008, 25(11): 114034. doi: 10.1088/0264-9381/25/11/114034
[19]	WU S F, GIULICCHI L, FENAL T, et al. Attitude stabilization of LISA pathfinder spacecraft using colloidal micro-newton thrusters[C]//Proceedings of the AIAA Guidance, Navigation, and Control Conference. Reston, Virigina: AIAA, 2010: AIAA2010-8198.
[20]	WU S F, GIULICCHI L, FENAL T, et al. Attitude control of LISA pathfinder spacecraft with micro-newton FEEP thrusters under multiple failures[C]//Proceedings of the AIAA Guidance, Navigation, and Control Conference. Reston: AIAA, 2010: AIAA2010-8199.