A fault propagation path analysis method for flight control system based on improved FPPN
-
摘要:
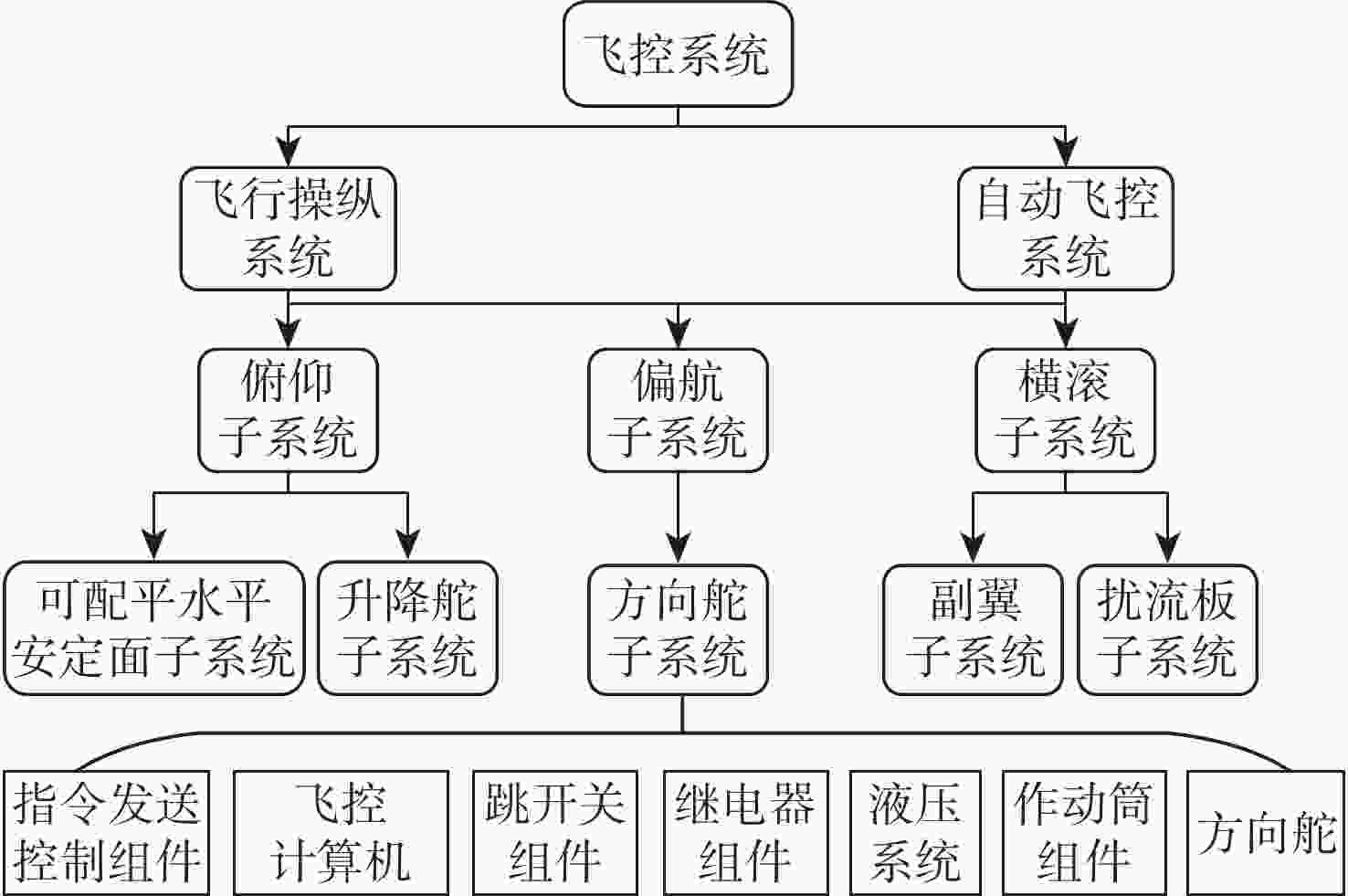
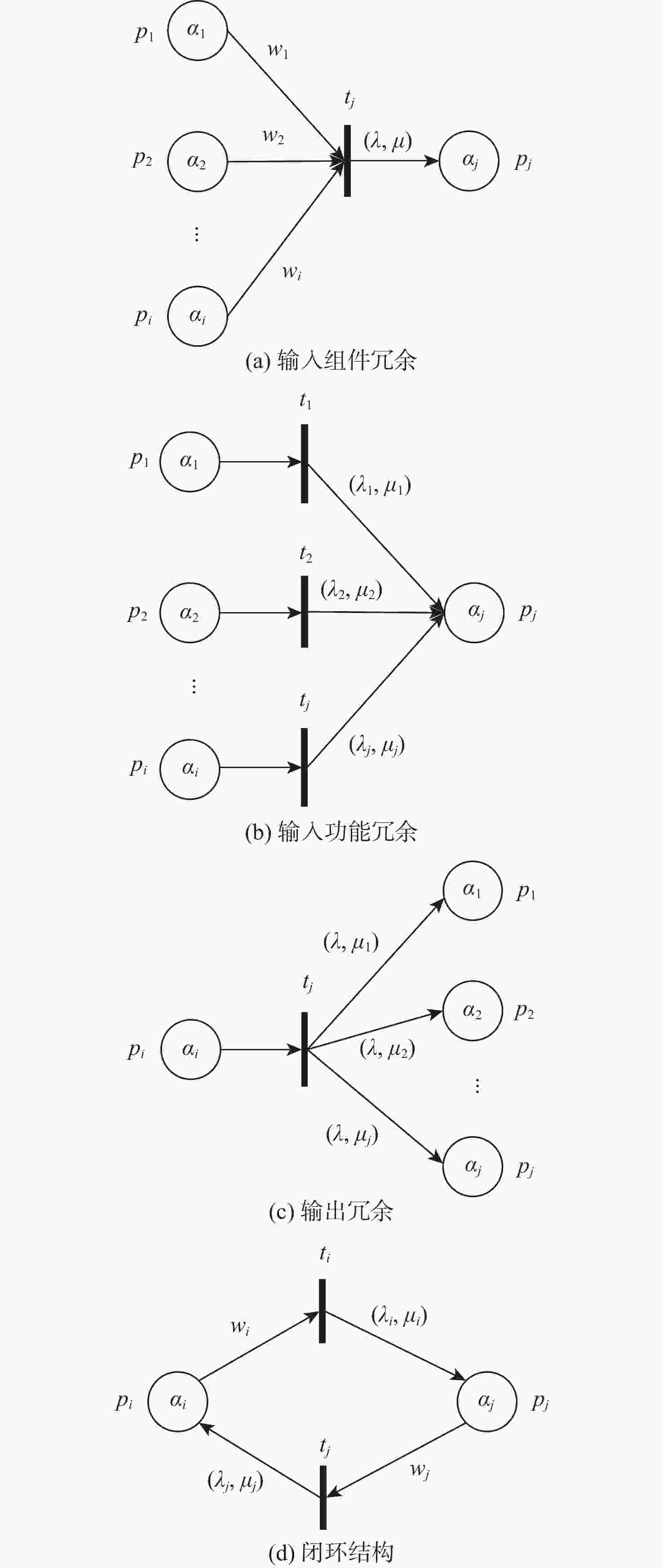
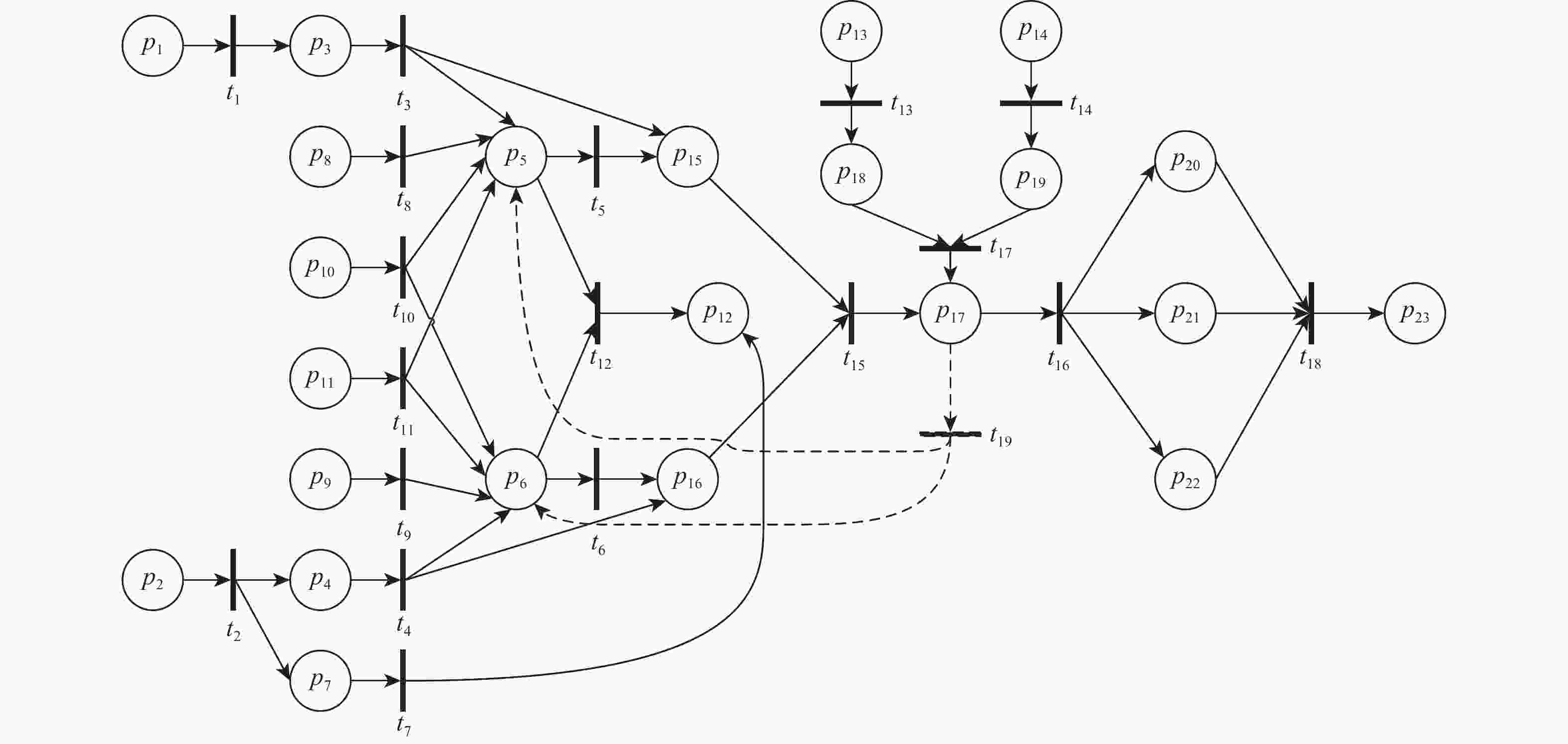
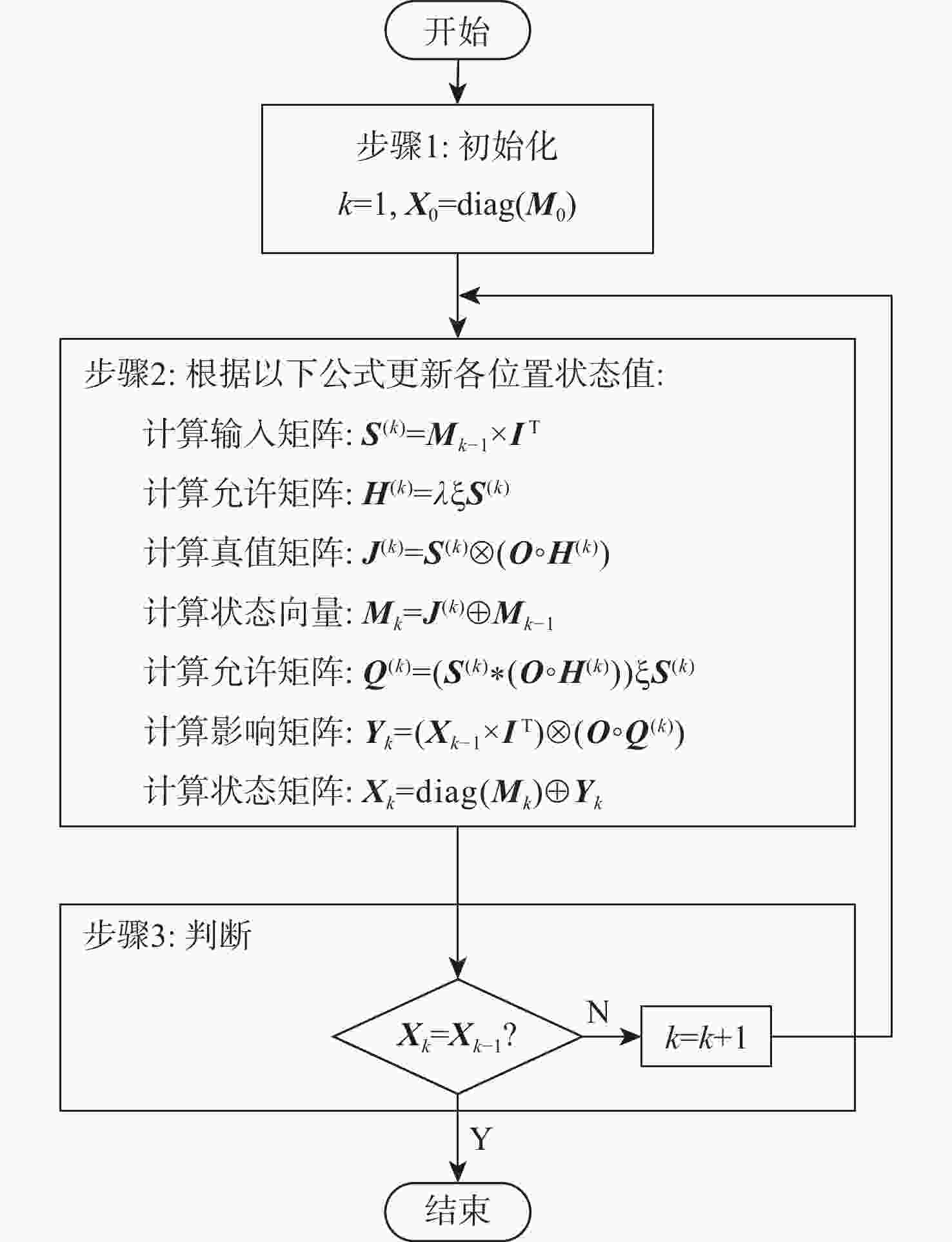
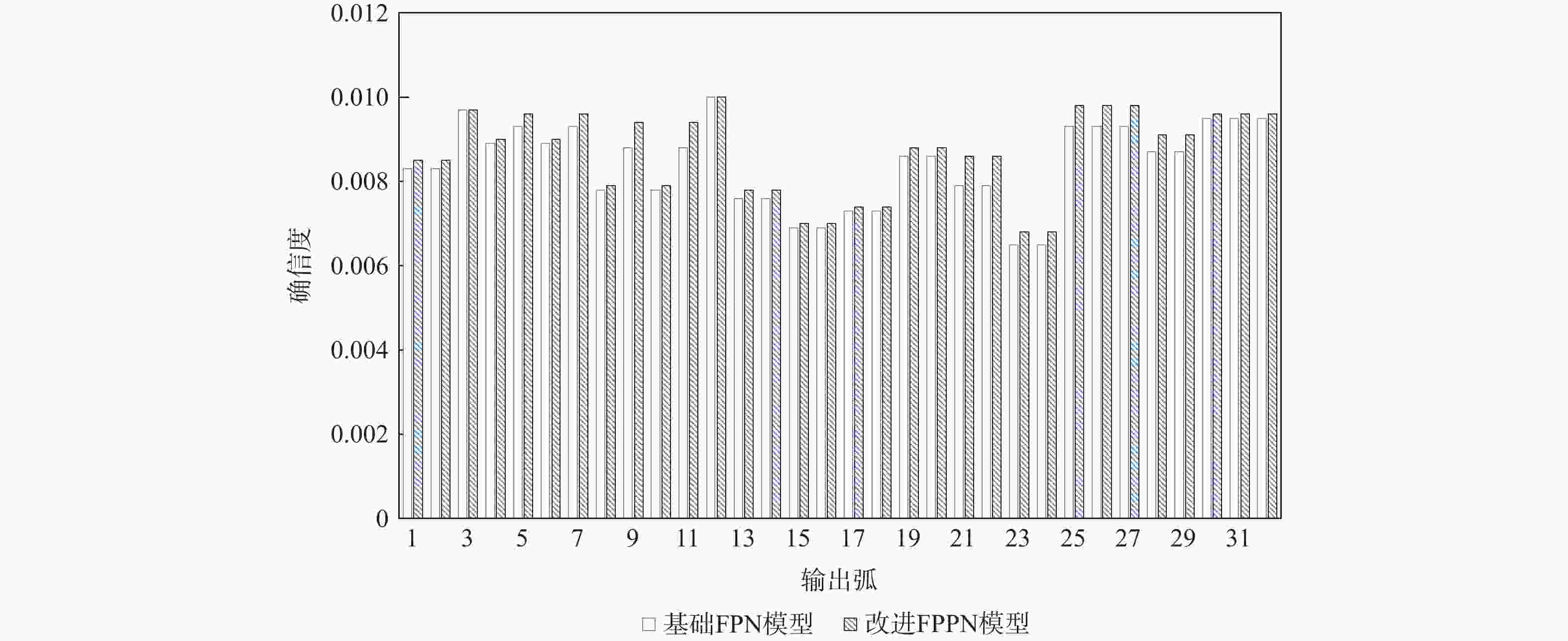
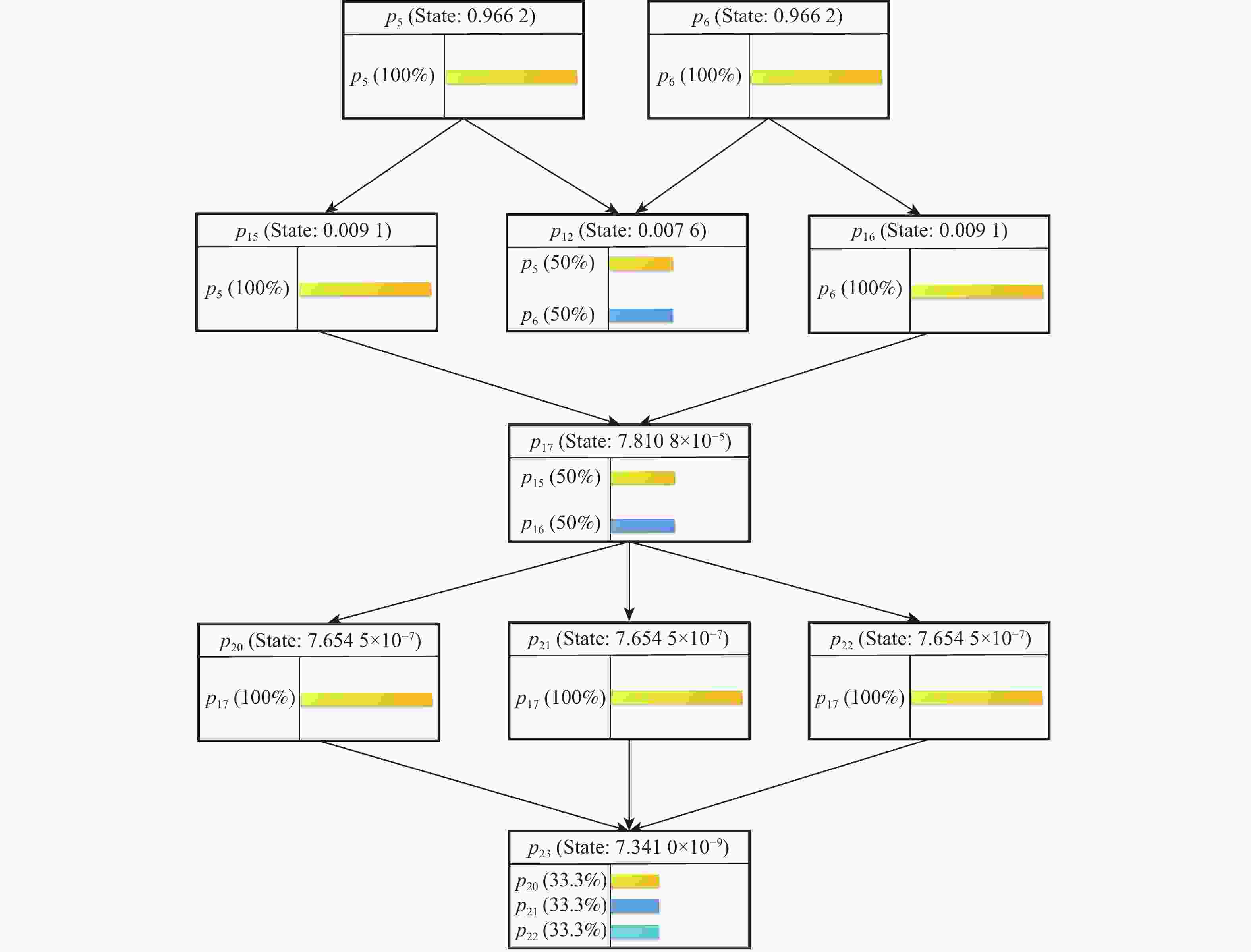
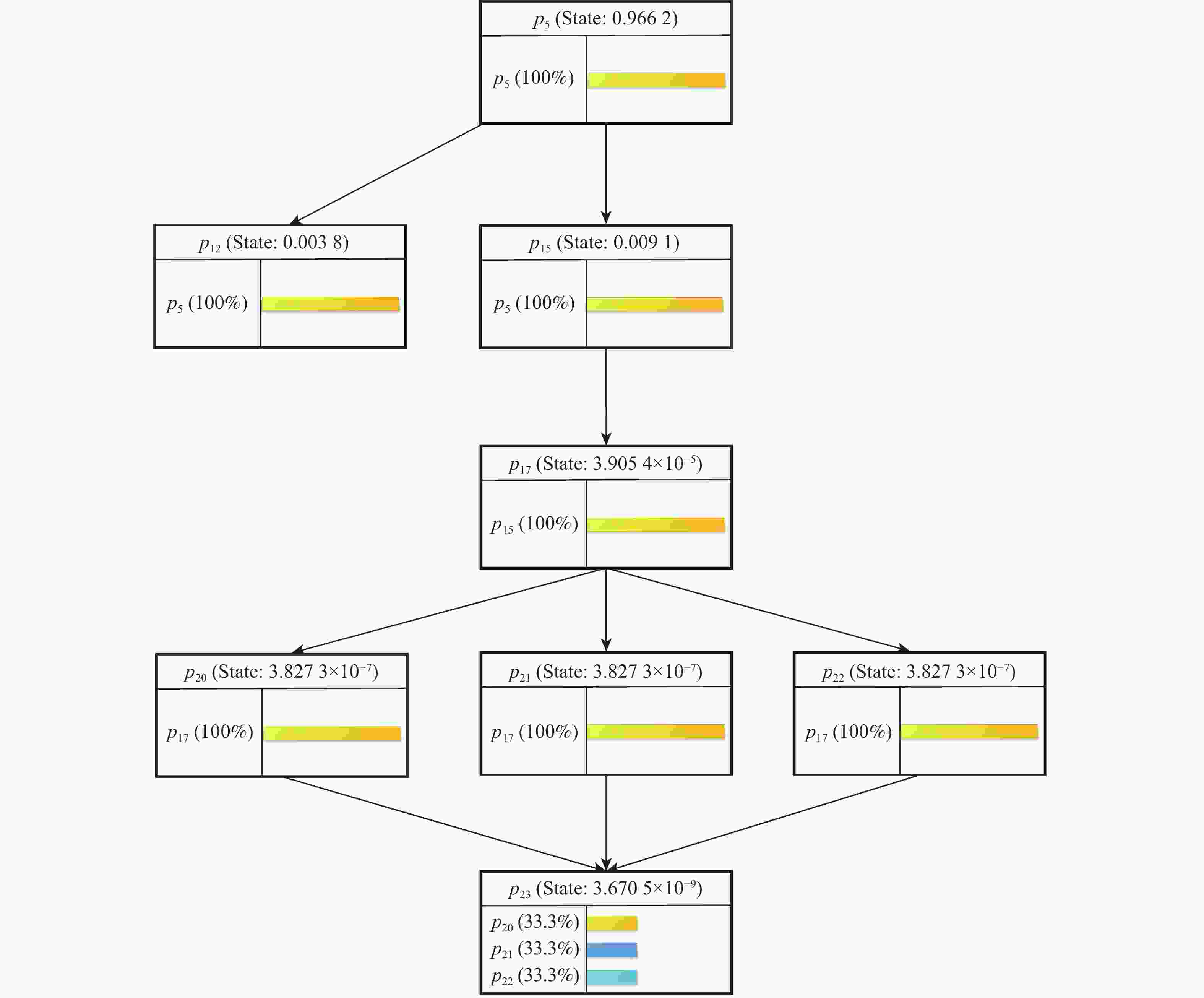
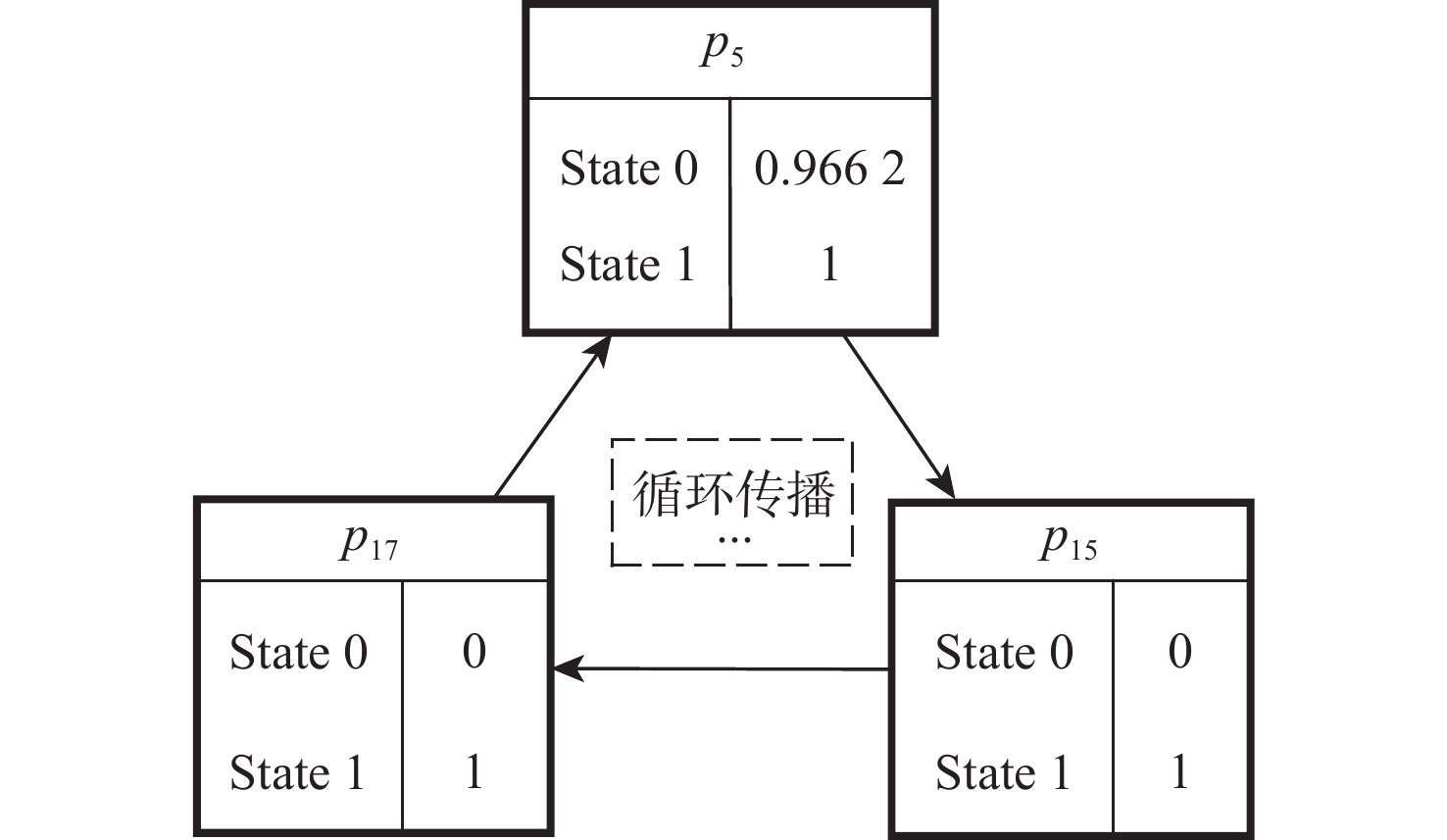
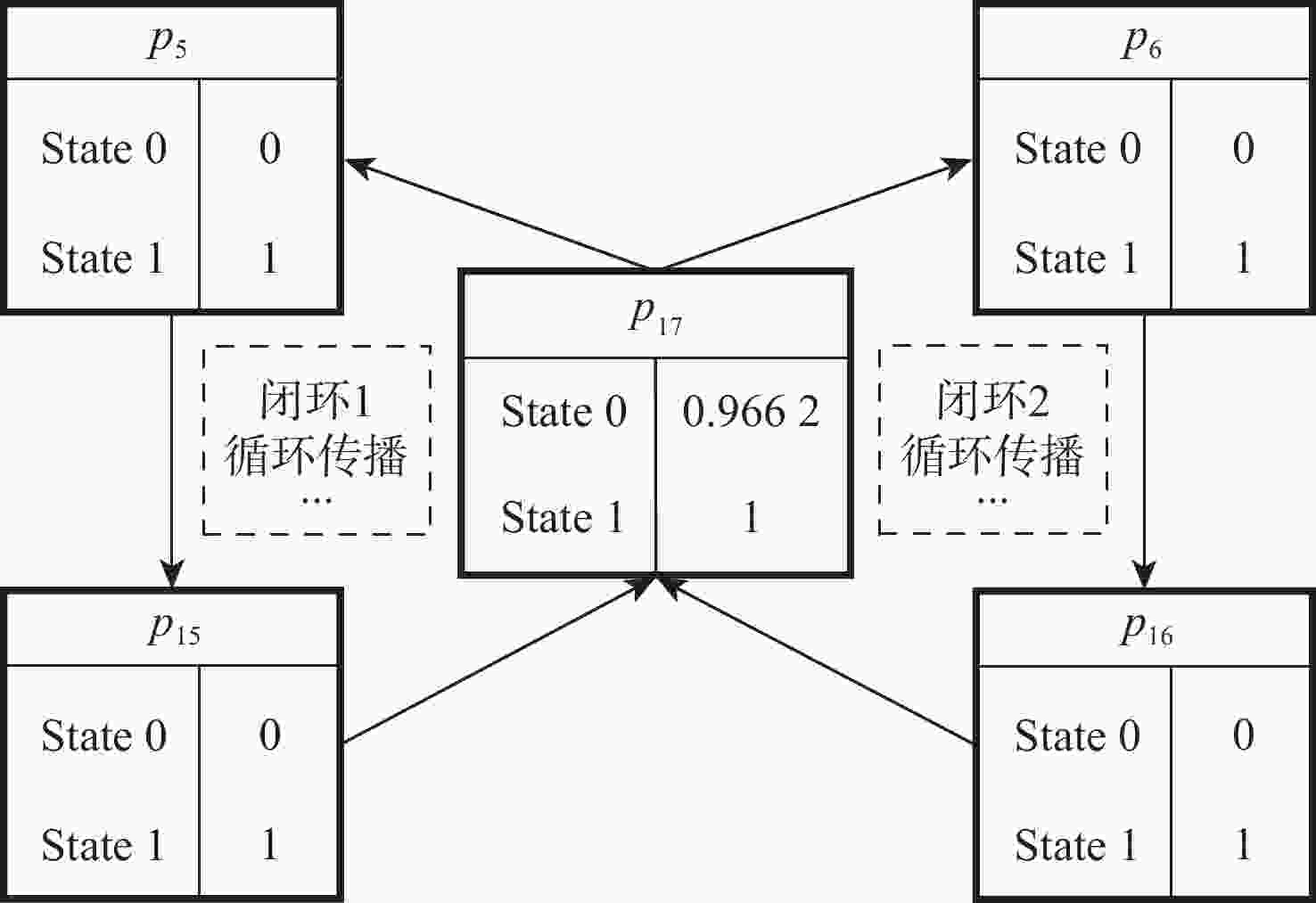
针对飞控系统多冗余、多闭环的结构特性，结合有向图模型和模糊Petri网（ FPN ）模型，构建飞控系统故障传播模糊概率Petri网（ FPPN ）模型，以解决飞控系统特定结构下的故障传播路径问题。改进的FPPN模型包含飞控系统有向图模型、故障传播特性量化计算模型和故障传播FPPN模型3个部分。采用面向对象技术分析飞控系统的功能行为和物理结构，综合复杂网络理论，构建系统故障传播有向图模型；引入Floyd算法，开展系统耦合关联分析，基于节点的度和边介数定义系统故障传播特性；在有向图模型的基础上，提出相应的结构映射规则，构建飞控系统故障传播FPPN模型，融合改进后的参数量化方法，设定2种推理算法对系统多冗余、闭环结构特性下的故障传播路径进行有效分析。通过数值分析与实例验证，获取飞控系统典型故障传播路径及路径上相关节点的状态值，验证所提方法的有效性。
-
关键词:
- 飞控系统 /
- 复杂网络理论 /
- 有向图模型 /
- 模糊概率Petri网模型 /
- 故障传播路径分析
Abstract:In view of the multi-redundancy and multi-closed-loop structural characteristics of the flight control system, the directed graph model and the fuzzy Petri net (FPN) model were used, and a fuzzy probability Petri net (FPPN) model for fault propagation of the flight control system was constructed, so as to solve the fault propagation path of the flight control system with a specific structure. The improved FPPN model consisted of three parts:directed graph model of flight control system, quantitative calculation model for fault propagation characteristics, and FPPN model for fault propagation. A directed graph model of system fault propagation was built by analyzing the functional behavior and physical structure of the flight control system through object-oriented technology and utilizing complex network theory. The Floyd algorithm was introduced to carry out the system coupling correlation analysis, and the system fault propagation characteristics were defined based on the two indicators of node degree and edge betweenness. On the basis of the directed graph model, the corresponding structure mapping rules were proposed. The FPPN model for fault propagation of the flight control system was constructed. With the improved parameter quantization method, two reasoning algorithms were set to effectively analyze the fault propagation paths of the system with multi-redundancy and closed-loop structure characteristics. Through numerical analysis and example verification, the typical fault propagation path of the flight control system and the status value of the relevant nodes on the path were obtained, so as to verify the effectiveness of the proposed method.
-
图 11 基础FPN模型与改进FPPN模型确信度对比
Figure 11. Comparison of confidence values between basic FPN and improved FPPN models
图 14 单闭环结构故障传播分析
Figure 14. Fault propagation analysis of single closed-loop structure
图 15 多闭环结构故障传播分析
Figure 15. Fault propagation analysis of multiple closed-loop structure
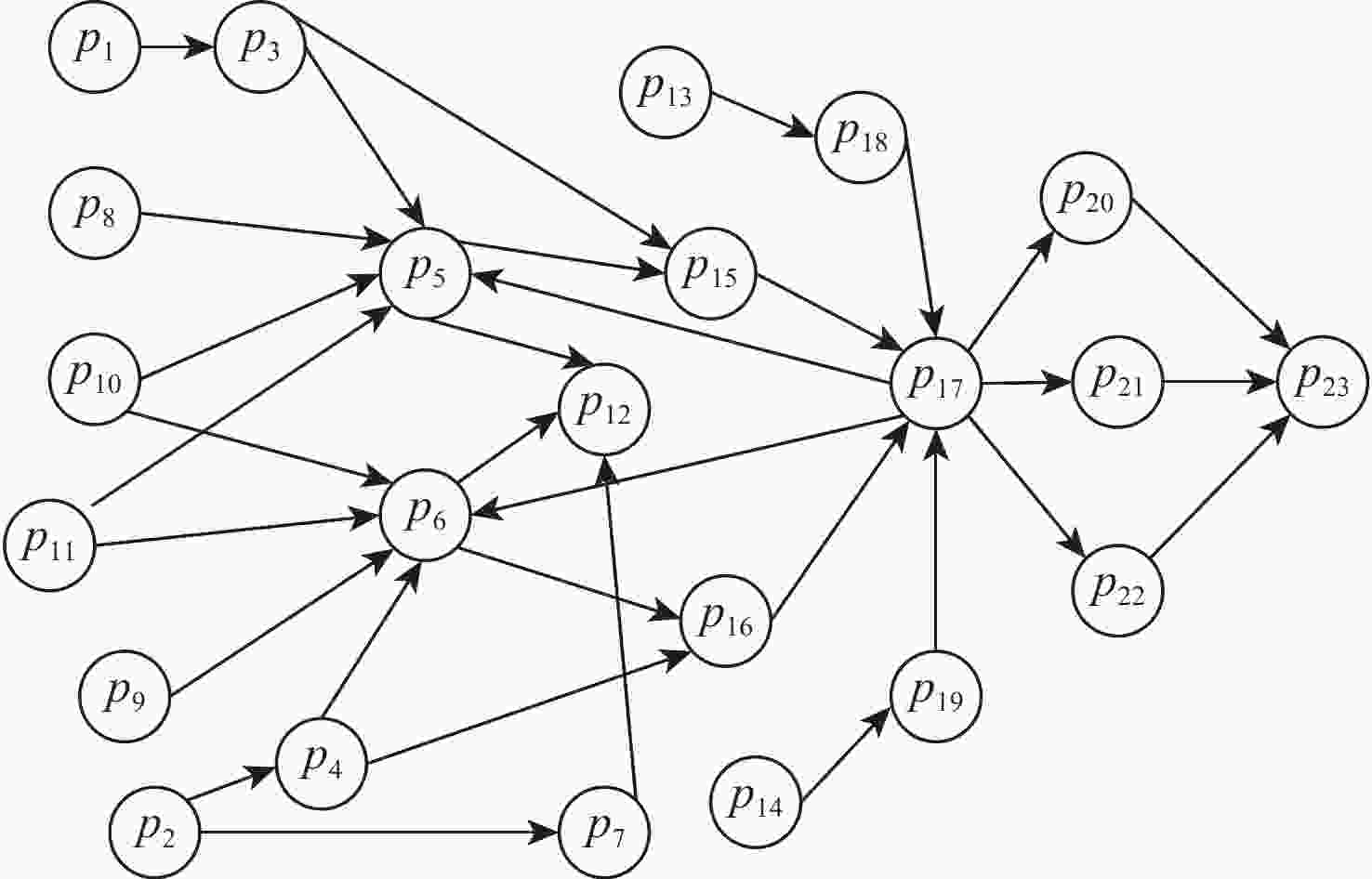
表 1 系统网络结构中各节点对应的部件编号
Table 1. Part number corresponding to each node in system network structure
节点pi 名称 1 直流汇流条1 2 直流汇流条2 3 飞行增稳计算机 1 的供电跳开关 4 飞行增稳计算机2的供电跳开关 5 飞行增稳计算机 1 6 飞行增稳计算机 2 7 供电跳开关 8 飞行增稳计算机 1 面板控制按钮 9 飞行增稳计算机 2 面板控制按钮 10 方向舵配平复位按钮 11 方向舵配平按钮 12 方向舵配平指示器 13 交流汇流条1 14 交流汇流条2 15 方向舵配平继电器 1 16 方向舵配平继电器 2 17 方向舵配平作动筒 18 偏航阻尼作动筒 1 供电跳开关 19 偏航阻尼作动筒 2 供电跳开关 20 方向舵伺服控制器G 21 方向舵伺服控制器B 22 方向舵伺服控制器Y 23 方向舵舵面 
下载: 导出CSV
表 2 各边的失效特性
Table 2. Failure characteristics of each edge
eij Hij eij Hij (1,3) 0.0083 (11,5) 0.0073 (2,4) 0.0083 (11,6) 0.0073 (2,7) 0.0097 (13,18) 0.0086 (3,5) 0.0089 (14,19) 0.0086 (3,15) 0.0093 (15,17) 0.0079 (4,6) 0.0089 (16,17) 0.0079 (4,16) 0.0093 (17,5) 0.0065 (5,12) 0.0078 (17,6) 0.0065 (5,15) 0.0088 (17,20) 0.0093 (6,12) 0.0078 (17,21) 0.0093 (6,16) 0.0088 (17,22) 0.0093 (7,12) 0.0100 (18,17) 0.0087 (8,5) 0.0076 (19,17) 0.0087 (9,6) 0.0076 (20,23) 0.0095 (10,5) 0.0069 (21,23) 0.0095 (10,6) 0.0069 (22,23) 0.0095
下载: 导出CSV
表 3 节点传播特性
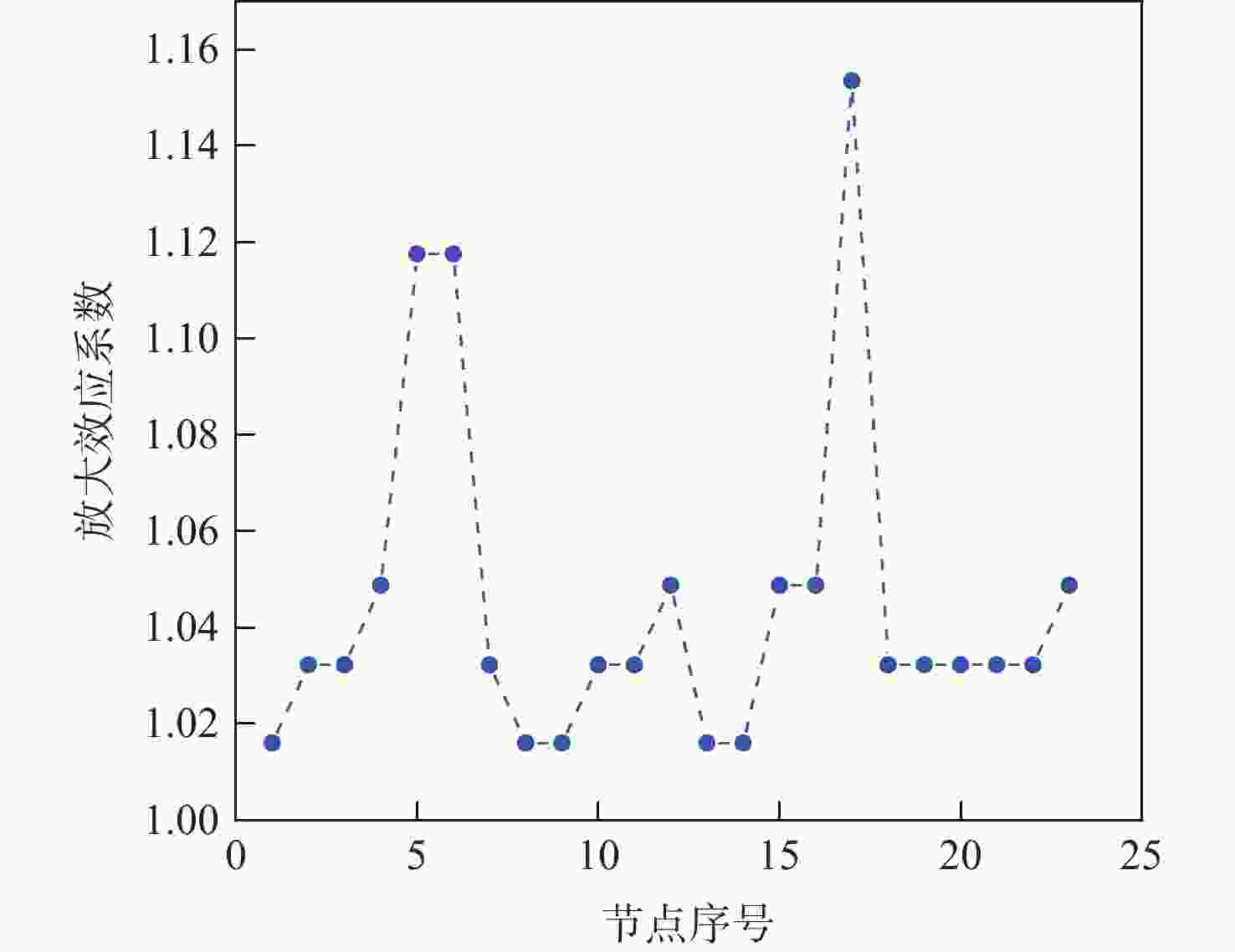
Table 3. Node propagation characteristics
pi si pi si 1 0.0159 13 0.0159 2 0.0317 14 0.0159 3 0.0317 15 0.0476 4 0.0476 16 0.0476 5 0.1111 17 0.1428 6 0.1111 18 0.0317 7 0.0317 19 0.0317 8 0.0159 20 0.0317 9 0.0159 21 0.0317 10 0.0317 22 0.0317 11 0.0317 23 0.0476 12 0.0476
下载: 导出CSV
表 4 边传播特性
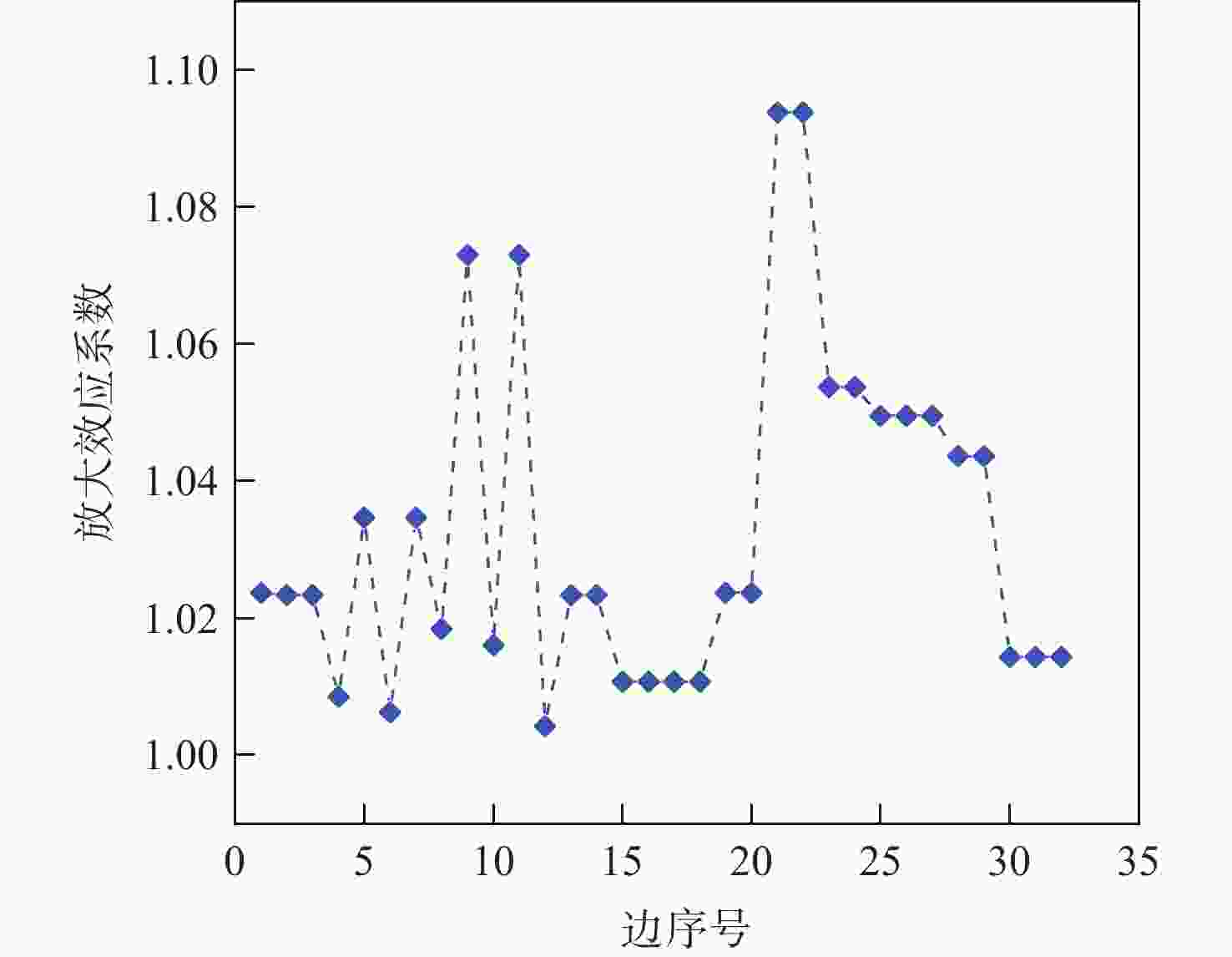
Table 4. Edge propagation characteristics
eij Sij eij Sij (1,3) 0.0234 (11,5) 0.0106 (2,4) 0.0213 (11,6) 0.0106 (2,7) 0.0042 (13,18) 0.0234 (3,5) 0.0085 (14,19) 0.0234 (3,15) 0.0314 (15,17) 0.0897 (4,6) 0.0063 (16,17) 0.0897 (4,16) 0.0341 (17,5) 0.0523 (5,12) 0.0182 (17,6) 0.0523 (5,15) 0.0705 (17,20) 0.0483 (6,12) 0.0160 (17,21) 0.0483 (6,16) 0.0705 (17,22) 0.0483 (7,12) 0.0042 (18,17) 0.0427 (8,5) 0.0213 (19,17) 0.0427 (9,6) 0.0213 (20,23) 0.0142 (10,5) 0.0106 (21,23) 0.0142 (10,6) 0.0106 (22,23) 0.0142
下载: 导出CSV
-
[1] ISERMANN R. Mechatronic systems—Innovative products with embedded control[J]. Control Engineering Practice, 2008, 16(1): 14-29. doi: 10.1016/j.conengprac.2007.03.010 [2] 康文文, 李浩敏. 基于模型的飞机系统架构多视图表达方法[J]. 系统工程与电子技术, 2021, 43(11): 3266-3277. doi: 10.12305/j.issn.1001-506X.2021.11.27KANG W W, LI H M. Multi-view representation method of aircraft system architecture based on model[J]. Systems Engineering and Electronics, 2021, 43(11): 3266-3277(in Chinese). doi: 10.12305/j.issn.1001-506X.2021.11.27 [3] WANG C N, XING L D, PENG R, et al. Competing failure analysis in phased-mission systems with multiple functional dependence groups[J]. Reliability Engineering & System Safety, 2017, 164: 24-33. [4] 管祥民, 赵帅喆. 面向航空网络的机场风险传播网络[J]. 北京航空航天大学学报, 2023, 49(6): 1342-1351.GUAN X M, ZHAO S Z. Airport risk propagation network oriented to aviation network[J]. Journal of Beijing University of Aeronautics and Astronautics, 2023, 49(6): 1342-1351(in Chinese). [5] 张宏, 吕悦晶. 基于复杂网络的车载自组织网络脆弱性分析[J]. 北京航空航天大学学报, 2021, 47(8): 1543-1549.ZHANG H, LYU Y J. Vulnerability of vehicular ad hoc network based on complex network[J]. Journal of Beijing University of Aeronautics and Astronautics, 2021, 47(8): 1543-1549(in Chinese). [6] XU Y F, WANG Z, JIANG Y, et al. Small-world network analysis on fault propagation characteristics of water networks in eco-industrial parks[J]. Resources, Conservation and Recycling, 2019, 149: 343-351. doi: 10.1016/j.resconrec.2019.05.040 [7] LIU X F, AN S Q. Failure propagation analysis of aircraft engine systems based on complex network[C]//Proceedings of the 3rd International Symposium on Aircraft Airworthiness. Amsterdam: Elseiver, 2014, 80: 506-521. [8] LUAN L, SHEN G X, ZHANG Y Z, et al. Identification of key components of CNC lathe based on dynamic influence of fault propagation[J]. Applied Sciences, 2022, 12(12): 6187. doi: 10.3390/app12126187 [9] 袁健宝, 王政, 徐一凡, 等. 基于复杂网络边负载分配理论的化工过程级联故障风险传播路径[J]. 化工进展, 2019, 38(8): 3525-3533.YUAN J B, WANG Z, XU Y F, et al. Risk propagation path of cascading fault in chemical process based on edge load distribution in complex network[J]. Chemical Industry and Engineering Progress, 2019, 38(8): 3525-3533(in Chinese). [10] MI J H, LI Y F, YANG Y J, et al. Reliability assessment of complex electromechanical systems under epistemic uncertainty[J]. Reliability Engineering & System Safety, 2016, 152: 1-15. [11] CHEN X L, WANG J, ZHOU J L. Probability density estimation and Bayesian causal analysis based fault detection and root identification[J]. Industrial & Engineering Chemistry Research, 2018, 57(43): 14656-14664. [12] AMRANI N B, SAINTIS L, SARSRI D, et al. Evaluating the predicted reliability of mechatronic systems: State of the art[EB/OL]. (2016-06-19)[2022-06-19]. [13] SHARMA R K, SHARMA P. Qualitative and quantitative approaches to analyse reliability of a mechatronic system: A case[J]. Journal of Industrial Engineering International, 2015, 11(2): 253-268. doi: 10.1007/s40092-015-0098-6 [14] KUBO K, JANG S, TAKASHI T, et al. Quasi-Monte Carlo sampling method for simulation-based dynamic probabilistic risk assessment of nuclear power plants[J]. Journal of Nuclear Science and Technology, 2022, 59(3): 357-367. doi: 10.1080/00223131.2021.1971119 [15] PICCIALLI F, CUOMO S, GIAMPAOLO F, et al. Path prediction in IoT systems through Markov chain algorithm[J]. Future Generation Computer Systems, 2020, 109: 210-217. doi: 10.1016/j.future.2020.03.053 [16] 阎芳, 向晨阳, 董磊, 等. DIMA架构下飞机全电刹车系统故障传播行为分析与评估[J]. 航空学报, 2021, 42(9): 324674.YAN F, XIANG C Y, DONG L, et al. Analysis and evaluation of fault propagation behavior of aircraft all-electric brake system under DIMA architecture[J]. Acta Aeronautica et Astronautica Sinica, 2021, 42(9): 324674(in Chinese). [17] 申桂香, 栾兰, 张英芝, 等. 加工中心组件故障传播影响力评估[J]. 吉林大学学报(工学版), 2022, 52(1): 63-69.SHEN G X, LUAN L, ZHANG Y Z, et al. Fault propagation impact assessment of machining center components[J]. Journal of Jilin University (Engineering and Technology Edition), 2022, 52(1): 63-69(in Chinese). [18] LIU H C, LUAN X, LIN W L, et al. Grey reasoning Petri nets for large group knowledge representation and reasoning[J]. IEEE Transactions on Fuzzy Systems, 2020, 28(12): 3315-3329. doi: 10.1109/TFUZZ.2019.2949770 [19] SHI H, WANG L, LI X Y, et al. A novel method for failure mode and effects analysis using fuzzy evidential reasoning and fuzzy Petri nets[J]. Journal of Ambient Intelligence and Humanized Computing, 2020, 11(6): 2381-2395. doi: 10.1007/s12652-019-01262-w [20] WANG X L, LU F M, ZHOU M C, et al. A synergy-effect-incorporated fuzzy Petri net modeling paradigm with application in risk assessment[J]. Expert Systems with Applications, 2022, 199: 117037. doi: 10.1016/j.eswa.2022.117037 [21] LI W J, HE M, SUN Y B, et al. A novel layered fuzzy Petri nets modelling and reasoning method for process equipment failure risk assessment[J]. Journal of Loss Prevention in the Process Industries, 2019, 62: 103953. doi: 10.1016/j.jlp.2019.103953 [22] CHENG H B, HE Z Y, WANG Q, et al. Fault diagnosis method based on Petri nets considering service feature of information source devices[J]. Computers and Electrical Engineering, 2015, 46: 1-13. doi: 10.1016/j.compeleceng.2015.06.016 [23] LI L, XIE Y F, CEN L H, et al. A novel cause analysis approach of grey reasoning Petri net based on matrix operations[J]. Applied Intelligence, 2022, 52(1): 1-18. doi: 10.1007/s10489-021-02377-4 [24] 刘久富, 张信哲, 汪恒宇, 等. 部分可观Petri网故障的量子贝叶斯诊断[J]. 北京航空航天大学学报, 2022, 48(7): 1125-1134.LIU J F, ZHANG X Z, WANG H Y, et al. Partial observable Petri nets fault diagnosis with quantum Bayesian learning[J]. Journal of Beijing University of Aeronautics and Astronautics, 2022, 48(7): 1125-1134(in Chinese). [25] 王国庆, 谷青范, 王淼, 等. 新一代综合化航空电子系统构架技术研究[J]. 航空学报, 2014, 35(6): 1473-1486.WANG G Q, GU Q F, WANG M, et al. Research on the architecture technology for new generation integrated avionics system[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(6): 1473-1486(in Chinese). [26] ZHOU J F. A fuzzy Petri-net approach for fault analysis considering factor influences[J]. IEEE Access, 2020, 8: 72229-72238. doi: 10.1109/ACCESS.2020.2986306 [27] WANG Y H, LI M, SHI H. A method of searching fault propagation paths in mechatronic systems based on MPPS model[J]. Journal of Central South University, 2018, 25(9): 2199-2218. doi: 10.1007/s11771-018-3908-3 -
下载:
点击查看大图
计量
- 文章访问数: 817
- HTML全文浏览量: 138
- PDF下载量: 20
- 被引次数: 0
