-
摘要:
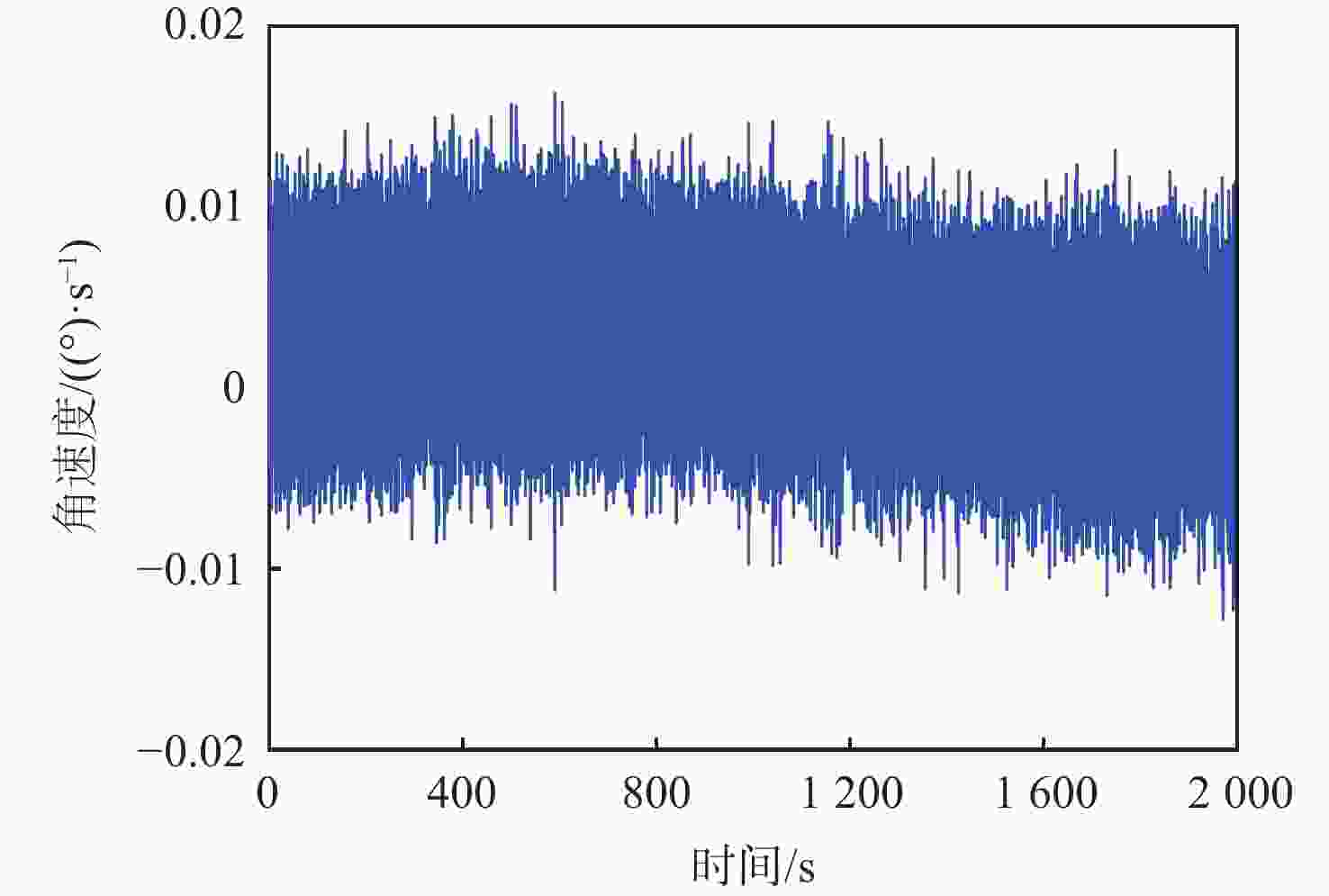
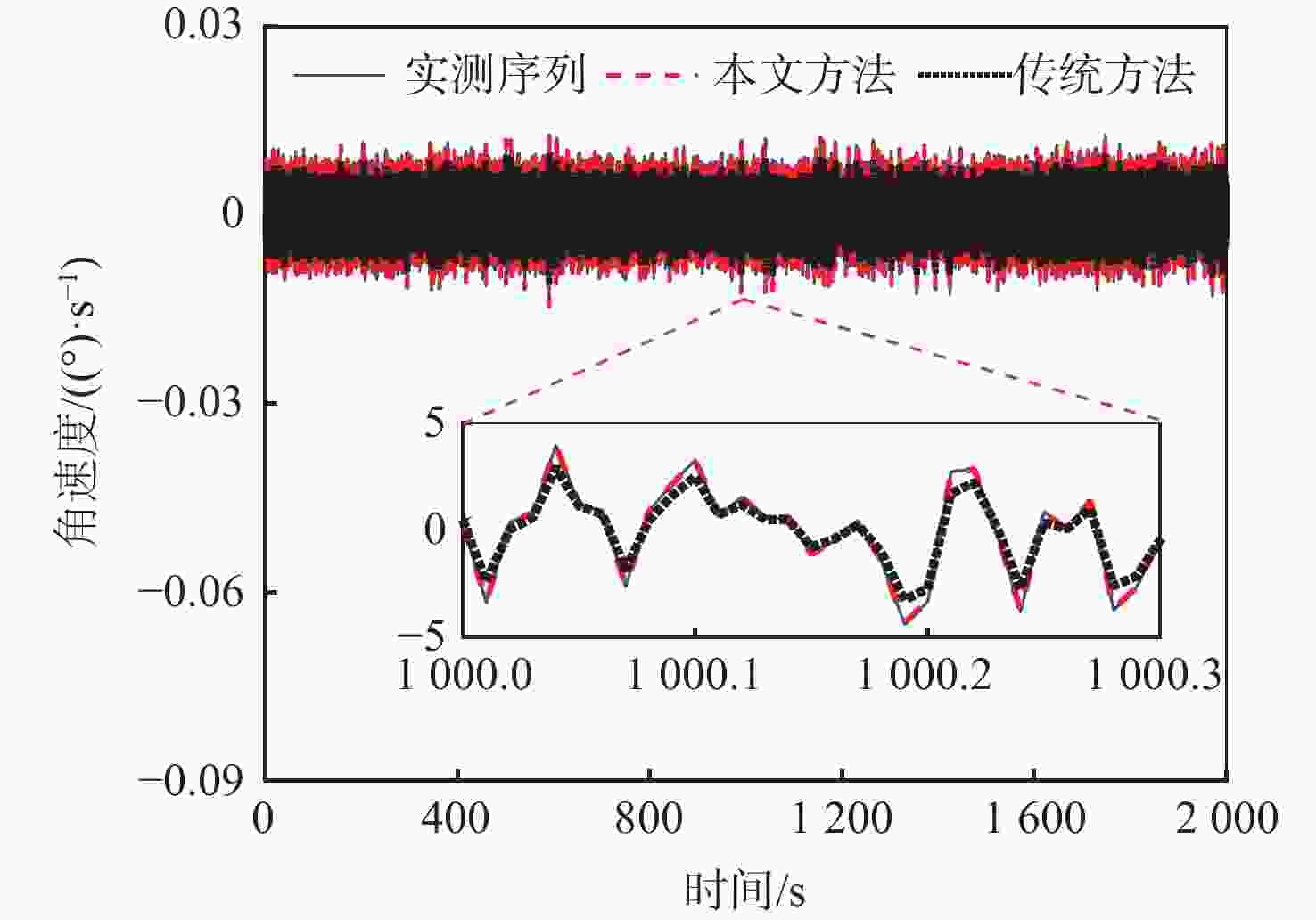
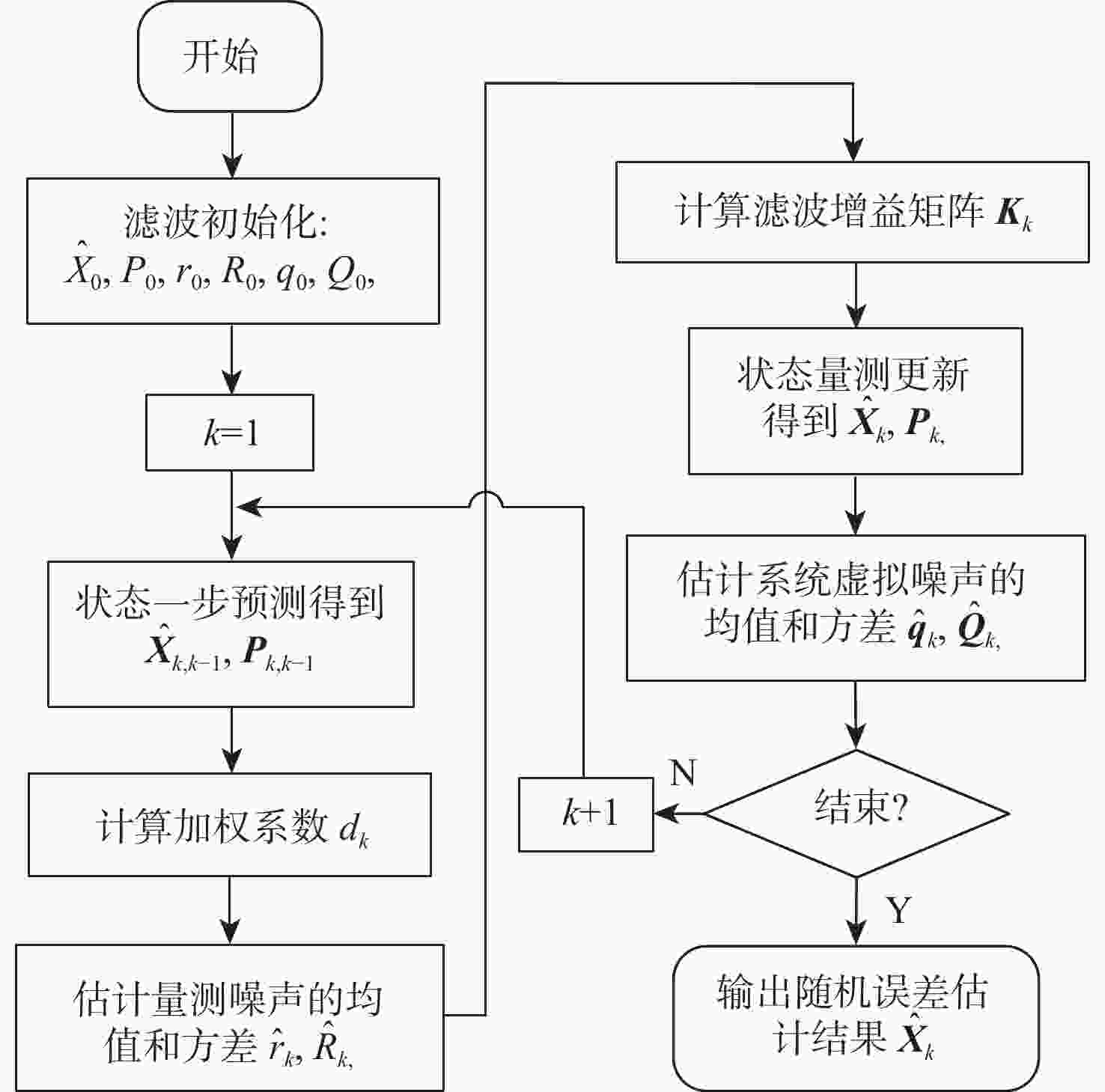
光学陀螺随机误差在线补偿方法通常先离线建立随机误差模型，再利用Kalman滤波在线补偿随机误差。受陀螺仪自身性能稳定性以及外界环境的影响，离线建立的随机误差模型应用于在线补偿时会出现偏差；外界环境变化导致量测噪声统计特性具有时变性，不满足Kalman滤波必须已知噪声先验统计的要求，这2个因素均会降低随机误差的在线估计精度。提出一种基于自适应滤波的随机误差在线补偿方法。通过引入虚拟噪声，将随机误差模型偏差的影响归结为时变虚拟系统噪声；进而利用渐消记忆时变噪声估值器，对虚拟系统噪声和量测噪声的统计特性进行估计与修正，消除随机误差模型偏差及量测噪声时变的影响。试验结果表明，所提方法可以实现对随机误差的高精度在线补偿，具有一定工程应用价值。
Abstract:The random error online compensation method of optical gyro establishes a random error model offline and compensates random error online by Kalman filter. However, when used for online compensation, the offline random error model has deviation due to the influence of the external environment and the stability of the gyro’s performance. In addition, changes in the external environment cause measurement noise with time-varying statistical characteristics, which does not meet the requirement that the Kalman filter must have known the noise’s prior statistics. The above factors reduce the online estimation accuracy of random error. Therefore, an online random error compensation method based on adaptive filtering is proposed. The influence of random error model deviation is reduced to time-varying virtual system noise by introducing virtual noise. In order to remove the effects of random error model deviation and time-varying measurement noise, the fading memory time-varying noise estimator is used to estimate and correct the statistical properties of the virtual system and measurement noise. The experimental results show that the proposed method can realize high-precision online compensation for random error, and has certain engineering application value.
-
Key words:
- random error /
- online compensation /
- model deviation /
- time-varying noise /
- adaptive filtering
-
图 1 基于自适应滤波的随机误差在线补偿方法的流程图
Figure 1. Flow chart of the random error online compensation method based on adaptive filtering
表 1 补偿前后的输出结果对比
Table 1. Comparison of output result before and after compensation
(°)/s 方法 均值 均方差 补偿前 −1.33×10−6 3.06×10−3 传统方法 −3.65×10−7 8.21×10−4 本文方法 4.33×10−8 1.79×10−5 
下载: 导出CSV
-
[1] XIONG Z Y, WEI G, GAO C F, et al. Precision temperature control for the laser gyro inertial navigation system in long-endurance marine navigation[J]. Sensors, 2021, 21(12): 4119. doi: 10.3390/s21124119 [2] YANG C, CAI Y W, XIN C J, et al. Research on temperature error compensation method of vehicle-mounted laser gyro SINS[J]. Journal of Physics:Conference Series, 2021, 1885(4): 042020. doi: 10.1088/1742-6596/1885/4/042020 [3] 刘文涛, 刘洁瑜, 沈强. 光纤陀螺随机误差的集成建模及滤波处理[J]. 光电工程, 2018, 45(10): 180082.LIU W T, LIU J Y, SHEN Q. Integrated modeling and filtering of fiber optic gyroscope’s random errors[J]. Opto-Electronic Engineering, 2018, 45(10): 180082(in Chinese). [4] NARASIMHAPPA M, NAYAK J, TERRA M H, et al. ARMA model based adaptive unscented fading Kalman filter for reducing drift of fiber optic gyroscope[J]. Sensors and Actuators A:Physical, 2016, 251: 42-51. doi: 10.1016/j.sna.2016.09.036 [5] TENG F, JIN J, HUANG Y L, et al. Noise analysis and measurement of high sensitivity photonic crystal fiber-optic gyroscope[J]. Optical Fiber Technology, 2015, 25: 1-6. doi: 10.1016/j.yofte.2015.06.002 [6] 金毅, 吴训忠, 谢聂, 等. 光纤陀螺随机漂移在线建模实时滤波技术[J]. 光电工程, 2015, 42(3): 13-19.JIN Y, WU X Z, XIE N, et al. Real-time filtering research based on on-line modeling random drift of FOG[J]. Opto-Electronic Engineering, 2015, 42(3): 13-19(in Chinese). [7] 朱枫, 张葆, 李贤涛, 等. 基于强跟踪卡尔曼滤波的陀螺信号处理[J]. 吉林大学学报(工学版), 2017, 47(6): 1868-1875.ZHU F, ZHANG B, LI X T, et al. Gyro signal processing based on strong tracking Kalman filter[J]. Journal of Jilin University (Engineering and Technology Edition), 2017, 47(6): 1868-1875(in Chinese). [8] SONG J L, SHI Z Y, DU B H, et al. MEMS gyroscope wavelet de-noising method based on redundancy and sparse representation[J]. Microelectronic Engineering, 2019, 217: 111112. doi: 10.1016/j.mee.2019.111112 [9] 冯小虎, 朱家海. 基于小波域维纳滤波的激光陀螺数据处理研究[J]. 航空精密制造技术, 2008, 44(6): 17-20.FENG X H, ZHU J H. Research on signal processing of laser gyro based on wavelet domain Wiener flter[J]. Aviation Precision Manufacturing Technology, 2008, 44(6): 17-20(in Chinese). [10] 孙伟, 孙鹏翔, 刘东雨. 基于PSO-WNN的MEMS陀螺随机误差建模普适性分析[J]. 传感技术学报, 2020, 33(9): 1292-1298.SUN W, SUN P X, LIU D Y. Universality analysis of stochastic error modeling for MEMS gyroscope based on PSO-WNN[J]. Chinese Journal of Sensors and Actuators, 2020, 33(9): 1292-1298(in Chinese). [11] 王新龙, 陈涛, 杜宇. 基于ARMA模型的光纤陀螺漂移数据建模方法研究[J]. 弹箭与制导学报, 2006, 26(1): 5-7,11.WANG X L, CHEN T, DU Y. The drift method of fiber optic gyros based on the ARMA model[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2006, 26(1): 5-7,11(in Chinese). [12] 王可东, 武雨霞. 一种MEMS陀螺随机漂移的高精度建模方法[J]. 北京航空航天大学学报, 2016, 42(8): 1584-1592.WANG K D, WU Y X. An accurate modeling method for random drift of MEMS gyro[J]. Journal of Beijing University of Aeronautics and Astronautics, 2016, 42(8): 1584-1592(in Chinese). [13] 傅军, 韩洪祥. 改进的MEMS陀螺随机噪声自适应Kalman实时滤波方法[J]. 光子学报, 2019, 48(12): 1212003. doi: 10.3788/gzxb20194812.1212003FU J, HAN H X. Modified adaptive real-time filtering algorithm for MEMS gyroscope random noise[J]. Acta Photonica Sinica, 2019, 48(12): 1212003(in Chinese). doi: 10.3788/gzxb20194812.1212003 [14] 王可东, 熊少锋. ARMA建模及其在Kalman滤波中的应用[J]. 宇航学报, 2012, 33(8): 1048-1055.WANG K D, XIONG S F. An ARMA modeling method and its application in Kalman filtering[J]. Journal of Astronautics, 2012, 33(8): 1048-1055(in Chinese). [15] 李鲁明, 赵鲁阳, 唐晓红, 等. 基于改进卡尔曼滤波的陀螺仪误差补偿算法[J]. 传感技术学报, 2018, 31(4): 538-544,550.LI L M, ZHAO L Y, TANG X H, et al. A compensation algorithm of gyroscope error based on modified Kalman filter[J]. Chinese Journal of Sensors and Actuators, 2018, 31(4): 538-544,550(in Chinese). [16] 柴嘉薪, 王新龙, 王盾, 等. 一种光纤陀螺随机振动误差高精度建模方法[J]. 航空兵器, 2017, 24(4): 49-54.CHAI J X, WANG X L, WANG D, et al. A high precision modeling method for random vibration error of fiber optic gyroscope[J]. Aero Weaponry, 2017, 24(4): 49-54(in Chinese). -
下载:
点击查看大图
计量
- 文章访问数: 335
- HTML全文浏览量: 98
- PDF下载量: 11
- 被引次数: 0
