-
摘要:
多目标进化算法(MOEA)因其良好的全局探索能力备受关注,但其在最优值附近的局部搜索能力却相对较弱,且对于具有大规模决策变量的优化问题,MOEA所需的种群数量与迭代次数都十分庞大,优化效率较低。基于梯度的优化算法能够很好地克服这些问题,但梯度搜索算法很难应用于多目标问题(MOPs)。在加权平均梯度的基础上引入随机权函数,发展多目标梯度算子,将其与基于参考点的第三代非支配排序遗传算法(NSGA-Ⅲ)结合,发展了多目标梯度优化算法(MOGBA)和多目标混合进化算法(HMOEA)。HMOEA在保留NSGA-Ⅲ良好的全局探索能力的同时,极大地增强了局部搜索能力。数值实验表明:HMOEA对于各种Pareto阵面都具有优秀的捕获能力,与典型的多目标算法相比效率提升了5~10倍。进一步将HMOEA应用于RAE2822翼型的多目标气动优化问题中,得到了理想的Pareto前沿,表明HMOEA是一种高效的优化算法,在气动优化设计中具有潜在的应用价值。
Abstract:Because of its strong global exploration ability, the current multi-objective evolutionary algorithm (MOEA) has received a lot of attention. However, its local search ability close to the optimal value is relatively weak, and for optimization problems involving large-scale decision variables, MOEA requires a very large number of populations and iterations, which results in a low optimization efficiency. Gradient-based optimization algorithms can overcome these problems well, but they are difficult to be applied to multi-objective problems (MOPs). Therefore, this paper introduced a random weight function on the basis of a weighted average gradient, developed a multi-objective gradient operator, and combined it with a non-dominated sorting genetic algorithm-Ⅲ (NSGA- Ⅲ) based on reference points to develop multi-objective optimization algorithm (MOGBA) and multi-objective Hybrid Evolutionary algorithm (HMOEA). The latter greatly enhances the local search capability while retaining the good global exploration capability of NSGA-Ⅲ. Experiments with numbers demonstrate that HMOEA can effectively capture a wide range of Pareto forms, and that it is 5–10 times more efficient than standard multi-objective algorithms. And further, HMOEA is applied to the multi-objective aerodynamic optimization problem of the RAE2822 airfoil, and the ideal Pareto front is obtained, indicating that HMOEA is an efficient optimization algorithm with potential applications in aerodynamic optimization design.
-
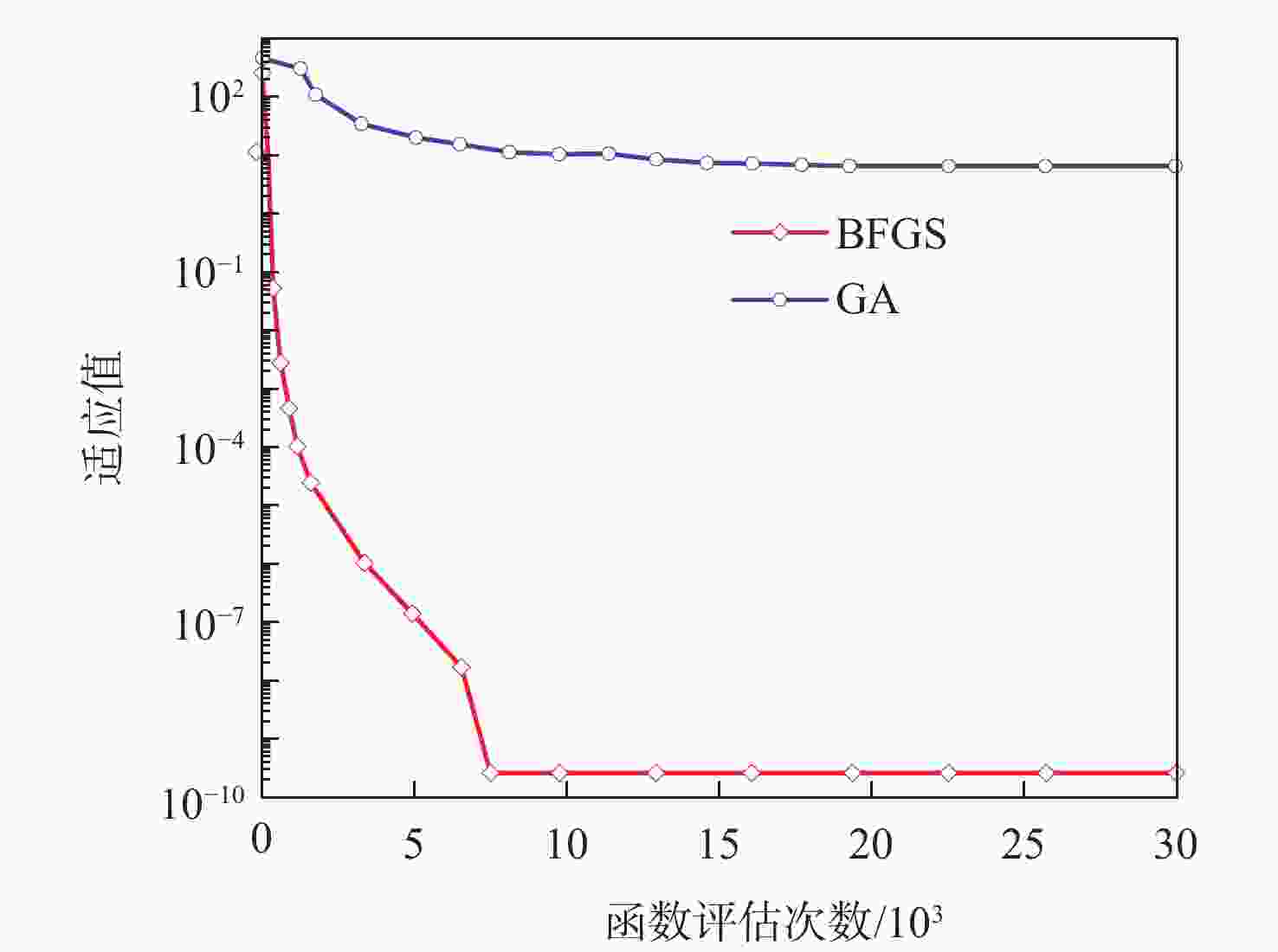
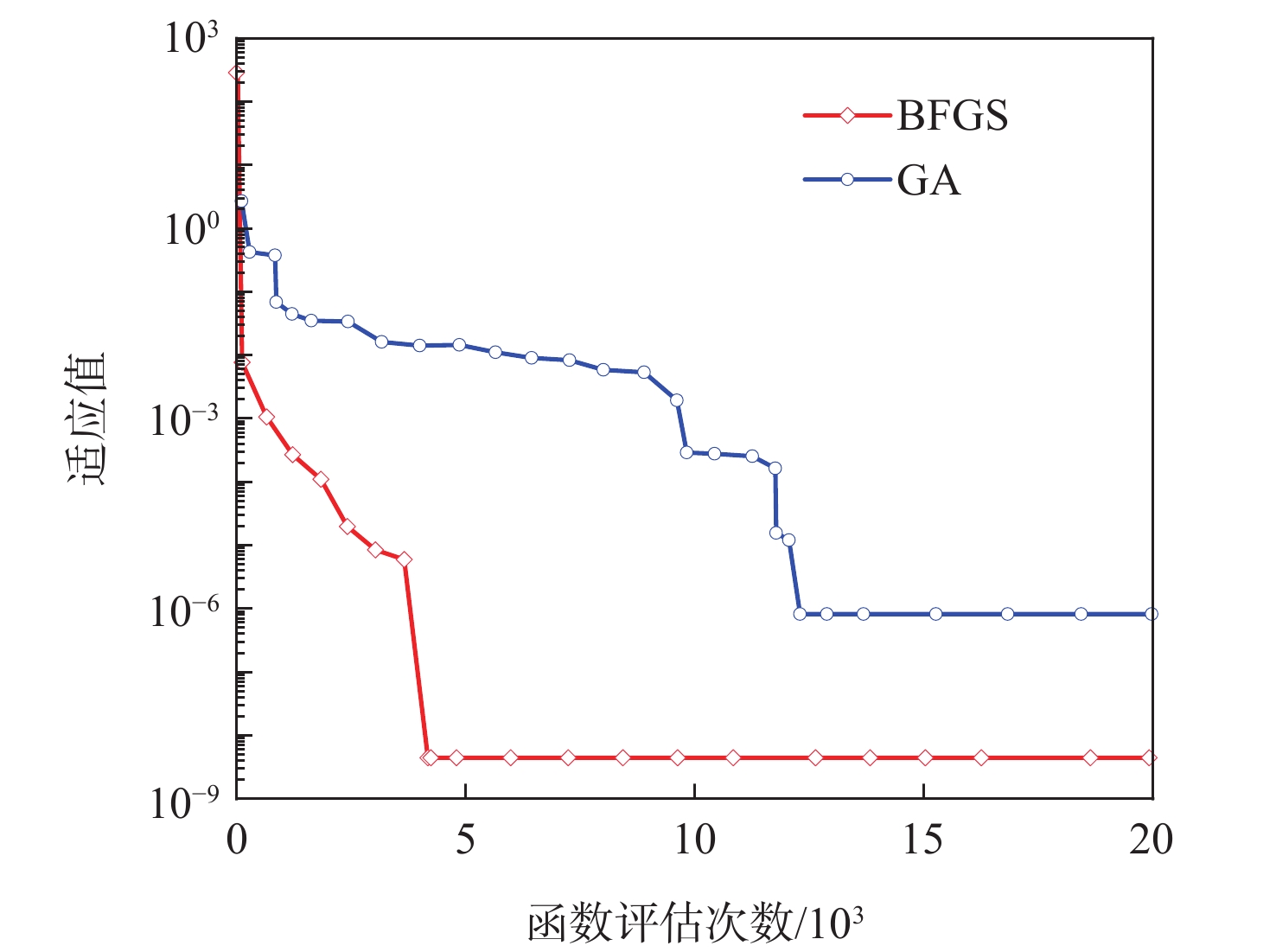
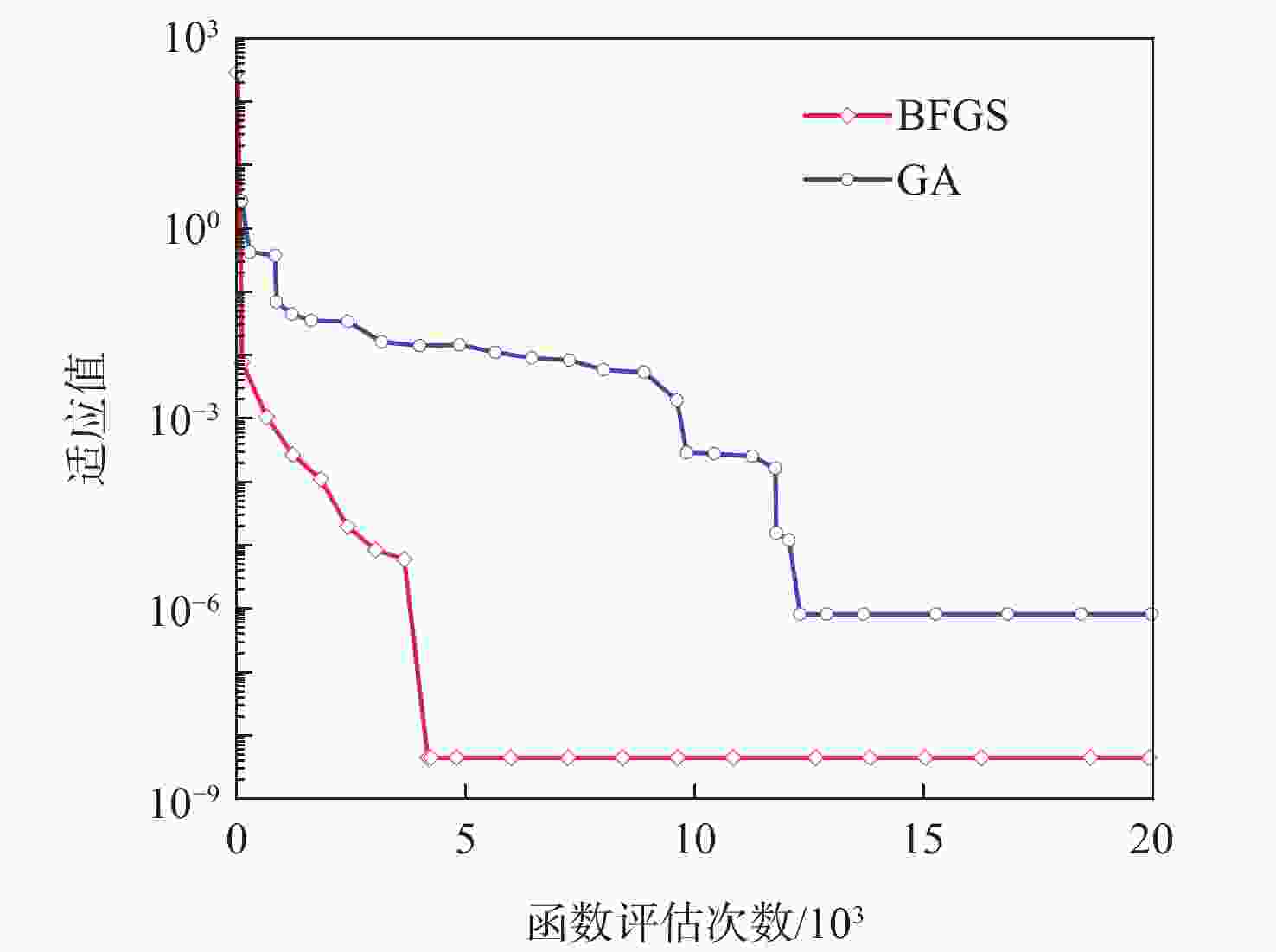
表 1 基于ROSENBROCK函数的算法性能验证
Table 1. Performance verification of algorithm based on ROSENBROCK function
维度 算法 函数评估次数 收敛精度 2 BFGS 1480 10−5 GA 12320 10−5 10 BFGS 400 10 GA 7600 10 表 2 测试函数参数设置
Table 2. Test function parameter Settings
函数 变量维度 目标数 ZDT1~ZDT3 30 2 ZDT4、ZDT6 10 2 DTLZ1 7 3 DTLZ2~DTLZ6 12 3 DTLZ7 22 4 表 3 6种优化算法参数设置
Table 3. Six optimization algorithm parameter settings
算法 $ {p}_{{\mathrm{c}}} $ $ {p}_{{\mathrm{m}}} $ $ {\eta }_{{\mathrm{c}}} $ $ {\eta }_{{\mathrm{m}}} $ $ N $ $ L $ $ T $ $ \delta $ $ K $ HMOEA 1.0 $ 1/n $ 20 20 100 5 MOGBA 100 5 NSGA-Ⅱ 1.0 $ 1/n $ 20 20 100 NSGA-Ⅲ 1.0 $ 1/n $ 20 20 100 MOEA/D 1.0 $ 1/n $ 20 20 100 20 0.9 5 RVEA 1.0 $ 1/n $ 20 20 100 注:$ n $为变量维度,$ {p}_{{\mathrm{c}}} $为交叉概率,$ {p}_{{\mathrm{m}}} $为变异概率,$ L $为多权重的权重数目,$ {\eta }_{{\mathrm{c}}} $为交叉分布指数,$ {\eta }_{{\mathrm{m}}} $为变异分布指数,$ N $为种群大小,$ T $为MOEA/D的邻居个数,$ \delta $为MOEA/D中邻居种群内相邻个体之间发生交叉的概率,$ K $为MOEA/D中子问题的个数。 表 4 6种优化算法的IGD指标
Table 4. Six optimization algorithms IGD metrics
函数 均值 HMOEA MOGBA NSGA-Ⅱ NSGA-Ⅲ MOEA/D RVEA ZDT1 $ 3.89\times {10}^{-3} $ $ 3.89\times {10}^{-3}$ $ 4.61\times {10}^{-3}$ $ 3.99\times {10}^{-3} $ $ 3.89\times {10}^{-3}$ $ 1.88\times {10}^{-2} $ ZDT2 $ 3.81\times {10}^{-3}$ $ 3.82\times {10}^{-3} $ $ 5.66\times {10}^{-1} $ $ 7.59\times {10}^{-1}$ $ 9.89\times {10}^{-2} $ $ 1.42 $ ZDT3 $ 5.61\times {10}^{-3}$ $ 9.22\times {10}^{-3} $ $ 1.28\times {10}^{-2}$ $ 1.78\times {10}^{-2} $ $ 1.97\times {10}^{-2} $ $ 1.59\times {10}^{-1}$ ZDT4 $ 3.89\times {10}^{-3} $ $ 3.89\times {10}^{-3} $ $ 2.38\times {10}^{-1}$ $ 4.79\times {10}^{-1} $ $ 4.24\times {10}^{-2} $ $ 1.24 $ ZDT6 $ 3.15\times {10}^{-3} $ $ 7.91\times {10}^{-3} $ $ 4.65\times {10}^{-2} $ $ 1.82\times {10}^{-1} $ $ 5.32\times {10}^{-3} $ $ 3.39\times {10}^{-1} $ DTLZ1 $ 2.06\times {10}^{-2} $ $ 3.41\times {10}^{-2} $ $ 5.35\times {10}^{-2} $ $ 3.44\times {10}^{-2} $ $ 2.35\times {10}^{-2} $ $ 9.09\times {10}^{-2} $ DTLZ2 $ 5.45\times {10}^{-2} $ $ 6.06\times {10}^{-2} $ $ 6.98\times {10}^{-2} $ $ 5.51\times {10}^{-2} $ $ 5.53\times {10}^{-2} $ $ 5.64\times {10}^{-2} $ DTLZ3 $ 6.58\times {10}^{-2} $ $ 4.80\times {10}^{-1} $ $ 8.29 $ $ 1.18\times {10}^{1} $ $ 2.32\times {10}^{1} $ $ 2.41\times {10}^{1} $ DTLZ4 $ 5.46\times {10}^{-2} $ $ 3.85\times {10}^{-1} $ $ 1.92\times {10}^{-1} $ $ 2.17\times {10}^{-1} $ $ 4.58\times {10}^{-1} $ $ 5.66\times {10}^{-2} $ DTLZ5 $ 3.50\times {10}^{-3} $ $ 1.46\times {10}^{-2} $ $ 6.02\times {10}^{-3} $ $ 1.30\times {10}^{-2} $ $ 3.33\times {10}^{-2} $ $ 8.88\times {10}^{-2} $ DTLZ6 $ 3.65\times {10}^{-3} $ $ 3.32\times {10}^{-1} $ $ 6.14\times {10}^{-3} $ $ 1.71\times {10}^{-2} $ $ 2.95\times {10}^{-1} $ $ 1.56\times {10}^{-1} $ DTLZ7 $ 7.71\times {10}^{-2} $ $ 1.23\times {10}^{-1} $ $ 9.61\times {10}^{-2} $ $ 1.29\times {10}^{-1} $ $ 1.86\times {10}^{-1} $ $ 2.34\times {10}^{-1} $ 函数 秩和检验结果 标准差 HMOEA MOGBA NSGA-Ⅱ NSGA-Ⅲ MOEA/D RVEA HMOEA MOGBA NSGA-Ⅱ NSGA-Ⅲ MOEA/D RVEA ZDT1 $ - $ $ + $ $ ++ $ $ ++ $ $ += $ $ ++ $ $ 2.41\times {10}^{-6} $ $ 2.48\times {10}^{-6} $ $ 2.05\times {10}^{-4} $ $ 6.51\times {10}^{-5} $ $ 1.42\times {10}^{-5} $ $ 3.48\times {10}^{-3} $ ZDT2 $ + $ $ + $ $ ++ $ $ ++ $ $ ++ $ $ ++ $ $ 3.27\times {10}^{-7} $ $ 2.86\times {10}^{-6} $ $ 1.07\times {10}^{-1} $ $ 1.01\times {10}^{-1} $ $ 1.11\times {10}^{-1} $ $ 5.81\times {10}^{-1} $ ZDT3 $ - $ $ + $ $ += $ $ ++ $ $ ++ $ $ ++ $ $ 1.29\times {10}^{-4} $ $ 1.65\times {10}^{-3} $ $ 8.94\times {10}^{-3} $ $ 7.89\times {10}^{-3} $ $ 1.25\times {10}^{-2} $ $ 2.41\times {10}^{-2} $ ZDT4 $ - $ $ + $ $ ++ $ $ ++ $ $ ++ $ $ ++ $ $ 1.29\times {10}^{-4} $ $ 2.43\times {10}^{-6} $ $ 1.68\times {10}^{-1} $ $ 2.33\times {10}^{-1} $ $ 4.11\times {10}^{-2} $ $ 3.40\times {10}^{-1} $ ZDT6 $ - $ $ + $ $ ++ $ $ ++ $ $ +- $ $ ++ $ $ 6.55\times {10}^{-7} $ $ 1.71\times {10}^{-3} $ $ 2.39\times {10}^{-2} $ $ 6.88\times {10}^{-2} $ $ 2.92\times {10}^{-3} $ $ 7.76\times {10}^{-2} $ DTLZ1 $ - $ $ + $ $ += $ $ +- $ $ +- $ $ ++ $ $ 1.77\times {10}^{-4} $ $ 7.98\times {10}^{-3} $ $ 6.96\times {10}^{-2} $ $ 4.87\times {10}^{-2} $ $ 2.81\times {10}^{-3} $ $ 6.85\times {10}^{-2} $ DTLZ2 $ - $ $ + $ $ ++ $ $ +- $ $ +- $ $ +- $ $ 3.63\times {10}^{-5} $ $ 2.02\times {10}^{-2} $ $ 2.37\times {10}^{-3} $ $ 2.07\times {10}^{-4} $ $ 5.23\times {10}^{-4} $ $ 5.94\times {10}^{-4} $ DTLZ3 $ - $ $ + $ $ ++ $ $ ++ $ $ ++ $ $ ++ $ $ 7.42\times {10}^{-3} $ $ 3.17\times {10}^{-3} $ $ 3.97 $ $ 4.67 $ $ 1.60\times {10}^{1} $ $ 6.93 $ DTLZ4 $ - $ $ + $ $ +- $ $ +- $ $ += $ $ +- $ $ 6.40\times {10}^{-5} $ $ 1.22\times {10}^{-2} $ $ 2.35\times {10}^{-1} $ $ 2.29\times {10}^{-1} $ $ 3.43\times {10}^{-1} $ $ 1.26\times {10}^{-3} $ DTLZ5 $ - $ $ + $ $ +- $ $ +- $ $ ++ $ $ ++ $ $ 5.29\times {10}^{-4} $ $ 2.30\times {10}^{-3} $ $ 2.68\times {10}^{-4} $ $ 1.02\times {10}^{-3} $ $ 2.51\times {10}^{-4} $ $ 1.78\times {10}^{-2} $ DTLZ6 $ - $ $ + $ $ +- $ $ +- $ $ += $ $ +- $ $ 3.72\times {10}^{-4} $ $ 5.85\times {10}^{-2} $ $ 3.31\times {10}^{-4} $ $ 6.49\times {10}^{-3} $ $ 5.41\times {10}^{-1} $ $ 1.62\times {10}^{-1} $ DTLZ7 $ - $ $ + $ $ +- $ $ +- $ $ ++ $ $ ++ $ $ 5.79\times {10}^{-3} $ $ 1.35\times {10}^{-2} $ $ 9.18\times {10}^{-3} $ $ 9.25\times {10}^{-2} $ $ 1.76\times {10}^{-1} $ $ 5.91\times {10}^{-2} $ 表 5 6种优化算法HV指标
Table 5. Six optimization algorithms HV metrics
函数 均值 HMOEA MOGBA NSGA-Ⅱ NSGA-Ⅲ MOEA/D RVEA ZDT1 $ 7.20\times {10}^{-1} $ $ 7.20\times {10}^{-1} $ $ 7.19\times {10}^{-1} $ $ 7.20\times {10}^{-1} $ $ 7.20\times {10}^{-1} $ $ 6.99\times {10}^{-1} $ ZDT2 $ 4.45\times {10}^{-1} $ $ 4.45\times {10}^{-1} $ $ 3.89\times {10}^{-2} $ $ 1.19\times {10}^{-6} $ $ 3.52\times {10}^{-1} $ $ 0 $ ZDT3 $ 5.83\times {10}^{-1} $ $ 5.82\times {10}^{-1} $ $ 5.83\times {10}^{-1} $ $ 5.78\times {10}^{-1} $ $ 6.0\times {10}^{-1} $ $ 4.64\times {10}^{-1} $ ZDT4 $ 7.20\times {10}^{-1} $ $ 7.20\times {10}^{-1} $ $ 4.92\times {10}^{-1} $ $ 2.71\times {10}^{-1} $ $ 6.76\times {10}^{-1} $ $ 7.87\times {10}^{-3} $ ZDT6 $ 4.17\times {10}^{-1} $ $ 4.13\times {10}^{-1} $ $ 3.63\times {10}^{-1} $ $ 2.22\times {10}^{-1} $ $ 4.13\times {10}^{-1} $ $ 9.78\times {10}^{-2} $ DTLZ1 $ 8.42\times {10}^{-1} $ $ 8.18\times {10}^{-1} $ $ 7.56\times {10}^{-1} $ $ 8.05\times {10}^{-1} $ $ 8.28\times {10}^{-1} $ $ 6.84\times {10}^{-1} $ DTLZ2 $ 5.60\times {10}^{-1} $ $ 5.57\times {10}^{-1} $ $ 5.29\times {10}^{-1} $ $ 5.55\times {10}^{-1} $ $ 5.54\times {10}^{-1} $ $ 5.51\times {10}^{-1} $ DTLZ3 $ 5.42\times {10}^{-1} $ $ 2.49\times {10}^{-1} $ $ 0 $ $ 0 $ $ 0 $ $ 0 $ DTLZ4 $ 5.59\times {10}^{-1} $ $ 2.87\times {10}^{-1} $ $ 4.80\times {10}^{-1} $ $ 4.83\times {10}^{-1} $ $ 3.6\times {10}^{-1} $ $ 5.51\times {10}^{-1} $ DTLZ5 $ 2.00\times {10}^{-1} $ $ 1.92\times {10}^{-1} $ $ 1.99\times {10}^{-1} $ $ 1.93\times {10}^{-1} $ $ 1.82\times {10}^{-1} $ $ 1.44\times {10}^{-1} $ DTLZ6 $ 2.00\times {10}^{-1} $ $ 1.01\times {10}^{-1} $ $ 1.99\times {10}^{-1} $ $ 1.91\times {10}^{-1} $ $ 1.39\times {10}^{-1} $ $ 1.09\times {10}^{-1} $ DTLZ7 $ 2.74\times {10}^{-1} $ $ 2.60\times {10}^{-1} $ $ 2.47\times {10}^{-1} $ $ 2.43\times {10}^{-1} $ $ 2.51\times {10}^{-1} $ $ 1.85\times {10}^{-1} $ 函数 秩和检验结果 标准差 HMOEA MOGBA NSGA-Ⅱ NSGA-Ⅲ MOEA/D RVEA HMOEA MOGBA NSGA-Ⅱ NSGA-Ⅲ MOEA/D RVEA ZDT1 $ = $ $ = $ $ ++ $ $ ++ $ $ ++ $ $ ++ $ $ 7.72\times {10}^{-6} $ $ 6.32\times {10}^{-6} $ $ 2.53\times {10}^{-4} $ $ 2.04\times {10}^{-4} $ $ 4.15\times {10}^{-5} $ $ 4.26\times {10}^{-3} $ ZDT2 $ - $ $ + $ $ ++ $ $ ++ $ $ ++ $ $ ++ $ $ 4.20\times {10}^{-7} $ $ 3.66\times {10}^{-6} $ $ 3.61\times {10}^{-2} $ $ 6.40\times {10}^{-6} $ $ 9.42\times {10}^{-2} $ $ 0 $ ZDT3 $ - $ $ + $ $ ++ $ $ ++ $ $ == $ $ ++ $ $ 1.51\times {10}^{-4} $ $ 3.55\times {10}^{-4} $ $ 2.92\times {10}^{-2} $ $ 2.43\times {10}^{-2} $ $ 4.4\times {10}^{-2} $ $ 1.73\times {10}^{-2} $ ZDT4 $ - $ $ + $ $ ++ $ $ ++ $ $ ++ $ $ ++ $ $ 3.92\times {10}^{-6} $ $ 6.51\times {10}^{-6} $ $ 1.55\times {10}^{-1} $ $ 1.70\times {10}^{-1} $ $ 4.22\times {10}^{-2} $ $ 2.24\times {10}^{-2} $ ZDT6 $ - $ $ + $ $ ++ $ $ ++ $ $ += $ $ ++ $ $ 6.23\times {10}^{-7} $ $ 1.43\times {10}^{-3} $ $ 2.76\times {10}^{-2} $ $ 5.74\times {10}^{-2} $ $ 3.08\times {10}^{-3} $ $ 4.08\times {10}^{-2} $ DTLZ1 $ - $ $ + $ $ += $ $ +- $ $ +- $ $ ++ $ $ 2.49\times {10}^{-4} $ $ 1.49\times {10}^{-2} $ $ 1.71\times {10}^{-1} $ $ 1.17\times {10}^{-1} $ $ 9.67\times {10}^{-2} $ $ 1.49\times {10}^{-1} $ DTLZ2 $ - $ $ + $ $ ++ $ $ ++ $ $ ++ $ $ ++ $ $ 7.98\times {10}^{-5} $ $ 3.64\times {10}^{-3} $ $ 3.69\times {10}^{-3} $ $ 9.01\times {10}^{-4} $ $ 1.64\times {10}^{-3} $ $ 1.35\times {10}^{-3} $ DTLZ3 $ - $ $ + $ $ ++ $ $ ++ $ $ ++ $ $ ++ $ $ 1.13\times {10}^{-2} $ $ 5.52\times {10}^{-4} $ $ 0 $ $ 0 $ $ 0 $ $ 0 $ DTLZ4 $ - $ $ + $ $ +- $ $ +- $ $ +- $ $ +- $ $ 1.31\times {10}^{-4} $ $ 2.37\times {10}^{-2} $ $ 1.04\times {10}^{-1} $ $ 1.01\times {10}^{-1} $ $ 1.77\times {10}^{-1} $ $ 2.65\times {10}^{-3} $ DTLZ5 $ - $ $ + $ $ +- $ $ += $ $ ++ $ $ ++ $ $ 4.43\times {10}^{-4} $ $ 1.55\times {10}^{-3} $ $ 2.12\times {10}^{-4} $ $ 1.03\times {10}^{-3} $ $ 1.44\times {10}^{-4} $ $ 1.03\times {10}^{-2} $ DTLZ6 $ - $ $ + $ $ +- $ $ +- $ $ += $ $ += $ $ 3.61\times {10}^{-4} $ $ 1.65\times {10}^{-2} $ $ 2.08\times {10}^{-4} $ $ 4.59\times {10}^{-3} $ $ 7.65\times {10}^{-2} $ $ 4.24\times {10}^{-2} $ DTLZ7 $ - $ $ + $ $ ++ $ $ ++ $ $ ++ $ $ ++ $ $ 2.15\times {10}^{-3} $ $ 4.21\times {10}^{-3} $ $ 5.41\times {10}^{-3} $ $ 8.75\times {10}^{-3} $ $ 1.32\times {10}^{-2} $ $ 2.39\times {10}^{-2} $ 表 6 6种优化算法综合指标
Table 6. Six optimization algorithms comprehensive metrics
算法 平均秩 总平均秩 获得+的数目 获得−的数目 获得=的数目 ZDT DTLZ HMOEA MOGBA HMOEA MOGBA HMOEA MOGBA HMOEA 1.200 1.000 1.083 0 23 1 MOGBA 2.200 3.786 3.125 23 0 1 NSGA-Ⅱ 4.000 3.500 3.708 24 14 0 7 0 3 NSGA-Ⅲ 4.700 3.500 4.000 24 14 0 9 0 1 MOEA/D 2.900 4.143 3.625 23 13 0 5 1 6 RVEA 6.000 4.643 5.208 24 19 0 4 0 1 表 7 设计参数范围
Table 7. Range of design parameters
${R_{{\mathrm{le}}}}/c$ $\beta/{\mathrm{rad}}$ $ {\beta '}/{\mathrm{rad}} $ ${b_1}/c$ ${b_2}/c$ ${b_3}/c$ $b_1'/c$ $b_2'/c$ $b_3'/c$ [0.004,0.012] [0.14,0.28] [0.00,0.14] [0.05,0.20] [0.10,0.30] [0.10,0.30] [0.05,0.30] [0.05,0.30] [0.10,0.25] 表 8 3个选择点翼型气动参数
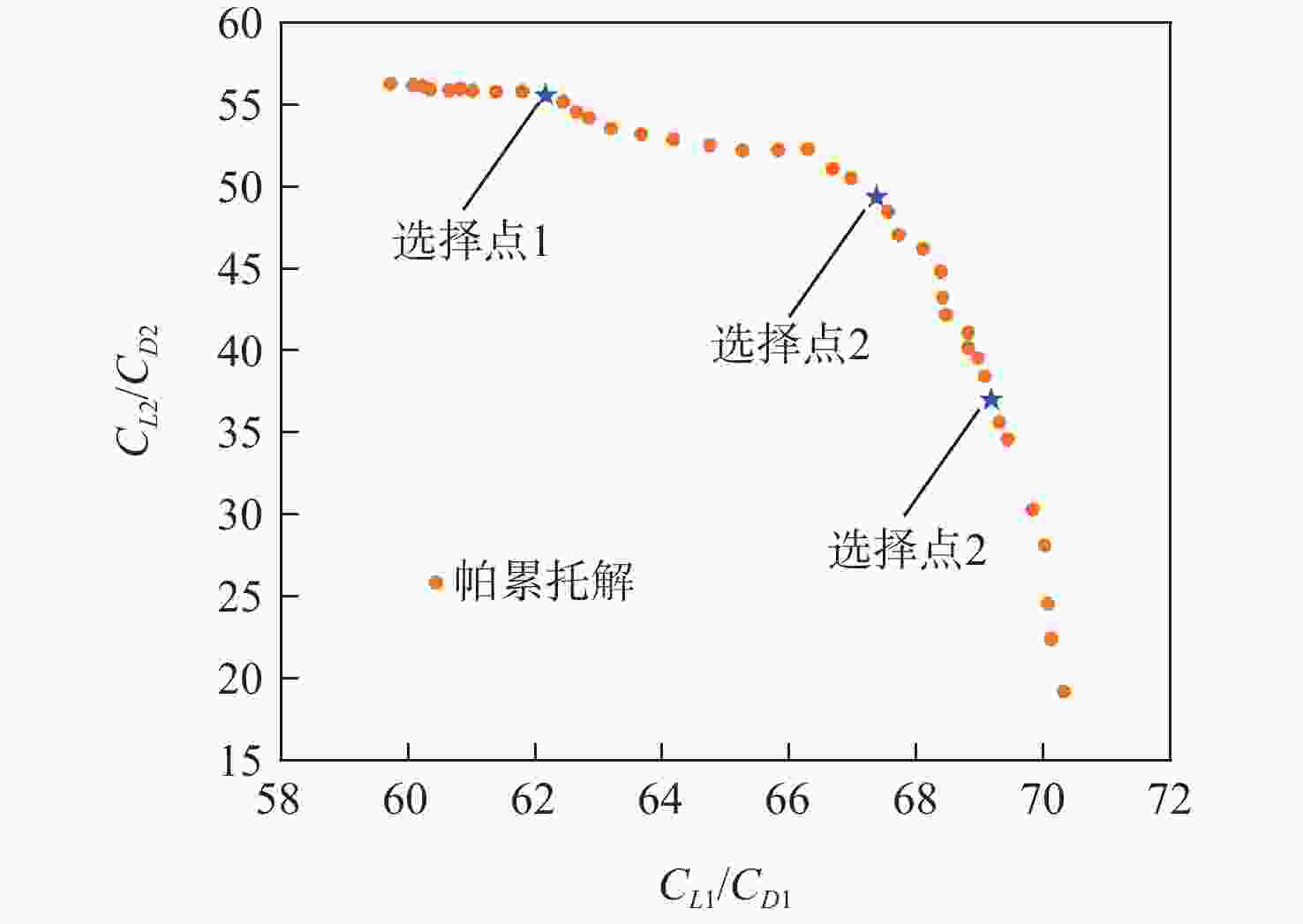
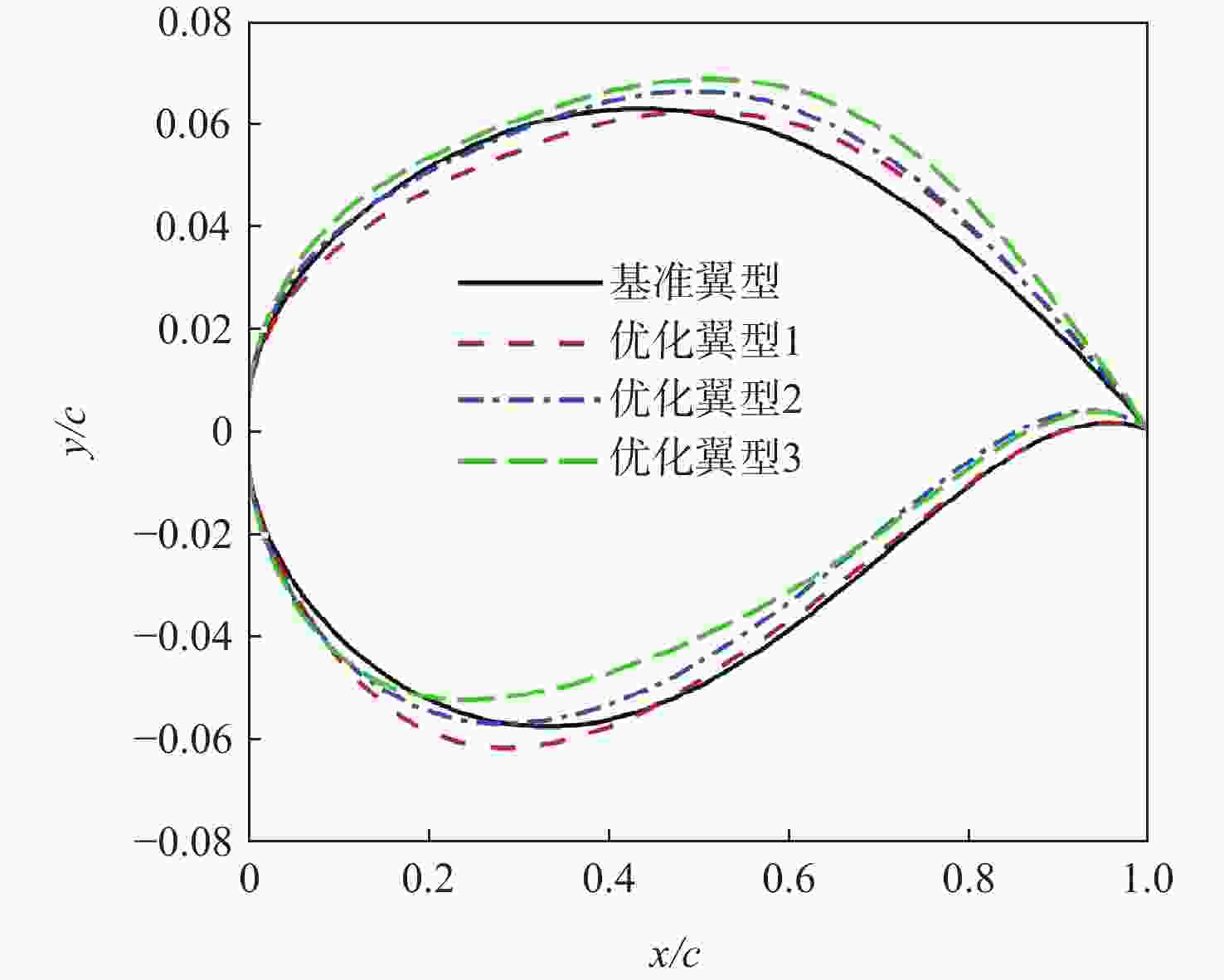
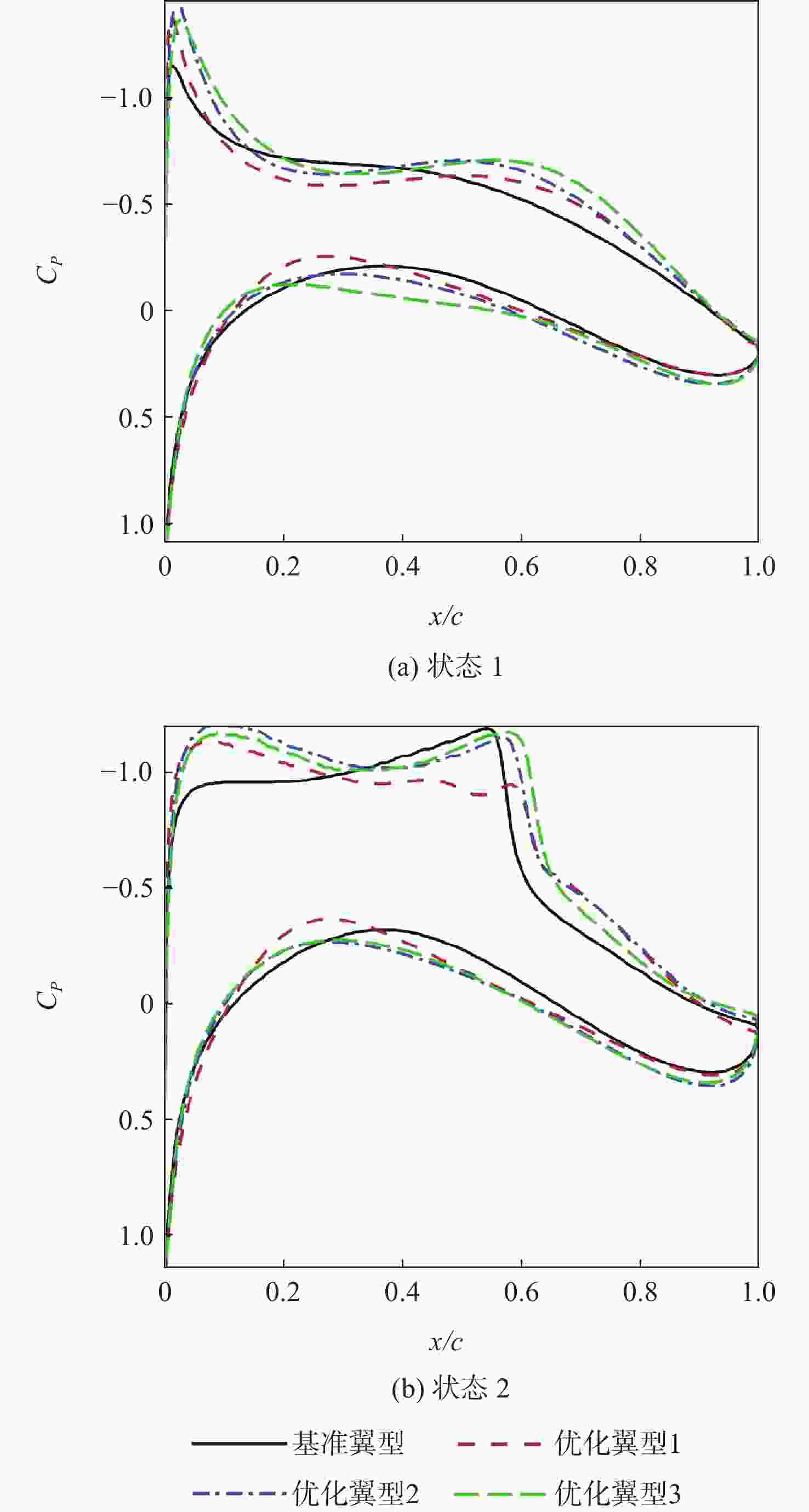
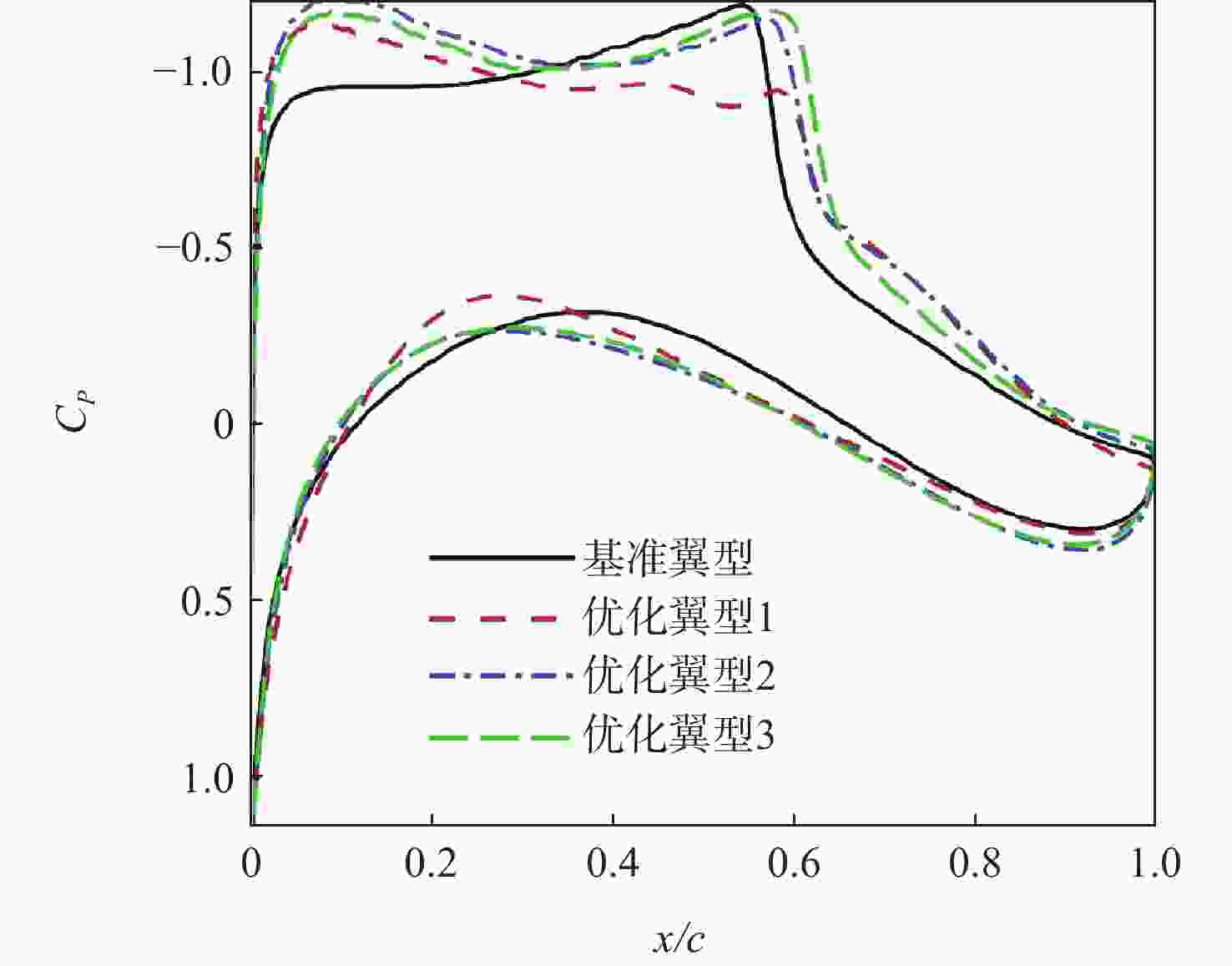
Table 8. Aerodynamic parameters of the three choice point airfoils
翼型 工况 $ {C}_{L}/{C}_{D} $ 基准翼型 1 56.3354 2 37.3572 优化翼型1 1 62.4824(+10.91%) 2 55.0731(+47.72%) 优化翼型2 1 67.3352(+19.53%) 2 49.4523(+32.38%) 优化翼型3 1 69.0864(+22.63%) 2 37.4338(+0.023%) -
[1] 刘加会. 无导数优化的直接搜索算法研究[D]. 西安: 西安电子科技大学, 2017: 5-14.LIU J H. Research on direct search algorithm for derivative-free optimization[D]. Xi’an: Xidian University, 2017: 5-14 (in Chinese) . [2] 常永虎, 李虎阳. 基于梯度的优化算法研究[J]. 现代计算机, 2019(17): 3-8. doi: 10.3969/j.issn.1007-1423.2019.17.001CHANG Y H, LI H Y. Comparison of gradient based optimization algorithms[J]. Modern Computer, 2019(17): 3-8 (in Chinese). doi: 10.3969/j.issn.1007-1423.2019.17.001 [3] 王向慧, 连志春, 徐志英, 等. 基于Pareto最优概念的多目标进化算法研究[J]. 计算机工程与应用, 2008, 44(27): 58-61. doi: 10.3778/j.issn.1002-8331.2008.27.019WANG X H, LIAN Z C, XU Z Y, et al. Research on Pareto optimal-based multiobjective evolutionary algorithms[J]. Computer Engineering and Applications, 2008, 44(27): 58-61 (in Chinese). doi: 10.3778/j.issn.1002-8331.2008.27.019 [4] MIRJALILI S. Genetic algorithm[C]// Evolutionary Algorithms and Neural Networks. Berlin: Springer, 2019: 43-55. [5] JAMESON A. Aerodynamic design via control theory[J]. Journal of Scientific Computing, 1988, 3(3): 233-260. doi: 10.1007/BF01061285 [6] AHMADIANFAR I, BOZORG-HADDAD O, CHU X F. Gradient-based optimizer: A new metaheuristic optimization algorithm[J]. Information Sciences, 2020, 540: 131-159. doi: 10.1016/j.ins.2020.06.037 [7] CHIOU J P, WANG F S. A hybrid method of differential evolution with application to optimal control problems of a bioprocess system[C]// Proceedings of the IEEE International Conference on Evolutionary Computation Proceedings. Piscataway: IEEE Press, 1998: 627-632. [8] TANG Z, HU X, PÉRIAUX J. Multi-level hybridized optimization methods coupling local search deterministic and global search evolutionary algorithms[J]. Archives of Computational Methods in Engineering, 2020, 27(3): 939-975. doi: 10.1007/s11831-019-09336-w [9] DEB K, PRATAP A, AGARWAL S, et al. A fast and elitist multiobjective genetic algorithm: NSGA-Ⅱ[J]. IEEE Transactions on Evolutionary Computation, 2002, 6(2): 182-197. doi: 10.1109/4235.996017 [10] DEB K, JAIN H. An evolutionary many-objective optimization algorithm using reference-point-based nondominated sorting approach, part I: Solving problems with box constraints[J]. IEEE Transactions on Evolutionary Computation, 2014, 18(4): 577-601. [11] JAIN H, DEB K. An evolutionary many-objective optimization algorithm using reference-point based nondominated sorting approach, part Ⅱ: Handling constraints and extending to an adaptive approach[J]. IEEE Transactions on Evolutionary Computation, 2013, 18(4): 602-622. [12] SIERRA M R, COELLO COELLO C A. Improving PSO-based multi-objective optimization using crowding, mutation and ε-dominance[C]//International Conference on Evolutionary Multi-Criterion Optimization. Berlin: Springer, 2005: 505-519. [13] ZHANG Q F, LI H. MOEA/D: A multiobjective evolutionary algorithm based on decomposition[J]. IEEE Transactions on Evolutionary Computation, 2007, 11(6): 712-731. doi: 10.1109/TEVC.2007.892759 [14] CHENG R, JIN Y C, OLHOFER M, et al. A reference vector guided evolutionary algorithm for many-objective optimization[J]. IEEE Transactions on Evolutionary Computation, 2016, 20(5): 773-791. doi: 10.1109/TEVC.2016.2519378 [15] LIU D C, NOCEDAL J. On the limited memory BFGS method for large scale optimization[J]. Mathematical Programming, 1989, 45(1): 503-528. [16] BROYDEN C G. The convergence of a class of double-rank minimization algorithms[J]. IMA Journal of Applied Mathematics, 1970, 6(3): 222-231. doi: 10.1093/imamat/6.3.222 [17] FLETCHER R. A new approach to variable metric algorithms[J]. The Computer Journal, 1970, 13(3): 317-322. doi: 10.1093/comjnl/13.3.317 [18] GOLDFARB D. A family of variable-metric methods derived by variational means[J]. Mathematics of Computation, 1970, 24(109): 23-26. doi: 10.1090/S0025-5718-1970-0258249-6 [19] SHANNO D F. Conditioning of quasi-Newton methods for function minimization[J]. Mathematics of Computation, 1970, 24(111): 647-656. doi: 10.1090/S0025-5718-1970-0274029-X [20] LYU Z, XU Z, MARTINS J. Benchmarking optimization algorithms for wing aerodynamic design optimization[C]//Proceedings of the 8th International Conference on Computational Fluid Dynamics. Oxford : International Journal of Computational Fluid Dynamics, 2014, 1-18. [21] KENWAY G K W, MADER C A, HE P, et al. Effective adjoint approaches for computational fluid dynamics[J]. Progress in Aerospace Sciences, 2019, 110: 100542. doi: 10.1016/j.paerosci.2019.05.002 [22] HUA Y C, JIN Y C, HAO K R. A clustering-based adaptive evolutionary algorithm for multiobjective optimization with irregular Pareto fronts[J]. IEEE Transactions on Cybernetics, 2019, 49(7): 2758-2770. doi: 10.1109/TCYB.2018.2834466 [23] COOK P H, MCDONALD M A, FIRMIN M C P. Aerofoil RAE 2822:Pressure distributions, and boundary layer and wake measurements: ADA073982[R]. Experimental Data Base for Computer Program Assessment: AGARD Report AR 138, 1979: A6. -






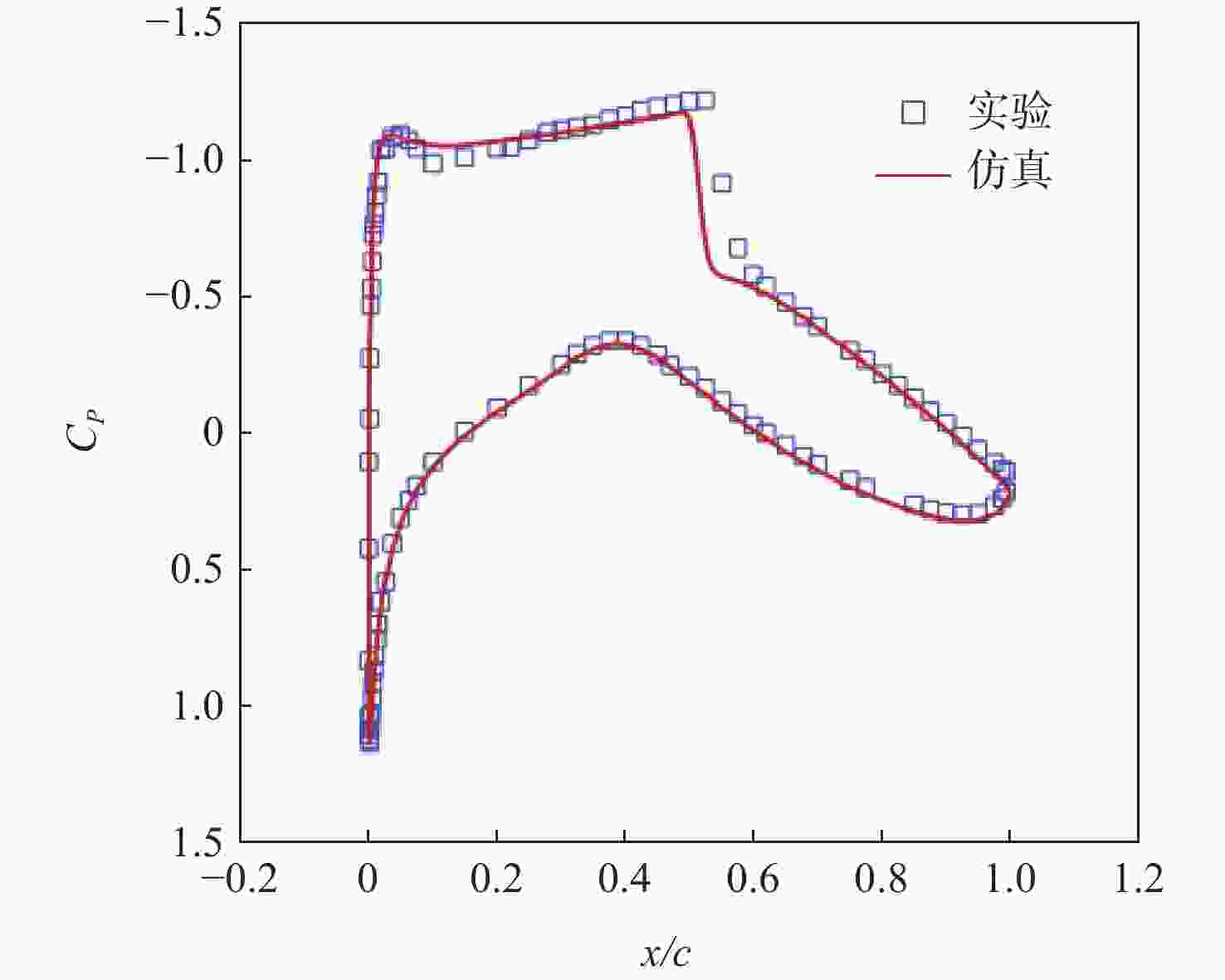
 下载:
下载: