基于反吸引速度更新机制的改进蜉蝣算法

毛清华; 王迎港; 牛晓辉

doi:10.13700/j.bh.1001-5965.2022.0550

基于反吸引速度更新机制的改进蜉蝣算法

doi: 10.13700/j.bh.1001-5965.2022.0550

燕山大学经济管理学院，秦皇岛 066004

基金项目: 国家自然科学基金(71704151)

详细信息

通讯作者:
E-mail：maoqh@ysu.edu.cn

中图分类号: TP301.6
计量
- 文章访问数: 146
- HTML全文浏览量: 90
- PDF下载量: 9
- 被引次数: 0
出版历程
- 收稿日期: 2022-06-29
- 录用日期: 2022-08-15
- 网络出版日期: 2022-09-16
- 整期出版日期: 2024-06-27

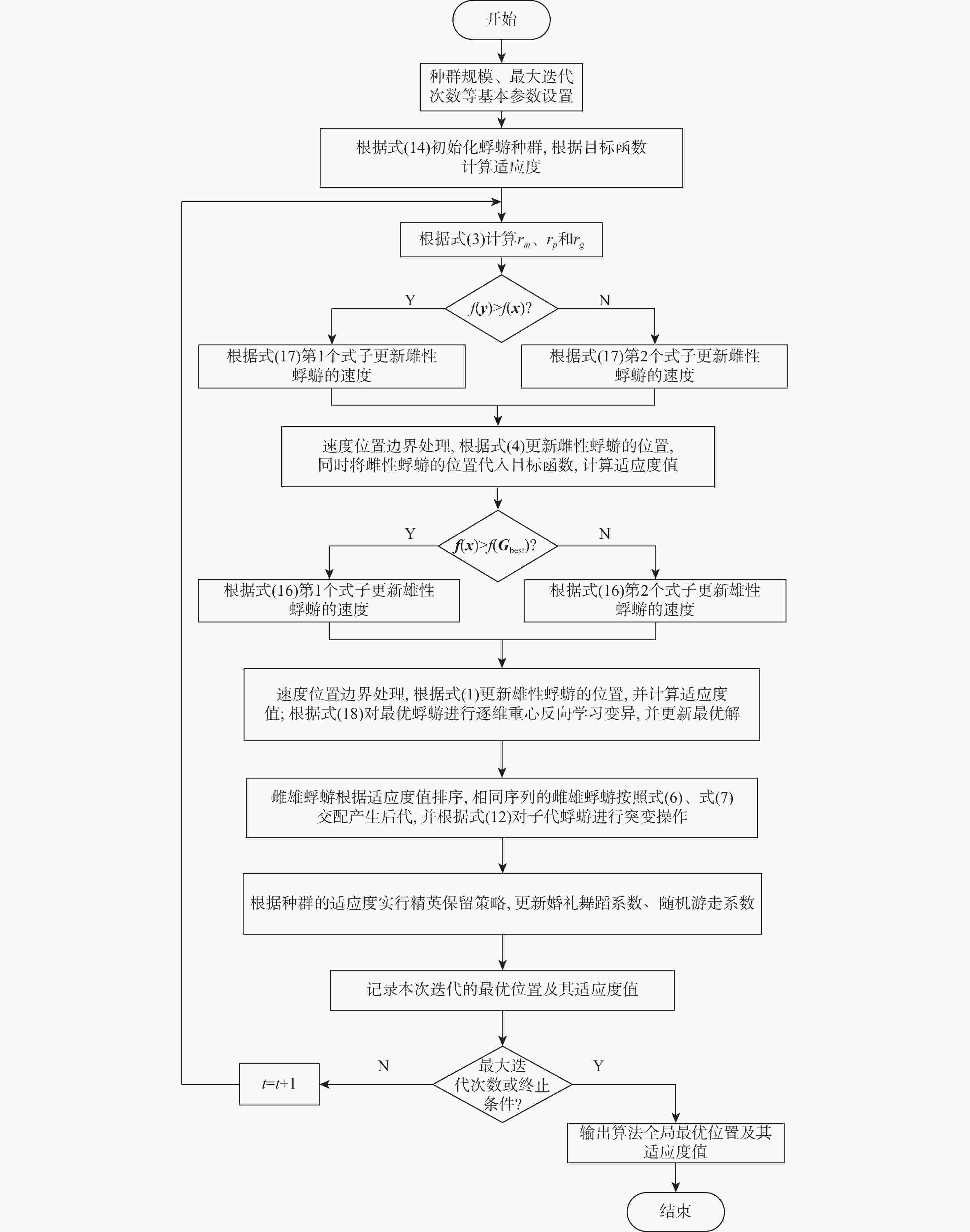
Improved mayfly optimization algorithm based on anti-attraction velocity update mechanism

School of Economics and Management，Yanshan University，Qinhuangdao 066004，China

Funds: National Natural Science Foundation of China (71704151)

More Information

Corresponding author: E-mail：maoqh@ysu.edu.cn

摘要

摘要:
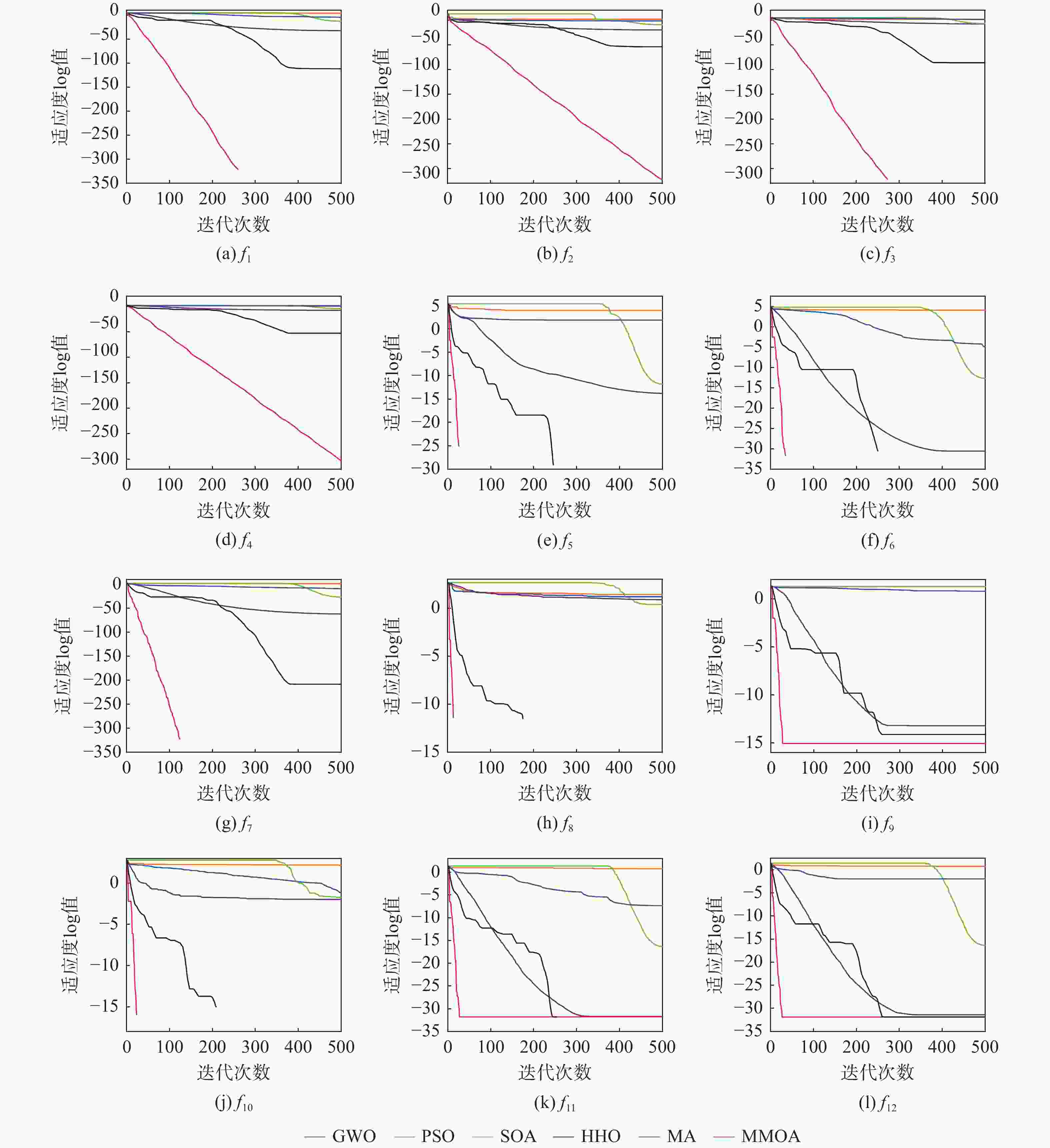
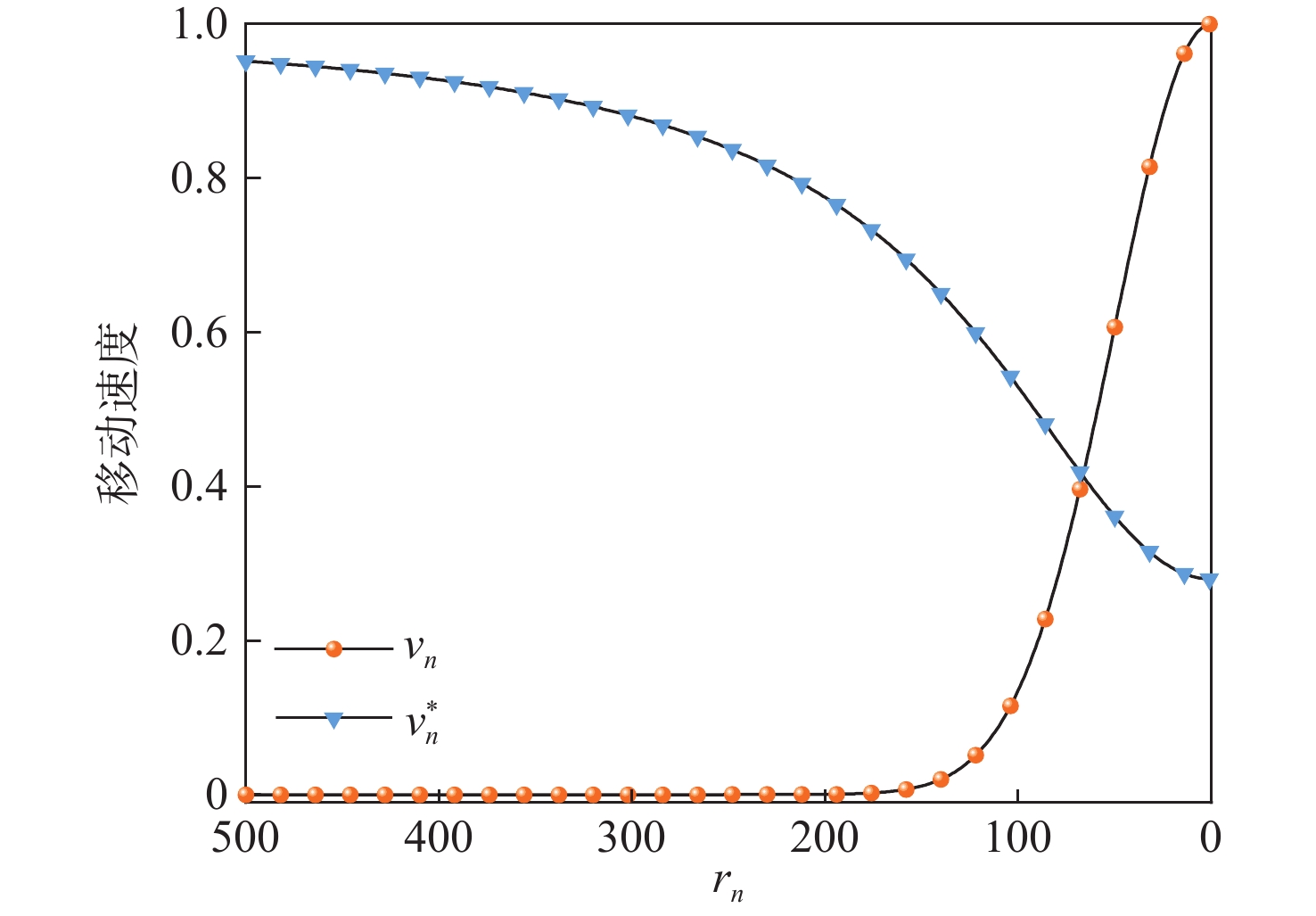
针对蜉蝣算法(MA)前期收敛速度较慢、后期寻优精度不高等问题，提出一种基于反吸引速度更新机制的改进蜉蝣算法(MMOA)。采用改进型Tent混沌序列初始化蜉蝣种群，使蜉蝣分布更加均匀，提升了种群的多样性；结合MA的特点，引入反吸引速度更新机制指导蜉蝣速度更新，平衡算法的全局搜索和局部寻优能力，进而提升算法的收敛性能；对全局最优蜉蝣进行逐维的重心反向学习变异，降低各维度间的干扰，帮助算法跳出局部最优并加速收敛。基于12个标准测试函数和部分CEC2017测试函数进行对比仿真实验，结果表明：MMOA较灰狼优化(GWO)算法、MA等算法在收敛速度、寻优精度和稳定性等方面都具有明显优势。
- 蜉蝣算法 /
- 改进Tent混沌 /
- 反吸引速度 /
- 逐维变异 /
- 重心反向学习
Abstract:
To address the problem that the mayfly optimization algorithm (MA) has a slow convergence speed in the early stage and not high accuracy in the later stage of the search, a modified mayfly optimization algorithm (MMOA) based on the anti-attraction speed update mechanism is proposed. Firstly, an improved Tent chaotic sequence is used to initialize the mayfly population, which makes the mayfly distribution more uniform and improves the diversity of the population. Secondly, in order to enhance the algorithm’s convergence performance, an anti-attraction speed update mechanism is presented to direct the mayfly speed update depending on the properties of the MA. Finally, the dimension-by-dimension centroid opposition-based learning strategy is performed on the global best mayfly, which reduces the interference between dimensions, helps the algorithm jump out of the local optimum and accelerates the convergence. Based on a comparison of simulation experiments using 12 conventional test functions and a few CEC2017 test functions, the findings indicate that MMOA clearly outperforms algorithms such as grey wolf optimizer (GWO) and MA in terms of convergence speed, stability, and optimization accuracy.
- mayfly algorithm /
- improved Tent chaos /
- anti-attraction velocity /
- dimension-by-dimension mutation /
- centroid opposition-based learning

HTML全文

图 1 $ {{v}}_n^ * $与${v_n}$对比

Figure 1. Comparison of $ {v}_n^ * $ and ${v_n}$

下载: 全尺寸图片幻灯片

图 2 $ {{v}}_n^ * $变化曲线

Figure 2. $ {{v}}_n^ * $ change curves

下载: 全尺寸图片幻灯片

图 3 MMOA流程

Figure 3. MMOA flow chart

下载: 全尺寸图片幻灯片

图 4 算法收敛次数随参数${{P}}$取值的变化曲线

Figure 4. Variation curves of algorithm convergence times with value of parameter ${{P}}$

下载: 全尺寸图片幻灯片

图 5 适应度值随参数${{P}}$取值的变化曲线

Figure 5. Variation curve of fitness value with value of parameter ${{P}}$

下载: 全尺寸图片幻灯片

图 6 标准测试函数平均收敛曲线

Figure 6. Standard test function average convergence curves

下载: 全尺寸图片幻灯片

表 1 寻优结果对比

Table 1. Comparison of optimization results

函数	固定寻优值	迭代次数
函数	固定寻优值	MA	OMA
Sphere	1.00×10⁻⁵	428	37
Schwefel’s 1.2	25	550	26
Rosenbrock’s	10	586	17
Quartic	1.00×10⁻¹⁰	430	32
Ackely’s	5	459	11
Penalized1	1.00×10⁻¹⁵	833	66

下载: 导出CSV

表 2 标准测试函数

Table 2. Standard test functions

类型	函数	函数名称	取值范围	最优解
单峰函数	f₁	Sphere	[−100,100]	0
	f₂	Schwefel’s 2.22	[−10,10]	0
	f₃	Schwefel’s 1.2	[−100,100]	0
	f₄	Schwefel’s 2.21	[−100,100]	0
	f₅	Rosenbrock’s	[−30,30]	0
	f₆	Step	[−100,100]	0
	f₇	Quartic	[−1.28,1.28]	0
多峰函数	f₈	Rastrigin’s	[−5.12,5.12]	0
	f₉	Ackely’s	[−32,32]	0
	f₁₀	Griewank’s	[−600,600]	0
	f₁₁	Penalized1	[−50,50]	0
	f₁₂	Penalized2	[−50,50]	0

下载: 导出CSV

表 3 部分CEC2017测试函数

Table 3. Some CEC2017 test functions

函数	特征	取值范围	最优解
CEC03	UN	[−100,100]	300
CEC06	MN	[−100,100]	600
CEC09	MN	[−100,100]	900
CEC12	HF	[−100,100]	1200
CEC15	HF	[−100,100]	1500
CEC18	HF	[−100,100]	1800
CEC21	CF	[−100,100]	2100
CEC24	CF	[−100,100]	2400
CEC27	CF	[−100,100]	2700
注：UN表示单峰函数，MN表示简单多峰函数，HF表示混合函数，CF表示组合函数。

下载: 导出CSV

表 4 不同策略寻优结果

Table 4. Optimal results of different strategies

函数	算法	平均值			标准差
函数	算法	d=10	d=50	d=100	d=10	d=50	d=100
f₁	MA	5.53×10⁻³⁶	2.78×10⁻²	1.38×10²	9.57×10⁻³⁶	5.17×10⁻²	1.53×10²
	TMA	8.42×10⁻³⁸	3.96×10⁻⁵	7.87×10¹	1.52×10⁻³⁷	1.96×10⁻⁴	8.57×10¹
	VMA	4.38×10⁻¹³	2.76×10⁻²	1.93×10¹	4.77×10⁻¹³	4.57×10⁻²	7.57×10¹
	OMA	2.30×10⁻¹²⁰	8.09×10⁻⁹⁶	7.93×10⁻⁹⁵	3.55×10⁻¹²⁰	1.41×10⁻⁹⁵	1.08×10⁻⁹⁴
	MMOA	0	0	0	0	0	0
f₄	MA	3.50×10⁻⁴	1.79×10¹	2.98×10¹	5.91×10⁻⁴	4.75×10¹	3.96×10¹
	TMA	1.22×10⁻⁴	1.85	3.19	1.39×10⁻⁴	4.55	5.07
	VMA	4.97×10⁻¹	2.69×10¹	3.65×10¹	1.06	3.95×10¹	4.29×10¹
	OMA	4.15×10⁻⁴⁹	5.06×10⁻⁴⁸	9.41×10⁻⁴⁸	2.19×10⁻⁴⁸	2.39×10⁻⁴⁸	3.45×10⁻⁴⁸
	MMOA	7.02×10⁻³⁰⁰	1.14×10⁻²⁸⁴	8.99×10⁻²⁸⁸	0	3.25×10⁻²⁸⁴	9.35×10⁻²⁸⁸
f₈	MA	3.16	6.32×10¹	1.54×10²	4.83	8.83	3.71×10¹
	TMA	1.06	3.28×10¹	1.39×10²	2.52	4.13	2.75×10¹
	VMA	1.46	4.54×10¹	1.28×10²	1.67	5.82	2.11×10¹
	OMA	0	0	0	0	0	0
	MMOA	0	0	0	0	0	0
f₁₂	MA	1.10×10⁻³	4.26×10⁻²	1.68	3.41×10⁻³	1.05×10⁻¹	2.95
	TMA	3.66×10⁻⁴	1.42×10⁻²	1.31	2.01×10⁻³	7.63×10⁻²	1.86
	VMA	1.51×10⁻³	8.80×10⁻³	3.91×10⁻¹	3.80×10⁻³	2.21×10⁻²	2.57×10⁻¹
	OMA	1.35×10⁻³²	1.35×10⁻³²	1.35×10⁻³²	5.57×10⁻⁴⁸	5.57×10⁻⁴⁸	5.57×10⁻⁴⁸
	MMOA	1.35×10⁻³²	1.35×10⁻³²	1.35×10⁻³²	5.57×10⁻⁴⁸	5.57×10⁻⁴⁸	5.57×10⁻⁴⁸
CEC03	MA	3.00×10²	3.01×10⁵	7.46×10⁵	8.54×10⁻¹²	9.68×10⁴	1.66×10⁵
	TMA	3.00×10²	2.75×10⁵	6.71×10⁵	7.54×10⁻¹⁴	9.21×10⁴	1.68×10⁵
	VMA	3.00×10²	7.68×10⁴	3.90×10⁵	6.68×10⁻¹⁴	4.42×10⁴	1.33×10⁵
	OMA	3.00×10²	2.53×10⁵	5.09×10⁵	7.01×10⁻¹⁴	7.95×10⁴	1.76×10⁵
	MMOA	3.00×10²	5.57×10⁴	2.56×10⁵	3.50×10⁻¹⁴	2.27×10⁴	4.95×10⁴
CEC09	MA	1.01×10³	1.17×10⁴	2.41×10⁴	1.24×10²	2.09×10³	2.96×10³
	TMA	9.84×10²	1.10×10⁴	2.29×10⁴	6.76×10¹	1.59×10³	2.23×10³
	VMA	9.53×10²	1.12×10⁴	2.31×10⁴	5.49×10¹	2.14×10³	2.47×10³
	OMA	9.42×10²	1.07×10⁴	2.03×10⁴	4.31×10¹	1.51×10³	1.71×10³
	MMOA	9.05×10²	9.57×10³	1.79×10⁴	3.25×10¹	7.41×10²	1.42×10³
CEC15	MA	1.84×10³	8.33×10³	1.03×10⁴	1.56×10³	3.05×10³	7.19×10³
	TMA	1.72×10³	6.94×10³	9.53×10³	4.57×10²	2.61×10³	6.59×10³
	VMA	1.66×10³	5.83×10³	8.82×10³	3.64×10²	3.88×10³	6.24×10³
	OMA	1.56×10³	5.77×10³	8.21×10³	1.17×10²	3.45×10³	6.43×10³
	MMOA	1.52×10³	5.38×10³	8.05×10³	3.11×10¹	1.89×10³	5.66×10³

下载: 导出CSV

表 5 标准测试函数下寻优结果

Table 5. Optimal results under standard test functions

函数	算法	最优值	平均值	标准差	函数	算法	最优值	平均值	标准差
f₁	GWO	3.23×10⁻³⁵	3.17×10⁻³³	3.42×10⁻³³	f₇	GWO	1.48×10⁻⁶²	8.37×10⁻⁶⁰	4.30×10⁻⁵⁹
	PSO	5.17×10³	1.26×10⁴	4.26×10³		PSO	1.49×10¹	1.48×10¹	7.25
	SOA	6.31×10⁻¹⁵	3.63×10⁻¹³	8.53×10⁻¹³		SOA	1.94×10⁻²⁷	4.85×10⁻²⁸	8.91×10⁻²⁸
	HHO	2.86×10⁻¹¹²	2.92×10⁻⁹⁸	1.57×10⁻⁹⁷		HHO	5.38×10⁻²⁰⁹	6.22×10⁻¹⁹⁸	6.58×10⁻¹⁹⁸
	MA	8.99×10⁻⁷	2.49×10⁻⁵	3.68×10⁻⁵		MA	5.18×10⁻¹⁰	1.44×10⁻¹⁰	3.39×10⁻¹⁰
	MMOA	0	0	0		MMOA	0	0	0
f₂	GWO	9.88×10⁻²¹	8.08×10⁻²⁰	6.12×10⁻²⁰	f₈	GWO	7.42	2.26	3.40
	PSO	4.83×10¹	1.67×10³	4.27×10³		PSO	3.35×10²	3.12×10²	2.83×10¹
	SOA	3.74×10⁻¹⁰	4.52×10⁻⁹	5.85×10⁻⁹		SOA	2.10×10⁻¹²	1.78	7.02
	HHO	1.89×10⁻⁵⁴	2.84×10⁻⁵³	1.09×10⁻⁵²		HHO	0	0	0
	MA	4.55×10⁻⁵	7.90×10⁻³	2.03×10⁻²		MA	2.59×10¹	2.70×10¹	9.02
	MMOA	0	3.39×10⁻³⁰⁶	7.32×10⁻³⁰⁶		MMOA	0	0	0
f₃	GWO	8.52×10⁻¹²	1.92×10⁻⁸	4.43×10⁻⁸	f₉	GWO	6.13×10⁻¹⁴	4.35×10⁻¹⁴	5.75×10⁻¹⁵
	PSO	2.70×10⁴	4.40×10⁴	8.20×10³		PSO	1.89×10¹	1.62×10¹	1.45
	SOA	1.08×10⁻⁸	2.31×10⁻⁶	3.82×10⁻⁶		SOA	1.99×10¹	1.99×10¹	1.70×10⁻³
	HHO	1.31×10⁻⁸⁶	5.35×10⁻⁸⁵	2.89×10⁻⁸⁴		HHO	4.44×10⁻¹⁵	7.64×10⁻¹⁵	1.08×10⁻¹⁵
	MA	8.79×10⁻¹	1.74×10¹	2.28×10¹		MA	6.23	4.93	1.22
	MMOA	0	0	0		MMOA	8.88×10⁻¹⁶	8.88×10⁻¹⁶	0
f₄	GWO	2.58×10⁻⁸	2.32×10⁻⁸	1.82×10⁻⁸	f₁₀	GWO	0	3.20×10⁻³	6.80×10⁻³
	PSO	5.77×10¹	5.86×10¹	5.02		PSO	1.44×10²	1.09×10²	3.31×10¹
	SOA	1.01×10⁻⁴	3.24×10⁻⁴	3.37×10⁻⁴		SOA	1.01×10⁻¹²	1.78×10⁻²	2.71×10⁻²
	HHO	2.85×10⁻⁵³	2.73×10⁻⁵¹	1.25×10⁻⁵⁰		HHO	0	0	0
	MA	5.28	6.76	3.15		MA	5.60×10⁻²	4.44×10⁻¹	6.66×10⁻¹
	MMOA	2.85×10⁻³⁰⁵	3.02×10⁻²⁹⁷	8.52×10⁻²⁹⁷		MMOA	0	0	0
f₅	GWO	1.71×10⁻¹⁴	6.83×10⁻²	3.35×10⁻¹	f₁₁	GWO	2.014×10⁻³²	1.87×10⁻³²	1.36×10⁻³³
	PSO	9.32×10³	1.95×10⁴	1.04×10⁴		PSO	5.79	7.29	1.83
	SOA	1.54×10⁻¹²	7.53×10⁻¹¹	1.87×10⁻¹⁰		SOA	4.75×10⁻¹⁷	1.15×10⁻¹⁶	2.69×10⁻¹⁶
	HHO	0	0	0		HHO	1.57×10⁻³²	1.57×10⁻³²	5.57×10⁻⁴⁸
	MA	7.53×10¹	4.89×10¹	3.51×10¹		MA	4.49×10⁻⁸	3.46×10⁻²	7.38×10⁻²
	MMOA	0	0	0		MMOA	1.57×10⁻³²	1.57×10⁻³²	5.57×10⁻⁴⁸
f₆	GWO	2.87×10⁻³¹	2.76×10⁻³¹	8.11×10⁻³²	f₁₂	GWO	4.06×10⁻³²	9.39×10⁻³²	1.40×10⁻³¹
	PSO	1.28×10⁴	1.26×10⁴	4.26×10³		PSO	5.79	6.75	2.16
	SOA	2.00×10⁻¹³	3.63×10⁻¹³	8.53×10⁻¹³		SOA	4.26×10⁻¹⁷	1.96×10⁻¹⁶	2.55×10⁻¹⁶
	HHO	0	0	0		HHO	1.35×10⁻³²	1.35×10⁻³²	5.57×10⁻⁴⁸
	MA	1.14×10⁻⁵	2.49×10⁻⁵	3.68×10⁻⁵		MA	9.58×10⁻⁸	5.50×10⁻³	9.40×10⁻³
	MMOA	0	0	0		MMOA	1.35×10⁻³²	1.35×10⁻³²	5.57×10⁻⁴⁸

下载: 导出CSV

表 6 Wilcoxon秩和检验$p$值

Table 6. Wilcoxon rank sum test $p$-value

函数	MMOA & GWO	MMOA & PSO	MMOA & SOA	MMOA & HHO	MMOA & MA
f₁	1.21×10⁻¹²	1.21×10⁻¹²	1.21×10⁻¹²	1.21×10⁻¹²	1.21×10⁻¹²
f₂	2.86×10⁻¹¹	2.86×10⁻¹¹	2.86×10⁻¹¹	2.63×10⁻¹¹	2.86×10⁻¹¹
f₃	1.21×10⁻¹²	1.21×10⁻¹²	1.21×10⁻¹²	1.21×10⁻¹²	1.21×10⁻¹²
f₄	3.02×10⁻¹¹	3.02×10⁻¹¹	3.02×10⁻¹¹	3.02×10⁻¹¹	3.02×10⁻¹¹
f₅	1.21×10⁻¹²	1.21×10⁻¹²	1.21×10⁻¹²	N/A	1.21×10⁻¹²
f₆	1.20×10⁻¹²	1.21×10⁻¹²	1.21×10⁻¹²	N/A	1.21×10⁻¹²
f₇	1.21×10⁻¹²	1.21×10⁻¹²	1.21×10⁻¹²	1.21×10⁻¹²	1.21×10⁻¹²
f₈	4.87×10⁻¹¹	1.21×10⁻¹²	1.21×10⁻¹²	N/A	1.21×10⁻¹²
f₉	8.77×10⁻¹³	1.21×10⁻¹²	1.21×10⁻¹²	6.12×10⁻¹⁴	1.21×10⁻¹²
f₁₀	1.10×10⁻²	1.21×10⁻¹²	1.21×10⁻¹²	N/A	1.21×10⁻¹²
f₁₁	1.20×10⁻¹²	1.21×10⁻¹²	1.21×10⁻¹²	N/A	1.21×10⁻¹²
f₁₂	1.20×10⁻¹²	1.21×10⁻¹²	1.21×10⁻¹²	N/A	1.21×10⁻¹²
注：N/A表示两者之间无法比较，性能相当。

下载: 导出CSV

表 7 MIWMA和MMOA性能对比

Table 7. Performance comparison of MIWMA and MMOA algorithms

函数	最优值		平均值		标准差
函数	MIWMA	MMOA	MIWMA	MMOA	MIWMA	MMOA
f₁	3.81×10⁻¹⁴³	0	1.40×10⁻¹³⁵	0	6.50×10⁻¹³⁴	0
f₂	3.42×10⁻⁶⁹	9.06×10⁻²⁵³	2.05×10⁻⁶⁰	9.55×10⁻²⁴²	9.61×10⁻⁶⁰	2.26×10⁻²⁴¹
f₃	3.15×10⁻¹³⁵	0	2.55×10⁻¹¹³	0	1.70×10⁻¹¹²	0
f₄	5.55×10⁻⁷⁰	3.16×10⁻²⁴⁰	1.88×10⁻⁶⁰	3.34×10⁻²³⁴	1.17×10⁻⁵⁹	7.28×10⁻²³⁴
f₇	4.17×10⁻⁷	0	5.62×10⁻⁵	0	4.08×10⁻⁵	0
f₈	0	0	0	0	0	0
f₉	8.88×10⁻¹⁶	8.88×10⁻¹⁶	8.88×10⁻¹⁶	8.88×10⁻¹⁶	0	0
f₁₀	0	0	0	0	0	0
f₁₁	5.45×10⁻¹⁴	1.57×10⁻³²	6.43×10⁻¹³	1.57×10⁻³²	6.72×10⁻¹³	5.53×10⁻⁴⁸

下载: 导出CSV

表 8 CEC2017测试函数下寻优结果

Table 8. Optimal results under CEC2017 test functions

函数	算法	平均值	标准差
CEC03	AFSMA	4.80×10⁴	1.44×10⁴
	EGSWA	8.39×10⁴	6.63×10³
	IGWO	1.84×10⁴	3.46×10³
	HHO	5.59×10⁴	8.15×10³
	MA	1.35×10⁵	6.39×10⁴
	MMOA	1.09×10⁴	3.41×10³
CEC06	AFSMA	6.24×10²	1.02×10¹
	EGSWA	6.83×10²	1.21×10¹
	IGWO	7.02×10²	1.11×10²
	HHO	6.69×10²	9.50
	MA	6.67×10²	7.48
	MMOA	6.19×10²	5.84
CEC09	AFSMA	5.05×10³	1.56×10³
	EGSWA	1.08×10⁴	1.32×10³
	IGWO	1.14×10³	3.32×10³
	HHO	8.78×10³	1.37×10³
	MA	6.03×10³	1.25×10³
	MMOA	4.10×10³	4.99×10²
CEC12	AFSMA	3.37×10⁶	3.13×10⁶
	EGSWA	2.02×10⁹	8.57×10⁸
	IGWO	4.86×10⁶	4.14×10⁶
	HHO	1.09×10⁸	1.37×10⁸
	MA	1.43×10⁷	1.55×10⁷
	MMOA	1.85×10⁶	1.57×10⁶
CEC15	AFSMA	1.33×10⁴	1.33×10⁴
	EGSWA	7.88×10⁷	8.33×10⁷
	IGWO	6.04×10⁴	4.06×10⁴
	HHO	1.17×10⁵	6.78×10⁴
	MA	2.23×10⁴	1.82×10⁴
	MMOA	2.29×10³	4.75×10³
CEC18	AFSMA	2.45×10⁶	2.72×10⁶
	EGSWA	1.84×10⁷	1.82×10⁷
	IGWO	4.56×10⁵	2.91×10⁵
	HHO	4.49×10⁶	8.33×10⁶
	MA	2.02×10⁵	1.96×10⁵
	MMOA	1.58×10⁵	1.52×10⁵
CEC21	AFSMA	2.45×10³	3.67×10¹
	EGSWA	2.67×10³	5.12×10¹
	IGWO	3.21×10³	1.31×10²
	HHO	2.73×10³	9.21×10¹
	MA	2.58×10³	5.01×10¹
	MMOA	2.43×10³	3.59×10¹
CEC24	AFSMA	2.98×10³	4.81×10¹
	EGSWA	3.44×10³	1.16×10²
	IGWO	2.74×10³	6.83×10²
	HHO	3.54×10³	1.69×10²
	MA	3.73×10³	1.75×10²
	MMOA	3.27×10³	1.40×10²
CEC27	AFSMA	3.25×10³	2.09×10¹
	EGSWA	3.20×10³	1.80×10⁻⁹
	IGWO	3.21×10³	7.02×10²
	HHO	3.58×10³	2.12×10²
	MA	4.55×10³	7.31×10²
	MMOA	3.32×10³	1.93×10²

下载: 导出CSV

参考文献(21)

[1]	MIRJALILI S, MIRJALILI S M, LEWIS A. Grey wolf optimizer[J]. Advances in Engineering Software, 2014, 69: 46-61.
[2]	MIRJALILI S, GANDOMI A H, MIRJALILI S Z, et al. Salp swarm algorithm[J]. Advances in Engineering Software, 2017, 114: 163-191. doi: 10.1016/j.advengsoft.2017.07.002
[3]	ARORA S, SINGH S. Butterfly optimization algorithm: A novel approach for global optimization[J]. Soft Computing, 2019, 23(3): 715-734. doi: 10.1007/s00500-018-3102-4
[4]	DHIMAN G, KUMAR V. Seagull optimization algorithm: Theory and its applications for large-scale industrial engineering problems[J]. Knowledge-Based Systems, 2019, 165: 169-196. doi: 10.1016/j.knosys.2018.11.024
[5]	FARAMARZI A, HEIDARINEJAD M, STEPHENS B, et al. Equilibrium optimizer: A novel optimization algorithm[J]. Knowledge-Based Systems, 2020, 191: 105190. doi: 10.1016/j.knosys.2019.105190
[6]	ZERVOUDAKIS K, TSAFARAKIS S. A mayfly optimization algorithm[J]. Computers & Industrial Engineering, 2020, 145: 106559.
[7]	王尔申, 贾超颖, 曲萍萍, 等. 基于混沌粒子群优化的北斗/GPS组合导航选星算法[J]. 北京航空航天大学学报, 2019, 45(2): 259-265. WANG E S, JIA C Y, QU P P, et al. BDS /GPS integrated navigation satellite selection algorithm based on chaos particle swarm optimization[J]. Journal of Beijing University of Aeronautics and Astronautics, 2019, 45(2): 259-265(in Chinese).
[8]	王志华, 王浩帆, 程漫漫. 基于启发式遗传算法的模糊测试样本集优化方案[J]. 北京航空航天大学学报, 2022, 48(2): 217-224. WANG Z H, WANG H F, CHENG M M. Fuzzing testing sample set optimization scheme based on heuristic genetic algorithm[J]. Journal of Beijing University of Aeronautics and Astronautics, 2022, 48(2): 217-224(in Chinese).
[9]	刘景森, 毛艺楠, 李煜. 具有振荡约束的自然选择萤火虫优化算法[J]. 控制与决策, 2020, 35(10): 2363-2371. LIU J S, MAO Y N, LI Y. Natural selection firefly optimization algorithm with oscillation and constraint[J]. Control and Decision, 2020, 35(10): 2363-2371(in Chinese).
[10]	ABD ELAZIZ M, SENTHILRAJA S, ZAYED M E, et al. A new random vector functional link integrated with mayfly optimization algorithm for performance prediction of solar photovoltaic thermal collector combined with electrolytic hydrogen production system[J]. Applied Thermal Engineering, 2021, 193: 117055.
[11]	HU A H, DENG Z L, YANG H, et al. An optimal geometry configuration algorithm of hybrid semi-passive location system based on mayfly optimization algorithm[J]. Sensors, 2021, 21(22): 7484. doi: 10.3390/s21227484
[12]	SHAHEEN M A M, HASANIEN H M, EL MOURSI M S, et al. Precise modeling of PEM fuel cell using improved chaotic mayfly optimization algorithm[J]. International Journal of Energy Research, 2021, 45(13): 18754-18769.
[13]	LIU Y H, CHAI Y, LIU B W, et al. Bearing fault diagnosis based on energy spectrum statistics and modified mayfly optimization algorithm[J]. Sensors, 2021, 21(6): 2245. doi: 10.3390/s21062245
[14]	李浩, 杨海潇, 张兰, 等. 改进离散蜉蝣算法的多目标动态网络社区发现[J]. 计算机科学与探索, 2023, 17(4): 942-952. LI H, YANG H X, ZHAMG L, et al. Improved discrete mayfly algorithm for multi-objective dynamic network community detection[J]. Journal of Frontiers of Computer Science and Technology, 2023, 17(4): 942-952(in Chinese).
[15]	邵瑞凝, 杨博, 束洪春, 等. 基于改进蜉蝣算法的光伏阵列最优重构方法[J]. 电力系统自动化, 2022, 46(11): 142-150. SHAO R N, YANG B, SHU H C, et al. Improved mayfly algorithm for optimal PV array reconfiguration[J]. Automation of Electric Power Systems, 2022, 46(11): 142-150(in Chinese).
[16]	张娜, 赵泽丹, 包晓安, 等. 基于改进的Tent混沌万有力搜索算法[J]. 控制与决策, 2020, 35(4): 893-900. ZHANG N, ZHAO Z D, BAO X A, et al. Gravitational search algorithm based on improved Tent chaos[J]. Control and Decision, 2020, 35(4): 893-900(in Chinese).
[17]	罗强, 季伟东, 徐浩天, 等. 一种最优粒子逐维变异的粒子群优化算法[J]. 小型微型计算机系统, 2020, 41(2): 259-263. LUO Q, JI W D, XU H T, et al. Particle swarm optimization with global best particle dimension-by-dimension mutation[J]. Journal of Chinese Computer Systems, 2020, 41(2): 259-263(in Chinese).
[18]	王义, 张达敏, 邹诚诚. 增强全局搜索和自适应蜉蝣算法[J]. 哈尔滨工业大学学报, 2022, 54(11): 137-150. WANG Y, ZHANG D M, ZOU C C. Enhance global search and adaptive mayfly algorithm[J]. Journal of Harbin Institute of Technology, 2022, 54(11): 137-150(in Chinese).
[19]	ABDEL-BASSET M, MOHAMED R, CHAKRABORTTY R K, et al. An efficient binary slime mould algorithm integrated with a novel attacking-feeding strategy for feature selection[J]. Computers & Industrial Engineering, 2021, 153(11): 107078.
[20]	肖子雅, 刘升. 精英反向黄金正弦鲸鱼算法及其工程优化研究[J]. 电子学报, 2019, 47(10): 2177-2186. doi: 10.3969/j.issn.0372-2112.2019.10.020 XIAO Z Y, LIU S. Study on elite opposition-based golden-sine whale optimization algorithm and its application of project optimization[J]. Acta Electronica Sinica, 2019, 47(10): 2177-2186(in Chinese). doi: 10.3969/j.issn.0372-2112.2019.10.020
[21]	NADIMI-SHAHRAKI M H, TAGHIAN S, MIRJALILI S. An improved grey wolf optimizer for solving engineering problems[J]. Expert Systems with Applications, 2021, 166: 113917. doi: 10.1016/j.eswa.2020.113917