Short linkable-and-redactable ring signature and its blockchain correcting application
-
摘要:
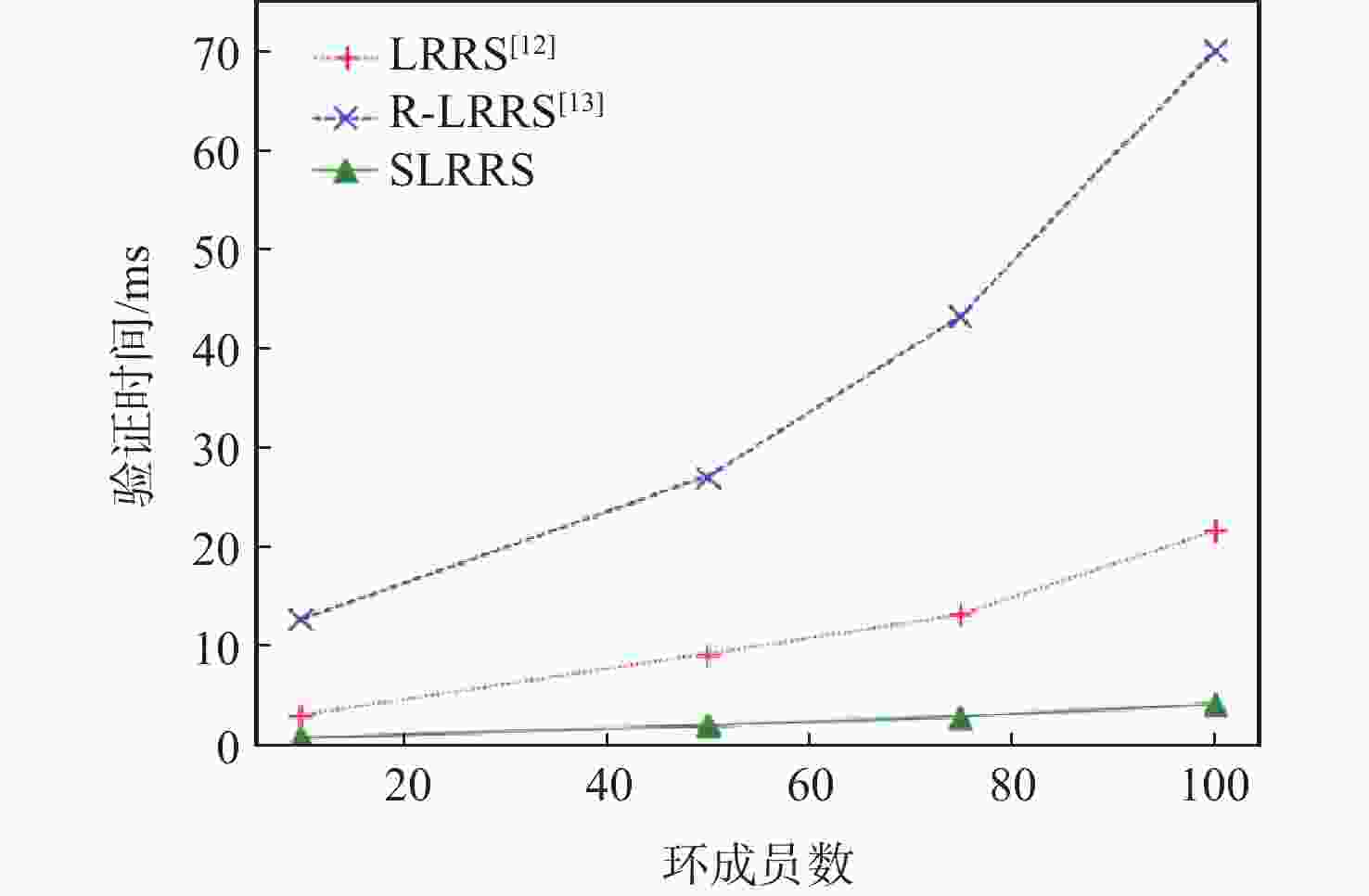
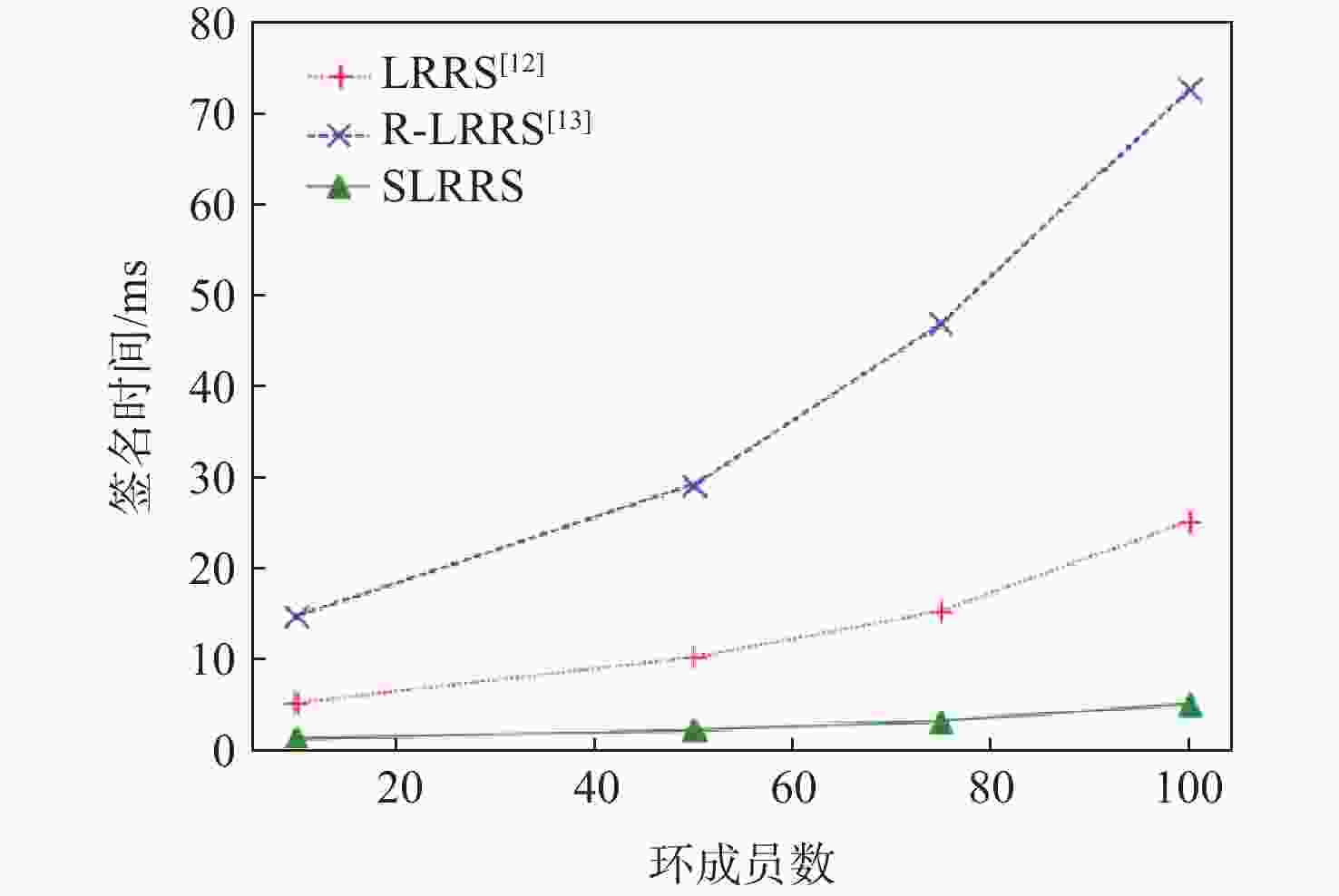
关联可编辑环签名(LRRS)可提升区块链的匿名性,防止双花攻击,修正区块链数据,但其签名大小随环成员的增多而增大。针对该问题,结合已有LRRS和简短关联环签名方案,利用动态累加器对环成员的公钥进行累加计算,依据原知识证明签名(SPK)构造出新的SPK,提出简短LRRS(SLRRS)方案,基于该签名又提出新的区块链修正协议。在随机谕言机模型下,证明所提签名具有不可伪造性、匿名性、关联性。性能评估表明:随着环成员的增多,已有签名的大小在增大,而所提签名不变;同时此类签名所消耗的时间均在增多,而所提签名的时间增速较缓且最少。
-
关键词:
- 知识证明签名 /
- 动态累加器 /
- 简短关联可编辑环签名 /
- 时间更新变色龙哈希 /
- 区块链修正
Abstract:Linkable-and-redactable ring signatures (LRRS) could improve the anonymity of blockchain, prevent double-flower attacks and correct blockchain data, but its signature size increased with the increase of ring members. With the aim of addressing the issue, this paper combined the existing LRRS and short ring signature with a dynamic accumulator to gather the public keys of ring members. Subsequently, new signatures were created based on knowledge proofs (SPK) derived from the original SPK, a short LRRS (SLRRS) was suggested, and a new blockchain correcting protocol was suggested based on the signature. In the random oracle model, the proposed signature is proved to be unforgeable, anonymous and linkable. Performance analysis demonstrates that as the number of ring members rises, the size of the current signatures grows, but the size of the proposed signature stays constant. In addition, the duration of these signatures increases, but the proposed signature's time climbs the slowest.
-
表 1 各签名方案性能对比
Table 1. Performance comparison of signature schemes
方案 签名生成 签名验证 编辑 更新 签名大小 LRRS[12] $\begin{gathered} (5n + 1){T_{\rm{e}}} + (4n + 2){T_{\rm{m}}}+ \\\quad\quad (n + 2){T_{\rm{H}}} + {T_{\rm{i}}} \\\end{gathered} $ $\begin{gathered}(2n + 2){T_{\rm{e}}} + (3n + 1){T_{\rm{m}}}+ \\\quad\quad(n + 1){T_{\rm{H}}}\\\end{gathered} $ $\begin{gathered} (4n + 2){T_{\rm{e}}} + (7n + 1){T_{\rm{m}}}+\\\quad\quad (n + 2){T_{\rm{H}}} \\\end{gathered} $ $\begin{gathered}2n{T_{\rm{e}}} + 4n{T_{\rm{m}}} +\\ \quad\quad(n + 1){T_{\rm{H}}} + 2{T_{\rm{i}}} \\\end{gathered} $ $\begin{gathered} (2n + 1)||G|| + \\\quad\quad n||{\bf{Z}}_q^*|| + ||{{\bf{Z}}_q}|| \\\end{gathered} $ R-LRRS[13] $\begin{gathered}(3n + 4){T_{\rm{e}}} + 3n{T_{\rm{m}}} +\\\quad\quad(n + 3){T_{\rm{H}}} + (3n + 1){T_{\rm{P}}} \\\end{gathered} $ $\begin{gathered} (3n + 1){T_{\rm{e}}} + (3n - 2){T_{\rm{m}}} +\\\quad\quad(n + 2){T_{\rm{H}}} + (3n - 2){T_{\rm{P}}}\end{gathered} $ $\begin{gathered}6{T_{\rm{e}}} + (3n + 2){T_{\rm{m}}} + 3{T_{\rm{H}}} +\\\quad\quad (3n + 1){T_{\rm{P}}} + {T_{\rm{i}}}\\\end{gathered} $ $\begin{gathered}(2n + 1)||G|| +\\\quad\quad n||{\bf{Z}}_q^*|| + ||{{\bf{Z}}_q}|| \\\end{gathered} $ SLRRS $ 10{T_{\rm{e}}} + (n + 5){T_{\rm{m}}} + 3{T_{\rm{H}}} $ $5{T_{\rm{e}}} + (n + 3){T_{\rm{m}}} + 3{T_{\rm{H}}} + 2{T_{\rm{i}}} $ $10{T_{\rm{e}}} + (n + 9){T_{\rm{m}}} + 4{T_{\rm{H}}} + 2{T_{\rm{i}}} $ $\begin{gathered}10{T_{\rm{e}}} + (n + 9){T_{\rm{m}}} + \\\quad\quad 3{T_{\rm{H}}} + 4{T_{\rm{i}}} \\\end{gathered} $ $\begin{gathered}5||G|| + 2||{U_f}|| +\\\quad\quad 2||{{\bf{Z}}_q}||\\\end{gathered} $ -
[1] YANG D, LONG C N, XU H, et al. A review on scalability of blockchain[C]//Proceedings of the 2nd International Conference on Blockchain Technology. New York: ACM, 2020: 1-6. [2] 袁勇, 王飞跃. 可编辑区块链: 模型、技术与方法[J]. 自动化学报, 2020, 46(5): 831-846.YUAN Y, WANG F Y. Editable blockchain: Models, techniques and methods[J]. Acta Automatica Sinica, 2020, 46(5): 831-846 (in Chinese). [3] 李佩丽, 徐海霞, 马添军, 等. 可更改区块链技术研究[J]. 密码学报, 2018, 5(5): 501-509.LI P L, XU H X, MA T J, et al. Research on fault-correcting blockchain technology[J]. Journal of Cryptologic Research, 2018, 5(5): 501-509 (in Chinese). [4] 高伟, 陈利群, 唐春明, 等. 一次变色龙哈希函数及其在可修正区块链中的应用[J]. 计算机研究与发展, 2021, 58(10): 2310-2318. doi: 10.7544/issn1000-1239.2021.20210653GAO W, CHEN L Q, TANG C M, et al. One-time chameleon hash function and its application in redactable blockchain[J]. Journal of Computer Research and Development, 2021, 58(10): 2310-2318(in Chinese). doi: 10.7544/issn1000-1239.2021.20210653 [5] ATENIESE G, MAGRI B, VENTURI D, et al. Redactable blockchain–or–rewriting history in Bitcoin and friends[C]//Proceedings of the IEEE European Symposium on Security and Privacy. Piscataway: IEEE Press, 2017: 111-126. [6] RIVEST R L, SHAMIR A, TAUMAN Y. How to leak a secret[C]//Proceedings of the 7th International Conference on the Theory and Application of Cryptology and Information Security: Advances in Cryptology. New York: ACM, 2001: 552-565. [7] REN Y L, CAI X J, HU M Q. Privacy-preserving redactable blockchain for internet of things[J]. Security and Communication Networks, 2021, 2021: 4485311. [8] 任艳丽, 徐丹婷, 张新鹏, 等. 基于门限环签名的可删除区块链[J]. 通信学报, 2019, 40(4): 71-82. doi: 10.11959/j.issn.1000-436x.2019084REN Y L, XU D T, ZHANG X P, et al. Deletable blockchain based on threshold ring signature[J]. Journal on Communications, 2019, 40(4): 71-82(in Chinese). doi: 10.11959/j.issn.1000-436x.2019084 [9] LIU J K, WEI V K, WONG D S. Linkable spontaneous anonymous group signature for ad hoc groups[C]//Proceedings of the 9th Australasian Conference on Information Security and Privacy. Berlin: Springer, 2004: 325-335. [10] KYAZHIN S, POPOV V. Yet another E-voting scheme implemented using hyperledger fabric blockchain[C]//Proceedings of the 20th International Conference on Computational Science and Its Applications. Berlin: Springer, 2020, 12251: 37-47. [11] 张小松, 黄可, 牛伟纳, 等. 一种可编辑、可链接、不可抵赖的环签名方法: CN110071812B[P]. 2021-06-08.ZHANG X S, HUANG K, NIU W N, et al. Editable, linkable and non-repudiation ring signature method: CN110071812B[P]. 2021-06-08 (in Chinese). [12] HUANG K, ZHANG X S, MU Y, et al. Scalable and redactable blockchain with update and anonymity[J]. Information Sciences, 2021, 546: 25-41. doi: 10.1016/j.ins.2020.07.016 [13] HUANG K, MU Y, REZAEIBAGHA F, et al. BA2P : Bidirectional and anonymous auction protocol with dispute-freeness[J]. Security and Communication Networks, 2021, 2021: 6690766. [14] TSANG P P, WEI V K. Short linkable ring signatures for E-voting, E-cash and attestation[C]//Proceedings of the 1st Information Security Practice and Experience Conference. Berlin: Springer, 2005: 48-60. [15] AU M H, CHOW S S M, SUSILO W, et al. Short linkable ring signatures revisited[C]//Proceedings of the 3rd European Public Key Infrastructure Workshop. Berlin: Springer, 2006: 101-115. [16] YU B, LIU J K, SAKZAD A, et al. Platform-independent secure blockchain-based voting system[C]//Proceedings of the International Conference on Information Security. Berlin: Springer, 2018: 369- 386. [17] 严新成, 陈越, 贾洪勇, 等. 支持高效密文密钥同步演化的安全数据共享方案[J]. 通信学报, 2018, 39(5): 123-133. doi: 10.11959/j.issn.1000-436x.2018083YAN X C, CHEN Y, JIA H Y, et al. Secure data sharing scheme supporting efficient synchronous evolution for ciphertext and key[J]. Journal on Communications, 2018, 39(5): 123-133(in Chinese). doi: 10.11959/j.issn.1000-436x.2018083 [18] CAMENISCH J, LYSYANSKAYA A. Dynamic accumulators and application to efficient revocation of anonymous credentials[C]//Proceedings of the 22nd Annual International Cryptology Conference. Berlin: Springer, 2002, 2442: 61-76. [19] CAMENISCH J, STADLER M. Efficient group signature schemes for large groups (extended abstract)[C]//Proceedings of Annual International Cryptology Conference. Berlin: Springer, 1997: 410-424. [20] 杨波. 现代密码学[M]. 4版. 北京: 清华大学出版社, 2017: 273-274.YANG B. Modern cryptography [M]. 4th ed. Beijing: Tsinghua University Press, 2017: 273-274(in Chinese). [21] LAUTER K. The advantages of elliptic curve cryptography for wireless security[J]. IEEE Wireless Communications, 2004, 11(1): 62-67. doi: 10.1109/MWC.2004.1269719 [22] YOSHITOMI M, TAKAGI T, KIYOMOTO S, et al. Efficient implementation of the pairing on mobilephones using BREW[C]//Proceedings of the 8th International Conference on Information Security Applications. New York: ACM, 2007: 203–214. -






 下载:
下载: