ARAIM-related fault subset optimization algorithm based on sparrow search algorithm
-
摘要:
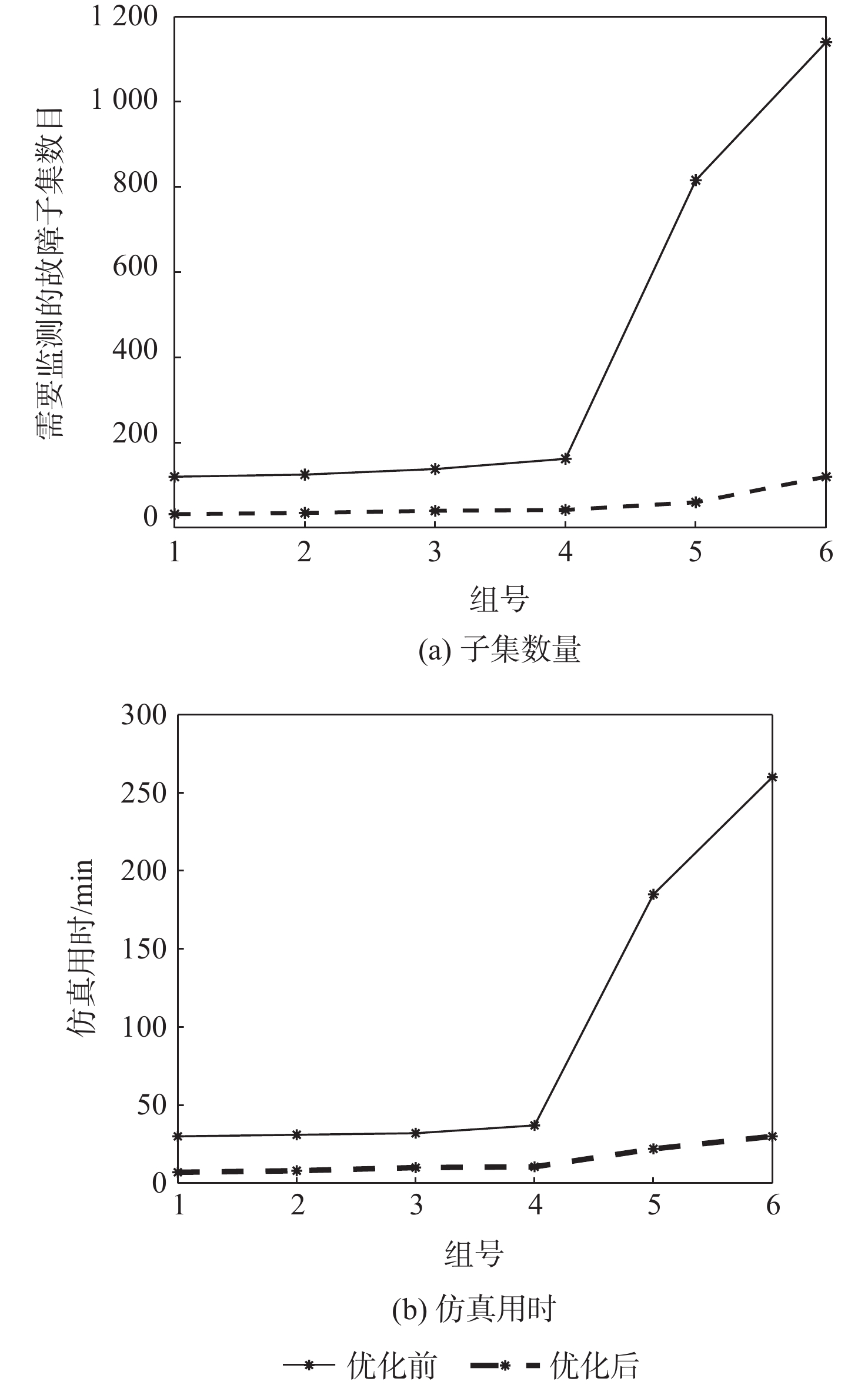
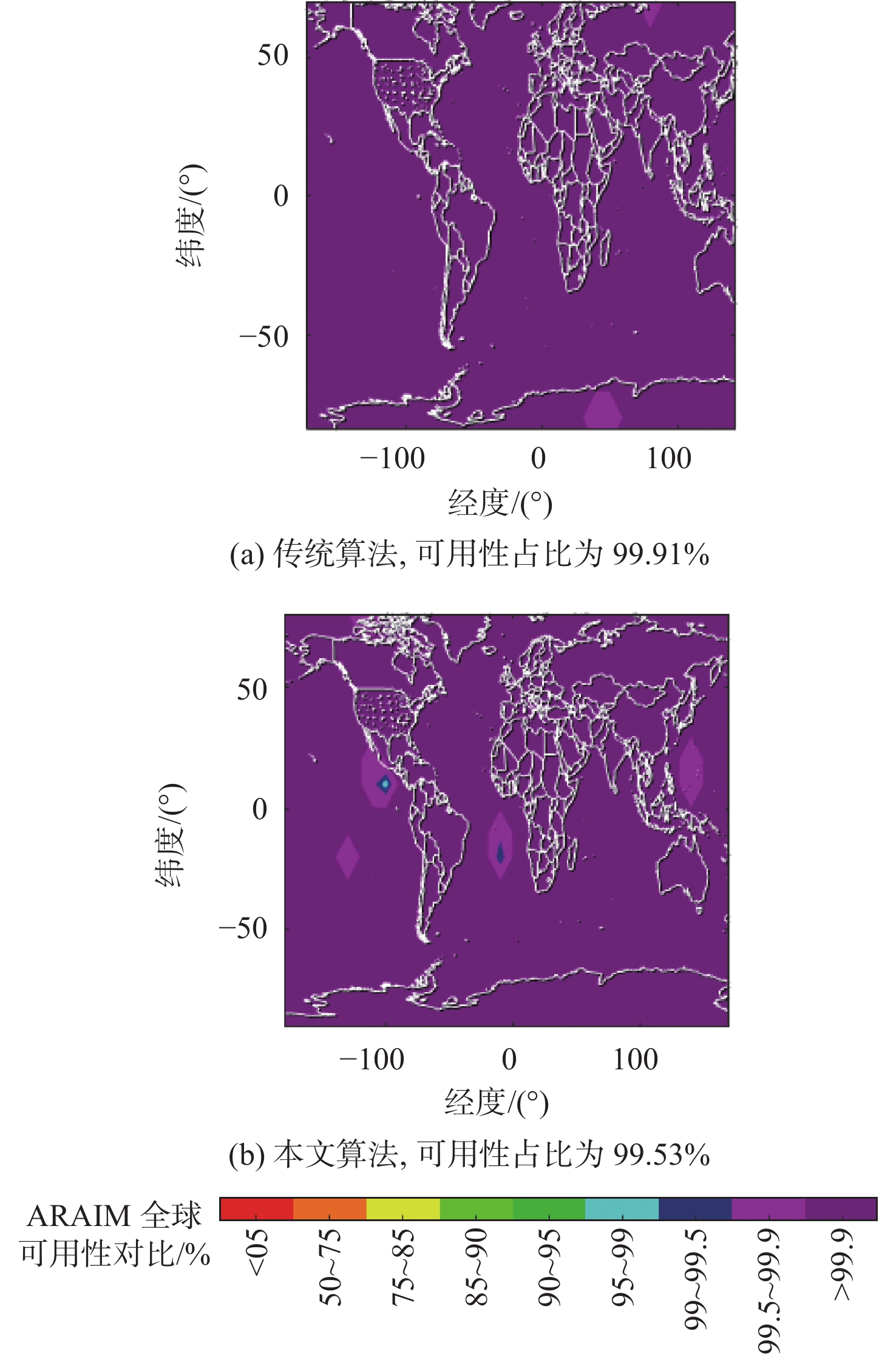
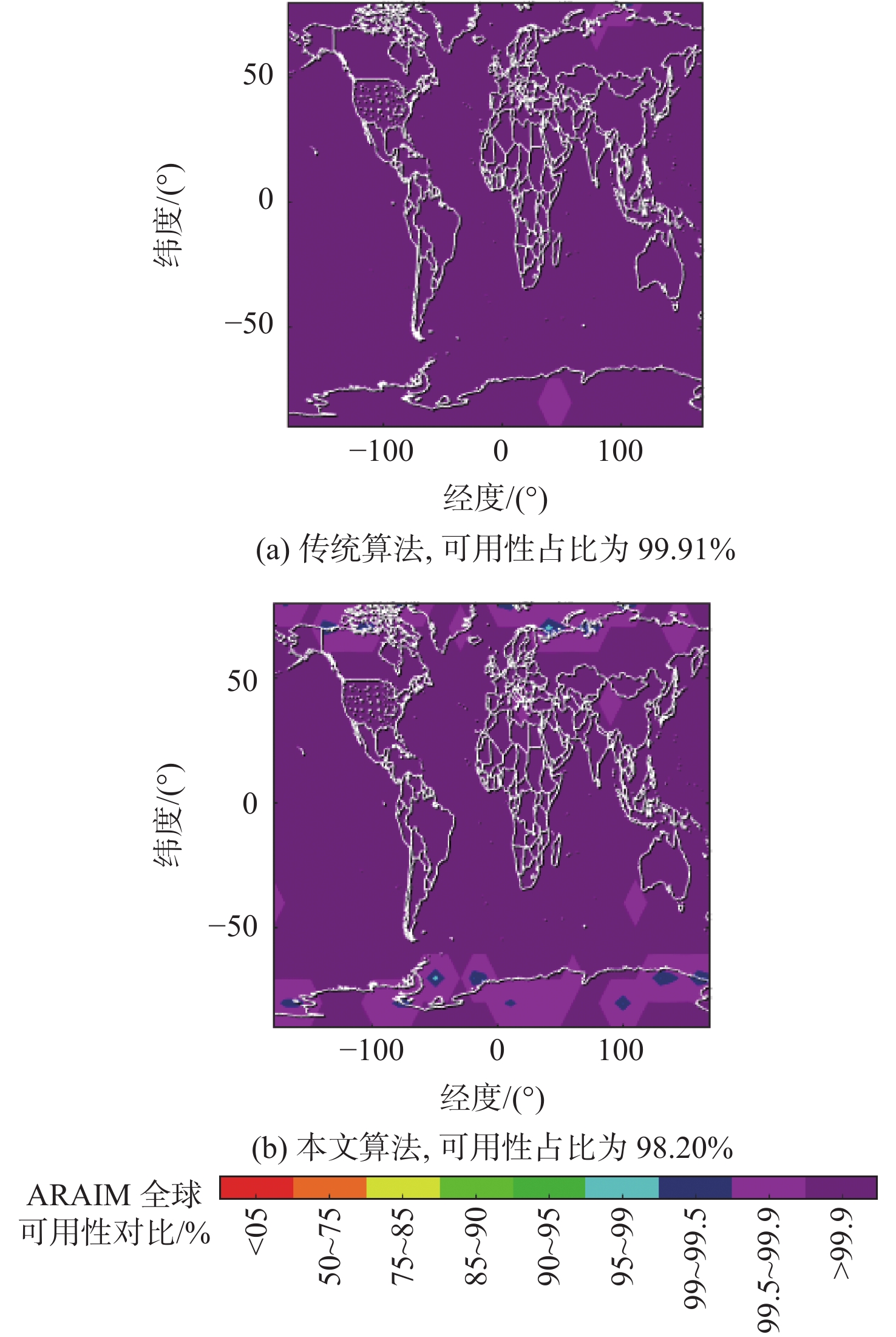
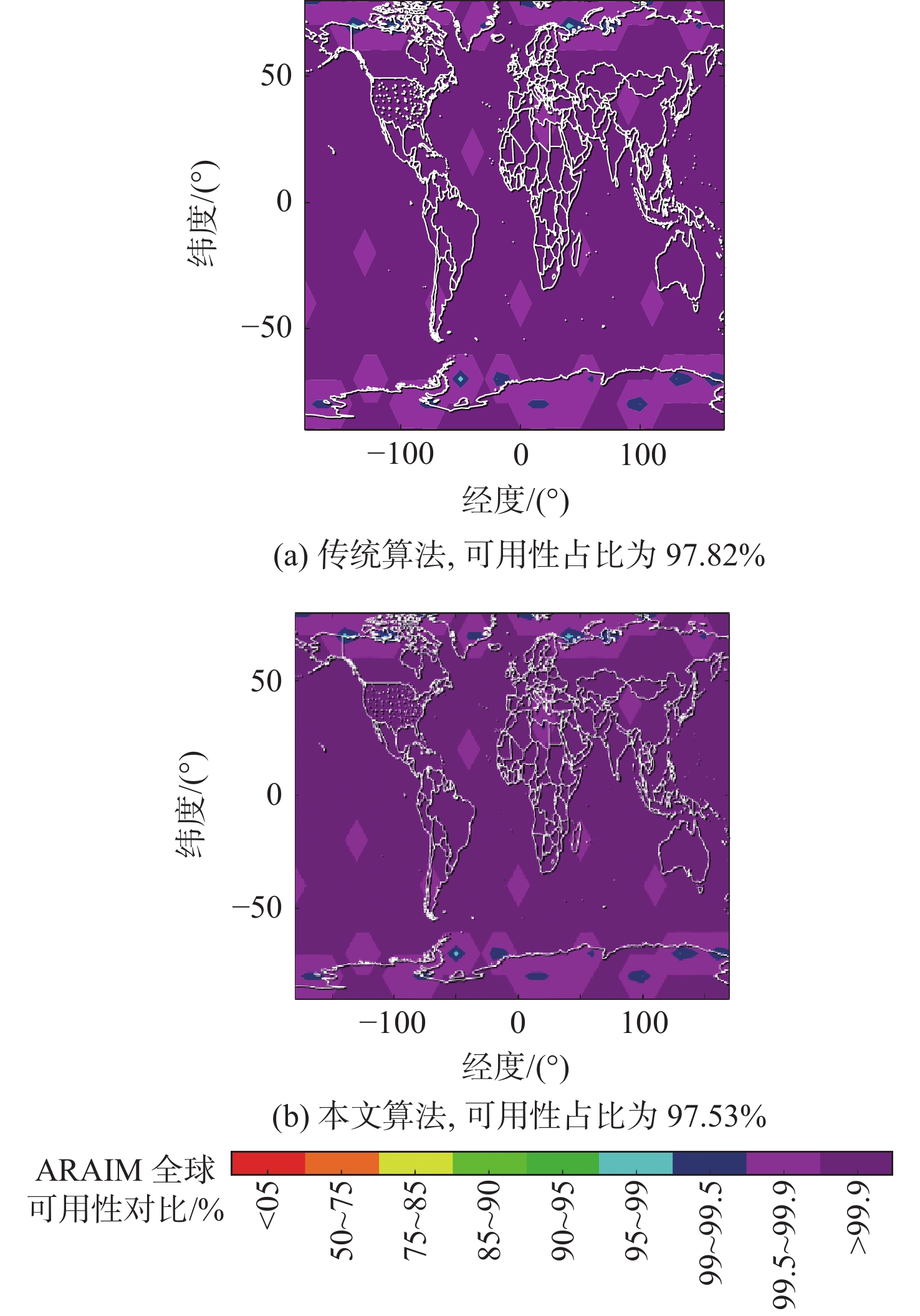
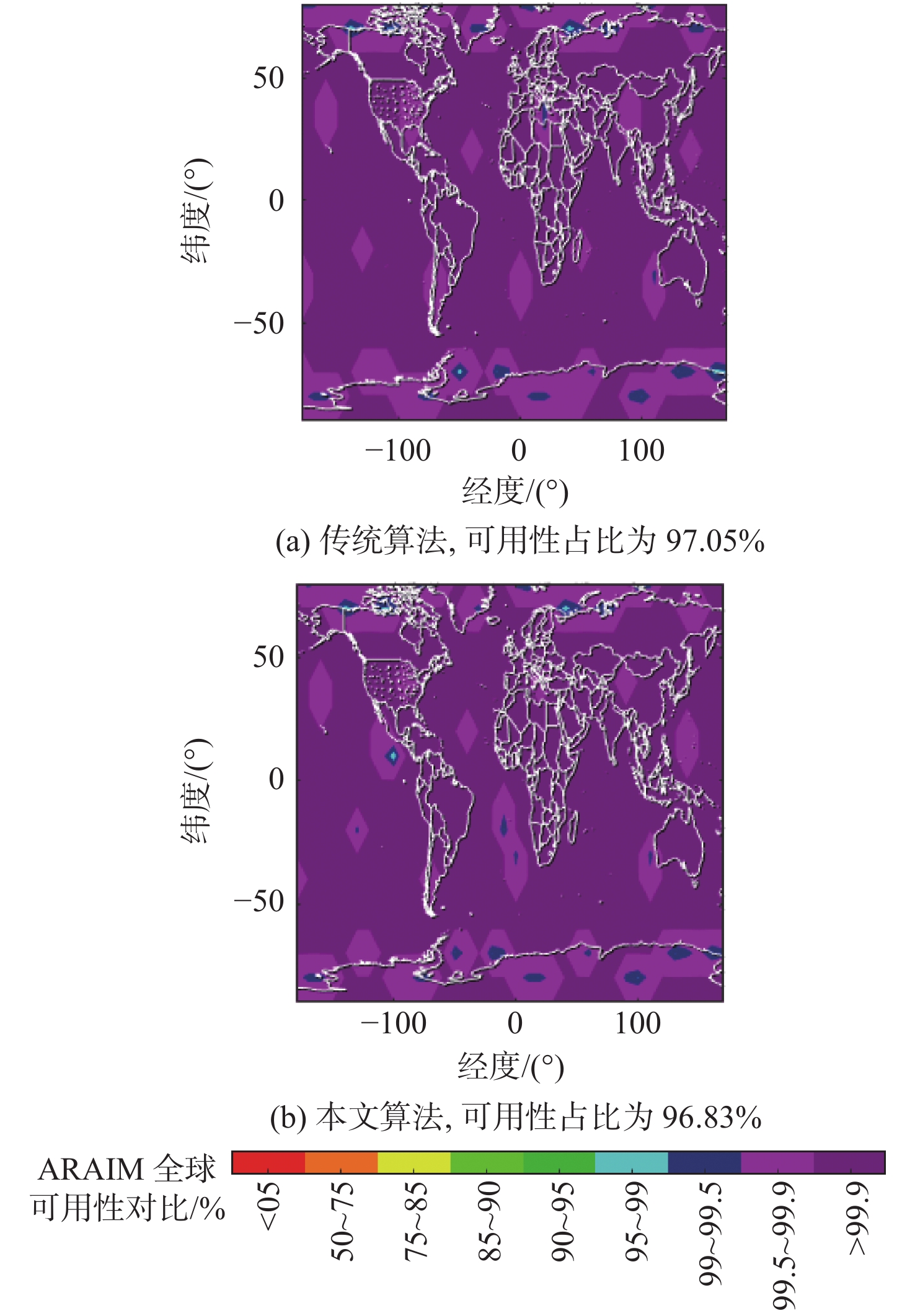
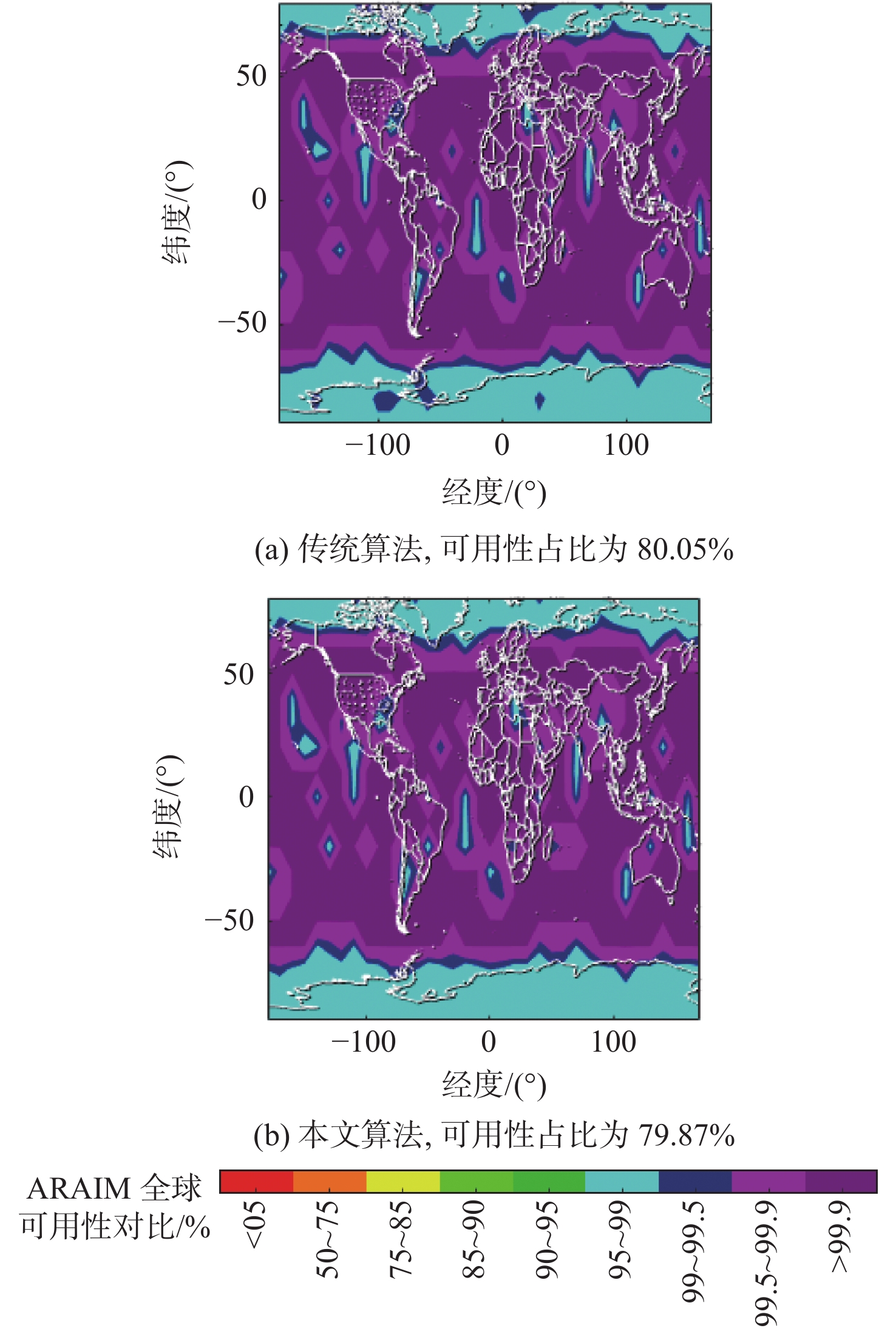
针对多假设解分离(MHSS)测试受卫星数目增加、潜在故障概率提高的影响，使得需要监测的子集数量增长而带来计算负担增加的问题，提出一种基于麻雀搜索算法(SSA)的高级接收机自主完好性监测(ARAIM)故障子集优化算法。结合SSA将可见卫星分配为发现者、跟随者和侦查预警者，通过剔除能量较低的个体降低计算冗余。在搜索过程中，引入自适应步长提升迭代速度，提高算法的执行效率。在双星座情况下，对完好性支持信息(ISM)参数进行3种假设，验证了所提算法的可用性，并与传统算法进行了对比分析。结果表明：通过所提算法得到的子集数量较传统算法减少了75%～90%，相同条件下，仿真用时降低了68%～88%，ARAIM可用性变化不超过2%。
-
关键词:
- 高级接收机自主完好性监测 /
- 双星座 /
- 故障子集 /
- 麻雀搜索算法 /
- 完好性支持信息
Abstract:The multiple hypothesis solution separation (MHSS) test is affected by the increase in the number of satellites and the potential fault probability. This results in a sharp increase in the number of subsets to be monitored and brings more computational burdens. In order to solve the above problems, an advanced receiver autonomous integrity monitoring (ARAIM)-related fault subset optimization algorithm based on the sparrow search algorithm (SSA) was proposed. According to the SSA, the satellites were divided into detectors, followers, and premonitors. Computational redundancy was reduced by eliminating individuals with lower energy. The adaptive step size was introduced during the search, so as to improve the iteration speed and the execution efficiency of the algorithm. In the dual constellation scenario, three hypotheses were made for the integrity supported message (ISM) parameters to verify the availability of the improved algorithm and compare it with traditional algorithms. The results show that the number of subsets obtained by the proposed algorithm is reduced by 75%–90% compared with traditional algorithms, and the computing time under the same condition is reduced by 68%–88%. In addition, the availability of ARAIM changes by no more than 2%.
-
图 2 第1组参数下ARAIM全球可用性对比
Figure 2. Comparison of global availability of ARAIM with parameters of group 1
图 3 第2组参数下ARAIM全球可用性对比
Figure 3. Comparison of global availability of ARAIM with parameters of group 2
图 4 第3组参数下ARAIM全球可用性对比
Figure 4. Comparison of global availability of ARAIM with parameters of group 3
图 5 第4组参数下ARAIM全球可用性对比
Figure 5. Comparison of global availability of ARAIM with parameters of group 4
图 6 第5组参数下ARAIM全球可用性对比
Figure 6. Comparison of global availability of ARAIM with parameters of group 5
图 7 第6组参数下ARAIM全球可用性对比
Figure 7. Comparison of global availability of ARAIM with parameters of group 6
表 1 ISM参数设置
Table 1. Setting of ISM parameters
假设状态 组号 星座 $ {P_{{\mathrm{sat}}}} $ $ {P_{{\mathrm{const}}}} $ $ {b_{{\mathrm{nom}}}} $ $ {\sigma _{{\mathrm{URA}}}} $ $ {\sigma _{{\mathrm{URE}}}} $ 理想状态 1 GPS 10−5 10−8 0.75 1 0.66 BDS 10−4 10−8 0.75 1 0.66 2 GPS 10−4 10−8 0.75 1 0.66 BDS 10−5 10−8 0.75 1 0.66 差异状态 3 GPS 10−5 10−4 0.75 1 0.66 BDS 10−4 10−5 0.75 1 0.66 4 GPS 10−4 10−5 0.75 1 0.66 BDS 10−5 10−4 0.75 1 0.66 保守状态 5 GPS 10−4 10−4 0.75 2.4 1.6 BDS 10−3 10−4 0.75 2.4 1.6 6 GPS 10−3 10−4 0.75 2.4 1.6 BDS 10−4 10−4 0.75 2.4 1.6 
下载: 导出CSV
表 2 不同ISM参数下$ {N_{\max }} $取值
Table 2. $ {N_{\max }} $ under different ISM parameters
Pevent Nmax N=10 N=15 N=20 N=20 N=30 N=35 N=40 10−5 1 1 1 1 1 1 1 10−4 2 2 2 2 2 2 2 5×10−4 2 2 3 3 3 3 3 10−3 3 3 3 3 3 3 4
下载: 导出CSV
-
[1] 胡自全, 何秀凤. 组合GNSS系统可见卫星分析[J]. 全球定位系统, 2015, 40(3): 1-5.HU Z Q, HE X F. Analysis the visible satellites of combined GNSS system[J]. GNSS World of China, 2015, 40(3): 1-5(in Chinese). [2] 王尔申, 孙彩苗, 黄煜峰, 等. 改进粒子群优化的卫星导航选星算法[J]. 北京航空航天大学学报, 2021, 47(1): 1-6.WANG E S, SUN C M, HUANG Y F, et al. Satellite navigation satellite selection algorithm based on improved particle swarm optimization[J]. Journal of Beijing University of Aeronautics and Astronautics, 2021, 47(1): 1-6(in Chinese). [3] 崔瑞云, 倪育德, 王琳琳, 等. 北斗卫星导航系统完好性参数研究[J]. 现代导航, 2015, 6(1): 17-22.CUI R Y, NI Y D, WANG L L, et al. Research on integrity parameters of BeiDou satellite navigation system[J]. Modern Navigation, 2015, 6(1): 17-22(in Chinese). [4] CHANG J, ZHAN X Q, ZHAI Y W, et al. Analysis of BDS GEO satellite multipath effect for GNSS integrity monitoring in civil aviation[J]. Aerospace Systems, 2021, 4(2): 133-141. doi: 10.1007/s42401-020-00074-7 [5] WANG S Z, ZHAI Y W, ZHAN X Q. Characterizing BDS signal-in-space performance from integrity perspective[J]. Navigation, 2021, 68(1): 157-183. doi: 10.1002/navi.409 [6] 韩清清, 王利, 罗思龙, 等. ARAIM算法的风险概率优化分配[J]. 测绘学报, 2021, 50(12): 1751-1761. doi: 10.11947/j.AGCS.2021.20200260HAN Q Q, WANG L, LUO S L, et al. Optimal allocation of risk probability based on ARAIM algorithm[J]. Acta Geodaetica et Cartographica Sinica, 2021, 50(12): 1751-1761(in Chinese). doi: 10.11947/j.AGCS.2021.20200260 [7] 王尔申, 孙彩苗, 佟刚, 等. 基于PSO的多星座GNSS垂直保护级优化方法[J]. 北京航空航天大学学报, 2021, 47(11): 2175-2180.WANG E S, SUN C M, TONG G, et al. Optimization method of multi-constellation GNSS vertical protection level based on particle swarm optimization algorithm[J]. Journal of Beijing University of Aeronautics and Astronautics, 2021, 47(11): 2175-2180(in Chinese). [8] CHANG J, ZHAN X Q, ZHAI Y W. Real-time integrity monitoring for civil aviation with improved navigation performance[C]//Proceedings of the International Conference on Aerospace System Science and Engineering. Berlin: Springer, 2020: 107-127. [9] LIU B Y, GAO Y, GAO Y T, et al. HPL calculation improvement for Chi-squared residual-based ARAIM[J]. GPS Solutions, 2022, 26(2): 45. doi: 10.1007/s10291-021-01220-0 [10] BLANCH J, WALKER T, ENGE P, et al. Baseline advanced RAIM user algorithm and possible improvements[J]. IEEE Transactions on Aerospace and Electronic Systems, 2015, 51(1): 713-732. doi: 10.1109/TAES.2014.130739 [11] ZHANG Y B, WANG L, FAN L, et al. MHSS ARAIM algorithm combined with gross error detection[J]. Journal of Geodesy and Geoinformation Science, 2020, 3(1): 38-46. [12] GAO Y T, JIANG Y, GAO Y, et al. A linear Kalman filter-based integrity monitoring considering colored measurement noise[J]. GPS Solutions, 2021, 25(2): 59. doi: 10.1007/s10291-021-01086-2 [13] WALTER T, BLANCH J, ENGE P. Reduced subset analysis for multi-constellation ARAIM[C]//Proceedings of the International Technical Meeting of the Institute of Navigation. Washington, D.C.: INST Navigation, 2014: 89-98. [14] GE Y S, WANG Z P, ZHU Y B. Reduced ARAIM monitoring subset method based on satellites in different orbital planes[J]. GPS Solutions, 2017, 21(4): 1443-1456. doi: 10.1007/s10291-017-0658-x [15] BLANCH J, WALTER T, ENGE P. Fixed subset selection to reduce advanced RAIM complexity[C]//Proceedings of the International Technical Meeting of the Institute of Navigation. Washington, D.C.: INST Navigation, 2018: 88-98. [16] MENG Q, LIU J Y, ZENG Q H, et al. Improved ARAIM fault modes determination scheme based on feedback structure with probability accumulation[J]. GPS Solutions, 2019, 23(1): 16. [17] LUO S L, WANG L, TU R, et al. Satellite selection methods for multi-constellation advanced RAIM[J]. Advances in Space Research, 2020, 65(5): 1503-1517. doi: 10.1016/j.asr.2019.12.015 [18] 刘金鑫, 滕继涛, 李锐, 等. 基于子集包含减少ARAIM子集数量的方法[J]. 北京航空航天大学学报, 2020, 46(8): 1592-1600.LIU J X, TENG J T, LI R, et al. Method for reducing number of ARAIM subsets based on subset inclusion[J]. Journal of Beijing University of Aeronautics and Astronautics, 2020, 46(8): 1592-1600(in Chinese). [19] XUE J K, SHEN B. A novel swarm intelligence optimization approach: Sparrow search algorithm[J]. Systems Science & Control Engineering, 2020, 8(1): 22-34. [20] WANG Z, HU W, WANG E S, et al. Enhancement dataset for low altitude unmanned aerial vehicle detection[J]. Transactions of Nanjing University of Aeronautics and Astronautics, 2021, 38(6): 914-926. [21] 王尔申, 郭靖, 宏晨, 等. 改进目标收益函数的无人机集群空地对抗模型[J]. 南京航空航天大学学报, 2021, 53(6): 888-897.WANG E S, GUO J, HONG C, et al. UAV swarm air-ground engagement model with improved payoff[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2021, 53(6): 888-897(in Chinese). [22] BLANCH J, WALKER T, ENGE P, et al. Advanced RAIM user algorithm description: Integrity support message processing, fault detection, exclusion, and protection level calculation[C]//Proceedings of the 25th International Technical Meeting of the Satellite Division of the Institute of Navigation. Washington, D.C.: INST Navigation, 2012: 2828-2849. -
下载:
点击查看大图
计量
- 文章访问数: 518
- HTML全文浏览量: 87
- PDF下载量: 47
- 被引次数: 0
