Vibration control of flexible spacecraft with output constraints and external disturbances
-
摘要:
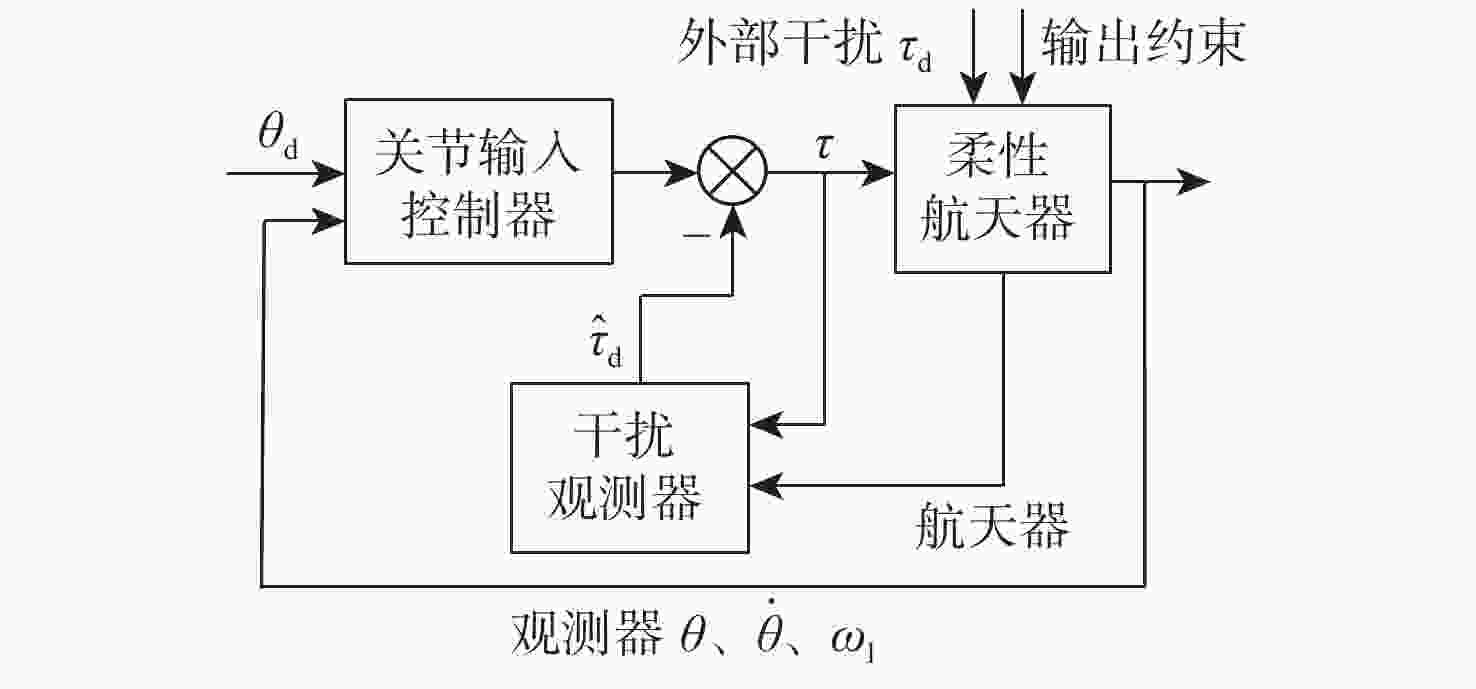
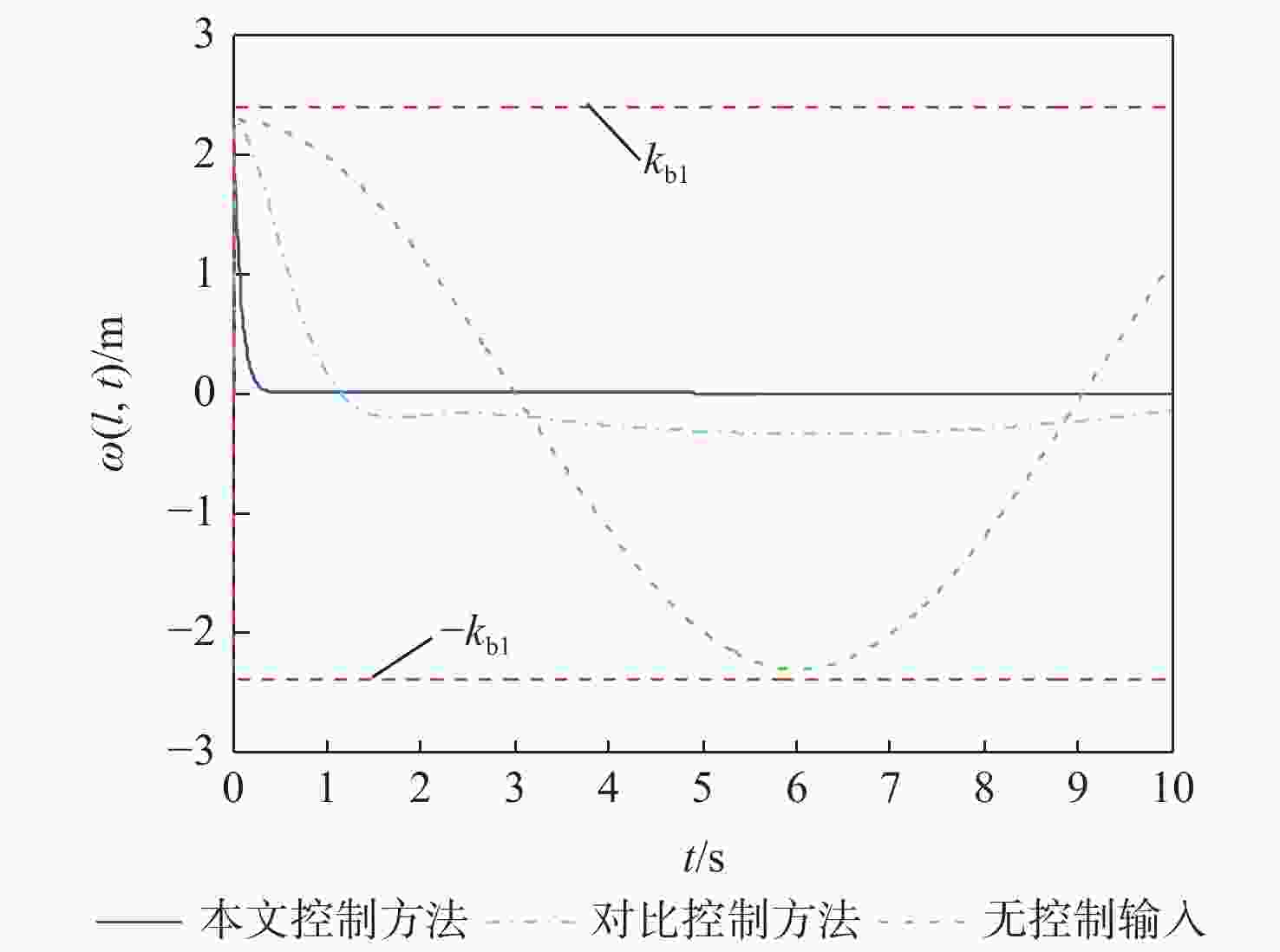
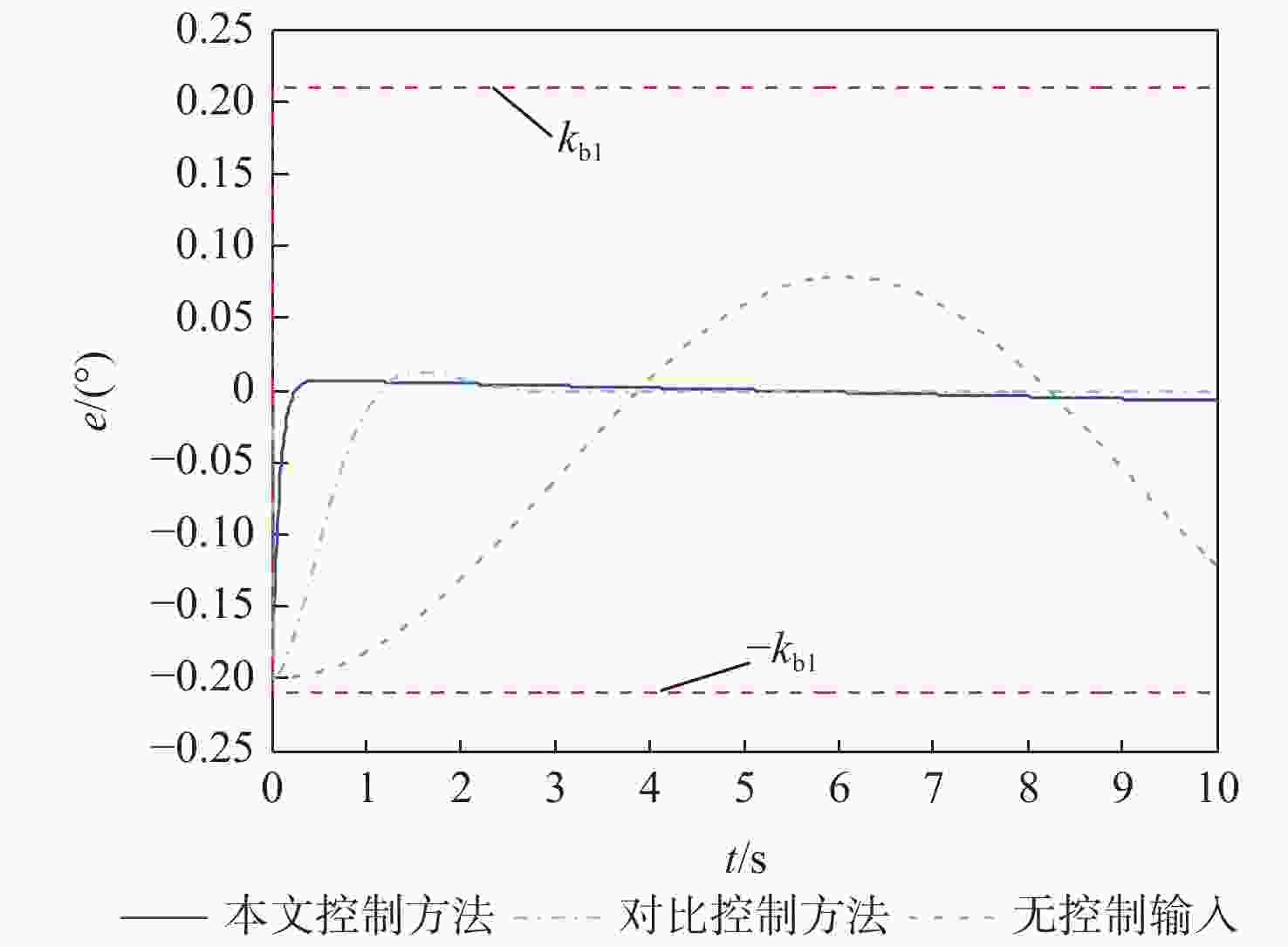
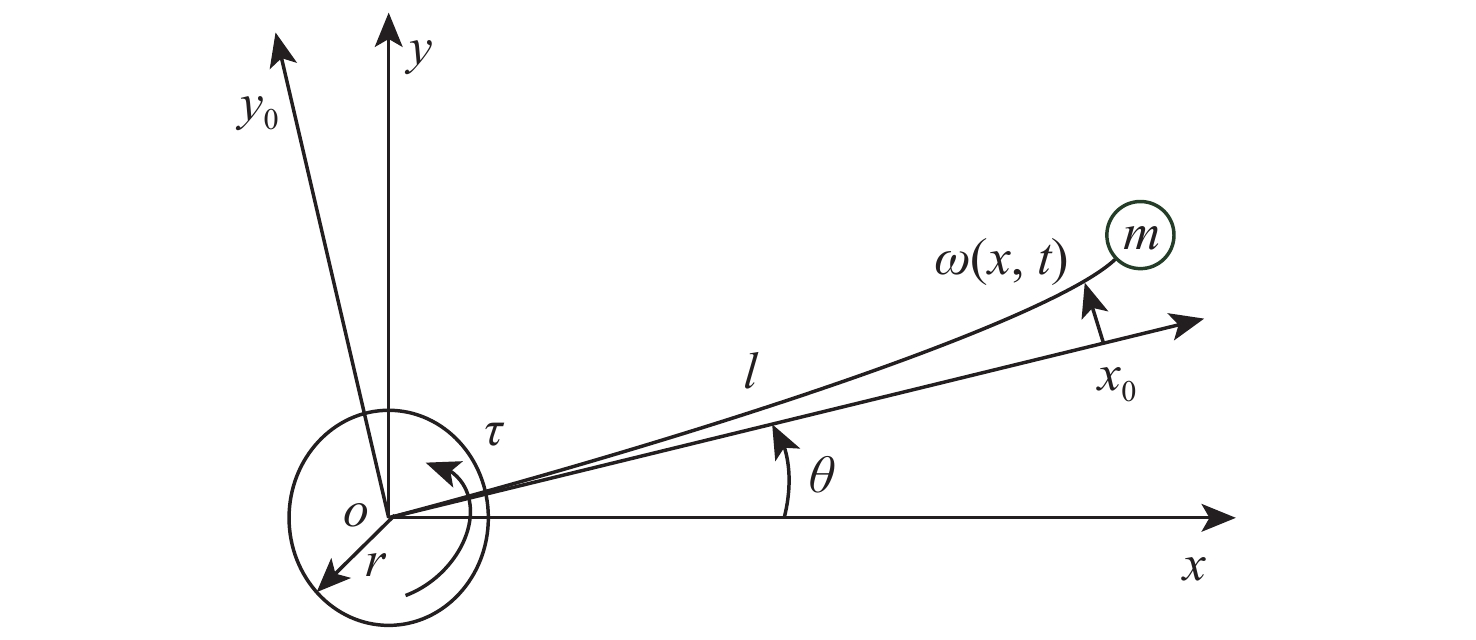
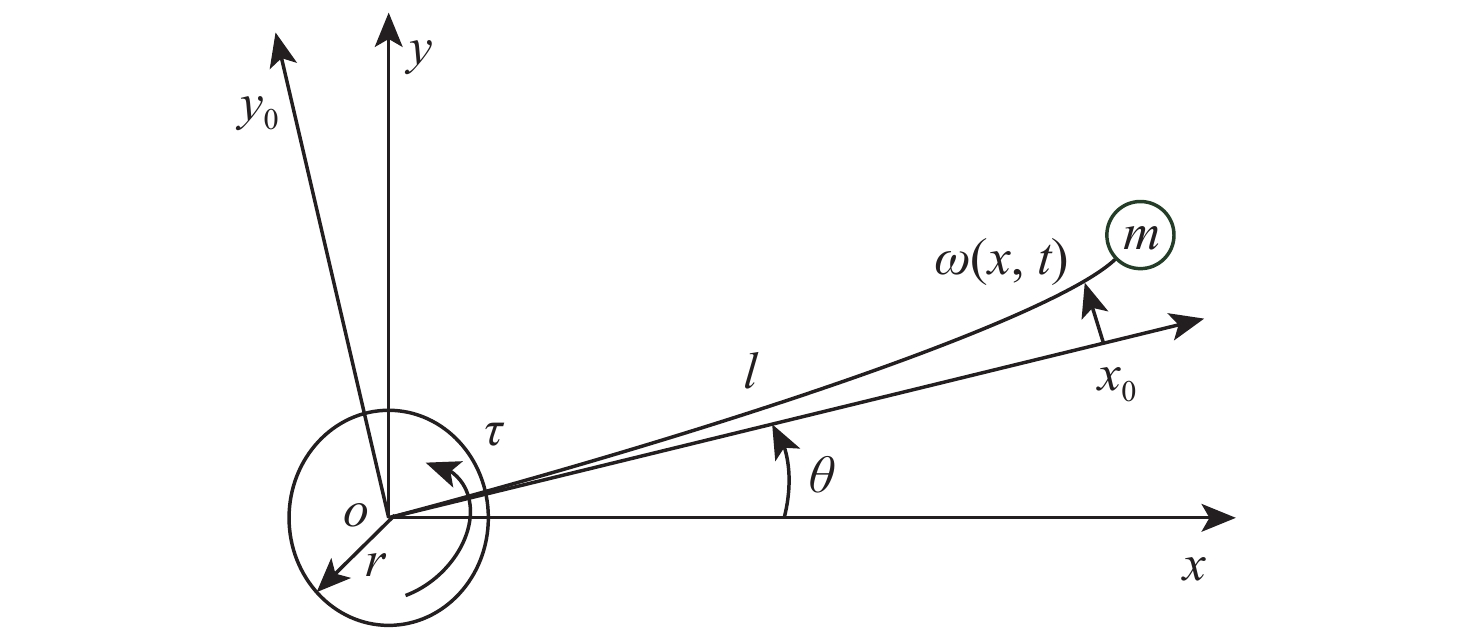
针对具有输出约束及外部干扰的柔性航天器系统，提出一种直接关节力矩输入的振动控制方法。利用哈密顿原理，系统动力学特性由偏微分方程（PDE）和常微分方程（ODE）耦合组成的分布参数模型来描述。设计了非线性干扰观测器补偿外界干扰，并基于正切型障碍李雅普诺夫函数解决了航天器姿态角度误差和振动误差的多输出约束问题。利用扩展的拉塞尔不变集原理和半群理论证明了系统的渐近稳定性。不仅实现了姿态角的位置控制，还抑制了柔性航天器的弹性振动。通过对比仿真验证了所提方法的有效性。
Abstract:A vibration control with direct joint torque input is presented for flexible spacecraft systems subject to external disturbances and output limits. Firstly, the dynamic characteristics of the system are described by a distributed parameter model which is composed of partial differential equation (PDE) and ordinary differential equation (ODE). Secondly, the tangential barrier Lyapunov function is used to ensure that the output constraints of vibration errors and attitude angle errors are met by a nonlinear disturbance observer that is intended to adjust for external disturbances. The asymptotic stability of the system is proved by extended LaSalle’s invariance principle and semigroup theory. It not only realizes the position control of attitude angle, but also restrains the elastic vibration of flexible spacecraft. Finally, the effectiveness of the proposed control method is verified by comparison simulations.
-
图 3 无控制输入的弹性挠度$\omega (x,t)$
Figure 3. Elastic deflection $\omega (x,t)$ without control input
图 4 PD应变力及剪切力反馈控制方法的弹性挠度$\omega (x,t)$
Figure 4. Elastic deflection $\omega (x,t)$ with PD strain force and share force control
图 9 末端的弹性变形$\omega (l,t)$
Figure 9. Elastic deformation $\omega (l,t)$ of the end point
图 5 本文控制方法的弹性挠度$\omega (x,t)$
Figure 5. Elastic deflection $\omega (x,t)$ with the proposed control method
图 6 姿态角度$\theta $及角速度$\dot \theta $的跟踪曲线
Figure 6. Tracking curves of attitude angle $\theta $ and angular velocity $\dot \theta $
图 7 外部干扰${\tau _{\mathrm{d}}}$及其观测值${\hat \tau _{\mathrm{d}}}$
Figure 7. External disturbance ${\tau _{\mathrm{d}}}$ and its estimate ${\hat \tau _{\mathrm{d}}}$
表 1 航天器物理参数
Table 1. The physical parameters of spacecraft
悬臂梁长度l/m 悬臂梁尖端质量m/kg 单位长度均匀质量$ \rho $/(kg·m−1) 刚性轮轴半径r/m 弯曲刚度E/(N·m) 转动惯量$ {I_{\rm{h}}} $/(N·m2) 10 5 8 1 300 120 
下载: 导出CSV
表 2 系统控制参数
Table 2. System control parameters
角度误差约束值$ {k_{{\rm{b}}1}} $ 控制参数$ \lambda $ 控制参数$ {k_{\mathrm{f}}} $ 控制参数$ {k_{\mathrm{s}}} $ 控制参数$ K $ 振动约束值$ {k_{{\rm{b}}2}} $ 控制参数$ {k_{\mathrm{p}}} $ 控制参数$ {k_{\mathrm{d}}} $ 控制参数$ {k_{\mathrm{v}}} $ 0.21 5 10 400 150 2.4 550 400 2
下载: 导出CSV
-
[1] 王长国, 卫剑征, 刘宇艳, 等. 航天柔性展开结构技术及其应用研究进展[J]. 宇航学报, 2020, 41(6): 761-769.WANG C G, WEI J Z, LIU Y Y, et al. Some advances in technologies of aerospace flexible deployable structure and their applications[J]. Journal of Astronautics, 2020, 41(6): 761-769(in Chinese). [2] 王涵斌, 贺曦, 王晋军. 柔性翼气动力和变形特性的实验研究[J]. 北京航空航天大学学报, 2022, 48(4): 665-673.WANG H B, HE X, WANG J J. Experimental study on aerodynamic and deformation characteristics of flexible membrane wing[J]. Journal of Beijing university Aeronautics and Astronautics, 2022, 48(4): 665-673(in Chinese). [3] HE W, TANG X Y, WANG T T, et al. Trajectory tracking control for a three-dimensional flexible wing[J]. IEEE Transactions on Control Systems Technology, 2022, 30(5): 2243-2250. doi: 10.1109/TCST.2021.3139087 [4] 颜奇民, 胡俊华, 陈国明, 等. 变体航行器动力学建模与仿真[J]. 北京航空航天大学学报, 2021, 47(12): 2602-2610.YAN Q M, HU J H, CHEN G M, et al. Dynamic modeling and simulation of morphing vehicle[J]. Journal of Beijing University of Aeronautics and Astronautics, 2021, 47(12): 2602-2610(in Chinese). [5] LIU S Y, LANGARI R, LI Y C. Non-linear direct joint control for manipulator handling a flexible payload with input constraints[J]. International Journal of Robotics and Automation, 2019, 34(6): 645-653. [6] LIU Y, CHEN X B, WU Y L, et al. Adaptive neural network control of a flexible spacecraft subject to input nonlinearity and asymmetric output constraint[J]. IEEE Transactions on Neural Networks and Learning Systems, 2022, 33(11): 6226-6234. doi: 10.1109/TNNLS.2021.3072907 [7] MA J T, WEN H, JIN D P. PDE model-based boundary control of a spacecraft with double flexible appendages under prescribed performance[J]. Advances in Space Research, 2020, 65(1): 586-597. doi: 10.1016/j.asr.2019.09.050 [8] CHEN T, WEN H, WEI Z T. Distributed attitude tracking for multiple flexible spacecraft described by partial differential equations[J]. Acta Astronautica, 2019, 159: 637-645. doi: 10.1016/j.actaastro.2019.02.010 [9] HE W, MENG T T, HE X Y, et al. Iterative learning control for a flapping wing micro aerial vehicle under distributed disturbances[J]. IEEE Transactions on Cybernetics, 2019, 49(4): 1524-1535. doi: 10.1109/TCYB.2018.2808321 [10] CAO F F, LIU J K. Adaptive neural network control of an arm-string system with actuator fault based on a PDE model[J]. Journal of Vibration and Control, 2019, 25(1): 172-181. doi: 10.1177/1077546318772476 [11] 刘增波, 乔建忠, 郭雷, 等. 基于非线性干扰观测器的航天器相对姿轨耦合控制[J]. 北京航空航天大学学报, 2020, 46(10): 1907-1915.LIU Z B, QIAO J Z, GUO L, et al. Nonlinear disturbance observer based control for relative position and attitude coupled spacecraft[J]. Journal of Beijing University of Aeronautics and Astronautics, 2020, 46(10): 1907-1915(in Chinese). [12] 张秀云, 宗群, 窦立谦, 等. 柔性航天器振动主动抑制及姿态控制[J]. 航空学报, 2019, 40(4): 233-242.ZHANG X Y, ZONG Q, DOU L Q, et al. Active vibration suppression and attitude control for flexible spacecraft[J]. Acta Aeronautica et Astronautica Sinica, 2019, 40(4): 233-242(in Chinese). [13] ZHAO Z J, AHN C K, LI H X. Boundary antidisturbance control of a spatially nonlinear flexible string system[J]. IEEE Transactions on Industrial Electronics, 2020, 67(6): 4846-4856. doi: 10.1109/TIE.2019.2931230 [14] LIU S Y, LIU Z J, LI Y C, et al. Nonlinear disturbance observer- based direct joint control for manipulation of a flexible payload with output constraints[J]. International Journal of Control, 2023, 96(5): 1377-1388. doi: 10.1080/00207179.2022.2046858 [15] HE W, KANG F S, KONG L H, et al. Vibration control of a constrained two-link flexible robotic manipulator with fixed-time convergence[J]. IEEE Transactions on Cybernetics, 2022, 52(7): 5973-5983. doi: 10.1109/TCYB.2021.3064865 [16] MA G, TAN Z F, LIU Y M, et al. Adaptive robust barrier-based control of a 3D flexible riser system subject to boundary displacement constraints[J]. International Journal of Robust and Nonlinear Control, 2022, 32(5): 3062-3077. doi: 10.1002/rnc.5693 [17] TANG Z L, TEE K P, HE W. Tangent barrier Lyapunov functions for the control of output-constrained nonlinear systems[J]. IFAC Proceedings Volumes, 2013, 46(20): 449-455. doi: 10.3182/20130902-3-CN-3020.00122 [18] 彭聪, 缪卫东, 曾聪. 基于机器视觉的轻型梁三维振动测量方法[J]. 北京航空航天大学学报, 2021, 47(2): 207-212.PENG C, MIAO W D, ZENG C. Three-dimensional vibration measurement method for lightweight beam based on machine vision[J]. Journal of Beijing University of Aeronautics and Astronautics, 2021, 47(2): 207-212(in Chinese). [19] TEE K P, GE S S, TAY E H. Barrier Lyapunov functions for the control of output-constrained nonlinear systems[J]. Automatica (Journal of IFAC), 2009, 45(4): 918-927. doi: 10.1016/j.automatica.2008.11.017 [20] PAZY A. Semigroups of linear operators and applications to partial differential equations[M]. Berlin: Springer, 1983: 14-15. -
下载:
点击查看大图
计量
- 文章访问数: 654
- HTML全文浏览量: 75
- PDF下载量: 13
- 被引次数: 0
