Model correction method for CFD numerical simulation under mixed aleatory and epistemic uncertainty
-
摘要:
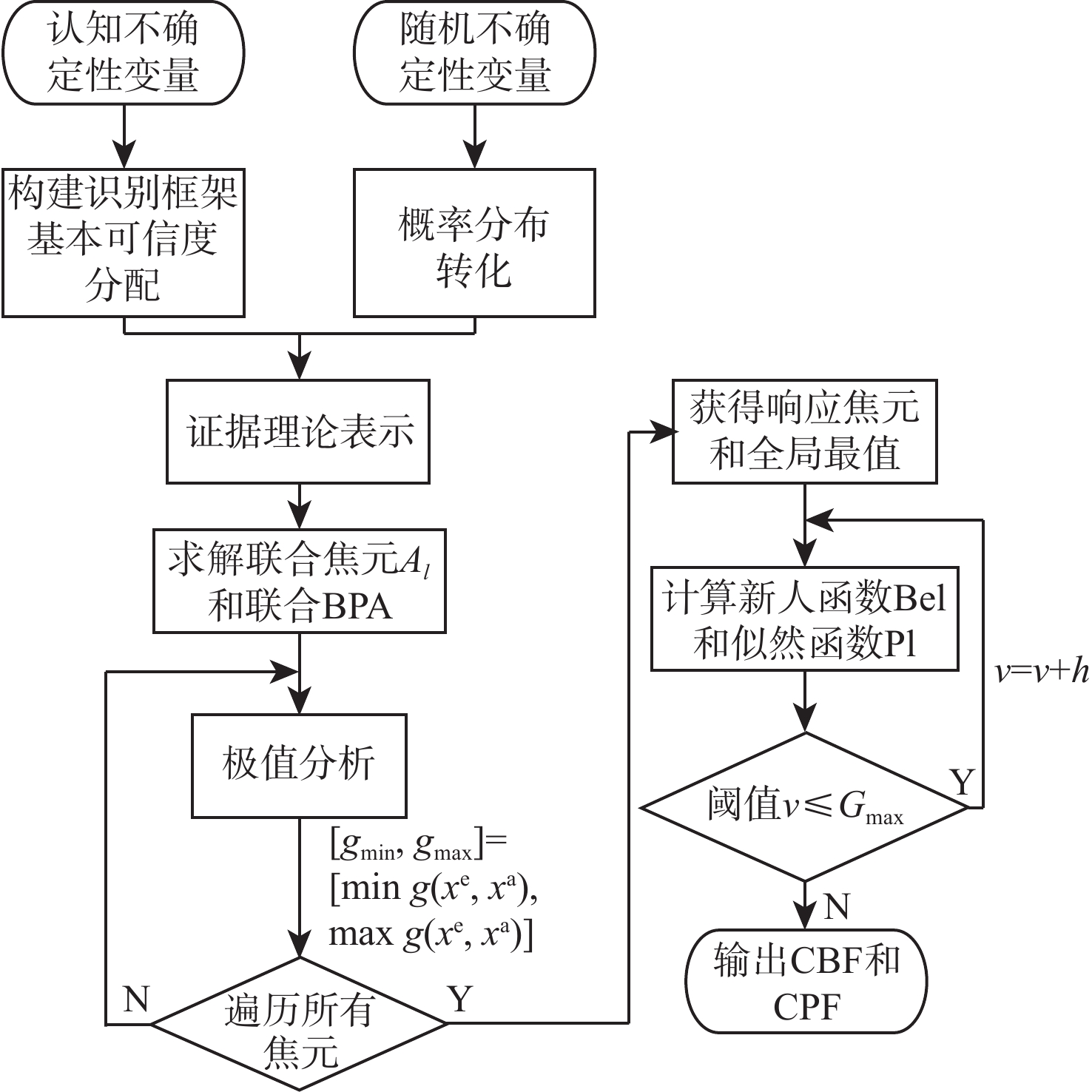
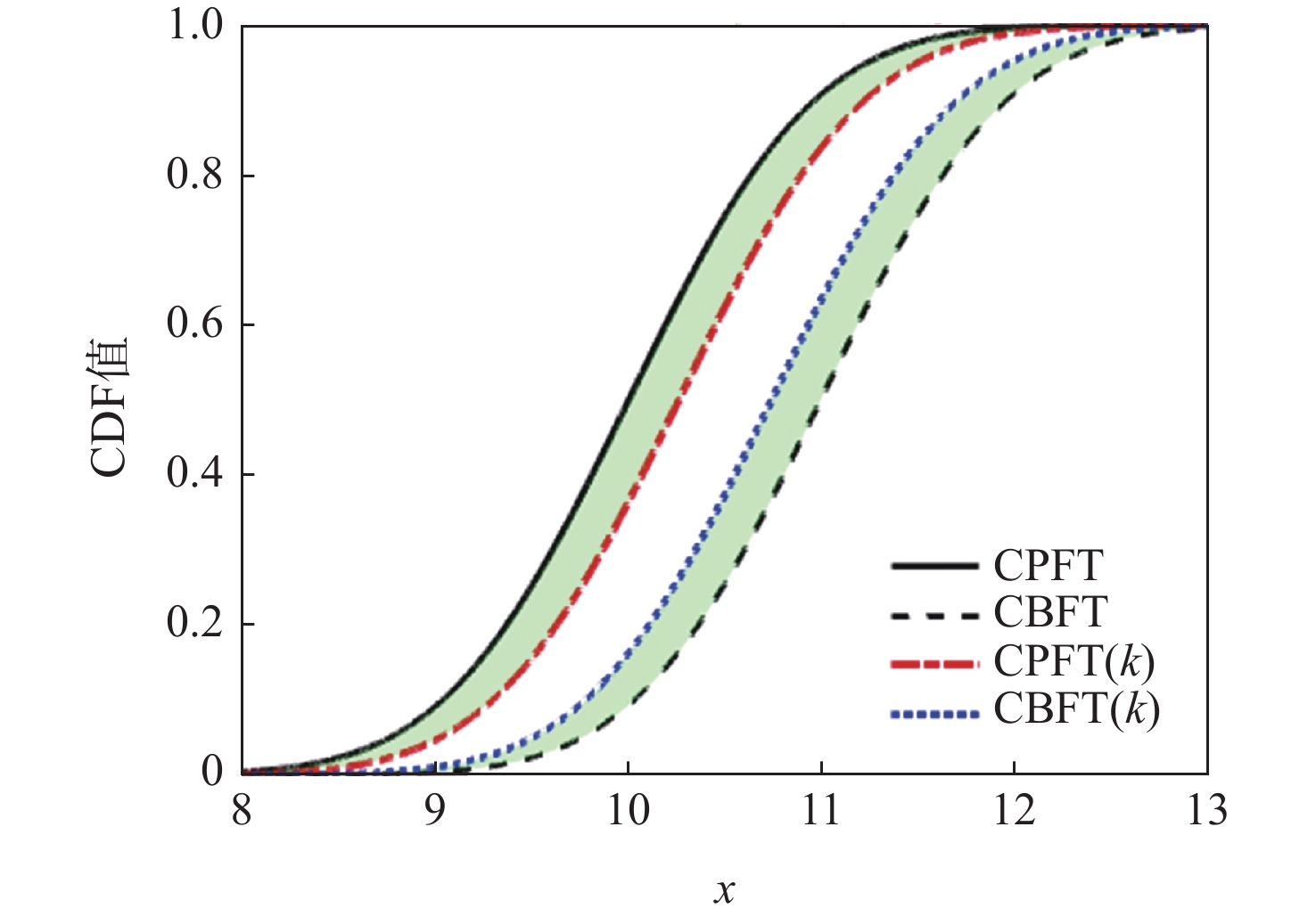
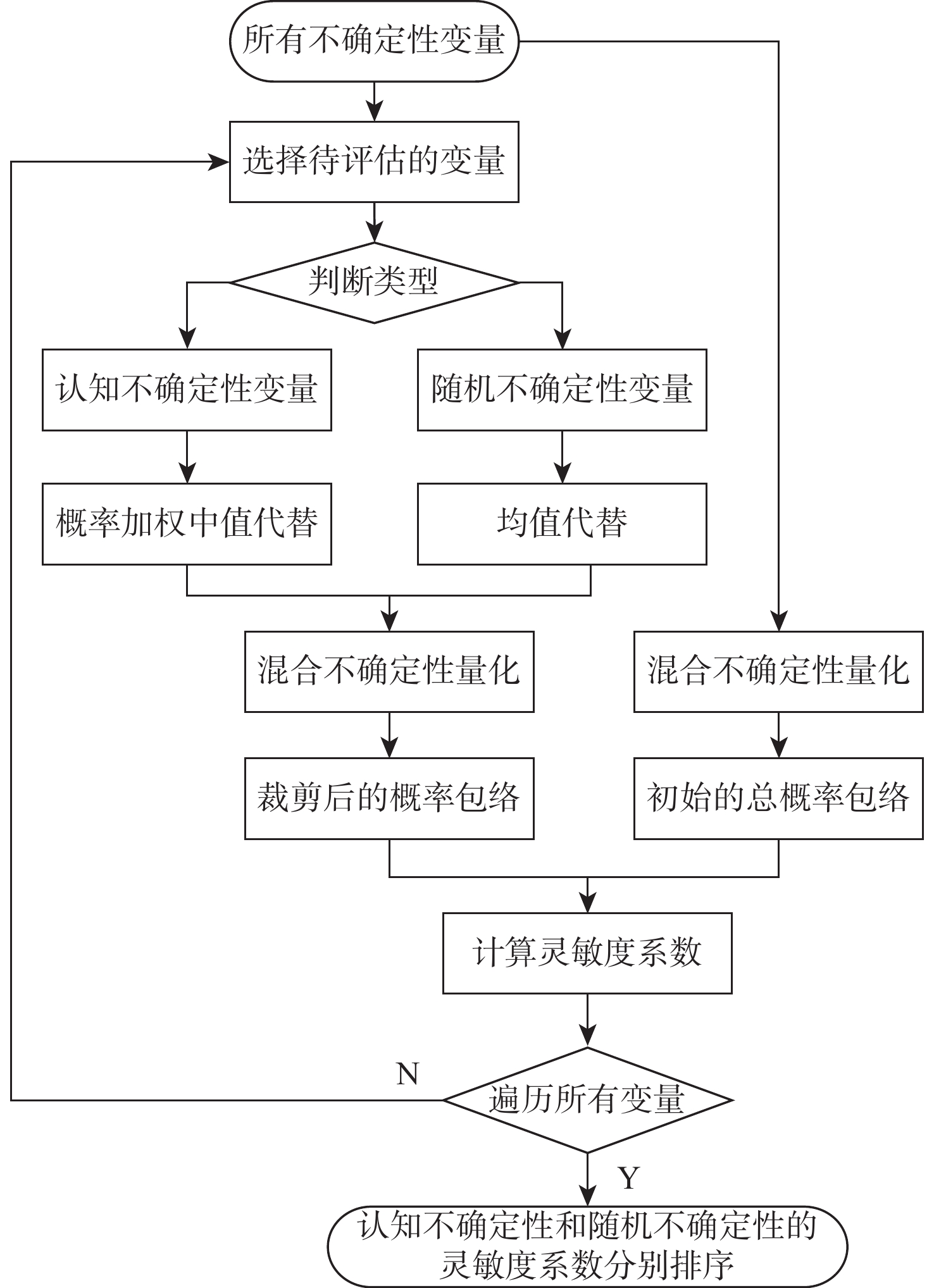
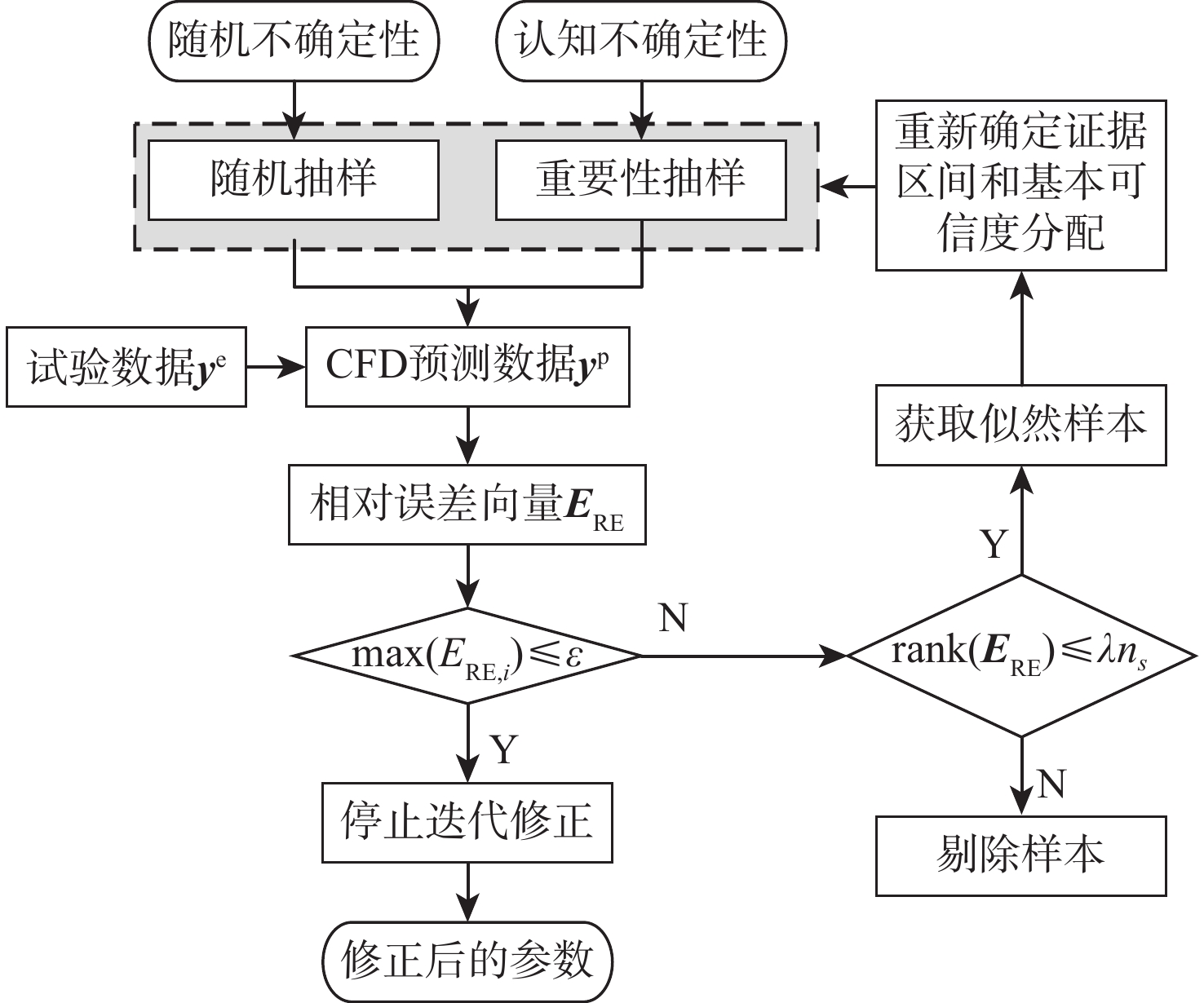
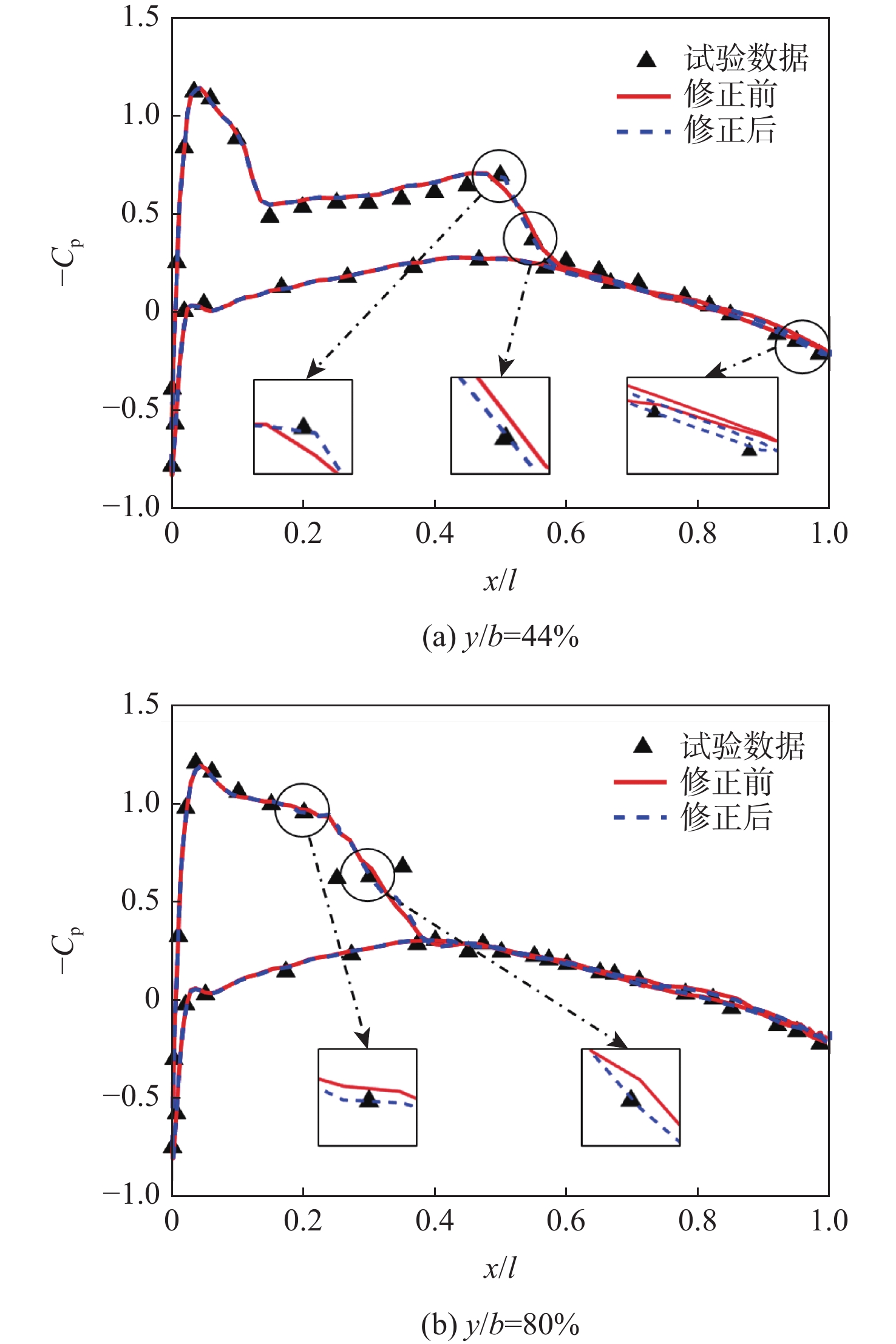
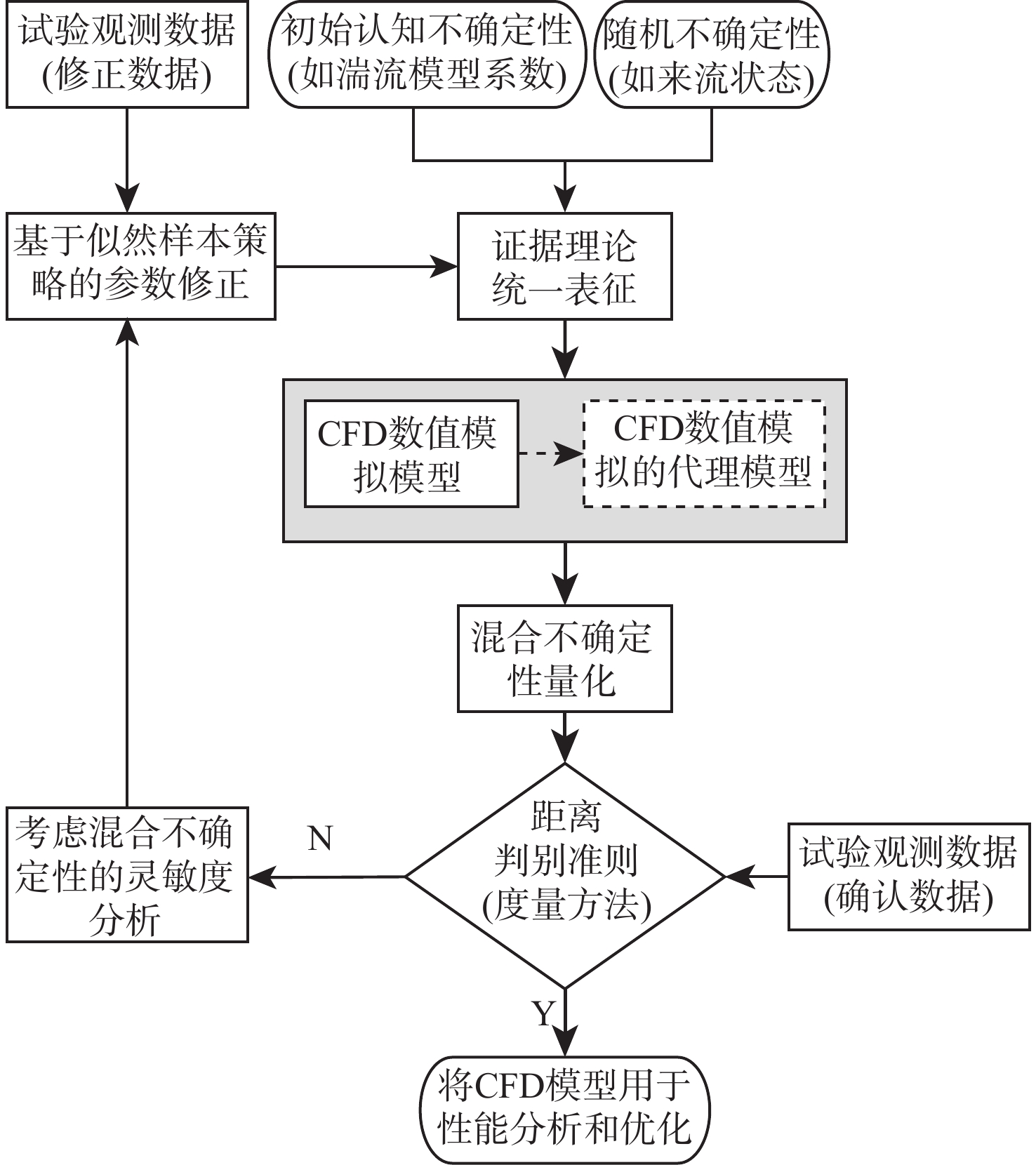
针对随机和认知混合不确定性下的CFD模型修正问题，提出了一种融合混合不确定性量化、全局灵敏度分析、参数修正的模型修正架构，建立了基于证据理论的混合不确定性量化方法，在此基础上构建了基于概率包络面积变化率的混合不确定性灵敏度分析指标，提出了基于似然样本策略的参数修正方法。针对三维机翼ONERA M6的CFD数值模拟，在考虑湍流模型封闭系数认知不确定性和来流条件随机不确定性的情况下，通过混合不确定性量化得到升力系数的概率分布包络，并开展全局灵敏度分析发掘影响较大的封闭系数，降低模型修正的复杂度和计算量，并根据似然样本策略对关键系数加以修正。经过参数迭代修正，修正后的CFD仿真结果与试验数据高度吻合，证明了提出的CFD模型修正方法的有效性。
Abstract:A type of model updating framework is proposed, aiming at the challenge of CFD model updating under mixed aleatory and epistemic uncertainty. The framework integrates mixed uncertainty quantification, global sensitivity analysis and parameter updating strategy. The method of mixed uncertainty quantification is established based on evidence theory, and sensitivity analysis index——change rate of probability envelope area for mixed uncertainty is constructed based on evidence theory. A parameter updating method based on the likelihood samples strategy is proposed. For the CFD numerical simulation of the three-dimensional wing ONERA M6, the probability envelope representation of the lift coefficient is obtained by quantifying mixed uncertainty, considering epistemic uncertainty of the turbulence model coefficients and aleatory uncertainty of the incoming flow conditions. Based on this, the global sensitivity analysis is carried out to explore the key turbulence model coefficients that have a great impact on the output, so as to reduce the complexity and calculation of the model updating. The key coefficients are updated according to the likelihood samples strategy. The updated CFD simulation results following parameter iterative updating show a strong degree of consistency with the experimental data, demonstrating the efficacy of the suggested CFD model updating technique.
-
Key words:
- mixed uncertainty /
- model updating /
- evidence theory /
- sensitivity analysis /
- turbulence model
-
图 3 基于证据理论的随机和认知混合不确定性量化流程
Figure 3. Flow chart of mixed aleatory and epistemic uncertainty quantification based on evidence theory
图 5 基于概率包络面积变化率的灵敏度分析流程
Figure 5. Flow chart of sensitivity analysis based on change rate of probability envelope area
图 6 基于似然样本策略的模型参数修正流程
Figure 6. Flow chart of model parameter correction process based on likelihood samples strategy
图 7 基于似然样本的参数修正示意图
Figure 7. Diagram of parameter correction based on likelihood samples
图 8 修正前后的y的概率分布上下界
Figure 8. Upper and lower bounds of probability distribution of y before and after correction
图 9 裁剪${C_{{\text{b1}}}}$、${C_{{\text{w3}}}}$、${C_{{\text{b2}}}}$后的概率包络变化情况
Figure 9. Change in probability envelope after cutting ${C_{{\text{b1}}}}$, ${C_{{\text{w3}}}}$ and ${C_{{\text{b2}}}}$
表 1 响应焦元与阈值区间3种可能的位置关系
Table 1. Three possible positional relationships between response focal element and threshold interval
图示 不等关系 包含关系 Bel Pl 
$v \geqslant {g_{\max }}$ $ {Y_l} \subseteq {G_v} $ √ √ 
${g_{\min }} \leqslant v \leqslant {g_{\max }}$ $ {Y_l} \cap {G_v} \ne \varnothing $ × √ 
$v \leqslant {g_{\min }}$ $ {Y_l} \cap {G_v} = \varnothing $ × × 注：√表示BPA计入Bel或Pl，×表示不计入。 
下载: 导出CSV
表 2 c1、c2的识别框架及基本可信度分配
Table 2. Evidence structure assignments and identification frameworks of c1 and c2
参数 焦元 BPA $ {c_1} $ [0.5, 0.8] 0.4 [0.8, 1.2] 0.3 [1.2, 1.5] 0.3 $ {c_2} $ [7.0, 7.5] 0.2 [7.5, 8.5] 0.5 [8.5, 9.0] 0.3
下载: 导出CSV
表 3 c1、c2的修正迭代结果
Table 3. Results of modified iteration for c1 and c2
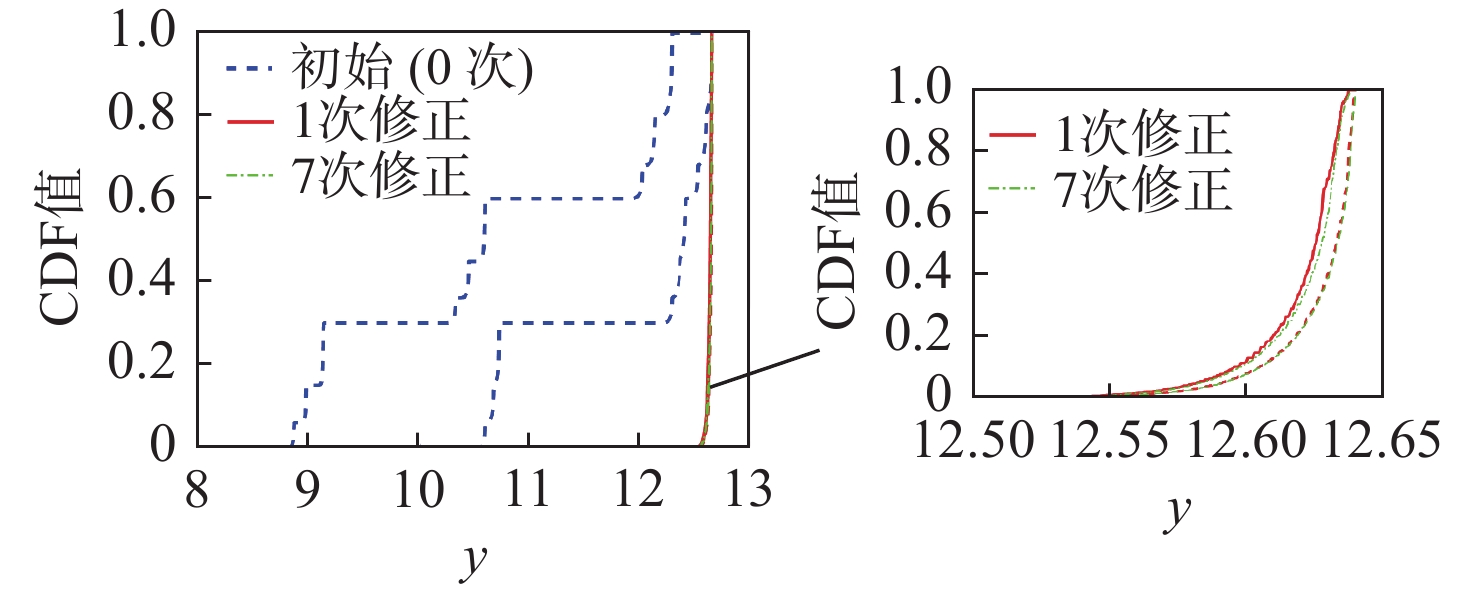
修正迭代次数 $ {c_1} $ $ {c_2} $ ${E_{{\mathrm{RE}},\max }}$/% 0 [0.5, 1.5] [7, 9] 29.82 1 [0.591 1, 0.645 8] [7.979 2, 8.251 8] 0.94 7 [0.598 6, 0.642 3] [7.995 3, 8.231 0] 0.65 注：c1、c2的证据区间的真值分别为0.618 0和8.115 0。
下载: 导出CSV
表 4 各认知不确定性变量的证据结构
Table 4. Evidence structure for each cognitive uncertainty variables
变量 默认值 焦元 BPA ${C_{{\text{b1}}}}$ 0.1355 [0.129, 0.133] 0.05 [0.133, 0.137] 0.95 ${C_{{\text{b2}}}}$ 0.622 [0.61, 0.65] 0.80 [0.65, 0.69] 0.20 ${C_{{\text{v1}}}}$ 7.1 [6.9, 7.1] 0.50 [7.1, 7.3] 0.50 ${C_{{\text{w2}}}}$ 0.3 [0.055, 0.204] 0.30 [0.204, 0.353] 0.70 ${C_{{\text{w3}}}}$ 2 [1.75, 2.25] 0.85 [2.25, 2.50] 0.15 $\sigma $ 0.667 [0.6, 0.8] 0.90 [0.8, 1.0] 0.10
下载: 导出CSV
表 5 各参数的抽样区间
Table 5. Sampling interval of each parameters
变量 抽样区间 变量 抽样区间 ${C_{{\text{b1}}}}$ [0.12, 0.14] ${C_{{\text{w3}}}}$ [1.7, 2.5] ${C_{{\text{b2}}}}$ [0.6, 0.7] $\sigma $ [0.6, 1.0] ${C_{{\text{v1}}}}$ [6.9, 7.3] $Ma$ [0.819 5, 0.839 5] ${C_{{\text{w2}}}}$ [0.05, 0.40] $\alpha $ [3.01°, 3.11°]
下载: 导出CSV
表 6 灵敏度分析结果(测试1)
Table 6. Results of sensitivity analysis (Case1)
类型 变量 裁剪值 $S_k^{\text{T}}$ ${s_k}$/% 排序 认知 ${C_{{\text{b1}}}}$ 0.135 3.871×10−3 58.57 1 ${C_{{\text{b2}}}}$ 0.638 9.165×10−3 1.94 6 ${C_{{\text{v1}}}}$ 7.100 8.933×10−3 4.42 5 ${C_{{\text{w2}}}}$ 0.234 8.827×10−3 5.56 3 ${C_{{\text{w3}}}}$ 2.056 7.764×10−3 16.93 2 $\sigma $ 0.720 8.845×10−3 5.37 4 随机 $Ma$ 0.840 9.093×10−3 2.71 2 $\alpha $ 3.060 8.926×10−3 4.50 1
下载: 导出CSV
表 7 模型参数修正的迭代结果(测试1)
Table 7. Results of model parameter corrections (Case1)
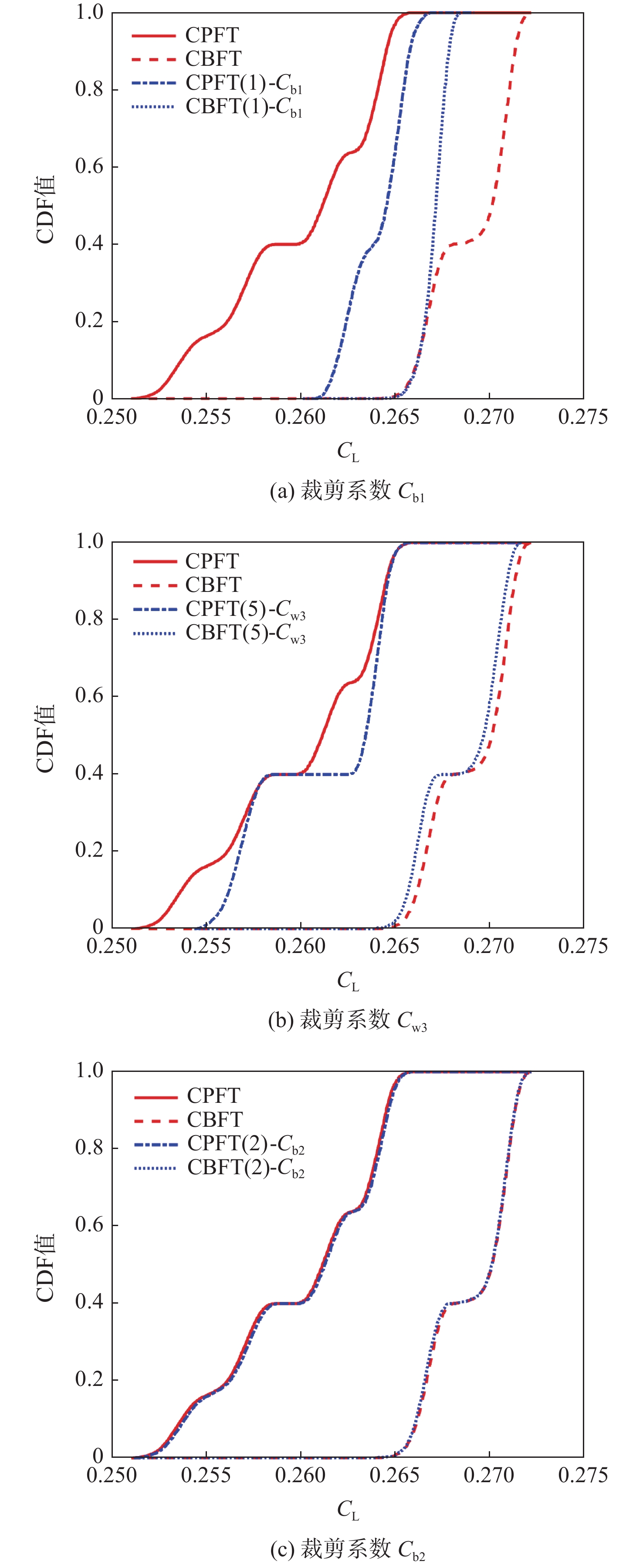
修正取值/区间 ${C_{{\text{b1}}}}$ ${C_{{\text{w3}}}}$ niter ${E_{{\mathrm{RE}},\max }}$/% ${C_{\text{L}}}$ 默认值 0.135 5 2.000 0 0.268 9 修正前 [0.129 0,0.137 0] [1.75,2.50] 0 5.06 [0.255 3,0.273 6] 精度达标后 [0.132 6,0.136 9] [1.913 7,2.108 1] 4 0.98 [0.266 3,0.271 4] 区间收敛后 [0.134 9,0.136 5] [1.996 4,2.055 6] 17 0.55 [0.267 4,0.270 2]
下载: 导出CSV
表 8 灵敏度分析结果(测试2)
Table 8. Results of sensitivity analysis (Case2)
变量 裁剪值 $S_k^{\text{T}}$ ${s_k}$/% 排序 ${C_{{\text{b1}}}}$ 0.135 3.202×10−3 63.07 1 ${C_{{\text{b2}}}}$ 0.638 8.485×10−3 2.14 6 ${C_{{\text{v1}}}}$ 7.100 8.249×10−3 4.86 5 ${C_{{\text{w2}}}}$ 0.234 8.120×10−3 6.35 3 ${C_{{\text{w3}}}}$ 2.056 7.083×10−3 18.31 2 $\sigma $ 0.720 8.212×10−3 5.28 4
下载: 导出CSV
表 9 模型参数修正的迭代结果(测试2)
Table 9. Results of model parameter updating (Case2)
修正取值/区间 ${C_{{\text{b1}}}}$ ${C_{{\text{w3}}}}$ niter ${E_{{\mathrm{RE}},\max }}$/% ${C_{\text{L}}}$ 默认值 0.135 5 2.000 0 0.26 修正前 [0.129 0, 0.137 0] [1.75, 2.50] 0 4.92 [0.256 6, 0.272 8] 精度达标后 [0.131 2, 0.134 8] [1.754 5, 1.936 8] 3 0.81 [0.259 5, 0.262 1] 区间收敛后 [0.133 1, 0.134 0] [1.754 7, 1.758 1] 12 0.19 [0.259 5, 0.260 3]
下载: 导出CSV
-
[1] 罗磊, 高振勋, 蒋崇文. CFD技术发展及其在航空领域中的应用进展[J]. 航空制造技术, 2016, 59(20): 77-81.LUO L, GAO Z X, JIANG C W. CFD development and application in aviation[J]. Aeronautical Manufacturing Technology, 2016, 59(20): 77-81(in Chinese). [2] 阎超, 屈峰, 赵雅甜, 等. 航空航天CFD物理模型和计算方法的述评与挑战[J]. 空气动力学学报, 2020, 38(5): 829-857. doi: 10.7638/kqdlxxb-2020.0072YAN C, QU F, ZHAO Y T, et al. Review of development and challenges for physical modeling and numerical scheme of CFD in aeronautics and astronautics[J]. Acta Aerodynamica Sinica, 2020, 38(5): 829-857(in Chinese). doi: 10.7638/kqdlxxb-2020.0072 [3] XU H C, QIN D T, LIU C Z, et al. An improved dynamic model updating method for multistage gearbox based on surrogate model and sensitivity analysis[J]. IEEE Access, 2021, 9: 18527-18537. doi: 10.1109/ACCESS.2021.3053395 [4] MARGHERI L, MELDI M, SALVETTI M V, et al. Epistemic uncertainties in RANS model free coefficients[J]. Computers & Fluids, 2014, 102: 315-335. [5] 张皓, 李东升, 李宏男. 有限元模型修正研究进展: 从线性到非线性[J]. 力学进展, 2019, 49: 542-575.ZHANG H, LI D S, LI H N. Recent progress on finite element model updating: from linearity to nonlinearity[J]. Advances in Mechanics, 2019, 49: 542-575(in Chinese). [6] 王纪森, 贾倩, 陈晨, 等. 液压管路油液流动的湍流模型参数修正研究[J]. 系统仿真学报, 2018, 30(5): 1665-1671.WANG J S, JIA Q, CHEN C, et al. Research of turbulence model parameters correction for oil flow of pipeline[J]. Journal of System Simulation, 2018, 30(5): 1665-1671(in Chinese). [7] 张亦知. 基于数据驱动的湍流模型修正方法研究[D]. 上海: 上海交通大学, 2020.ZHANG Y Z. Data-augmented correction of turbulence modeling[D]. Shanghai: Shanghai Jiao Tong University, 2020(in Chinese). [8] SCHAEFER J, ROMERO V, SHAFER S, et al. Approaches for quantifying uncertainties in computational modeling for aerospace applications[C]// AIAA Scitech 2020 Forum. Reston: AIAA, 2020. [9] MARES C, MOTTERSHEAD J E, FRISWELL M I. Stochastic model updating: part 1—theory and simulated example[J]. Mechanical Systems and Signal Processing, 2006, 20(7): 1674-1695. doi: 10.1016/j.ymssp.2005.06.006 [10] 陈鑫, 王刚, 叶正寅, 等. CFD不确定度量化方法研究综述[J]. 空气动力学学报, 2021, 39(4): 1-13. doi: 10.7638/kqdlxxb-2021.0012CHEN X, WANG G, YE Z Y, et al. A review of uncertainty quantification methods for Computational Fluid Dynamics[J]. Acta Aerodynamica Sinica, 2021, 39(4): 1-13(in Chinese). doi: 10.7638/kqdlxxb-2021.0012 [11] 郭惠昕, 锁斌. 随机和认知混合不确定系统的全局灵敏度分析方法[J]. 系统工程理论与实践, 2018, 38(7): 1888-1896. doi: 10.12011/1000-6788(2018)07-1888-09GUO H X, SUO B. Approach to global sensitivity analysis of hybrid uncertain system with aleatory and epistemic uncertainties[J]. Systems Engineering-Theory & Practice, 2018, 38(7): 1888-1896(in Chinese). doi: 10.12011/1000-6788(2018)07-1888-09 [12] SHAH H R, HOSDER S, WINTER T. A mixed uncertainty quantification approach with evidence theory and stochastic expansions[C]// Proceedings of the 16th AIAA Non-Deterministic Approaches Conference. Reston: AIAA, 2014: AIAA2014-0298. [13] 屈小章, 余江鸿, 姚齐水, 等. 基于随机-区间混合不确定性的风机性能可靠性分析[J]. 中国科学: 技术科学, 2020, 50(3): 299-311. doi: 10.1360/SST-2019-0243QU X Z, YU J H, YAO Q S, et al. Random-interval hybrid reliability analysis for fan performance in the presence of epistemic uncertainty[J]. Scientia Sinica (Technologica), 2020, 50(3): 299-311(in Chinese). doi: 10.1360/SST-2019-0243 [14] GUO J, DU X P. Sensitivity analysis with mixture of epistemic and aleatory uncertainties[J]. AIAA Journal, 2007, 45(9): 2337-2349. doi: 10.2514/1.28707 [15] FERSON S, TROY TUCKER W. Sensitivity analysis using probability bounding[J]. Reliability Engineering & System Safety, 2006, 91(10/11): 1435-1442. [16] 胡政文, 张保强, 邓振鸿. 概率盒全局灵敏度和活跃子空间跨层降维[J]. 航空学报, 2021, 42(9): 224582.HU Z W, ZHANG B Q, DENG Z H. Cross-layer dimension reduction based on probability box global sensitivity analysis and active subspace method[J]. Acta Aeronautica et Astronautica Sinica, 2021, 42(9): 224582(in Chinese). [17] 刘宇, 吴沐宸, 陈江涛, 等. 一种混合不确定性下的灵敏度分析方法: CN113051851B[P]. 2022-09-09.LIU Y, WU M C, CHEN J T, et al. Sensitivity analysis method under hybrid uncertainty: CN113051851B[P]. 2022-09-09(in Chinese). [18] FLOREA M C, JOUSSELME A L. Fusion of imperfect information in the unified framework of random sets theory: application to target identification[R]. Ottawa: Defence R&D Canada-Valcartier, 2007. [19] 许泽伟. 基于多项式混沌展开的不确定性模型修正方法研究[D]. 兰州: 兰州交通大学, 2021.XU Z W. Uncertainty finite element model updating method based on polynomial chaotic expansion[D]. Lanzhou: Lanzhou Jiatong University, 2021(in Chinese). [20] SHAFER G. A mathematical theory of evidence[M]. Princeton: Princeton University Press, 1976. [21] DA RONCH A, PANZERI M, DROFELNIK J, et al. Sensitivity and calibration of turbulence model in the presence of epistemic uncertainties[J]. CEAS Aeronautical Journal, 2020, 11(1): 33-47. doi: 10.1007/s13272-019-00389-y [22] HE X, ZHAO F Z, VAHDATI M. Uncertainty quantification of Spalart-Allmaras turbulence model coefficients for simplified compressor flow features[J]. Journal of Fluids Engineering, 2020, 142(9): 091501. doi: 10.1115/1.4047026 [23] SPALART P, ALLMARAS S. A one-equation turbulence model for aerodynamic flows[C]// Proceedings of the 30th Aerospace Sciences Meeting and Exhibit. Reston: AIAA, 1992: AIAA1992-439. [24] SCHAEFER J, HOSDER S, WEST T, et al. Uncertainty quantification of turbulence model closure coefficients for transonic wall-bounded flows[J]. AIAA Journal, 2017, 55(1): 195-213. doi: 10.2514/1.J054902 [25] NASA. ONERA M6 wing[EB/OL]. (2022-07-19)[2021-02-10]. https://www.grc.nasa.gov/www/wind/valid/m6wing/m6wing.html. [26] 韩忠华. Kriging模型及代理优化算法研究进展[J]. 航空学报, 2016, 37(11): 3197-3225.HAN Z H. Kriging surrogate model and its application to design optimization: a review of recent progress[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(11): 3197-3225(in Chinese). [27] ARAYA G. Turbulence model assessment in compressible flows around complex geometries with unstructured grids[J]. Fluids, 2019, 4(2): 81-95. doi: 10.3390/fluids4020081 -
下载:
点击查看大图
计量
- 文章访问数: 368
- HTML全文浏览量: 109
- PDF下载量: 17
- 被引次数: 0
