Migration control strategy for swarm density based on PDE-constrained heat conduction
-
摘要:
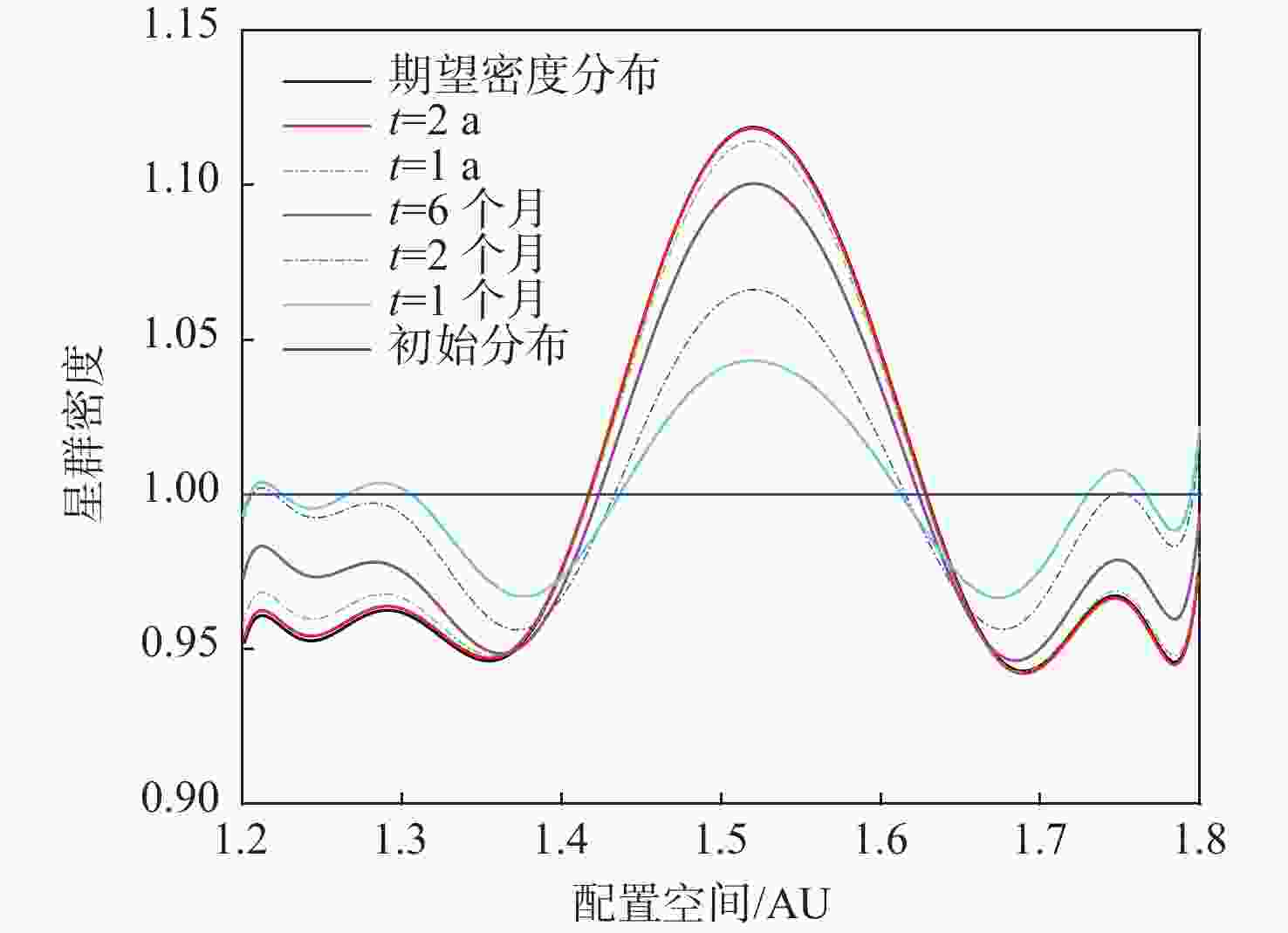
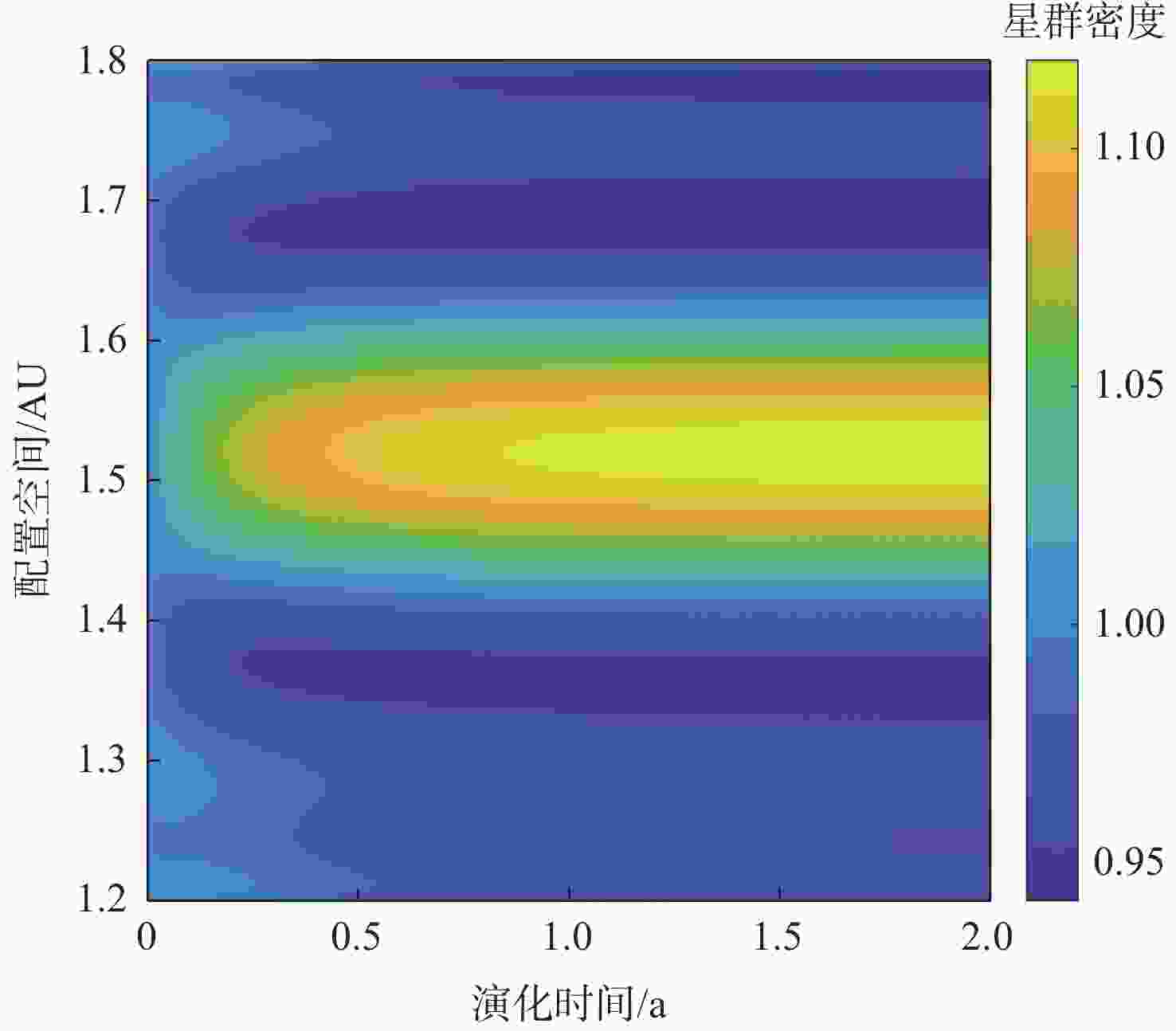
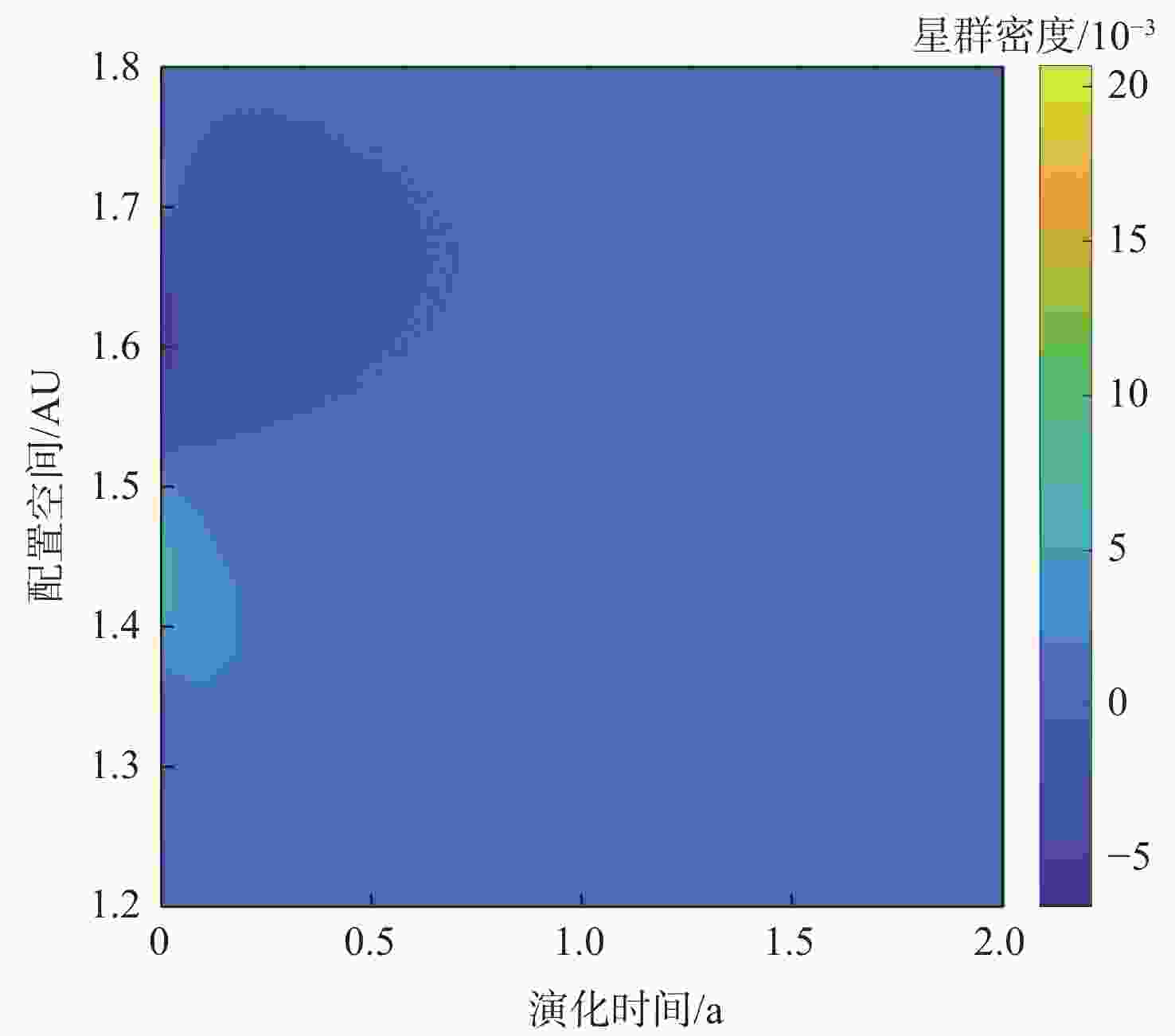
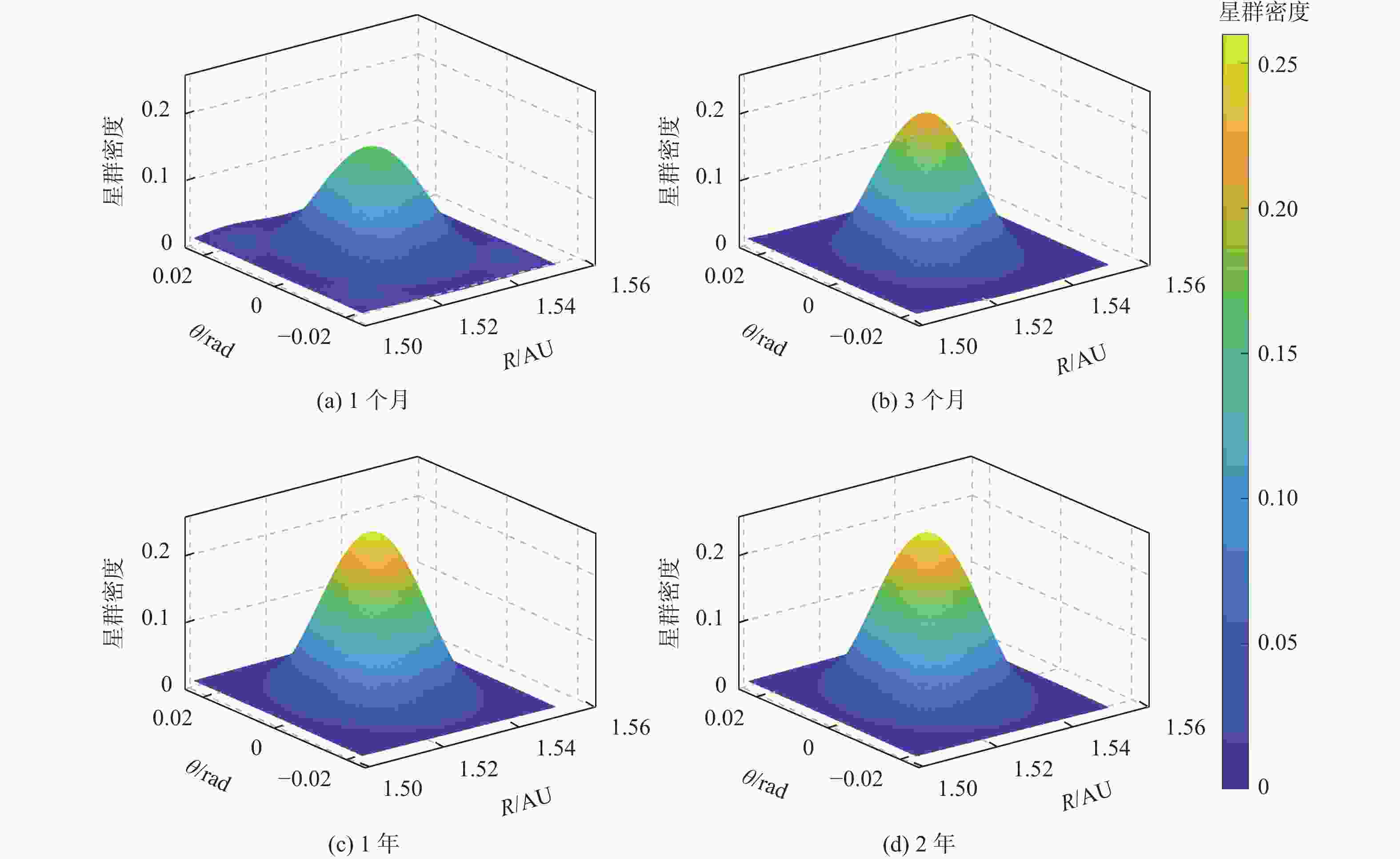
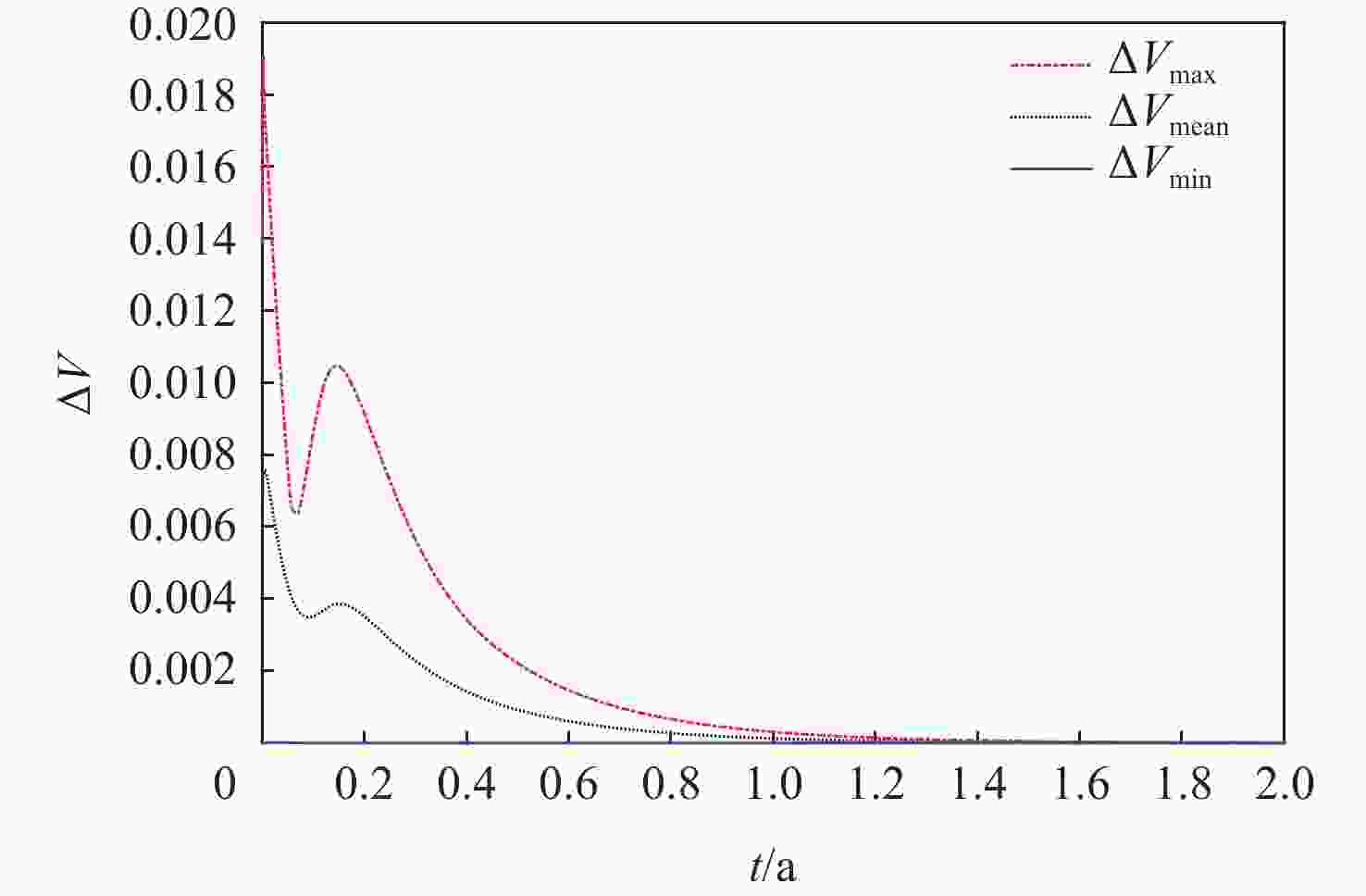
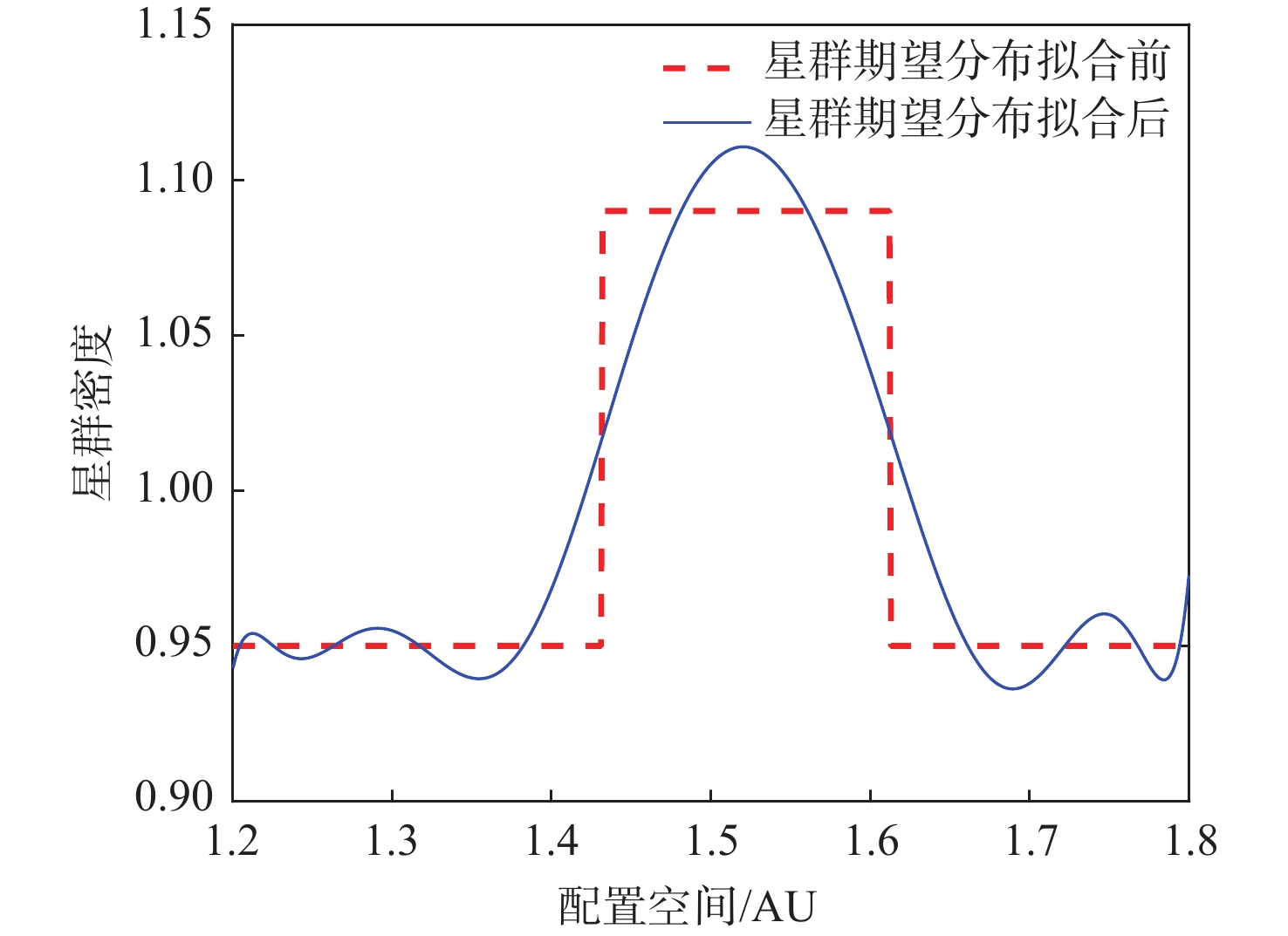
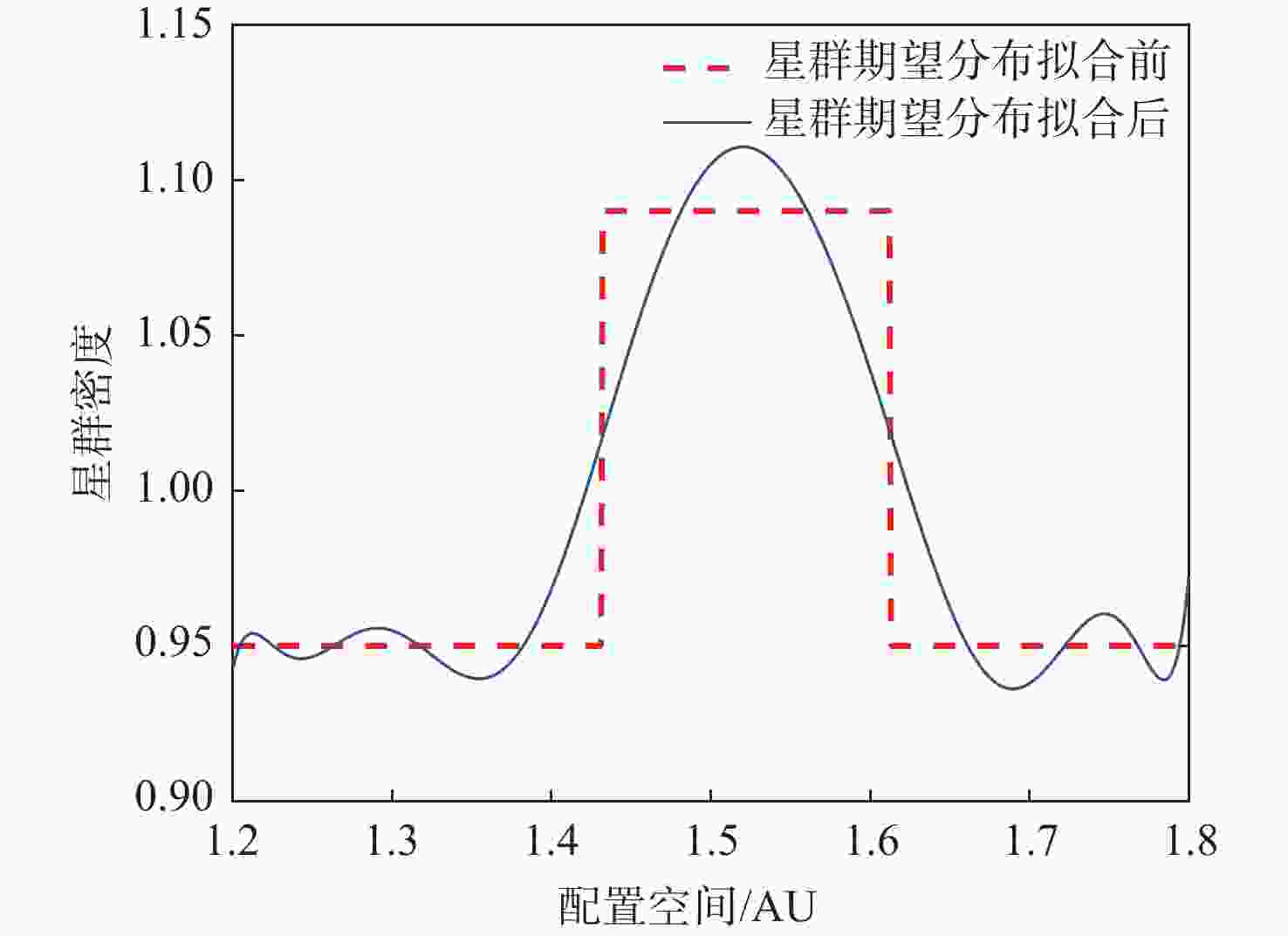
面向分布式星群在侦查监测，攻防作战等未来空间任务中的潜在应用，在偏微分动力学框架下，提出一种基于热传导特性的星群时空分布演化控制方法。通过类比热力学，以星群整体密度分布为参量，利用热传导偏微分方程描述星群宏观空间密度分布及其随时空的演化模型；基于热扩散机理构建速度场函数以实现集群期望密度分布的迁移控制，并分析论证了基于速度场反馈控制的渐近收敛性和稳定性；分别在一维空间与二维空间中模拟微纳星群迁移控制场景，分别利用Richardson外推法与交替方向隐式格式数值求解一维与二维热传导方程初边值问题，结果表明：所提方法有效收敛，星群迁移前期收敛速度快，在有限时间内可生成所需的密度分布。
Abstract:Advances in miniaturization are enabling the development of microscale swam with the advantages of high functional density, lower cost and high flexibility for the potential applications of reconnaissance monitoring, and space offensive and defensive operations. Facing the development trend of spacecraft formation in the huge quantification and intelligence, this paper investigates the model and control of swarm orbit evolution in potential applications for deep space missions. The spatial density distribution and its change with time and space are described by the partial differential equation of heat conduction, drawing an analogy with thermodynamics. The controller which generates a smooth velocity field is constructed based on the thermal diffusion mechanism, to enable the swarm to move to the desired density distribution. The asymptotic convergence and stability analysis of the velocity field feedback control is also provided. As an example, simulations are operated for the evolution of swarm density in one- and two-dimensional spaces. The findings show that the proposed method work well and can produce the desired swarm distribution in a predetermined amount of time.
-
Key words:
- partial differential equations /
- heat conduction /
- swarm /
- distribution functions /
- density control
-
图 1 一维星群密度在配置空间中的期望分布
Figure 1. Desired distribution of one-dimensional swarm density in configuration space
图 2 一维星群密度分布在配置空间中的演化
Figure 2. Evolution of one-dimensional swarm density in configuration space
图 4 一维空间中速度场函数随时间的变化历程
Figure 4. The history of the velocity field function inside the one-dimensional workspace with time
图 5 二维星群密度在配置空间中的初始分布及期望分布
Figure 5. Initial and desired distributions of two-dimensional swarm density inside the workspace
图 6 二维星群密度分布ρ(t, R, θ)在配置空间中的演化
Figure 6. Evolution of two-dimensional swarm density ρ(t, R, θ) in configuration space
图 7 二维星群密度差Φ(t, R, θ)在随时间的演化云图
Figure 7. Cloud view of the evolution of the 2D cluster density difference Φ(t, R, θ) over time
图 8 二维星群速度场v(t, R, θ)在随时间的演化云图
Figure 8. Cloud view of the evolution of the velocity field v(t, R, θ) inside the two-dimensional workspace over time
-
[1] JONES N. Tiny ‘chipsat’ spacecraft set for first flight[J]. Nature, 2016, 534: 15-16. doi: 10.1038/534015a [2] 韩耀昆, 陈琪锋. 全方向长期伴飞卫星集群轨道设计与仿真[J]. 飞控与探测, 2020, 3(3): 33-39.HAN Y K, CHEN Q F. Design and simulation of long-term bounded satellite cluster orbit in all directions[J]. Flight Control & Detection, 2020, 3(3): 33-39(in Chinese). [3] 王燕燕, 袁健全, 郝明瑞, 等. 基于时空协同的飞行器集群制导技术现状与应用[J]. 飞控与探测, 2021, 4(4): 32-39.WANG Y Y, YUAN J Q, HAO M R, et al. Research status and application of the cooperative guidance technology for aerial vehicle swarm systems based on spatiotemporal coordination[J]. Flight Control & Detection, 2021, 4(4): 32-39(in Chinese). [4] HADAEGH F Y, CHUNG S J, MANOHARA H M. On development of 100-gram-class spacecraft for swarm applications[J]. IEEE Systems Journal, 2016, 10(2): 673-684. doi: 10.1109/JSYST.2014.2327972 [5] BARNHART D J, VLADIMIROVA T, BAKER A M, et al. A low-cost femtosatellite to enable distributed space missions[J]. Acta Astronautica, 2009, 64(11-12): 1123-1143. doi: 10.1016/j.actaastro.2009.01.025 [6] 何艳超, 徐明. 长周期高精度回归轨道与脉冲轨道控制策略设计[J]. 北京航空航天大学学报, 2021, 47(11): 2256-2267.HE Y C, XU M. Design of long-duration high-precision repeat ground-track orbit and its impulsive orbital control strategy[J]. Journal of Beijing University of Aeronautics and Astronautics, 2021, 47(11): 2256-2267(in Chinese). [7] 高婉莹, 李克行. 基于人工势场的星群松散编队控制[J]. 空间控制技术与应用, 2021, 47(3): 33-39. doi: 10.3969/j.issn.1674-1579.2021.03.005GAO W Y, LI K H. Loose formation control of satellite clusters based on artificial potential field[J]. Aerospace Control and Application, 2021, 47(3): 33-39(in Chinese). doi: 10.3969/j.issn.1674-1579.2021.03.005 [8] ZHENG T J, HAN Q, LIN H. PDE-based dynamic density estimation for large-scale agent systems[J]. IEEE Control Systems Letters, 2021, 5(2): 541-546. doi: 10.1109/LCSYS.2020.3004417 [9] HEARD W B. Dispersion of ensembles of non-interacting particles[J]. Astrophysics and Space Science, 1976, 43(1): 63-82. doi: 10.1007/BF00640556 [10] MCINNESC R. An analytical model for the catastrophic production of orbital debris[J]. ESA Journal, 1993, 17: 293-305. [11] GOR’KAVYI N N, OZERNOY L M, MATHER J C. A new approach to dynamical evolution of interplanetary dust[J]. The Astrophysical Journal, 1997, 474(1): 496-502. doi: 10.1086/303440 [12] MCINNES C R. A Simple analytic model of the long term evolution of nanosatellite constellations[J]. Journal of Guidance, Control, and Dynamics, 2000, 23(2): 332-338. doi: 10.2514/2.4527 [13] LETIZIA F, COLOMBO C, LEWIS H G. Multidimensional extension of the continuity equation method for debris clouds evolution[J]. Advances in Space Research, 2016, 57(8): 1624-1640. doi: 10.1016/j.asr.2015.11.035 [14] COLOMBO C, MCINNES C R. Orbit design for future SpaceChip swarm missions in a planetary atmosphere[J]. Acta Astronautica, 2012, 75: 25-41. doi: 10.1016/j.actaastro.2012.01.004 [15] XU M, MCINNES C R. Closed-loop control of the orbit evolution of “smart dust” swarms[J]. Journal of Guidance, Control, and Dynamics, 2017, 40(7): 1806-1814. doi: 10.2514/1.G002386 [16] NAZARENKO A I. Prediction of the space debris spatial distribution on the basis of the evolution equations[J]. Acta Astronautica, 2014, 100: 47-56. doi: 10.1016/j.actaastro.2014.02.023 [17] MCINNES C R. A continuum model for the orbit evolution of self-propelled ‘smart dust’ swarms[J]. Celestial Mechanics and Dynamical Astronomy, 2016, 126(4): 501-517. doi: 10.1007/s10569-016-9707-y [18] EREN U, ACIKMESE B. Field generation for density control of swarms using heat equation and smoothing kernels[J]. International Federation of Automatic Control, 2017, 50(1): 9405-9411. [19] LI P, YAU S T. On the schrödinger equation and the eigenvalue problem[J]. Communications in Mathematical Physics, 1983, 88(3): 309-318. doi: 10.1007/BF01213210 [20] GU Y X, LIAO W Y, ZHU J P. An efficient high-order algorithm for solving systems of 3-D reaction-diffusion equations[J]. Journal of Computational and Applied Mathematics, 2003, 155(1): 1-17. doi: 10.1016/S0377-0427(02)00889-0 [21] 陆金甫, 关治. 偏微分方程数值解法[M]. 2版. 北京: 清华大学出版社, 2003: 110-115.LU J F, GUAN Z. Numerical solution of partial differential equation[M]. 2nd ed. Beijing: Tsinghua University Press, 2003: 110-115(in Chinese). -
下载:
点击查看大图
计量
- 文章访问数: 211
- HTML全文浏览量: 77
- PDF下载量: 9
- 被引次数: 0
